Xác định thiết diện bằng phương pháp giao tuyến gốc
Để xác định thiết diện của một hình chóp khi cắt bởi một mặt phẳng, chúng ta có hai phương pháp là phương pháp xác định thiết diện bằng giao tuyến gốc và xác định thiết diện bằng phép chiếu xuyên tâm. Bài viết này xin trình bày chi tiết phương pháp giao tuyến gốc và các ví dụ vận dụng.
1. Phương pháp giao tuyến gốc là gì?
Bài toán. Xác định thiết diện của một hình chóp khi cắt bởi mặt phẳng $(\alpha)$.
Phương pháp giao tuyến gốc (Trace method).
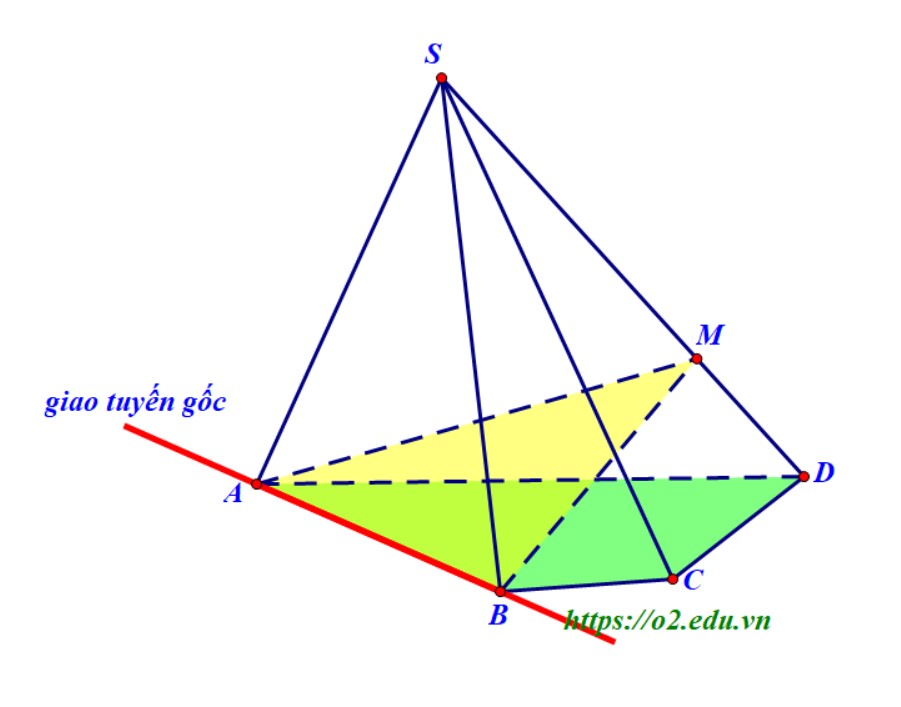
- Xác định giao tuyến $ d $ của mặt phẳng $(\alpha)$ với một mặt $ \mathcal{H} $ của hình chóp (thường là với mặt đáy).
- Tìm các giao điểm của giao tuyến $ d $ với các cạnh, đường chéo của mặt $ \mathcal{H} $.
- Dựa vào các giao điểm này và giao tuyến $ d, $ tìm tiếp các giao tuyến của mặt phẳng $(\alpha)$ với những mặt còn lại của hình chóp.
2. Ví dụ tìm thiết diện bằng phương pháp giao tuyến gốc
Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy không là hình thang. Giả sử $ M $ là một điểm trên $ SD $, xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM).$

Hướng dẫn.
- Rõ ràng rằng giao tuyến của mặt phẳng $ (ABM)$ với mặt đáy $ (ABCD)$ là đường thẳng $AB$, nên chúng ta lựa chọn đường thẳng $AB$ làm giao tuyến gốc.
- Tiếp theo, ta xác định các giao điểm của đường thẳng $AB$ với các cạnh của đáy, nếu không được thì sẽ sử dụng đến giao điểm với đường chéo. Vì tứ giác $ ABCD$ không là hình thang nên kéo dài hai đường thẳng $ AB$ và $ CD$ thì chúng sẽ cắt nhau, giả sử là điểm $ I$.
- Lúc này, đường thẳng $ IM$ nằm trong mặt phẳng $ (SCD)$ nên nó sẽ cắt được đường thẳng $ SC$, giả sử cắt tại điểm $ N$.
- Rõ ràng, mặt phẳng $ (ABM)$ lần lượt cắt các mặt của hình chóp $S.ABCD$ theo các giao tuyến tạo thành một tứ giác là $ AMNB$ nên thiết diện chính là tứ giác $ AMNB.$
Ví dụ 2. Cho tứ diện $ ABCD $ có $ M,N $ là trung điểm của $ AB,CD. $ Giả sử $ P $ là một điểm nằm trên cạnh $ AD $ nhưng không là trung điểm. Xác định thiết diện của mặt phẳng $ (MNP) $ và tứ diện.
Ví dụ 3. Cho tứ diện $ ABCD $ có $ I,J $ lần lượt là trọng tâm các tam giác $ ABC $ và $ ACD. $ Trên cạnh $ AB $ lấy điểm $ K $ sao cho $ AK>BK. $ Xác định thiết diện của tứ diện khi cắt bởi mặt phẳng $ (IJK). $
Ví dụ 4. Cho hình chóp $ S.ABCD $ có điểm $ M $ là trung điểm $ SC,N $ là một điểm trên cạnh $ SD $ sao cho $ SN<DN. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ AMN $.
Ví dụ 5. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ BC,CD $ và $ SA. $ Xác định thiết diện của hình chóp và mặt phẳng $ (MNP) $.
Ví dụ 6. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ CD,BC $ và $ SB. $ Xác định thiết diện của hình chóp và mặt phẳng $ (MNP) $.
Hướng dẫn. Trong mặt phẳng $ (ABCD) $ gọi $ E,F $ lần lượt là giao điểm của $ MN $ với $ AB $ và $ AD. $ Trong mặt phẳng $ (SAB) $ gọi $ Q=PE\cap SA, $ trong mặt phẳng $ (SAD) $ gọi $ R=QF\cap SD. $ Thiết diện là ngũ giác $ MNPQR. $
Ví dụ 7. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $ O. $ Gọi $ M,N $ lần lượt là trung điểm của $ BC,CD. $ Trên đoạn $ SO $ lấy điểm $ P $ sao cho $ SP>OP. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (MNP)$.
Hướng dẫn. Trong mặt phẳng $ (ABCD) $ gọi $ E,F,G $ lần lượt là giao điểm của $ MN $ với $ AB,AD,AC. $ Trong mặt phẳng $ (SAC) $ gọi $ J= GP\cap SA, $ trong $ (SAB) $ gọi $ K=JE\cap SB, $ trong $ (SAD) $ gọi $ I=JF\cap SD. $ Thiết diện là ngũ giác $ MNIJK. $
Ví dụ 8. Cho hình chóp $ S.ABCD $ có $ G $ là trọng tâm tam giác $ SCD $ và $ M $ là trung điểm cạnh $ SD. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (AGM)$.
Ví dụ 9. Cho hình chóp $S.ABCD$ có $ G $ là trọng tâm tam giác $ SCD, H$ là một điểm thuộc cạnh $ SA $ sao cho $ SH>AH. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (CGH). $
Hướng dẫn. Gọi $ M $ là trung điểm $ SD,E=HM\cap AD,K=CE\cap AB. $ Thiết diện là tứ giác $ CMHK. $
Ví dụ 10. Cho hình chóp $S.ABCD$ có $ G $ là trọng tâm tam giác $ SCD, H$ là một điểm thuộc cạnh $ SA $ sao cho $ SH<AH. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (CGH). $
Hướng dẫn. Gọi $ M $ là trung điểm $ SD,E=HM\cap AD,F=CE\cap AB,K=HF\cap SB. $ Thiết diện là tứ giác $ CMHK. $