Toán 10 – Giá trị lượng giác của góc từ 0 đến 180 độ
1. Giá trị lượng giác của một góc từ 0 đến 1800
1.1. Nửa đường tròn đơn vị
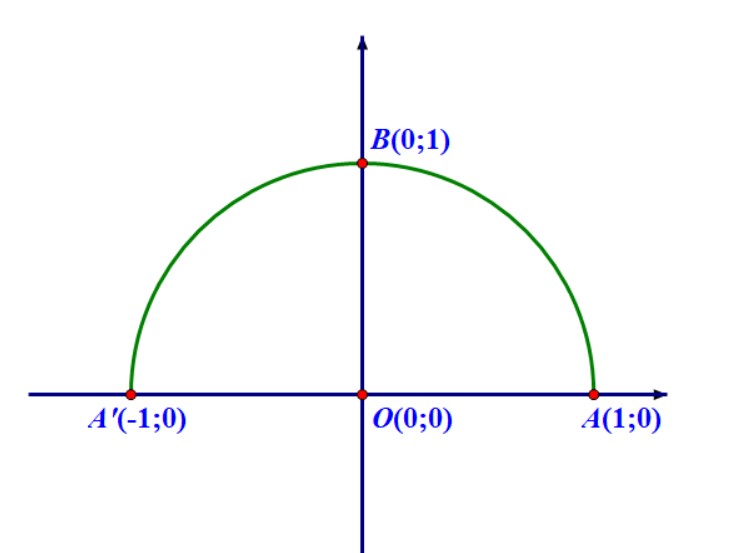
- Trong mặt phẳng tọa độ $Oxy$, nửa đường tròn đơn vị là nửa đường tròn có tâm $ O(0;0)$, bán kính bằng $ 1$ và đi qua các điểm $ A(1;0), B(0;1), A'(-1;0)$.
1.2. Giá trị lượng giác của một góc từ $0^\circ$ đến $180^\circ$
- Với mỗi góc $0^\circ \leqslant \alpha \leqslant 180^\circ$ thì có đúng một điểm $ M$ trên nửa đường tròn đơn vị sao cho $ \widehat{AOM}=\alpha$. Ngược lại, với mỗi điểm $ M$ trên nửa đường tròn đơn vị thì tồn tại đúng một góc $0^\circ \leqslant \alpha \leqslant 180^\circ$ sao cho $ \widehat{AOM}=\alpha$.
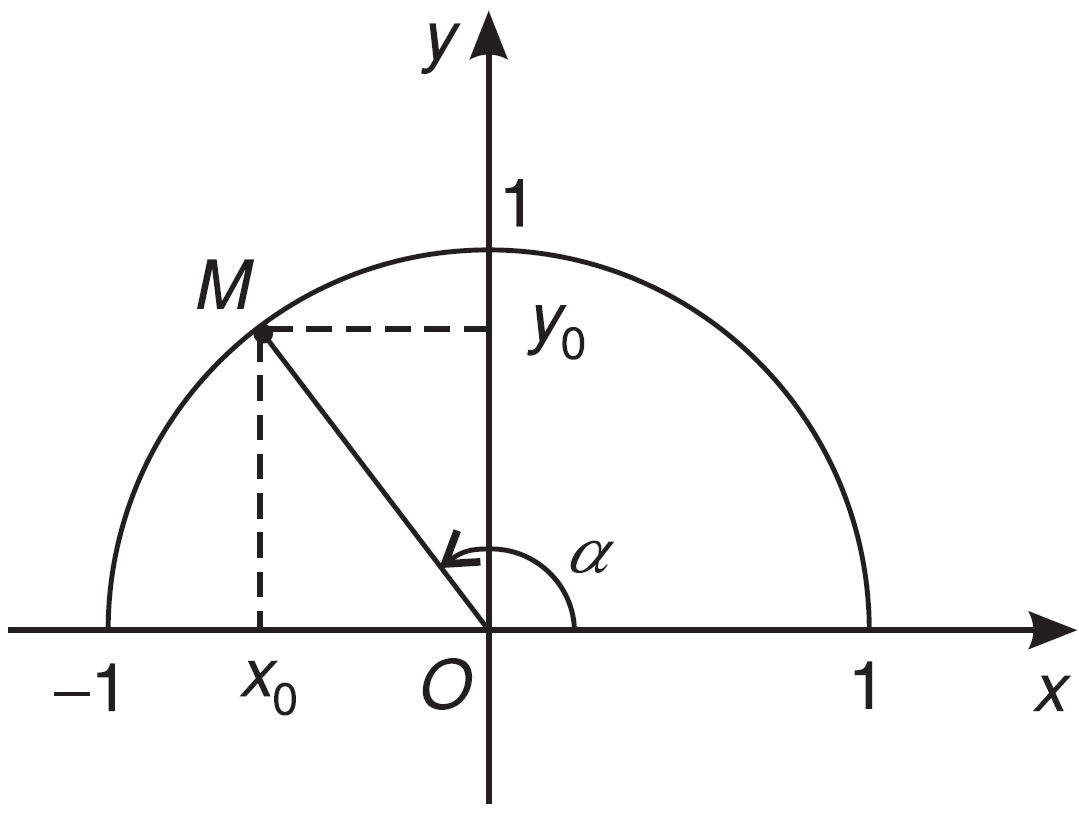
- Giả sử điểm $ M$ có tọa độ $ M(x_0;y_0)$ thì chúng ta định nghĩa:
- $ \sin \alpha =y_0$;
- $ \cos \alpha = x_0$;
- $ \tan \alpha =\frac{y_0}{x_0}=\frac{\sin x}{\cos x}$ nếu $ x_0\ne 0$;
- $ \cot \alpha =\frac{x_0}{y_0}=\frac{\cos x}{\sin x}$ nếu $ y_0\ne 0$.
Trục hoành – trục nằm ngang – còn được gọi là trục cos, trục tung – trục thẳng đứng – còn được gọi là trục sin.
1.3. Tính chất của giá trị lượng giác
- Nếu $ a+b=180^\circ$ (hai góc bù nhau) thì \begin{align} \sin a =\sin b,\\ \cos a = -\cos b,\\ \tan a =-\tan b, \\ \cot a =-\cot b.\end{align}
- Các hệ thức lượng giác cơ bản:
- $ \sin^2x+\cos^2x =1$
- $ \tan x =\frac{\sin x}{\cos x}$
- $ \cot x =\frac{\cos x}{\sin x}$
- $ \tan x \cdot \cot x =1$
1.4. Giá trị lượng giác của các góc đặc biệt
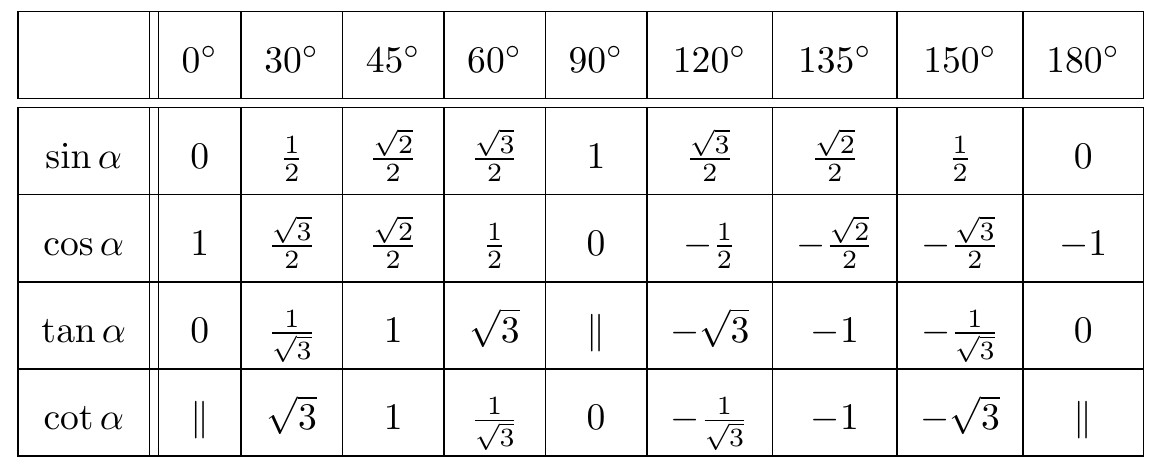
2. Bài tập giá trị lượng giác của một góc từ 0° đến 180°
Bài 1. Cho $\cos \alpha=-\frac{2}{3}$. Tính $\sin \alpha;\tan \alpha$ và $\cot \alpha$.
Bài 2. Cho góc $\alpha$ biết $0^\circ < \alpha < 90^\circ $ và $\tan \alpha =3$. Tính $\sin \alpha$ và $\cos \alpha$.
Bài 3. Cho $\sin \alpha =\frac{3}{4}$ với $90^\circ <\alpha < 180^\circ$. Tính $\cos \alpha$ và $\tan \alpha$.
Bài 4. Cho $\cos \alpha=-\frac{\sqrt{2}}{4}$. Tính $\sin \alpha;\tan \alpha$ và $\cot \alpha$.
Bài 5. Cho góc $\alpha$ biết $0^\circ < \alpha < 90^\circ $ và $\tan \alpha = 2\sqrt{2}$. Tính $\sin \alpha$ và $\cos \alpha$.
Bài 6. Biết $\tan \alpha = \sqrt{2}$. Tính giá trị của biểu thức $$A=\frac{3\sin \alpha -\cos \alpha}{2\sin \alpha+\cos \alpha}$$
Bài 7. Biết $\tan \alpha = \sqrt{2}$. Tính giá trị của biểu thức $$T=\frac{\sin \alpha -\cos \alpha}{\sin^3 \alpha+3\cos^3 \alpha+2\sin \alpha}$$
Bài 8. Biết $\sin \alpha = \frac{2}{3}$. Tính giá trị của biểu thức $$B=\frac{\cot \alpha -\tan \alpha}{\cot \alpha+2\tan \alpha}$$
Bài 9. Cho $0^\circ \leqslant \alpha \leqslant 180^\circ$. Chứng minh rằng:
- $(\sin \alpha +\cos \alpha)^2=1+2\sin \alpha\cos \alpha$.
- $(\sin \alpha -\cos \alpha)^2=1-2\sin \alpha\cos \alpha$.
- $\sin^4 \alpha +\cos^4 \alpha=1-2 \sin^2 \alpha\cos^2 \alpha$.
- $\sin^4 \alpha -\cos^4 \alpha=2\sin^2 \alpha -1$.
- $\sin^6 \alpha+\cos^6 \alpha = 1-3\sin^2 \alpha\cos^2 \alpha$.
- $\sin \alpha\cos\alpha (1+\tan \alpha)(1+\cot\alpha)=1+2\sin \alpha\cos \alpha$.
Bài 10. Chứng minh rằng các biểu thức sau đây không phụ thuộc $\alpha$
- $A=(\sin \alpha+\cos \alpha)^2+(\sin \alpha -\cos \alpha)^2$.
- $B=\sin^4 \alpha-\cos^4 \alpha -2\sin^2 \alpha +1$.