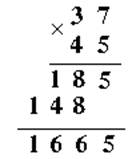O₂ Education

Tag: thuật toán

  • 150 bài Toán Tin

    150 bài Toán Tin

    150 bài Toán Tin

    Chúng tôi xin giới thiệu 150 bài Toán Tin của thầy Lê Minh Hoàng (ĐHSP Hà Nội) để bạn đọc tham khảo.

    01. TÍNH TOÁN SONG SONG

    Biểu thức đủ là một dãy ký tự gồm các biến ký hiệu bằng chữ cái thường tiếng Anh: a..z, các phép toán cộng ký hiệu +, nhân ký hiệu * và các dấu ngoặc (,). Được định nghĩa như sau:

    1. Mỗi biến a,b,…,z là một biểu thức đủ
    2. Nếu X và Y là biểu thức đủ thì (X+Y) và (X*Y) cũng là biểu thức đủ.
    3. Những biểu thức nào không xây dựng được theo 2 nguyên tắc trên không là biểu thức đủ.

    VD: Theo cách định nghĩa trên thì (a+(b+(c+d))) hoặc ((a+b)+(c*d)) là các biểu thức đủ.

    Cho biết thời gian tính phép + là P, thời gian tính phép * là Q, người ta định nghĩa thời gian tính toán một biểu thức đủ như sau:

    • Nếu biểu thức đủ chỉ gồm 1 biến (a..z) thì thời gian tính toán là 0
    • Nếu X và Y là 2 biểu thức đủ; thời gian tính X là TX thời gian tính Y là TY thì thời gian tính

    (X+Y) là max(TX,TY)+P thời gian tính (X*Y) là max(TX,TY)+Q

    Từ 1 biểu thức đủ người ta có thể biến đổi về một biểu thức tương đương bằng các luật:

    • Giao hoán: (X+Y) ⇔ (Y+X); (X*Y) ⇔ (Y*X)
    • Kết hợp: (X+(Y+Z)) ⇔((X+Y)+Z); (X*(Y*Z)) ⇔ ((X*Y)*Z)

    Yêu cầu: Cho trước một biểu thức đủ E dưới dạng xâu ký tự hãy viết chương trình:

    1. Tìm thời gian tính toán biểu thức E
    2. Hãy biến đổi biểu thức E thành biểu thức E’ tương đương với nó sao cho thời gian tính E’ là ít nhất có thể.

    Dữ liệu vào được đặt trong file văn bản PO.INP như sau:

    • Dòng thứ nhất ghi 2 số P, Q cách nhau 1 dấu cách (P,Q≤100)
    • Tiếp theo là một số dòng, mỗi dòng ghi 1 biểu thức đủ. Kết quả ra đặt trong file văn bản PO.OUT như sau:

    Với mỗi biểu thức E trong file PO.INP ghi ra file PO.OUT 3 dòng

    • Dòng thứ nhất: Ghi thời gian tính toán E
    • Dòng thứ hai: Ghi biểu thức E’
    • Dòng thứ ba: Ghi thời gian tính toán E’

    Chú ý: Để cho gọn, mỗi biểu thức đủ trong input/output file có thể viết mà không cần đến cặp dấu ngoặc ngoài cùng, dữ liệu vào được coi là đúng đắn và không cần kiểm tra.

    Ví dụ:

    150 bài Toán Tin 1

    02. BẢNG SỐ

    Cho một bảng hình chữ nhật kích thước M x N với M, N nguyên dương. M, N ≤ 50. Hình chữ nhật này được chia thành M x N ô vuông bằng nhau với kích thước đơn vị bởi các đường song song với các cạnh, trên ô vuông [i, j] ghi số nguyên A[i, j] (2 ≤ A[i, j] ≤ 50).

    Từ mảng A ta lập mảng B mà B[i, j] được xây dựng như sau:

    Biểu diễn số A[i, j] thành tổng các số nguyên tố với ràng buộc: trong biểu diễn đó có nhiều nhất chỉ một số nguyên tố xuất hiện hai lần. Trong các cách biểu diễn, chọn ra biểu diễn nhiều hạng tử nhất thì B[i, j] bằng số số hạng của biểu diễn này kể cả bội (nếu có).

    Ví dụ:

    Nếu A[i, j] = 10 = 2 + 3 + 5 thì B[i, j] = 3;

    Nếu A[i, j] = 12 = 2 + 2 + 3 + 5 thì B[i, j] = 4;

    Chú ý: Không được biểu diễn A[i, j] = 10 = 2 + 2 + 2 + 2 + 2 để có B[i, j] = 5 vì như vậy không thoả mãn ràng buộc

    1. Dữ liệu vào được cho bởi Text file INP trong đó:
      • Dòng đầu ghi hai số M, N
      • M dòng sau, dòng thứ i ghi N phần tử trên dòng i của bảng A: A[i, 1], A[i, 2], …, A[i, N] hai phần tử liên tiếp cách nhau ít nhất một dấu trống.
    2. Kết quả ghi ra Text file OUT.
      Giá trị bảng B, mỗi dòng của bảng ghi trên một dòng của file, hai phần tử liên tiếp cách nhau ít nhất một dấu trống.
    3. Hãy tìm hình chữ nhật lớn nhất được tạo bởi các ô mang giá trị bằng nhau của bảng B. Ghi tiếp ra file OUT.B1 một dòng gồm 5 số là: diện tích lớn nhất tìm được, toạ độ trên trái và dưới phải của hình chữ nhật có diện tích lớn nhất đó.

    03.   CARGO

    Bản đồ một kho hàng hình chữ nhật kích thước mxn được chia thành các ô vuông đơn vị (m hàng, n cột: các hàng đánh số từ trên xuống dưới, các cột đánh số từ trái qua phải). Trên các ô của bản đồ có một số ký hiệu:

    • Các ký hiệu # đánh dấu các ô đã có một kiện hàng xếp sẵn,
    • Một ký hiệu *: Đánh dấu ô đang có một xe đẩy
    • Một ký hiệu $: Đánh dấu ô chứa kiện hàng cần xếp
    • Một ký hiệu @: Đánh dấu vị trí ô mà cần phải xếp kiện hàng B vào ô đó
    • Các ký hiệu dấu chấm “.”: Cho biết ô đó trống

    Cần phải dùng xe đẩy ở * để đẩy kiện hàng ở $ đến vị trí @ sao cho trong quá trình di chuyển cũng như đay hàng, không chạm vào những kiện hàng đã được xếp sẵn. (Xe đay có thể di chuyển sang một trong 4 ô chung cạnh với ô đang đứng). Nếu có nhiều phương án thì chỉ ra một phương án sao cho xe đay phải di chuyển qua ít bước nhất.

    Các hướng di chuyển được chỉ ra trong hình dưới đây

    150 bài toán tin lê minh hoàng

    Dữ liệu: Vào từ file văn bản CARGO.INP

    • Dòng 1: Ghi hai số nguyên dương m, n cách nhau một dấu cách (m, n ≤ 80)
    • m dòng tiếp theo, dòng thứ i ghi đủ n ký hiệu trên hàng thứ i của bản đồ theo đúng thứ tự từ trái qua phải. Các ký hiệu được ghi liền nhau

    Kết quả: Ghi ra file văn bản CARGO.OUT

    • Dòng 1: Ghi số bước di chuyển xe đNy để thực hiện mục đích yêu cầu, nếu không có phương án khả thi thì dòng này ghi số -1
    • Dòng 2: Nếu có phương án khả thi thì dòng này ghi các ký tự liền nhau thể hiện hướng di chuyển của xe đNy R (East, West, South, North). Các chữ cái thường (e,w,s,n) thể hiện bước di chuyển không đNy hàng, các chữ cái in hoa (E,W,S,N) thể hiện bước di chuyển có đNy hàng.

    Ví dụ:

    150 bài Toán Tin 2

    04.   DÃY CON

    Cho một dãy gồm n ( n ≤ 1000) số nguyên dương A1, A2, …, An và số nguyên dương k (k ≤ 50). Hãy tìm dãy con gồm nhiều phần tử nhất của dãy đã cho sao cho tổng các phần tử của dãy con này chia hết cho k.

    Dữ liệu vào: file văn bản DAY.INP

    • Dòng đầu tiên chứa hai số n, k ghi cách nhau bởi ít nhất 1 dấu trống.
    • Các dòng tiếp theo chứa các số A1, A2, …, An được ghi theo đúng thứ tự cách nhau ít nhất một dấu trống hoặc xuống dòng (CR-LF).

    Kết quả: ghi ra file văn bản DAY.OUT

    • Dòng đầu tiên ghi m là số phần tử của dãy con tìm được.
    • Các dòng tiếp theo ghi dãy m chỉ số các phần tử của dãy đã cho có mặt trong dãy con tìm được. Các chỉ số ghi cách nhau ít nhất một dấu trắng hoặc một dấu xuống dòng.

    Ví dụ: 

    DAY.INP DAY.OUT
    10 3 9
    2 3 5 7 1 3 2 4 5
    9 6 12 7 6 7 10 8
    11 15

    05. XÂU FIBINACCI

    Xét dãy các xâu F1, F2, F3, …, FN, … trong đó:

    F1 = ‘A’

    F2 = ‘B’

    FK+1 = FK + FK-1 (K ³ 2).

    Ví dụ:

    F1 = ‘A’

    F2 = ‘B’ F3 = ‘BA’ F4 = ‘BAB’

    F5 = ‘BABBA’

    F6 = ‘BABBABAB’

    F7 = ‘BABBABABBABBA’

    F8 = ‘BABBABABBABBABABBABAB’

    F9 = ‘BABBABABBABBABABBABABBABBABABBABBA’

    Cho xâu S độ dài không quá 25, chỉ bao gồm các ký tự ‘A’ và ‘B’. Hãy xác định số lần xuất hiện xâu S trong xâu FN, N ≤ 35. Chú ý: hai lần xuất hiện của S trong FN không nhất thiết phải là các xâu rời nhau hoàn toàn.

    Dữ liệu: vào từ file văn bản FIBISTR.INP, bao gồm nhiều dòng, mỗi dòng có dạng N S. Giữa N và S có đúng 1 dấu cách. Dữ liệu vào là chuNn, không cần kiểm tra.

    Kết quả: Đưa ra file văn bản FIBISTR.OUT, mỗi dòng dữ liệu ứng với một dòng kết quả ra.

    06.   VÒNG SỐ NGUYÊN TỐ

    Một vòng tròn chứa 2n vòng tròn nhỏ (Xem hình vẽ). Các vòng tròn nhỏ được đánh số từ 1 đến n theo chiều kim đồng hồ. Cần điền các số tự nhiên từ 1 đến 2n mỗi số vào một vòng tròn nhỏ sao cho tổng của hai số trên hai vòng tròn nhỏ liên tiếp là số nguyên tố. Số điền ở vòng tròn nhỏ 1 luôn là số 1.

    vong so nguyen to

    Dữ liệu: Vào từ file văn bản CIRCLE.INP chứa số nguyên dương n (1 < n < 10)

    Kết quả: Ghi ra file văn bản CIRCLE.OUT:

    • Dòng đầu tiên ghi số lượng các cách điền số tìm được (k).
    • Dòng thứ i trong số k dòng tiếp theo ghi các số trong các vòng tròn nhỏ bắt đầu từ vòng tròn nhỏ 1 đọc theo thứ tự của các vòng tròn nhỏ.

    07.   ĐÔI BẠN

    Trước kia Tuấn và Mai là hai bạn cùng lớp còn bây giờ hai bạn học khác trường nhau. Cứ mỗi sáng, đúng 6 giờ cả hai đều đi từ nhà tới trường của mình theo con đường mất ít thời gian nhất (có thể có nhiều con đường đi mất thời gian bằng nhau và đều ít nhất). Nhưng hôm nay, hai bạn muốn gặp nhau để bàn việc họp lớp cũ nhân ngày 20-11.

    Cho biết sơ đồ giao thông của thành phố gồm N nút giao thông được đánh số từ 1 đến N và M tuyến đường phố (mỗi đường phố nối 2 nút giao thông). Vị trí nhà của Mai và Tuấn cũng như trường của hai bạn đều nằm ở các nút giao thông. Cần xác định xem Mai và Tuấn có cách nào đi thoả mãn yêu cầu nêu ở trên, đồng thời họ lại có thể gặp nhau ở nút giao thông nào đó trên con đường tới trường hay không ? (Ta nói Tuấn và Mai có thể gặp nhau tại một nút giao thông nào đó nếu họ đến nút giao thông này tại cùng một thời điểm). Nếu có nhiều phương án thì hãy chỉ ra phương án để Mai và Tuấn gặp nhau sớm nhất.

    Dữ liệu vào được đặt trong tệp FRIEND.INP:

    • Dòng đầu tiên chứa 2 số nguyên dương N, M (1 ≤ N ≤ 100);
    • Dòng tiếp theo chứa 4 số nguyên dương Ha, Sa, Hb, Sb lần lượt là số hiệu các nút giao thông tương ứng với: Nhà Tuấn, trường của Tuấn, nhà Mai, trường của
    • Dòng thứ i trong số M dòng tiếp theo chứa 3 số nguyên dương A, B, T. Trong đó A & B là hai đầu của tuyến đường phố i. Còn T là thời gian (tính bằng giây ≤ 1000) cần thiết để Tuấn (hoặc Mai) đi từ A đến B cũng như từ B đến A.

    Giả thiết là sơ đồ giao thông trong thành phố đảm bảo để có thể đi từ một nút giao thông bất kỳ đến tất cả các nút còn lại.

    Kết quả : Ghi ra tệp văn bản FRIEND.OUT

    • Dòng 1: Ghi từ YES hay NO tuỳ theo có phương án giúp cho hai bạn gặp nhau hay không. Trong trường hợp có phương án:
    • Dòng 2: Ghi thời gian ít nhất để Tuấn tới trường
    • Dòng 3: Ghi các nút giao thông theo thứ tự Tuấn đi qua
    • Dòng 4: Ghi thời gian ít nhất để Mai tới trường
    • Dòng 5: Ghi các nút giao thông theo thứ tự Mai đi qua
    • Dòng 6: Ghi số hiệu nút giao thông mà hai bạn gặp nhau
    • Dòng 7: Thời gian sớm nhất tính bằng giây kể từ 6 giờ sáng mà hai bạn có thể gặp nhau.

    Các số trên một dòng của Input/Output file ghi cách nhau ít nhất một dấu cách.

    Ví dụ : Với sơ đồ giao thông sau: (N=6,M=7, Ha=1, Sa=6, Hb=2, Sb=5)

    150 bài Toán Tin 3

    08.   CỬA SỔ VĂN BẢN

    Xét văn bản T gồm N ký tự (N ≤ 1000000, N không cho trước) và văn bản P gồm M ký tự (0 < M ≤ 100). Cửa sổ độ dài W là một đoạn văn bản gồm W ký tự liên tiếp của T (M < W ≤ 1000). Nói cửa sổ W chứa mẫu P nếu tồn tại một cách xoá một số ký tự liên tiếp của W để nhận được P.

    Hai cửa sổ của T gọi là khác nhau nếu chúng bắt đầu từ những vị trí khác nhau trong T. Hãy xác định số cửa sổ khác nhau trong văn bản T chứa P.

    Dữ liệu:

    • File văn bản INP
    • Dòng đầu chứa hai số nguyên W, M
    • Dòng thứ hai chứa M ký tự của văn bản P;
    • File TXT chứa văn bản T

    Kết quả:

    Đưa ra file WINDOW.OUT một số nguyên xác định số cửa sổ tìm được theo yêu cầu.

    Lưu ý: Đa số trường hợp, file WINDOWT.TXT không phải là Text file, có nghĩa là nó chứa các ký tự trong khoảng  #0..#255 (file of Char). Như vậy tính cả CR(#13) và LF(#10)

    Ví dụ:
    WINDOWP.INP WINDOWT.TXT WINDOW.OUT
    4 2

    is

    		 This is a sample text for the

    first task on the contest

    		 8

    09. VÒNG TRÒN CON

    Cho hai dãy số nguyên a1, a2, …, am và b1, b2, …, bn (2 ≤ m, n ≤ 100)

    Các số này được xếp quanh hai vòng tròn A và B: các số ai quanh vòng tròn A và các số bj quanh vòng tròn B. Vòng tròn C được gọi với các số quanh nó c1, c2, …, cp được gọi là vòng tròn con của A (hoặc của B) nếu tồn tại một cách xoá bớt các số của A (hoặc của B) để được vòng tròn C. Hãy tìm vòng tròn C là vòng tròn con của cả A và B với số phần tử (p) lớn nhất có thể.

    Chú ý: Các số trên 3 vòng tròn A, B, C được xếp theo đúng thứ tự trong dãy theo cùng một chiều kim đồng hồ.

    Dữ liệu: Vào từ file văn bản CIRCLE.INP

    • Dòng đầu chứa hai số nguyên m, n cách nhau ít nhất một dấu cách.
    • m dòng tiếp theo, dòng thứ i ghi số ai
    • n dòng tiếp theo, dòng thứ j ghi số bj

    Kết quả: Đưa ra file văn bản CIRCLE.OUT

    • Dòng đầu ghi số nguyên p
    • p dòng sau, dòng thứ k ghi số ck.

    10.   BỐ TRÍ PHÒNG HỌP

    Có n cuộc họp đánh số từ 1 đến n đăng ký làm việc tại một phòng hội thảo. Cuộc họp i cần được bắt đầu ngay sau thời điểm si và kết thúc tại thời điểm fi. Hỏi có thể bố trí phòng hội thảo phục vụ được nhiều nhất bao nhiêu cuộc họp, sao cho khoảng thời gian làm việc của hai cuộc họp bất kỳ là không giao nhau.

    Dữ liệu vào từ file văn bản ACTIVITY.INP

    • Dòng đầu tiên chứa số nguyên dương n ( n ≤ 10000)
    • Dòng thứ i trong số n dòng tiếp theo chứa hai số nguyên dương si, fi (si < fi ≤ 32000) (i: 1 ≤ i ≤n).

    Kết quả: Ghi ra file ACTIVITY.OUT

    • Dòng đầu tiên ghi số K là số các cuộc họp được chấp nhận phục vụ
    • K dòng tiếp theo liệt kê số hiệu các cuộc họp được chấp nhận theo thứ tự từ cuộc họp đầu tiên tới cuộc họp cuối cùng , mỗi dòng ghi số hiệu một cuộc họp.

    11.   MUA VÉ TÀU HOẢ

    Tuyến đường sắt từ thành phố A đến thành phố B đi qua một số nhà ga. Tuyến đường có thể biểu diễn bởi một đoạn thẳng, các nhà ga là các điểm trên đó. Tuyến đường bắt đầu từ A và kết thúc ở B, vì thế các nhà ga sẽ được đánh số bắt đầu từ A (có số hiệu là 1) và B là nhà ga cuối cùng.

    Giá vé đi lại giữa hai nhà ga chỉ phụ thuộc vào khoảng cách giữa chúng. Cách tính giá vé được cho trong bảng sau đây:

    Khoảng cách giữa hai nhà ga (X) Giá vé
    0 < X ≤ L1 C1
    L1 < X ≤ L2 C2
    L2 < X ≤ L3 C3

    Vé để đi thẳng từ nhà ga này đến nhà ga khác chỉ có thể đặt mua nếu khoảng cách giữa chúng không vượt quá L3. Vì thế nhiều khi để đi từ nhà ga này đến nhà ga khác ta phải đặt mua một số vé. Hơn thế nữa, nhân viên đường sắt yêu cầu hành khách chỉ được giữ đúng một vé khi đi trên tàu và vé đó sẽ bị huỷ khi hành khách xuống tàu.

    Ví dụ, trên tuyến đường sắt cho như sau:

    bai toan tin mua ve tau hoa

    Để đi từ ga 2 đến ga 6 không thể mua vé đi thẳng. Có nhiều cách mua vé để đi từ ga 2 đến ga 6: Chẳng hạn đặt mua vé từ ga 2 đến ga 3 mất chi phí C2 sau đó mua vé từ ga 3 đến ga 6 mất chi phí C3, và chi phí tổng cộng khi đi theo cách này là C2 + C3. Hoặc mua vé từ ga 2 đến ga 4 mất chi phí C2, sau đó mua vé từ ga 4 đến ga 5 mất chi phí C2 và mua vé từ ga 5 đến ga 6 mất chi phí C1, như vậy chi phí tổng cộng là 2C2 + C1. Lưu ý rằng mặc dù khoảng cách giữa ga 2 và ga 6 bằng 12 = 2 L2 nhưng không được phép mua 2 vé với giá C2 để đi thẳng từ ga 2 đến ga 6.

    Yêu cầu: Tìm cách đặt mua vé để đi lại giữa hai nhà ga cho trước với chi phí mua vé là nhỏ nhất.

    Dữ liệu vào từ file văn bản RTICKET.INP

    • Dòng đầu tiên ghi các số nguyên L1, L2, L3, C1, C2, C3 (1 ≤ L1 < L2 < L3 ≤ 109; 1 ≤ C1 < C2 < C3≤ 109) theo đúng thứ tự liệt kê ở trên.
    • Dòng thứ hai chứa số lượng nhà ga N ( 2 ≤ N ≤ 10000).
    • Dòng thứ ba ghi hai số nguyên s, f là các chỉ số của hai nhà ga cần tìm cách đặt mua vé với chi phí nhỏ nhất để đi lại giữa chúng.
    • Dòng thứ i trong số N – 1 dòng tiếp theo ghi số nguyên là khoảng cách từ nhà ga A (ga 1) đến nhà ga thứ i + 1. Chi phí ít nhất từ nhà ga đầu tiên A đến nhà ga cuối cùng B không vượt quá 109.

    Kết quả ghi ra file văn bản RTICKET.OUT chi phí nhỏ nhất tìm được.

    12.   XIN CHỮ KÝ

    Giám đốc một công ty trách nhiệm hữu hạn muốn xin chữ ký của ông Kiến trúc sư trưởng thành phố phê duyệt dự án xây dựng trụ sở làm việc của công ty. Ông kiến trúc sư trưởng chỉ ký vào giấy phép khi bà thư ký của ông ta đã ký duyệt vào giấy phép. Bà thư ký làm việc tại tầng thứ M của toà nhà trụ sở làm việc gồm M tầng của Văn phòng Kiến trúc sư trưởng thành phố. Các tầng của toà nhà được đánh số từ 1 đến M, từ thấp đến cao. Mỗi tầng của toà nhà có N phòng được đánh số từ 1 đến N từ trái qua phải. Trong mỗi phòng chỉ có một nhân viên làm việc. Giấy phép chỉ được bà thư ký ký duyệt khi đã có ít nhất một nhân viên ở tầng M đã ký xác nhận. Ngoài bà thư ký, một nhân viên bất kỳ chỉ ký xác nhận vào giấy phép khi có ít nhất một trong các điều kiện sau được thoả mãn:

    1. Nhân viên đó làm việc ở tầng 1
    2. Giấy phép đã được ký xác nhận bởi nhân viên làm việc ở cùng số phòng trong tầng sát dưới
    3. Giấy phép đã được ký xác nhận bởi nhân viên làm việc ở cùng số phòng trong tầng sát trên
    4. Giấy phép đã được ký xác nhận bởi nhân viên làm việc ở phòng bên cạnh

    Mỗi một nhân viên (kể cả bà thư ký) khi ký xác nhận đều đòi một khoản lệ phí. Hãy chỉ ra cách xin được chữ ký của Kiến trúc sư trưởng đòi hỏi tổng lệ phí phải trả là nhỏ nhất (giả thiết rằng riêng chữ ký của Kiến trúc sư trưởng không mất lệ phí).

    Dữ liệu vào từ file văn bản SIGN.INP

    • Dòng đầu tiên chứa ba số M, N, P (1 ≤ M ≤ 50; 1 ≤ N ≤ 100; 1 ≤ P ≤ N) ở đây P là số phòng bà thư ký.
    • Dòng thứ i trong số M dòng tiếp theo chứa N số nguyên dương theo thứ tự là lệ phí phải trả cho các nhân viên ở các phòng 1, 2, …, N trên tầng Các số này không vượt quá 109 và giả thiết rằng tổng chi phí cần trả cũng không vượt quá 109.

    Kết quả: Ghi ra file văn bản SIGN.OUT 

    • Dòng đầu tiên ghi 2 số F, K theo thứ tự là chi phí cần trả và số lượng phòng cần đi qua.
    • K dòng tiếp theo, mỗi dòng ghi số tầng và số phòng của một phòng theo thứ tự cần đi qua. (Các số trên 1 dòng của input/output file cách nhau ít nhất 1 dấu trống)

    13.   LẮC NẠM KIM CƯƠNG

    Lắc là một đồ trang sức rất được các cô gái ưa chuộng. Chính vì vậy mà chúng phải được chế tạo thật đẹp và đa dạng. Xét việc chế tạo lắc có m mắt xích, mỗi mắt được nạp một viên kim cương. Có n loại viên kim cương khác nhau, n ≤ 7; 2  ≤  m  ≤  27-n + 19.

    Hai lắc được gọi là khác nhau nếu ta không thể tìm cách đặt sao cho các mắt tương ứng có kim cương cùng loại. Lưu ý rằng lắc có hình vòng.

    Với m và n cho trước, hãy xác định xem có thể tồn tại bao nhiêu loại lắc khác nhau.

    Các loại kim cương được ký hiệu là A, B, C, … Một cấu hình lắc được xác định bởi một xâu m ký tự A, B, C, … và bắt đầu bằng ký tự nhỏ nhất.

    Cho số thứ tự l, hãy xác định cấu hình tương ứng (Các cấu hình được sắp xếp theo thứ tự từ điển).

    Dữ liệu: Vào từ file BRASLET.INP có dạng

    m n l1

    l2

    …

    Kết quả: Đưa ra file BRASLET.OUT

    K – Số lượng lắc khác nhau s1

    s2

    … (si xác định cấu hình lắc tương ứng với li)

    14.   RẢI SỎI

    Xét trò chơi rải sỏi với một người chơi như sau: Cho cây T và một đống sỏi gồm K viên ở mỗi bước người ta lấy 1 viên sỏi từ đống sỏi và đặt vào một nút lá tuỳ chọn.

    Nếu nút p có r nút lá và tất cả và tất cả các nút lá đều có sỏi thì người ta gom tất cả các viên sỏi ở lá lại, đặt 1 viên ở nút p, xoá các nút lá của nó và hoàn trả r – 1 viên sỏi còn lại vào đống sỏi.

    Trò chơi kết thúc khi đã đặt được 1 viên sỏi vào nút gốc.

    Nhiệm vụ đặt ra là theo cấu trúc của cây T, xác định số viên sỏi tối thiểu ban đầu để trò chơi có thể kết thúc bình thường. Cây có n nút ( N ≤ 400), nút gốc được đánh số là 1.

    Dữ liệu: vào từ file văn bản STONE.INP

    • Dòng đầu: số n
    • Dòng thứ i trong số n dòng tiếp theo có dạng: i m i1 i2 … im. Trong đó m là số nút con của nút i; i1, i2, …, im: Các nút con của nút i.

    Kết quả: đưa ra file STONE.OUT số lượng viên sỏi tối thiểu cần thiết

    15.   ĐIỆP VIÊN

    Địa bàn hoạt động của một điệp viên là một khu phố mà ở đó chỉ có các đường phố ngang, dọc tạo thành một lưới ô vuông. Với mục đích bảo mật, thay vì tên đường phố, điệp viên đánh số các phố ngang từ 0 đến m và các phố dọc từ 0 đến n. ở một số ngã ba hoặc ngã tư có các trạm kiểm soát. Anh ta đang đứng ở nút giao của hai đường (i1, j1) (j1 – đường ngang; i1 – đường dọc) và cần tới điểm hẹn ở giao của hai đường (i2, j2). Để tránh bị theo dõi, đường đi phải không qua các trạm kiểm soát và cứ tới chỗ rẽ thì nhất thiết phải đổi hướng đi, thậm chí có thể sang đường và đi ngược trở lại. Việc đổi hướng chỉ được thực hiện ở ngã ba hoặc ngã tư. Hãy xác định đường đi ngắn nhất tới điểm hẹn hoặc cho biết không có đường đi đáp ứng được yêu cầu đã nêu.

    Dữ liệu: vào từ file SPY.INP

    Dòng đầu: m n i1 j1 i2 j2 ( 0 ≤ m, n ≤ 100)

    Các dòng sau: mỗi dòng 2 số i, j (toạ độ trạm kiểm soát).

    Kết quả: đưa ra file SPY.OUT

    Dòng đầu: độ dài đường đi ngắn nhất hoặc thông báo NO nếu không có đường đi.

    Các dòng sau: mỗi dòng 2 số i, j chỉ nút tiếp theo cần tới theo đường đi tìm được, bắt đầu là i1 j1 và kết thúc là i2 j2.

    16.   KHOẢNG CÁCH GIỮA HAI XÂU

    Cho hai xâu ký tự S1 và S2, mỗi xâu có độ dài không quá 100 ký tự. Cho phép thực hiện các phép biến đổi sau đây đối với xâu ký tự:

    1. Thay thế một ký tự nào đó bởi ký tự khác
    2. Đổi chỗ hai ký tự liền nhau
    3. Chèn một ký tự vào sau vị trí nào đó
    4. Xoá bớt 1 ký tự

    Ta gọi khoảng cách giữa hai xâu S1 và S2 là số ít nhất các phép biến đổi nêu trên cần áp dụng đối với xâu S1 để biến nó thành xâu S2.

    Yêu cầu: Tính khoảng cách giữa 2 xâu S1, S2 cho trước và chỉ ra thứ tự các phép biến đổi.

     Ví dụ: Giả sử S1 = ‘Barney’; S2 = ‘brawny’. Khoảng cách giữa 2 xâu là 4. Dãy các phép biến đổi cần thực hiện là:

    1. Thay ký tự 1 của S1 (B) bởi b
    2. Đổi chỗ ký tự thứ 2 (a) và thứ 3 (r) của S1.
    3. Chèn ký tự w vào S1 sau ký tự thứ
    4. Xoá ký tự thứ 5 của S1.

    Dãy các phép biến đổi có thể mô tả như sau:

    ‘Barney’ ® ‘barney’ ® ‘braney’ ® ‘brawney’ ® ‘brawny’

    Dữ liệu: vào từ file văn bản STREDIT.INP có cấu trúc như sau:

    • Dòng đầu tiên chứa xâu S1
    • Dòng thứ hai chứa xâu S2

    Kết quả: Ghi ra file văn bản STREDIT.OUT

    • Dòng đầu tiên ghi số lượng các phép biến đổi cần sử dụng K
    • Mỗi dòng i trong số K dòng tiếp theo mô tả phép biến đổi được sử dụng ở lần thứ i gồm các tham số sau: các tham số ghi trên 1 dòng ghi cách nhau 1 dấu cách.
      • 1, P, C (nếu là phép thay ký tự tại vị trí P bằng ký tự C)
      • 2, I, I + 1 (nếu là phép đổi chỗ 2 ký tự thứ I và thứ I + 1)
      • 3, P, C (nếu là phép chèn ký tự C vào sau vị trí P)
      • 4, P (nếu là phép xoá ký tự thứ P)

    17.   XẾP LẠI BẢNG SỐ

    Cho một bảng ô vuông gồm m hàng và n cột. Các ô được đánh chỉ số theo (hàng, cột) từ (0, 0) đến (m – 1, n – 1). Trên m x n ô người ta viết các số tự nhiên từ 0 đến m x n – 1 theo một thứ tự tuỳ ý. Cho phép đổi chỗ hai số đặt trong hai ô ở thế mã giao chân. Cần tìm cách đổi chỗ các số sao cho thu được bảng có tính chất: Số ở ô (i, j) là n x i + j.

    Dữ liệu vào từ file văn bản BOARD.INP: các số ghi trên 1 dòng cách nhau ít nhất 1 dấu trống.

    • Dòng đầu ghi 2 số m, n (5 ≤ m, n ≤ 80)
    • m dòng tiếp theo, dòng thứ i ghi n số tự nhiên theo đúng thứ tự các số ghi trên hàng i của bảng.

    Kết quả đưa ra file BOARD.OUT

    • Dòng thứ i chứa 4 số X1, Y1, X2, Y2 cho biết tại bước thứ i cần đổi chỗ 2 số tại hai ô (X1, Y1) và (X2, Y2)

    18.   THĂM KHU TRIỂN LÃM

    Một khu triển lãm nghệ thuật có mxn phòng được bố trí trong một hình chữ nhật kích thước mxn (2≤m,n≤ 20). Mỗi phòng biểu diễn bởi một ô và đều có cửa thông với các phòng chung cạnh với nó. Với mỗi một phòng, ta đánh chỉ số theo toạ độ (x, y) của ô (1 ≤hàng x≤m; 1≤cột y≤n) và gán cho nó một chữ cái in hoa (‘A’..’Z’) thể hiện loại nghệ thuật trưng bày tại phòng đó. Có thể vào khu triển lãm ở các phòng có toạ độ (x bất kỳ, y = 1) và có thể đi ra ở các phòng có toạ độ (x bất kỳ, y = n)

    150 bài Toán Tin 4
    Ví dụ với m=10 và n=11

    Một vị thủ tướng đi thăm triển lãm có sở thích đặc biệt với một loại nghệ thuật. Yêu cầu của ông ta “rất đơn giản” là không nhất thiết phải đi thăm tất cả các phòng chứa loại nghệ thuật mà ông ta thích nhưng không được đi qua các phòng chứa loại nghệ thuật khác.

    Ví dụ: Để đi thăm loại nghệ thuật B, Thủ tướng có thể đi:

    (1,1), (1,2), (1,3), (1,4), (1,5), (1,6), (2,6), (3,6), (4,6), (4,7), (4,8), (4,9), (4,10), (5,10), (6,10),(6,11).

    Nhưng không phải luôn tồn tại đường đi như vậy, ví dụ : nếu Thủ tướng muốn đi thăm loại nghệ thuật A thì không thể tìm được một đường đi (Bởi cột 6 của bảng không có một chữ A nào).

    Để có đường đi của vị thủ tướng đi thăm loại nghệ thuật A thì những người quản lý triển lãm phải tìm cách đổi loại nghệ thuật tại hai phòng nào đó. Trong ví dụ này thì để có đường đi chúng ta có thể đổi loại nghệ thuật B ở phòng (5,6) cho loại nghệ thuật A ở phòng (3,1) hoặc phòng (3,7), (3,8),

    …

    Trong những cách đổi đó, người ta thường quan tâm đến việc phải đổi sao cho tổng số phòng phải đổi là ít nhất có thể được. Trong những cách đổi với số cặp phòng phải đổi ít nhất hãy chỉ ra cách đổi mà con đường thủ tướng phải đi là ngắn nhất có thể được. Có thể có nhiều nghiệm thì chỉ cần chỉ ra một nghiệm.

    Dữ liệu vào từ file văn bản TL.INP bao gồm:

    • Dòng đầu tiên ghi số m, n
    • Dòng thứ hai ghi một chữ cái in hoa thể hiện loại nghệ thuật thủ tướng muốn thăm.
    • m dòng tiếp theo, dòng thứ i là một xâu ký tự độ dài n biểu diễn các loại nghệ thuật trong các phòng trên hàng i theo đúng thứ tự từ cột 1 đến cột n.

    Kết quả cho ra file văn bản TL.OUT bao gồm:

    • Dòng đầu tiên là số cặp phòng cần đổi (p).
    • p dòng tiếp theo mỗi dòng gồm 4 số a, b, c, d có nghĩa là ta cần đổi loại nghệ thuật tại phòng (a,b) cho phòng (c,d).
    • Dòng tiếp theo ghi số phòng trên con đường đi ngắn nhất tìm được (q).
    • q dòng tiếp theo, mỗi dòng ghi toạ độ x,y thể hiện cho con đường ngắn nhất đó theo đúng thứ tự phòng đi qua.
    • Nếu không tồn tại phương án đổi phòng để có đường đi thì ghi vào file OUT một dòng:

    NO SOLUTION

    Ví dụ: Với khu triển lãm như trên:

    TL.INP TL.OUT
    10 11 0
    B 16
    BBBBBBFFFFF 1 1
    AAAAABDCCFF 1 2
    AFFFABAACFC 1 3
    BFEFABBBBBD 1 4
    FFDEABAAABA 1 5
    EEDEEEEEABB 1 6
    DDDEEEEEAAB 2 6
    DCCFFFCCABA 3 6
    DCCFFFCCAAA 4 6
    CCCCCCCCCCC 4 7
    4 8
    4 9
    4 10
    5 10
    6 10
    6 11

      

    TL.INP TL.OUT
    10 11 1
    A 5 6 3 1
    BBBBBBFFFFF 18
    AAAAABDCCFF 2 1
    AFFFABAACFC 2 2
    BFEFABBBBBD 2 3
    FFDEABAAABA 2 4
    EEDEEEEEABB 2 5
    DDDEEEEEAAB 3 5
    DCCFFFCCABA 4 5
    DCCFFFCCAAA 5 5
    CCCCCCCCCCC 5 6
    5 7
    5 8
    5 9
    6 9
    7 9
    8 9
    9 9
    9 10
    9 11

    19.   DÒ MÌN

    Cho một bãi mìn kích thước mxn ô vuông, trên một ô có thể có chứa một quả mìn hoặc không, để biểu diễn bản đồ mìn đó, người ta có hai cách:

    • Cách 1: dùng bản đồ đánh dấu: sử dụng một lưới ô vuông kích thước mxn, trên đó tại ô (i, j) ghi số 1 nếu ô đó có mìn, ghi số 0 nếu ô đó không có mìn
    • Cách 2: dùng bản đồ mật độ: sử dụng một lưới ô vuông kích thước mxn, trên đó tại ô (i, j) ghi một số trong khoảng từ 0 đến 8 cho biết tổng số mìn trong các ô lân cận với ô (i, j) (ô lân cận với ô (i, j) là ô có chung với ô (i, j) ít nhất 1 đỉnh).

    Giả thiết rằng hai bản đồ được ghi chính xác theo tình trạng mìn trên hiện trường.

    Ví dụ: Bản đồ đánh dấu và bản đồ mật độ tương ứng: (m = n = 10)

    150 bài Toán Tin 5

    Về nguyên tắc, lúc cài bãi mìn phải vẽ cả bản đồ đánh dấu và bản đồ mật độ, tuy nhiên sau một thời gian dài, khi người ta muốn gỡ mìn ra khỏi bãi thì vấn đề hết sức khó khăn bởi bản đồ đánh dấu đã bị thất lạc !!. Công việc của các lập trình viên là: Từ bản đồ mật độ, hãy tái tạo lại bản đồ đánh dấu của bãi mìn.

     Dữ liệu: Vào từ file văn bản MINE.INP, các số trên 1 dòng cách nhau ít nhất 1 dấu cách

    • Dòng 1: Ghi 2 số nguyên dương m, n (2 ≤ m, n ≤ 80)
    • m dòng tiếp theo, dòng thứ i ghi n số trên hàng i của bản đồ mật độ theo đúng thứ tự từ trái qua phải.

    Kết quả: Ghi ra file văn bản MINE.OUT, các số trên 1 dòng ghi cách nhau ít nhất 1 dấu cách

    • Dòng 1: Ghi tổng số lượng mìn trong bãi
    • m dòng tiếp theo, dòng thứ i ghi n số trên hàng i của bản đồ đánh dấu theo đúng thứ tự từ trái qua phải.

    Các bài tiếp theo, mời bạn đọc tải tại đây 150 BAI TOAN TIN – LE MINH HOANG

  • Bài tập HSG Tin học THPT

    Bài tập HSG Tin học THPT

    Chúng tôi xin giới thiệu 16 Bài tập HSG Tin học THPT gồm các bài tập: Điệp viên, Trư bát giới, Bàn cờ 4 * 4, Đội cờ, Hệ thống xe buýt, Bố trí phòng họp, Phân phối kênh, Trò chơi với ô chữ, Công việc, Mã hoá Burrows wheeler, Mặt phẳng, Truyền tin ngắn nhất, Robot quét vôi, Vườn Táo, Dãy lồi.

    Quý thầy cô và các em học sinh có thể tham khảo thêm Giải thuật Đệ quy là gì?

    1. Bài tập HSG Tin học THPT: Điệp viên

    Một điệp viên trưởng phụ trách một nước nọ trước khi về nước muốn gặp nhân viên của mình để nghe báo cáo. Hai người đang ở hai thành phố khác nhau vì vậy họ phải di chuyển để gặp nhau. Quy tắc di chuyển như sau:

    • Họ di chuyển vào ban ngày và nghỉ tại một thành phố vào buổi tối.
    • Trong ngày, họ chỉ có thể di chuyển từ một thành phố tới thành phố bên cạnh (có đường đi trực tiếp và các đường đi này là 1 chiều).
    • Để bảo đảm an toàn, các điệp viên luôn luôn di chuyển (không dừng tại một thành phố quá một đêm).
    • Hai người có thể gặp nhau nếu họ ở cùng1 thành phố vào buổi tối.

    Yêu cầu: Lập chương trình kiểm tra xem hai người có gặp nhau không.

    Dữ liệu: agent.inp

    • Dòng đầu ghi 2 số: n là số thành phố, m là số các đường đi trực tiếp giữa các thành phố (n <=50, m<=100).
    • Dòng tiếp theo là 2 số p, q là vị trí hiện thời của hai điệp viên.
    • M dòng tiếp theo mỗi dòng chứa 2 số ai, aj là số hiêu các thành phố và từ ai có đường đi trực tiếp (một chiều) đến aj.

    Kết quả: agent.out

    • Nếu 2 người không gặp nhau in ra từ “No”
    • Nếu 2 người gặp nhau in ra t là số ngày ngắn nhất mà hai người có thể gặp nhau.

    Ví dụ:

    Agent.in1 Agent.ou1 Agent.in2 Agent.ou2 Agent.in3 Agent.ou3 Agent.in4 Agent.ou4
    6 7

    1 5

    1 2

    4 5

    2 3

    3 4

    4 1

    5 4

    5 6

    		 3 3 3

    1 3

    1 2

    2 3

    3 1

    		 No 8 9

    1 8

    1 2

    2 3

    3 4

    4 1

    1 5

    5 6

    6 7

    7 8

    8 1

    		 5 8 9

    2 8

    1 2

    2 3

    3 4

    4 1

    1 5

    5 6

    6 7

    7 8

    8 1

    		 11

    Hướng dẫn: Sử dụng thuật toán: Loang theo lớp

    Bài toán này là một điển hình cho thuật toán “loang theo lớp”. Ta loang theo chiều rộng đường đi của 2 điệp viên theo trình tự: loang đường đi của người thứ nhất tại thời điểm i một lần rồi loang đường đi của người thứ hai tại thời điểm đó một lần. Lặp lại việc loang  đó cho đến khi không thể loang được tiếp hoặc kiểm tra thấy 2 người gặp nhau (tức cả 2 bên loang cùng đến được một địa điểm) hoặc kiểm tra thấy một đỉnh nào đó lặp lại quá nhiều một số lần cho phép (tức người đó rơi vào một chu trình mà không thể gặp được người kia) hay nếu queue vơi giới hạn cao cũng không thể chứa được nữa.

    Giả mã

    While Not Stop Do
   Begin
   Loangr1(đau1, cuoi1, Stop1);
   Loangr2(đau2,cuoi2, Stop2);
   If  kiemtra (dau1, cuoi1, dau2, cuoi2) then begin found := true; break end;
   Stop := Stop 1 or Stop2;
End;

    Trong chương trình con Loangr1(dau1, cuoi1, Stop1) đó biến stop1 trả giá trị true nếu chưa vượt quá giới hạn queue1 và solanlaplai[i] < Ghanchophep (co the là 10000 – tuy theo ban thich đo chinh xac nao).

    Hàm Loangr2(đau2,cuoi2, Stop2) cũng tương tự.

    Hàm Kiemtra (dau1, cuoi1, dau2, cuoi2) tra gia tri true nếu với các đỉnh được đi đến (vừa kết nạp vào queue1 và queue 2) trong lần loangr1 (co cuoi1 – dau1 đỉnh) và trong lần loangr2 (có cuoi2 – dau2 đỉnh) có một đỉnh chung.

    2. Bài tập HSG Tin học THPT: Trư bát giới

    Trên đường đi thỉnh kinh, một lần Bát Giới được Tôn Ngộ Không giao cho nhiệm vụ đi hầu Tam Tạng. Tam Tạng đi với tốc độ không đổi và đường đi của ông là đường gấp khúc (có thể tự cắt) gồm n điểm gãy. Mỗi điểm gãy được cho bởi cặp số nguyên (xi, yi) là toạ độ trên mặt phẳng xoy. Theo hầu Tam Tạng, Bát Giới đi chơi theo con đường riêng của mình nhưng luôn gặp Tam Tạng tại n điểm gãy nói trên. Hai người bắt đầu xuất phát từ điểm (x1, y1) và kết thúc chuyến đi đồng thời tại điểm (xn, yn) để chờ Tôn Ngộ Không và Sa Tăng. Bát Giới có thể đi với tốc độ không vượt quá hai lần tốc độ của Tam Tạng. Khi Tam Tạng đi theo đường thẳng từ điểm gãy này đến điểm gãy kế tiếp, Bát Giới có thể chạy đến các điểm hấp dẫn được cho bởi m cặp số nguyên (x’i, y’i). Tuy nhiên, sau khi tách rời Sư phụ tại điểm (xi, yi) Bát Giới chỉ có thể thăm không quá một điểm hấp dẫn ông để rồi gặp lại Sư phụ tại điểm (xi+1, yi+1).

    Yêu cầu:

    Tìm đường đi của Bát Giới thoả mãn các điều kiện nêu trên và sao cho số điểm hấp dẫn của Bát Giới thăm được là nhiều nhất.

    Dữ liệu: Bg.inp.

    • Dòng đầu tiên chứa hai số nguyên dương n và m (2n100, 0m100)
    • Dòng thứ hai chứa n cặp số nguyên: x1, y1, …, xn, yn.
    • Dòng thứ ba chứa m cặp số nguyên: x’1, y’1, …, x’m, y’m.

    Các điểm trong file dữ liệu là khác nhau từng đôi một và toạ độ của chúng là các số nguyên có trị tuyệt đối không vượt quá 1000. Các số ghi cách nhau bởi dấu cách.

    Kết quả: Bg.out.

    • Dòng đầu tiên ghi số nguyên dương k là số điểm gãy trên đường đi của Bát Giới.
    • Dòng thứ hai ghi cặp toạ độ u1, v1, …, uk, vk biểu diễn đường đi của Bát Giới. Các toạ độ ghi cách nhau bởi dấu cách..

    Ví dụ:

    Bg.INP Bg.OUT
    4 5

    1 4 5 7 5 2 -2 4

    -4 -2 3 9 1 2 -1 3 8 -3

    		 6

    1 4 3 9 5 7 5 2 1 2 -2 4

    Hướng dẫn:

    Dùng cặp ghép

    • Xây dựng tập X: tập các gồm n – 1 phần tử. Với các phần tử đó là các cạnh trên đường đi của Bát Giới.
    • Xây dựng tập Y: tập gồm m phần tử. Các phần tử là các điểm hấp dẫn.
    • Xây dựng ma trận quan hệ giữa X và Y. Nếu ở phần tử i (i của tập X – tức là các cạnh trên đường đi của Tam Tạng), Bát Giới có thể đi đến điểm hấp dẫn j (j thuộc Y) thì a[i,j] = true và ngược lại. Tức là a[i,j] = true ó kc(xi, yi, x’j, y’j) + kc(xi+1, yi+1, x’j, y’j) 2kc(xi, yi, xi+1, yi+1).
    • Dùng thuật toán cặp ghép tối đa để giải.

    3. Bài tập HSG Tin học THPT: Bàn cờ 4 * 4

    Một bàn cờ có dạng bảng vuông kích thước 4 * 4, trên đó có một số quân cờ. Một quân cờ chỉ có thể di chuyển sang 1 ô kề cạnh còn trống, mỗi di chuyển như vậy được gọi là 1 bước di chuyển. Cho hai trạng thái của bàn cờ, hãy chỉ ra một dãy các bước di chuyển để đưa bảng từ trạng thái xuất phát đến trạng thái đích với số phép di chuyển là ít nhất. Mỗi trạng thái được mô tả là một ma trận 4 * 4 trong đó số ô ở hàng I, cột j là 1 nếu tại vị trí (i,j) tương ứng có quân cờ đang đứng hoặc bằng 0 nếu không có.

    Dữ liệu: chess.inp

    • Gồm 2 * 4 dòng thể hiện ma trận mô tả trạng thái xuất phát và trạng thái đích. 4 dòng đầu tiên thể hiện ma trận xuất phát, 4 dòng tiếp theo là ma trận đích.
    • Input luôn đảm bảo là có nghiệm.

    Kết quả: chess.out

    • Dòng đầu tiên ghi k là số ít nhất các phép biến đổi tìm được.
    • K dòng tiếp, mỗi dòng mô tả 1 phép biến đổi, theo đúng trình tự biến đổi, gồm 4 số nguyên dương u, v, x, y thể hiện di chuyển quân cờ ở vị trí (u, v) sang vị trí (x, y).

    Ví dụ:

    Chess.inp Chess.out
    1111

    1111

    0000

    0000

    0000

    0000

    1111

    1111

    		 16

    2 1 3 1

    1 1 2 1

    2 2 3 2

    1 2 2 2

    2 3 3 3

    1 3 2 3

    2 4 3 4

    1 4 2 4

    3 1 4 1

    2 1 3 1

    3 2 4 2

    2 2 3 2

    3 3 4 3

    2 3 3 3

    3 4 4 4

    2 4 3 4

    4. Bài tập HSG Tin học THPT: Đội cờ             

    Có hai đội cờ vua A và B thi đấu với nhau. Mỗi đội cử ra n kì thủ, mỗi kì thủ của đội B chỉ đấu một trận và đấu với 1 kì thủ của đội A và ngược lại. Vậy có tất cả n trận đấu. Đội nào thắng được 2 điểm, hoà được 1 điểm và thua không được điểm nào.

    Cho đội B được quyền chọn cặp thi đấu.

    Yêu cầu: lập trình để đội B chọn được các cặp thi đấu sao cho tổng số điểm của đội B là cao nhất. Cho biết trình độ của kì thủ thứ i của hai đội A và B là ai và bi (I = 1, 2, …, n) và giả sử trong thi đấu, hai kì thủ có trình độ bằng nhau sẽ hoà và cầu thủ nào có trình độ cao hơn sẽ thắng.

    Dữ liệu: Doico.inp

    • Dòng đầu ghi số nguyên dương n (1n10000).
    • Trên dòng thứ I trong số n dòng tiếp theo ghi hai số nguyên dương ai, bi (1ai, bi1000), cách nhau một khoảng trắng.

    Kết quả: Doico.out

    • Dòng đầu là số nguyên t là tổng số điểm cao nhất mà đội B có thể đạt được.
    • Trên dòng thứ hai là n số nguyên dương xi, trong đó xi là số thứ tự của kì thủ đội B phải đấu với kì thủ thứ i của đội A để tổng số điểm đội B đạt được là lớn nhất.

    Ví dụ:

    Doico.inp Doico.out
    4

    7 8

    5 6

    4 3

    9 4

    		 5

    1 2 4 3

    Hướng dẫn thuật giải:

    • Sắp xếp hai mảng A, B theo thứ tự không giảm, nhớ lưu vị trí cũ của A, B vào hai mảng chỉ số.
    • Ta thực hiện phương pháp tối ưu từng bước, cụ thể:
    • Ở chương trình này cần chú ý khi sắp xếp 2 dãy A, B thì vị trí các kì thủ đã đổi, do đó mảng x là mảng ứng với vị trí mới của mảng A và B ta cần đổi về vị trí cũ.

    5. Bài tập HSG Tin học THPT: Hệ thống xe buýt.

    Một hệ thống các xe buýt có nhiệm vụ chuyên chở hành khách đi lại giữa một số ga sao cho đảm bảo tính liên thông hai chiều giữa các ga này. Hệ thống bao gồm một số tuyến đường, mỗi tuyến đường gồm một số ga khác nhau theo thứ tự mà xe buýt đi qua. Xe buýt thuộc tuyến đường nào chỉ chạy trên tuyến đường đó, lần lượt qua các ga thuộc tuyến cho đến hết, sau đó lại quay đầu chạy theo hướng ngược lại. Có thể có một số ga chung cho một số tuyến đường. Một hành khách muốn đi từ ga đầu đến ga cuối, có thể đi trên một tuyến hoặc phải chuyển tuyến một số lần ở những nơi có ga chung. Bài toán đặt ra là, cần tìm một hành trình cho phép đi từ ga đầu đến ga cuối sao cho số lần phải chuyển tuyến là ít nhất. Nếu tồn tại nhiều phương án như vậy, hãy tìm phương án đi qua ít ga nhất.

    Dữ liệu: busway.inp

    • Dòng đầu là số tuyến đường.
    • Các dòng tiếp mỗi dòng mô tả một tuyến đường, gồm một chuỗi các kí tự viết liền nhau, mỗi kí tự mô tả một tên ga theo đúng thứ tự các ga tren tuyến (chú ý các ga trên cùng một tuyến là khác nhau, nhưng các ga trên các tuyến khác nhau có thể trùng nhau, tên ga có thể là một kí tự bất kì hiển thị được trong bảng mã ACSII)
    • Dòng tiếp theo là số hành trình cần tìm.
    • Các dòng tiếp theo, mỗi dòng mô tả một hành trình cần tìm, gồm cặp kí tự viết liền nhau, xác định các tên ga đầu và ga cuối.

    Giả thiết các dữ liệu là hợp lệ, không cần kiểm tra. Giới hạn kích thước 100 cho số các tuyên đường và 50 cho số các ga trên cùng một tuyến đường.

    Kết quả: busway.out

    • Mỗi hành trình được viết trên một dòng, gồm các kí tự biểu diễn tên ga viết theo thứ tự đi được. Các tên ga này được viết thành từng nhóm theo tuyến đường: nếu thuộc cùng một tuyến thì viết liền nhau, nếu sang tuyến khác thì viết cách nhau một dấu cách (space), tên ga chung được viết lặp lại.

    Ví dụ

    Busway.inp Busway.out
    3

    ABC

    DBE

    GAEH

    2

    HC

    GB

    		 HEA ABC

    GA AB

    Hướng dẫn:

    • Xây dựng đồ thị đường đi giữa các ga là ma trận hai chiều (lưu vào mảng trọng số a). Coi mỗi kí tự là một đỉnh của đồ thị (dùng hàm ord(kítự) lấy giá trị là số). a[i,j] = 0 nếu các kí tự “chr(i)”, “ chr(j)” (cũng là các ga) không thuộc cùng một tuyến đường nào cả. a[i,j] > 0 và là giá trị nhỏ nhất của đoạn đường đi giữa hai ga (chr(i), chr(j)).
    • Dùng thuật toán Dijstra để tìm đường đi ngắn nhất từ ga đầu tới ga cuối. Trong thuật toán ta có hai ưu tiên sau:
      • Số ga giữa đường đi là ít nhất (ưu tiên cao nhất).
      • Tổng đường đi giữa các ga là nhỏ nhất.
    • Với ưu tiên thứ nhất ta có thể coi đồ thị vừa lập là một đồ thị mới: đồ thị quan hệ: a[i,j] = 0 tức không có đường đi từ i tới j và a[i,j] > 0 tức có đường đi giữa i và j. Với ưu tiên thứ nhất ta coi a[i,j] > 0 thì a[i,j] = 1 trong đồ thị mới lập.
    • Khi ưu tiên thứ nhất được thoả mãn ta xét đến ưu tiên thứ hai, khi đó coi như thuật toán Dijstra dùng cho đồ thị cũ đã lập lúc đầu – đồ thị trọng số.

    6. Bài tập HSG Tin học THPT: Bố trí phòng họp.

    Có n cuộc họp được đánh số từ 1 đến n đăng kí làm việc tại một phòng hội thảo. Cuộc họp i cần bắt đầu vào thời điểm ai và kết thúc vào thời điểm bi (i = 1..n). Hai cuộc họp có thể nhận phục vụ nếu các khoảng thời gian làm việc tương ứng chỉ có thể giao nhau tại đầu mút hoặc tách rời nhau.

    Yêu cầu: Hãy tìm một lịch cho phòng hội thảo để có thể phục vụ nhiều cuộc họp nhất.

    Dữ liệu:  Activity.inp.

    • Dòng đầu tiên là giá trị n (n <= 1000000).
    • Dòng thứ i trong n dòng tiếp theo ghi 2 số ai và bi cách nhau ít nhất một dấu cách. (ai, bi <=32000 và là các số nguyên dương).

    Kết quả: Activity.out.

    • Dòng đầu tiên ghi số k là số cuộc họp tối đa có thể bố trí.
    • Dòng tiếp theo ghi số hiệu của cuộc họp được phục vụ theo trình tự lịch bố trí.

    Ví dụ:

    Activity.inp Activity.out
    5

    1 3

    2 4

    1 6

    3 5

    7 9

    		 3

    1 4 5

    Hướng dẫn:

    Do n lớn nên ta cần lưu dữ liệu theo mảng thời gian.

    Khai báo:        tr: array [1..32000] of integer;

    Dùng mảng trước đánh dấu thời gian cuối của cuộc họp. Tức là nếu tr[c]  <> 0 thì tồn tại cuộc họp có thời điểm kết thúc là c và tr[c] mang ý nghĩa là thời điểm ban đầu của cuộc họp. Đọc dữ liệu và đánh dấu mảng tr sao cho tr[c] gần c nhất có thể.

    Với cuộc họp có thời điểm kết thúc c mà ta chọn, ta cần lưu chỉ số của cuộc họp đó.

    Khai báo:        Cs: array [1..32000] of longint; {vì n lớn}.

    Do mảng này không thể khai báo được -> lưu chỉ số theo 2 giá trị: n div 32, n mod 32 -> thay mảng cs bằng hai mảng sau:

    Khai báo:        Trx, try: array [1..32000] off integer

    Ý nghĩa  :        trx[c] = I div 32; try[c] := I mod 32.

    Mảng try có thể khai báo bằng kiểu byte. Hai mảng này dùng mảng động.

    Xử lí: Gọi max là thời gian kết thúc lớn nhất trong các cuộc họp. Duyệt từ 1 đến max, nếu có cuộc họp i nào có tr[i] >= cuối thì kết nạp vào mảng lưu. Với cuoi là giá trị thời gian kết thúc của cuộc họp được chọn trước đó (đầu tiên cuối = 0).

    7. Bài tập HSG Tin học THPT: Phân phối kênh

    Công ty dịch vụ mạng máy tính cần phân phối kênh hoạt động phục vụ n yêu cầu của khách hàng (n <= 5000) đánh số thứ tự từ 1 tới n. Với mỗi khách hàng thứ i ta biết khoảng thời gian yêu cầu sử dụng kênh là (si, ti), i =1, 2, …, n (khách hàng sẽ sử dụng kênh từ thời điểm si tới thời điểm ti). Thời gian chuyển giao kênh từ khách hàng này tới khách hàng khác là không đáng kể. Như vậy, nếu hai khách hàng nào đó được bố trí làm việc trên cùng một kênh thì các khoảng thời gian sử dụng của họ chỉ có thể có nhiều nhất là một điểm chung.

    Yêu cầu: hãy tìm cách phân phối sử dụng ít kênh nhất.

    Dữ liệu: Chanel.inp

    • Dòng đầu tiên ghi số n.
    • Dòng thứ i trong số n dòng tiếp theo mỗi dòng ghi 2 số nguyên dương si, ti (i =1, 2, …, n).

    Kết quả: Chanel.out

    • Dòng đầu tiên ghi số lượng kênh cần sử dụng p.
    • Mỗi dòng thứ i trong số p dòng tiếp theo chứa các chỉ số của mỗi khách hàng sử dụng kênh thứ i, i = 1, 2, …, p.

    Ví dụ:

    Chanel.inp Chanel.out
    7

    0 3

    3 5

    6 8

    0 7

    7 8

    0 2

    2 6

    		 3

    4 5

    1 2 3

    6 7

    Hướng dẫn.

    Ở bài này ta cần xác định các khách hàng với khoảng thời gian (si, ti) đó vào các tập sao cho các khoảng thời gian trong mỗi tập chỉ có thể có duy nhất là một điểm chung và số tập là ít nhất có thể được. Ta sắp xếp lại các khoảng thời gian đó theo thứ tự tăng dần của si, nếu si, sj bằng nhau thì sắp xếp theo thứ tự tăng dần của ti, tj … Khi đó ta duyệt các khách hàng theo thứ tự từ 1 tới n, với mỗi khách hàng thì ta duyệt các tập đã xây dựng được, nếu có thể kết nạp khách hàng này vào tập hợp nào thì ta kết nạp vào (và có thể thấy đó là cách kết nạp tối ưu do hiệu quả của sắp xếp), nếu không thì cho khách hàng này vào tập hợp mới. Ta thấy độ phức tạp của thuật toán chỉ cỡ .

    8. Bài tập HSG Tin học THPT: Trò chơi với ô chữ.

    Tiếp tục phát triển trò chơi với ô chữ, người ta đã đánh số cho các từ có độ dài từ 1 đến 26 theo quy tắc là ưu tiên độ dài từ, sau đó là theo vần ABC. Với:

    a                      1

    b                      2

    …

    z                      26

    aa                    27

    …

    snowfall          157.118.051.752

    Như vậy, mỗi một số ta có tương ứng là một từ gồm các chữ cái thường và ngược lại ứng với mỗi từ ta có một số tương ứng. Công việc đặt ra là: giả sử ta có một số hãy tìm từ tương ứng với nó, và cho một từ hãy cho biết từ đó ứng với số bao nhiêu.

    Dữ liệu: Game.inp.

    • Dòng đầu là một số nguyên.
    • Dòng thứ hai là một xâu kí tự (gồm các kí tự thường).

    Kết quả: Game.out.

    • Dòng thứ nhất là một từ tương ứng với số trong file input.
    • Dòng thứ hai là một số tương ứng với từ trong file input.

    Ví dụ:

    Game.inp Game.out
    157118051752

    snowfall

    		 snowfall

    157118051752

    9. Bài tập HSG Tin học THPT: Công việc

    Có n công viêc đánh số từ 1 đến n, n <= 10000. Mỗi việc làm đều phải làm liên tục trong một giờ mới xong. Việc u nếu làm không muộn hơn giờ thứ du sẽ thu được một giá trị nguyên dương gu; các giá trị du, gu nguyên dương và không lớn hơn 60000. Tại mỗi thời điểm không được làm hơn một việc và bắt đầu từ thời điểm 0, giờ thứ I xem như bắt đầu từ thời điểm I – 1.

    Yêu cầu: Hãy chọn một số việc làm sao cho tổng giá trị thu được là lớn nhất. Các số phát sinh trong phạm vi longint.

    Dữ liệu: Job.inp

    • Dòng thứ nhất ghi số n.
    • N dòng tiếp theo, dòng thứ u ghi hai số du, gu.

    Kết quả: Job.out

    • Dòng thứ nhất ghi tổng giá trị thu được.
    • Tiếp theo là các dòng, mỗi dòng ghi hai số x, y với ý nghĩa việc x làm trong giờ thứ y.

    Ví dụ:

    Job.inp Job.out
    6

    3 7

    3 20

    1 10

    1 15

    1 5

    3 3

    		 42

    3

    2 3

    4 1

    1 2

    10. Bài tập HSG Tin học THPT: Mã hoá Burrows wheeler.

    Burrows Wheeler đề xuất phương pháp mã hóa thông tin như sau: ví dụ cần mã hóa BANANA, các bước tiến hành là:

    • Bước 1: Từ cần mã hóa được dịch chuyển vòng tròn và tạo thành một ma trận l * l kí tự, trong đó l là độ dài của từ.
    • Bước 2: Sắp xếp lại các dòng của ma trận theo thứ tự từ điển.
    • Bước 3: trích xâu từ các kí tự cuối của cột, thông báo xâu này và cho biết từ gốc là thứ mấy trong ma trận nhận được ở bước 2. Ta có: (NNBAAA, 4).

    BANANA                               ABANAN

    ANANAB                               ANABAN

    NANABA                               ANANAB

    ANABAN                               BANANA

    NABANA                               NABANA

    ABANAN                               NANABA.

    Yêu cầu: cho kết quả mã hóa (kết quả bước 3). Hãy xác định từ ban đầu.

    Dữ liệu: mahoa.inp:

    • Bao gồm một hoặc nhiều nhóm 2 dòng , dòng đầu là xâu kí tự độ dài không quá 100, dòng sau là số nguyên dương cho biết vị trí từ gốc.

    Kết quả: mahoa.out:

    • Xuất ra các từ ban đầu, mỗi từ trên 1 dòng.

    Ví dụ:

    Mahoa.inp Mahoa.out
    NNBAAA

    4

    OMOEULCG

    1

    		 BANANA

    COGUMELO

    11. Bài tập HSG Tin học THPT: Mặt phẳng

    Trên mặt phẳng cho n hình chữ nhật có cạnh song song với trục toạ độ. Hãy đếm số miền mặt phẳng được tạo ra bởi các cạch của hình chữ nhật. Một miền mặt phẳng là một vùng liên tục khép kín giới hạn bởi các cạnh của hình chữ nhật và không chứa một miền mặt phẳng nào khác.

    Dữ liệu: Matphang.inp.

    Dòng đầu là số nguyên dương n (<30) là số hình chữ nhật.

    N dòng tiếp theo, mỗi dòng chứa 4 số nguyên dương lần lượt là toạ độ theo hai trục toạ độ của hai đỉnh đối của hình chữ nhật.

    Kết quả: Matphang.out.

    Số miền mặt phẳng tìm được.

    Ví dụ:

    Matphang.inp Matphang.out
    2

    10 10 30 30

    20 20 40 40

    		 3

     

    Matphang.inp Matphang.out
    2

    20 10 30 40

    10 20 40 30

    		 5

    12. Bài tập HSG Tin học THPT: Truyền tin ngắn nhất.

    Trong một mạng gồm n máy tính đánh số từ 1 đến n. Sơ đồ nối mạng được cho bởi hệ thống gồm m kênh nối trực tiếp giữa một số cặp máy trong mạng. Biết chi phí truyền cho 1 đơn vị thông tin theo mỗi kênh nối của mạng.

    Người ta cần chuyển 1 bức thông điệp từ máy s -> t. Để đảm bảo an ninh, người ta muốn chuyển bức thông điệp này theo 2 đường truyền tin khác nhau (tức là không có kênh nào của mạng được sử dụng trong cả 2 đường truyền tin). Chi phí của 1 đường truyền được hiểu là tổng chi phí trên các kênh của nó.

    Yêu cầu: giả sử bức thông điệp có độ dài một đơn vị thông tin, hãy tìm cách chuyển thông điệp từ s -> t sao cho tổng chi phí chuyển thông tin ( bằng tổng chi phí theo cả hai đường truyền tin) là nhỏ nhất.

    Dữ liệu: May.inp

    • Dòng đầu ghi n, m, s, t cách nhau bởi dấu cách (n<=100).
    • Mỗi dòng thứ i trong số m dòng tiếp theo ghi thông tin về kênh nối thứ i của mạng gồm 3 số di, ci, gi: di, ci là chỉ số 2 máy tương ứng và gi là chi phí để truyền theo kênh này (đường truyền là hai chiều).

    Kết quả: May.out

    • Dòng đầu ghi tổng chi phí.
    • Dòng thứ hai ghi đường truyền 1: s-> t.
    • Dòng thứ ba ghi đường truyền 2: s ->t.

    Ví dụ:

    May.inp May.out
    5 7 15

    1 2 3

    1 4 8

    2 3 5

    2 4 4

    3 5 5

    4 3 8

    4 5 3

    		 24

    1 2 3 5

    1 4 5

    13. Bài tập HSG Tin học THPT: Robot quét vôi

    Có 9 căn phòng (đánh số từ 1 đến 9) đã được quét vôi với mầu trắng, xanh hoặc vàng. Có 9 rôbôt (đánh số từ 1 đến 9) phụ trách việc quét vôi các phòng. Mỗi rôbôt chỉ quét vôi một số phòng nhất định. Việc quét vôi được thực hiện nhờ một chương trình cài sẵn theo qui tắc:

    • nếu phòng đang có mầu trắng thì quét mầu xanh,
    • nếu phòng đang có mầu xanh thì quét mầu vàng,
    • nếu phòng đang có mầu vàng thì quét mầu trắng.

    Cần phải gọi lần lượt một số các rôbôt ra quét vôi (mỗi lần một rôbôt, một rôbôt có thể gọi nhiều lần và có thể có rôbôt không được gọi. Rôbôt được gọi sẽ quét vôi tất cả các phòng mà nó phụ trách) để cuối cùng các phòng đều có mầu trắng. Hãy tìm một phương án như vậy sao cho lượng vôi phải quét là ít nhất. Giả thiết rằng luợng vôi cho mỗi lượt quét đối với các phòng là như nhau.

    Dữ liệu: đọc từ file văn bản ROBOT.INP gồm các dòng:

    • 9 dòng đầu, mỗi dòng mô tả danh sách các phòng được quét vôi bởi một rôbôt theo thứ tự từ rôbôt 1 đến rôbôt 9. Mỗi dòng như vậy gồm các số hiệu phòng viết sát nhau. Chẳng hạn dòng thứ 2 có nội dung:
      3578 mô tả rôbôt 2 phụ trách việc quét vôi các phòng 3, 5, 7, 8.
    • dòng cuối mô tả mầu vôi ban đầu của các phòng. Dòng gồm 9 ký tự viết sát nhau, ký tự thứ i biểu diễn mầu vôi của phòng i với quy ước: ký tự T chỉ mầu trắng, ký tự X chỉ mầu xanh, ký tự V chỉ mầu vàng.

    Kết quả: đưa ra file văn bản ROBOT.OUT gồm một dòng dưới dạng:

    • nếu không có phương án thì ghi một chữ số 0,
    • trái lại ghi dãy thứ tự các rôbôt được gọi (các số hiệu rôbôt viết sát nhau).

    Thí dụ: 

    ROBOT.INP   ROBOT.OUT
    159

    123

    357

    147

    5

    369

    456

    789

    258

    XVXVXVTXT

    		 2455688

    14. Bài tập HSG Tin học THPT

    Cho 2 xâu:

    X = x1x2..xM. (Với xi là các kí tự số từ ‘0’ đến ‘9’)

    Y = y1y2..yN.( Với yi là các kí tự số từ ‘0’ đến ‘9’)

    (M, N <= 250)

    Ta gọi: Z = z1z2..zk là xâu chung của 2 xâu X, Y nếu xâu Z nhận đ­ợc từ xâu X bằng cách xoá đi một số kí tự và cũng nhận được từ xâu Y bằng cách xoá đi một số kí tự.

    Yêu cầu: Tìm một xâu chung của 2 xâu X, Y sao cho xâu nhận được tạo thành một số lớn nhất có thể được.

    Dữ liệu vào file: String.inp

    Gồm 2 dòng, dòng 1 là xâu X, dòng 2 là xâu Y.

    Kết quả ra file: String.out

    Gồm 1 dòng duy nhất là số lớn nhất có thể nhận được.

    Ví dụ:

    String.inp String.out
    19012304 034012 34

    15. Bài tập HSG Tin học THPT: Vườn Táo

    Trong một mảnh vờn hình vuông cạnh 1000 m có trồng N cây táo . Vị trí mỗi cây táo đợc xác định bởi toạ độ (x,y) trong hệ toạ độ vuông góc với gốc toạ đọ là góc trái dới của vờn và các trục toạ độ song song với các cạnh vờn . Hãy tìm hình chữ nhật lớn nhất sao cho các cạnh song song với các cạnh của vờn , và trong nó không chứa cây táo nào ( mà chỉ có thể chứa trên biên ) .

    Dữ Liệu vào từ file     Tao.Inp

    • Dòng thứ nhất ghi N số từ 1 đến 600 .
    • Trong N dòng sau mỗi dòng ghi hai số nguyên dơng x,y ,0<x,y<1000 là toạ độ của các cây táo .

    Kết Quả ghi ra file   Tao.Out

    • Dòng thứ nhất ghi diện tích hình chữ nhật
    • Dòngthứ hai ghi số hai số là toạ độ của đỉnh trái dới
    • Dòng thứ ba ghi hai số là toạ độ của đỉnh trên phải của hình chữ nhật .

    Ví Dụ:

    TAO.INP

    7 280 100 200 600 400 200 135 800 800 400 600 800 900 210

    TAO.OUT

    360000 200 200 800 800

    Hướng dẫn.

    Ta thêm vào tập các cây những cây giả là hình chiếu của các cây thật trên bốn cạnh của khu vờn . Sắp xếp lại các cây theo thứ tự tăng dần của hoành độ . Thực chất ta đã chia chúng thành các hình nhỏ hơn . Sau đó tìm từng hình một thoả mãn điều kiện của hình chữ nhật ( không chứa táo , diện tích lớn nhất ) .

    16. Bài tập HSG Tin học THPT Dãy lồi

    Dãy giá trị nguyên A=(a1, a2, …, an) được gọi là dãy lồi nếu nó giảm dần từ a1 tới ai nào đó, rồi tăng dần tới an. Ví dụ: dãy 10 5 4 2 -1 4 6 8 12 là dãy lồi.

    Yêu cầu: lập trình nhập vào một dãy số nguyên, bằng cách xoá bớt một số phần tử của dãy và giữ nguyên trình tự các phần tử còn lại, ta nhận được dãy con lồi dài nhất.

    Dữ liệu: dayloi.inp.

    • Dòng đầu là số tự nhiên n (n<=5000).
    • Dòng tiếp theo là n số nguyên của dãy số(các số kiểu integer).

    Kết quả: dayloi.out.

    • Dòng đầu tiên ghi số phần tử lớn nhất của dãy con tìm được (ghi ra 0 nếu không tồn tại dãy lồi).
    • Dòng tiếp theo ghi các số thuộc dãy con (không thay đổi trật tự các phần tử trong dãy ban đầu).

    Ví dụ:

    Dayloi.inp Dayloi.out
    10

    1 2 3 4 2 5 1 2 3 4

    		 6

    4 2 1 2 3 4

  • 100 ĐỀ THI HỌC SINH GIỎI TIN HỌC – ĐỀ THI TIN HỌC TRẺ

    100 ĐỀ THI HỌC SINH GIỎI TIN HỌC – ĐỀ THI TIN HỌC TRẺ

    Bài 1: Viết chương trình nhập vào tọa độ tâm I(a;b) và bán kính r của một đường tròn (a, b, r là các số nguyên). Sau đó nhập vào một điểm A(x, y) bất kì và kiểm tra xem nó có thuộc đường tròn hay không?

    Bài 2: Viết chương trình tính tích xy (với x, y là hai số thực có độ lớn tùy ý).

    Bài 3: Tìm tất cả các chữ số có ba chữ số, sao cho tổng các lập phương của các chữ số thì bằng chính số đó.

    Bài 4: Nhập 3 loại tiền và số tiền cần đổi. Hãy tìm tất cả các tổ hợp có được của 3 loại tiền trên cho số tiền vừa nhập.

    Bài 5: Viết chương trình giải bài toán cổ sau:

    Trăm trâu trăm cỏ
    Trâu đứng ăn năm
    Trâu nằm ăn ba
    Trâu già ba con một bó.

    Hỏi có bao nhiêu con mỗi loại?

    Bài 6: Lập tam giác PASCAL, dùng chương trình con.

    Bài 7: Viết các chương trình con  tính diện tích tam giác, tròn, vuông, chữ nhật trong một chương trình. Sau  đó hỏi chọn  một trong các phương án  tính diện  tích bằng  cách chọn trong bảng chọn lệnh sau:

    1. Không làm gì hết và trở về màn hình soạn thảo.
    2. Tính diện tích hình vuông
    3. Tính diện tích hình tròn
    4. Tính diện tích tam giác
    5. Tính diện tích hình chữ nhật

    Bài 8: Viết chương trình nhập vào một dãy số nguyên   có n phần tử. In ra màn hình phần tử nhỏ nhất, phần tử lớn nhất và giá trị trung bình của danh sách ra màn hình.

    Bài 9: Viết chương trình nhập vào một dãy số nguyên  có n phần tử.

    1. Đưa những phần tử lẻ ra đầu danh sách, những phần tử chẵn về cuối danh sách và in kết quả ra màn hình.
    2. Sắp xếp các phần tử lẻ đầu danh sách theo thứ tứ tăng dần, sắp xếp các phần tử chẵn cuối danh sách theo thứ tự giảm dần. In danh sách ra màn hình.

    Bài 10: Viết chương trình nhập vào một chuỗi kí tự, sau đó nhập vào một kí tự bất kì và đếm số lần của nó trong chuỗi đã nhập.

    Bài 11: Viết chương trình nhập vào một chuỗi ký tự. Kiểm tra xem nó có đối xứng hay không (Ví dụ: Chuỗi đối xứng RADAR, MADAM).

    Bài 12: Viết chương trình nhập vào họ tên của một người. Sau đó in chuỗi họ tên ra màn hình với các ký tự đầu đổi thành chữ hoa, toàn bộ chuỗi họ và tên đổi thành chữ hoa.

    Bài 13: Viết chương trình nhập vào một dãy số nguyên  có n phần tử.

    1. Sắp xếp dãy theo thứ tự tăng dần và in kết quả ra màn hình.
    2. Nhập vào một số x bất kì, đếm số lần xuất hiện của nó trong dãy trên.
    3. In ra màn hình số phần tử nhỏ hơn hoặc bằng x.
    4. In ra màn hình số phần tử lớn hơn x.

    Bài 14: Sử dụng lệnh lặp để tính tổng của 11 số hạng đầu tiên

    S = 100 + 105 + 110  +...

    Bài 15:  Tìm số P, biết rằng

    P/4 = 1 - 1/3   + 1/5 - 1/7  +...

    Với độ chính xác: |1/2n-1| < 10^-5

    Bài 16: Cho một dãy số nguyên A(i) với i=1,...N. Viết chương trình:

    1. Tính và in ra trung bình cộng cuả các số dương trong dãy.
    2. Đếm xem có bao nhiêu số chia hết cho 3.
    3. In ra vị trí các số bằng 0 (nếu có) trong dãy đã cho.

    Bài 17:  Viết chương trình tìm các số có 3 chữ số mà tổng lập phương các chữ số của nó bằng chính nó (các số Amstrong).

    Bài 18:  Nhập một số thực x rồi tính

    S = 1 + x/1! + x^2/2! + x^3/3! +...+ x^n/n!

    với độ chính xác | x^n/n! | < 10^-5.

    Bài 19:  Dãy Fibonaxi được định nghĩa như sau:

    A1=A2=1, An=A(n-1) + A(n-2) với n>=2.

    Hãy:

    1. Nhập một số n và in ra n số Fibonaxi đầu tiên.
    2. Nhập một số n và in ra các số Fibonaxi nhỏ hơn hoặc bằng n.

    Bài 20:  Cho một dãy số. Viết chương trình:

    1. Gom tất cả các số chia hết cho 7 về đầu dãy và tất cả các số chia hết cho 5 vể cuối dãy.
    2. Sắp xếp phần số đã gom theo thứ tự tăng dần.

    Bài 21:   Cho một dãy số. Hãy viết chương trình Tìm phần tử nhỏ nhất và phần tử nhỏ thứ hai. Hãy cho biết vị trí đầu tiên của phần tử lớn nhất.

    Bài 22: Cho một dãy ký tự. Hãy viết chương trình tách dãy trên thành hai nửa, nửa đầu gồm các số, nửa sau là các chữ cái. Sắp xếp nửa đầu giảm dần, nửa sau tăng dần.

    Bài 23: Xét dãy các xâu F1, F2,... Fn trong đó:

    F1 = 'A'; F2 = 'B'; Fk+1 = Fk + F(k-1) với k=>2

    Ví dụ:

    F1 = 'A'
F2 = 'B'
F3 = 'BA'
F4 = 'BAB'
F5 = 'BABBA'
F6 = 'BABBABAB'...

    Cho xâu S độ dài không quá 25, chỉ bao gồm các kí tự 'A' và 'B'. Yêu cầu:

    1. Hãy xác định số lần xuất hiện xâu S trong xâu Fn, n<=35. Chú ý: Hai lần xuất hiện của S trong Fn không nhất thiết phải là các xâu rời nhau hoàn toàn.
    2. Dữ liệu vào: Đọc từ file văn bản FIBISTR.INP có cấu trúc như sau: Gồm nhiều dòng, mỗi dòng gồm n và S. Giữa n và S có đúng 1 dấu cách. Dữ liệu vào là chuẩn, không cần kiểm tra.
    3. Dữ liệu ra: Ghi ra file văn bản FIBISTR.OUT có cấu trúc như sau: Gồm nhiều dòng, mỗi dòng dữ liệu ứng với một dòng kết quả ra.

    Bài 24: SỐ PHẢN NGUYÊN TỐ. Một số tự nhiên n được gọi là số phản nguyên tố nếu nó có nhiều ước số nhất trong n số tự nhiên đầu tiên.

    Yêu cầu: Cho số K không vượt quá 10000. Ghi ra số phản nguyên tố lớn nhất nhỏ hơn hoặc bằng K.

    Dữ liệu vào: Đọc từ file văn bản OPNT.INP có cấu trúc như sau:

    • Dòng đầu tiên là số M (1<M<=100) là số lượng các số cần tìm số phản nguyên tố lớn nhất của nó.
    • M dòng tiếp theo là các số K1,K2,..KM

    Dữ liệu ra: Ghi ra file văn bản SOPNT.OUT có cấu trúc như sau:

    • Gồm M dòng.
    • Dòng thứ i (1<=i<=M) là số phản nguyên tố lớn nhất nhỏ hơn hoặc bằng Ki.

    Bài 25: Ngồi nhà quá rỗi, Sơn có ý tưởng dùng các que diêm tạo thành các số hập phân. Một cách đại diện cho 10 chữ số thập phân như sau:

    ĐỀ THI HỌC SINH GIỎI TIN HỌC - ĐỀ THI TIN HỌC TRẺ

    Cho N que diêm, Sơn có thể tạo ra một loạt các chữ số. Sơn kinh gạc phát hiện ra số nhỏ nhất và lớn nhất trong số đó có thể tạo được bằng cách sử dụng tất cả các que diêm của Sơn.

    Yêu cầu: Xác định số nhỏ nhất và lớn nhất mà Sơn có thể tạo ra.

    Dữ liệu vào: Đọc từ file văn bản MATCH.INP có cấu trúc như sau:

    • Dòng đầu tiên là số test K (1<K<=100)
    • K dòng tiếp theo, mỗi test gồm một dòng chứa số nguyên n (2<=n<=100) là số que diêm

    Bài 26: Dãy số được gọi là dãy số đối xứng nếu đọc các phần tử của dãy số này từ trái sang phải hay đọc ngược lại đều được cùng kết quả. Ví dụ: 1, 2, 1 hoặc 1, 2, 2, 1 là các dãy số đối xứng.

    Dãy số P được gọi là dãy số con của dãy số A nếu các phần tử thuộc P có mặt liên tiếp trong dãy số A với thứ tự không đổi. Ví dụ: 2, 1, 3 là dãy số con của 1, 2, 2, 1, 3.

    Cho dãy số tự nhiên A gồm n phần tử a1, a2, a3…an (ai <35000, 5<n<100)

    Yêu cầu: Hãy viết phương trình tìm dãy số P là dãy số con đối xứng dài nhất của dãy số A.

    Dữ liệu vào: Nhập vào số tự nhiên n và n phần tử của dãy số A.

    Kết quả: Xuất ra màn hình kết quả vừa tìm được

    Ví dụ:

    Dữ liệu vào: (nhập từ bàn phím)

    N=5   1 2 2 1

    Kết quả: (xuất ra màn hình)

    A: 1 2 2 1 2

    Bài 27:   Xâu s1 có độ dài m và s2 có độ dài n ( m,n là hai số tự nhiên; n,m<250). Biết rằng s1,s2 chỉ chứa các kí tự ‘A’…’Z’.

    Yêu cầu: Hãy viết phương trình tìm xâu con chung dài nhất của xâu s1 và s2.

    Dữ liệu vào: Nhập từ bàn phím 2 xâu s1 và s2.

    Kết quả: Xuất ra màn hình xâu con chung của 2 xâ s1 và s2.

    Ví dụ:

    Dữ liệu vào: kết quả: ABBA

    S1:ABBABC

    S2:ABABBA

    Bài 28: Cho xâu S có độ dài N (N<100). Xâu S chỉ chứa các k‎ tự số ‘0’…’9’.

    Yêu cầu: Hãy viết chương trình tìm xâu S1 bằng cách hoán vị các k‎ tự số trong xâu S sao cho xâu S1 có giá trị nhỏ nhất lớn hơn S.

    Đữ liệu vào: Cho trong tệp tin so.inp, gồm 1 dòng ghi xâu S.

    Kết quả: Ghi trong tập tin so.out, gồm 1 dòng ghi kết quả vừa tìm được.

    Ví dụ:

    Dữ liệu vào: (So.inp)     Kết quả: (so.out)

    ‘1234’   ‘1324’

    Bài 29: Viết chương tìm ước số chung lớn nhất của hai số nguyên a và b khác 0, với a, b được nhập từ bàn phím.

    Bài 30:  Viết chương trình nhập vào một mảng gồm n phần tử (n<=100). Kiểm tra và in ra màn hình các số là số nguyên tố sắp xếp theo thứ tự tăng dần.

    Bài 31: Cho số tự nhiên N (N<=50). Hãy viết chương trình thực hiện:

    1. Nhập số N, sau đó nhập N số nguyên từ bàn phím. thứ tự của các số gọi là chỉ số.
    2. Hãy tính trong dãy số trên có bào nhiêu số dương chẵn.
    3. Tìm (các) chỉ số của giá trị âm lớn nhất của dãy số nếu có.
    4. Tìm tất cả các dãy con dài nhất các số khác không cùng dấu.

    Bài 32:  Nhập vào từ bàn phím một số N nguyên dương (N<=5000).

    1. Hãy phân tích N thành tổng của hai số nguyên tố (nếu được) và thông báo không được nếu không có phương án nào.
    2. Nếu N thoả mãn câu a, hãy đưa càng nhiều càng tốt các phương án phân tích (2 phương án có cùng các số hạng chỉ coi là một)

    Bài 33:  Cho trước một dãy số bao gồm toàn các số 0 và 1. Dãy này có độ dài nhỏ hơn 255.

    1. Viết chương trình nhập dãy số trên từ bàn phím. Các số được nhập liên tiếp từ bàn phím, quá trình nhập dữ liệu kết thúc nhấn phím <Enter>. Nếu việc nhập dữ liệu sai trên màn hình kết quả “Bạn đã nhập sai, đề nghị nhập lại” và cho phép nhập lại ngay dữ liệu.
    2. Một dãy con đúng của dãy trên được gọi là một dãy con liên tục bất kỳ của dãy trên bao gồm các số hạng giống nhau. Hãy tính độ dài lớn nhất của một dãy con đúng của dãy trên.
    3. Một dãy con đúng bậc 1 của dãy trên được coi là một dãy con liên tục bất kỳ của dãy trên bao gồm toàn các số hạng giống nhau ngoại trừ 1 phần tử. Hãy tính độ dài lớn nhất của một dãy con đúng bậc 1 của dãy trên.

    Bài 34:  Cho số nguyên N trong phạm vi từ 1000 đến 999999. Cần xác định số này có phải là thông tin về một ngày tháng có trong thế kỷ 21 không. (Thế kỷ 21 bắt đầu từ 1 tháng 1 năm 2001 và kết thúc vào ngày 31 tháng 12 năm 3000. Biết rằng 2  chữ số cuối của N là chỉ hai chữ số cuối của năm, các chữ số còn lại (ở đầu) xác định ngày và tháng.

    Ví dụ:

    1111       tương ứng với 1 tháng 1 năm 2011;

    21290     tương ứng với 2 tháng 12 năm 2090 hoặc 21 tháng 2 năm 2090;

    131192 tương ứng với 13 tháng 11 năm 2092;

    32392     Không phải là thông tin về một ngày tháng nào cả;

    311198 Không phải là thông tin về một ngày tháng nào cả;

    29205     Không phải là thông tin về một ngày tháng nào cả;

    Dữ liệu: Nhập vào số N từ bàn phím.

    Kết quả: Đưa ra màn hình các ngày tháng năm tương ứng với N hoặc thông báo là KHONG nếu N không phải là thông tin về một ngày tháng nào cả.

    Ví dụ:

    Giá trị của N Thông báo ra màn hình tương ứng
    1111

    21290

    29205

    		 1-1-2011

    2-12-2090 HOAC 21-2-2090

    KHONG

    Bài 35:    Cho dãy số nguyên a1, a2,…, an (n <= 1000).

    Hãy tìm cách thực hiện một số ít nhất phép đổi chỗ hai số hạng bất kỳ của dãy để thu được dãy số mà số lẻ đứng ở vị trí lẻ, số chẵn đứng ở vị trí chẵn.

    Dữ liệu: Vào từ file văn bản DAYSO.INP:

    • Dòng đầu tiên chứa số nguyên dương n;
    • Dòng thứ i trong số n dòng tiếp theo chứa số hạng ai của dãy đã cho (-32767 à 32767, i = 1, 2,…, n).

    Kết quả: ghi ra file văn bản DAYSO.OUT:

    • Dòng đầu tiên ghi số lượng phép đổi chỗ cần thực hiện k (qui ước k = -1, nếu không thể biến đổi được dãy đã cho thành dãy thoả mãn yêu cầu đầu bài);
    • Nếu k > 0, thì dòng thứ j trong số k dòng tiếp theo ghi chỉ số của hai số hạng cần đổi chỗ cho nhau ở lần đổi chỗ thứ j  ( j =1, 2,…, k).

    Ví dụ:

     DAYSO.INP DAYSO.OUT DAYSO.INP DAYSO.OUT
    6

    1

    2

    3

    4

    6

    5

    		 1

    5 6

    		 4

    1

    3

    2

    5

    		 -1

    Bài 36:  Một nhóm gồm n bạn học sinh của một lớp tham gia một câu lạc bộ tin học vào dịp nghỉ hè. Biết rằng khoảng thời gian mà bạn thứ i có mặt tại câu lạc bộ là [ai, bi] (ai<bi tương ứng là các thời điểm đến và rời khỏi câu lạc bộ). Cô giáo chủ nhiệm lớp muốn tới thăm các bạn trong nhóm này. Hãy giúp cô giáo chủ nhiệm xác định thời điểm đến câu lạc bộ sao cho tại thời điểm đó cô giáo có thể gặp được nhiều bạn trong nhóm nhất.

    Dữ liệu: Vào từ file văn bản MEETING.INP:

    • Dòng đầu tiên ghi số nguyên dương n (n <= 1000);
    • Dòng thứ i trong số n dòng tiếp theo ghi 2 số nguyên không âm ai, bi, i = 1, 2,…, n.

    Kết quả: Ghi ra file văn bản MEETING.OUT:

    • Dòng đầu tiên ghi số nguyên dương k là số lượng bạn đang có mặt ở câu lạc bộ tại thời điểm cô giáo đến;
    • Trong k dòng tiếp theo ghi chỉ số của k bạn có mặt ở câu lạc bộ tại thời điểm cô giáo đến, mỗi dòng ghi một chỉ số của một bạn.

    Ví dụ:

     MEETING.INP MEETING.OUT MEETING.INP MEETING.OUT
    6

    1  2

    2  3

    2  5

    5  7

    6  7

    9 11

    		 3

    1

    2

    3

    		 5

    1 2

    3 5

    7 9

    11 15

    17 21

    		 1

    1

    Bài 37:  Ứng với mỗi số tự nhiên x, ta có số tự nhiên f(x) bằng tổng bình phương các chữ số của x. Từ x ta xây dựng dãy (Xn) như sau:

    X1 = x ; X2 = f(X1) ; X3 = f(X2) ; …; Xi = f(Xi – 1)    với   1 <= I <= n

    Ví dụ:

    x = 12 ta có dãy: 12; 5; 25; 29; 85; 89; 145; 42; 20; 4; 16; 37; 58; 89

    x = 4 ta có dãy: 4; 16; 37; 58; 89; 145; 42; 20; 4

    Viết chương trình nhập vào từ bàn phím số tự nhiên x và in ra màn hình dãy (Xn)

    Dữ liệu vào: Số tự nhiên x.

    Dữ liệu ra: In ra màn hình dãy (Xn)

    Bài 38:  Tạo một dãy gồm n (3 < n < 20) số nguyên nhận các giá trị ngẫu nhiên từ 1 đến 99.  Xuất dãy  và xuất ra vị trí các số nguyên tố của dãy.

    Dữ liệu vào: Số nguyên n có giới hạn theo đề.

    Kết quả ra: Mảng a ngẫu nhiên và vị trí các số nguyên tố trong mảng.

    Ví dụ:

    Dữ liệu vào Dữ liệu ra
    19

     

    		 So phan tu cua mang: 19

    Mang a la:

    74 98 69 94  5 11 11 50 21 61 89 73 14 19 55 31 71 50  1

    Vi tri cac so nguyen to co trong a la:  5  6  7 10 11 12 14 16 17

    Lưu ý: số 1 không phải là số nguyên tố

    Bài 39:  Viết chương trình in ra màn hình các số từ x đến y là số chẵn và chia hết cho 3. với x, y nhập từ bàn phím? Đếm xem có tất cả bao nhiêu số?

    Dữ liệu vào: Số nguyên x và y (x < y).

    Kết quả ra: Các số chẵn chia hết cho 3 trong phạm vi từ x đến y và đếm có bao nhiêu số.

    Ví dụ:

    Dữ liệu vào Dữ liệu ra
    3

    40

    		 12  18  24  30  36

    Co tat ca: 6 so

    Các bài từ 40 đến 64 sau đây lấy từ 100 đề Toán Tin (Tin học &#038; Nhà trường)

    Bài 65: Bạn Huy không tập trung tư tưởng trong giờ toán vì vậy thầy giáo cho thêm bài tập về nhà rèn luyện khả năng tập trung tư tưởng và tính cẩn thận chu đáo. Nội dung bài tập là cho n xâu chỉ bao gồm các ký tự la tinh thường và chữ số. Đoạn các ký tự số liên tục tạo thành một số nguyên. Ở mỗi đoạn ký tự số liên tục Huy phải trích ra số lớn nhất có thể, sắp xếp các số nhận được từ các xâu đã cho và đưa ra theo thứ tự không giảm, mỗi số được đưa ra dưới dạng không có các số 0 không có nghĩa.

    Ví dụ, với n = 1 và xâu là 01a2b3456cde478 dãy số cần đưa ra là 1, 2, 478, 3456.

    Yêu cầu: Cho số nguyên n (1 ≤ n ≤ 100) và n xâu, mỗi xâu có độ dài không quá 100. Hãy đưa ra dãy số nhận được đã sắp xếp theo thứ tự không giảm, mỗi số trên một dòng.

    Dữ liệu: Vào từ file văn bản numbers.inp:

    Dòng đầu tiên chứa số nguyên n,

    Mỗi dòng trong n dòng sau chứa một xâu chỉ gồm các ký tự la tinh thường và số.

    Dữ liệu đảm bảo có không quá 500 số được tách ra.

    Kết quả: Đưa ra file văn bản NUMBERS.OUT dãy số nhận được đã sắp xếp theo thứ tự không giảm, mỗi số trên một dòng.

    Ví dụ:

    numbers.inp numbers.out
    4

    43silos0

    zita002

    le2sim

    231233

    		 0

    2

    2

    43

    231233

    Bài 66: Hãy viết chương trình đổi tờ giấy bạc có mệnh giá n (Việt Nam đồng) ra ba loại giấy bạc có mệnh giá 500, 200, 100 (Việt Nam đồng) sao cho số tờ gấy bạc phải sử dụng là ít nhất (n được nhập từ bàn phím).

    Bài 67: Tuổi của cha hiện nay là b tuổi, tuổi của con là c tuổi (b-c > 0 và b, c là các số nguyên dương). Hãy viết chương trình (với b, c được nhập từ bàn phím) để kiểm tra xem tuổi cha có gấp đôi tuổi con hay không? Nếu đúng thì đưa ra màn hình thông báo “hiện nay tuổi cha gấp đôi tuổi con”; trường hợp ngược lại, hãy tính số năm n (trước đó hoặc sau đó) tuổi cha gấp đôi tuổi con và đưa ra màn hình thông báo “n năm trước đây tuổi cha gấp đôi tuổi con” hay “sau n năm tuổi cha sẽ gấp đôi tuổi con”.

    Bài 68: Hàng tháng, các hộ dân sử dụng điện đều nhận được một hóa đơn thanh toán tiền điện. Giá tiền điện phải trả được tính như sau:

    • 100 số đầu tiên, mỗi số phải trả 550 đồng,
    • Từ số 101 đến số 150, mỗi số phải trả 1100 đồng,
    • Từ số 151 đến số 200, mỗi số phải trả 1470 đồng,
    • Từ số 201 trở đi, mỗi số phải trả 1600 đồng.

    Số tiền điện mà mỗi hộ dân phải trả ở hóa đơn là tổng số tiền điện mà người đó đã sử dụng với 10% thuế VAT.     Hãy viết chương trình tính số tiền điện mà người tiêu dùng phải trả trong tháng với a là số KW điện mà người tiêu dùng đã sử dụng và được nhập từ bàn phím.

    Bài 69: Nhập vào số tự nhiên n (0 < n < 10) và hai mảng số nguyên A, B có n phần tử đại diện cho hai tập hợp theo yêu cầu không có hai phần tử trùng nhau trong cùng một tập hợp. (Do đó, trong quá trình nhập nếu phần tử vừa nhập vào đã có trong mảng thì không bổ sung vào mảng). In ra màn hình tập hợp A, tập hợp B và các phần tử là giao của hai tập hợp A và B.

    Bài 70:

    1. Nhập một dãy số nguyên có n phần tử (0< n <= 100)
    2. Sắp xếp dãy vừa nhập theo thứ tự tăng dần, in ra màn hình dãy đã sắp thứ tự
    3. Tìm trên dãy đã sắp xếp có phần tử x hay không, với x được nhập từ bàn phím.

    Bài 71: Cho đa thức bậc n:

    A = anxn + an-1xn-1+…+ a1x + a0

    Trong đó an, an-1,…a1,a0 là các hệ số nguyên có giá trị tuyệt đối không quá 100.

    Biết rằng phương trình A = 0 nếu có nghiệm nguyên thì nghiệm nguyên đó chỉ có thể là ước số của hệ số a0.

    Yêu cầu: Hãy tìm tất cả các nghiệm nguyên (nếu có) của phương trình A = 0.

    Bài 72: Kỳ thi học sinh giỏi năm học 2008-2009 của tỉnh Bà Rịa-Vũng Tàu có 8 đội tuyển dự thi đến từ các huyện (TX, TP), số thứ tự các huyện được đánh số lần lượt từ 1 đến 8 là Vũng Tàu, Bà Rịa, Tân Thành, Châu Đức, Xuyên Mộc, Đất Đỏ, Long Điền, Côn Đảo. Mỗi thí sinh dự thi có một số báo danh duy nhất (là một số nguyên dương), mỗi đội tuyển của huyện tối đa 90 thí sinh. Sau khi thi xong Sở Giáo dục- Đào tạo tổ chức cho các thí sinh  giao lưu với nhau, Ban tổ chức sắp xếp các thí sinh đứng thành một vòng tròn, để tạo điều kiện cho các thí sinh trong tỉnh được giao lưu với nhau Ban tổ chức yêu cầu các thí sinh cùng huyện không đứng gần nhau, các thí sinh thuộc 2 huyện có số thứ tự liền kề cũng không được đứng gần nhau.

    Yêu cầu: Hãy giúp Ban tổ chức chỉ ra một cách xếp thỏa mãn yêu cầu trên

    Dữ liệu vào: file ‘pupil.inp’

    Gồm có 8 dòng, dòng thứ i chứa các số báo danh của các thí sinh huyện thứ i, các số báo danh cách nhau ít nhất một dấu cách.

    Dữ liệu ra: file ‘pupil.out’

    (Mô tả cách xếp n thí sinh theo yêu cầu trên một vòng tròn, ta có thể mô tả trên một đường thẳng, trong đó thí sinh đầu và thí sinh cuối đứng gần nhau trên vòng tròn)

    Gồm n dòng (n là tổng số thí sinh), mỗi dòng là số báo danh của thí sinh. Trong trường hợp không có cách nào thỏa mãn yêu cầu thì ghi là -1

    Ví dụ

    Pupil.inp Pupil.out
    1 2 3

    4 5 6

    7 8 9

    10 11 12

    13 14 15

    16 17 18

    19 20 21

    22 23

    		 1

    22

    16

    7

    17

    23

    2

    18

    8

    3

    9

    10

    4

    11

    5

    12

    6

    13

    19

    14

    20

    15

    21

    Bài 73: Nhập vào một số tự nhiên N với (0 < N ≤ 65535). Hãy cho biết chữ số lớn nhất của số tự nhiên vừa nhập. Hãy in đảo ngược số N.

    Ví dụ: N=6548. Chữ số lớn nhất là: 8. Số in ngược là: 8456.

    Bài 74: Nhập vào một số tự nhiên N với (0 < N ≤ 65535), phân tích số vừa nhập thành các thừa số nguyên tố, nếu số vừa nhập là số nguyên tố thì chỉ thông báo ra màn hình đây là số nguyên tố.

    Ví dụ:

    • Nếu số vừa nhập là 300, thì in ra màn hình 300 = 2. 2. 3. 5. 5
    • Nếu số vừa nhập là 307, thì in ra màn hình “307 là số nguyên tố”

    Bài 75: Tìm tất cả các số nguyên dương x, y, z  thỏa mãn phương trình: ax + by + cz = n; trong đó a, b, c, n là các số nguyên dương (a, b, c ≤ 65535; n ≤ 2.147.483.647)

    Yêu cầu kỹ thuật:

    1. Kiểm tra việc nhập dữ liệu thỏa mãn yêu cầu của đề bài. Nếu người sử dụng nhập sai thì thông báo nhập sai và hỏi người dùng có muốn nhập lại hay không, nếu không thì kết thúc chương trình.
    2. Không được dùng quá 2 vòng lặp lồng nhau và điều kiện dừng của mỗi vòng lặp không được vượt quá ngưỡng mà từ đó ta biết chắc chắn phương trình không có nghiệm.
    3. Nếu phương trình có nghiệm thì liệt kê có thứ tự các bộ nghiệm của phương trình theo dạng sau:

    Giả sử phương trình có dạng 15x + 28y + 24z = 454, ta in ra màn hình như sau:

    STT     x          y          x

    1          10        10        1

    2          14        7          2

    Ngược lại không thì thông báo phương trình không có nghiệm.

    Bài 76: Một số có tổng các ước nhỏ hơn nó bằng chính nó được gọi là số hoàn chỉnh.

    Ví dụ: 6 có các ước nhỏ hơn nó là 1, 2, 3. Tổng là 1 + 2 + 3 = 6.

    Viết chương trình xét xem một số n được nhập từ bàn phím có phải là số hoàn chỉnh không.

    Bài 77: Viết chương trình tìm các số hoàn chỉnh nhỏ hơn n (Với n được nhập từ bàn phím).

    Bài 78: Dãy Fibonacy có hai phần tử đầu là 1, 1. Các phần tử sau bằng tổng hai phần tử đứng ngay trước nó:

    1, 1, 2, 3, 5, 8, 13, 21,…

    Viết chương trình in ra dãy Fibonacy có phần tử lớn nhất nhỏ hơn n?

    Bài 79: Viết chương trình nhập n số, xoá số thứ k trong n số vừa nhập. In ra n-1 số còn lại.

    Bài 80: Viết chương trình cho phép nhập một dãy gồm n số nguyên. Nhập thêm một số và chèn thêm vào dãy sau phần tử k.

    Bài 81: Viết chương trình in ra màn hình tam giác Pascal. Ví dụ, với n=4 sẽ in ra hình sau:

    1          1

1          2          1

1          3          3          1

1          4          6          4          1

    Hàng thứ n được xác định từ hàng n-1:

    • Phần tử đầu tiên và phần tử cuối cùng đều bằng 1.
    • Phần tử thứ 2 là tổng của phần tử thứ nhất và thứ 2 của hàng n-1
    • Phần tử thứ k của hàng thứ n là tổng của phần tử thứ k-1 và k của hàng thứ n-1.

    Bài 82: Viết chương trình tính giai thừa của số n (Viết là n!). Với yêu cầu:

    • Nếu người dùng nhập số n < 0 thì yêu cầu nhập lại.
    • Sử dụng chương trình con để tính giai thừa của một số.

    Bài 83: Viết chương trình cho phép cộng hai phân số.

    Bài 84: Nhập vào một số nguyên dương n. Hãy in ra số nguyên tố nhỏ nhất lớn hơn n. VD: Nhập n = 10. Kết quả in ra số 11.

    Bài 85: Tìm các số tự nhiên nhỏ hơn hoặc bằng n mà sau khi làm phép phân tích ra thừa số nguyên tố có nhiều nhân tử nhất. Ví dụ n=9. Các số có nhiều nhân tử nhất sau khi làm phép phân tích là: 8 = 2.2.2

    Viết chương trình cho phép phân tích một số ra thừa số nguyên tố và ghi kết quả dưới dạng tích các lũy thừa. Ví dụ: 300 = 2^2.3.5^2

    Bài 86: Mọi số tự nhiên đều có thể viết được dưới dạng tổng của hai số nguyên tố. Viết chương trình thực hiện tách một số tự nhiên thành tổng của hai số nguyên tố.

    Bài 87: Hai số tự nhiên A, B được coi là hữu nghị nếu như số này bằng tổng các ước số của số kia và ngược lại. Lập trình tìm và in ra màn hình các cặp số hữu nghị trong phạm vi từ 1 đến 10000. (Lưu ý, số 1 được coi là ước số của mọi số còn mỗi số không được coi là ước số của chính nó).

    Bài 88: Cho dãy số gồm n số. Tìm dãy con lớn nhất các phần tử tăng (giảm) dần.

    Bài 89: Cho dãy số gồm n số. Tìm dãy con lớn nhất các phần tử có cùng dấu, (đan dấu).

    Bài 90: Cho dãy gồm n số. Tìm dãy con lớn nhất đơn điệu (liên tục tăng, giảm hoặc giảm, tăng).

    Bài 91:  Cho dãy số gồm n số nguyên. Tìm dãy con có tổng lớn nhất

    Hướng dẫn. Sử dụng kỹ thuật vét cạn các dãy con, dùng hàm tính tổng dãy con để kiểm tra.

    Bài 92: Gọi abcd là một số có 4 chữ số. Hãy lập chương trình tìm tất cả các số có 4 chữ số thỏa mãn biểu thức: abcd=(ab + cd)^2. Ví dụ 2025=(20 + 25)^2.

    Bài 93:  Viết chương trình cho nhập hai số tự nhiên N và k. Hãy cho biết chữ số thứ k tính từ trái sang phải trong số N là chữ số nào? Nếu k lớn hơn độ dài của N hoặc k bằng 0 thì thông báo không tìm được.

    Bài 94:  Một số được gọi là số bậc thang nếu biểu diễn thập phân của nó có nhiều hơn một chữ số đồng thời theo chiều từ trái qua phải, chữ số đứng sau không nhỏ hơn chữ số đứng trước. Viết chương trình in ra các số bậc thang trong đoạn [n1, n2] với n1, n2 được nhập từ bàn phím.

    Bài 95: Viết chương trình cho phép đổi một số từ cơ số 10 sang cơ số bất kỳ.

    Thuật toán:

    • Dùng mảng CS để lưu các chữ số.
    • Lặp khi n <> việc: Chia n cho s lấy phần dư. Lấy phần dư làm chỉ số để lấy và lưu chữ số. Gán n = n div s.

    Chú ý chữ số lấy sau sẽ nằm trước.

    Bài 96: Viết chương trình cho phép đổi một số từ cơ số bất kỳ sang cơ số 10.

    Bài 97: Năm 1973, nhà Toán học Neil Sloan đưa ra khái niệm độ bền của một số nguyên không âm N như sau:

    • Nếu N có một chữ số thì độ bền của N bằng 0.
    • Nếu N có từ hai chữ số trở lên thì độ bền của N bằng độ bền của số nguyên là tích các chữ số của N cộng 1.

    Cho N từ 0  đến 2.000.000.000, tìm số bé hơn N có độ bền lớn nhất.

    Ví dụ

    Persist.inp Persist.out Giải thích
    100 77 Doben(77)=Doben(49)+1=Doben(36)+1+1=Doben(18)+1+1+1=Doben(8)+1+1+1+1=0+1+1+1+1=4

    Hướng dẫn.

    • Để tìm độ bền một số cần một hàm TICH(n) tính tích các chữ số của n.
    • Cho d = 0. Lặp lại điều kiện n >9 việc tăng d lên 1 thay n = TICH(n).
  • Thuật toán kiểm tra Số Nguyên Tố

    Thuật toán kiểm tra Số Nguyên Tố

    Thuật toán kiểm tra Số Nguyên Tố

    Thuật toán kiểm tra Số Nguyên Tố của một số nguyên dương, cùng với thuật toán tìm UCLN của hai số tự nhiên là những bài toán quan trọng trong Lập trình.

    Kiểm tra tính nguyên tố là bài toán kiểm tra xem một số tự nhiên n có phải là số nguyên tố hay không. Bài toán này đặc biệt trở nên quan trọng khi các hệ mật mã khoá công khai ra đời.

    1. Số nguyên tố là gì?

    Số nguyên tố (prime) là số tự nhiên lớn hơn 1, chỉ có hai ước số là 1 và chính nó. Theo định nghĩa này thì các số 2, 3, 5, 7, 11,… là các số nguyên tố, trong đó số 2 là số nguyên tố chẵn duy nhất.

    số nguyên tố là gì

    Ví dụ: 7 là số nguyên tố vì trong khoảng từ 2 đến 6 không tồn tại số nào mà 7 chia hết cả.

    2. Các Thuật toán kiểm tra Số Nguyên Tố Đơn Giản

    Phương pháp đơn giản nhất để kiểm tra một số n có là số nguyên tố không là kiểm tra xem nó có chia hết cho các số m nằm trong khoảng 2 đến n-1 hay không.

    Nếu n chia hết cho một trong các số m nào đó thì n không là số nguyên tố (còn được gọi là hợp số composite). Ngược lại, nếu n không chia hết cho bất kì số m nào thì kết lianaj n là số nguyên tố.

    Thực ra việc kiểm tra với m từ 2 đến n-1 là không cần thiết, mà chỉ cần kiểm tra đến $\sqrt{n}$ là đủ. Vì nếu n là hợp số thì nó chắc chắn có ước số không vượt quá sqrt(n).

    Lặp từng phần tử với bước nhảy 1 đến n-1

    Giả sử cần kiểm tra số n có phải là số nguyên tố hay không thì các bước thực hiện như sau:

    • Bước 1: Nhập vào n
    • Bước 2: Kiểm tra nếu n < 2 thì kết luận n không phải là số nguyên tố
    • Bước 3: Lặp từ 2 tới (n-1), nếu trong khoảng này tồn tại số mà n chia hết thì kết luận n không phải là số nguyên tố, ngược lại n là số nguyên tố.

    Độ phức tạp của thuật toán trên là $O(n)$.

    Lặp từng phần tử với bước nhảy 2

    Theo định nghĩa thì số 2 là số nguyên tố chẵn duy nhất, vì vậy ta sẽ loại 2 ra khỏi vòng lặp và trong thân vòng lặp chỉ kiểm tra các số lẻ mà thôi, cách này sẽ tối ưu hơn cách 1 rất nhiều.

    • Bước 1: Nhập vào n;
    • Bước 2: Kiểm tra nếu n < 2 thì kết luận n không phải là số nguyên tố;
    • Bước 3: Kiểm tra nếu n = 2 thì kết luận n là số nguyên tố;
    • Bước 4: Kiểm tra nếu n > 2 và chẵn thì kết luận n không phải là số nguyên tố;
    • Bước 5. Lặp từ 3 tới (n-1), bước nhảy là 2 nếu trong khoảng này tồn tại số mà n chia hết thì kết luận n không phải là số nguyên tố, ngược lại n là số nguyên tố.

    Lặp từng phần tử đến $\sqrt{n}$

    Để tối ưu hơn, thay vì lặp tới n-1, chúng ta chỉ cần lặp các số từ 2 đến sqrt(n), nếu n chia hết cho một trong những số đó thì n không phải là số nguyên tố. Ngược lại thì n là số nguyên tố.

    Độ phức tạp của thuật toán trên là $O(\sqrt{n})$.

    Xem mã nguồn viết bằng ngôn ngữ Dart tại đây https://divin.dev/dart/2021/10/14/bai-tap-dart-17.html

    3. Tối ưu thuật toán kiểm tra số nguyên tố

    Chúng ta có thể tối ưu thuật toán trên bằng cách chỉ ra n không chia hết cho những số nguyên tố nhỏ hơn nó. Tuy nhiên, chúng ta lại chưa biết được các số nguyên tố nhỏ hơn nó là những số nào (Bạn có thể sử dụng phương pháp sàng số nguyên tố – Sàng Eratosthenes để tìm ra các số nguyên tố nhỏ hơn số n cho trước). Nên ta sử dụng kết quả sau đây:

    Tất cả những số nguyên tố lớn hơn 3 đều có dạng 6k ± 1 (vì 6k, 6k ± 2, là những số chẵn; 6k + 3 thì chia hết cho 3).

    Do đó, chúng ta chỉ cần kiểm tra các số có dạng 6k ± 1 từ 2 đến √n, nếu n chia hết cho một trong những số đó thì n không phải là số nguyên tố. Ngược lại thì n là số nguyên tố.

    def is_prime(n: int) -> bool:
    """Primality test using 6k+-1 optimization."""
    if n <= 3:
        return n > 1
    if n % 2 == 0 or n % 3 == 0:
        return False
    i = 5
    while i ** 2 <= n:
        if n % i == 0 or n % (i + 2) == 0:
            return False
        i += 6
    return True

    4. Các Thuật toán kiểm tra Số Nguyên Tố Nâng Cao

    Các cách kiểm tra số nguyên tố kể trên có độ chính xác tuyệt đối nhưng khối lượng tính toán rất lớn. Theo Wiki thì chúng ta còn có những cách khác để kiểm tra tính nguyên tố của một số với một độ chính xác cho trước.

    Kiểm tra theo xác suất

    Các phép kiểm tra tính nguyên tố hay dùng nhất là các thuật toán ngẫu nhiên.

    Giả sử có một mệnh đề Q(p,a) nào đó đúng với mọi số nguyên tố p và một số tự nhiên a <= p. Nếu n là một số tự nhiên lẻ và mệnh đề Q(n,a) đúng với một a<= n được lấy ngẫu nhiên, khi đó a có khả năng là một số nguyên tố.

    Ta đưa ra một thuật toán, kết luận rằng n là số nguyên tố. Nó là một thuật toán ngẫu nhiên hay thuật toán xác suất. Trong các thuật toán loại này, dùng một kiểm tra ngẫu nhiên sẽ không bao giờ kết luận một số nguyên tố là hợp số nhưng lại có thể kết luận một hợp số là số nguyên tố. Do đó, phương pháp này không chính xác một cách tuyệt đối.

    Xác suất sai của phép kiểm tra có thể giảm xuống nhờ việc chọn một dãy độc lập các số a; nếu với mỗi số a xác suất để thuật toán kết luận một hợp số là số nguyên tố là nhỏ hơn một nửa thì sau k lần thử độc lập, xác suất sai là nhỏ hơn 2^k, độ tin cậy của thuật toán sẽ tăng lên theo k.

    Cấu trúc cơ bản của một phép kiểm tra ngẫu nhiên là:

    • Chọn một số ngẫu nhiên a.
    • Kiểm tra một hệ thức nào đó giữa số a và số n đã cho. Nếu hệ thức sai thì chắc chắn n là một hợp số (số a là “bằng chứng” chứng tỏ n là hợp số) và dừng thuật toán.
    • Nếu hệ thức đúng, chúng ta lặp lại hai bước trên cho đến khi đạt được một số lần định trước hoặc gặp trường hợp dừng thuật toán.

    Sau nhiều lần thử, nếu hệ thức đúng với nhiều giá trị của a, ta có thể nói rằng n “có khả năng cao” là số nguyên tố chứ không thể chắc chắn n là số nguyên tố. Tất nhiên là chúng ta sẽ tìm cách tăng “khả năng” này lên bằng cách thực hiện nhiều tính toán hơn.

    Các hệ thức thường sử dụng

    Nếu p là một số nguyên tố thì

    • 2p - 1 ≡ 1 (mod p) (đây là nội dung của định lí Fermat nhỏ)
    • fp + 1 ≡ 0 (mod p) (với fp + 1 là số Fibonacci thứ p + 1 và p có dạng 5k ± 2)
    • (p - 1)! ≡ -1 (mod p) khi và chỉ khi p nguyên tố. Đây là nội dung của định lí Wilson, nhưng việc tính toán biểu thức (n - 1)! % n sẽ có độ phức tạp lớn hơn log n.

    Các phép kiểm tra tính nguyên tố ngẫu nhiên là:

    • Phép kiểm tra tính nguyên tố của Fermat (kiểm tra Fermat). Đây là phép thử heuristic; tuy nhiên ít người sử dung phép thử này.
    • Kiểm tra Miller-Rabin và Kiểm tra Solovay-Strassen. Với mỗi hợp số n, ít nhất 3/4 (với kiểm tra Miller-Rabin) hoặc 1/2 (Với kiểm tra Solovay-Strassen) các số a là bằng chứng chứng tỏ n là hợp số).

    thuật toán kiểm tra số nguyên tố

    Các phép kiểm tra tất định

    Vào năm 2002, Manindra Agrawal, Nitin Saxena và Neeraj Kayal đề xuất một giải thuật tất định kiểm tra tính nguyên tố, là kiểm tra AKS, có khả năng chạy trong O((log n)12). Trên thực tế thuật toán này chạy chậm hơn các phương pháp xác suất.

    Các phương pháp này, mời bạn đọc tham khảo thêm tại https://en.wikipedia.org/wiki/Primality_test

     

  • 100 đề Toán Tin (Tin học & Nhà trường)

    100 đề Toán Tin (Tin học & Nhà trường)

    100 đề Toán Tin (Tin học & Nhà trường)

    O2 Education xin gửi tới bạn đọc TUYỂN TẬP 100 ĐỀ TOÁN TIN (100 đề Toán Tin được trích từ tạp chí Tin học & Nhà trường). Bản PDF và Word, mời các bạn tải ở cuối bài viết

    Phần 1: ĐỀ BÀI 100 đề Toán Tin (Tin học & Nhà trường)

    Bài 1/1999 – Trò chơi cùng nhau qua cầu

    (Dành cho học sinh Tiểu học)

    Bốn người cần đi qua một chiếc cầu. Do cầu yếu nên mỗi lần đi không quá hai người, và vì trời tối nên phải cầm đèn mới đi được. Bốn người đi nhanh chậm khác nhau, qua cầu với thời gian tương ứng là 10 phút, 5 phút, 2 phút và 1 phút. Vì chỉ có một chiếc đèn nên mỗi lần qua cầu phải có người mang đèn trở về cho những người kế tiếp. Khi hai người đi cùng nhau thì qua cầu với thời gian của người đi chậm hơn. Ví dụ sau đây là một cách đi:

    • Người 10 phút đi với người 5 phút qua cầu, mất 10 phút.
    • Người 5 phút cầm đèn quay về, mất 5 phút.
    • Người 5 phút đi với người 2 phút qua cầu, mất 5 phút.
    • Người 2 phút cầm đèn quay về, mất 2 phút.
    • Người 2 phút đi với người 1 phút qua cầu, mất 2 phút.

    Thời gian tổng cộng là 10+5+5+2+2 = 24 phút.

    Em hãy tìm cách đi khác với tổng thời gian càng ít càng tốt, và nếu dưới 19 phút thì thật tuyệt vời!

    Bài 2/1999 – Tổ chức tham quan

    (Dành cho học sinh THCS)

    Trong đợt tổ chức đi tham quan danh lam thắng cảnh của thành phố Hồ Chí Minh, Ban tổ chức hội thi Tin học trẻ tổ chức cho $N$ đoàn (đánh từ số $1$ đến $N$) mỗi đoàn đi thăm quan một địa điểm khác nhau. Đoàn thứ $i$ đi thăm địa điểm ở cách Khách sạn Hoàng Đế $d_i$ km ($i=1,2,…,N$). Hội thi có $M$ xe taxi đánh số từ $1$ đến $M$ ($M\geqslant N$) để phục vụ việc đưa các đoàn đi thăm quan. Xe thứ $j$ có mức tiêu thụ xăng là $v_j$ đơn vị thể tích/km.

    Yêu cầu: Hãy chọn $N$ xe để phục vụ việc đưa các đoàn đi thăm quan, mỗi xe chỉ phục vụ một đoàn, sao cho tổng chi phí xăng cần sử dụng là ít nhất.

    Dữ liệu: File văn bản P2.INP:

    • Dòng đầu tiên chứa hai số nguyên dương $N$, $M$ ($N \leqslant M\leqslant 200$)
    • Dòng thứ hai chứa các số nguyên dương $d_1, d_2, …, d_N$
    • Dòng thứ ba chứa các số nguyên dương $v_1, v_2, …, V_M$
    • Các số trên cùng một dòng được ghi khác nhau bởi dấu trắng

    Kết quả: Ghi ra file văn bản P2.OUT:

    • Dòng đầu tiên chứa tổng lượng xăng dầu cần dùng cho việc đưa các đoàn đi thăm quan (không tính lượt về);
    • Dòng thứ i trong số $N$ dòng tiếp theo ghi chỉ số xe phục vụ đoàn $i$ ($i=1, 2, …, N$).

    Ví dụ:

    P2.INP

    P2.OUT

    3 4

    7 5 9

    17 13 15 10

    256

    2

    3

    4

    Bài 3/1999 – Mạng tế bào

    (Dành cho học sinh THPT)

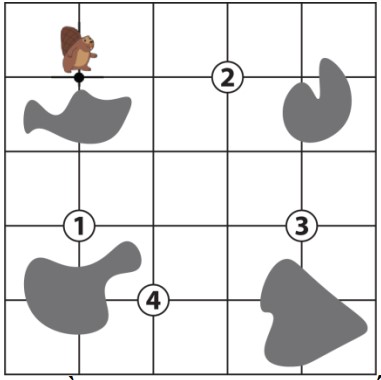
    Mạng tế bào có dạng một lưới ô vuông hình chữ nhật. Tại mỗi nhịp thời gian: mỗi ô của lưới chứa tín hiệu là 0 hoặc 1 và có thể truyền tín hiệu trong nó cho một số ô kề cạnh theo một qui luật cho trước. Ô ở góc trên bên trái có thể nhận tín hiệu từ bên ngoài đưa vào. Sau nhịp thời gian đó, tín hiệu ở một ô sẽ là 0 nếu tất cả các tín hiệu truyền đến nó là 0, còn trong trường hợp ngược lại tín hiệu trong nó sẽ là 1. Một ô không nhận được tín hiệu nào từ các ô kề cạnh với nó sẽ giữ nguyên tín hiệu đang có trong nó. Riêng đối với ô trên trái, sau khi truyền tín hiệu chứa trong nó đi, nếu có tín hiệu vào thì ô trên trái sẽ chỉ nhận tín hiệu này, còn nếu không có tín hiệu nào thì ô trên trái cũng hoạt động giống như các ô khác. ở trạng thái đầu tín hiệu trong tất cả các ô là 0.

    Yêu cầu: Cho trước số nhịp thời gian $T$ và dãy tín hiệu vào $S$ là một dãy gồm T ký hiệu $S_1$,…, $S_T$, trong đó $S_i$ là 0 hoặc 1 thể hiện có tín hiệu vào, ngược lại $S_i$ là $X$ thể hiện không có tín hiệu vào tại nhịp thời gian thứ $i$ ($1 \leqslant i \leqslant T$), hãy xác định trạng thái của lưới sau nhịp thời gian thứ $T$.

    Dữ liệu: vào từ file văn bản P3.INP:

    • Dòng đầu tiên chứa 3 số nguyên $M$, $N$, $T$ theo thứ tự là số dòng, số cột của lưới và số nhịp thời gian ($1<M, N \leqslant 200$; $T \leqslant 100$);
    • Dòng thứ hai chứa xâu tín hiệu vào $S$;
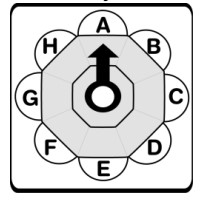
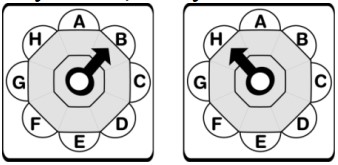
    • $M$ dòng tiếp theo mô tả qui luật truyền tin. Dòng thứ $i$ trong số $M$ dòng này chứa $N$ số $a_{i1}, a_{i2}, …, a_{iN}$, trong đó giá trị của $a_{ij}$ sẽ là 1, 2, 3, 4, 5, 6, 7, 8 tương ứng lần lượt nếu ô $(i, j)$ phải truyền tin cho ô kề cạnh bên trái, bên phải, bên trên, bên dưới, bên trên và bên dưới, bên trái và bên phải, bên trên và bên trái, bên dưới và bên phải (xem hình vẽ); còn nếu ô $(i, j)$ không phải truyền tín hiệu thì $a_{ij}=0$.

    tuyển tập 100 đề toán tin

    Kết quả: Ghi ra file văn bản P3.OUT gồm M dòng, mỗi dòng là một xâu gồm N ký tự 0 hoặc 1 mô tả trạng thái của lưới sau nhịp thời gian thứ T.

    Ví dụ:

    P3.INP

    P3.OUT

    2 2 5

    101XX

    2 4

    2 1

    11

    01

    Quá trình biến đổi trạng thái được diễn tả trong hình dưới đây:

    0

    0

    1

    0

    0

    1

    1

    0

    1

    1

    1

    1

    0

    0

    0

    0

    0

    0

    0

    1

    1

    0

    0

    1

    Bài 4/1999 – Trò chơi bốc sỏi

    (Dành cho học sinh Tiểu học)

    Trên mặt đất có một đống sỏi có 101 viên. Hai em học sinh Hoàng và Huy chơi trò chơi như sau: Mỗi em đến lượt đi phải bốc ra từ đống sỏi trên tối thiểu là 1 viên và tối đa là 4 viên. Người thua là người phải bốc viên sỏi cuối cùng. Giả sử Hoàng là người được bốc trước, Huy bốc sau. Các em thử nghĩ xem ai là người thắng cuộc, Hoàng hay Huy? Và người thắng cuộc phải suy nghĩ gì và thực hiện các bước đi của mình ra sao?

    Bài 5/1999 – 12 viên bi

    (Dành cho học sinh THCS)

    Có 12 hòn bi giống hệt nhau về kích thước, hình dáng và khối lượng. Tuy nhiên trong chúng lại có đúng một hòn bi kém chất lượng: hoặc nhẹ hơn hoặc nặng hơn bình thường. Dùng một cân bàn hai bên, bạn hãy dùng 3 lần cân để tìm ra được viên bi đó. Cần chỉ rõ rằng viên bi đó là nặng hơn hay nhẹ hơn.

    Viết chương trình mô phỏng việc tổ chức cân các hòn bi trên. Dữ liệu về hòn bi kém chất lượng do người sử dụng chương trình nắm giữ. Yêu cầu trình bày chương trình đẹp và mỹ thuật.

    Bài 6/1999 – Giao điểm các đường thẳng

    (Dành cho học sinh THPT)

    Trên mặt phẳng cho trước n đường thẳng. Hãy tính số giao điểm của các đường thẳng này. Yêu cầu tính càng chính xác càng tốt.

    Các đường thẳng trên mặt phẳng được cho bởi 3 số thực A, B, C với phương trình Ax + By + C = 0, ở đây các số A, B không đồng thời bằng 0.

    Dữ liệu vào của bài toán cho trong tệp B6.INP có dạng sau:

    • Dòng đầu tiên ghi số n
    • n dòng tiếp theo, mỗi dòng ghi 3 số thực A, B, C cách nhau bởi dấu cách.
    • Kết quả của bài toán thể hiện trên màn hình.

    Bài 7/1999 – Miền mặt phẳng chia bởi các đường thẳng

    (Dành cho học sinh THPT)

    Xét bài toán tương tự như bài 6/1999 nhưng yêu cầu tính số miền mặt phẳng được chia bởi n đường thẳng này:

    Trên mặt phẳng cho trước n đường thẳng. Hãy tính số miền mặt phẳng được chia bởi các đường thẳng này. Yêu cầu tính càng chính xác càng tốt.

    Các đường thẳng trên mặt phẳng được cho bởi 3 số thực A, B, C với phương trình Ax + By + C = 0, ở đây các số A, B không đồng thời bằng 0.

    Dữ liệu vào của bài toán cho trong tệp B7.INP có dạng sau:

    • Dòng đầu tiên ghi số n
    • n dòng tiếp theo, mỗi dòng ghi 3 số thực A, B, C cách nhau bởi dấu cách.

    Kết quả của bài toán thể hiện trên màn hình.

    Bài 8/1999 – Cân táo

    (Dành cho học sinh Tiểu học)

    Mẹ đi chợ về mua cho Nga 27 quả táo giống hệt nhau về kích thước và khối lượng. Tuy nhiên người bán hàng nói rằng trong số các quả táo trên có đúng một quả có khối lượng nhẹ hơn. Em hãy dùng một chiếc cân bàn hai bên để tìm ra quả táo nhẹ đó. Yêu cầu số lần cân là nhỏ nhất.

    Các em hãy giúp bạn Nga tìm ra quả táo nhẹ đó đi. Nếu các em tìm ra quả táo đó sau ít hơn 5 lần cân thì đã là tốt lắm rồi.

    Bài 9/1999 – Bốc diêm

    (Dành cho học sinh Tiểu học)

    Trên bàn có 3 dãy que diêm, số lượng que diêm của các dãy này lần lượt là 3, 5 và 8. Hai bạn Nga và An chơi trò chơi sau: Mỗi bạn đến lượt mình được quyền (và phải) bốc một số que diêm bất kỳ từ một dãy trên. Người thắng là người bốc được que diêm cuối cùng.

    Ai là người thắng cuộc trong trò chơi trên? Và bạn đó phải bốc diêm như thế nào? Các bạn hãy cùng suy nghĩ với Nga và An nhé.

    Bài 10/1999 – Dãy số nguyên

    (Dành cho học sinh THCS)

    Dãy các số tự nhiên được viết ra thành một dãy vô hạn trên đường thẳng:

    1234567891011121314... (1)

    Hỏi số ở vị trí thứ 1000 trong dãy trên là số nào?

    Em hãy làm bài này theo hai cách: Cách 1 dùng suy luận logic và cách 2 viết chương trình để tính toán và so sánh hai kết quả với nhau.

    Tổng quát bài toán trên: Chương trình yêu cầu nhập số K từ bàn phím và in ra trên màn hình kết quả là số nằm ở vị trì thứ K trong dãy (1) trên. Yêu cầu chương trình chạy càng nhanh càng tốt.

    Bài 11/1999 – Dãy số Fibonaci

    (Dành cho học sinh THCS)

    Như các bạn đã biết dãy số Fibonaci là dãy 1, 1, 2, 3, 5, 8, …. Dãy này cho bởi công thức đệ qui sau:

    F1 = 1, F2 =1, Fn = Fn-1 + Fn-2 với n > 2

    1. Chứng minh khẳng định sau:

    Mọi số tự nhiên N đều có thể biểu diễn duy nhất dưới dạng tổng của một số số trong dãy số Fibonaci.

    N = akFk + ak-1Fk-1 +…+a1F1

    Với biểu diễn như trên ta nói N có biểu diễn Fibonaci là akak-1a2a1

    2. Cho trước số tự nhiên N, hãy tìm biểu diễn Fibonaci của số N.

    Input:

    Tệp văn bản P11.INP bao gồm nhiều dòng. Mỗi dòng ghi một số tự nhiên.

    Output:

    Tệp P11.OUT ghi kết quả của chương trình: trên mỗi dòng ghi lại biểu diễn Fibonaci của các số tự nhiên tương ứng trong tệp P11.INP.

    Bài 12/1999 – N-mino

    (Dành cho học sinh THPT)

    N-mino là hình thu được từ N hình vuông $1\times 1$ ghép lại (cạnh kề cạnh). Hai n-mino được gọi là đồng nhất nếu chúng có thể đặt chồng khít lên nhau.

    Bạn hãy lập chương trình tính và vẽ ra tất cả các N-mino trên màn hình. Số n nhập từ bàn phím.

    Ví dụ: Với N=3 chỉ có hai loại N-mino sau đây:

    100 đề Toán Tin (Tin học & Nhà trường)

    3-mino thẳng    và      3-mino hình thước thợ

    Chú ý: Gọi Mn là số các n-mino khác nhau thì ta có M1=1, M2=1, M3=2, M4=5, M5=12, M6=35,…

    Yêu cầu bài giải đúng và trình bày đẹp.

    Bài 13/1999 – Phân hoạch hình chữ nhật

    (Dành cho học sinh THPT)

    Một hình vuông có thể chia thành nhiều hình chữ nhật có các cạnh song song với cạnh hình vuông (xem Hình vẽ). Xây dựng cấu trúc dữ liệu và lập chương trình mô tả phép chia đó. Tính xem có bao nhiêu cách chia như vậy.

    100 đề Toán Tin (Tin học & Nhà trường) 6

    Input

    Dữ liệu nhập vào từ tệp P13.INP bao gồm hai số tự nhiên là n, m – kích thước hình chữ nhật.

    Output

    Dữ liệu ra nằm trong tệp P13.OUT có dạng sau:

    • Dòng đầu tiên ghi số K là tổng số các phép phân hoạch.
    • Tiếp theo là K nhóm, mỗi nhóm cách nhau bằng một dòng trống.
    • Mỗi nhóm dữ liệu bao gồm các cặp tọa độ của các hình chữ nhật nằm trong phân hoạch.

    Bài 14/2000 – Tìm số trang sách của một quyển sách

    (Dành cho học sinh Tiểu học)

    Để đánh số các trang sách của 1 quyển sách cần tất cả 1392 chữ số. Hỏi quyển sách có tất cả bao nhiêu trang?

    Bài 15/2000 – Hội nghị đội viên

    (Dành cho học sinh Tiểu học)

    Trong một hội nghị liên chi đội có một số bạn nam và nữ. Biết rằng mỗi bạn trai đều quen với N các bạn gái và mỗi bạn gái đều quen với đúng N bạn trai. Hãy lập luận để chứng tỏ rằng trong hội nghị đó số các bạn trai và các bạn gái là như nhau.

    Bài 16/2000 – Chia số

    (Dành cho học sinh THCS)

    Bạn hãy chia N2 số 1, 2, 3, …., N2-1, N2 thành N nhóm sao cho mỗi nhóm có số các số hạng như nhau và có tổng các số này cũng bằng nhau.

    Bài 17/2000 – Số nguyên tố tương đương

    (Dành cho học sinh THCS)

    Hai số tự nhiên được gọi là Nguyên tố tương đương nếu chúng có chung các ước số nguyên tố. Error: Reference source not foundVí dụ các số 75 và 15 là nguyên tố tương đương vì cùng có các ước nguyên tố là 3 và 5. Cho trước hai số tự nhiên N, M. Hãy viết chương trình kiểm tra xem các số này có là nguyên tố tương đương với nhau hay không.

    Bài 18/2000 – Sên bò

    (Dành cho học sinh THCS và THPT)

    Trên lưới ô vuông một con sên xuất phát từ đỉnh (0,0) cần phải đi đến điểm kết thúc tại (N,0) (N là số tự nhiên cho trước).

    Qui tắc đi: Mỗi bước (x1, y1) –> (x2, y2) thoả mãn điều kiện (sên bò):

    • x2 = x1 + 1
    • y1 – 1 <= y2 <= y1 + 1

    Tìm một cách đi sao cho trong quá trình đi nó có thể lên cao nhất trên trục tung (tức là tọa độ y đạt cực đại). Chỉ cần đưa ra một nghiệm.

    Input

    Số N được nhập từ bàn phím.

    Output

    Output ra file P5.OUT có dạng:

    • Dòng đầu tiên ghi 2 số: m, h. Trong đó m là số các bước đi của con sên để đến được vị trí đích, h ghi lại độ cao cực đại đạt được của con sên.
    • m dòng tiếp theo, mỗi dòng ghi ra lần lượt các tọa độ (x,y) là các bước đi của sên trên lưới.

    Yêu cầu kỹ thuật

    Các bạn có thể mô tả các bước đi của con sên trên màn hình đồ họa. Để đạt được mục đích đó số N cần được chọn không vượt quá 50. Mặc dù không yêu cầu nhưng những lời giải có mô phỏng đồ họa sẽ có điểm cao hơn nếu không mô phỏng đồ họa.

    Bài 19/2000 – Đa giác

    (Dành cho học sinh THPT)

    Hãy tìm điều kiện cần và đủ để N số thực dương a1, a2, …, aN tạo thành các cạnh liên tiếp của một đa giác N cạnh trên mặt phẳng. Giả sử cho trước N số a1, a2, …, aN thỏa mãn điều kiện là các cạnh của đa giác, bạn hãy lập chương trình biểu diễn và vẽ đa giác trên.

    Input

    Input của bài toán là tệp P6.INP bao gồm 2 dòng, dòng đầu tiên ghi số N, dòng thứ hai ghi N số thực cách nhau bởi dấu cách.

    Output

    Đầu ra của bài toán thể hiện trên màn hình.

    Chú ý: Phần lý thuyết của bài toán cần được chứng minh một cách chặt chẽ.

    Bài 20/2000 – Bạn Lan ở căn hộ số mấy?

    (Dành cho học sinh Tiểu học)

    Nhà Lan ở trong một ngôi nhà 8 tầng, mỗi tầng có 8 căn hộ. Một hôm, các bạn trong lớp hỏi Lan:

    “Nhà bạn ở căn hộ số mấy?”.

    “Các bạn hãy thử hỏi một số câu, mình sẽ trả lời tất cả câu hỏi của các bạn, nhưng chỉ nói “đúng” hoặc “không” thôi. Qua các câu hỏi đó các bạn thử đoán xem mình ở căn hộ số bao nhiêu”- Lan trả lời.

    Bạn Huy nói:

    “Mình sẽ hỏi, có phải bạn ở căn hộ số 1, số 2,…, số 63 không. Như vậy với nhiều nhất 63 câu hỏi mình sẽ biết được bạn căn hộ nào.”

    Bạn Nam nói:

    “Còn mình chỉ cần đến 14 câu, 7 câu đủ để biết bạn ở tầng mấy và 7 câu có thể biết chính xác bạn ở căn hộ số mấy”.

    Còn em, em phải hỏi nhiều nhất mấy lần để biết được bạn Lan ở căn hộ số bao nhiêu?

    Bài 21/2000 – Những trang sách bị rơi

    (Dành cho học sinh Tiểu học)

    Một cuốn sách bị rơi mất một mảng. Trang bị rơi thứ nhất có số 387, còn trang cuối cũng gồm 3 chữ số 3, 8, 7 nhưng được viết theo một thứ tự khác.

    Hỏi có bao nhiêu trang sách bị rơi ra?

    Bài 22/2000 – Đếm đường đi

    (Dành cho học sinh THCS)

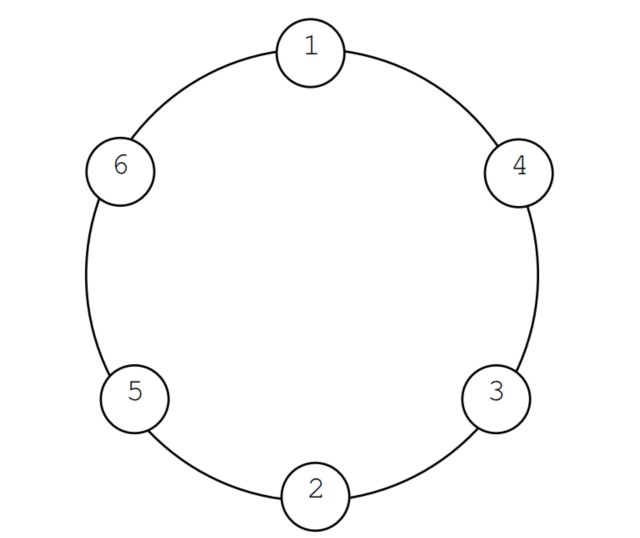
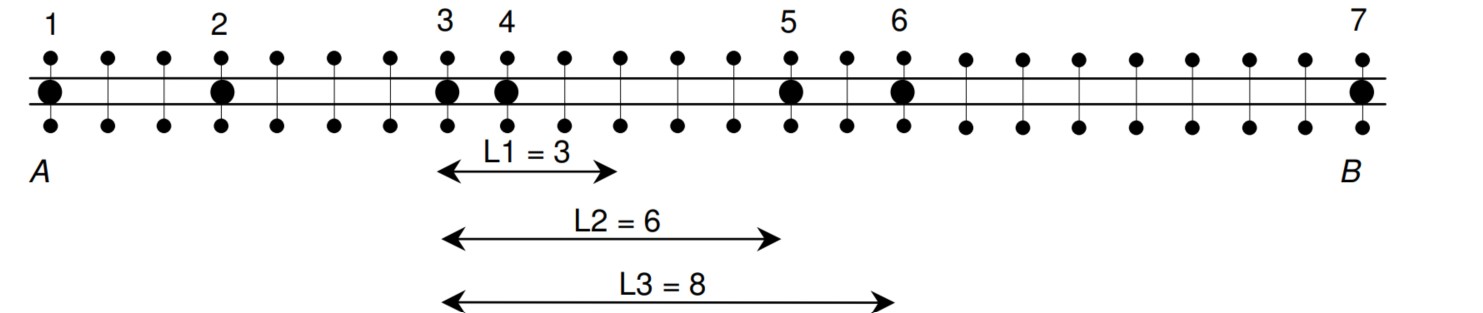
    Cho hình sau:

    a) Bạn hãy đếm tất cả các đường đi từ A đến B. Mỗi đường đi chỉ được đi qua mỗi đỉnh nhiều nhất là 1 lần.

    b) Bạn hãy tìm tất cả các đường đi từ A đến D, sao cho đường đi đó qua mỗi cạnh đúng một lần.

    c) Bạn hãy tìm tất cả các đường đi qua tất cảc các cạnh của hình, mỗi cạnh đúng một lần, sao cho:

    • Điểm bắt đầu và điểm kết thúc trùng nhau.
    • Điểm bắt đầu và điểm kết thúc không trùng nhau

    Bài 23/2000 – Quay Rubic

    (Dành cho học sinh THPT)

    Rubic là một khối lập phương gồm 3´3´3 = 27 khối lập phương con. Mỗi mặt rubic gồm 3´3 = 9 mặt của một lớp 9 khối lập phương con. ở trạng thái ban đầu, mỗi mặt rubic được tô một màu. Các mặt khác nhau được tô các màu khác nhau. Giả sử ta đang nhìn vào một mặt trước của rubic. Có thể kí hiệu màu các mặt như sau: F: màu mặt trước là mặt ta đang nhìn; U: màu mặt trên; R: màu mặt phải; B: màu mặt sau; L: màu mặt bên trái; D: màu mặt dưới.

    Một lớp gồm 3´3 khối lập phương con có thể quay 90 độ nhiều lần, trục quay đi qua tâm và vuông góc với mặt đang xét. Kết quả sau khi quay là khối lập phương 3´3´3 với các màu mặt đã bị đổi khác.

    Một xâu vòng quay liên tiếp rubic có thể mô tả bằng xâu các chữ cái của U, R, F, D, B, L, trong đó mỗi chữ cái là kí hiệu một vòng quay cơ sở: quay mặt tương ứng 90 độ theo chiều kim đồng hồ. Hãy viết chương trình giải 3 bài toán dưới đây:

    1. Cho 2 xâu INPUT khác nhau, kiểm tra xem liệu nếu áp dụng với trạng thái đầu có cho cùng một kết quả hay không?
    2. Cho một xâu vào, hãy xác định số lần cần áp dụng xâu vào đó cho trạng thái đầu rubic để lại nhận được trạng thái đầu đó.

    1. Cho 2 xâu INPUT khác nhau, kiểm tra xem liệu nếu áp dụng với trạng thái đầu có cho cùng một kết quả hay không?

    2. Cho một xâu vào, hãy xác định số lần cần áp dụng xâu vào đó cho trạng thái đầu rubic để lại nhận được trạng thái đầu đó.

    Bài 24/2000 – Sắp xếp dãy số

    (Dành cho học sinh Tiểu học)

    Cho dãy số: 3, 1, 7, 9, 5. Cho phép 3 lần đổi chỗ, mỗi, lần được đổi chỗ hai số bất kỳ. Em hãy sắp xếp lại dãy số trên theo thứ tự tăng dần.

    Bài 25/2000 – Xây dựng số

    (Dành cho học sinh THCS)

    Cho các số sau: 1, 2, 3, 5, 7. Chỉ dùng phép toán cộng hãy dùng dãy trên để tạo ra số: 43, 52.

    Ví dụ để tạo số 130 bạn có thể làm như sau: 123 + 7 = 130.

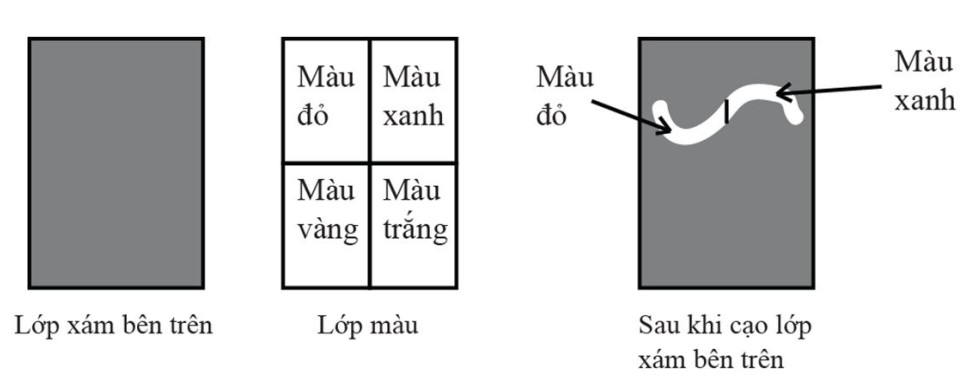
    Bài 26/2000 – Tô màu

    (Dành cho học sinh THCS)

    Cho lưới ô vuông 4×4, cần phải tô màu các ô của lưới. Được phép dùng 3 màu: Xanh, đỏ, vàng. Điều kiện tô màu là ba ô bất kỳ liền nhau theo chiều dọc và ngang phải khác màu nhau. Hỏi có bao nhiêu cách như vậy, hãy liệt kê tất cả các cách.

    Bài 27/2000 – Bàn cờ

    (Dành cho học sinh THPT)

    Cho một bàn cờ vuông 8×8, trên đó cho trước một số quân cờ. Ví dụ hình vẽ sau là một bàn cờ như vậy:

    100 bai toan tin - ban co

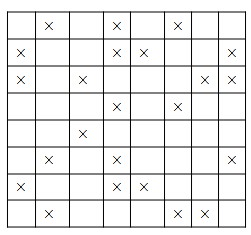
    Dữ liệu nhập được ghi trên tệp BANCO.TXT bao gồm 8 dòng, mỗi dòng là một sâu nhị phân có độ dài bằng 8. Vị trí các quân cờ ứng với số 1, các ô trống ứng với số 0. Ví dụ tệp BANCO.TXT ứng với bàn cờ trên:

    01010100
10011001
10100011
00010100
00100000
01010001
10011000
01000110

    Hãy viết chương trình tính số quân cờ liên tục lớn nhất nằm trên một đường thẳng trên bàn cờ. Đường thẳng ở đây có thể là đường thẳng đứng. đường nằm ngang hoặc đường chéo. Kết quả thể hiện trên màn hình.

    Với ví dụ nêu trên, chương trình phải in trên màn hình kết quả là 4.

    Bài 28/2000 – Đổi tiền

    (Dành cho học sinh Tiểu học)

    Giả sử bạn có nhiều tờ tiền loại 1, 2 và 5 ngàn đồng. Hỏi với các tờ tiền đó bạn có bao nhiêu cách đổi tờ 10 ngàn đồng? Hãy liệt kê các cách đổi.

    Bài 29/2000 – Chọn bạn

    (Dành cho học sinh THCS)

    Trong một trại hè người ta tình cờ chọn ra một nhóm 6 học sinh. Chứng minh rằng sẽ tìm được 3 trong số 6 bạn đó sao cho 3 bạn này hoặc đã quen nhau (đôi một) từ trước hoặc chưa hề quen nhau. Em hãy chỉ ra cách tìm 3 bạn đó.

    Bài 30/2000 – Phần tử yên ngựa

    (Dành cho học sinh THCS)

    Cho bảng A kích thước MxN. Phần tử Aij được gọi là phần tử yên ngựa nếu nó là phần tử nhỏ nhất trong hàng của nó đồng thời là phần tử lớn nhất trong cột của nó. Ví dụ trong bảng số sau đây:

    15 3 9
55 4 6
76 1 2

    thì phần tử A22 chính là phần tử yên ngựa.

    Bạn hãy lập chương trình nhập từ bàn phím một bảng số kích thước MxN và kiểm tra xem nó có phần tử yên ngựa hay không?

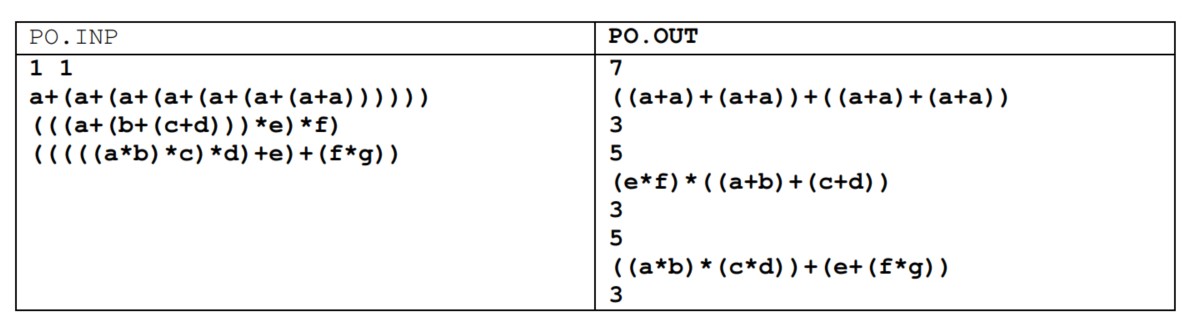
    Bài 31/2000 – Biểu diễn phân số

    (Dành cho học sinh PTTH)

    Một phân số luôn luôn có thể được viết dưới số thập phân hữu hạn hoặc vô hạn tuần hoàn. Ví dụ:

    23/5 = 4.6

    3/8 = 0.375

    1/3 = 0.(3)

    45/56 = 0.803(571428)

    ….

    Trong các ví dụ trên thì các chữ số đặt trong dấu ngoặc chỉ phần tuần hoàn của số thập phân.

    Nhiệm vụ của bạn là viết một chương trình nhập tử số (N) và nhập mẫu số (D), sau đó đưa ra kết quả là dạng thập phân của phân số N/D.

    Ví dụ chạy chương trình:

    Nhap N, D:1 7

    1/7 = 0.(142857)_

    Bài 32/2000 – Bài toán 8 hậu

    (Dành cho học sinh Tiểu học)

    Trên bàn cờ vua hãy sẵp xếp đúng 8 quân Hậu sao cho không còn con nào có thể ăn được con nào. Hãy tìm ra nhiều cách sắp nhất?

    Bài 33/2000 – Mã hoá văn bản

    (Dành cho học sinh THCS)

    Bài toán sau mô tả một thuật toán mã hoá đơn giản (để tiện ta lấy ví dụ tiếng Anh, các bạn có thể mở rộng cho tiếng Việt):

    Tập hợp các chữ cái tiếng Anh bao gồm 26 chữ cái được đánh sô thứ tự từ 0 đến 25 như sau:

    0

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    a

    b

    c

    d

    e

    f

    g

    h

    i

    j

    k

    l

    m

    n

    o

    p

    q

    r

    s

    t

    u

    v

    w

    x

    y

    Z

    Quy tắc mã hoá một ký tự như sau (lấy ví dụ ký tự X):

    – Tìm số thứ tự tương ứng của ký tự ta được 23

    – Tăng giá trị số này lên 5 ta được 28

    – Tìm số dư trong phép chia số này cho 26 ta được 2

    – Tra ngược bảng chữ cái ta thu được C.

    a. Sử dụng quy tắc trên để mã hoá các dòng chữ sau:

    PEACE

    HEAL THE WORLD

    I LOVE SPRING

    b. Hãy tìm ra quy tắc giải mã các dòng chữ sau:

    N FR F XYZIJSY

    NSKTVRFYNHX

    MFSTN SFYNTSFQ ZSNBJVXNYD

    Bài 34/2000 – Mã hoá và giải mã

    (Dành cho học sinh THCS)

    Theo quy tắc mã hoá ở bài trên (33/2000), hãy viết chương trình cho phép:

    – Nhập một xâu ký tự và in ra xâu ký tự đã được mã hóa

    – Nhập một xâu ký tự đã được mã hoá và in ra sâu ký tự đã được giải mã.

    Ví dụ khi chạy chương trình:

    Nhap xau ky tu:

    PEACE

    Xau ky tu tren duoc ma hoa la:

    UJFHJ

    Nhap xau ky tu can giai ma:

    FR

    Xau ky tu tren duoc giai ma la:

    AM_

    Bài 35/2000 – Các phân số được sắp xếp

    (Dành cho học sinh THPT)

    Xét tập F(N) tất cả các số hữu tỷ trong đoạn [0,1] với mẫu số không vượt quá N.

    Ví dụ tập F(5):

    0/1 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1/1

    Hãy viết chương trình cho phép nhập số nguyên N nằm trong khoẳng từ 1 đến 100 và xuất ra theo thứ tự tăng dần các phân số trong tập F(N) cùng số lượng các phân số đó.

    Ví dụ khi chạy chương trình:

    Nhap so N: 5

    0/1 1/5 1/4 1/3 2/5 1/2 3/5 2/3 3/4 4/5 1/1

    Tat ca co 11 phan so_

    Bài 36/2000 – Anh chàng hà tiện

    (Dành cho học sinh Tiểu học)

    Một chàng hà tiện ra hiệu may quần áo. Người chủ hiệu biết tính khách nên nói với anh ta: “Tôi tính tiền công theo 2 cách: cách thứ nhất là lấy đúng 11700 đồng. Cách thứ hai là lấy theo tiền cúc: chiếc cúc thứ nhất tôi lấy 1 đồng, chiếc cúc thứ 2 tôi lấy 2 đồng gấp đôi chiếc thứ nhất, chiếc cúc thứ 3 tôi lấy 4 đống gấp đôi lần chiếc cúc thứ 2 và cứ tiếp tục như thế cho đến hết. áo của anh có 18 chiếc cúc. Nếu anh thấy cách thứ nhất là đắt thì anh có thể trả tôi theo cách thứ hai.”

    Sau một hồi suy nghĩ chàng hà tiện quyết định chọn theo cách thứ hai. Hỏi anh ta phải trả bao nhiêu tiền và anh ta có bị “hố” hay không?

    Bài 37/2000 – Số siêu nguyên tố

    (Dành cho học sinh THCS)

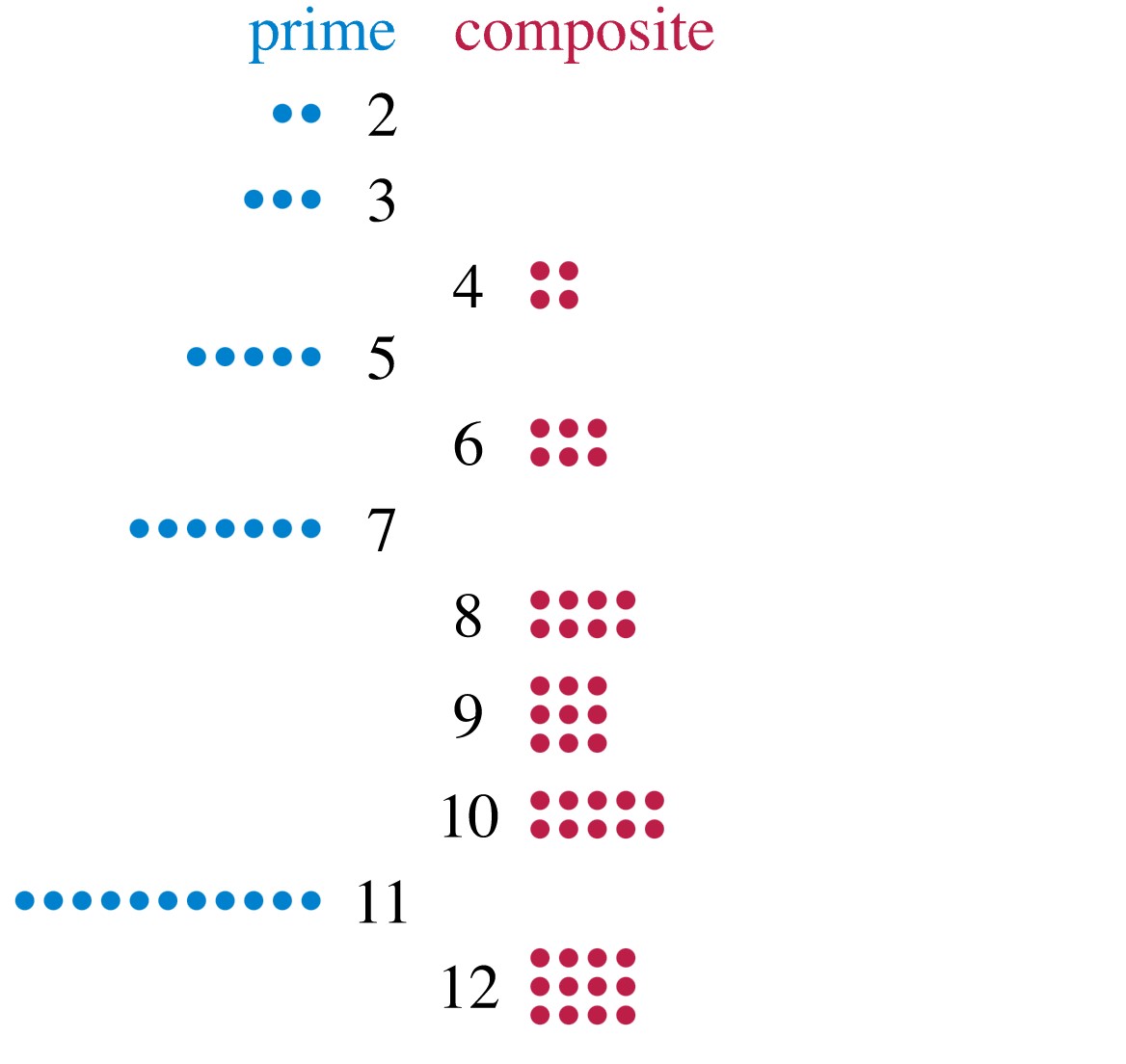
    Số siêu nguyên tố là số nguyên tố mà khi bỏ một số tuỳ ý các chữ số bên phải của nó thì phần còn lại vẫn tạo thành một số nguyên tố.

    Ví dụ 7331 là một số siêu nguyên tố có 4 chữ số vì 733, 73, 7 cũng là các số nguyên tố.

    Nhiệm vụ của bạn là viết chương trình nhập dữ liệu vào là một số nguyên N (0< N <10) và đưa ra kết quả là một số siêu nguyên tố có N chữ số cùng số lượng của chúng.

    Ví dụ khi chạy chương trình:

    Nhap so N: 4

    Cac so sieu nguyen to có 4 chu so la: 2333 2339 2393 2399 2939 3119 3137 3733 3739 3793 3797 5939 7193 7331 7333 7393

    Tat ca co 16 so_

    Bài 38/2000 – Tam giác số

    (Dành cho học sinh THPT)

    Hình sau mô tả một tam giác số có số hàng N=5:

    7

    3

    8

    8

    1

    0

    2

    7

    4

    4

    4

    5

    2

    6

    5

    Đi từ đỉnh (số 7) đến đáy tam giác bằng một đường gấp khúc, mỗi bước chỉ được đi từ số ở hàng trên xuống một trong hai số đứng kề bên phải hay bên trái ở hàng dưới, và cộng các số trên đường đi lại ta được một tổng.

    Ví dụ: đường đi 7 8 1 4 6 có tổng là S=26, đường đi 7 3 1 7 5 có tổng là S=23

    Trong hình trên, tổng Smax=30 theo đường đi 7 3 8 7 5 là tổng lớn nhất trong tất cả các tổng.

    Nhiệm vụ của bạn và viết chương trình nhận dữ liệu vào là một tam giác số chứa trong text file INPUT.TXT và đưa ra kết quả là giá trị của tổng Smax trên màn hình.

    File INPUT.TXT có dạng như sau:

    Dòng thứ 1: có duy nhất 1 số N là số hàng của tam giác số (0<N<100).

    N dòng tiếp theo, từ dòng thứ 2 đến dòng thứ N+1: dòng thứ i có (i-1) số cách nhau bởi dấu trống (space).

    Ví dụ: với nội dung của file INPUT.TXT là

    5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

    thì kết quả chạy chương trình sẽ là: Smax=30.

    Bài 39/2000 – Ô chữ

    (Dành cho học sinh THCS và THPT)

    Trò chơi ô chữ thông dụng 30 năm trước của trẻ em gồm một khung ô chữ kích thước 5×5 chứa 24 hình vương nhỏ kích thước như nhau. Trên mặt mỗi hình vuông nhỏ có in một chữ cái trong bảng chữ cái. Vì chỉ có 24 hình vuông trong ô chữ nên trong ô chữ còn thừa ra một ô trống, có kích thước đúng bằng kích thước các hình vuông. Một hình vuông có thể đẩy trượt vào ô trống đó nếu nó nằm ngay sát bên trái, bên phải, bên trên hay bên dưới ô trống. Mục tiêu của trò chơi là trượt các hình vuông vào ô trống sao cho cuối cùng các chữ cái trong ô chữ được xếp theo đúng thứ tự của chúng trong bảng chữ cái. Hình sau đây minh hoạ một ô chữ với cấu hình ban đầu và cấu hình của nó sau 6 nước đi sau:

    1.Trượt hình vuông phía trên ô trống.

    2.Trượt hình vuông bên phải ô trống.

    3.Trượt hình vuông bên phải ô trống.

    4.Trượt hình vuông phía dưới ô trống.

    5.Trượt hình vuông phía dưới ô trống.

    6.Trượt hình vuông bên trái ô trống.

    100 đề Toán Tin (Tin học & Nhà trường) 7

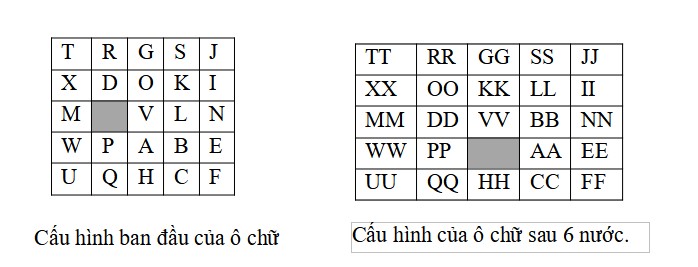
    Bạn hãy viết một chương trình của bạn chứa cấu hình ban đầu của ô chữ cùng các nước đi để vẽ ra ô chữ kết quả.

    Input

    Đầu vào của chương trình của bạn chứa cấu hình ban đầu của một ô chữ và một dẫy các nước đi trong ô chữ đó.

    Năm dòng đầu tiên mô tả cấu hình ban đầu của ô chữ, mỗi dòng tương ứng với một hàng của ô chữ và chứa đúng 5 ký tự tương ứng với 5 hình vuông của ô chữ trên hàng đó. Ô trống được diễn tả bằng một dấu cách.

    Các dòng tiếp theo sau là dẫy các nước đi. Dãy các nước đi được ghi bằng dãy các chữ A,B,R và L để thể hiện hình vuông nào được trượt vào ô trống. A thể hiện hình vuông phía trên ô trống được trượt vào ô trống, tương ứng: B-phía dưới, R-bên phải, L-bên trái. Có thể có những nước đi không hợp cách, ngay cả khi nó được biểu thị bằng những chữ cái trên. Nếu xuất hiện một nước đi không hợp cách thì ô chữ coi như không có cấu hình kết quả. Dãy các nước đi có thể chiếm một số dòng, nhưng nó sẽ được xem là kết thúc ngay khi gặp một số 0.

    Out put

    Nếu ô chữ không có cấu hình kết quả thì thông báo ‘This puzzle has no final configuration.’; ngược lại thì hiển thị cấu hình ô chữ kết quả. Định dạng mỗi dòng kết quả bằng cách đặt một dấu cách vào giữa hai kí tự kế tiếp nhau. Ô trống cũng được sử lý như vậy. Ví dụ nếu ô trống nằm bên trong hàng thì nó được xuất hiện dưới dạng 3 dấu cách: một để ngăn cách nó với kí tự bên trái, một để thể hiện chính ô trống đó, còn một để ngăn cách nó với kí tự bên phải.

    Chú ý: Input mẫu đầu tiên tương ứng với ô chữ được minh hoạ trong ví dụ trên.

    Sample Input 1

    TRGSJ
XDOKI
M VLN
WPABE
UQHCF
ARRBBL0

    Sample Output 1

    T R G S J

    X O K L I

    M D V B N

    W P A E

    U Q H C F

    Sample Input 2

    AB C DE

    F G H I J

    KLMNO

    PQRS

    TUVWX

    AAA

    LLLL0

    Sample Output 2

    A B C D

    F G H I E

    K L M N J

    P Q R S O

    T U V W X

    Sample Input 3

    ABCDE

    FGHIJ

    KLMNO

    PQRS

    TUVWX

    AAAAABBRRRLL0

    Sample Output 3

    This puzzle has no final configuration.

    Bài 40/2000 – Máy định vị Radio

    Một con tàu được trang bị ăng-ten định hướng có thể xác định vị trí hiện thời của mình nhờ các lần đọc đèn hiệu địa phương. Mỗi đèn hiệu được đặt ở một vị trí đã biết và phát ra một tín hiệu đơn nhất. Mỗi khi bắt được tín hiệu, tàu liền quay ăng-ten của mình cho đến khi đạt được tín hiệu cực đại. Điều đó cho phép xác định được phương vị tương đối của đèn hiệu. Cho biết dữ liệu của lần đọc trước (thời gian, phương vị tương đối, vị trí của đèn), một lần đọc mới đủ để xác định vị trí hiện thời của tàu. Bạn phải viết một chương trình xác định vị trí hiện thời của tàu từ hai lần đọc đèn hiệu.

    Vị trí của các đèn hiệu và các con tàu được cho trong hệ toạ độ vuông góc, trục Ox hướng về phía đông, còn Oy hướng về phía bắc. Hướng đi của con tàu được đo bằng độ, theo chiều kim đồng hồ tính từ hướng bắc. Như vậy, hướng bắc sẽ là 00, hướng đông là 900, hướng nam là 1800 và hướng tây là 2700. Phương vị tương đối của đèn hiệu cũng được đo bằng độ, tương đối với hướng đi của tàu và theo chiều kim đồng hồ. ăng ten không thể chỉ ra đèn hiệu nằm ở hướng nào trên phương vị. Như vậy, một phương vị 900 có nghĩa là đèn hiệu có thể nằm ở hướng 900 hoặc 2700.

    Input

    Dòng đầu tiên của input là một số nguyên chỉ số lượng các đèn hiệu (nhiều nhất là 30). Mỗi dòng tiếp theo cho một đèn hiệu. Mỗi dòng bắt đầu bằng tên đèn (là một chuỗi kí tự không vượt quá 20 kí tự), sau đó là vị trí của đèn cho bằng hoành độ và tung độ. Các trường này phân cách bởi một dấu cách.

    Dòng tiếp theo ngay sau các dữ liệu về đèn hiệu là một số nguyên chỉ số lượng các kịch bản đường đi của tàu. Mỗi kịch bản chứa 3 dòng gồm một dòng cho biết hướng đi của tàu so với hướng Bắc và vận tốc vận tốc thực của tàu, và hai dòng chỉ hai lần đọc đèn hiệu. Thời gian được đo bằng phút, tính từ lúc nửa đêm trong vòng 24 giờ. Vận tốc đo bằng đơn vị độ dài (như các đơn vị của hệ trục toạ độ) trên đơn vị thời gian. Dòng thứ hai của kịch bản là lần đọc thứ nhất gồm thời gian (là một số nguyên), tên đèn và góc phương vị tương đối với hướng đi của tàu. Ba trường được ngăn cách nhau bởi một dấu cách. Dòng thứ ba của kịch bản là lần đọc thứ hai. Thời gian của lần đọc này luôn lớn hơn lần đọc thứ nhất.

    Output

    Với mỗi kịch bản, chương trình của bạn phải chỉ ra được số thứ tự của kịch bản (Scenario 1, Scenario 2,…), và một thông báo về vị trí của con tàu (được làm tròn đến hai chữ số thập phân) tại thời điểm của lần đọc thứ hai. Nếu vị trí của tàu không thể xác định thì thông báo: ”Position cannot be determined.”

    Mẫu input và output chính xác tương ứng được cho như sau:

    Sample Input

    4

    First 2.0 4.0

    Second 6.0 2.0

    Third 6.0 7.0

    Fourth 10.0 5.0

    2

    0.0 1.0

    1 First 270.0

    2 Fourth 90.0

    116.5651 2.2361

    4 Third 126.8699

    5 First 319.3987

    Sample Output

    Scenario 1: Position cannot be determined

    Scenario 2: Position is (6.00, 5.00)

    Bài 41/2000 – Cờ Othello

    (Dành cho học sinh THCS và THPT)

    Cờ Othello là trò chơi cho 2 người trên một bàn cờ kích thước 8×8 ô, dùng những quân tròn một mặt đen, một mặt trắng. Các đấu thủ sẽ được lần lượt đi một quân vào ô còn trống trên bàn cờ. Khi đi một quân, đấu thủ phải lật được ít nhất một quân của đấu thủ kia. Các quân sẽ lật được nếu chúng nằm liên tiếp trên cùng một đường thẳng (ngang, dọc hoặc chéo) mà ở hai đầu của đường đó là hai quân có mầu của đấu thủ đang đi. Khi xong một lượt đi, tất cả các quân đã bị lật đã được đổi sang màu của đấu thủ vừa đi. Trong một lượt đi có thể lật được nhiều hàng.

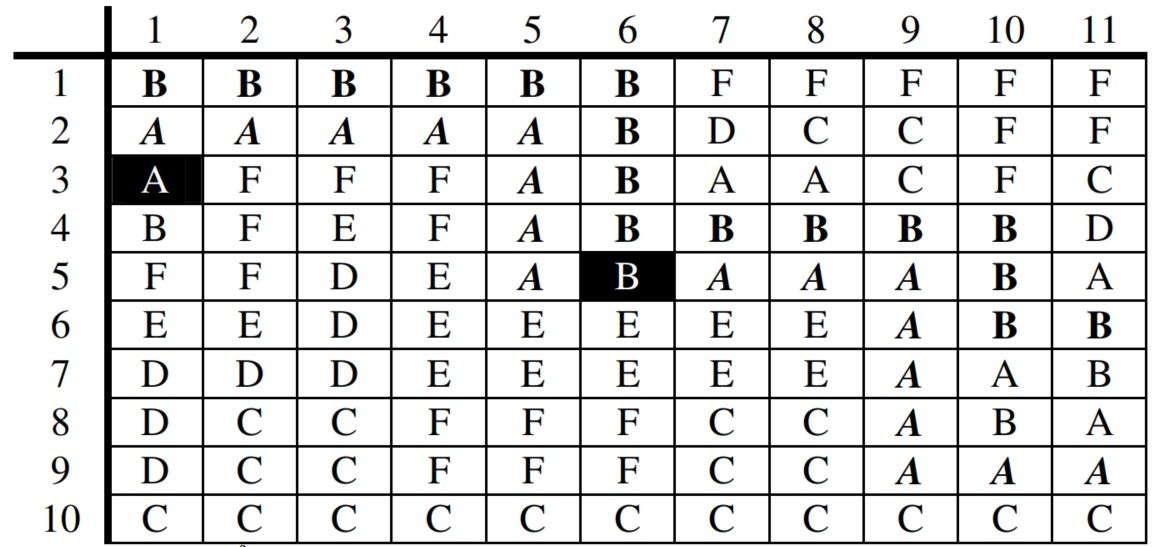
    Ví dụ: Nếu thế cờ hiện thời ở bàn cờ bên trái và lượt đi là của đấu thủ trắng, thì anh ta có thể đi được một trong các nước sau: (3,5) (4,6) (5,3) (6,4). Nếu anh ta đi nước (3,5) thì sau nước đi thế cờ sẽ như ở bàn cờ bên phải.

    Vẽ bàn cờ

    Bạn hãy viết một chương trình để đọc một ván cờ từ một text file có qui cách:

    8 dòng đầu tiên là bàn cờ thế, mỗi dòng chứa 8 kí tự, mỗi kí tự có thể là:

    ‘-‘ thể hiện một ô trống,

    ‘B’ thể hiện một ô có quân đen,

    ‘W’ thể hiện một ô có quân trắng.

    Dòng thứ 9 chứa một trong hai kí tự ‘B’ hoặc ‘W’ để chỉ nước đi thuộc về đấu thủ nào.

    Các dòng tiếp theo là các lệnh. Mỗi lệnh có thể là: liệt kê tất cả các nước đi có thể của đấu thủ hiện thời, thực hiện một nước đi, hay thôi chơi ván cờ đó. Mỗi lệnh ghi trên một dòng theo qui cách sau:

    Liệt kê tất cả các nước đi có thể của đấu thủ hiện thời:

    Lệnh là một chữ ‘L’ ở cột đầu tiên của dòng. Chương trình phải kiểm tra cả bàn cờ và in ra tất cả các nước đi hợp lệ của đấu thủ hiện thời theo dạng (x,y) trong đó x là hàng và y là cột của nước đi. Các nước đi này phải được in theo qui cách:

    + Mọi nước đi trên hàng i sẽ được in trước mỗi nước đi trên hàng j nếu j>i.

    + Nếu trên hàng i có nhiều hơn 1 nước đi thì các nước đi được in theo thứ tự của cột.

    Mọi nước đi hợp lệ phải in trên một dòng. Nếu không có nước đi nào hợp lệ vì đấu thủ hiện thời không thể lật bất cứ một quân nào thì phải in ra thông báo ‘No legal move’.

    Thực hiện một nước đi

    Lệnh là một chữ ‘M’ ở cột đầu tiên của dòng, tiếp theo sau là 2 chữ số ở cột thứ hai và thứ ba của dòng. Các chữ số chỉ ra hàng và cột của ô trống trên bàn cờ nơi đấu thủ hiện thời sẽ đặt quân của mình, trừ phi anh ta không có nước đi hơp lệ nào. Nếu đấu thủ hiện thời không có nước đi hợp lệ nào thì anh ta được thay bởi đấu thủ kia và bây giờ nước đi là của đấu thủ mới. Chương trình phải kiểm tra khi đó nước đi là hợp lệ. Bạn sẽ phải ghi nhận sự thay đổi trên bàn cờ, kể cả việc thêm các quân mới lẫn việc thay đổi màu sắc quân cờ bị lật. Cuối mỗi nước đi hãy in ra số lượng tất cả các quân cờ mỗi màu trên bàn cờ theo qui cách ‘Black – xx White – yy, trong đó xx là số lượng các quân đen còn yy là số lượng các quân trắng. Sau một nước đi, đấu thủ hiện thời được thay bởi đấu thủ kia.

    Thôi chơi ván cờ đó

    Lệnh là một chữ ‘Q’ ở cột đầu tiên của dòng, dòng lệnh này kết thúc Input cho ván cờ đang xét. Chương trình phải in thế cờ cuối cùng của ván cờ theo qui cách được dùng ở input.

    Bạn phải kiểm tra tính chính xác của các lệnh. Không được để dòng trắng ở bất cứ nơi nào trong output.

    Bài 42/2000 – Một chút về tư duy số học

    (Dành cho học sinh Tiểu học)

    Tìm số tự nhiên nhỏ nhất khi chia cho 2, 3, 4, 5, 6, 7, 8, 9, 10 cho phần dư tương ứng là 1, 2, 3, 4, 5, 6, 7, 8, 9.

    Bài 43/2000 – Kim giờ và phút gặp nhau bao nhiêu lần trong ngày

    (Dành cho học sinh Tiểu học)

    Đồng hồ quả lắc có 2 kim: giờ và phút. Tính xem trong vòng 1 ngày đêm (từ 0h – 24h) có bao nhiêu lần 2 kim gặp nhau và đó là những lúc nào.

    Bài 44/2000 – Tạo ma trận số

    (Dành cho học sinh THCS)

    Cho trước số nguyên dương N bất kỳ. Hãy viết thuật toán và chương trình để tạo lập bảng NxN phần tử nguyên dương theo quy luật được cho trong ví dụ sau:

    1 2 3 4 5 6

    2 4 6 8 10 12

    3 6 9 12 2 4

    4 8 12 2 4 6

    5 10 2 4 6 8

    6 12 4 6 8 10

    Thực hiện chương trình đó trên máy với N=12, đưa ra màn hình ma trận kết quả (có dạng như trong ví dụ).

    Bài 45/2000 – Các vòng tròn Olimpic

    (Dành cho học sinh THPT)

    Có 5 vòng tròn Olimpic chia mặt phẳng thành 15 phần (không kể phần vô hạn) (hình vẽ). Hãy đặt vào mỗi phần đó một số sao cho tổng số các số trong mỗi vòng tròn bằng 39.

    Lập chương trình giải quyết bài toán trên và cho biết có bao nhiêu cách xếp như vậy.

    Bài 46/2000 – Đảo chữ cái

    (Dành cho học sinh THCS và THPT)

    Bạn phải viết chương trình đưa ra tất cả các từ có thể có phát sinh từ một tập các chữ cái.

    Ví dụ: Cho từ “abc”, chương trình của bạn phải đưa ra được các từ “abc”, “acb”, “bac”, “bca”, “cab” và “cba” (bằng cách khảo sát tất cả các trường hợp khác nhau của tổ hợp ba chữ cái đã cho).

    Input

    Dữ liệu vào được cho trong tệp input.txt chứa một số từ. Dòng đầu tiên là một số tự nhiên cho biết số từ được cho ở dưới. Mỗi dòng tiếp theo chứa một từ. Trong đó, một từ có thể chứa cả chữ cái thường hoặc hoa từ A đến Z. Các chữ thường và hoa được coi như là khác nhau. Một chữ cái nào đó có thể xuất hiện nhiều hơn một lần.

    Output

    Với mỗi từ đã cho trong file Input.txt, kết quả nhận được ra file Output.txt phải chứa tất cả các từ khác nhau được sinh từ các chữ cái của từ đó. Các từ được sinh ra từ một từ đã cho phải được đưa ra theo thứ tự tăng dần của bảng chữ cái.

    Sample Input

    2

    abc

    acba

    Sample Output

    abc

    acb

    bac

    bca

    cab

    cba

    aabc

    aacb

    abac

    abca

    acab

    acba

    baac

    baca

    bcaa

    caab

    caba

    cbaa

    Bài 47/2000 – Xoá số trên vòng tròn

    (Dành cho học sinh THCS và PTTH)

    Các số từ 1 đến 2000 được xếp theo thứ tự tăng dần trên một đường tròn theo chiều kim đồng hồ. Bắt đầu từ số 1, chuyển động theo chiều kim đồng hồ, cứ bước qua một số lại xoá đi một số. Công việc đó tiếp diễn cho đến khi trên vòng tròn còn lại đúng một số. Lập chương trình tính và in ra số đó.

    Bài 48/2000 – Những chiếc gậy

    (Dành cho học sinh THCS và THPT)

    George có những chiếc gậy với chiều dài như nhau và chặt chúng thành những đoạn có chiều dài ngẫu nhiên cho đến khi tất cả các phần trở thành đều có chiều dài tối đa là 50 đơn vị. Bây giờ anh ta muốn ghép các đoạn lại như ban đầu nhưng lại quên mất nó như thế nào và chiều dài ban đầu của chúng là bao nhiêu. Hãy giúp George thiết kế chương trình để ước tính nhỏ nhất có thể của chiều dài những cái gậy này. Tất cả chiều dài được biểu diễn bằng đơn vị là những số nguyên lớn hơn 0.

    Input

    Dữ liệu vào trong file Input.txt chứa các khối mỗi khối 2 dòng. Dòng đầu tiên chứa số phần của chiếc gậy sau khi cắt. Dòng thứ 2 là chiều dài của các phần này cách nhau bởi một dấu cách. Dòng cuối cùng kết thúc file Input là số 0.

    Output

    Kết quả ra trong file Output.txt chứa chiều dài nhỏ nhất có thể của những cái gậy, mỗi chiếc trong mỗi khối trên một dòng.

    Sample Input

    9

    5 2 1 5 2 1 5 2 1

    4

    1 2 3 4

    0

    Sample Output

    6

    5

    Bài 49/2001 – Một chút nhanh trí

    (Dành cho học sinh Tiểu học)

    Số tự nhiên A có tính chất là khi chia A và lập phương của A cho một số lẻ bất kỳ thì nhận được số dư như nhau. Tìm tất cả các số tự nhiên như vậy.

    Bài 50/2001 – Bài toán đổi màu bi

    (Dành cho học sinh THCS và THPT)

    Trên bàn có N1 hòn bi xanh, N2 hòn bi đỏ và N3 hòn bi vàng. Luật chơi như sau:

    Nếu 2 hòn bi khác màu nhau chạm nhau thì chúng sẽ cùng biến thành màu thứ 3 (ví dụ: xanh, vàng –> đỏ, đỏ).

    Tìm thuật toán và lập chương trình cho biết rằng có thể biến tất cả các hòn bi đó thành một màu đỏ có được không?

    Bài 51/2001 – Thay thế từ

    (Dành cho học sinh THCS và PTTH)

    Hai file INPUT1.TXT và INPUT2.TXT được cho như sau: File INPUT1.TXT chứa một đoạn văn bản bất kì. File INPUT2.TXT chứa không quá 50 dòng, mỗi dòng gồm hai từ: từ đầu là từ đích và từ sau là từ nguồn. Hãy tìm trong file INPUT1.TXT tất cả các từ là từ đích và thay thế chúng bằng các từ nguồn tương ứng. Kết quả ghi vào file KQ.OUT (sẽ là một đoạn văn bản tương tự như trong file INPUT1.TXT nhưng đã được thay thế từ đích bởi từ nguồn).

    Sample INPUT

    • File INPUT1.TXT chứa đoạn văn bản sau:

    Nam moi sap den roi, ban co zui khong?

    Chuc cac ban don mot cai Tet that vui ve va hanh phuc.

    Chuc ban luon hoc gioi!

    • File INPUT2.TXT chứa các dòng sau:
    ban em
zui vui

    Sample OUTPUT

    • File KQ.OUT sẽ chứa đoạn văn bản sau:
    Nam moi sap den roi, em co vui khong?
Chuc cac em don mot cai Tet that vui ve va hanh phuc.
Chuc em luon hoc gioi!

    Bài 52/2001 – Xác định các tứ giác đồng hồ trong ma trận

    (Dành cho học sinh THCS và THPT)

    Cho ma trận vuông A[i,j] (i,j = 1, 2 … n). Các phần tử của A được đánh số từ 1 đến nn.

    Gọi S là số l­ượng các “tứ giác” có bốn đỉnh là: A[i,j]; A[i,j+1]; A[i+1,j]; A[i+1,j+1] sao cho các số ở đỉnh của nó xếp theo thứ tự tăng dần theo chiều kim đồng hồ (tính từ một đỉnh nào đó).

    1) Lập ch­ương trình tính số l­ượng S.

    2) Lập thuật toán xác định A sao cho số S là:

    a. Lớn nhất.

    b. Nhỏ nhất.

    Bài 53/2001 – Lập lịch tháng kỳ ảo

    (Dành cho học sinh THCS và THPT)

    Lịch của các tháng đ­ược biểu diễn bằng một ma trận có số cột bằng 7 và số hàng nhỏ hơn hoặc bằng 6.

    1

    2

    3

    4

    5

    6

    7

    8

    9

    10

    11

    12

    13

    14

    15

    16

    17

    18

    19

    20

    21

    22

    23

    24

    25

    26

    27

    28

    29

    30

    Ví dụ: Trong hình vẽ, lịch này thỏa mãn tính chất sau: Mọi ma trận con 33 không có ô trống đều là ma trận “kỳ ảo” theo nghĩa: Tổng các số của mỗi đ­ường chéo bằng tổng của trung bình cộng của tất cả các cột và hàng. Hãy xây dựng tất cả các lịch tháng có tính chất nh­ư trên. Lập ch­ương trình mô tả tất cả các khả năng xảy ra.

    Bài 54/2001 – Bạn hãy gạch số

    (Dành cho học sinh Tiểu học và THCS)

    Chúng ta viết liên tiếp 10 số nguyên tố đầu tiên theo thứ tự tăng để tạo thành một số có nhiều chữ số. Trong số này hãy gạch đi một nửa số chữ số để số còn lại là:

    a. Nhỏ nhất

    b. Lớn nhất

    Trong từng trường hợp phải nêu cụ thể thuật giải (tại sao lại gạch như vậy)?

    Bài 55/2001 – Bài toán che mắt mèo

    (Dành cho học sinh THCS và THPT)

    Trên bàn cờ ô vuông NxN tại mỗi ô có thể xếp hoặc một con mèo con, hoặc một quân cờ. Hai con mèo trên bàn cờ sẽ nhìn thấy nhau nếu trên đ­ường thẳng nối chúng theo hàng ngang, hàng dọc hay đ­ường chéo không có quân cờ nào cả.

    Hãy tìm cách xếp mèo và quân cờ nh­ư trên sao cho số mèo lớn nhất mà không có hai con mèo nào nhìn thấy nhau?

    Bài 56/2001 – Chia l­ưới

    (Dành cho học sinh THPT)

    Cho l­ưới MN (m, n <= 20) ô vuông, trong mỗi ô cho trước một số tự nhiên. Hãy tìm cách chia lưới trên làm hai phần (chia theo cạnh l­ưới) sao cho trị tuyệt đối hiệu số của tổng các số trong mỗi phần có giá trị nhỏ nhất (như hình dưới đây).

    7

    1

    3

    5

    12

    2

    5

    9

    2

    10

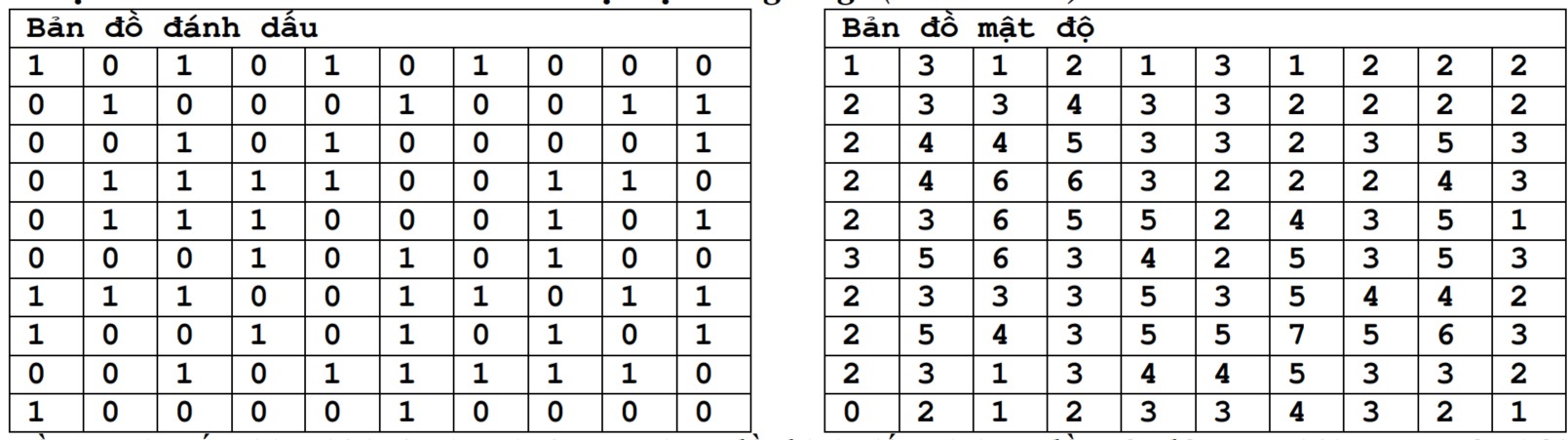
    Dữ liệu được cho trong file LUOI.INP, được cho như sau:

    – Dòng đầu tiên gồm 2 số m, n là kích thước của ô lưới.

    – m dòng tiếp theo, mỗi dòng gồm n số cách nhau bởi dấu cách, ô nào không có giá trị được cho bằng 0.

    Dữ liệu ra trong file LUOI.OUT miêu tả lưới sau khi chia thành hai phần: là một ma trận kích thước mn gồm các số 0 và 1 (số 0 kí hiệu cho các ô tương ứng với phần thứ nhất, và số 1 kí hiệu cho các ô tương ứng với phần thứ hai).

    Sample Input:

    Dữ liệu cho sau đây tương ứng với hình trên:

    5 6

    0 0 0 0 7 0

    0 1 3 5 0 0

    0 12 2 5 0 0

    0 9 2 10 0 0

    0 0 0 0 0 0

    Sample Output:

    0 1 1 1 1 1

    0 1 0 1 1 1

    0 0 0 1 1 1

    0 0 0 1 1 1

    0 0 0 0 0 1

    Bài 57/2001 – Chọn số

    (Dành cho học sinh Tiểu học và THCS )

    Cho 2000 số a1, a2,…, a2000 mỗi số là +1 hoặc -1. Hỏi có thể hay không từ 2000 số đó chọn ra các số nào đó để tổng các số được chọn ra bằng tổng các số còn lại? Giả sử cho 2001 số, liệu có thể có cách chọn không? Nêu cách giải tổng quát.

    Bài 58/2001 – Tổng các số tự nhiên liên tiếp

    (Dành cho học sinh THCS và THPT)

    Cho trước số tự nhiên n. Lập thuật toán cho biết n có thể biểu diễn thành tổng của hai hoặc nhiều số tự nhiên liên tiếp hay không?

    Trong trường hợp có, hãy thể hiện tất cả các cách có thể có.

    Bài 59/2001 – Đếm số ô vuông

    (Dành cho học sinh THCS và THPT)

    Cho một bảng vuông gồm NxN điểm nằm trên các mắt lưới ô vuông. Các điểm kề nhau trên một hàng hay một cột có thể được nối với nhau bằng một đoạn thẳng hoặc không được nối. Các đoạn đó sẽ tạo ra các ô vuông trên bảng. Ví dụ với bảng sau đây thì n = 4 và có 3 ô vuông:

    100 đề Toán Tin (Tin học & Nhà trường) 8

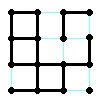
    Trên mỗi hàng có thể có nhiều nhất n-1 đoạn thẳng nằm ngang và có tất cả n hàng như vậy. Tương tự như vậy có tất cả n-1 hàng các đoạn thẳng nằm dọc và trên mỗi hàng có thể có nhiều nhất n đoạn.

    Để mô tả người ta dùng hai mảng nhị phân: một mảng ghi các đoạn nằm ngang kích thước n x (n-1), và một mảng ghi các đoạn nằm dọc kích thước (n-1) xn. Trong mảng, số 1 dùng để mô tả đoạn thẳng nối giữa 2 điểm, còn số 0 miêu tả giữa hai điểm không có đoạn thẳng nối. Trong ví dụ trên thì ma trận “ngang” là:

    và ma trận “dọc” là:

    Cho trước ma trận “ngang” và ma trận “dọc”, dữ liệu nhập từ các tệp văn bản có tên là NGANG.INP và DOC.INP. Hãy lập trình đếm số các ô vuông trên bảng.

    Bài 60/2001 – Tìm số dư của phép chia

    (Dành cho học sinh Tiểu học)

    Một số nguyên khi chia cho 1976 và 1977 đều dư 76. Hỏi số đó khi chia cho 39 dư bao nhiêu?

    Bài 61/2001 – Thuật toán điền số vào ma trận

    (Dành cho học sinh THCS và THPT)

    Hãy lập thuật toán điền các phần tử của ma trận NN các số 0, 1 và -1 sao cho:

    a) Tổng các số của mọi hình vuông con 2×2 đều bằng 0.

    b) Tổng các số của ma trận trên là lớn nhất.

    Bài 62/2001 – Chèn Xâu

    (Dành cho học sinh THCS và THPT)

    Cho một xâu S = ’123456789’ hãy tìm cách chèn vào S các dấu ‘+’ hoặc ‘-‘ để thu được số M cho trước (nếu có thể). Số M nguyên được nhập từ bàn phím. Trong file Output Chenxau.Out ghi tất cả các phương án chèn (nếu có) và ghi “Khong co” nếu như không thể thu được M từ cách làm trên.

    Ví dụ: Nhập M = 8, một trong các phương án đó là: ‘-1+2-3+4+5-6+7’;

    M = -28, một trong các phương án đó là: ‘-1+2-34+5’;

    (Đề ra của bạn: Lê Nhân Tâm – 12 Tin Trường THPT Lam Sơn)

    Bài 63/2001 – Tìm số nhỏ nhất

    (Dành cho học sinh Tiểu học)

    Hãy viết ra số nhỏ nhất bao gồm tất cả các chữ số 0, 1, 2, 3, … 9 mà nó:

    • a. Chia hết cho 9
    • b. Chia hết cho 5
    • c. Chia hết cho 20

    Có giải thích cho từng trường hợp?

    Bài 64/2001 – Đổi ma trận số

    (Dành cho học sinh THCS và THPT)

    Cho mảng số thực vuông A kích thước 2nx2n. Hãy lập các mảng mới bằng cách đổi chỗ các khối vuông kích thước nxn của A theo các cách sau:

    100 đề Toán Tin (Tin học & Nhà trường) 9 100 đề Toán Tin (Tin học & Nhà trường) 10

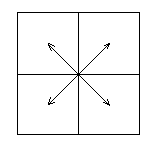
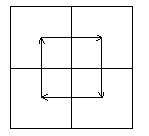
    Bài 65/2001 – Lưới ô vuông vô hạn

    (Dành cho học sinh THCS và THPT)

    Cho lưới ô vuông vô hạn về hai phía (trên và phải). Các ô của lưới được đánh số theo quy tắc sau:

    • Ô trái dưới – vị trí (0,0) – được đánh số 0.
    • Các ô còn lại được đánh số theo nguyên tắc lan toả từ vị trí (0,0) và theo quy tắc: tại một vị trí số được điền vào là số nguyên không âm nhỏ nhất chưa được điền trên hàng và cột chứa ô hiện thời. Ví dụ, ta có hình dạng của một số ô của lưới như sau:

    3

    2

    1

    0

    2

    3

    0

    1

    1

    0

    3

    2

    0

    1

    2

    3

    Cho trước cặp số tự nhiên M, N – kích thước ô lưới. Hãy viết chương trình mô tả lưới trên, kết quả được ghi vào file KQ.TXT.

    Bài 66/2001 – Bảng số 9 x 9

    (Dành cho học sinh Tiểu họcvà THCS)

    Hãy xếp các số 1, 2, 3, …, 81 vào bảng 9 x 9 sao cho:

    a) Trên mỗi hàng các số được xếp theo thứ tự tăng dần (từ trái qua phải).

    b) Tổng các số ở cột 5 là lớn nhất.

    Yêu cầu:

    • Đối với các bạn học sinh khối Tiểu học chỉ cần viết ra bảng số thoả mãn tính chất trên.
    • Các bạn học sinh khối THCS thì phải lập trình hiển thị kết quả ra màn hình.

    Bài 67/2001 – Về các phép biến đổi “Nhân 2 trừ 1”

    (Dành cho học sinh THCS và THPT)

    Cho ma trận A kích thước M x N, Aij – là các số tự nhiên. Các phép biến đổi có thể là:

    • Nhân tất cả các số của một hàng với 2.
    • Trừ tất cả các số của một cột cho 1.

    Tìm thuật toán sao cho sau một số phép biến đổi trên ma trận A trở thành toàn số 0.

    Bài 68/2001 – Hình tròn và bảng vuông

    (Dành cho học sinh THPT)

    Một đường tròn đường kính 2n -1 đơn vị được vẽ giữa bàn cờ 2n2n. Với n = 3 được minh hoạ như dưới đây:

    100 đề Toán Tin (Tin học & Nhà trường) 11

    Viết chương trình xác định số ô vuông của bảng bị cắt bởi hình tròn và số ô vuông nằm hoàn toàn trong hình tròn.

    Dữ liệu vào trong file Input.txt bao gồm: Mỗi dòng là một số nguyên dương không lớn hơn 150 – là các giá trị của n.

    Dữ liệu ra trong file Output.txt: Với mỗi giá trị vào n, kết quả ra phải tính được số ô vuông bị cắt bởi hình tròn và số ô vuông nằm hoàn toàn trong hình tròn, mỗi số trên một dòng. Mỗi kết quả tương ứng với một giá trị n phải cách nhau một dòng.

    Sample Input

    3

    4

    Sample Output

    20

    12

    28

    24

    Bài 69/2001 – Bội của 36

    (Dành cho học sinh Tiểu học)

    Tìm số tự nhiên nhỏ nhất chia hết cho 36 mà trong dạng viết thập phân của nó có chứa tất cả các chữ số từ 1 tới 9.

    Bài 70/2001 – Mã hoá theo khoá

    (Dành cho học sinh THCS và THPT)

    Cho trước khoá là một hoán vị của n số (1, 2, …, n). Khi đó để mã hoá một xâu kí tự ta có thể chia xâu thànhtừng nhóm n kí tự (riêng nếu nhóm cuối cùng không đủ n kí tự thì ta coa thể thêm các dấu cách vào sau cho đủ) rồi hoán vị các kí tự trong từng nhóm. Sau đó, ghép lại theo thứ tự các nhóm ta được một xâu đã mã hoá.

    Chẳng hạn: với khoá 3241 (n=4) thì ta có thể mã hoá xâu ‘english’ thành ‘gnlehs i’.

    Hãy viết chương trình mã hoá một xâu kí tự cho trước.

    Bài 71/2001 – Thực hiện phép nhân

    (Dành cho học sinh THCS và THPT)

    Bạn hãy lập chương trình nhập 2 số nguyên dương a và b. Sau đó thực hiện phép nhân (a x b) như cách nhân bằng tay thông thường. Ví dụ:

    100 đề Toán Tin (Tin học & Nhà trường) 12

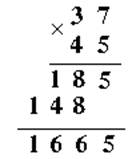
    Bài 72/2001 – Biến đổi trên lưới số

    (Dành cho học sinh THCS và THPT)

    Trên một lưới N x N các ô được đánh số 1 hoặc -1. Lưới trên được biến đổi theo quy tắc sau: một ô nào đó được thay thế bằng tích của các số trong các ô kề nó (kề cạnh). Lập chương trình thực hiện sao cho sau một số bước toàn lưới còn lại chữ số 1.

    Bài 73/2001 – Bài toán chuỗi số

    (Dành cho học sinh Tiểu họcvà THCS)

    Cho một chuỗi số có quy luật. Bạn có thể tìm được hai số cuối của dãy không, thay thế chúng trong dấu hỏi chấm (?). Bài toán không dễ dàng lắm đâu, vì chúng được tạo ra bởi một quy luật rất phức tạp. Bạn thử sức xem?

    5 8 11 14 17 23 27 32 35 41 49 52 ? ?

    Bài 74/2001 – Hai hàng số kỳ ảo

    (Dành cho học sinh THCS và THPT)

    Hãy xếp 2N số tự nhiên 1, 2, …, 2N thành 2 hàng số:

    A1, A2 … An

    B1, B2 … Bn

    Thỏa mãn điều kiện: tổng các số theo n cột bằng nhau, tổng các số theo các hàng bằng nhau.

    Bài 75/2001 – Trò chơi Tích – Tắc vuông

    (Dành cho học sinh THCS và THPT)

    Trên một lưới kẻ ô vuông có 2 người chơi như sau: người thứ nhất mỗi lần chơi sẽ đánh dấu x vào 1 ô trống. Người thứ hai được đánh dấu 0 vào 1 ô trống. Người thứ nhất muốn đạt được mục đích là đánh được 4 dấu x tạo thành 4 đỉnh của 1 hình vuông. Người thứ hai có nhiệm vụ ngăn cản mục đích đó của người thứ nhất.

    Lập chương trình tìm thuật toán tối ưu cho người thứ nhất (người thứ nhất có thể luôn thắng).

    Chú ý: Lưới ô vuông được coi là vô­ hạn về cả hai phía.

    Bài76/2001 – Đoạn thẳng và hình chữ nhật

    (Dành cho học sinh THPT)

    Hãy viết một chương trình xác định xem một đoạn thẳng có cắt hình chữ nhật hay không?

    Ví dụ:

    Cho tọa độ điểm bắt đầu và điểm kết thúc của đường thẳng: (4,9) và (11,2);

    Và tọa độ đỉnh trái trên và đỉnh phải dưới của hình chữ nhật: (1,5) và (7,1);

    100 đề Toán Tin (Tin học & Nhà trường) 13
    Đoạn thẳng không cắt hình chữ nhật

    Đoạn thẳng được gọi là cắt hình chữ nhật nếu đoạn thẳng và hình chữ nhật có ít nhất một điểm chung.

    Chú ý: mặc dù tất cả dữ liệu vào đều là số nguyên, nhưng tọa độ của các giao điểm tính ra chưa chắc là số nguyên.

    Input

    Dữ liệu vào trong file Input.Inp kiểm tra N trường hợp (N <= 1000). Dòng đầu tiên của file dữ liệu vào là số N. Mỗi dòng tiếp theo chứa một trường hợp kiểm tra theo quy cách sau:

    xstart ystart xend yend xleft ytop xright yboottm

    trong đó: (xstart, ystart) là điểm bắt đầu và (xend, yend) là điểm kết thúc của đoạn thẳng. Và (xleft, ytop) là đỉnh trái trên, (xright, ybottom) là đỉnh phải dưới của hình chữ nhật. 8 số này được cách nhau bởi một dấu cách.

    Output

    Với mỗi một trường hợp kiểm tra trong file Input.txt, dữ liệu ra trong file Output.out phải đưa ra một dòng gồm hoặc là chữ cái “T” nếu đoạn thẳng cắt hình chữ nhật, hoặc là “F” nếu đoạn thẳng không cắt hình chữ nhật.

    Ví dụ

    Input.Inp

    1

    4 9 11 2 1 5 7 1

    Output.out

    F

    Bài 77/2001 – Xoá số trên bảng

    (Dành cho học sinh Tiểu học)

    Trên bảng đen cô giáo ghi lên 23 số tự nhiên: 1, 2, 3, …, 23

    Các bạn được phép xoá đi 2 số bất kỳ trên bảng và thay vào đó một số mới là hiệu của chúng.

    1. Hỏi có thể thực hiện sau một số bước trên bảng còn lại toàn số 0 hay không? Nếu được hãy chỉ ra một cách làm cụ thể.
    2. Bài toán còn đúng không nếu thay số 23 bằng 25.

    Bài 78/2001 – Cà rốt và những chú thỏ

    (Dành cho học sinh Tiểu học)

    Các số ở mỗi ô trong hình thoi dưới đây biểu thị số lượng củ cà rốt. Chú thỏ đi từ góc dưới với 14 củ cà rốt và đi lên đỉnh trên với 13 củ cà rốt, chỉ được đi theo đường chéo, đi đến đâu ăn hết tổng số cà rốt trong ô đó. Hỏi rằng chú thỏ có thể ăn được nhiều nhất bao nhiêu củ cà rốt?

    100 đề Toán Tin (Tin học & Nhà trường) 14

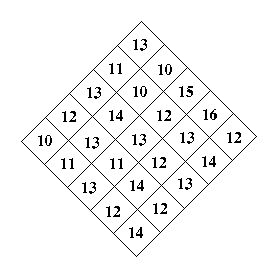
    Bài 79/2001 – Về một ma trận số

    (Dành cho học sinh THCS)

    Mô tả thuật toán, lập chương trình xây dựng ma trận A[10,10] thoả mãn các tính chất:

    • A[i,j] là các số nguyên từ 0..9 (1 <= i, j <= 10),
    • Mỗi số từ 0..9 được gặp 10 lần trong ma trận A,
    • Mỗi hàng và mỗi cột của A chứa không quá 4 số khác nhau.

    Bài 80/2001 – Xếp số 1 trên lưới

    (Dành cho học sinh THCS)

    Hãy xếp 16 số 1 lên ma trận 10×10 sao cho nếu xoá đi bất kỳ 5 hàng và 5 cột thì vẫn còn lại ít nhất là một số 1. Nêu thuật toán và lập trình hiển thị ra màn hình kết quả ma trận thoả mãn tính chất trên.

    Bài 81/2001 – Dãy nghịch thế

    (Dành cho học sinh THPT)

    Cho dãy số (a1, a2, a3, …, an) là một hoán vị bất kỳ của tập hợp (1, 2, 3, …, n). Dãy số (b1, b2, b3, …, bn) gọi là nghịch thế của dãy a nếu bi là các phần tử đứng trước số i trong dãy a mà lớn hơn i.

    Ví dụ:

    Dãy a là: 3 2 5 7 1 4 6

    Dãy b là: 4 1 0 2 0 1 0

    a. Cho dãy a, hãy xây dựng chương trình tìm dãy b.

    b. Cho dãy b, xây dựng chương trình tìm dãy a.

    Dữ liệu vào trong file NGICH.INP với nội dung:

    Dòng đầu tiên là số n (1 <= n <= 10 000).

    Các dòng tiếp theo là n số của dãy a, mỗi số cách nhau một dấu cách,

    Các dòng tiếp theo là n số của dãy b, mỗi số cách nhau bởi một dấu cách.

    Dữ liệu ra trong file NGHICH.OUT với nội dung:

    n số đầu tiên là kết quả của câu a,

    Tiếp đó là một dòng trống và sau đó là n số kết quả của câu b (nếu tìm được dãy a).

    Bài 82/2001 – Gặp gỡ

    (Dành cho học sinh THPT)

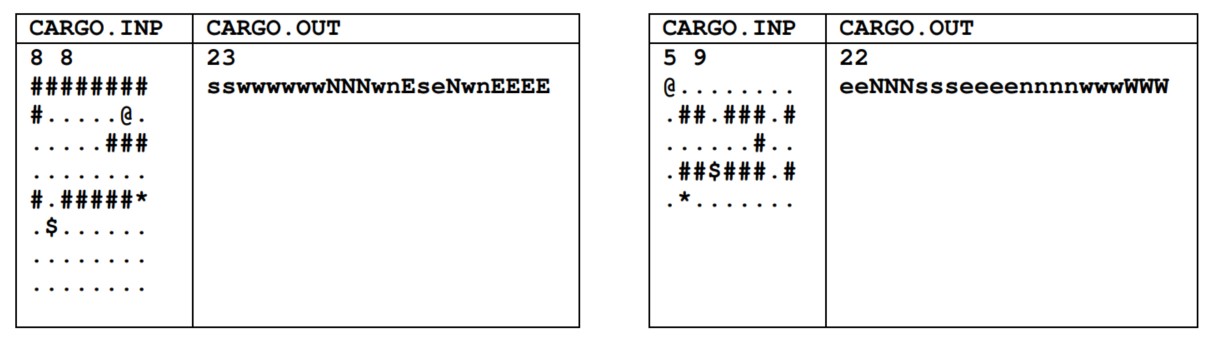
    Trên một lưới ô vuông kích thước MN (M dòng, N cột) người ta đặt k rôbôt. Rôbôt thứ i được đặt ở ô (xi,,yi). Mỗi ô của lưới có thể đặt một vật cản hay không. Tại mỗi bước, mỗi rôbôt chỉ có thể di chuyển theo các hướng lên, xuống, trái, phải – vào các ô kề cạnh không có vật cản. k rôbôt sẽ gặp nhau nếu chúng cùng đứng trong một ô. k rôbôt bắt đầu di chuyển đồng thời và mỗi lượt cả k rôbôt đều phải thực hiện việc di chuyển (nghĩa là không cho phép một rôbôt dừng lại một ô nào đó trong khi rôbôt khác thực hiện bước di chuyển). Bài toán đặt ra là tìm số bước di chuyển ít nhất mà k rôbôt phải thực hiện để có thể gặp nhau. Chú ý rằng, tùy trạng thái của lưới, k rôbôt có thể không khi nào gặp được nhau.

    Dữ liệu vào cho trong file văn bản MEET.INP, bao gồm:

    + Dòng đầu tiên chứa 3 số M,N và k (M,N<=50;k<=10)

    + k dòng sau, dòng thứ i gồm 2 số xi,yi là vị trí của rôbốt thứ i.

    + M dòng tiếp theo, mỗi dòng ghi N số gồm 0 và 1 mô tả trạng thái dòng tương ứng của lưới, trong đó mỗi số mô tả một ô với quy ước: 0 – không có vật cản, 1 – có vật cản.

    Các số trên cùng một dòng của file dữ liệu được ghi cách nhau ít nhất một dấu trắng.

    Dữ liệu ra ghi lên file văn bản MEET.OUT: nếu k rôbôt không thể gặp nhau thì ghi một dòng gồm một ký tự #, trái lại ghi k dòng, mỗi dòng là một dãy các ký tự viết liền nhau mô tả các bước đi của rôbôt: U-lên trên, D-xuống dưới, L-sang trái, R-sang phải.

    Ví dụ:

    MEET.INP

    4 6 2

    1 1

    4 6

    0 1 1 0 0 0

    0 0 0 0 0 1

    0 0 1 0 0 1

    0 1 0 1 0 0

    MEET.OUT

    DRRR

    LUUL

    Bài 83/2001 – Các đường tròn đồng tâm

    (Dành cho học sinh Tiểu học)

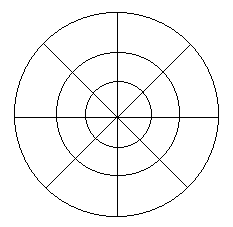
    Ba đường tròn đồng tâm, mỗi hình được chia thành 8 phần (như hình dưới).

    Hãy đặt các số trong danh sách dưới đây vào các phần trong các hình tròn sao cho: mỗi đường tròn gồm 8 số trong tám phần có tổng bằng 80, mỗi phần của hình tròn ngoài gồm 3 số (mỗi phần của hình tròn ngoài chứa cả phần của hai hình tròn trong) có tổng bằng 30.

    Các số bạn được sử dụng là:

    14, 11, 10, 12, 7, 9, 9, 8, 9, 9, 11, 11, 10, 10, 10, 10, 14, 9, 7, 11, 10, 8, 12, 9.

    100 đề Toán Tin (Tin học & Nhà trường) 15

    Bài 84/2001 – Cùng một tích

    (Dành cho học sinh THCS và THPT)

    Cho n số x1, x2, …, xn chỉ nhận một trong các giá trị -1, 0, 1. Và cho một số nguyên P. Hãy tính số lượng tất cả các cách gán giá trị khác nhau của n số trên sao cho: $\sum x_i x_j = P$ (với i =1..n, j =1..n, i $\ne$ j). Hai cách gán được gọi là khác nhau nếu số lượng các số xi­ = 0 là khác nhau.

    Input: gồm 2 số n, P.

    Output: số các cách chọn khác nhau.

    Giới hạn: 2 <= n <= 1010 ; |P| <= 1010.

    (Đề ra của bạn Lý Quốc Vinh – Tp. Hồ Chí Minh)

    Bài 85/2001 – Biến đổi 0 – 1

    (Dành cho học sinh THPT)

    Cho 2 lưới ô vuông A và B cùng kích thước M xN, mỗi ô có chỉ nhận các giá trị 0 hoặc 1 (A khác B). Các ô lưới được đánh số từ trên xuống dưới, từ trái qua phải bắt đầu từ 1. Cho phép thực hiện phép biến đổi sau đây với lưới A:

    – Chọn ô (i, j) và đảo giá trị của ô đó và các ô chung cạnh với nó (0 thành 1, 1 thành 0).

    Hãy xác định xem bằng cách áp dụng dãy biến đổi trên có thể đưa A về B được hay không? Nếu có hãy chỉ ra cách sử dụng một số ít nhất phép biến đổi.

    Dữ liệu nhập vào từ file văn bản BIENDOI.INP:

    • Dòng đầu tiên ghi hai số M, N – kích thước ô lưới (M, N <= 100),
    • M dòng tiếp theo, mỗi dòng một xâu N kí tự 0, 1 ứng với dòng tương ứng của A,
    • Tiếp theo là một dòng trống,
    • M dòng cuối mỗi dòng 1 xâu N kí tự 0, 1 ứng với dòng tương ứng của B.

    Dữ liệu ra trong file BIENDOI.OUT:

    • Dòng đầu số nguyên k là số lượng phép biến đổi ít nhất cần áp dụng (k = 0 nếu không biến đổi được)
    • Dòng thứ i trong số k dòng tiếp theo ghi hai số nguyên xác định ô cần chọn để thực hiện phép biến đổi.

    Ví dụ:

    BIENDOI. INP

    4 5
1 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 1 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 1 0 0
0 0 0 0 0

    BIENDOI.OUT

    2
2 1
3 2

    (Đề ra của bạn Nguyễn Văn Đức – Cần Thơ)

    Bài 86/2001 – Dãy số tự nhiên logic

    (Dành cho học sinh Tiểu học)

    Đây là một chuỗi các số tự nhiên được sắp xếp theo một logic nào đó. Hãy tìm con số đầu tiên và cuối cùng của dãy số để thay thế cho dấu ?

    ? 12 14 15 16 18 20 21 22 ?

    Bài 87/2001 – Ghi số trên bảng

    (Dành cho học sinh THCS)

    Trên bảng ghi số 0. Mỗi lần được tăng số đã viết lên bảng thêm 1 đơn vị hoặc tăng gấp đôi. Hỏi sau ít nhất là bao nhiêu bước sẽ thu được số nguyên dương N?

    Bài 88/2001 – Về các số đặc biệt có 10 chữ số

    (Dành cho học sinh THCS và THPT)

    Lập chương trình tính (và chỉ ra) tất cả các số có 10 chữ số a0a1a2…a9 thoả mãn các tính chất sau:
    a0 bằng số chữ số 0 của số trên;

    a1 bằng số chữ số 1 của số trên;

    a2 bằng số chữ số 2 của số trên;

    …….

    a9 bằng số chữ số 9 của số trên;

    Bài 89/2001 – Chữ số thứ N

    (Dành cho học sinh THCS và THPT)

    Khi viết các số tự nhiên tăng dần từ 1, 2, 3,… liên tiếp nhau, ta nhận được một dãy các chữ số thập phân vô hạn, ví dụ:

    234567891011121314151617181920...

    Yêu cầu: Hãy tìm chữ số thứ N của dãy số vô hạn trên.

    Dữ liệu vào từ file ‘Number.inp’ gồm một số dòng, mỗi dòng ghi một số nguyên dương N (N<109).

    Kết quả ra file ’Number.out’, với mỗi số N đọc được từ file Number.inp, ghi trên dòng tương ứng chữ số thứ N của dãy.

    Ví dụ:

    Number.inp

    Number.out

    5

    10

    54

    5

    1

    3

    Bài 90/2002 – Thay số trong bảng 9 ô

    (Dành cho học sinh Tiểu học)

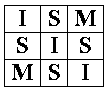
    Cho một bảng vuông gồm 9 ô. Đầu tiên các ô được điền bởi các chữ cái I, S, M. Bạn hãy thay những số thích hợp vào các ô sao cho tổng các số trong các ô điền cùng chữ cái ban đầu là bằng nhau và là một số chia hết cho 4.

    Chú ý: các ô cùng chữ cái phải thay bởi những số như nhau.

    100 đề Toán Tin (Tin học & Nhà trường) 16

    Bài 91/2002 – Các số lặp

    (Dành cho học sinh THCS và THPT)

    Cho dãy số nguyên gồm N phần tử. Lập chương trình in ra số được lặp nhiều nhất trong dãy.

    Bài 92/2002 – Dãy chia hết

    (Dành cho học sinh THPT)

    Xét một dãy gồm N số nguyên tuỳ ý. Giữa các số nguyên đó ta có thể đặt các dấu + hoặc – để thu được các biểu thức số học khác nhau. Ta nói dãy số là chia hết cho K nếu một trong các biểu thức thu được chia hết cho K. Hãy viết chương trình xác định tính chia hết của một dãy số đã cho.

    Dữ liệu vào: Lấy từ một file văn bản có tên là DIV.INP có cấu trúc như sau:

    – Dòng đầu là hai số N và K (2 ≤ N ≤ 10 000, 2 ≤ K ≤ 100), cách nhau bởi dấu trống.

    – Các dòng tiếp theo là dãy N số có trị tuyệt đối không quá 10 000 cách nhau bởi dấu trống hoặc dấu xuống dòng.

    Dữ liệu ra: Ghi ra file văn bản DIV.OUT số 1 nếu dãy đã cho chia hết cho K và số 0 nếu ngược lại.

    Ví dụ:

    DIV.INP DIV.OUT DIV.INP DIV.OUT

    4 6 0 4 7 1

    1 2 3 5 1 2 3 5

    (Đề ra của bạn Trần Đình Trung – Lớp 11A Tin – Khối PTCT – ĐH Vinh)

    Bài 93/2002 – Trò chơi bắn bi

    (Dành cho học sinh Tiểu học)

    Cho bảng bắn bi sau:

    100 đề Toán Tin (Tin học & Nhà trường) 17

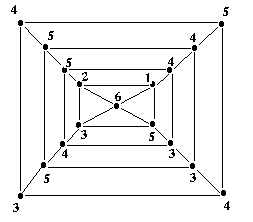
    Bạn có thể bắn bi vào từ một trong số các đỉnh ở ngoài cùng. Khi được bắn vào trong, hòn bi chỉ có thể tiếp tục đi vào trong ở đỉnh gần đó nhất hoặc lăn theo nhiều nhất là một cạnh để đi vào ở đỉnh kề đó. Biết rằng khi đến hình chữ nhật trong cùng, hòn bi không đ­ợc lăn trên một cạnh nào mà phải đi thẳng vào tâm.

    Hãy tìm đường đi sao cho tổng số điểm mà nó đi qua là lớn nhất và có bao nhiêu đường đi để có được số điểm đó.

    Bài 94/2002 – Biểu diễn tổng các số Fibonaci

    (Dành cho học sinh THCS)

    Cho số tự nhiên N và dãy số Fibonaci: 1, 1, 2, 3, 5, 8, ….

    Bạn hãy viết ch­ơng trình kiểm tra xem N có thể biểu diễn thành tổng của của các số Fibonaci khác nhau hay không?

    Bài 95/2002 – Dãy con có tổng lớn nhất

    (Dành cho học sinh THPT)

    Cho dãy gồm n số nguyên a1, a2, …, an. Tìm dãy con gồm một hoặc một số phần tử liên tiếp của dãy đã cho với tổng các phần tử trong dãy là lớn nhất.

    Dữ liệu: Vào từ file văn bản SUBSEQ.INP

    • Dòng đầu tiền chứa số nguyên d­ơng n (n < 106).
    • Dòng thứ i trong số n dòng tiếp theo chứa số ai (|ai|  1000).

    Kết quả: Ghi ra file văn bản SUBSEQ.OUT

    • Dòng đầu tiên ghi vị trí của phần tử đầu tiên của dãy con tìm được.
    • Dòng thứ hai ghi vị trí của phần tử cuối cùng của dãy con tìm được
    • Dòng thứ ba ghi tổng các phần tử của dãy con tìm được.

    Ví dụ:

    SUBSEQ.INP

    SUBSEQ.OUT

    8 12 -14 1 23 -6 22 -34 13

    3 6 40

    Bài 96/2002 – Số chung lớn nhất

    (Dành cho học sinh THPT)

    Cho 2 xâu:

    X = x1x2..xM. (Với xi là các kí tự số từ ‘0’ đến ‘9’)

    Y = y1y2..yN.( Với yi là các kí tự số từ ‘0’ đến ‘9’)

    (M, N <= 250)

    Ta gọi: Z = z1z2..zk là xâu chung của 2 xâu X, Y nếu xâu Z nhận đ­ợc từ xâu X bằng cách xoá đi một số kí tự và cũng nhận được từ xâu Y bằng cách xoá đi một số kí tự.

    Yêu cầu: Tìm một xâu chung của 2 xâu X, Y sao cho xâu nhận được tạo thành một số lớn nhất có thể được.

    Dữ liệu vào file: String.inp

    Gồm 2 dòng, dòng 1 là xâu X, dòng 2 là xâu Y.

    Kết quả ra file: String.out

    Gồm 1 dòng duy nhất là số lớn nhất có thể nhận được.

    Ví dụ:

    String.inp

    String.out

    19012304 034012

    34

    Bài 97/2002 – Thay số trong bảng

    (Dành cho học sinh Tiểu học)

    Bảng dưới gồm 9 ô, ban đầu được điền bởi các chữ cái. Bạn hãy thay các chữ cái bởi các chữ số từ 0 đến 8 vào ô sao cho tất cả các số theo hàng ngang, hàng dọc đều là số có 3 chữ số (chữ số hàng trăm phải khác 0) và thoả mãn:

    4

    5

    6

    1 2 3

    a

    b

    c

    d

    e

    f

    g

    h

    i

    Ngang

    4 – Bội số nguyên của 8;

    5 – Tích của các số tự nhiên liên tiếp đầu tiên;

    6 – Tích các số nguyên tố kề nhau

    Dọc

    1 – Bội nguyên của 11;

    2 – Tích của nhiều thừa số 2;

    3 – Bội số nguyên của 11.

    (Đề ra của bạn Đào Tuấn Anh – Lớp 10A Trường THPT Năng Khiếu Ngô Sĩ Liên – thị xã Bắc Giang)

    Bài 98/2002 – Số phản nguyên tố

    (Dành cho học sinh THCS và THPT)

    Một số n gọi là số phản nguyên tố nếu số ước số của nó là nhiều nhất trong n số tự nhiên đầu tiên. Cho số K (K <= 2 tỷ). Hãy ghi ra số phản nguyên tố lớn nhất nhỏ hơn hoặc bằng K.

    Dữ liệu vào trong file PNT.INP nội dung gồm:

    – Dòng đầu tiên là số M (1 < M <= 100) – số các số cần tìm số phản nguyên tố lớn nhất của nó;

    – M dòng tiếp theo lần lượt là các số K1, K2, K3, …, KM;

    Dữ liệu ra trong file PNT.OUT gồm M dòng: dòng thứ i là số phản nguyên tố lớn nhất nhỏ hơn hoặc bằng Ki.

    Ví dụ:

    PNT.INP

    1

    1000

    PNT.OUT

    840

    (Tác giả: Master – gửi bài qua Website của Tin học & Nhà trường)

    Bài 99/2002 – Bài toán chúc Tết

    (Dành cho học sinh THPT)

    Một người quyết định dành một ngày Tết để đến chúc Tết các bạn của mình. Để chắc chắn, hôm trước anh ta đã điện thoại đến từng người để hỏi khoảng thời gian mà người đó có thể tiếp mình. Giả sử có N người được hỏi (đánh số từ 1 đến N), người thứ i cho biết thời gian có thể tiếp trong ngày là từ Ai đến Bi (i = 1, 2, …, N). Giả thiết rằng, khoảng thời gian cần thiết cho mỗi cuộc gặp là H và khoảng thời gian chuẩn bị từ một cuộc gặp đến một cuộc gặp kế tiếp là T. Bạn hãy xây dựng giúp một lịch chúc Tết để anh ta có thể chúc Tết được nhiều người nhất.

    File dữ liệu vào trong file CHUCTET.INP gồm dòng đầu ghi số N, dòng thứ i trong số N dòng tiếp theo ghi khoảng thời gian có thể tiếp khách của người i gồm 2 số thực Ai và Bi (cách nhau ít nhất một dấu trắng). Dòng tiếp theo ghi giá trị H (số thực) và dòng cuối cùng ghi giá trị T (số thực). Giả thiết rằng các giá trị thời gian đều được viết dưới dạng thập phân theo đơn vị giờ, tính đến 1 số lẻ (thí dụ 10.5 có nghĩa là m­ời giờ r­ỡi) và đều nằm trong khoảng từ 8 đến 21 (từ 8 giờ sáng đến 9 giờ tối). Số khách tối đa không quá 30.

    Kết quả ghi ra file CHUCTET.OUT gồm dòng đầu ghi K là số người được thăm, K dòng tiếp theo ghi trình tự đi thăm, mỗi dòng gồm 2 số (ghi cách nhau ít nhất một dấu trắng): số đầu là số hiệu người được thăm, số tiếp theo là thời điểm gặp tương ứng.

    Thí dụ:

    CHUCTET.INP

    20

    10.5 12.6

    15.5 16.6

    14.0 14.1

    17.5 21.0

    15.0 16.1

    10.5 10.6

    19.0 21.0

    10.5 13.6

    12.5 12.6

    11.5 13.6

    12.5 15.6

    16.0 18.1

    13.5 14.6

    12.5 17.6

    13.0 13.1

    18.5 21.0

    9.0 13.1

    10.5 11.6

    10.5 12.6

    18.0 21.0

    0.5

    0.1

    CHUCTET.OUT

    16

    17 9.0

    1 10.5

    18 11.1

    19 11.7

    8 12.3

    10 12.9

    11 13.5

    13 14.1

    5 15.0

    2 15.6

    12 16.2

    14 16.8

    4 17.5

    7 19.0

    16 19.6

    20 20.2

    (Đề ra của bạn Đinh Quang Huy – ĐHKHTN – ĐHQG Hà Nội )

    Bài 100/2002 – Mời khách dự tiệc

    (Dành cho học sinh THPT)

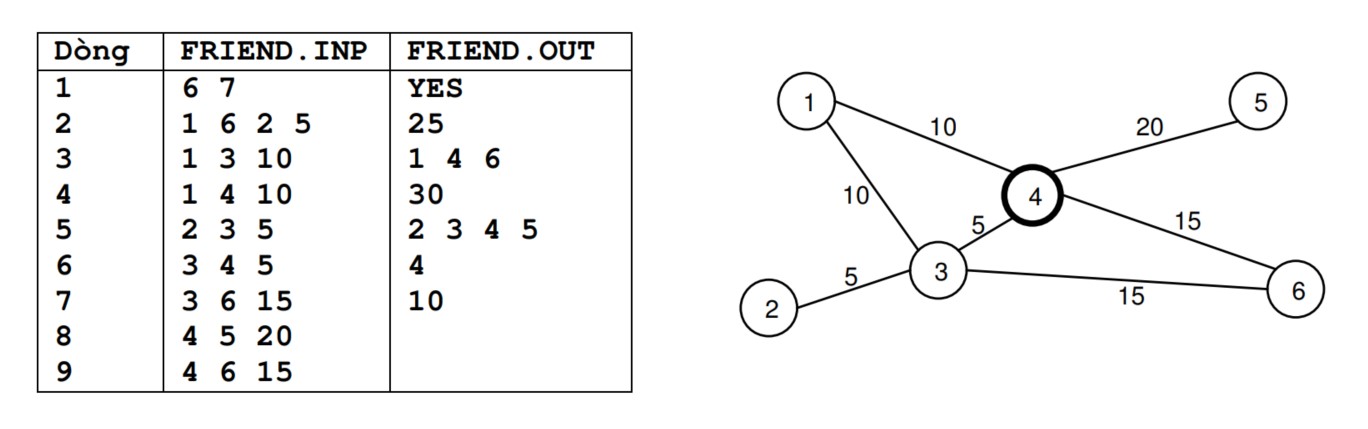
    Công ty trách nhiệm hữu hạn “Vui vẻ” có n cán bộ đánh số từ 1 đến n. Cán bộ i có đánh giá độ vui tính là vi (i = 1, 2, …, n). Ngoại trừ Giám đốc Công ty, mỗi cán bộ có 1 thủ trưởng trực tiếp của mình.

    Bạn chỉ cần giúp Công ty mời một nhóm cán bộ đến dự dạ tiệc “Vui vẻ” sao cho trong số những người được mời không đồng thời có mặt nhân viên và thủ trưởng trực tiếp và đồng thời tổng đánh giá độ vui tính của những người dự tiệc là lớn nhất.

    Giả thiết rằng mỗi một thủ trưởng có không quá 20 cán bộ trực tiếp dưới quyền.

    Dữ liệu: Vào từ file văn bản GUEST.INP

    • Dòng đầu tiên ghi số cán bộ của Công ty: n (1 < n < 1001);
    • Dòng thứ i trong số n dòng tiếp theo ghi hai số nguyên dương ti, vi; trong đó ti là số hiệu của thủ trưởng trực tiếp và vi là độ vui tính của cán bộ i (i = 1, 2, …, n). Quy ước ti = 0 nếu i là số hiệu của Giám đốc Công ty.

    Kết quả: Ghi ra file văn bản GUEST.OUT

    • Dòng đầu tiên ghi hai số m, v; trong đó m là tổng số cán bộ được mời còn v là tổng độ vui tính của các cán bộ được mời dự tiệc;
    • Dòng thứ i trong số m dòng tiếp theo ghi số hiệu của cán bộ được mời thứ i (i = 1, 2, …, m).

    Ví dụ:

    GUEST.INP

    GUEST.OUT

    3

    0 3

    1 6

    2 4

    2 7

    1

    3

    GUEST.INP

    GUEST.OUT

    7

    0 1

    1 1

    1 12

    2 50

    2 1

    3 1

    3 1

    3 63

    3

    4

    5

    (Đề ra của bạn Lưu Văn Minh)

    Phần 2: LỜI GIẢI 100 đề Toán Tin (Tin học & Nhà trường)

    Lời giải cho các bài toán, mời bạn đọc xem trong file: [PDF]100DeToanTin_o2.edu.vn

  • Đề thi BEBRAS 2020 lớp 3 4 và đáp án

    Đề thi BEBRAS 2020 lớp 3 4 và đáp án

    Đề thi BEBRAS 2020 lớp 3 4

    Hướng dẫn giải đề thi Bebras 2020 lớp 3 – 4

    Phần A. Với mỗi câu trả lời đúng, thí sinh được 6 điểm

    Câu 1. Trong mạng xã hội TeeniGram, mỗi người tham gia có thể theo dõi những người tham gia khác. Nếu trong một nhóm người tham gia TeeniGram có một người được tất cả những người còn lại theo dõi và người này không theo dõi bất cứ ai trong nhóm thì người này được gọi là “Thần tượng”. Biết rằng trong nhóm 5 bạn hải ly Alan, Don, Frances, Grace và Robin:

    • Alan theo dõi Don và Grace.
    • Don theo dõi Grace và Robin.
    • Fraces theo dõi Alan, Grace và Robin.
    • Robin theo dõi Alan và Grace.

    Hỏi ai là thần tượng trong nhóm bạn?
    A) Alan

    B) Don

    C) Grace

    D) Robin

    Câu 2. Hải ly chạy thể dục buổi sáng. Bạn ấy dự định đi tới các vị trí 1, 2, 3 và 4 (không nhất thiết theo thứ tự) theo các đường kẻ trong công viên như hình dưới đây.

    De thi Bebras nam 2020 lop 3 4 cau 2
    Mỗi hình vuông đơn vị có cạnh 100 mét.

    Trong công viên có một số vũng lầy màu xám mà bạn ấy không thể đi qua. Hỏi quãng đường ngắn nhất để hải ly đi tới tất cả các vị trí 1, 2, 3 và 4 là bao nhiêu mét?

    A) 1200

    B) 1000

    C) 800

    D) 600

    Câu 3. Hải ly phải đóng gói 5 quả bóng lớn, 2 quả bóng trung bình và 5 quả bóng nhỏ vào hộp. Bạn ấy có 3 hộp lớn, 5 hộp trung bình và 3 hộp nhỏ. Một quả bóng có thể được đặt vừa vào chiếc hộp tương ứng hoặc lớn hơn. Đồng thời mỗi hộp chỉ có thể chứa đúng một quả bóng.

    De thi Bebras nam 2020 lop 3 4 cau 3
    Hỏi hải ly có thể đóng gói được tối đa bao nhiêu quả bóng?
    A) 8

    B) 9

    C) 10

    D) 11

    Câu 4. Ba nhóm người tuyết, mỗi nhóm có 5 người đứng thành hàng. Mỗi bạn lần lượt từ trái sang phải lấy một chiếc mũ theo thứ tự từ trên xuống dưới.

    De thi Bebras nam 2020 lop 3 4 cau 4

    Hỏi các nhóm người tuyết phải lấy các chiếc mũ trong các nhóm nào để mỗi bạn lấy được chiếc mũ theo đúng kích thước của mình?

    Câu 5. Hải ly có cách vẽ tranh bằng cách cạo đi lớp màu xám bên trên của tờ giấy màu như hình dưới đây:

    bebras 2020 lop 3 4 cau 5
    Hỏi trong các bức tranh dưới đây, bức tranh nào xuất hiện đúng ba màu của lớp màu bên dưới?

    bebras 2020 lop 3 4 cau 5 2.jpg

    Phần B. Với mỗi câu trả lời đúng, thí sinh được 9 điểm.

    Câu 6. Hải ly Rebecca có một số khối lập phương kích thước khác nhau như hình dưới đây. Các số biểu diễn cho kích thước của các khối lập phương.

    bebras 2020 lop 3 4 cau 6.jpg

    Bạn ấy muốn sắp xếp các khối lập phương từ trái sang phải theo thứ tự từ bé tới lớn bằng cách lần lượt đổi chỗ các khối lập phương cạnh nhau. Hỏi bạn ấy cần đổi chỗ các khối lập phương ít nhất bao nhiêu lần?
    A) 9

    B) 8

    C) 7

    D) 6

    Câu 7. Đầu bếp hải ly có một chiếc két sắt để cất giữ những công thức bí mật. Chiếc két sắt được khóa bằng chiếc khóa dưới đây.

    bebras 2020 lop 3 4 cau 7

    Để mở được chiếc két sắt, hải ly phải lần lượt xoay mũi tên sang bên trái, sang bên phải để mũi tên chỉ vào các chữ cái có trong mật mã mở khóa. Ví dụ để xoay được chữ cái B và chữ cái H thì hải ly lần lượt xoay Đề thi BEBRAS 2020 lớp 3 4 và đáp án 18 như hình dưới đây.

    bebras 2020 lop 3 4 cau 72

    Hỏi hải ly phải quay khóa như thế nào để mở két sắt nếu mật khẩu là CHEFDG?

    bebras 2020 lop 3 4 cau 73

    Câu 8. Ở thành phố hải ly, các bạn hải ly thường sử dụng xe buýt để di chuyển. Dưới đây là một số chuyến xe buýt và lịch trình di chuyển.

    bebras 2020 lop 3 4 cau 8
    Hải ly xuất phát tại trạm A lúc 11:05 và muốn tới trạm D. Hỏi bạn ấy có thể tới trạm D sớm nhất vào lúc mấy giờ?

    A) 12:00

    B) 11:20

    C) 13:00

    D) 12:20

    Câu 9. Hải ly Diana nhận nhiệm vụ trang trí 5 bàn tiệc cho ngày lễ sắp tới. Bạn ấy được sử dụng:

    • Hai loại thảm trải bàn;
    • Ba loại hoa.

    Các bàn được trang trí phải thỏa mãn điều kiện:

    • Dùng tất cả các loại hoa hoặc chỉ dùng đúng một loại hoa.
    • Hai bàn cạnh nhau không được trải cùng loại thảm trải bàn.

    Hỏi trong các cách trải bàn dưới đây, cách nào thỏa mãn điều kiện đã cho?