Thuật toán giải sudoku bằng quay lui backtracking
Trong bài này chúng ta sẽ sử dụng thuật toán quay lui để giải quyết bài toán giải Sudoku. Để hiểu thuật toán quay lui là gì mời bạn xem bài Thuật toán quay lui và minh họa.
Xem thêm: Python: Bài toán xếp hậu sử dụng đệ quy
Bài viết tham khảo từ techwithtim.net
1. Giới thiệu luật chơi và cách giải Sudoku
Sudoku là một trò chơi giải đố theo wiki định nghĩa như sau:
Sudoku (数独すうどく (số độc) sūdoku?) (suːˈdoʊkuː/, /-ˈdɒ-/, /sə-/, ban đầu có tên gọi là Number Place) là một trò chơi câu đố sắp xếp chữ số dựa trên logic theo tổ hợp. Mục tiêu của trò chơi là điền các chữ số vào một lưới 9×9 sao cho mỗi cột, mỗi hàng, và mỗi phần trong số chín lưới con 3×3 cấu tạo nên lưới chính (cũng gọi là “hộp”, “khối”, hoặc “vùng”) đều chứa tất cả các chữ số từ 1 tới 9. Câu đố đã được hoàn thành một phần, người chơi phải giải tiếp bằng việc điền số. Mỗi câu đố được thiết lập tốt có một cách làm duy nhất.
Cách giải trò chơi Sudoku, mời các bạn xem video hướng dẫn sau:
2. Thuật toán giải Sudoku
Sau đây ta sẽ tìm thuật toán giải Sudoku bằng kỹ thuật backtracking, ngôn ngữ lập trình sử dụng là Python. Các bước tiến hành như sau:
- Viết hàm in câu đố Sudoku ra màn hình.
- Tìm vị trí các ô trống trong Sudoku.
- Với mỗi vị trí ô trống vừa tìm được, lần lượt thử đặt
sốtừ 1 đến 9 vào ô trống đó. Kiểm tra xem sau khi thử đặtsốđó vào ô trống đó thì có hợp lệ (thỏa mãn các điều kiện về luật chơi của Sudoku hay không). Nếu hợp lệ thì tiếp tục tìm các ô trống tiếp theo và lại thử, nếu không thì thử vớisố_tiếp_theo - Lặp lại quy trình trên cho đến khi không còn ô trống nào trên câu đố, hoặc không tìm được lời giải.
Input, một câu đố sudoku biểu diễn bởi danh sách list 2 chiều (một danh sách gồm 9 phần tử, mỗi phần tử là dòng – lại là một danh sách gồm 9 phần tử tương ứng với 9 ô trong một dòng) với các ô trống được quy ước điền bởi số 0, ví dụ Sudoku cau_do được biểu diễn như sau:
cau_do = [
[7,8,0,4,0,0,1,2,0],
[6,0,0,0,7,5,0,0,9],
[0,0,0,6,0,1,0,7,8],
[0,0,7,0,4,0,2,6,0],
[0,0,1,0,5,0,9,3,0],
[9,0,4,0,6,0,0,0,5],
[0,7,0,3,0,0,0,1,2],
[1,2,0,0,0,7,4,0,0],
[0,4,9,2,0,6,0,0,7]
]
Chú ý rằng chỉ số index trong Python được đánh từ 0 trở đi, do đó các vị trí của từng ô trong bảng số sẽ là cau_d0[0][0] cho đến cau_do[8][8], ở đây cau_do[d][c] là ô số ở vị trí dòng d và cột c.
2.1. Viết hàm in câu đố Sudoku ra màn hình
Ở đây chúng ta sử dụng giao diện dòng lệnh, chưa sử dụng giao diện đồ họa GUI nên sẽ sử dụng hàm print() của Python để in một đối tượng ra màn hình CMD.
Ta sẽ viết hàm in_sudoku để in một câu đố Sudoku có tên là q ra màn hình, sử dụng biến d và c để biểu diễn dòng và cột.
Nếu dòng d là dòng thứ 3 hoặc 6 thì ta sẽ in ra màn hình một dòng gồm các kí tự - - - - - - - - - - - để ngăn cách, mục đích là biểu diễn cho các khối ô vuông 3x3 của Sudoku. Tương tự, nếu cột ở vị trí 3 hoặc 6 thì ta sẽ in ra kí tự | để ngăn cách. Nếu cột ở vị trí thứ 8 thì ta sẽ xuống dòng mới.
def in_sudoku(q):
for d in range(len(q)):
if d % 3 == 0 and d != 0:
print("- - - - - - - - - - -")
for c in range(len(q[0])):
if c % 3 == 0 and c != 0:
print("| ", end ="")
if c == 8:
print(str(q[d][c]))
else:
print(str(q[d][c]) + " ", end = "")
Thử in với cau_do ở phần đầu, chúng ta được kết quả như sau, ở đây tôi dùng SublimeText để code:
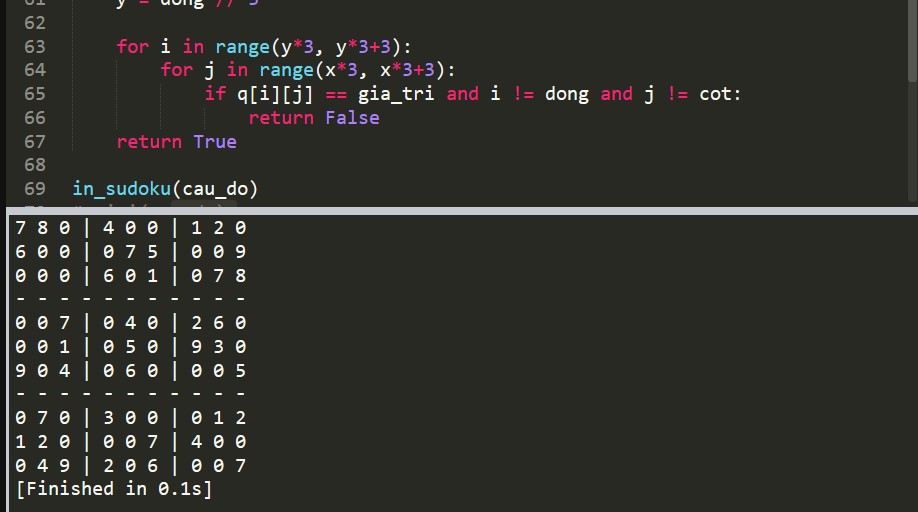
2.2. Viết hàm tìm các ô trống trong Sudoku
Mục tiêu của chúng ta là tìm các vị trí ô trống trong câu đố q
def tim_o_trong(q):
for d in range(len(q)):
for c in range(len(q[0])):
if q[d][c] == 0:
return d, c
return None
2.3. Viết hàm kiểm tra tính hợp lệ của một câu đố
def kiem_tra(q, gia_tri, dong, cot):
for i in range(len(q[0])):
if q[i][cot] == gia_tri and i != dong:
return False
for i in range(len(q)):
if q[dong][i] == gia_tri and i != cot:
return False
x = cot // 3
y = dong // 3
for i in range(y*3, y*3+3):
for j in range(x*3, x*3+3):
if q[i][j] == gia_tri and i != dong and j != cot:
return False
return True
2.4. Viết hàm chính để tìm lời giải cho một câu đố Sudoku
def giai(q):
tim_thay = tim_o_trong(q)
if not tim_thay:
return True
else:
d, c = tim_thay
for i in range(1,10):
if kiem_tra(q, i, d, c):
q[d][c] = i
if giai(q):
return True
else:
q[d][c] = 0
return False
3. Chương trình Python giải Sudoku hoàn chỉnh
cau_do = [
[7,8,0,4,0,0,1,2,0],
[6,0,0,0,7,5,0,0,9],
[0,0,0,6,0,1,0,7,8],
[0,0,7,0,4,0,2,6,0],
[0,0,1,0,5,0,9,3,0],
[9,0,4,0,6,0,0,0,5],
[0,7,0,3,0,0,0,1,2],
[1,2,0,0,0,7,4,0,0],
[0,4,9,2,0,6,0,0,7]
]
def in_sudoku(q):
for d in range(len(q)):
if d % 3 == 0 and d != 0:
print("- - - - - - - - - - -")
for c in range(len(q[0])):
if c % 3 == 0 and c != 0:
print("| ", end ="")
if c == 8:
print(str(q[d][c]))
else:
print(str(q[d][c]) + " ", end = "")
def giai(q):
tim_thay = tim_o_trong(q)
if not tim_thay:
return True
else:
d, c = tim_thay
for i in range(1,10):
if kiem_tra(q, i, d, c):
q[d][c] = i
if giai(q):
return True
else:
q[d][c] = 0
return False
def tim_o_trong(q):
for d in range(len(q)):
for c in range(len(q[0])):
if q[d][c] == 0:
return d, c
return None
def kiem_tra(q, gia_tri, dong, cot):
for i in range(len(q[0])):
if q[i][cot] == gia_tri and i != dong:
return False
for i in range(len(q)):
if q[dong][i] == gia_tri and i != cot:
return False
x = cot // 3
y = dong // 3
for i in range(y*3, y*3+3):
for j in range(x*3, x*3+3):
if q[i][j] == gia_tri and i != dong and j != cot:
return False
return True
in_sudoku(cau_do)
giai(cau_do)
print('Loi giai cua Sudoku tren la:')
in_sudoku(cau_do)
Cho chạy chương trình, chúng ta được kết quả như hình sau:



