Tag: thể tích

100 bài tập khối nón, khối trụ, khối cầu VDC

100 bài tập khối nón, khối trụ, khối cầu VDC

Bài tập khối nón khối trụ khối cầu có lời giải

Câu 1. Cắt hình nón $\left( N \right)$ bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng \(4\). Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng

A. \(\frac{8\pi }{3}\).
B. \(\frac{32\pi }{3}\).
C. \(8\pi \).
D. \(64\pi \).

Lời giải. Chọn A

Gọi tam giác \(SAB\) vuông cân tại S là thiết diện của hình nón cắt bởi mặt phẳng.

Ta có \(S{}_{\Delta SAB}=\frac{1}{2}S{{A}^{2}}=4\Rightarrow SA=2\sqrt{2}\Rightarrow AB=4\).

Khi đó bán kính đáy của hình nón \(r=\frac{AB}{2}=2\) và \(SO=r=2\).

Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho là:

\(V=\frac{1}{3}\pi {{r}^{2}}h=\frac{8\pi }{3}\).

Câu 2. Cho hình trụ có hai đáy là hai hình tròn \(\left( O;R \right)\) và \(\left( {O}’;R \right)\). \(AB\) là một dây cung của đường tròn \(\left( O;R \right)\) sao cho tam giác \({O}’AB\) là tam giác đều và mặt phẳng \(\left( {O}’AB \right)\) tạo với mặt phẳng chứa đường tròn \(\left( O;R \right)\) một góc \(60{}^\circ \). Tính theo \(R\) thể tích \(V\) của khối trụ đã cho.

A.\(V=\frac{\pi \sqrt{7}{{R}^{3}}}{7}\).
B. \(V=\frac{3\pi \sqrt{5}{{R}^{3}}}{5}\).
C. \(V=\frac{\pi \sqrt{5}{{R}^{3}}}{5}\).
D. \(V=\frac{3\pi \sqrt{7}{{R}^{3}}}{7}\).

Lời giải. Chọn D

Đặt độ dài cạnh $AB=x$ $\left( x>0 \right)$ và \(M\) là trung điểm \(AB\).

Vì tam giác ${O}’AB$ đều nên ${O}’A={O}’B=AB=x$$\Rightarrow {O}’M=\frac{x\sqrt{3}}{2}$.

Vì mặt phẳng \(\left( {O}’AB \right)\) tạo với mặt phẳng chứa đường tròn \(\left( O;R \right)\) góc \(60{}^\circ \) nên $\widehat{{O}’MO}=60{}^\circ $.

Xét tam giác ${O}’OM$ vuông tại \(O\) ta có: $\cos \widehat{{O}’MO}=\frac{OM}{{O}’M}$. Suy ra

$\cos 60{}^\circ =\frac{OM}{\frac{x\sqrt{3}}{2}}\Leftrightarrow OM=\frac{x\sqrt{3}}{4}$

Xét tam giác $OAM$vuông ở \(M\) có: $O{{A}^{2}}=O{{M}^{2}}+A{{M}^{2}}$ nên

${{R}^{2}}={{\left( \frac{x\sqrt{3}}{4} \right)}^{2}}+{{\left( \frac{x}{2} \right)}^{2}}\Leftrightarrow {{R}^{2}}=\frac{7}{16}{{x}^{2}}\Rightarrow x=\frac{4\sqrt{7}}{7}R$

Do đó: ${O}’M=\frac{x\sqrt{3}}{2}=\frac{2\sqrt{21}}{7}R$ và $OM=\frac{x\sqrt{3}}{4}=\frac{\sqrt{21}}{7}R$. Vì vậy, ta có

$O{O}’=\sqrt{{O}'{{M}^{2}}-O{{M}^{2}}}=\frac{3\sqrt{7}}{7}R$.

Vậy thể tích khối trụ là $V=\pi {{R}^{2}}.h=\pi {{R}^{2}}.\frac{3\sqrt{7}}{7}R\Rightarrow V=\frac{3\pi \sqrt{7}{{R}^{3}}}{7}$.

Câu 3. Một hình trụ có chiều cao bằng $10$ và bán kính mặt đáy bằng $5$. Một mặt phẳng song song với trục của hình trụ và cách trục một khoảng bằng 2 cắt hình trụ theo thiết diện có diện tích bằng

A. $40\pi $.
B. $80\pi $.
C. $100\pi $.
D. $50\pi $.

Lời giải. Chọn B

Thiết diện là hình chữ nhật và giả sử là $ABCD$ như hình vẽ.

Gọi $M$là trung điểm $AB$. Ta có: $\left\{ {\begin{array}{*{20}{c}} {AD = OO’ = 10}\\ {OB = 5,OM = 3} \end{array}} \right. \Rightarrow MB = \sqrt {O{B^2} – O{M^2}} = 4 \Rightarrow AB = 8$.

Suy ra, diện tích thiết diện bằng: ${S_{ABCD}} = AD.AB = 10.8 = 80 \Rightarrow $Chọn B

Câu 4. Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, cạnh bên bằng $2a$. Khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$bằng

A. $\frac{a\sqrt{165}}{45}$.
B. $\frac{a\sqrt{165}}{15}$.
C. $\frac{2a\sqrt{165}}{15}$.
D. $\frac{a\sqrt{165}}{30}$.

Lời giải.Chọn B

Gọi $G$ là trọng tâm tam giác $ABC$. Do hình chóp $S.ABC$ đều nên $SO\bot \left( ABC \right)$

$SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{4{{a}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{33}}{3}$; $GM=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$

$d\left( A,\left( SBC \right) \right)=3d\left( G,\left( SBC \right) \right)=\frac{3SG.GM}{\sqrt{S{{G}^{2}}+G{{M}^{2}}}}$ $=\frac{a\sqrt{165}}{15}$.

Câu 5. Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và $SAO = {30^0}$; $SAB = {60^0}$. Tính diện tích xung quanh hình nón?

A. $4\pi \sqrt 3 $
B. $\frac{{3\pi \sqrt 2 }}{4}$
C. $2\pi \sqrt 3 $
D. $3\pi \sqrt 2 $

Lời giải. Chọn A

Gọi I là trung điểm của AB thì $OI \bot AB;SI \bot AB;OI = 2$

Lại có $\left\{ {\begin{array}{*{20}{c}}

{AO = SA.\cos SAO = SA.\frac{{\sqrt 3 }}{2}}\\

{AI = SA.\cos SAI = \frac{{SA}}{2}}

\end{array}} \right.$

Từ đó ta có $\frac{{AI}}{{AO}} = \frac{1}{{\sqrt 3 }}$. Mặt khác $\frac{{AI}}{{AO}} = \cos IAO \Rightarrow \sin IAO = \frac{{\sqrt 6 }}{3} = \frac{2}{{OA}} \Rightarrow OA = \sqrt 6 $

Mà $SA = \frac{{OA}}{{\cos 30}} = \sqrt 6 .\frac{2}{{\sqrt 3 }} = 2\sqrt 2 $

Diện tích xung quanh cần tính là: ${S_{xq}} = \pi .OA.SA = 4\pi \sqrt 3 $

Download bài tập khối nón khối trụ khối cầu file word

Các câu còn lại, mời thầy cô và các em download tại đây 100 bai tap khoi non khoi tru khoi cau o2.edu.vn

01/11/2021
Phương pháp so sánh thể tích
Phương pháp so sánh thể tích

Để tính thể tích của một khối chóp, khối lăng trụ chúng ta có thể tính trực tiếp bằng cách xác định diện tích đáy và chiều cao như trong bài Tính thể tích khối chóp. Tuy nhiên, có một cách rất hiệu quả để tính thể tích của khối chóp, khối lăng trụ, khối đa diện mà đề bài yêu cầu là so sánh chúng với các khối có thể tích dễ dàng tính được.

1. Lý thuyết Phương pháp so sánh thể tích

Từ công thức tính thể tích khối chóp, ta thấy thể tích của khối chóp không đổi khi:
- Đáy cố định, đỉnh của hình chóp di chuyển trên một mặt phẳng hoặc một đường thẳng song song với đáy.
- Đỉnh của hình chóp cố định, đáy của hình chóp biến đổi trên một mặt phẳng cố định thành những đa giác tương đương (tức là những đa giác có cùng diện tích).
Do đó, khi tính thể tích khối chóp, chúng ta thường sử dụng các kết quả:
- Hai khối chóp có chung đáy thì ta đi so sánh vị trí của hai đỉnh.
- Hai khối chóp có chung đỉnh thì ta đi so sánh diện tích của hai đáy.
- Sử dụng công thức tỉ số thể tích.
2. Ví dụ Phương pháp so sánh thể tích

Ví dụ 1. Chia khối lăng trụ $ABC.A’B’C’$ thành ba khối tứ diện bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$. Hãy kể tên ba khối tứ diện đó và chứng tỏ rằng chúng có cùng thể tích.

Lời giải
- Chia khối lăng trụ $ABC.A’B’C’$ bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$ thành ba khối tứ diện: $CC’A’B’$, $CBA’B’$, $CABA’$.
- Xét hai hình chóp $C.ABA’$ và $C.BA’B’$ có cùng độ dài đường cao là khoảng cách từ $C$ tới mặt phẳng $(ABB’A’)$ và đáy là các tam giác $ABA’$, $BB’A’$ là hai tam giác cùng diện tích (cùng bằng một nửa diện tích của hình bình hành $ABB’A’$). Vậy \[{{V}_{C.{ABA}}}={{V}_{C.{BA}B’}}\] hay \[{{V}_{{CABA}}}={{V}_{{CBA}B’}}\]
- Ta có: $BB’//(ACC’A’)$ nên suy ra $d(B; (ACC’A’))=d(B’; (ACC’A’))$ hay $$d(B; (ACA’))=d(B’; (CC’A’)).$$
- Lại có $ACA’$ và $CC’A’$ la hai tam giác có cùng diện tích nên \[V_{B.ACA’}=V_{B’.CC’A}\] hay \[V_{CABA’}=V_{CC’AB’}\]
Từ đó suy ra điều phải chứng minh.

Ví dụ 2. [CĐ2011] Cho hình chóp $ S.ABC $ có đáy là tam giác vuông cân tại $ B, AB=a,SA $ vuông góc với đáy. Góc giữa hai mặt phẳng $ (SBC) $ và $ (ABC) $ bằng $ 30^\circ. $ Gọi $ M,N $ lần lượt là trung điểm $ SC,AB $. Tính thể tích các khối chóp $ S.ABM, S.BMN. $

Hướng dẫn. Chỉ ra $ \widehat{SBA}=30^\circ $ và $ V_{S.ABM}=\frac{1}{2}V_{S.ABC} =\frac{a^3\sqrt{3}}{36}. $

Ví dụ 3. Cho hình chóp $ S.ABC $ có đáy là $ \Delta ABC $ vuông cân ở $ B$, $AC=a\sqrt{2},SA\perp\left( ABC \right), SA=a $. Gọi $ G $ là trọng tâm của $ \Delta SBC $, mặt phẳng $ \left( \alpha \right) $ đi qua $ AG $ và song song với $ BC $ cắt $ SC,SB $ lần lượt tại $ M,N $. Tính thể tích khối chóp $ S.AMN $?

Hướng dẫn. Tính được $ V_{S.ABC}=\frac{{{a}^{3}}}{6}. $ Ta có \[ \frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=\frac{4}{9} \] Suy ra $ {{V}_{S.AMN}}=\frac{4}{9}.{{V}_{S.ABC}}=\frac{4}{9}.\frac{{{a}^{3}}}{6}=\frac{2{{a}^{3}}}{27}. $

Ví dụ 4. [D2006] Cho hình chóp $ S.ABC $ có đáy là $ \Delta ABC $ đều cạnh $ a $ và $ SA\perp \left( ABC \right), SA=2a $. Gọi $ H,K $ lần lượt là hình chiếu vuông góc của điểm $ A $ lần lượt lên cạnh $ SB,SC $. Tính thể tích khối $ A.BCKH $ theo $ a $.

Hướng dẫn. Tính ngay được \[{{V}_{S.ABC}}=\frac{1}{3}.{{S}_{\Delta ABC}}.SA=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.2a=\frac{{{a}^{3}}\sqrt{3}}{6}\] Mặt khác lại có \[\frac{{{V}_{S.AHK}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SH}{SB}.\frac{SK}{SC}=\frac{SH.SB}{S{{B}^{2}}}.\frac{SK.SC}{S{{C}^{2}}}=\frac{16}{25}\] Suy ra \[ {{V}_{A.BCKH}}={{V}_{S.ABC}}-{{V}_{S.AHK}}=\frac{9}{25}.{{V}_{S.ABC}}=\frac{3{{a}^{3}}\sqrt{3}}{50} \]

Ví dụ 5. Cho hình chóp tứ giác đều $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh bên tạo với đáy một góc $ 60^\circ $. Gọi $ M $ là trung điểm $ SC $. Mặt phẳng đi qua $ AM $ và song song với $ BD $, cắt $ SB $ tại $ E $ và cắt $ SD $ tại $ F $. Tính thể tích khối chóp $ S.AEMF $.

Hướng dẫn. $ {{V}_{SAMF}}=\frac{1}{3}{{V}_{SACD}}=\frac{1}{6}{{V}_{S.ABCD}}=\frac{{{a}^{3}}\sqrt{6}}{36}\Rightarrow {{V}_{S.AEMF}}=2.\frac{{{a}^{3}}\sqrt{6}}{36}=\frac{{{a}^{3}}\sqrt{6}}{18} $

Ví dụ 6. Cho hình chóp $S.ABC$ có các góc $ \widehat{ASB}=\widehat{BSC}=\widehat{CSA}=60^\circ $. Độ dài các cạnh $ SA,SB,SC $ lần lượt là $ a,b,c $. Tính thể tích khối chóp $ S.ABC. $

Hướng dẫn.
Trên các cạnh $ SB,SC $ lần lượt lấy $ B’,C’ $ sao cho $ SB’=SC’=SA=a $. Như vậy, hình chóp $S.AB’C’$ là một tứ diện đều cạnh bằng $ a $ nên có thể tích \[ V_{SAB’C’}=\frac{a^3\sqrt{2}}{12}. \] Mặt khác, theo tỉ số thể tích thì
\[ \frac{V_{S.ABC}}{V_{S.AB’C’}}=\frac{SA}{SA}\cdot\frac{SB}{SB’}\cdot\frac{SC}{SC’}=\frac{bc}{a^2}\]
Do đó, thể tích khối chóp cần tìm là \[ V_{S.ABC}=\frac{abc\sqrt{2}}{12}. \]

Ví dụ 7. [CĐ2008] Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$?

Hướng dẫn. Vì $MS=MA$ nên $ d\left(A,(MNP) \right)=d\left(S,(MNP) \right)$. Do đó $ V_{A.MNP}=V_{S.MNP} $. Mặt khác \[\frac{{{V}_{S.MNP}}}{{{V}_{S.ABP}}}=\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SP}=\frac{1}{4}\]
Từ đó tìm được $ {{V}_{A.MNP}}=\frac{{{a}^{3}}\sqrt{6}}{48}. $

3. Bài tập sử dụng Phương pháp so sánh thể tích

Bài 1. [CĐ2009] Cho hình chóp tứ giác đều $ S.ABCD $ có $ AB=a,SA=a\sqrt{2} $. Gọi $ M,N,P $ lần lượt là trung điểm của các cạnh $ SA,SB,CD $. Chứng minh rằng đường thẳng $ MN $ vuông góc với đường thẳng $ SP $. Tính theo $ a $ thể tích khối tứ diện $ AMNP $.

Hướng dẫn. Vì $ MN\parallel CD $ mà $ CD\perp SP $ nên $ MN\perp SP. $ Ta có $ V_{AMNP}=\frac{1}{4}V_{ABSP}= \frac{1}{8}V_{S.ABCD}$. Đáp số. $ V=\frac{a^3\sqrt{6}}{48} $

Bài 2. Cho tứ diện đều $ ABCD $ có cạnh $ a $. Lấy các điểm $ B’,C’ $ trên $ AB $ và $ AC $ sao cho $ AB’=\frac{a}{2},AC’=\frac{2a}{3} $. Tính thể tích khối tứ diện $ AB’C’D $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{2}}{36} $.

Bài 3. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a, SC\perp(ABCD) $ cho $ SA=a\sqrt{3} $. Gọi $ H $ là hình chiếu của $ C $ lên $ SB,K $ là trung điểm của $ SD. $ Tính thể tích khối chóp $ S.ABCD $ và khối chóp $ C.BDKH? $

Hướng dẫn. Xét tam giác vuông $ SCB $ có $ SH.SB=SC^2 $ nên $ \frac{SH}{SB}=\frac{SC^2}{SB^2}=\frac{2}{3}. $ Suy ra \[ \frac{V_{S.CKH}}{V_{S.CDB}}=\frac{SC}{SC}.\frac{SK}{SD}.\frac{SH}{SB}=\frac{1}{3} \] Do đó, $ V_{C.BDKH}=\frac{2}{3}V_{S.CBD}=\frac{1}{3}V_{S.ABCD} $

Đáp số. $ V_{S.ABCD}=\frac{a^3\sqrt{2}}{3}$, $V_{C.BDKH}=\frac{a^3\sqrt{2}}{9}. $

Bài 4. Cho hình chóp $ S.ABCD $ có đáy là hình chữ nhật với $ AB=a,\,AD=2a, $ cạnh $ SA $ vuông góc với đáy, cạnh $ SB $ tạo với mặt đáy một góc $ {{60}^{\circ }} $. Trên cạnh $ SA $ lấy điểm $ M $ sao cho $ AM=\frac{a\sqrt{3}}{3} $. Mặt phẳng $ (BCM) $ cắt cạnh $ SD $ tại $ N $. Tính thể tích khối chóp $ S.BCMN? $

Hướng dẫn. $ {{V}_{S.BCMN}}={{V}_{SMBC}}+{{V}_{SMNC}}=\frac{5}{9}{{V}_{S.ABCD}}=\frac{5}{9}.\frac{1}{3}.SA.{{S}_{ABCD}}=\frac{10\sqrt{3}}{27}{{a}^{3}} $

Bài 5. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh bên $ SA $ vuông góc với đáy và $ SA = a $. Gọi $ M $ là một điểm trên cạnh $ SA $ sao cho $ AM = x $. Mặt phẳng $ (MBC) $ cắt $ SD $ tại $ N $. Tính thể tích khối đa diện $ ABCDMN $ theo $ a $ và $ x $.

Đáp số. $ V=\frac{ax.(3a-x)}{6} $

Bài 6. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác đều cạnh $ a\sqrt{3} $, đường cao $ SA=a $. Mặt phẳng qua điểm $ A $ và vuông góc với $ SB $ tại $ H $ và cắt $ SC $ tại $ K $. Tính thể tích hình chóp $ S.AHK $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{3}}{40} $.

Bài 7. Cho hình chóp $ S.ABCD $ có $ ABCD $ là hình bình hành, $ M $ thuộc cạnh $ SA $ và $ \frac{SM}{SA}=x $. Tìm $ x $ để mặt phẳng $ (MBC) $ chia hình chóp thành hai phần có thể tích bằng nhau?

Hướng dẫn. Mặt phẳng $ (MBC) $ cắt $ (SAD) $ theo giao tuyến $ MN\parallel AD. $ Phân chia $ V_{S.MNBC} =V_{S.MBC}+V_{S.MNC} $ để so sánh.

Đáp số. $ x=\frac{-1+\sqrt{5}}{2} $

Bài 8. [DB B2006] Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thoi cạnh $ a $ và góc $ \widehat{BAD}={{60}^\circ} $. Biết rằng $ SA\perp \left( ABCD \right),SA=a $. Gọi $ C’ $ là trung điểm của cạnh $ SC $. Mặt phẳng $ \left( P \right) $ đi qua $ AC’ $ và song song với $ BD $, cắt các cạnh $ SB,SD $ lần lượt tại $ B’ $ và $ D’ $. Tính thể tích khối chóp $ S.ABC’D’ $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{3}}{18} $.

Bài 9. Cho hình chóp $ S.ABCD $ có thể tích là $ V.$ Tứ giác $ ABCD $ là hình bình hành, $ M $ là trung điểm của $ BC $ và $ G $ là trọng tâm tam giác $ SCD $. Tính thể tích tứ diện $ SAMG? $

Hướng dẫn. So sánh thể tích hình chóp $ S.AMG $ với thể tích hình chóp $ S.AMN $ bằng cách coi $ \Delta SAM $ làm đáy chung.

Đáp số. $ V_{SAMG}=\frac{1}{4}V $

Bài 10. Cho hình chóp $ S.ABCD $ có thể tích là $ V.$ Tứ giác $ ABCD $ là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ BC,CD,SD $. Tính thể tích tứ diện $ AMNP? $

Bài 11. Cho hình chóp $ S.ABC $ có điểm $ M\in SA,N\in SB $ sao cho $ \frac{SM}{MA}=\frac{1}{2},\frac{SN}{NB}=2. $ Gọi $ (\alpha) $ là mặt phẳng qua $ MN $ và song song với $ SC $. Mặt phẳng này cắt $ AC $ tại $ E,BC $ tại $ F. $
1. Chứng minh rằng $ AB,MN,EF $ đồng quy, gọi điểm này là $ I, $ tính tỉ số $ \frac{BI}{BA}? $
2. Mặt phẳng $ (\alpha) $ chia hình chóp thành hai phần. Tính tỉ số thể tích của hai phần này?
Hướng dẫn. Gọi $ L $ là trung điểm của $ SN. $

Đáp số. $ \frac{BI}{BA}=\frac{1}{3},\frac{V_1}{V_2}=\frac{4}{5}. $
24/09/2021
Phương pháp phân chia khối đa diện
Phương pháp phân chia khối đa diện

Để tính thể tích của một khối đa diện, nếu đó là các khối cơ bản như khối chóp, khối lăng trụ thì chúng ta có thể tính trực tiếp (xem trong bài Tính thể tích khối chóp) hoặc so sánh thể tích của chúng với các khối dễ tính thể tích hơn.

Tuy nhiên, đối với các khối đa diện phức tạp, hoặc việc tính thể tích của chúng một cách trực tiếp gặp khó khăn, chúng ta có thể nghĩ tới việc phân chia khối đa diện thành các khối đơn giản, dễ tính thể tích hơn.

Để làm quen với việc phân chia và lắp ghép khối đa diện, chúng ta sẽ làm một số ví dụ trước khi đi vào các bài tập tính thể tích.

Ví dụ phương pháp phân chia khối đa diện

Ví dụ 1. Chia khối lăng trụ $ABC.A’B’C’$ thành ba khối tứ diện bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$. Hãy kể tên ba khối tứ diện đó.

Hướng dẫn

Chia khối lăng trụ $ABC.A’B’C’$ bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$ ta được ba khối tứ diện: $CC’A’B’$, $CBA’B’$, $CABA’$.

Ví dụ 2. Có thể chia một khối lập phương thành bao nhiêu khối tứ diện bằng nhau?

Hướng dẫn

Dùng mặt phẳng $(BDD’B’)$ ta chia thành hai khối lập phương thành hai khối lăng trụ $ABD.A’B’D’$ và $BCD.B’C’D’$. Tương tự như ví dụ 1, chúng ta có:
- Khối lăng trụ tam giác $ABD.A’B’D’$ ta lần lượt dùng các mặt phẳng $(ABD’)$ và $(A’BD’)$ chia thành ba khối tứ diện bằng nhau.
- Tương tự với khối lăng trụ tam giác $BCD.B’C’D’$, ta cũng chia được thành ba khối tứ diện đều bằng nhau.
Vậy có tất cả 6 khối tứ diện bằng nhau.

Ví dụ 3. Mặt phẳng $( AB’C’)$ chia khối lăng trụ $ABC.A’B’C’$ thành các khối đa diện nào?

Hướng dẫn

Dựa vào hình vẽ, ta thấy mặt phẳng $(AB’C’)$ chia khối lăng trụ $ABC.A’B’C’$ thành một khối chóp tam giác $A.A’B’C’$ và một khối chóp tứ giác $A.BCC’B’$.

Ví dụ 4. Cho khối chóp $S. ABCD$, hỏi hai mặt phẳng $(SAC)$ và $(SBD)$ chia khối chóp $S.ABCD$ thành bao nhiêu khối chóp?

Hướng dẫn

Gọi $O$ là giao điểm của $AC$ và $BD$. Mặt phẳng $(SAC)$ và $(SBD)$ chia khối chóp $S.ABCD$ thành 4 khối chóp: $S.ABO$, $S.ADO$, $S.CDO$ và $S.BCO$.

Ví dụ 5. Cho tứ diện $ABCD$. Lấy một điểm $M$ nằm trong đoạn $AB$, điểm $N$ nằm trong đoạn $CD$. Chia tứ diện đã cho bằng hai mặt phẳng $(MCD)$ và $(NAB)$ ta được 4 khối tứ diện nào?

Hướng dẫn
- Mặt phẳng $(MCD)$ chia tứ diện đã cho thành hai khối $(MACD)$ và $(MBCD)$.
- Mặt phẳng $(ABN)$ chia khối $(MACD)$ thành hai khối $(MANC)$ và $(MAND)$.
- Mặt phẳng $(ABN)$ chia khối $(MBCD)$ thành hai khối $(MBCN)$ và $(MBND)$.
Ví dụ 6. Chia một khối tứ diện đều thành bốn tứ diện bằng nhau.

Hướng dẫn.
- Xét tứ diện đều $ $A B C D$ . Gọi $ $G$ là giao điểm của các đường thẳng nối đỉnh với trọng tâm của mặt đối diện.
- Dễ thấy các tứ diện $ $G A B C, G B C D, G C D A, G D A B$ bằng nhau.
- Thật vậy, các tứ diện trên đều có đáy là các tam giác đều có cạnh bằng nhau, các cạnh bên $ $G A = G B = G C = G D$ . Vậy ta đã chia được tứ diện đều thành $4$ tứ diện bằng nhau.
Ví dụ 7. Hãy dùng 4 mặt phẳng để chia một khối tứ diện đã cho thành 9 khối tứ diện.

Hướng dẫn.
- Giả sử $ABCD$ là khối tứ diện đã cho.
- Chia cạnh $AB$ thành ba đoạn thẳng bởi các điểm chia $M$ và $M’$. Chia cạnh $CD$ thành ba đoạn thẳng bởi các điểm $N$ và $N’$.
- Khi đó 4 mặt phẳng $(ABN)$, $(ABN’)$, $(CDM)$, $(CDM’)$ sẽ phân chia khối tứ diện $ABCD$ thành 9 khối tứ diện.
Sử dụng Phương pháp phân chia khối đa diện để tính thể tích

Ví dụ 1. Cho khối hộp ABCD.A’B’C’D’. Tính thể tích của khối hộp này biết tứ diện ACB’D’ có thể tích bằng V.

Ví dụ 2. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a , chiều cao AA’ = b . Gọi M là trung điểm cạnh CC’ . Tính thể tích khối tứ diện BDA’M .

(đang tiếp tục bổ sung)
23/09/2021
Tính thể tích khối chóp
Tính thể tích khối chóp

Tính thể tích khối chóp là một dạng toán quan trọng trong các kì thi tốt nghiệp và xét tuyển vào ĐH CĐ. Để tính được thể tích của một khối chóp đòi hỏi học sinh ghi nhớ và vận dụng được nhiều phần kiến thức của hình học không gian, đặc biệt là kiến thức về góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng trong không gian.

Dưới đây là cách tính thể tích khối chóp trực tiếp, ngoài ra còn cách tính gián tiếp bằng Phương pháp so sánh thể tích.

1. Công thức tính thể tích khối chóp

Khối chóp đỉnh $ S $ và đáy là một đa giác có diện tích $ B $ thì $$ V=\frac{1}{3}B\times h $$

Trong công thức trên, việc tính được diện tích $B$ của đáy là bài toán tính diện tích đa giác (tam giác, tứ giác…) quen thuộc trong chương trình hình học cấp 2. Mọi khó khăn của bài toán tính thể tích khối chóp quy về việc xác định và tính được chiều cao của khối chóp. Dưới đây là các cách xác định đường cao của khối chóp.

2. Cách xác định chiều cao của hình chóp

Đường cao của một hình chóp là đoạn thẳng hạ vuông góc từ đỉnh hình chóp xuống mặt đáy tương ứng của nó. Trong thực tế, đối khi người ta không cần dựng đường cao mà chỉ cần tính chiều cao khối chóp, tức là tính khoảng cách từ đỉnh tới mặt đáy của nó. (Bạn đọc có thể xem lại cách tính khoảng cách từ một điểm đến một mặt phẳng)

Dĩ nhiên, ngoài các kiến thức nêu dưới đây, thì các em học sinh cần ôn tập kĩ lại phần kiến thức về góc trong không gian:
- Cách tính góc giữa đường thẳng và mặt phẳng trong không gian
- Cách tính góc giữa hai mặt phẳng trong không gian
2.1. Hình chóp có một cạnh bên vuông góc với đáy

Hình chóp có một cạnh bên vuông góc với đáy thì đường cao khối chóp là cạnh bên đó.

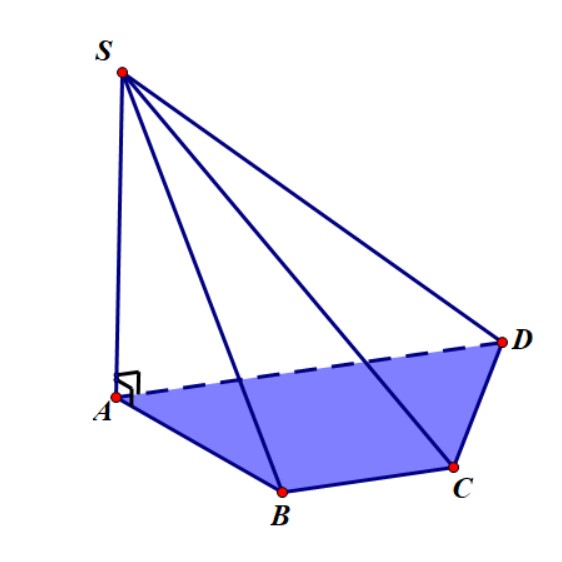
Ví dụ, hình chóp $S.ABCD$ có cạnh bên $SA$ vuông góc với mặt phẳng đáy thì thể tích của nó là $$ V =\frac{1}{3} SA\cdot S_{ABCD}$$

2.2. Hình chóp chứa hai mặt phẳng vuông góc với đáy

Hình chóp chứa hai mặt phẳng vuông góc với đáy thì đường cao là giao tuyến của hai mặt phẳng đó.

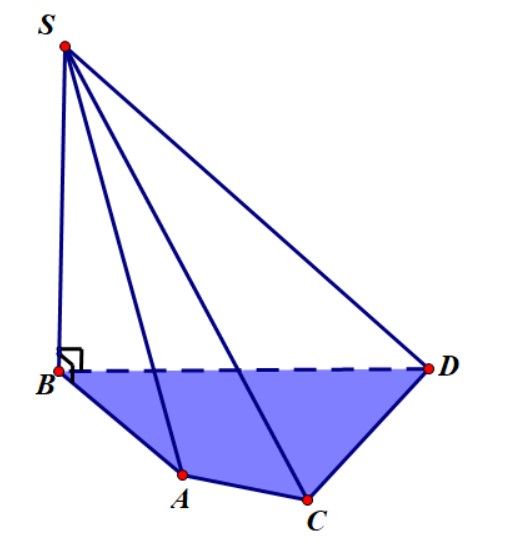
Ví dụ, hình chóp $S.ABCD$ có hai mặt phẳng $(SAB)$ và $(SBC)$ cùng vuông góc với mặt phẳng đáy thì đường cao của hình chóp chính là giao tuyến của hai mặt phẳng $(SAB)$ và $(SBC)$. Tức là đường thẳng $SB$. Do đó, thể tích của hình chóp là $$
V =\frac{1}{3} SB\cdot S_{ABCD} $$

2.3. Hình chóp chứa một mặt phẳng vuông góc với đáy

Hình chóp chứa một mặt phẳng vuông góc với đáy, mặt phẳng đó thường là một tam giác thì đường cao của hình chóp chính là đường cao của tam giác đó.

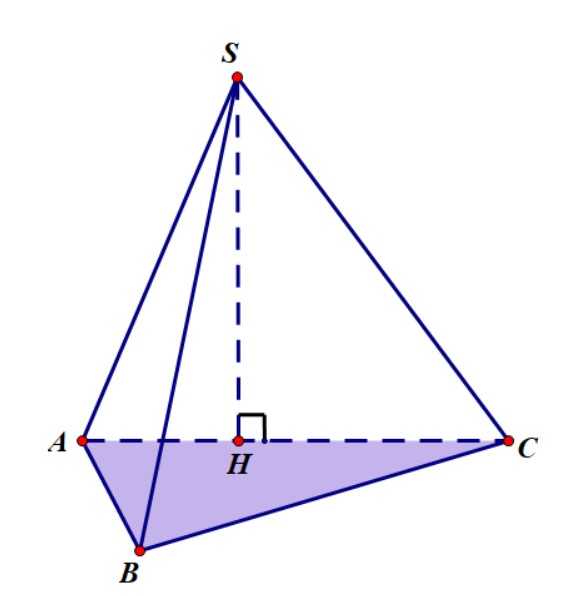
Cho hình chóp $S.ABC$ có $ (SAC) $ vuông góc với mặt phẳng đáy. Khi đó, để xác định đường cao của hình chóp chúng ta làm như sau:
- Trong mặt phẳng $ (SAC) $ kẻ $ SH $ vuông góc với $ AC $, $ H $ thuộc $ AC $.
- Sử dụng tính chất của Hai mặt phẳng vuông góc với nhau , ta chứng minh được $ SH $ vuông góc với $ (ABC) $ hay $ SH $ là đường cao của hình chóp.
Do đó, thể tích khối chóp $ S.ABC $ là $$ V=\frac{1}{3}SH\cdot S_{ABC} $$

2.4. Hình chóp có các cạnh bên bằng nhau và hình chóp đều

Hình chóp có các cạnh bên bằng nhau và hình chóp đều thì đường cao đi qua đỉnh và tâm đường tròn ngoại tiếp của đáy.
- Các em học sinh cần lưu ý hình chóp đều là hình chóp có đáy là một đa giác đều và có các cạnh bên bằng nhau. Các cạnh bên này và cạnh đáy có thể bằng nhau hoặc không bằng nhau đều được.
- Một hình chóp đều thì có các cạnh bên bằng nhau nhưng hình chóp có các cạnh bên bằng nhau thì chưa đủ điều kiện để là một hình chóp đều. Tuy nhiên, một hình chóp mà có các cạnh bên bằng nhau (bao gồm cả hình chóp đều) thì có tính chất:
- Hình chiếu vuông góc của đỉnh hình chóp lên mặt đáy trùng với tâm đường tròn ngoại tiếp của đáy.
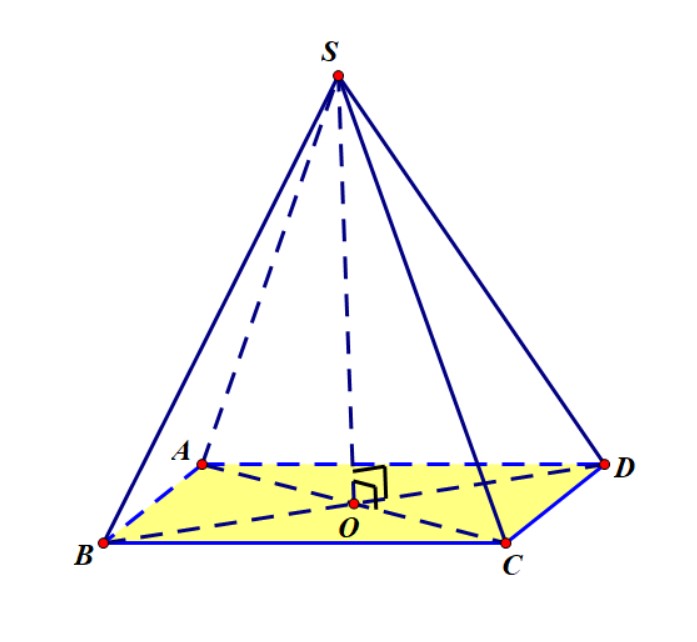
Chẳng hạn, với hình chóp đều tứ giác $S.ABCD$ thì gọi $ O $ là tâm hình vuông (tức là giao điểm hai đường chéo của hình vuông, đồng thời cũng là tâm đối xứng, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp hình vuông) thì chứng minh được $ SO $ vuông góc với mặt phẳng đáy.

Như vậy, chiều cao hình chóp $S.ABCD$ là $ SO $ và thể tích của khối chóp $ S.ABCD $ là $$ V=\frac{1}{3}SO\cdot S_{ABCD} $$

3. Các dạng toán tính thể tích khối chóp

3.1. Hình chóp có một cạnh bên vuông góc với đáy

Ví dụ 1. [TN2013] Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $ và $ SA $ vuông góc với đáy. Cạnh $ SD $ tạo với mặt phẳng $ (SAB) $ góc $ 30^\circ. $ Tính thể tích khối chóp.

Đáp số $ V=\frac{a^3\sqrt{3}}{3} $.

Ví dụ 2. [TN2011] Cho hình chóp $ S.ABCD $ có đáy là hình thang vuông tại $ A $ và $ D. $ Cạnh $ AD=CD=a,$ cạnh $AB=3a. $ Cạnh $ SA $ vuông góc với đáy và $ SC $ tạo với đáy một góc $ 45^\circ. $ Tính thể tích khối chóp $ S.ABCD $.

Đáp số $ V=\frac{2a^3\sqrt{2}}{3} $.

Ví dụ 3. [TN2010] cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh $ SA $ vuông góc với đáy. Góc giữa mặt phẳng $ (SBD) $ và đáy là $ 60^\circ. $ Tính thể tích khối chóp $ S.ABCD $?

Hướng dẫn. Gọi $ O $ là tâm của đáy thì $ \widehat{SOA}=60^\circ. $ Đáp số $ V=\frac{a^3\sqrt{6}}{6}. $

Ví dụ 4. [TN2009] Cho hình chóp $ S.ABC $ có mặt bên $ SBC $ là tam giác đều cạnh $ a $, cạnh $ SA $ vuông góc với đáy, $ \widehat{BAC}=120^\circ. $ Tính thể tích khối chóp $ S.ABC $.

Hướng dẫn. Hai tam giác vuông $ SAB $ và $ SAC $ bằng nhau nên $ AB=AC. $ Áp dụng định lí cosin có $ BC=\frac{a\sqrt{3} }{3}. $ Từ đó tìm được $ SA =\frac{a\sqrt{3}}{6} $ và thể tích bằng $ \frac{a^3\sqrt{2}}{36}. $

Ví dụ 5. Cho hình chóp $ S.ABCD $ có đáy là hình chữ nhật, cạnh $ AB=a,AD=2a. $ Cạnh $ SB $ vuông góc với đáy và khoảng cách từ $ B $ tới $ (SAD) $ bằng $ \frac{2a}{\sqrt{5}}. $ Tính thể tích khối chóp.

Hướng dẫn. Dựng $ BH $ vuông góc với $ SA $ thì $ BH=\frac{2a}{\sqrt{5}}. $ Suy ra $ SB=2a $, và từ đó tìm được $ V=\frac{4}{3}a^3. $

3.2. Hình chóp chứa hai mặt phẳng vuông góc với đáy

Ví dụ 1. Cho hình chóp $ S.ABC $ đáy là tam giác vuông tại $ A,AB=3a,AC=4a, $ SC $ =5a $. Hai mặt bên $ (SAB) $ và $ (SAC) $ cùng vuông góc với đáy. Tính thể tích khối chóp?

Hướng dẫn. Từ giả thiết suy ra $ SA $ vuông góc với đáy và tìm được $ SA=3a. $ Đáp số $ V=6a^3. $

Ví dụ 2. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình chữ nhật với $ AB=a,BC=2a. $ Hai mặt phẳng $ (SAB) $ và $ (SAD) $ cùng vuông góc với đáy, cạnh $ SC $ hợp với đáy góc $ 60^\circ. $ Tính thể tích khối chóp $ S.ABCD $?

Hướng dẫn. Chỉ ra $ \widehat{SCA}=60^\circ $ và tìm được $ SA=a\sqrt{15} $. Từ đó tìm được đáp số $ {{V}_{ABCD}}=\frac{2{{a}^{3}}\sqrt{15}}{3}. $

Ví dụ 3. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $. Các mặt bên $ (SAB) $ và $ (SAD) $ cùng vuông góc với mặt phẳng đáy, góc giữa mặt phẳng $ (SBD) $ và đáy bằng $ {{45}^\circ} $. Tính thể tích khối chóp $ S.ABCD $ theo $ a $.

Đáp số $ V = \frac{{a^3}\sqrt{2}}{6} $

Ví dụ 4. [A2009] Cho hình chóp $ S.ABCD $ có đáy là hình thang vuông tại $ A $ và $ D,$ cạnh $AB=AD=2a,$ cạnh $CD=a,$ góc giữa hai mặt phẳng $ \left( SBC \right) $ và $ \left( ABCD \right) $ bằng $ {{60}^\circ} $. Gọi $ I $ là trung điểm của $ AD $. Biết rằng hai mặt phẳng $ \left( SBI \right) $ và $ \left( SCI \right) $ cùng vuông góc với mặt đáy. Tính thể tích khối chóp $ S.ABCD $?

Hướng dẫn. Vì hai mặt phẳng $ \left( SBI \right) $ và $ \left( SCI \right) $ cùng vuông góc với mặt đáy nên giao tuyến của chúng cũng vuông góc với đáy, tức là $ SI\perp (ABCD) $. Kẻ $ IK\perp BC $ với $ K\in BC $ thì $ \widehat{SKI}=60^\circ. $ Gọi $ J $ là trung điểm $ BC $ từ tam giác vuông $ IKJ $ tìm được $ IK= \frac{3a\sqrt{5}}{5}. $ Từ đó tìm được $ SI=\frac{3a\sqrt{15}}{5}$. Đáp số $ V=\frac{3{{a}^{3}}\sqrt{15}}{5}. $

Ví dụ 5. [A2011] Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác vuông cân tại $ B, AB = BC = 2a $, hai mặt phẳng $ (SAB) $ và $ (SAC) $ cùng vuông góc với đáy. Gọi $ M $ là trung điểm của $ AB, $ mặt phẳng qua $ SM $ và song song với $ BC $, cắt $ AC $ tại $ N $. Biết góc giữa hai mặt phẳng $ (SBC) $ và $ (ABC) $ bằng $ 60^\circ $. Tính thể tích khối chóp $ S.BCNM $.

Hướng dẫn. Chỉ ra $ SA\perp(ABC) $ và góc giữa hai mặt phẳng $ (SBC) $ và $ (ABC) $ là $ \widehat{SBA} $. Mặt khác, chứng minh được $ N $ là trung điểm $ AC $. Từ đó, tìm được đáp số là $ {V_{S.BCNM}} = \sqrt 3 {a^3}. $

Ví dụ 6. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thoi, $ AC = 2\sqrt{3}a, BD = 2a.$ Hai cạnh $AC $ và $ BD $ cắt nhau tại $ O. $ Hai mặt phẳng $ (SAC) $ và $ (SBD) $ cùng vuông góc với đáy. Biết khoảng cách từ điểm $ O $ đến mặt phẳng $ (SAB) $ bằng $ \frac{a\sqrt{3}}{4} $.Tính thể tích khối chóp $ S.ABCD $ theo $ a $.

Hướng dẫn. Hai mặt phẳng $ (SAC) $ và $ (SBD) $ cùng vuông góc với đáy nên giao tuyến $ SO $ của chúng chính là đường cao của hình chóp. Chỉ ra tam giác $ ABD $ đều. Gọi $ H $ là trung điểm của $ AB, K $ là trung điểm của $ HB $ và $ I $ là hình chiếu của $ O $ lên $ SK $ thì $ OI $ chính là khoảng cách từ điểm $ O $ đến mặt phẳng $ (SAB) $. Sử dụng hệ thức lượng trong tam giác vuông, có $$ \frac{1}{{O{I^2}}} = \frac{1}{{O{K^2}}} + \frac{1}{{S{O^2}}} $$ và tìm được $SO = \frac{a}{2} $. Đáp số $ {{V}_{S.ABCD}}=\frac{\sqrt{3}{{a}^{3}}}{3}. $

3.3. Hình chóp chứa một mặt phẳng vuông góc với đáy

Ví dụ 1. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác vuông tại $ A $, cho $ AB=a,AC=a\sqrt{3} $, mặt bên $ SBC $ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích của khối chóp $ S.ABC $.

Đáp số $ \frac{a^3}{2}. $

Ví dụ 2. [CĐ2010] Hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $. Mặt phẳng $ (SAB) $ vuông góc với đáy và $ SA=SB. $ Góc giữa $ SC $ và đáy là $ 45^\circ. $ Tính thể tích khối chóp $ S.ABCD $.

Hướng dẫn. Gọi $ I $ là trung điểm $ AB $ thì $ SI\perp (ABCD). $ Đáp số $ V=\frac{a^3\sqrt{5}}{6}. $

Ví dụ 3. Cho hình chóp $ S.ABCD $, đáy là hình thang vuông tại $ A $ và $ B,$ cạnh $AB=BC=a,$ cạnh $AD=2a. $ Mặt phẳng $ SAD $ vuông góc với đáy và tam giác $ SAD $ vuông tại $ S. $ Biết $ SB=a\sqrt{2} $, tính thể tích khối chóp $ S.ABCD $.

Ví dụ 4. Cho hình chóp $ S.ABC $ có $ BC=2a $ và đáy là tam giác vuông tại $ C. $ Tam giác $ SAB $ vuông cân tại $ S $ và nằm trong mặt phẳng vuông góc với đáy. Mặt phẳng $ (SAC) $ hợp với đáy một góc $ 60^\circ. $ Tính thể tích khối chóp $ S.ABC $.

Hướng dẫn. Gọi $ H,K $ là trung điểm của $ AB,AC $ thì $ SH\perp(ABC) $ và $ \widehat{SKH}=60^\circ. $ Đáp số $ V=\frac{2{{a}^{3}}\sqrt{6}}{3}. $

Ví dụ 5. [B2008] Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ 2a, SA = a, SB = a\sqrt{3} $ và mặt phẳng $ (SAB) $ vuông góc với mặt phẳng đáy. Gọi $ M, N $ lần lượt là trung điểm $ AB, BC $. Tính theo $ a $ thể tích khối chóp $ S.BMDN $ và tính cosin góc giữa hai đường thẳng $ SM, DN $.

Đáp số: $ V=\frac{{{a}^{3}}}{\sqrt{3}}$ và $\cos (SM,DN)=\frac{1}{\sqrt{5}} $.

Ví dụ 6. [B2006] Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình chữ nhật với $ AB=a,$ $AD=a\sqrt{2},$ cạnh $SA=a $ và vuông góc với mặt phẳng đáy. Gọi $ M,N $ lần lượt là trung điểm của $ AD,SC $ và $ I $ là giao điểm của $ BM $ và $ AC $. Tính thể tích khối tứ diện $ ANIB $.

Hướng dẫn. Chỉ ra đường thẳng $ NO$ vuông góc với mặt phẳng $(ABCD) $ nên ${{V}_{ANIB}}={{V}_{N.AIB}}$ và được tính bởi công thức $$\frac{1}{3}.{{S}_{\Delta AIB}}.NO$$ Tính được $ AI,BI $ và suy ra tam giác $ AIB $ vuông tại $ I $. Từ đó tìm được đáp số ${{V}_{N.AIB}}=\frac{{{a}^{3}}\sqrt{2}}{36} $

Ví dụ 7. [A2007] Cho hình chóp $ S.ABCD $ đáy $ ABCD $ là hình vuông cạnh $ a $, mặt bên $ SAD $ là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $ M,N,P $ lần lượt là trung điểm của $ SB,BC,CD $. Chứng minh rằng $ AM\perp PB $ và tính thể tích khối tứ diện $ CMNP $.

Hướng dẫn. Gọi $ H $ là trung điểm của $ AD $ thì $ SH\perp AD $. Kẻ $ MK\parallel SH$ với $K\in HB $ thì chứng minh được $ MK\perp(ABCD) $ và $ MK=\frac{SH}{2}=\frac{a\sqrt{3}}{4}. $ Do đó, thể tích khối chóp cần tính là \begin{align}
V&=V_{M.CNP}\\
&=\frac{1}{3}MK.S_{CNP}\\
&=\frac{{{a}^{3}}\sqrt{3}}{96}
\end{align}

3.4. Hình chóp đều – Hình chóp có các cạnh bên bằng nhau

Ví dụ 1. Hình chóp tam giác đều $ S.ABC $ có đáy là tam giác đều cạnh bằng $ a $, các cạnh bên tạo với đáy một góc $ 60^\circ $. Hãy tính thể tích của khối chóp $ S.ABC $.

Hướng dẫn. Gọi $ M $ là trung điểm $ BC $ và $ O $ là tâm của đáy thì $ \widehat{SAO}=60^\circ $. Từ đó tìm được $ SO=a $ và $ V=\frac{{{a}^{3}}\sqrt{3}}{12} $

Ví dụ 2. Cho hình chóp tứ giác đều $ S.ABCD $ có cạnh đáy $ 2a $, góc giữa mặt bên và mặt đáy bằng $ {{60}^\circ} $. Tính thể tích của khối chóp $ S.ABCD $.

Hướng dẫn. Gọi $ O $ là tâm của đáy, $ M $ là trung điểm của $ AB $ thì $ \widehat{SMO}=60^\circ. $ Đáp số $ V=\frac{4{{a}^{3}}\sqrt{3}}{3}. $

Ví dụ 3. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình chữ nhật, $ AB = a , AD = 2a $. Đỉnh $ S $ cách đều các đỉnh $ A,B,C,D $ của mặt đáy và $ SB = a\sqrt{5} $. Tính thể tích khối chóp $ S.ABCD. $

Hướng dẫn. Đáp số \begin{align} {V} &= \frac{1}{3}SO.{S_{ABCD}} \\ &= \frac{1}{3}.\frac{{a\sqrt {15} }}{2}.2{a^2} \\ &= \frac{{{a^3}\sqrt {15} }}{3} \end{align}

Ví dụ 4. Cho hình chóp $ S.ABCD $ có đáy là hình thoi cạnh $ a,\widehat{ABC} =60^\circ$, cạnh $SB = 2a $. Đỉnh $ S $ cách đều các đỉnh $ A,B,C $ của mặt đáy $ ABCD $. Tính thể tích khối chóp $ S.ABCD.$

Hướng dẫn. Chỉ ra tam giác $ ABC $ đều và gọi $ H $ là tâm của tam giác $ ABC $ thì $ SH\perp(ABCD). $ Từ đó tìm được \begin{align}
{{V}}&=\frac{1}{3}SH.{{S}_{ABCD}}\\
&=\frac{1}{3}.\frac{a\sqrt{33}}{9}.\frac{{{a}^{2}}\sqrt{3}}{2}\\
&=\frac{{{a}^{3}}\sqrt{11}}{18}
\end{align}

Ví dụ 5. Cho hình chóp $ S.ABCD $ có đáy là hình thoi cạnh $ a $ và $SA=a$. Các góc $\widehat{SAB},\widehat{SAD} ,\widehat{BAD}$ cùng bằng $60^\circ $. Tính thể tích khối chóp $ S.ABCD $.

Hướng dẫn. Gọi $ O $ là tâm hình thoi $ ABCD $. Từ $ SA=AB=AD=a $ và $ \widehat{SAB}=\widehat{SAD}=60^\circ $ suy ra các tam giác $ SAB,SAD $ đều.

Do đó, $ SA=SB=SD $ nên hình chiếu của đỉnh $S$ lên mặt đáy sẽ trùng với tâm $ H $ của tam giác $BAD $.

Có cạnh $ BD=a$ nên suy ra $ AC=a\sqrt{3}$ và tính được diện tích $ABCD$ là $\frac{1}{2}AC.BD=\frac{a^2\sqrt{3}}{2}. $

Trong tam giác $ BAD $ có $ AH=\frac{2}{3}AO=\frac{a\sqrt{3}}{3} $ nên suy ra $ SH=\sqrt{SA^2-AH^2}$. Từ đó tính được $SH=\frac{a\sqrt{6}}{3}. $
Suy ra $ V=\frac{a^3\sqrt{2}}{6}. $

4. Bài tập . thể tích khối chóp

Hình chóp có chứa một cạnh bên vuông góc với đáy

Bài tập 1. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác vuông tại $ B $ với $ AC=a,SA\perp \left( ABC \right) $ và $ SB $ hợp với mặt phẳng đáy $ (ABC) $ một góc $ {{60}^\circ} $. Tính thể tích của khối chóp.
Đáp số: $ V=\frac{{{a}^{3}}\sqrt{6}}{24} $.

Bài tập 2. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác vuông tại $ B,SA\perp \left( ABC \right) $. Biết rằng $ AB=a, AC=2a $, góc giữa hai mặt phẳng $ \left( SBC \right) $ và $ \left( ABC \right) $ bằng $ {{60}^\circ} $. Tính thể tích khối chóp $ S.ABC $ theo $ a $.
Đáp số: $ V=\frac{a^3}{2} $.

Bài tập 3. [CĐ2008] Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thang, các góc $ \widehat{BAD}$, $\widehat{ABC}$ cùng bằng ${{90}^\circ}$, $AB=BC=a,$ $AD=2a$, cạnh $ SA$ vuông góc với $\left( ABCD \right)$ và dài bằng $2a $. Gọi $ M,N $ lần lượt là trung điểm của $ SA,SD $. Chứng minh rằng $ BCNM $ là hình chữ nhật và tính thể tích của khối chóp $ S.BNM $?
Hướng dẫn. Có \begin{align}
V_{S.BNM}&=V_{N.BMS}\\
&=\frac{1}{3}NM.S_{\Delta BMS} \\
&=\frac{a^3}{6}
\end{align}

Bài tập 4. [CĐKT Cao Thắng 2007] Cho hình chóp $ S.ABC $ có đáy $ \Delta ABC $ là tam giác vuông tại $ B $ và $ SA\perp \left( ABC \right) $ với $ \widehat{ACB}={{60}^\circ} $, $ BC=a,SA=a\sqrt{3} $. Gọi $ M $ là trung điểm của cạnh $ SB $. Chứng minh $ \left( SAB \right)\perp \left( SBC \right) $ và tính thể tích khối tứ diện $ MABC $.
Hướng dẫn. Có \begin{align}
V_{MABC }&=V_{C.MAB}\\
&=\frac{1}{3}CB.S_{\Delta MAB} \\
&=\frac{{{a}^{3}}}{4}.
\end{align}

Bài tập 5. Cho hình chóp $S.ABC$ có đáy là $\Delta ABC$ vuông tại $A$ và $SB\perp \left( ABC \right)$. Biết $SB=a,SC$ hợp với mặt phẳng $\left( SAB \right)$ một góc ${{30}^\circ}$ và mặt phẳng $\left( SAC \right)$ hợp với mặt phẳng $\left( SAB \right)$ một góc ${{60}^\circ}$. Chứng minh $SC^2=SB^2+AB^2+AC^2$ và tính thể tích khối chóp $S.ABC$.

Hướng dẫn. Chỉ ra $ AC\perp (SAB) $ nên tam giác $ SAC $ vuông. Do đó $ SC^2=SA^2+AC^2$ và suy ra $SC^2=SB^2+AB^2+AC^2. $ Thể tích $V=\frac{{{a}^{3}}\sqrt{3}}{27}$.

Bài tập 6. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình chữ nhật với $ AB=3a, BC=4a $. Biết $ SD $ vuông góc với đáy và tam giác $ SBC $ có diện tích $ 6\sqrt{2} a^2 $. Tính thể tích khối chóp $ S.ABCD $ theo $ a $.
Đáp số: $ 12a^3 $

Bài tập 7. [A2010] Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình vuông cạnh $ a $. Gọi $ M $ và $ N $ lần lượt là trung điểm của các cạnh $ AB $ và $ AD,H $ là giao điểm của $ CN $ và $ DM $. Biết $ SH\perp \left( ABCD \right) $ và $ SH=a\sqrt{3} $. Tính thể tích khối chóp $ S.CDNM $.
Hướng dẫn. Tính diện tích của tứ giác $ CDNM$ bằng cách lấy diện tích ${ABCD}$ trừ đi diện tích tam giác ${AMN}$ và ${BMC} $. Đáp số $ V=\frac{5{{a}^{3}}\sqrt{3}}{24}$.

Bài tập 8. [DB A2006] Cho hình hộp đứng $ABCD.A’B’C’D’$ có $AB=AD=a,$ cạnh bên $AA’=\frac{a\sqrt{3}}{2},$ góc ${BAD}={{60}^{0}}$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $A’D’$ và $A’B’$. Chứng minh rằng: $AC’\bot \left( BDMN \right)$ và tính thể tích khối chóp $A.BDMN$.

Hướng dẫn. Nhận thấy $ABCD$ là hình thoi nên chứng minh được $ BD\perp(ACC’A’) $. Do đó $ AC’\perp BD. $ Gọi $ E=MD\cap AA’ $ thì $ A’ $ là trung điểm $ AE $ và $ AA’,BN,DM $ đồng quy tại $ E. $ Hai tam giác vuông $ AOE $ và $ CC’A $ bằng nhau nên suy ra $ AC’\perp OE. $ Như vậy $ AC’ $ vuông góc với $ BD $ và $ OE $ nên $ AC’\perp(BDMN) $. Gọi $ H=AC’\cap OE $ thì $ AH $ là đường cao của hình chóp $ A.BDMN $. Khi đó, $ V=\frac{1}{3}AH.S_{BDMN}=\frac{3{{a}^{3}}}{16}. $

Hình chóp có chứa hai mặt phẳng vuông góc với đáy

Bài tập 9. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình vuông cạnh $ a $, hai mặt bên $ \left( SAB \right) $ và $ \left( SAD \right) $ cùng vuông góc với $ \left( ABCD \right) $. Cho $ SB=3a $. Gọi $ M $ là trung điểm của $ CD $. Tính thể tích của khối chóp $ S.ABCM $.
Đáp số: $ V=\frac{3\sqrt{2}a^3}{2} $

Bài tập 10. Hình chóp $ S.ABC $ có các cạnh $ SB,SC,BC,CA$ bằng nhau và cùng bằng $a, $ hai mặt $ (ABC) $ và $ (ASC) $ cùng vuông góc với $ (SBC). $ Tính thể tích khối chóp $S.ABC$.
Đáp số: Chọn $ A $ làm đỉnh hình chóp. Đáp số $ V=\frac{a^3\sqrt{3}}{12} $

Bài tập 11. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình chữ nhật, các mặt bên $ \left( SAB \right) $ và $ \left( SAD \right) $ cùng vuông góc với mặt đáy $ \left( ABCD \right) $, cho $ AB=a,AD=2a,$ cạnh $SC $ tạo với mặt đáy $ \left( ABCD \right) $ một góc $ {{45}^\circ} $. Tính thể tích của khối chóp $ S.ABCD $.
Đáp số: $ V=\frac{2\sqrt{3}a^3}{3}.$

Bài tập 12. Hình chóp $ S.ABC $ có hai mặt bên $ (SAB) $ và $ (SAC) $ cùng vuông góc với mặt đáy. Biết rằng đáy $ ABC $ là tam giác vuông cân đỉnh $ A $ với trung tuyến $ AD = a $, cạnh bên $ SB $ tạo với đáy một góc $ \alpha $. Biết $ $SA$=a\sqrt{6} $, hãy tìm góc $ \alpha $ và tính thể tích khối chóp $ S.ABC$.
Đáp số:
$ \alpha=\widehat{SBA}=60^\circ $, $ V=\frac{{{a}^{3}}\sqrt{6}}{3} $.

Bài tập 13. Cho hình chóp $ S.ABC $ có các mặt bên đôi một vuông góc. Diện tích các mặt bên lần lượt là $ 4a^2,6a^2 $ và $ 12a^2. $ Tính thể tích khối chóp.

Hướng dẫn. Chỉ ra $ SA,SB,SC $ đôi một vuông góc. Đặt $ SA=x,$ $SB=y,$ $SC=z $ và biểu diễn tích $ xyz $ theo $ a. $ Từ đó tìm được thể tích $ V=8a^3 $.

Bài tập 14. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thang vuông tại $ A $ và $ D $, $ AD=DC=a,AB=2a $. Biết rằng hai mặt phẳng $ \left( SAB \right) $ và $ \left( SAD \right) $ cùng vuông góc với mặt đáy $ \left( ABCD \right),SC $ tạo với mặt phẳng đáy $ \left( ABCD \right) $ một góc $ {{60}^\circ} $. Gọi $ I $ là trung điểm của $ SB $.
1. Tính thể tích của khối chóp $ S.ABCD $ theo $ a $.
2. Chứng minh tam giác $ SBC $ vuông và tính thể tích khối chóp $ S.ACI $.
Hướng dẫn. Có \begin{align}
V&=V_{I.SAC}\\
&=\frac{1}{3}d(I,(SAC)).S_{\Delta SAC}\\
&= \frac{1}{3}.\frac{1}{2}d(B,(SAC)).S_{\Delta SAC}
\end{align} Đáp số $ V_{S.ABCD}=\frac{\sqrt{6}a^3}{2},$ và $V_{S.ACI}=\frac{a^3\sqrt{6}}{6}. $

Hình chóp có chứa một mặt phẳng vuông góc với đáy

Bài tập 15. Cho hình chóp $ S.ABCD $ có đáy là hình thang cân với $ AD\parallel BC $. Mặt phẳng $ (SAD) $ vuông góc với đáy. Cho $ AB=BC=CD=a$ và $SA=SD=AD=2a $. Tính thể tích khối chóp $ S.ABCD. $ Tính thể tích khối chóp $ S.ABC$.

Đáp số: $ V_{S.ABCD}=\frac{3a^3}{4}$ và $V_{S.ABC}=\frac{a^3}{4}. $

Bài tập 16. Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thang vuông tại $ A $ và $ D,AD=DC=a,AB=2a $. Biết rằng $ \Delta SAB $ đều và nằm trong mặt phẳng vuông góc với $ \left( ABCD \right) $. Tính thể tích khối chóp $ S.ABCD $.

Đáp số: $ V=\frac{{{a}^{3}}\sqrt{3}}{2} $.

Bài tập 17. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a, $ mặt phẳng $ (SAC) $ vuông góc với đáy, $ \widehat{ASC}=90^\circ $ và $ SA $ tạo với đáy một góc $ \alpha. $ Tính thể tích khối chóp.

Hướng dẫn. Kẻ $ AH $ vuông góc với $ AC $ tại $ H $ thì $ AH $ là đường cao của hình chóp. Đáp số: $ V=\frac{a^3\sqrt{2}\sin2\alpha}{6} $

Bài tập 18. Hình chóp $ S.ABC $ có $ \widehat{BAC}=90^\circ,$ $\widehat{ABC}=\alpha.$ Tam giác $SBC $ là tam giác đều cạnh $ a $ và $ (SAB)\perp (ABC). $ Tính thể tích khối chóp $ S.ABC $.

Hướng dẫn. Hạ $ SH\perp AB $ thì có hai tam giác $ SHB,SHC $ bằng nhau nên suy ra $ HB=HC $. Gọi $ I $ là trung điểm $ BC $ thì $ HI $ là đường trung tuyến và đường cao của tam giác cân $ HBC $ nên tính được $ HB =\frac{a}{2\cos\alpha} $. Từ đó tìm được $ SH=\frac{a\sqrt{4\cos^2\alpha-1}}{2\cos\alpha} $. Đáp số: $ \frac{1}{12}a^3\sin\alpha\sqrt{4\cos^2\alpha-1} $

Bài tập 19. Hai hình thang $ ABCD $ và $ ABEF $ cùng vuông tại $ A,B $ và nằm trong hai mặt phẳng vuông góc với nhau. Cho $ AB=5a$, $AD=AF=a$, $BC=4a$, $BE=x. $ Định $ x $ để hai tứ diện $ ABDF $ và $ ABCE $ có thể tích bằng nhau.

Đáp số: $ x=\frac{a}{4}. $

Hình chóp đều và hình chóp có các cạnh bên bằng nhau

Bài tập 20. [TN2008] Cho hình chóp đều $ S.ABC $ có cạnh đáy bằng $ a $, cạnh bên bằng $ 2a $. Gọi $ I $ là trung điểm của cạnh $ BC $. Chứng minh: $ SA\perp BC $ và tính thể tích khối chóp $ S.ABI $ theo $ a $.

Bài tập 21. Tính thể tích tứ diện đều có các cạnh bằng $ a $.

Đáp số: $ \frac{a^2\sqrt{2}}{12} $

Bài tập 22. Tính thể tích khối chóp tứ giác đều có cạnh bên và cạnh đáy cùng bằng $ a $.

Đáp số: $ \frac{a^2\sqrt{2}}{6} $

Bài tập 23. Hình chóp tứ giác đều $ S.ABCD $ có cạnh đáy bằng $ a $, các cạnh bên tạo với mặt đáy góc $ {{60}^\circ} $. Tính thể tích hình chóp đó.
Đáp số: $ \frac{{{a}^{3}}}{\sqrt{6}} $

Bài tập 24. Cho hình chóp đều $ S.ABCD $ có cạnh đáy bằng $ a $, các cạnh bên tạo với mặt đáy góc $ {{45}^\circ} $. Tính thể tích khối chóp.
Đáp số: $ \frac{{{a}^{3}}\sqrt{2}}{6} $

Bài tập 25. Hình chóp tứ giác đều $ S.ABCD $ có chiều cao $ SH = h $, góc giữa mặt bên và mặt đáy bằng $ \alpha $. Tính thể tích khối chóp theo $ h $ và $ \alpha $.

Đáp số: $ \frac{4{{h}^{3}}{{\cot }^{2}}\alpha }{3} $

Bài tập 26. [Cao Đẳng Kinh Tế Đối Ngoại 2007]
Cho hình chóp $ S.ABCD $ có tất cả các cạnh đều bằng nhau. Chứng minh rằng $ S.ABCD $ là hình chóp đều. Tính độ dài cạnh của hình chóp này khi biết thể tích của nó bằng $ \frac{9{{a}^{3}}\sqrt{2}}{2} $.
Đáp số: $ 3a $.

Bài tập 27. [DB D2006] Cho hình chóp tứ giác đều $ S.ABCD $ có cạnh đáy bằng $ a $. Gọi $ SH $ là đường cao của hình chóp. Khoảng cách từ trung điểm $ I $ của $ SH $ đến mặt bên $ \left( SBC \right) $ bằng $ b $. Tính thể tích khối chóp $ S.ABCD $.

Hướng dẫn. Gọi $ M $ là trung điểm của $ CD $, hạ $ IK\perp SM $ thì $ IK $ chính là khoảng cách từ $ I $ đến mặt phẳng $ (SCD). $ Đáp số: $ V=\frac{2{{a}^{3}}b}{3\sqrt{{{a}^{2}}-16{{b}^{2}}}} $.

Bài tập 29. [B2004] Cho hình chóp tứ giác đều $ S.ABCD $ có cạnh đáy bằng $ a $, góc giữa cạnh bên và mặt phẳng đáy bằng $ \varphi$. Tính tang góc giữa hai mặt phẳng $ \left( SAB \right) $ và mặt phẳng $ \left( ABCD \right) $ theo $ \varphi $. Tính thể tích khối chóp theo $ a $ và $ \varphi $.

Đáp số: $ \sqrt{2}\tan \varphi$, $V=\frac{{{a}^{3}}\sqrt{2}.\tan \varphi }{6} $.
11/04/2021