Phương pháp phân chia khối đa diện
Để tính thể tích của một khối đa diện, nếu đó là các khối cơ bản như khối chóp, khối lăng trụ thì chúng ta có thể tính trực tiếp (xem trong bài Tính thể tích khối chóp) hoặc so sánh thể tích của chúng với các khối dễ tính thể tích hơn.
Tuy nhiên, đối với các khối đa diện phức tạp, hoặc việc tính thể tích của chúng một cách trực tiếp gặp khó khăn, chúng ta có thể nghĩ tới việc phân chia khối đa diện thành các khối đơn giản, dễ tính thể tích hơn.
Để làm quen với việc phân chia và lắp ghép khối đa diện, chúng ta sẽ làm một số ví dụ trước khi đi vào các bài tập tính thể tích.
Ví dụ phương pháp phân chia khối đa diện
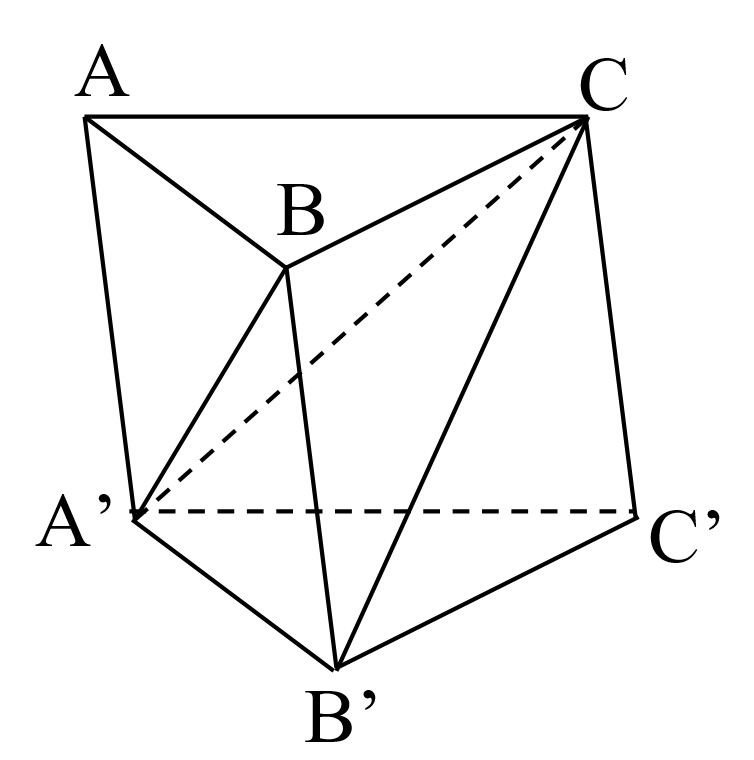
Ví dụ 1. Chia khối lăng trụ $ABC.A’B’C’$ thành ba khối tứ diện bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$. Hãy kể tên ba khối tứ diện đó.
Hướng dẫn
Chia khối lăng trụ $ABC.A’B’C’$ bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$ ta được ba khối tứ diện: $CC’A’B’$, $CBA’B’$, $CABA’$.
Ví dụ 2. Có thể chia một khối lập phương thành bao nhiêu khối tứ diện bằng nhau?
Hướng dẫn
Dùng mặt phẳng $(BDD’B’)$ ta chia thành hai khối lập phương thành hai khối lăng trụ $ABD.A’B’D’$ và $BCD.B’C’D’$. Tương tự như ví dụ 1, chúng ta có:
- Khối lăng trụ tam giác $ABD.A’B’D’$ ta lần lượt dùng các mặt phẳng $(ABD’)$ và $(A’BD’)$ chia thành ba khối tứ diện bằng nhau.
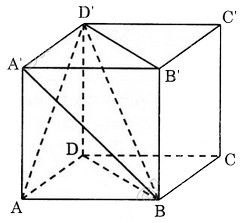
- Tương tự với khối lăng trụ tam giác $BCD.B’C’D’$, ta cũng chia được thành ba khối tứ diện đều bằng nhau.
Vậy có tất cả 6 khối tứ diện bằng nhau.
Ví dụ 3. Mặt phẳng $( AB’C’)$ chia khối lăng trụ $ABC.A’B’C’$ thành các khối đa diện nào?
Hướng dẫn

Dựa vào hình vẽ, ta thấy mặt phẳng $(AB’C’)$ chia khối lăng trụ $ABC.A’B’C’$ thành một khối chóp tam giác $A.A’B’C’$ và một khối chóp tứ giác $A.BCC’B’$.
Ví dụ 4. Cho khối chóp $S. ABCD$, hỏi hai mặt phẳng $(SAC)$ và $(SBD)$ chia khối chóp $S.ABCD$ thành bao nhiêu khối chóp?

Hướng dẫn
Gọi $O$ là giao điểm của $AC$ và $BD$. Mặt phẳng $(SAC)$ và $(SBD)$ chia khối chóp $S.ABCD$ thành 4 khối chóp: $S.ABO$, $S.ADO$, $S.CDO$ và $S.BCO$.
Ví dụ 5. Cho tứ diện $ABCD$. Lấy một điểm $M$ nằm trong đoạn $AB$, điểm $N$ nằm trong đoạn $CD$. Chia tứ diện đã cho bằng hai mặt phẳng $(MCD)$ và $(NAB)$ ta được 4 khối tứ diện nào?
Hướng dẫn

- Mặt phẳng $(MCD)$ chia tứ diện đã cho thành hai khối $(MACD)$ và $(MBCD)$.
- Mặt phẳng $(ABN)$ chia khối $(MACD)$ thành hai khối $(MANC)$ và $(MAND)$.
- Mặt phẳng $(ABN)$ chia khối $(MBCD)$ thành hai khối $(MBCN)$ và $(MBND)$.
Ví dụ 6. Chia một khối tứ diện đều thành bốn tứ diện bằng nhau.
Hướng dẫn.
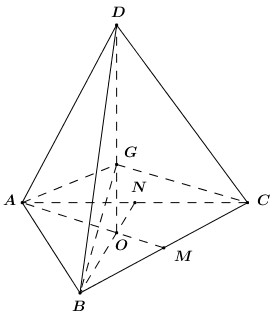
- Xét tứ diện đều $. Gọi $ là giao điểm của các đường thẳng nối đỉnh với trọng tâm của mặt đối diện.
- Dễ thấy các tứ diện $ bằng nhau.
- Thật vậy, các tứ diện trên đều có đáy là các tam giác đều có cạnh bằng nhau, các cạnh bên $. Vậy ta đã chia được tứ diện đều thành tứ diện bằng nhau.
Ví dụ 7. Hãy dùng 4 mặt phẳng để chia một khối tứ diện đã cho thành 9 khối tứ diện.
Hướng dẫn.
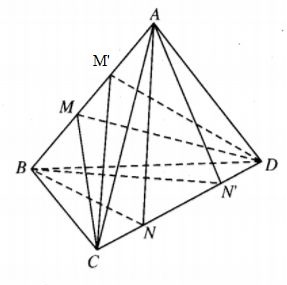
- Giả sử $ABCD$ là khối tứ diện đã cho.
- Chia cạnh $AB$ thành ba đoạn thẳng bởi các điểm chia $M$ và $M’$. Chia cạnh $CD$ thành ba đoạn thẳng bởi các điểm $N$ và $N’$.
- Khi đó 4 mặt phẳng $(ABN)$, $(ABN’)$, $(CDM)$, $(CDM’)$ sẽ phân chia khối tứ diện $ABCD$ thành 9 khối tứ diện.
Sử dụng Phương pháp phân chia khối đa diện để tính thể tích
Ví dụ 1. Cho khối hộp ABCD.A’B’C’D’. Tính thể tích của khối hộp này biết tứ diện ACB’D’ có thể tích bằng V.

Ví dụ 2. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a , chiều cao AA’ = b . Gọi M là trung điểm cạnh CC’ . Tính thể tích khối tứ diện BDA’M .
(đang tiếp tục bổ sung)