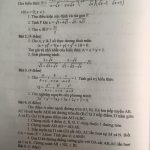Tag: vào 10

Đề thi vào 10 môn Toán Hà Nội 2021
Đề thi vào 10 môn Toán Hà Nội 2021

1. Đề thi vào 10 môn Toán Hà Nội 2021

Bài I. (2,0 điểm)

Cho hai biểu thức $ A=\dfrac{\sqrt{x}}{\sqrt{x}+3} $ và $ B=\dfrac{2\sqrt{x}}{\sqrt{x}-3} -\dfrac{3x+9}{x-9}$ với $ x \geqslant 0, x\ne 9 $.
1. Tính giá trị biểu thức $ A $ khi $ x=16 $.
2. Chứng minh $ A+B=\dfrac{3}{\sqrt{x}+3} $.
Bài II. (2,5 điểm)

1. Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:

Một tổ sản xuất phải làm xong $ 4800 $ bộ đồ bảo hộ y tế trong một số ngày quy định. Thực tế, mỗi ngày tổ đó đã làm được nhiều hơn $ 100 $ bộ so với số bộ đồ y tế phải làm trong một ngày theo kế hoạch. Vì thế 8 ngày trước khi hết thời hạn, tổ sản xuất đã làm xong $ 4800 $ bộ đồ bảo hộ y tế đó. Hỏi theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu bộ đồ bảo hộ y tế? (Giả định rằng số bộ đồ y tế mà tổ đó làm xong trong mỗi ngày là bằng nhau.)

2. Một thùng nước có dạng hình trụ với chiều cao $ 1,6 $ m và bán kính đáy $ 0,5 $ m. Người ta sơn toàn bộ phía ngoài mặt xung quanh của thùng nước này (trừ hai mặt đáy). Tính diện tích bề mặt được sơn của thùng nước (lấy $ \pi \approx 3,14$).

Bài III (2,0 điểm)
1. Giải hệ phương trình \[ \begin{cases} \dfrac{3}{x+1}-2y=-1\\ \dfrac{5}{x+1}+3y=11 \end{cases} \]
2. Trong mặt phẳng tọa độ $Oxy$, cho parabol $ (P):y=x^2 $ và đường thẳng $ (d): y=2x+m-2$. Tìm tất cả các giá trị của $ m $ để $ (d) $ cắt $ (P) $ tại hai điểm phân biệt có hoành độ $ x_1,x_2 $ sao cho $ \big|x_1-x_2\big|=2$.
Bài IV (3,0 điểm)

Cho tam giác $ABC$ vuông tại $ A $. Vẽ đường tròn tâm $ C $, bán kính $ CA $. Từ điểm $ B $ kẻ tiếp tuyến $ BM $ với đường tròn $ (C;CA) $ ($ M $ là tiếp điểm, $ M $ và $ A $ nằm khác phía đối với đường thẳng $ BC $).
1. Chứng minh bốn điểm $ A,C,M , B $ cùng thuộc một đường tròn.
2. Lấy điểm $ N $ thuộc đoạn thẳng $ AB $ ($ N $ khác $ A,N $ khác $ B $). Lấy điểm $ P $ thuộc tia đối của tia $ MB $ sao cho $ MP=AN $. Chứng minh tam giác $ CPN $ là tam giác cân và đường thẳng $ AM $ đi qua trung điểm của đoạn thẳng $ NP $.
Bài V (0,5 điểm)

Với các số thực $ a $ và $ b $ thỏa mãn $ a^2+b^2=2, $ tìm giá trị nhỏ nhất của biểu thức $ P=3(a+b)+ab $.

2. Lời giải Đề thi vào 10 môn Toán Hà Nội 2021

Quý thầy cô và các em học sinh có thể tải file PDF lời giải tại đây.
14/06/2021

Đề thi tuyển sinh vào lớp 10 chuyên KHTN HN năm 2014

SỞ GD VÀ ĐT HÀ NỘI

ĐỀ CHÍNH THỨC

(Đề thi gồm 01 trang)

THI VÀO LỚP 10 CHUYÊN KHOA HỌC TỰ NHIÊN

NĂM HỌC 2014

MÔN: TOÁN ( VÒNG 1 )

(Thời gian làm bài 150 phút, không kể thời gian giao đề)

Bài 1.

Giả sử $x,y$ là những số thực dương thỏa mãn \[\frac{y}{x+y}+\frac{2{{y}^{2}}}{{{x}^{2}}+{{y}^{2}}}+\frac{4{{y}^{4}}}{{{x}^{4}}+{{y}^{4}}}+\frac{8{{y}^{4}}}{{{x}^{8}}-{{y}^{4}}}=4\] Chứng minh rằng: $5y=4x$.

Giải hệ phương trình: \[\left\{ \begin{array}{*{35}{l}} 2{{x}^{2}}-3{{y}^{2}}+xy=12 \\ 6x+{{x}^{2}}y=12+6y+{{y}^{2}}x \\ \end{array} \right.\]

Bài 2.

Cho $x,y$ là những số nguyên lớn hơn 1 sao cho $4{{x}^{2}}{{y}^{2}}-7x+7y$ là số chính phương. Chứng minh rằng: $x=y.$
Giả sử $x,y$ là những số thực không âm thỏa mãn: ${{x}^{3}}+{{y}^{3}}+xy={{x}^{2}}+{{y}^{2}}$. Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: \[P=\frac{1+\sqrt{x}}{2+\sqrt{y}}+\frac{2+\sqrt{x}}{1+\sqrt{y}}\]

Bài 3. Cho tam giác $ABC$ nhọn với $AB<BC$. Gọi $D$ là điểm thuộc cạnh BC sao cho $AD$ là phân giác của $\widehat{BAC}$. Đường thẳng qua $C$ song song với $AD$ cắt trung trực của $AC$ tại $E$. Đường thẳng qua $B$ song song với $AD$ cắt trung trực của $AB$ tại $F$.

Chứng minh tam giác $AFB$ đồng dạng với tam giác $AEC$.
Chứng minh rằng các đường thẳng $BE$, $CF$, $AD$ đồng quy tại một điểm, gọi điểm đó là $G$.
Đường thẳng qua $G$ song song với $AE$ cắt đường thẳng $BF$ tại $Q$. Đường thẳng $QE$ cắt đường tròn ngoại tiếp tam giác $GEC$ tại $P$ khác $E$. Chứng minh rằng các điểm $A$, $P$, $G$, $Q$, $F$ cùng thuộc một đường tròn.

Bài 4. Giả sử $a$, $b$, $c$ là các số thực dương thỏa mãn đẳng thức $ab+bc+ca=1$. Chứng minh rằng \[2abc(a+b+c)\le \frac{5}{9}+{{a}^{4}}{{b}^{2}}+{{b}^{4}}{{c}^{2}}+{{c}^{4}}{{a}^{2}}\]

—HẾT —

31/05/2021

100 đề thi HSG Toán 9 và thi vào 10 chuyên Toán

100 đề thi HSG Toán 9 và thi vào 10 chuyên Toán

Tổng hợp 100 đề thi HSG Toán 9 và thi vào lớp 10 chuyên của cá trường THCS, THPT trên địa bàn thành phố Hà Nội qua các năm. Mời thầy cô và các em học sinh tham khảo.

14/04/2020