100 bài tập khối nón, khối trụ, khối cầu VDC
Bài tập khối nón khối trụ khối cầu có lời giải
Câu 1. Cắt hình nón $\left( N \right)$ bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng \(4\). Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng
A. \(\frac{8\pi }{3}\).
B. \(\frac{32\pi }{3}\).
C. \(8\pi \).
D. \(64\pi \).

Lời giải. Chọn A
Gọi tam giác \(SAB\) vuông cân tại S là thiết diện của hình nón cắt bởi mặt phẳng.
Ta có \(S{}_{\Delta SAB}=\frac{1}{2}S{{A}^{2}}=4\Rightarrow SA=2\sqrt{2}\Rightarrow AB=4\).
Khi đó bán kính đáy của hình nón \(r=\frac{AB}{2}=2\) và \(SO=r=2\).
Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho là:
\(V=\frac{1}{3}\pi {{r}^{2}}h=\frac{8\pi }{3}\).
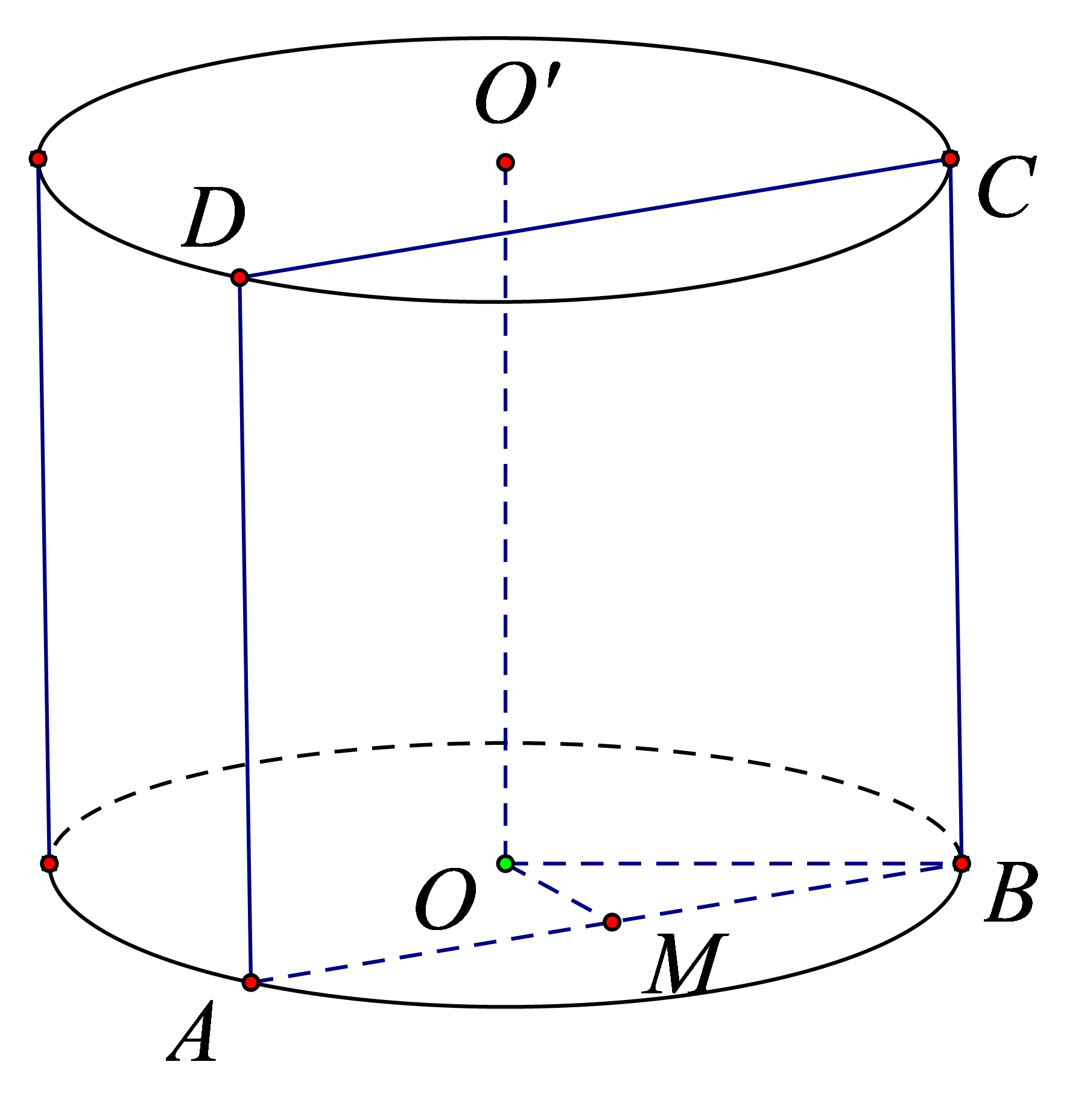
Câu 2. Cho hình trụ có hai đáy là hai hình tròn \(\left( O;R \right)\) và \(\left( {O}’;R \right)\). \(AB\) là một dây cung của đường tròn \(\left( O;R \right)\) sao cho tam giác \({O}’AB\) là tam giác đều và mặt phẳng \(\left( {O}’AB \right)\) tạo với mặt phẳng chứa đường tròn \(\left( O;R \right)\) một góc \(60{}^\circ \). Tính theo \(R\) thể tích \(V\) của khối trụ đã cho.
A.\(V=\frac{\pi \sqrt{7}{{R}^{3}}}{7}\).
B. \(V=\frac{3\pi \sqrt{5}{{R}^{3}}}{5}\).
C. \(V=\frac{\pi \sqrt{5}{{R}^{3}}}{5}\).
D. \(V=\frac{3\pi \sqrt{7}{{R}^{3}}}{7}\).
Lời giải. Chọn D

Đặt độ dài cạnh $AB=x$ $\left( x>0 \right)$ và \(M\) là trung điểm \(AB\).
Vì tam giác ${O}’AB$ đều nên ${O}’A={O}’B=AB=x$$\Rightarrow {O}’M=\frac{x\sqrt{3}}{2}$.
Vì mặt phẳng \(\left( {O}’AB \right)\) tạo với mặt phẳng chứa đường tròn \(\left( O;R \right)\) góc \(60{}^\circ \) nên $\widehat{{O}’MO}=60{}^\circ $.
Xét tam giác ${O}’OM$ vuông tại \(O\) ta có: $\cos \widehat{{O}’MO}=\frac{OM}{{O}’M}$. Suy ra
$\cos 60{}^\circ =\frac{OM}{\frac{x\sqrt{3}}{2}}\Leftrightarrow OM=\frac{x\sqrt{3}}{4}$
Xét tam giác $OAM$vuông ở \(M\) có: $O{{A}^{2}}=O{{M}^{2}}+A{{M}^{2}}$ nên
${{R}^{2}}={{\left( \frac{x\sqrt{3}}{4} \right)}^{2}}+{{\left( \frac{x}{2} \right)}^{2}}\Leftrightarrow {{R}^{2}}=\frac{7}{16}{{x}^{2}}\Rightarrow x=\frac{4\sqrt{7}}{7}R$
Do đó: ${O}’M=\frac{x\sqrt{3}}{2}=\frac{2\sqrt{21}}{7}R$ và $OM=\frac{x\sqrt{3}}{4}=\frac{\sqrt{21}}{7}R$. Vì vậy, ta có
$O{O}’=\sqrt{{O}'{{M}^{2}}-O{{M}^{2}}}=\frac{3\sqrt{7}}{7}R$.
Vậy thể tích khối trụ là $V=\pi {{R}^{2}}.h=\pi {{R}^{2}}.\frac{3\sqrt{7}}{7}R\Rightarrow V=\frac{3\pi \sqrt{7}{{R}^{3}}}{7}$.
Câu 3. Một hình trụ có chiều cao bằng $10$ và bán kính mặt đáy bằng $5$. Một mặt phẳng song song với trục của hình trụ và cách trục một khoảng bằng 2 cắt hình trụ theo thiết diện có diện tích bằng
A. $40\pi $.
B. $80\pi $.
C. $100\pi $.
D. $50\pi $.
 Lời giải. Chọn B
Lời giải. Chọn B
Thiết diện là hình chữ nhật và giả sử là $ABCD$ như hình vẽ.
Gọi $M$là trung điểm $AB$. Ta có: $\left\{ {\begin{array}{*{20}{c}} {AD = OO’ = 10}\\ {OB = 5,OM = 3} \end{array}} \right. \Rightarrow MB = \sqrt {O{B^2} – O{M^2}} = 4 \Rightarrow AB = 8$.
Suy ra, diện tích thiết diện bằng: ${S_{ABCD}} = AD.AB = 10.8 = 80 \Rightarrow $Chọn B
Câu 4. Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, cạnh bên bằng $2a$. Khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$bằng
A. $\frac{a\sqrt{165}}{45}$.
B. $\frac{a\sqrt{165}}{15}$.
C. $\frac{2a\sqrt{165}}{15}$.
D. $\frac{a\sqrt{165}}{30}$.
Lời giải. Chọn B
Chọn B
Gọi $G$ là trọng tâm tam giác $ABC$. Do hình chóp $S.ABC$ đều nên $SO\bot \left( ABC \right)$
$SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{4{{a}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{33}}{3}$; $GM=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$
$d\left( A,\left( SBC \right) \right)=3d\left( G,\left( SBC \right) \right)=\frac{3SG.GM}{\sqrt{S{{G}^{2}}+G{{M}^{2}}}}$ $=\frac{a\sqrt{165}}{15}$.
Câu 5. Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và $SAO = {30^0}$; $SAB = {60^0}$. Tính diện tích xung quanh hình nón?
A. $4\pi \sqrt 3 $
B. $\frac{{3\pi \sqrt 2 }}{4}$
C. $2\pi \sqrt 3 $
D. $3\pi \sqrt 2 $
 Lời giải. Chọn A
Lời giải. Chọn A
Gọi I là trung điểm của AB thì $OI \bot AB;SI \bot AB;OI = 2$
Lại có $\left\{ {\begin{array}{*{20}{c}}
{AO = SA.\cos SAO = SA.\frac{{\sqrt 3 }}{2}}\\
{AI = SA.\cos SAI = \frac{{SA}}{2}}
\end{array}} \right.$
Từ đó ta có $\frac{{AI}}{{AO}} = \frac{1}{{\sqrt 3 }}$. Mặt khác $\frac{{AI}}{{AO}} = \cos IAO \Rightarrow \sin IAO = \frac{{\sqrt 6 }}{3} = \frac{2}{{OA}} \Rightarrow OA = \sqrt 6 $
Mà $SA = \frac{{OA}}{{\cos 30}} = \sqrt 6 .\frac{2}{{\sqrt 3 }} = 2\sqrt 2 $
Diện tích xung quanh cần tính là: ${S_{xq}} = \pi .OA.SA = 4\pi \sqrt 3 $
Download bài tập khối nón khối trụ khối cầu file word
Các câu còn lại, mời thầy cô và các em download tại đây 100 bai tap khoi non khoi tru khoi cau o2.edu.vn
Leave a Reply