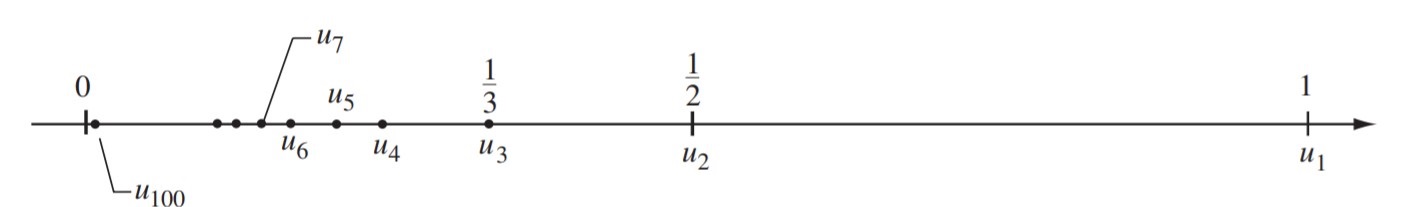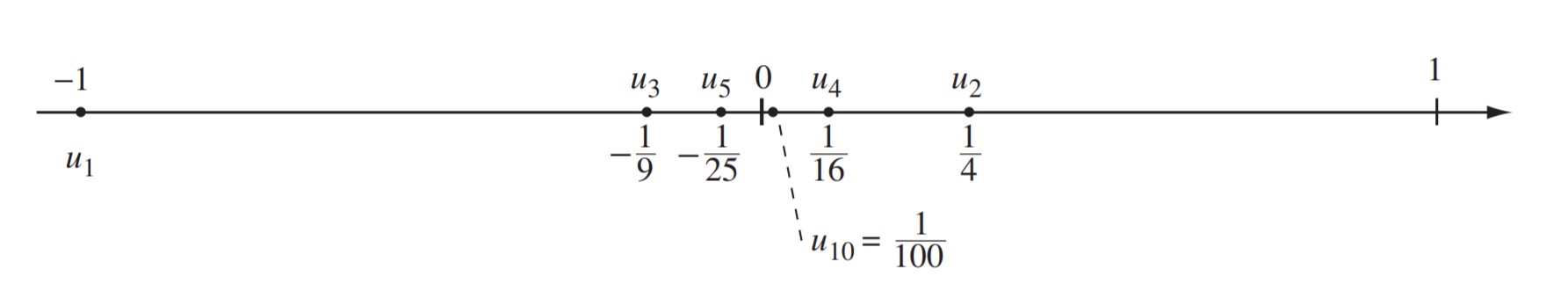Giới hạn của dãy số
Nếu nhìn các đại lượng vô hạn dưới con mắt hữu hạn, chúng ta sẽ gặp vô vàn nghịch lí, như nghịch lí Zeno:
Achilles và con rùa. Trong một cuộc chạy đua, người chạy nhanh nhất không bao giờ có thể bắt kịp được kẻ chậm nhất. Kể từ khi xuất phát, người đuổi theo trước hết phải đến được điểm mà kẻ bị đuổi bắt đầu chạy. Do đó, kẻ chạy chậm hơn luôn dẫn đầu.

Trong nghịch lý Achilles và rùa, Achilles chạy đua với rùa. Ví dụ Achilles chấp rùa một đoạn 100 mét. Nếu chúng ta giả sử rằng mỗi tay đua đều bắt đầu chạy với một tốc độ không đổi (Achilles chạy rất nhanh và rùa rất chậm), thì sau một thời gian hữu hạn, Achilles sẽ chạy được 100 mét, tức anh ta đã đến được điểm xuất phát của con rùa. Nhưng trong thời gian này, con rùa cũng đã chạy được một quãng đường ngắn, ví dụ 10 mét. Sau đó Achilles lại tốn một khoảng thời gian nữa để chạy đến điểm cách 10 mét ấy, mà trong thời gian đó thì con rùa lại tiến xa hơn một chút nữa, và cứ như thế mãi. Vì vậy, bất cứ khi nào Achilles đến một vị trí mà con rùa đã đến, thì con rùa lại cách đó một đoạn. Bởi vì số lượng các điểm Achilles phải đến được mà con rùa đã đi qua là vô hạn, do đó anh ta không bao giờ có thể bắt kịp được con rùa.
1. Giới hạn hữu hạn của dãy số
1.1. Dãy số có giới hạn bằng 0
Định nghĩa. Dãy số \( u_n \) được gọi là có giới hạn bằng \( 0 \) khi \( n \) dần tới dương vô cùng nếu \( \big|u_n\big| \) nhỏ hơn một số dương bé tùy ý kể từ một số hạng nào đó trở đi.
Kí hiệu \( \lim\limits_{n\to +\infty}u_n =0 \).
Ví dụ, xét dãy \( (u_n) \) có công thức số hạng tổng quát \( u_n=\frac{1}{n} \). Ta sẽ chỉ ra \( \big|u_n\big| \) nhỏ hơn một số dương bé tùy ý kể từ một số hạng nào đó trở đi.
- Chẳng hạn, chọn số dương bé tùy ý là \( 0{,}01 \) thì có \( \big|u_n\big| <0{,}01 \Leftrightarrow n>100\). Như vậy ta chỉ cần lấy các số hạng kể từ \( u_{101} \) trở đi là có \( \big|u_n\big| <0{,}01 \).
- Chọn số dương bé tùy ý là \( {0,0005} \) thì thì có \( \big|u_n\big| <0{,}0005 \Leftrightarrow n>2000\). Như vậy ta chỉ cần lấy các số hạng kể từ \( u_{2001} \) trở đi là có \( \big|u_n\big| <0{,}005 \).
- Tương tự, muốn \( \big|u_n\big| <0{,}000003 \Leftrightarrow n>333333{,}(3)\). Như vậy ta chỉ cần lấy các số hạng kể từ \( u_{333334} \) trở đi là có \( \big|u_n\big| <0{,}000003 \).
- Tổng quát, muốn \( \big|u_n\big| <\epsilon \) ta chỉ cần lấy từ số hạng thứ \( \left[\frac{1}{\epsilon} \right] +1\) trở đi, ở đây \( [*] \) là kí hiệu phần nguyên của \( * \).
Như vậy, ta nói dãy số \( \frac{1}{n}\) có giới hạn là \( 0 \) khi \( n \) dần tới dương vô cùng và viết \( \lim\limits_{n\to +\infty}\frac{1}{n} =0 \) hoặc \( \lim \frac{1}{n} =0 \).
Biểu diễn các số hạng của dãy trên trục số, chúng ta thấy khi \( n \) dần tới dương vô cùng thì các số hạng \( u_n \) ngày càng tiến gần tới số \( 0 \)
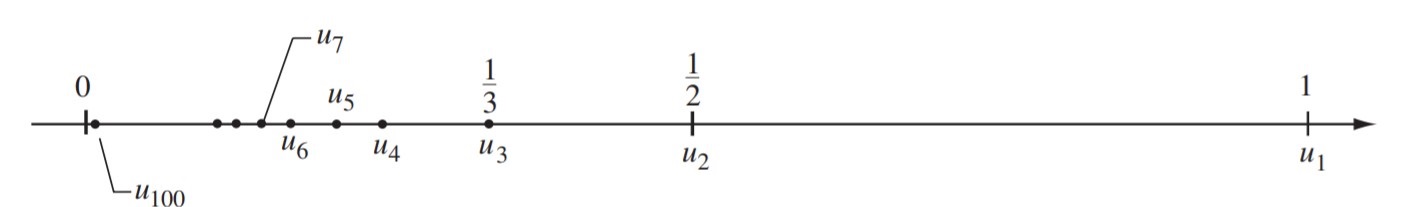
Xét thêm một dãy số khác nữa là dãy có công thức số hạng tổng quát \(u_n=\frac{(-1)^n}{n}\). Biểu diễn các số hạng của dãy trên trục số, ta được hình sau:
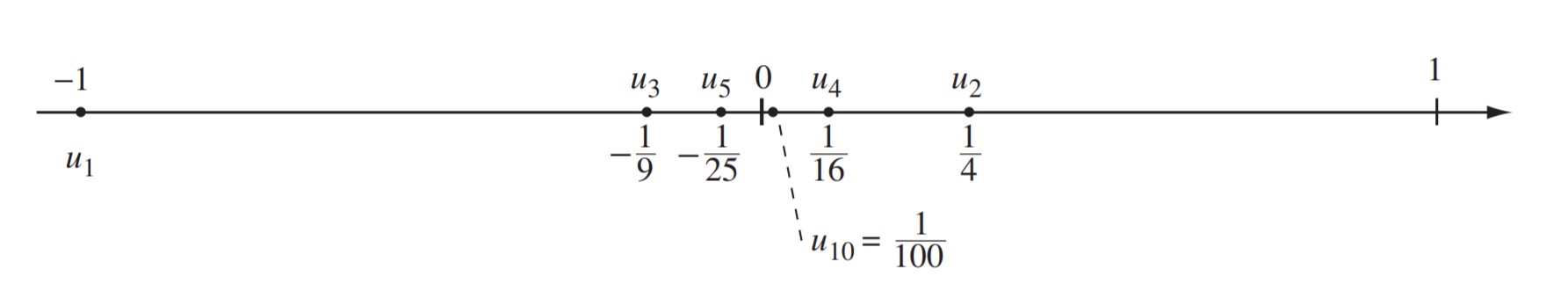
Về mặt hình ảnh, chúng ta thấy khi \( n \) dần tới dương vô cùng thì các số hạng \( u_n \) ngày càng tiến gần tới số \( 0 \) và chúng có xu hướng hội tụ tại điểm \( 0 \) đó. Chúng ta cũng nói dãy \(\frac{(-1)^n}{n}\) có giới hạn là \( 0 \) khi \( n \) dần tới dương vô cùng.
Ngoài ra, chúng ta còn gặp một số dãy có giới hạn \( 0 \) như \[ \lim\frac{1}{n^2} =0, \lim \frac{1}{\sqrt{n}} = 0,… \]
1.2. Định nghĩa giới hạn hữu hạn của dãy số
Định nghĩa. Dãy số \( u_n \) được gọi là có giới hạn bằng \( a \) khi \( n \) dần tới dương vô cùng nếu dãy \( v_n=u_n-a \) có giới hạn bằng \( 0 \) khi \( n \) dần tới dương vô cùng.
Tức là , \( \lim\limits_{n\to +\infty}u_n =a \) nếu \( \lim\limits_{n\to +\infty} \left (u_n-a\right ) =0 \).
Ví dụ, dãy \( u_n \) với công thức số hạng tổng quát \( u_n=\frac{2n+1}{n} \) có giới hạn bằng \( 2 \) khi \( n \) dần tới dương vô cực vì $$ \lim (u_n-2) = \lim \left(\frac{2n+1}{n}-2\right)=\lim \frac{1}{n} =0.$$
2. Quy tắc và tính chất về giới hạn hữu hạn của dãy số
Cho hai dãy \( u_n \) và \( v_n \) có \( \lim u_n=a, \lim v_n=b \) thì
- \( \lim \left(u_n \pm v_n\right) = a\pm b \)
- \( \lim \left(u_n v_n\right) = a b \)
- \( \lim \left(\frac{u_n}{v_n} \right) = \frac{a}{b}\) nếu \( b\ne 0 \)
Cho dãy \( u_n \) có \( u_n \geqslant 0\) và \( \lim u_n=a\) thì \( a \geqslant 0 \) và \( \lim \sqrt{u_n} =\sqrt{a} \).
Sử dụng các tính chất và định nghĩa trên, chúng ta có một vài giới hạn đặc biệt sau.
- \( \lim c =c\) với \( c \) là hằng số bất kì.
- \( \lim \frac{c}{n} = 0\) vì \( lim c=c\) và \( \lim \frac{1}{n} =0\)
- \( \lim \frac{1}{n^k}=0 \) với \( k \) nguyên dương.
- \( \lim q^n = 0 \) với \( |q| <1 \)
Với các giới hạn đặc biệt này, ta dễ dàng có các giới hạn sau:
- Vì \( \lim 2=2 \) và \( \lim \frac{3}{n} =0\) nên \( \lim \left(2+\frac{3}{n}\right) =2 \)
- Vì \( \lim 5=5 \) và \( \lim \frac{1}{n^2} =0\) nên \( \lim \left(5+\frac{1}{n^2}\right) =5 \)
Do đó, $$ \lim \frac{2+\frac{3}{n}}{5+\frac{1}{n^2}}=\frac{2}{5}. $$ Nhưng giới hạn này cũng chính là giới hạn của dãy có công thức số hạng tổng quát $$ u_n=\frac{2+\frac{3}{n}}{5+\frac{1}{n^2}} = \frac{2n^2+3n}{5n^2+1}.$$
Từ đó, chúng ta ý tưởng chung để tìm giới hạn của các dãy số là làm ngược lại quá trình trên. Tức là ta tìm cách biến đổi để đưa về các giới hạn đặc biệt rồi sử dụng tính chất về giới hạn của tổng, hiệu, tích, thương.
Ví dụ, tính giới hạn $$ \lim \frac{n+4}{3n-2} $$ chúng ta chia cả tử và mẫu của phân thức cho \( n \) thì được $$ \lim \frac{n+4}{3n-2} = \lim \frac{1+\frac{4}{n}}{3-\frac{2}{n}} = \frac{1+0}{3-0} =\frac{1}{3}. $$
Ví dụ, tính giới hạn $$ \lim \frac{\sqrt{n^2+3}}{4-n} $$ chúng ta chia cả tử và mẫu của phân thức cho \( n \) thì được $$ \lim \frac{\sqrt{n^2+3}}{4-n} =\lim \frac{\sqrt{1+\frac{3}{n^2}}}{\frac{4}{n}-1}=\frac{\sqrt{1+0}}{0-1}=-1.$$
Ví dụ. Tính các giới hạn sau:
- $ \lim \dfrac{2n^3-n^2+1}{n^3+1}=2 $
- $ \lim \dfrac{-n^7-n^6+1}{n+2n^7}=-\dfrac{1}{2} $
- $ \lim \dfrac{(n+1)(n^2-3n+5)}{n^3-2n(n^2+1)+2}=-1 $
- $ \lim \dfrac{n\sqrt{n}+n^2-1}{2n^2+1}=\dfrac{1}{2} $
- $ \lim \dfrac{n+\sqrt{n^2+1}}{3n-1}=\dfrac{2}{3} $
- $ \lim \dfrac{n+\sqrt{n^2+2n+1}}{2-\sqrt{4n^2+1}}=-1 $
- $ \lim \dfrac{2n+\sqrt{n^3+2n^2+1}}{n\sqrt{3n+2}-1}=\dfrac{1}{\sqrt{3}} $
- $ \lim \dfrac{\sqrt[3]{-27n^6+2n+1}}{4n^2+4n+1}=-\dfrac{3}{4} $
- $ \lim \sqrt{\dfrac{3n^2+2n-1}{n^2+5n}}=\sqrt{3} $
- $ \lim \left(\dfrac{2n^2}{n^2+3n+1}-\dfrac{2n}{3n+1}\right) $
- $ \lim \dfrac{n+1}{n^3+1}=0 $
- $ \lim \dfrac{11n^2-2n+1}{n^3+n^2+1}=0 $
- $ \lim \dfrac{(2n+1)(n-5)+n^2+1}{n^3+n^2}=0 $
- $ \lim \left(\dfrac{2n}{3n^2+1}-\dfrac{n}{3n^2+1}\right) $
- $ \lim \dfrac{n+\sqrt{n^3+1}}{2n^2+\sqrt{n}-1}=0 $
- $ \lim \dfrac{2}{\sqrt{n^2+1}-n} $
- $ \lim \dfrac{1}{\sqrt{n}\left(\sqrt{n+2}-\sqrt{n+1}\right)} $
- $ \lim \dfrac{3}{\sqrt{4n^2+1}-2n+1} $
- $ \lim \dfrac{2^n+3^n}{5\cdot3^n+2^n} $
- $ \lim \dfrac{2^n-1}{3^n+2^{n+1}} $
- $ \lim \dfrac{2^n-3^n+5^{n+2}}{5^n+3^{n+1}} $
- $ \lim \dfrac{(-2)^n-5^{n+1}}{5^{n-1}+3^{n+1}} $
3. Tổng của cấp số nhân lùi vô hạn
Cấp số nhân lùi vô hạn là cấp số nhân có vô hạn số hạng và công bội \( q \) thỏa mãn \( |q|<1 \). Ví dụ, cấp số nhân:
- \( \frac{1}{2}, \frac{1}{4}, \frac{1}{8},… \left(\frac{1}{2}\right)^n \) là cấp số nhân lùi vô hạn với công bội \( q=\frac{1}{2}
\)
- \( \frac{-1}{2}, \frac{1}{4}, \frac{-1}{8},… \left(\frac{-1}{2}\right)^n \) là cấp số nhân lùi vô hạn với công bội \( q=\frac{-1}{2}
\)
Cho cấp số nhân lùi vô hạn với số hạng đầu là \( u_1\) và công bội \( q \) thì tổng của \( n \) số hạng đầu tiên là $$ S_n=u_1+u_2 + u_3 +…+ u_n=u_1 \cdot \frac{1-q^n}{1-q} $$ Vì \( |q|<1 \) nên khi \( n\to +\infty \) thì \( q^n\to 0 \) do đó $$ \lim S_n = \frac{u_1}{1-q} $$
Giới hạn này được gọi là tổng của cấp số nhân lùi vô hạn \( (u_n) \) và kí hiệu là \( S=u_1+u_2 + u_3 +…+ u_n+… \)
4. Giới hạn vô cực
Định nghĩa dãy số có giới hạn vô cực
- Dãy số \( u_n \) được gọi là có giới hạn \( +\infty \) khi \( n \) dần tới dương vô cùng nếu \( u_n \) lớn hơn một số dương tùy ý kể từ một số hạng nào đó trở đi.
Kí hiệu \( \lim\limits_{n\to +\infty}u_n =+\infty \) hoặc \( \lim u_n =+\infty \) .
- Dãy số \( u_n \) được gọi là có giới hạn \( -\infty \) khi \( n \) dần tới dương vô cùng nếu \( \lim \left(-u_n\right) =+\infty \)
Kí hiệu \( \lim u_n =-\infty \).
Một vài giới hạn đặc biệt
- \( \lim n^k = +\infty \) với \( k \) nguyên dương;
- \( \lim \sqrt{n} = +\infty \);
- \( \lim q^n= +\infty \) nếu \( q >1\).
Tính chất giới hạn vô cực của dãy số
- Nếu \( \lim u_n=a\) và \(\lim v_n=\pm \infty \) thì \( \lim \left(\frac{u_n}{v_n} \right) = 0\).
- Nếu \( \lim u_n=a>0, \lim v_n=0 \) và \( v_n>0 \) với mọi \( n \) thì \( \lim \left(\frac{u_n}{v_n} \right) = +\infty \).
- Nếu \( \lim u_n=a\) và \(\lim v_n=+ \infty \) thì \( \lim \left(u_n v_n \right) = +\infty \).
Ví dụ. Tính các giới hạn sau:
- $ \lim (n^2+n-3)=+\infty $
- $ \lim (2n^2-n^3+4)=-\infty $
- $ \lim (n\sqrt{n}+3n-1)=+\infty $
- $ \lim \dfrac{2n^3-n^2+1}{n^2+1}=+\infty $
- $ \lim \dfrac{11n^4+1}{-5n^2+n+1}=-\infty $
- $ \lim \dfrac{2n\sqrt{n}-3}{n+\sqrt{n}-1} $
- $ \lim \dfrac{3^n+2^n}{2^{n+1}-1} $
Ví dụ. Tính các giới hạn sau:
- $ \lim (n\sqrt{n}+n-3)=+\infty $
- $ \lim (\sqrt{n^2+n+1}+3n)=+\infty $
- $ \lim (\sqrt{n^2+1}-3n)=-\infty $
- $ \lim (\sqrt{n+1}+\sqrt{n+2})=+\infty $
- $ \lim (\sqrt{n+1}-\sqrt{n+2})=0 $
- $ \lim \left(\dfrac{1}{n-\sqrt{n^2+1}}-\dfrac{1}{n+\sqrt{n^2+1}}\right)$
- $ \lim (\sqrt{n^2+n+1}-n)$
- $ \lim (\sqrt{n^2+n+1}-\sqrt{n^2-n+1})$
- $ \lim \dfrac{3n+2}{\sqrt{n^2+3}-\sqrt{n^2+1}}$
- $ \lim \dfrac{\sqrt{n^2+n}-n}{\sqrt{n^2+1}-\sqrt{n^2+2n}}$
- $ \lim (\sqrt[3]{n^3+1}-n)$
- $ \lim (2n+1+\sqrt[3]{1-8n^3})$
Ví dụ. Tính các giới hạn sau:
- $ \lim n(\sqrt{n^2+1}-n)=+\infty $
- $ \lim \sqrt{n+1}(\sqrt{n+2}-\sqrt{n}) $
- $ \lim n^2(\sqrt{3n^4+5}-\sqrt{3n^4+2}) $
- $ \lim \dfrac{n(n+\sqrt{n-n^3})}{n-\sqrt{n^2+4n}} $
- $ \lim (\sqrt{n^2+1}-\sqrt[3]{n^3+n})$
- $ \lim (\sqrt{n^2+n+1}+\sqrt[3]{1-n^3})$
- $ \lim (2n-\sqrt{9n^2+n}+\sqrt{n^2+2n}) $
- $ \lim \left(\sqrt{n^2+2n}+2\sqrt[3]{n^2-8n^3}+\sqrt{n^2+1}\right) $