TOÁN 9: LIÊN HỆ GIỮA CUNG VÀ DÂY CUNG
Cung và dây cung có mối liên hệ như thế nào? Đây là một kiến thức quan trọng trong chương trình lớp 9. Mời các em cùng tham khảo:
1. TÓM TẮT LÝ THUYẾT LIÊN HỆ GIỮA CUNG VÀ DÂY CUNG
- Với hai cung nhỏ trong một đường tròn hay hai đường tròn bằng nhau:
- Hai cung bằng nhau căng hai dây bằng nhau.
- Hai dây bằng nhau căng hai cung bằng nhau.
- Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:
- Cung lớn hơn căng dây lớn hơn.
- Dây lớn hơn căng cung lớn hơn.
- Đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
- Đường kính đi qua trung điểm của một dây không đi qua tâm thì đi qua điểm chính giữa của cung căng dây ấy.
- Đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
- Trong một đường tròn hai cung bị chắn giữa hai dây song song thì bằng nhau.
Ví dụ 1. Cho tam giác nhọn \(ABC\) nội tiếp đường tròn \(\left( O;R \right),\text{ }\left( AB\text{ }<\text{ }BC \right)\). Vẽ dây $BD$ của \(\left( O \right)\) và \(BD\bot OA\). So sánh \(\overset\frown{AD}\) và \(\overset\frown{BC}\).
Lời giải
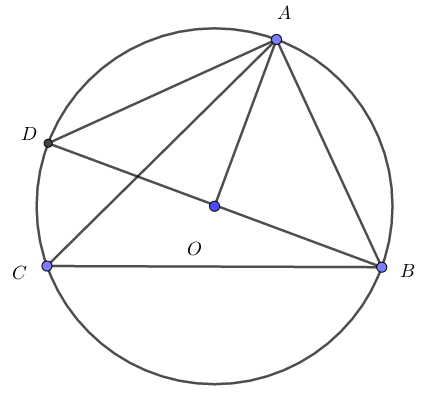
Ta có $BD\bot OA$ nên $OB=OD$.
Tam giác $ABD$ có $OA$ vừa là đường cao và là đường trung tuyến nên cân tại $A$.
Suy ra $AD=AB$.
Mà $AB<BC$ (gt). Suy ra $AD<BC\Rightarrow \overset\frown{AD}<\overset\frown{BC}$.
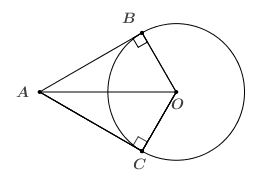
Ví dụ 2. Cho \(\left( O;R \right)\) và \(~A,\text{ }B\) thuộc \(\left( O \right)\) sao cho sđ\(\overset\frown{AB}=120{}^\circ \), \(C\)là điểm thuộc \(AB\) sao cho \(AC=R\). Chứng minh rằng \(OC\bot AB\).
Lời giải
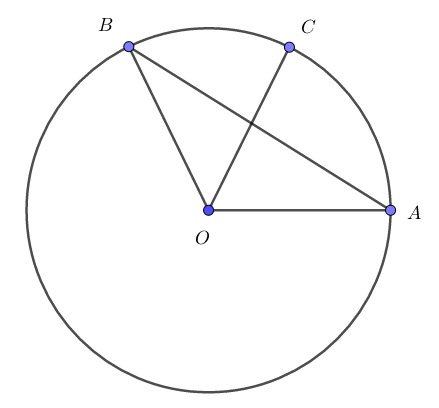
Tam giác $OAC$ có $OA=OB=AC=R$ nên là tam giác đều. Suy ra $\widehat{AOC}=60{}^\circ $. Mà sđ\(\overset\frown{AB}=120{}^\circ \Rightarrow \widehat{AOB}=120{}^\circ \).
Suy ra $\widehat{AOC}=\frac{1}{2}\widehat{AOB}\Rightarrow $$OC$ là phân giác $\widehat{AOB}$.
Tam giác $OAB$ cân tại $O$ có $OC$ là phân giác nên cũng là đường cao. Suy ra $OC\bot AB$.
2. BÀI TẬP CUNG VÀ DÂY CUNG TRONG ĐƯỜNG TRÒN
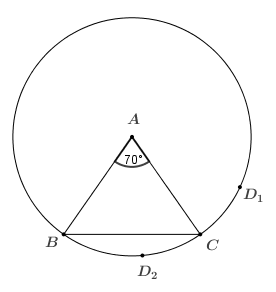
Bài 6. Cho \(\Delta ABC\)cân tại A nội tiếp \(\left( O;R \right)\), có \(\widehat{A}=80{}^\circ \). So sánh các cung:
\(\overset\frown{AB}\), \(\overset\frown{BC}\),\(\overset\frown{CA}\).

Lời giải
Vì $\Delta ABC$cân tại $A$ nên \(\widehat{ABC}=\widehat{ACB}=50{}^\circ \). Vì $\widehat{BAC}$ chắn \(\overset\frown{BC}\), $\widehat{ABC}$ chắn cung \(\overset\frown{CA}\) và $\widehat{ACB}$ chắn cung \(\overset\frown{AB}\) nên ta có \(\overset\frown{AB}\) = \(\overset\frown{CA}\) ; \(\overset\frown{BC}>\overset\frown{AB}\) ; \(\overset\frown{BC}\) > \(\overset\frown{CA}\).
Bài 7. Cho \(AB\) là dây cung của đường tròn \(\left( O;R \right)\text{ (AB}\ne \text{2R)}\). Vẽ \(OH\bot AB\)tại \(H\). Tia \(OH\) cắt đường tròn \((O)\) ở \(C\). Vẽ dây \(AD\) của (O) và $AD\,\text{//}\,BC$. Chứng minh rằng \(AC=\text{ }BC=\text{ }BD.\)
Lời giải
Nhận thấy $OC$ nằm trên đường kính của đường tròn $\left( O \right)$, mặt khác $OC$ lại đi qua trung điểm $H$của dây cung $AB$ và vuông góc với $AB$. Suy ra $OC$đi qua điểm chính giữa của cung $\overset\frown{AB}$,từ đó suy ra $\overset\frown{AC}=\overset\frown{BC}$. Vì hai cung bằng nhau căng hai dây bằng nhau nên suy ra $AC=BC$ (1) .
Mặt khác trong một đường tròn hai cung bị chắn bởi hai dây song song thì bằng nhau nên từ $AD\,\text{//}\,BC$ suy ra $AC=BD$ (2)
Từ (1) và (2) suy ra \(AC=\text{ }BC=\text{ }BD.\)
Bài 8. Cho nửa đường tròn $\left( O\,;\,R \right)$. Các điểm $M,N$ thuộc đường kính $BC$ sao cho $BM=MN=NC$. Các điểm $D,E$ thuộc $\overset\frown{BC}$ sao cho $BD=DE=EC$. Gọi $A$ là giao điểm của $DM$và $EN$. Chứng minh $\Delta ABC$ đều.
Lời giải
Nối $DO$, ta dễ dàng chứng minh được $DOCE$ là hình thoi. Suy ra $DE=OC=R$.
Vì $MN=\frac{BC}{3}=\frac{2R}{3}$ nên ta có $\frac{MN}{DE}=\frac{2R}{3}:R=\frac{2}{3}$.
Mặt khác $MN//DE$ nên $\frac{MA}{DA}=\frac{MN}{DE}=\frac{2}{3}$.
Từ đó suy ra $\Delta MDB\backsim \Delta MCA$ (c.g.c) $\Rightarrow $$AC=2BD=2R$. (1)
Chứng minh tương tự ta cũng có $AB=2R$(2)
Từ (1) và (2) suy ra $\Delta ABC$có $AB=AC=BC$ nên $\Delta ABC$đều.
Bài 9. Cho nửa đường tròn $\left( O\,;\,R \right)$, đường kính $AB=4cm$. Dây $CD\,\text{//}\,AB$ ($D$thuộc $\overset\frown{AC}$). Cho biết chu vi của hình thang $ABCD$ bằng $10cm$. Tính độ dài các cạnh của hình thang $ABCD$.
Lời giải
Vì $CD\,\text{//}\,AB$nên $\overset\frown{AD}=\overset\frown{CB}$$\Rightarrow $$AD=CB$. Gọi $AD=CB=x$$\left( x>0 \right)$ thì ta có $CD=10-2x-4=6-2x$.
Từ $D$ và $C$ dựng các đường thẳng vuông góc với $AB$ lần lượt tại $E$ và \(F\).
Suy ra $BF$= $\frac{AB-DC}{2}=\frac{2x-2}{2}$.
Áp dụng hệ thức liên hệ giữa cạnh huyền, cạnh góc vuông và hình chiếu vào tam giác $ACB$vuông tại $C$ ta có: $AB.BF=B{{C}^{2}}$ $\Leftrightarrow $$4.\frac{2x-2}{2}={{x}^{2}}$
$\Leftrightarrow $${{x}^{2}}-4x+4=0$$\Leftrightarrow $${{\left( x-2 \right)}^{2}}=0$$\Leftrightarrow $$x=2$.
Suy ra $CD=6-2.2=2cm$.
Vậy $AD=BC=CD=2cm$.
Bài 10. Cho nửa đường tròn \(\left( O;R \right)\) \(\left( AB\ne 2R \right)\), \(I\)là trung điểm của dây \(AB\); tia \(OI\) cắt \(\left( O \right)\)ở \(C\).
a) So sánh \(\overset\frown{AC}\) và \(\overset\frown{BC}\)
b) Vẽ dây \(MN\)qua \(I\). So sánh \(\overset\frown{MN}\) và \(\overset\frown{AB}\)
Lời giải
a) Có \(I\) là trung điểm của \(AB\) và \(AB\) là dây cung \((AB\ne 2R)\). Suy ra \( OI\bot AB\) tại \(I\) (đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây đó)
Mà: \(OA=OB\)
\(AI=IB\)(gt)
\(OI\bot AB\)(cmt)
\(\Rightarrow OC\)là đường trung trực của \(AB\)
\(\Rightarrow AC=BC\Rightarrow \overset\frown{AC}=\overset\frown{BC}\)
b) Kẻ \(OH\bot MN\)
\(\Rightarrow \Delta OHI\) vuông tại H nên \(OH<OI\) Mà \(OH,OI\) lần lượt là các khoảng cách từ \(O\) đến hai dây \(MN\) và \(AB\) \(\Rightarrow MN>AB\)\(\Rightarrow \overset\frown{MN}>\overset\frown{AB}\)
Bài 11. Cho tam giác \(ABC\) vuông tại \(A\), nội tiếp \(\left( O\,;\,R \right)\). Qua \(B\) vẽ dây cung \(BD\parallel AC\). Chứng minh rằng tứ giác \(ABCD\) là hình chữ nhật.
Lời giải
Xét đường tròn \((O)\) có
- \(BD\parallel AC\)(gt)
- \(AC\bot AB\)( vì \(\Delta ABC\) vuông tại \(A\))
\(\Rightarrow BD\bot AB\Rightarrow \widehat{ABD}=90{}^\circ \)
Xét \(\Delta BCD\) có \(D\in (O)\)
Suy ra \(\Delta BCD\) vuông tại \(D\). Do đó, \(BD\bot DC\Rightarrow \widehat{BDC}=90{}^\circ \)
Xét tứ giác \(ABCD\) có:
\(\begin{align}
& \widehat{ABD}=90{}^\circ \\
& \widehat{BDC}=90{}^\circ \\
& \widehat{BAC}=90{}^\circ \\
\end{align}\)
\(\Rightarrow \)Tứ giác \(ABCD\) là hình chữ nhật
Bài 12. Cho điểm \(A\) cố định nằm trong đường tròn $\left( O\,;\,R \right)$ $\left( A\ne O \right)$. \(BC\) là dây cung di động qua \(A\). Xác định vị trí của dây \(BC\) để cung \(BC\) nhỏ nhất.
Lời giải
Giả sử dây \(BC\)đi qua \(A\)và \(BC\bot OA\)tại \(A\)
Vẽ dây cung \(MN\) đi qua \(A\) \(\left( M,N\ne B,C \right)\)
Kẻ \(OH\bot MN\)
Xét \(\Delta OHA\) vuông tại \(H\)\(\Rightarrow OA>OH\)\(\Rightarrow d(O,BC)>d(O,MN)\Rightarrow BC<MN\)
Vậy dây \(BC\)nhỏ nhất khi đi qua \(A\)là dây vuông góc với \(OA\)