Phân dạng Bài tập công thức lượng giác
1. Lý thuyết công thức lượng giác
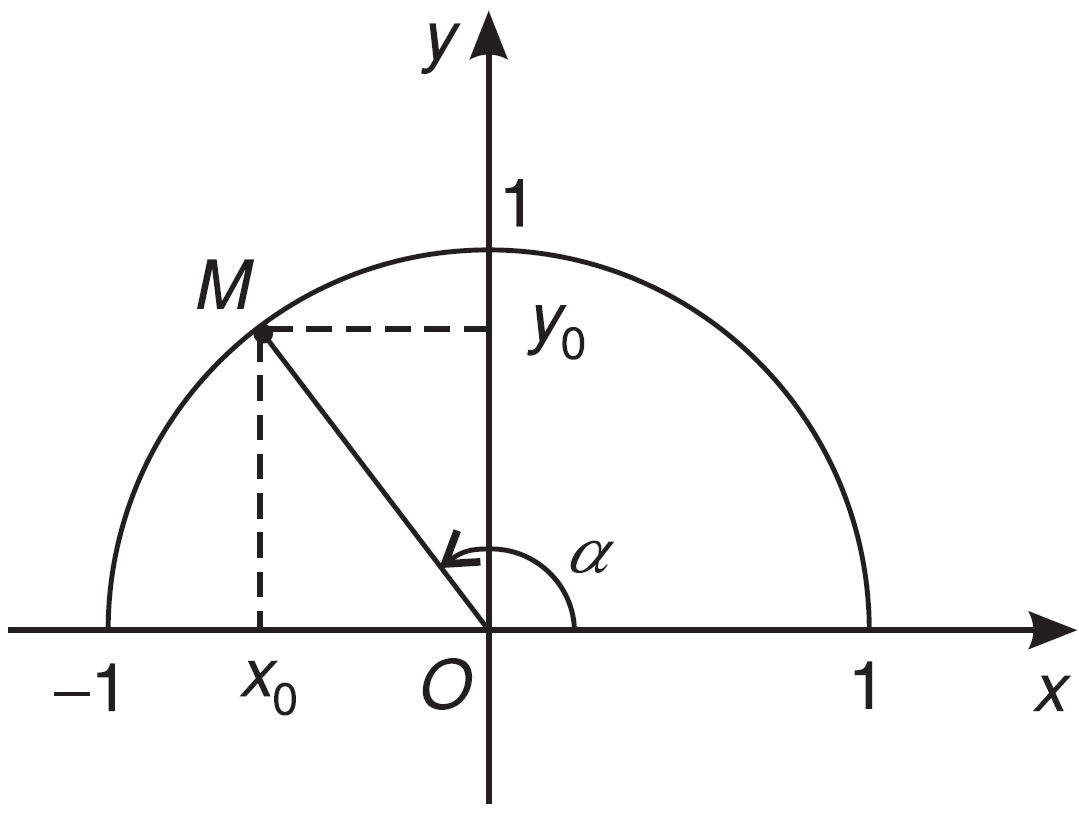
1.1. Khái niệm các giá trị lượng giác
Sử dụng đường tròn lượng giác, chúng ta có các khái niệm và kết quả sau:

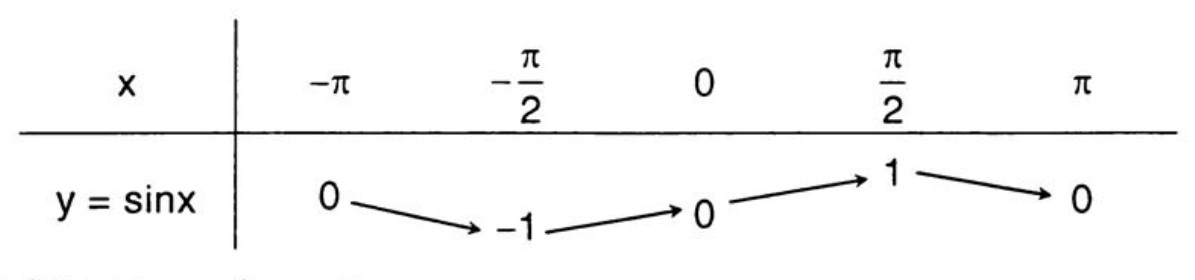
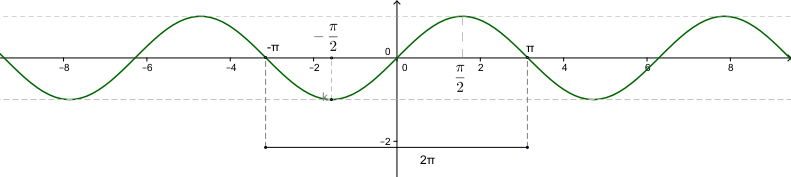
1.2. Giá trị lượng giác của các cung đặc biệt
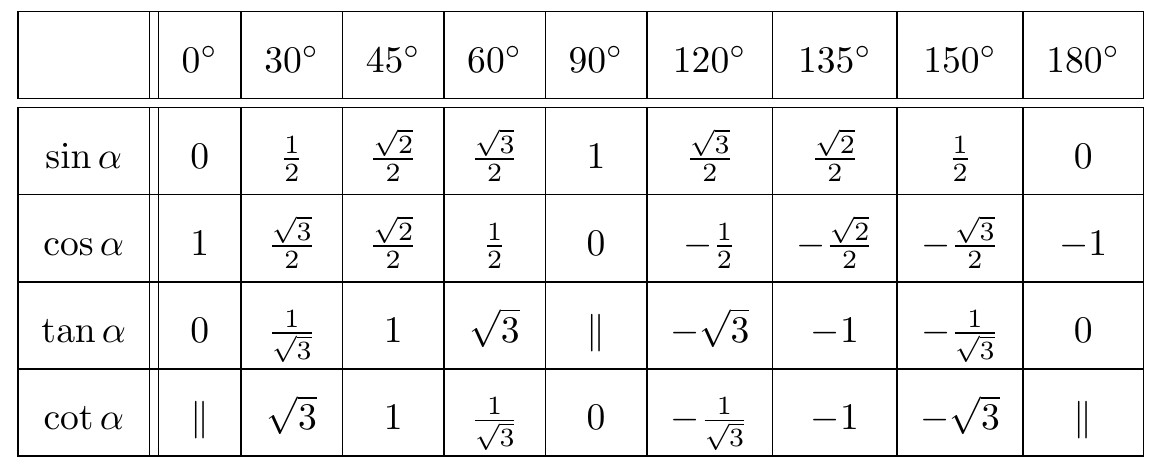
Bạn cần nhớ giá trị lượng giác của các góc đặc biệt $ 0,\dfrac{\pi}{6},\dfrac{\pi}{4},\dfrac{\pi}{3},\dfrac{\pi}{2},\pi $ như trong bảng sau:

1.3. Giá trị lượng giác của các cung có liên quan đặc biệt (cung liên kết)
Giá trị lượng giác của các cung có liên quan cos đối – sin bù – phụ chéo – khác $ \pi $ tan; hơn nhau ở tuổi 90…; hơn kém chẵn $ \pi $ thì sin-cos…
| STT |
Hai cung |
Gọi là hai cung |
Công thức |
Cách nhớ |
| 1 |
$\left( -a \right)$ và $a$ |
Đối nhau |
$\cos (-a)=\cos a$
$\sin (-a)=-\sin a$
$\tan (-a)=-\tan a$
$\cot (-a)=-\cot a$ |
Cos đối |
| 2 |
$\left( \pi -a \right)$ và$a$ |
Bù nhau |
$\sin (\pi -a)=\sin a$
$\cos(\pi -a)=-\cos a$
$\tan (\pi -a)=-\tan a$
$\cot (\pi -a)=-\cot a$ |
Sin bù |
| 3 |
$\left( \frac{\pi }{2}-a \right)$ và $a$
|
Phụ nhau |
$\sin \left( \frac{\pi }{2}-a \right)=\cos a$
$\cos\left( \frac{\pi }{2}-a \right)=\sin a$
$\tan \left( \frac{\pi }{2}-a \right)=\cot a$
$\cot \left( \frac{\pi }{2}-a \right)=\tan a$ |
Phụ chéo |
| 4 |
$\left( \pi +a \right)$ và $a$ |
Sai khác $\pi $ |
$\tan (\pi +a)=\tan a$
$\cot (\pi +a)=\cot a$
$\sin (\pi +a)=-\sin a$
$\cos(\pi +a)=-\cos a$ |
Khác $\pi $ tan, cot |
| 5 |
$\left( \frac{\pi }{2}+a \right)$ và $a$ |
Hơn $\frac{\pi }{2}$ |
$\sin \left( \frac{\pi }{2}+a \right)=\cos a$
$\cos\left( \frac{\pi }{2}+a \right)=-\sin a$
$\tan \left( \frac{\pi }{2}+a \right)=-\cot a$
$\cot \left( \frac{\pi }{2}+a \right)=-\tan a$ |
2 cung hơn nhau $\frac{\pi }{2}$ thì sin ( cung lớn) = cos ( cung nhỏ) |
Mời thầy cô và các em xem thêm ở bài Công thức lượng giác – Giá trị lượng giác của góc lớp 10
1.4. Các công thức lượng giác cơ bản
- $ \tan x=\dfrac{\sin x}{\cos x}, \cot x=\dfrac{\cos x}{\sin x},\tan x\cot x=1 $
- $ \sin^2x+\cos^2x=1, 1+\tan^2x=\dfrac{1}{\cos^2 x}, 1+\cot^2x=\dfrac{1}{\sin^2x} $
1.5. Công thức cộng
1.6. Công thức nhân và hạ bậc
1.7. Công thức biến đổi tổng thành tích và tích thành tổng
2. Các dạng toán và ví dụ điển hình
Ví dụ 1. Biểu diễn các cung có số đo: $ \dfrac{\pi}{4},\dfrac{5\pi}{4},\dfrac{\pi}{4}+k\pi,\dfrac{\pi}{6},\dfrac{13\pi}{6},\dfrac{\pi}{3}+k\dfrac{2\pi}{3},60^\circ+k120^\circ $ trên đường tròn lượng giác.
Ví dụ 2. Tính $ \tan 300^\circ,\sin(-780^\circ) $
Hướng dẫn.
$ \tan 300^\circ=-\sqrt{3},\sin(-780^\circ)=-\dfrac{\sqrt{3}}{2}. $
Ví dụ 3. Rút gọn các biểu thức
$ A=5\tan540^\circ+2\cos1170^\circ+4\sin990^\circ-3\cos540^\circ. $
$ B= 3\sin\dfrac{25\pi}{6}-3\tan\dfrac{13\pi}{4}+2\cos\dfrac{14\pi}{3}$
$ C=\dfrac{\sin(-234^\circ)-\cos216^\circ}{\sin144^\circ-\cos216^\circ}\cdot\tan36^\circ $
$ D=\sin(x+\pi)-\cos(\dfrac{\pi}{2}-x)+\cot(2\pi-x)+\tan(\dfrac{3\pi}{2}-x) $
Hướng dẫn.
$ A=-1, \quad B=-\dfrac{1}{2}, \quad C=1,\quad D=-2\sin x $
Ví dụ 4. Chứng minh các đẳng thức
- $ \sin^4x+\cos^4x=1-2\sin^2x\cos^2x $
- $ \sin^6x+\cos^6x=1-3\sin^2x\cos^2x $
- $ \dfrac{1-\cos x}{\sin x}=\dfrac{\sin x}{1+\cos x} $
- $ \dfrac{1+\cot x}{1-\cot x}=\dfrac{\tan x+1}{\tan x-1} $
Ví dụ 5. Rút gọn các biểu thức lượng giác sau:
$ A=(\tan x+\cot x)^2-(\tan x-\cot x)^2 $
$ B=(1-\sin^2x)\cot^2x+1-\cot^2x $
$ C=\tan x+\dfrac{\cos x}{1+\sin x} $
$ D=\dfrac{\cos x\tan x}{\sin^2x}-\cot x\cos x $
Hướng dẫn. $ A=4$, $B=\sin^2x$, $C=\dfrac{1}{\cos x}$, $D=\sin x $
Ví dụ 6. Chứng minh các biểu thức sau không phụ thuộc vào $ x $
$ A=\dfrac{\cot^2x-\cos^2x}{\cot^2x} $
$ B=\dfrac{(1-\tan^2x)^2}{4\tan^2x} $
$ C=2(\sin^6x+\cos^6x)-3(\sin^4x+\cos^4x) $
Hướng dẫn. $ A=1$, $B=-1$, $C=-1$
Ví dụ 7. Cho $ \cos\alpha=-\dfrac{3}{5} $ và $ 180^\circ<\alpha<270^\circ. $ Tính $ \sin\alpha,\tan\alpha,\cot\alpha? $
Hướng dẫn. $ \sin\alpha=-\dfrac{4}{5},\tan\alpha=\dfrac{4}{3},\cot\alpha=\dfrac{3}{4}. $
Ví dụ 8. Cho $ \tan\alpha=\dfrac{3}{4} $ và $ \pi<\alpha<\dfrac{3\pi}{2}. $ Tính Tính $ \sin\alpha,\tan\alpha,\cot\alpha? $
Hướng dẫn. $ \sin\alpha=-\dfrac{3}{5},\cos\alpha=-\dfrac{4}{5},\cot\alpha=\dfrac{4}{3}. $
3. Phân loại bài tập công thức lượng giác
Dạng 1. Tính giá trị lượng giác của một cung (góc)
Bài 1. Tính các giá trị lượng giác của góc, biết:
a) $\sin \alpha = \frac{2}{3},{\rm{ }}\frac{\pi }{2} < \alpha < \pi $
b) $\cos \alpha = \frac{4}{5},{\rm{ }}\frac{{3\pi }}{2} < \alpha < 2\pi $
c) $\cos \alpha = – \frac{5}{7},{\rm{ }} – \pi < \alpha < – \frac{\pi }{2}$
d) $\tan \alpha = \frac{4}{3},{\rm{ }}\pi < \alpha < \frac{{3\pi }}{2}$
e) $\cot \alpha = – \sqrt 3 ,{\rm{ }} – \frac{{3\pi }}{2} < \alpha < – \pi $
f) $\tan \alpha = \frac{7}{3},{\rm{ 0}} < \alpha < \frac{\pi }{2}$
Bài 2. Cho $\tan \alpha = 3$, tính giá trị các biểu thức
a) $A = \frac{{2\sin \alpha – 3\cos \alpha }}{{4\sin \alpha + 3\cos \alpha }}$
b) $B = \frac{{3\sin \alpha – 5\cos \alpha }}{{5{{\sin }^3}\alpha – 4{{\cos }^3}\alpha }}$.
Bài 3. Cho $\cot \alpha = \frac{3}{5}$, tính giá trị các biểu thức
a) $A = \frac{{\sin \alpha + \cos \alpha }}{{\sin \alpha – \cos \alpha }}$
b) $B = \frac{{\sin \alpha .\cos \alpha }}{{{{\sin }^2}\alpha – {{\cos }^2}\alpha }}$
c) $C = \frac{{3{{\sin }^2}\alpha + 12\sin \alpha \cos \alpha + 10{{\cos }^2}\alpha }}{{3{{\sin }^2}\alpha + \sin \alpha \cos \alpha – 2{{\cos }^2}\alpha }}$.
Bài 4. Tính giá trị các biểu thức lượng giác sau:
a) $A = \frac{{{{\sin }^2}\alpha – {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha – 2{{\cos }^2}\alpha }}$ biết $\cot \alpha = 3$.
b) $A = \frac{{2{{\sin }^2}\alpha – {{\cos }^2}\alpha – 1}}{{ – 2{{\sin }^2}\alpha + 3{{\cos }^2}\alpha }}$ biết $\tan \alpha = \frac{1}{4}$.
c) $C = \frac{{\cot \alpha + \tan \alpha }}{{\cot \alpha – \tan \alpha }}$ biết $\sin \alpha = \frac{3}{5},{\rm{ 0}} < \alpha < \frac{\pi }{2}$.
d) $D = \frac{{\sin \alpha + 3\cos \alpha }}{{\tan \alpha }}$ biết $\sin \alpha = – \frac{4}{5},{\rm{ }}\frac{{3\pi }}{2} < \alpha < 2\pi $.
e) $E = \frac{{4\cot \alpha + 3}}{{1 – 5\sin \alpha }}$ biết $\cos \alpha = – \frac{1}{3},{\rm{ }}\pi < \alpha < \frac{{3\pi }}{2}$.
f) $F = \frac{{\sin \alpha – 3\cos \alpha }}{{\cos \alpha – 2\sin \alpha }}$ biết $\tan \alpha = 3$.
Bài 5. Cho $\tan \alpha + \cot \alpha = m$. Hãy tính giá trị các biểu thức lượng giác sau $m$:
a) ${\tan ^2}\alpha + {\cot ^2}\alpha $
b) $\left| {\tan \alpha – \cot \alpha } \right|$
c) ${\tan ^3}\alpha + {\cot ^3}\alpha $
Bài 6. Cho $\sin \alpha + \cos \alpha = m$. Hãy tính:
a) $\sin \alpha \cos \alpha $
b) $\left| {\sin \alpha – \cos \alpha } \right|$
c) ${\sin ^3}\alpha + {\cos ^3}\alpha $
d) ${\sin ^4}\alpha + {\cos ^4}\alpha $ e) ${\sin ^6}\alpha + {\cos ^6}\alpha $
Dùng công thức cộng
Bài 8. Tính giá trị các biểu thức lượng giác sau:
a) $\cos \left( {x + \frac{\pi }{3}} \right)$, biết $\sin x = \frac{1}{{\sqrt 3 }}$ và $0 < x < \frac{\pi }{2}.$
b) $\tan \left( {x – \frac{\pi }{4}} \right)$, biết $\cos x = – \frac{1}{3}$ và $\frac{\pi }{2} < x < \pi .$
c) $\cos \left( {a + b} \right),{\rm{ }}\sin \left( {a – b} \right),$ biết $\sin a = \frac{4}{5},{\rm{ }}{0^0} < a < {90^0}$ và $\sin b = \frac{2}{3},{90^0} < a < {180^0}$.
Bài 9.
a) Cho $\sin a = – \frac{{12}}{{13}}$, với $\pi < a < \frac{{3\pi }}{2}$. Tính $\tan \left( {\frac{\pi }{3} – a} \right)$.
b) Cho $\sin a = \frac{5}{{13}},{\rm{ }}\cos b = \frac{3}{5}$ với $\frac{\pi }{2} < a < \pi ,{\rm{ }}\frac{\pi }{2} < b < \pi $. Tính $\sin \left( {a – b} \right),{\rm{ }}\cos \left( {a + b} \right)$.
c) Cho $\tan a = \frac{1}{2},{\rm{ sin}}b = \frac{3}{5}$ với $0 < b < \frac{\pi }{2}$. Tính $\cot \left( {a – b} \right),{\rm{ tan}}\left( {a + b} \right)$.
Bài 10. Cho $\tan \alpha = – \frac{{15}}{8}$ với $\frac{{3\pi }}{2} < b < 2\pi $.
a) Tính $\sin \alpha ,{\rm{ }}\cos \alpha ,{\rm{ }}\cot \alpha $.
b) Tính $\sin \left( {\alpha – 7\pi } \right),{\rm{ }}\cos \left( {\alpha + \frac{{2\pi }}{3}} \right),{\rm{ }}\cot \left( {\frac{{3\pi }}{4} – \alpha } \right)$.
Bài 11. Cho $\sin \alpha = \frac{8}{{17}},{\rm{ sin}}\beta = \frac{{15}}{{17}},{\rm{ 0}} < \alpha < \frac{\pi }{2},{\rm{ 0}} < \beta < \frac{\pi }{2}.$ Chứng minh $\alpha + \beta = \frac{\pi }{2}$.
Dùng công thức nhân
Bài 12. Tính $\sin 2a,{\rm{ }}\cos 2a,{\rm{ }}\tan 2a$, biết
a) $\sin a = – 0,6$ và $\pi < a < \frac{{3\pi }}{2}$.
b) $\sin a = \frac{3}{5}$ và $\frac{\pi }{2} < a < \pi $.
c) $\cos a = – \frac{5}{{13}}$ và $\frac{\pi }{2} < a < \pi $.
d) $\tan a = \frac{4}{3}$ và $\pi < a < \frac{{3\pi }}{2}$.
e) $\tan a = 2$.
f) $\cos a = \frac{1}{4}$ và $\frac{{3\pi }}{2} < a < 2\pi $.
g) $\sin a + \cos a = \frac{1}{2}$ và $\frac{{3\pi }}{4} < a < \pi $.
Bài 13. Cho $\cos a = – \frac{5}{{13}}$ với $\pi < a < \frac{{3\pi }}{2}$. Tính giá trị $$\sin 2a,{\rm{ }}\cos 2a,{\rm{ }}\cot \left( {\frac{\pi }{4} – a} \right),\sin \left( {{{30}^0} + a} \right)$$
Bài 14. Cho $\sin 2a = \frac{4}{5}{\rm{ }}\left( {\frac{\pi }{4} < a < \frac{\pi }{2}} \right)$. Tính $\sin a,{\rm{ }}\cos 2a,{\rm{ }}\cos 4a,{\rm{ tan}}\left( {\frac{\pi }{4} – 2a} \right).$
Bài 15. Cho $\sin 2a = – \frac{5}{9}{\rm{ }}\left( {\frac{\pi }{2} < a < \pi } \right)$. Tính $\sin a,{\rm{ }}\cos a.$
Bài 16. Cho $\cos 2a = \frac{3}{5}{\rm{ }}\left( {\frac{{3\pi }}{4} < a < \pi } \right)$. Tính $\sin a,{\rm{ }}\cos a,{\rm{ }}\tan a$.
Dạng 2. Rút gọn biểu thức lượng giác:
Bài 1. Rút gọn các biểu thức sau (không dùng máy tính):
a) $A = \sin {170^0}.\cos {80^0} + \cos {10^0}.\sin {80^0}.$
b) $B = \frac{{\cos \left( { – {{288}^0}} \right)\cot {{72}^0}}}{{\tan \left( { – {{162}^0}} \right)\sin {{108}^0}}} – \tan {18^0}$.
c) $C = \frac{{\sin \left( { – {{243}^0}} \right) + \sin {{126}^0}}}{{\sin {{144}^0} – \cos {{126}^0}}}.\tan {36^0}$.
d) $D = \frac{{\left( {\cot {{44}^0} + \tan {{226}^0}} \right).\cos {{406}^0}}}{{\cos {{316}^0}}} – \cot {72^0}.\cot {18^0}$.
Bài 2. Rút gọn các biểu thức sau ( không dùng máy tính ):
a) $A = {\sin ^2}\left( {{{180}^0} – x} \right) + {\tan ^2}\left( {{{180}^0} – x} \right).{\tan ^2}\left( {{{270}^0} + x} \right) + \sin \left( {{{90}^0} + x} \right).\cos \left( {x – {{360}^0}} \right)$.
b) $B = \frac{{\cos \left( {x – {{90}^0}} \right)}}{{\sin \left( {{{180}^0} – x} \right)}} + \frac{{\tan \left( {x – {{180}^0}} \right)\cos \left( {x + {{180}^0}} \right)\sin \left( {{{270}^0} + x} \right)}}{{\tan \left( {{{270}^0} + x} \right)}}$.
c) $C = \frac{{\sin {{20}^0}.\sin {{30}^0}.\sin {{40}^0}.\sin {{50}^0}.\sin {{60}^0}.\sin {{70}^0}}}{{\cos {{10}^0}.\cos {{50}^0}}}.$
d) $D = \tan {1^0}.\tan {2^0}.\tan {3^0}…..\tan {88^0}.\tan {89^0}.$
e) $E = \cos \frac{\pi }{7} + \cos \frac{{2\pi }}{7} + …. + \cos \frac{{6\pi }}{7}$.
Bài 3. Rút gọn các biểu thức sau:
a) $A = \cos \left( {x – \frac{\pi }{2}} \right) + \sin \left( {x – \pi } \right)$.
b) $B = \cos \left( {\pi – x} \right) + \sin \left( {x + \frac{\pi }{2}} \right)$.
c) $C = \cos \left( {\frac{\pi }{2} – x} \right) + \sin \left( {\frac{\pi }{2} – x} \right) – \cos \left( {\frac{\pi }{2} + x} \right) – \sin \left( {\frac{\pi }{2} + x} \right)$.
d) $D = \cos \left( {\frac{{3\pi }}{2} – x} \right) – \sin \left( {\frac{{3\pi }}{2} – x} \right) + \cos \left( {x – \frac{{7\pi }}{2}} \right) – \sin \left( {x – \frac{{7\pi }}{2}} \right).$
e) $E = \cos \left( {\frac{\pi }{2} – x} \right) + \cos \left( {\pi – x} \right) + \cos \left( {\frac{{3\pi }}{2} – x} \right) + \cos \left( {2\pi – x} \right).$
f) $F = \sin \left( {\frac{{5\pi }}{2} – x} \right) – \cos \left( {\frac{{13\pi }}{2} – x} \right) – 3\sin \left( {x – 5\pi } \right) – 2\sin x – \cos x.$
Bài 4. Rút gọn các biểu thức sau:
a) $A = \sin \left( {\pi – x} \right) – \cos \left( {\frac{\pi }{2} – x} \right) + \cot \left( {\pi + x} \right).\cot \left( {\frac{\pi }{2} – x} \right)$.
b) $B = \cos \left( {\frac{\pi }{2} + x} \right) + \cos \left( {2\pi – x} \right) + \cos \left( {3\pi + x} \right)$.
c) $C = \cot \left( {x – 4\pi } \right)\cos \left( {x – \frac{{3\pi }}{2}} \right) + \cos \left( {x + 6\pi } \right) – 2\sin \left( {x – \pi } \right)$.
d) $C = \sin \left( {x + 5\pi } \right) – \cos \left( {\frac{\pi }{2} – x} \right) + \cot \left( {4\pi – x} \right) + \tan \left( {\frac{\pi }{2} – x} \right)$.
e) $E = \cot \left( {x + 5\pi } \right).\cos \left( {x – \frac{{3\pi }}{2}} \right) + \cos \left( {x + 4\pi } \right) – 2\cos \left( {x + \frac{\pi }{2}} \right).$
f) $F = \cos \left( {x + 5\pi } \right) – 2\sin \left( {\frac{{11\pi }}{2} – x} \right) – \sin \left( {\frac{{11\pi }}{2} + x} \right).$
Công thức lượng giác cơ bản
Bài 5. Rút gọn các biểu thức sau:
a) $A = \left( {1 – {{\sin }^2}a} \right){\cot ^2}a + 1 – {\cot ^2}a.$ b) $B = {\cos ^4}a + {\sin ^2}a.{\cos ^2}a + {\sin ^2}a.$
c) $C = \frac{{{{\cos }^2}x – {{\cot }^2}x}}{{{{\sin }^2}x – {{\tan }^2}x}}$ d) $D = \frac{{{{\left( {\sin a + \cos a} \right)}^2} – 1}}{{\cot a – \sin a.\cos a}}$.
e) $E = \left( {1 + \cot a} \right).{\sin ^3}a + \left( {1 + \tan a} \right).{\cos ^3}a$ f) $F = \frac{{{{\sin }^2}x + 2{{\cos }^2}x – 1}}{{{{\cot }^2}a}}$.
Bài 6. Rút gọn các biểu thức sau:
a) $A = 1 – {\cos ^2}a + {\cot ^2}a.{\sin ^2}a$.
b) $B = \frac{{2{{\cos }^2}a – 1}}{{\sin a + \cos a}}$.
c) $C = \cot a – \frac{{\cos a}}{{\sin a + 1}}$
d) $D = \frac{{\sin a + 1}}{{\cos a}}.\left[ {1 – {{\left( {\frac{{1 – \sin a}}{{\cos a}}} \right)}^2}} \right].$
e) $E = \sqrt {\left( {1 + \cot a} \right).{{\sin }^2}a + \left( {1 + \tan a} \right).{{\cos }^2}a} $.
Bài 7. Chứng minh các biểu thức sau không phụ thuộc vào biến $x$.
a) $A = 3.{\cos ^2}x.\left( {1 + {{\tan }^2}x} \right) – {\sin ^2}x\left( {1 + {{\cot }^2}x} \right)$
b) $B = \frac{{{{\sin }^4}x + {{\cos }^4}x – 1}}{{{{\sin }^2}x.{{\cos }^2}x}}$.
c) $C = \frac{{\cot {}^2x – {{\cos }^2}x}}{{\cot {}^2x}} + \frac{{\sin x.\cos x}}{{\cot x}}$
d) $D = \frac{2}{{\tan x – 1}} + \frac{{\cot x + 1}}{{\cot x – 1}}$.
e) $E = 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) – 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)$ .
f) $F = {\left( {\tan x + \cot x} \right)^2} – {\left( {\tan x – \cot x} \right)^2}$.
g) $G = \sqrt {{{\sin }^4}x + 4{{\cos }^2}x} + \sqrt {{{\cos }^4}x + 4{{\sin }^2}x} $ .
h) $H = 2{\cos ^4}x – {\sin ^4}x + {\sin ^2}x.{\cos ^2}x + 3{\sin ^2}x$.
Công thức cộng, nhân, biến đổi
Bài 8. Rút gọn các biểu thức sau:
a) $A = \sin \left( {a + b} \right) + \sin \left( {\frac{\pi }{2} – a} \right).\sin \left( { – b} \right)$
b) $B = \cos \left( {\frac{\pi }{4} – a} \right).\cos \left( {\frac{\pi }{4} + a} \right) + \frac{1}{2}{\sin ^2}a$
c) $C = \cos \left( {\frac{\pi }{2} – a} \right).\sin \left( {\frac{\pi }{2} – b} \right) – \sin \left( {a – b} \right)$
d) $D = \cos a.\cos \left( {\frac{\pi }{3} – a} \right).\cos \left( {\frac{\pi }{3} + a} \right)$.
e) $E = \cos \left( {x + {{17}^0}} \right).\cos \left( {{{13}^0} – x} \right) – \sin \left( {{{17}^0} + x} \right).\sin \left( {{{13}^0} – x} \right)$.
f) $F = \sin \left( {2x + \frac{\pi }{3}} \right)\cos \left( {x – \frac{\pi }{6}} \right) – \cos \left( {2x + \frac{\pi }{3}} \right).\cos \left( {\frac{{2\pi }}{3} – x} \right)$.
Bài 9. Rút gọn các biểu thức sau:
a) $A = \frac{{\sin \left( {x + \frac{\pi }{4}} \right) – \cos \left( {x + \frac{\pi }{4}} \right)}}{{\sin \left( {x + \frac{\pi }{4}} \right) + \cos \left( {x + \frac{\pi }{4}} \right)}}$
b) $B = \frac{{\cot x – \tan x}}{{\cos 2x}}$.
c) $C = \frac{{\sin a + \sin 3a + \sin 5a}}{{\cos a + \cos 3a + \cos 5a}}$
d) $D = \frac{{\sin a.\cos 5a – \sin 5a.\cos 3a}}{{\cos 2a}}$.
e) $H = \sin x\left( {1 + 2\cos 2x + 2\cos 4x + 2\cos 6x} \right)$.
Bài 10. Rút gọn các biểu thức:
a) $A = \frac{{\sin a + \sin 2a}}{{1 + \cos a + \cos 2a}}$
b) $B = \frac{{4{{\sin }^2}a}}{{1 – {{\cos }^2}\frac{a}{2}}}$
c) $C = \frac{{1 + \cos a – \sin a}}{{1 – \cos a – \sin a}}$
d) $D = \frac{{1 + \sin a – 2{{\sin }^2}\left( {{{45}^0} – \frac{a}{2}} \right)}}{{4\cos \frac{a}{2}}}$.
e) $E = \frac{{\tan 2a}}{{\tan 4a – \tan 2a}}$
f) $F = \frac{{3 – 4\cos 2a + \cos 4a}}{{3 + 4\cos 2a + \cos 4a}}$
g) $G = \sqrt {1 + \sin a} – \sqrt {1 – \sin a} ,{\rm{ }}0 < a < \frac{\pi }{2}$ h) $H = \frac{{\sin a + \sin 3a + \sin 5a}}{{\cos a + \cos 3a + \cos 5a}}$
Bài 11. Chứng minh các biểu thức sau không phụ thuộc vào biến $x$.
a) $A = \sin 8x + 2{\cos ^2}\left( {{{45}^0} + 4x} \right)$
b) $B = \cos x + \cos \left( {x + \frac{{2\pi }}{3}} \right) + \cos \left( {x + \frac{{4\pi }}{3}} \right)$
c) $C = \cos \left( {x – \frac{\pi }{3}} \right)\cos \left( {x + \frac{\pi }{4}} \right) + \cos \left( {x + \frac{\pi }{6}} \right).\cos \left( {x + \frac{{3\pi }}{4}} \right)$
d) $D = \sin 2x – 2\sin \left( {x – {{15}^0}} \right).\cos \left( {x + {{15}^0}} \right)$.
e) $E = {\cos ^2}x + \sin \left( {x + {{30}^0}} \right).\sin \left( {x – {{30}^0}} \right)$
Bài 12. Chứng minh các biểu thức sau không phụ thuộc vào biến $x$.
a) $A = \sin 6x.\cot 3x – \cos 6x$
b) $B = \left( {\cot \frac{x}{3} – \tan \frac{x}{3}} \right).\tan \frac{{2x}}{3}$
c) $C = \frac{{{{\cos }^3}x – \cos 3x}}{{\cos x}} + \frac{{{{\sin }^3}x + \sin 3x}}{{\sin x}}$
d) $D = {\sin ^2}x + {\sin ^2}\left( {x + \frac{{2\pi }}{3}} \right) + {\sin ^2}\left( {\frac{{2\pi }}{3} – x} \right)$
e) $E = {\cos ^2}\left( {a – x} \right) + {\cos ^2}x – 2\cos a.\cos x.\cos \left( {a – x} \right)$
f) $F = {\left[ {\tan \left( {{{90}^0} – x} \right) – \cot \left( {{{90}^0} + x} \right)} \right]^2} – {\left[ {\cot \left( {{{180}^0} + x} \right) + \cot \left( {{{270}^0} + x} \right)} \right]^2}$.
Dạng 3. Chứng minh đẳng thức lượng giác
Bài 1. Chứng minh rằng với mọi góc $\alpha $ ta có:
a) $\sin \left( {\alpha + \frac{\pi }{2}} \right) = \cos \alpha $
b) $\cos \left( {\alpha + \frac{\pi }{2}} \right) = – \sin \alpha $
c) $\tan \left( {\alpha + \frac{\pi }{2}} \right) = – \cot \alpha $
d) $\cot \left( {\alpha + \frac{\pi }{2}} \right) = – \tan \alpha $.
Bài 2. Chứng minh các đẳng thức:
a) ${\tan ^2}\alpha – {\sin ^2}\alpha = {\tan ^2}\alpha .{\sin ^2}\alpha $
b) $\tan \alpha + \frac{{\cos \alpha }}{{1 + \sin \alpha }} = \frac{1}{{\cos \alpha }}$
c) $\frac{{{{\sin }^3}\alpha + {{\cos }^3}\alpha }}{{\sin \alpha + \cos \alpha }} = 1 – \sin \alpha .\cos \alpha $
d) $\frac{{{{\sin }^2}\alpha – {{\cos }^2}\alpha }}{{1 + 2\sin \alpha .\cos \alpha }} = \frac{{\tan \alpha – 1}}{{\tan \alpha + 1}}$
e) ${\sin ^4}\alpha + {\cos ^4}\alpha – {\sin ^6}\alpha – {\cos ^6}\alpha = {\sin ^2}\alpha .{\cos ^2}\alpha $
f) $2\left( {{{\sin }^6}\alpha – {{\cos }^6}\alpha } \right) + 1 = 3\left( {{{\sin }^4}\alpha + {{\cos }^4}\alpha } \right)$
g) ${\sin ^3}\alpha \left( {1 + \cot \alpha } \right) + {\cos ^3}\alpha \left( {1 + \tan \alpha } \right) = \sin \alpha + \cos \alpha $
Bài 3. Chứng minh các đẳng thức sau:
a) $\frac{{1 + {{\cos }^2}\alpha }}{{1 – {{\sin }^2}\alpha }} – \tan \alpha .\cot \alpha = \frac{1}{{{{\cos }^2}\alpha }}$ b)$\frac{{\sin \alpha + \cos \alpha – 1}}{{1 – \cos \alpha }} = \frac{{2\cos \alpha }}{{\sin \alpha – \cos \alpha + 1}}$
c) $\frac{{\sin \alpha }}{{\sin \alpha + \cos \alpha }} – \frac{{\cos \alpha }}{{\cos \alpha – \sin \alpha }} = \frac{{1 + {{\cot }^2}\alpha }}{{1 – {{\cot }^2}\alpha }}$
d) $\frac{{{{\sin }^2}\alpha }}{{\sin \alpha – \cos \alpha }} – \frac{{\sin \alpha + \cos \alpha }}{{{{\tan }^2}\alpha – 1}} = \sin \alpha + \cos \alpha $.
Sử dụng công thức cộng, nhân
Bài 4. Chứng minh các đẳng thức sau
a) $\cos x.\cos \left( {\frac{\pi }{3} – x} \right).\cos \left( {\frac{\pi }{3} + x} \right) = \frac{1}{4}\cos 3x$
b) $\frac{{\sin 2x + \sin x}}{{1 + \cos 2x + \cos x}} = \tan x$
c) $\sin 5x – 2\sin x\left( {\cos 4x + \cos 2x} \right) = \sin x$
d) $\frac{{1 + \cos x – \sin x}}{{1 – \cos x – \sin x}} = – \cot \frac{x}{2}$
e) $\frac{{\sin 2x}}{{1 + \cos 2x}}.\frac{{\cos x}}{{1 + \cos x}} = \tan \frac{x}{2}$
f) $\frac{{3 – 4\cos 2x + \cos 4x}}{{3 + 4\cos 2x + \cos 4x}} = {\tan ^4}x$
Bài 5. Chứng minh các đẳng thức sau:
a) $\sin \left( {a + b} \right).\sin \left( {a – b} \right) = {\sin ^2}a – {\sin ^2}b$
b) $\frac{{4\tan x\left( {1 – {{\tan }^2}x} \right)}}{{{{\left( {1 + {{\tan }^2}x} \right)}^2}}} = \sin 4x$
c) $\frac{{2\sin \left( {a + b} \right)}}{{\cos \left( {a + b} \right) + \cos \left( {a – b} \right)}} = \tan a + \tan b$
d) $\frac{{1 + {{\tan }^4}x}}{{{{\tan }^2}x + {{\cot }^2}x}} = {\tan ^2}x$
e) $\sin 2x – \sin 4x + \sin 6x = 4\sin x.\cos 2x.\cos 3x$
f) $\tan 3x – \tan 2x – \tan x = \tan x.\tan 2x.\tan 3x$
g) $\frac{{\cos x.\sin \left( {x – 3} \right) – \sin x.\cos \left( {x – 3} \right)}}{{\cos \left( {3 – \frac{\pi }{6}} \right) – \frac{1}{2}\sin 3}} = – \frac{{2\tan 3}}{{\sqrt 3 }}$
Dạng 4. Chứng minh đẳng thức lượng giác trong tam giác
Bài 1. Cho $\Delta ABC$. Chứng minh rằng:
a) $\sin \left( {A + B} \right) = \sin C$
b) $\cos \left( {A + B} \right) = – \cos C$
c) $\sin \frac{{A + B}}{2} = \cos \frac{C}{2}$
d) $\cos \frac{{A + B}}{2} = \sin \frac{C}{2}$
e) $\tan \frac{{A + B – C}}{2} = \cot C$.
Bài 2. Cho tam giác $ABC$. Chứng minh rằng:
a) $\sin A = \sin B.\cos C + \sin C.\cos B$
b) $\cos \frac{A}{2} = \sin \frac{B}{2}.\cos \frac{C}{2} + \sin \frac{C}{2}.\cos \frac{B}{2}$
c) $\sin 2A + \sin 2B + \sin 2C = 4\sin A.\sin B.\sin C$
d) $\cos A + \cos B + \cos C = 1 + 4\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2}$.
Bài 3. Cho tam giác $ABC$. Chứng minh rằng:
a) $\cos B.\cos C – \sin B.\sin C + \cos A = 0$.
b) $\sin A + \sin B + \sin C = 4\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}$.
c) $\cos 2A + \cos 2B + \cos 2C = – 1 – 4\cos A.\cos B.\cos C$.
d) $\tan \frac{A}{2}.\tan \frac{B}{2} + \tan \frac{B}{2}.\tan \frac{C}{2} + \tan \frac{C}{2}.\tan \frac{A}{2} = 1$