Biện luận hệ phương trình, hệ bất phương trình bằng đồ thị
Sử dụng sự tương giao của đường tròn và đường thẳng trong mặt phẳng tọa độ Oxy, chúng ta có thể dễ dàng Biện luận hệ phương trình, hệ bất phương trình có chứa tham số.
Xem thêm:
1. Lý thuyết biện luận hệ phương trình, hệ bất phương trình bằng đồ thị
Nhắc lại rằng, đối với hệ phương trình hai ẩn, hệ bất phương trình hai ẩn $ x,y$ thì mỗi nghiệm của nó là một cặp số $ (x;y)$ thỏa mãn hệ đã cho. Mỗi cặp số $ (x;y)$ này chính là tọa độ của một điểm ở trong mặt phẳng tọa độ $ Oxy$.
Để biện luận hệ phương trình, hệ bất phương trình đã cho, chúng ta biểu diễn các phương trình, bất phương trình của hệ bởi những đường thẳng, đường tròn hoặc miền mặt phẳng giới hạn bởi các đường thẳng, đường tròn trong mặt phẳng. Khi đó, số nghiệm của hệ phương trình, của hệ bất phương trình chính bằng số điểm chung của các đường thẳng và đường tròn này.
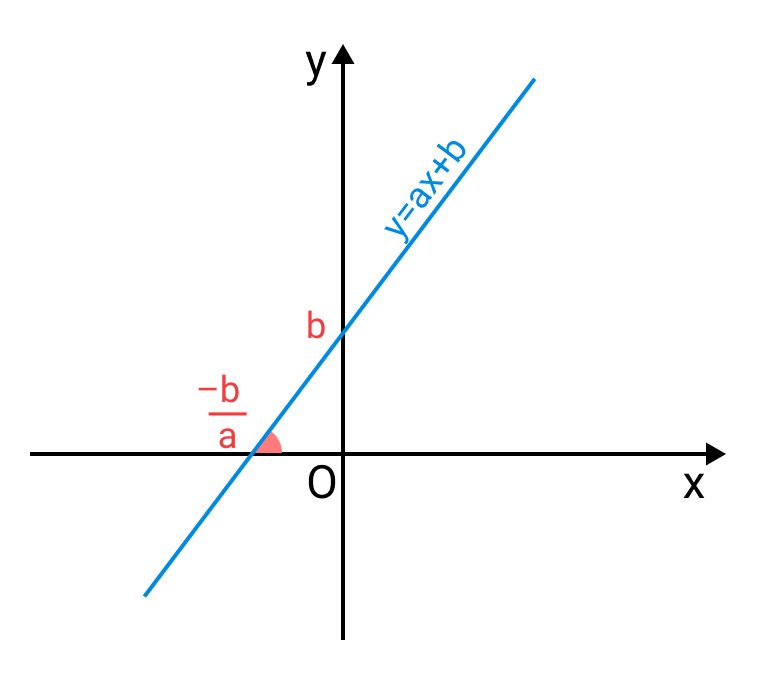
- Trong mặt phẳng $ Oxy$, phương trình đường thẳng có dạng tổng quát $$ ax+by+c=0 $$
- Phương trình đường tròn tâm $ I(a,b)$ bán kính $ R$ là $$ (x-a)^2+(y-b)^2=R^2 $$
- Khoảng cách từ điểm $ M(x_0;y_0)$ tới đường thẳng $ \Delta:ax+by+c=0$ là
$$ d(M,\Delta)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
- Vị trí tương đối của đường thẳng $ \Delta$ và đường tròn tâm $ I$, bán kính $ R$:
- có một điểm chung khi và chỉ khi $ d(I,\Delta)=R$
- có hai điểm chung khi và chỉ khi $ d(I,\Delta)<R$
- có không điểm chung khi và chỉ khi $ d(I,\Delta)>R$
2. Các ví dụ Biện luận hệ phương trình, hệ bất phương trình bằng đồ thị
Bài 1: Tìm $ a$ để hệ sau có nghiệm duy nhất: $$\left\{ \begin{array}{lr}
{x^2} + {y^2} – 2x \le 2&(1)\\
x – y + a = 0&(2)
\end{array} \right.$$
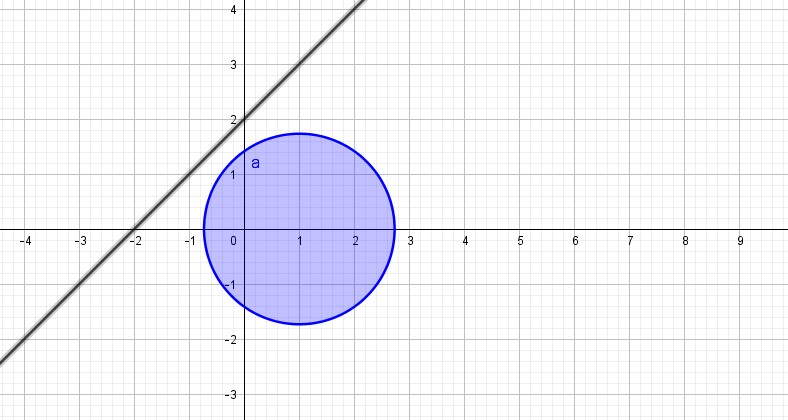
Lời giải: Ta có bất phương trình (1) tương đương với $$ {(x – 1)^2} + {y^2} \le 3$$ Bất phương trình này biểu diễn hình tròn $ (C)$ có tâm $ I(1;0)$ bán kính $R=\sqrt 3 $ trên mặt phẳng tọa độ $ Oxy$. Phương trình (2) biểu diễn đường thẳng $ \Delta:x-y+a=0$. Để hệ có nghiệm duy nhất thì đường thẳng phải tiếp xúc với đường tròn. Điều này xảy ra khi và chỉ khi
\begin{align*}
d\left( {I,\Delta } \right) &= R\\
\Leftrightarrow \frac{{\left| {1 – 0 – a} \right|}}{{\sqrt 2 }}& = \sqrt 3
\end{align*}
Giải hệ này, tìm được đáp số $ a = – 1 – \sqrt 6 ;a = – 1 + \sqrt 6 $.
Bài 2: Tìm $ a$ để hệ sau có nghiệm duy nhất: $$\left\{ \begin{array}{l}
x + y + \sqrt {2xy + m} \ge m\\
x + y \le 1
\end{array} \right.$$
Lời giải: Hệ bất phương trình đã cho tương đương với
\begin{align*}
&\left\{ \begin{array}{l}
\sqrt {2xy + m} \ge 1 – \left( {x + y} \right)\\
x + y \le 1
\end{array} \right.\\
\Leftrightarrow &\left\{ \begin{array}{l}
2xy + m \ge {\left( {1 – \left( {x + y} \right)} \right)^2}\\
x + y \le 1
\end{array} \right.\\
\Leftrightarrow &\left\{ \begin{array}{lr}
{\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} \le m + 1&\left( 3 \right)\\
x + y \le 1&\left( 4 \right)
\end{array} \right.
\end{align*}
- Với $m+1 \le 0$ hay $m \le -1$ thì hệ vô nghiệm.
- Với $ m+1 > 0$ hay $ m>-1$, thì bất phương trình (3) biểu diễn hình tròn $ (C)$ có tâm $ I(1;1)$ và bán kính $R=\sqrt {m + 1} $ trong mặt phẳng tọa độ Oxy. Bất phương trình (4) biểu diễn nửa mặt phẳng bờ là đường thẳng $ x+y=1$. Hệ có nghiệm duy nhất khi và chỉ khi đường thẳng $ x+y=1$ tiếp xúc với đường tròn $ (C)$. Điều kiện cần và đủ là
$$d(I,\Delta)=R \Leftrightarrow \frac{1}{{\sqrt 2 }} = \sqrt {m + 1} \Leftrightarrow m = – \frac{1}{2}$$
Bài 3: Tìm $ a$ để hệ sau có nghiệm: $$\left\{ \begin{array}{l}
4x – 3y + 2 \ge 0\\
{x^2} + {y^2} = a
\end{array} \right.$$
Lời giải:
- Nếu $ a\le 0$ hệ vô nghiệm.
- Nếu $ a> 0$ thì số nghiệm của hệ (nếu có) là số giao điểm của nửa mặt phẳng biểu diễn bởi bất phương trình $4x-3y+2 \le 0$ và đường tròn tâm $ O(0;0)$ bán kính $R=\sqrt a $. Do đó, hệ có nghiệm khi và chỉ khi $$\sqrt a \ge OH \Leftrightarrow a \ge \frac{4}{{25}},$$ trong đó, $ H$ là chân đường vuông góc hạ từ $ O$ xuống đường thẳng $ 4x-3y+2= 0$.
Bài 4: Cho hệ bất phương trình $$\left\{ \begin{array}{lr}
{\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} \le 2&(5)\\
x – y + m = 0&(6)
\end{array} \right.$$
Xác định $ m$ để hệ nghiệm đúng với mọi $x \in \left[ {0;2} \right]$.
Lời giải: Tập hợp các điểm $ (x;y)$ thỏa mãn (5) là các điểm nằm trong và trên đường tròn $${\left( {x – 1} \right)^2} + {\left( {y – 1} \right)^2} = 2$$
Đường tròn này có tâm $ I(1;1)$ và bán kính $R = \sqrt 2 $. Tập hợp các điểm $ (x;y)$ thỏa mãn (6) là các điểm nằm trên đường thẳng $\Delta $ có phương trình $x-y+m=0.$
Gỉa sử điểm $A \in \Delta $ sao cho ${x_A} = 0$ thì tọa độ của $ A$ là $ (0;m)$; $B \in \Delta $ sao cho ${x_B} = 2$ thì $ B(2;2+m)$.
Hệ có nghiệm với mọi $x \in \left[ {0;2} \right]$ khi và chỉ khi đoạn thẳng $ AB$ nằm trong đường tròn $ (I;R)$. Lúc đó
$$\left\{ \begin{array}{l} IA \le R\\ IB \le R
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{\left( {0 – 1} \right)^2} + {\left( {m – 1} \right)^2} \le 2\\
{\left( {2 – 1} \right)^2} + {\left( {2 + m – 1} \right)^2} \le 2
\end{array} \right. $$
Giải hệ này tìm được $ m = 0$
Bài 5: Cho hệ phương trình $$\left\{ \begin{array}{lr}
{x^2} + {y^2} – x = 0&(7)\\
x + ay – a = 0&(8)
\end{array} \right.$$
Tìm $ a$ để hệ có hai nghiệm phân biệt.
Lời giải: Phương trình (7) tương đương với $$ {\left( {x – \frac{1}{2}} \right)^2} + {y^2} = \frac{1}{4}$$
Đây là một đường tròn tâm $I\left( {\frac{1}{2};0} \right)$ bán kính $R=\frac{1}{2}$. Tập nghiệm của phương trình (8) là tọa độ những điểm nằm trên đường thẳng $ x+ay-a=0$. Họ đường thẳng này luôn di qua điểm $ A(0;1)$ cố định.
Nhận xét điểm $ A$ nằm ngoài đường tròn $ (I;R)$, nên từ $ A$ kẻ được hai tiếp tuyến với đường tròn $ (I;R)$.
Phương trình tiếp tuyến đó là: $ x=0$ và $x + \frac{4}{3}y – \frac{4}{3} = 0$.
Để hệ có hai nghiệm phân biệt thì đường thẳng $ x+ay-a=0$ phải cắt đường tròn (I;R) tại hai điểm phân biệt. Vậy đường thẳng $ x+ay-a=0$ phải nằm giữa hai tiếp tuyến trên. Điều này xảy ra khi và chỉ khi $0 <a < \frac{4}{3}$.
Bài 6: Tìm $ m$ để phương trình sau có nghiệm: $$\sqrt {1 – {x^2}} = m – x$$
Lời giải: Đặt $y = \sqrt {1 – {x^2}} $, điều kiện$y \ge 0$ thì phương tương đương với hệ bất phương trình
$$\left\{ \begin{array}{lr}
{x^2} + {y^2} = 1&(2)\\
x + y – m = 0&(3)
\end{array} \right.$$
Gọi hai đường thẳng song song với đường thẳng $ d:x+y-m=0$ và tiếp xúc với đường tròn $ {x^2} + {y^2} = 1$ là $d_1, d_2$. Chúng ta viết được phương trình của chúng là $$ x+y-1=0,\, x+y+\sqrt{2}=0 $$
Để phương trình đã cho có nghiệm thì đường thẳng $ d$ phải nằm giữa hai đường thẳng $ d_1$ và $ d_2$. Điều kiện cần và đủ là
$ – 1 \le m \le \sqrt 2 $.
Bài 7: Tìm GTLN của hàm số: $$y = x + \sqrt {a – {x^2}} (a > 0)$$
Lời giải: Đặt $t = \sqrt {{a^2} – {x^2}} \Leftrightarrow {x^2} + {t^2} = {a^2}$ và $ x+t-y=0$. Chúng ta cần tìm điều kiện để hệ sau có nghiệm
$$\left\{ \begin{array}{lr}
{x^2} + {t^2} = {a^2}&(1)\\
x + t – y = 0&(2)
\end{array} \right.$$
Bài 8: Hãy biện luận số nghiệm của hệ sau theo $ m$. $$\left\{ \begin{array}{lr}
x + y = 4(1)&\\
{x^2} + {y^2} = {m^2}&(2)
\end{array} \right.$$
Lời giải.
- Nếu $ m=0$ thì hệ vô nghiệm.
- Nếu $m \ne 0$ thì số nghiệm của hệ chính bằng số giao điểm của đường tròn ${x^2} + {y^2} = {m^2}$ và đường thẳng $\Delta 😡 + y = 4$
Điều kiện cần và đủ là $$ d(O,\Delta)= \frac{{\left| { – 4} \right|}}{{\sqrt 2 }} = 2\sqrt 2 $$
Vậy ta có:
- Nếu $\left| m \right| < 2\sqrt 2 $ hệ vô nghiệm.
- Nếu $m = \pm 2\sqrt 2 $ thì hệ có nghiệm duy nhất: $\left\{ \begin{array}{l}
x = 2\\ y = 2 \end{array} \right.$
- Nếu $\left| m \right| > 2\sqrt 2 $ thì hệ có hai nghiệm phân biệt.
Bài 9: Tìm $ a$ để bất phương trình sau có nghiệm $$\sqrt {a – x} + \sqrt {x + a} > a(a > 0)$$
Lời giải: Đặt $\left\{ \begin{array}{l}
u = \sqrt {a + x} \\
v = \sqrt {a – x}
\end{array} \right.$ với điều kiện $u,v \ge 0$. Bất phương trình đã cho tương đương với hệ:
$$\left\{ \begin{array}{lr}
u + v > a&(1)\\
{u^2} + {v^2} = 2a&(2)
\end{array} \right.$$
Làm tương tự các bài toán trước, đáp số là $ 0 < a < 4$.