Tag: hhkg

Cách chứng minh đường thẳng vuông góc với mặt phẳng
BỘ SÁCH HHKG GIÁ TỐT TRÊN SHOPEE

Cách chứng minh đường thẳng vuông góc với mặt phẳng, cách dựng một đường thẳng vuông góc với một mặt phẳng cho trước là bài toán quyết định của hình học không gian lớp 11, và cũng là cơ sở để giải quyết bài toán tính thể tích khối đa diện ở lớp 12.

Xem thêm Cách tìm giao tuyến của hai mặt phẳng

1. Lý thuyết đường thẳng vuông góc với mặt phẳng

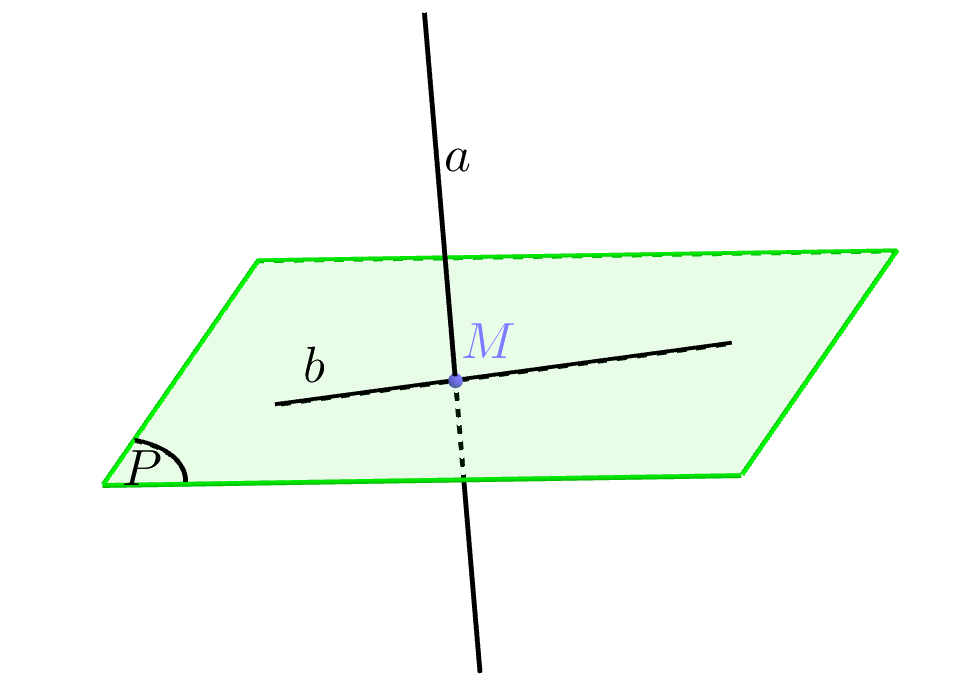
Định nghĩa. Một đường thẳng gọi là vuông góc với mặt phẳng nếu nó vuông góc với mọi đường thẳng nằm trong mặt phẳng ấy.

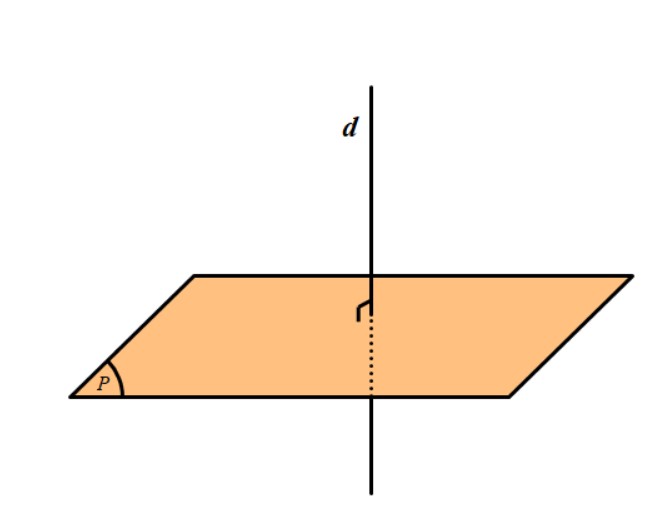
Tuy nhiên, để chứng minh một đường thẳng vuông góc với một mặt phẳng ta không cần chỉ ra nó vuông góc với mọi đường thẳng nằm trong mặt phẳng, mà ta chỉ cần sử dụng định lý sau.

Định lý. Nếu đường thẳng $d$ vuông góc với hai đường thẳng cắt nhau $a$ và $b$ cùng nằm trong mặt phẳng $(P)$ thì đường thẳng $d$ vuông góc với mặt phẳng $(P)$.

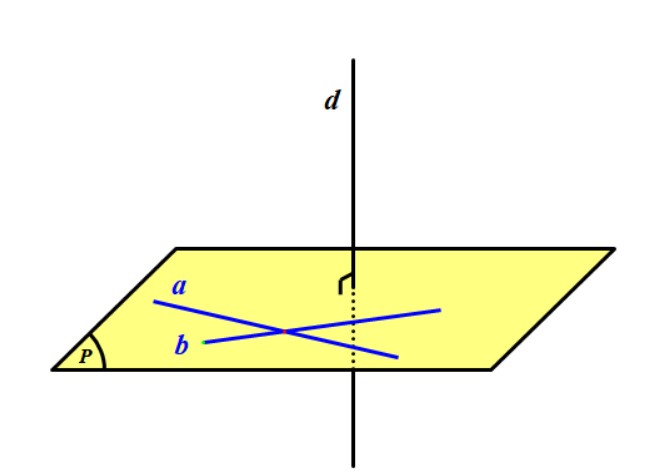
Như vậy, nếu một đường thẳng vuông góc với một mặt phẳng thì ta được sử dụng kết quả đường thẳng đó vuông góc với mọi đường thẳng của mặt phẳng đã cho. Nhưng để chứng minh thì ta chỉ cần chỉ ra nó vuông góc với hai đường thẳng cắt nhau của mặt phẳng đó là đủ.

Hệ quả: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì nó cũng vuông góc với cạnh thứ ba.

2. Ví dụ dạng toán chứng minh đường thẳng vuông góc mặt phẳng

Ví dụ 1. Cho hình chóp $S.ABC$ có $ SA$ vuông góc với đáy $(ABC), $ tam giác $ABC$ vuông tại $ B. $ Chứng minh rằng đường thẳng $ BC$ vuông góc với mặt phẳng $(SAB). $

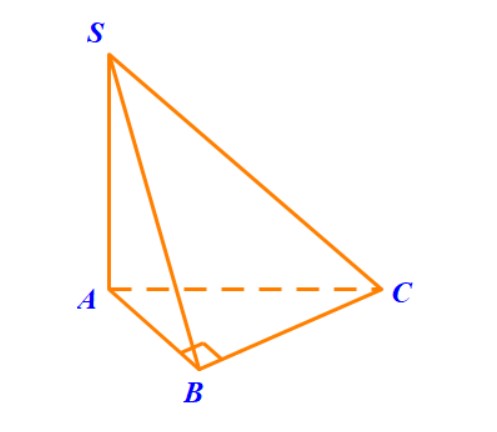
Hướng dẫn. Muốn chỉ ra đường thẳng $ BC$ vuông góc với mặt phẳng $(SAB) $ ta phải chỉ ra đường thẳng \(BC\) vuông góc với hai đường thẳng cắt nhau của mặt phẳng \( (SAB) \). Hiển nhiên ta đã có ngay \( BC\perp AB \) do tam giác \(ABC\) vuông tại \(B\). Cần phải tìm thêm một đường thẳng nữa cũng vuông góc với \( BC \) mà đường thẳng đó phải cắt \( AB \).
Chú ý rằng giả thiết cho \( SA \) vuông góc với mặt phẳng \( (ABC) \), tức là nó vuông góc với mọi đường thẳng nằm trong mặt phẳng \( (ABC) \). Nên, tất nhiên \( SA \) cũng vuông góc với \( BC \). Tóm lại, chúng ta có lời giải như sau.

Lời giải. Ta có \( SA\perp (ABC) \Rightarrow SA\perp BC \). Như vậy $$ \begin{cases}
BC\perp SA\\ BC\perp AB\\
AB,SA \subset (ABC)\\
AB,SA \text{ cắt nhau}
\end{cases}$$ Suy ra, $ BC$ vuông góc với mặt phẳng $(SAB). $

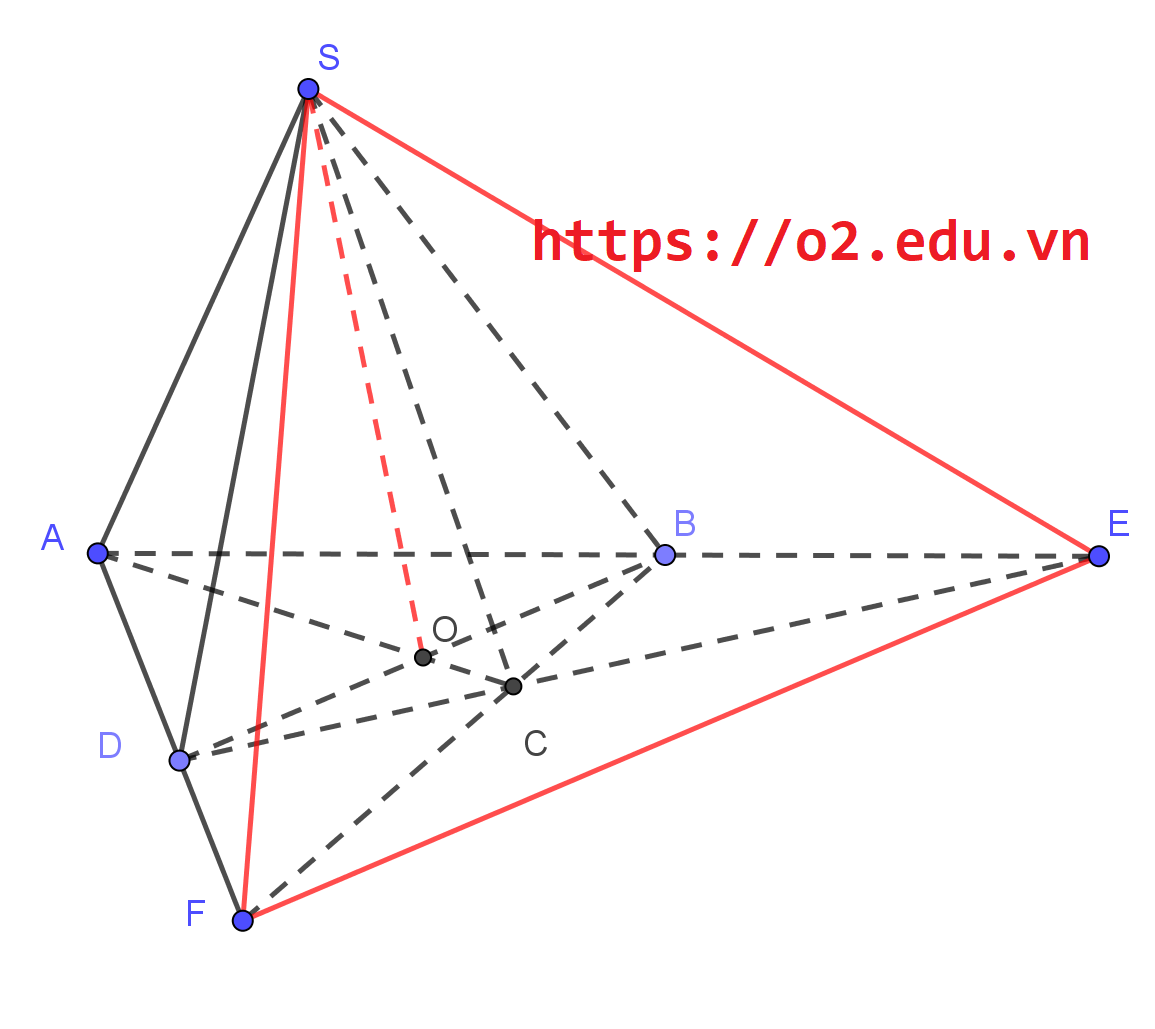
Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy là hình thoi tâm $ O, SA=SC $ và $ SB=SD. $

1. Chứng minh rằng đường thẳng $ SO $ vuông góc với mặt phẳng $ (ABCD).$

2. Gọi $ M, N $ lần lượt là trung điểm của $ SB $ và $ SD $. Chứng minh đường thẳng $ MN$ vuông góc với mặt phẳng $(SAC). $

Hướng dẫn.

1. Chỉ ra \( SO \) là đường cao trong tam giác cân \( SAC \) nên \( SO \perp AC\). Tương tự cũng chứng minh được \( SO\perp BD \). Mà \( AC \) và \( BD \) là hai đường thẳng cắt nhau, cùng nằm trong mặt phẳng \( (ABCD) \) nên suy ra \( SO \) vuông góc với \( (ABCD) \).

2. Ta chứng minh đường thẳng \( BD\) vuông góc với mặt phẳng \((SAC) \). Thật vậy, có
$$ \begin{cases}
BD\perp AC\\
BD\perp SO\\
AC,SO \subset (SAC)\\
AC, SO \text{ cắt nhau}
\end{cases} $$ Mặt khác \( MN \) là đường trung bình của tam giác \( SBD \) nên \( MN\parallel BD \). Do đó, đường thẳng \( MN \) vuông góc với mặt phẳng \( (SAC) \).

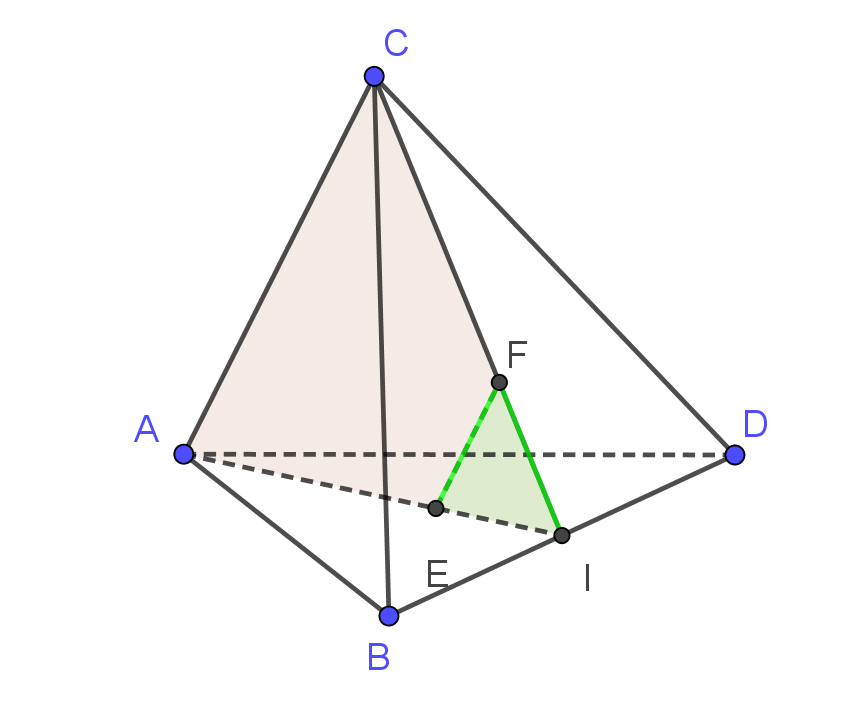
Ví dụ 3. Tứ diện $ ABCD $ có $ AC=AD $ và $ BC=BD. $ Chứng minh rằng đường thẳng $ CD$ vuông góc với đường thẳng $AB. $

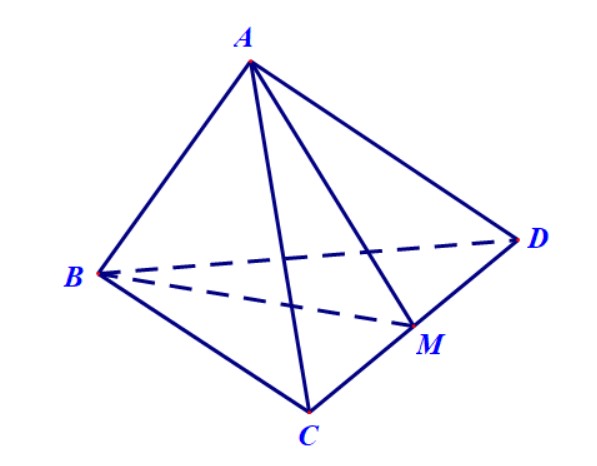
Hướng dẫn. Giả thiết $ AC=AD $ và $ BC=BD $ gợi cho chúng ta nghĩ đến các tính chất của tam giác cân. Mà tam giác cân thì yếu tố vuông góc chính là các đường cao đồng thời cũng là đường trung tuyến ứng với cạnh đáy. Do đó, chúng ta gọi trung điểm của \( CD \) là \( M \) thì có cách giải như sau.

Lời giải. Gọi trung điểm của cạnh \( CD \) là \( M \) thì ta có tam giác \( ACD \) cân tại \( A \) nên \( AM\perp CD \), tam giác \( BCD \) cân tại \( B \) nên \( BM\perp CD \). Tóm lại chúng ta có $$ \begin{cases}
CD\perp AM\\
CD\perp BM\\
AM,BM \subset (ABM)\\
AM,BM \text{ cắt nhau}
\end{cases} \Rightarrow CD \perp (ABM)$$ Mà đường thẳng \( AB \) nằm trong mặt phẳng \( (ABM) \) nên suy ra \( CD \) vuông góc với \( AB. \)

Ví dụ 4. Hình chóp $S.ABCD$ có đáy là hình chữ nhật và $ SA $ vuông góc với đáy. Chứng minh rằng đường thẳng $ CD $ vuông góc với mặt phẳng $ (SAD). $

Gợi ý. Hãy chỉ ra đường thẳng $ CD $ vuông góc với hai đường thẳng cắt nhau của mặt phẳng $ (SAD). $

Lời giải. Ta có \( ABCD \) là hình chữ nhật nên \( CD\perp AD \). Mặt khác, \( SA \) vuông góc với đáy \( (ABCD) \) nên \( SA \) vuông góc với mọi đường thẳng nằm trong \( (ABCD) \), đương nhiên trong đó có \( CD \). Tóm lại, chúng ta có được
$$ \begin{cases}
CD\perp AD\\
CD\perp SA\\
AD,SA\subset (SAD)\\
AD,SA \text{ cắt nhau}
\end{cases} $$ Suy ra, đường thẳng \( CD \) vuông góc với mặt phẳng \( (SAD). \)

Ví dụ 5. Hình chóp $ S.ABC $ có $ SA=SB=SC $. Chứng minh rằng $ O $ là hình chiếu của $ S $ lên mặt phẳng $(ABC)$ khi và chỉ khi $ OA=OB=OC. $

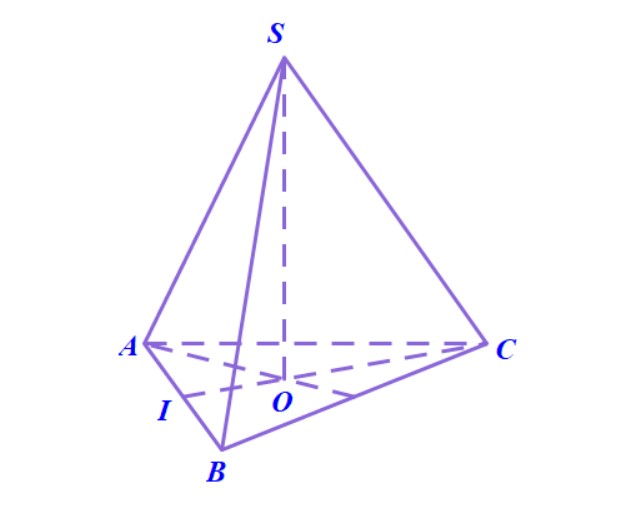
Hướng dẫn. Ta phải chứng minh cả hai chiều thuận và đảo của bài toán.
- Thuận: Có đường thẳng $ SO$ vuông góc với $(ABC) $ nên $ SO $ vuông góc với các đường thẳng $ OA,OB,OC. $ Ba tam giác vuông $ SOA,SOB,SOC $ bằng nhau nên suy ra $ OA=OB=OC. $
- Đảo: Từ $ OA=OB $ suy ra tam giác $ OAB $ cân tại $ O. $ Gọi $ I $ là trung điểm của $ AB $ thì $ AB $ vuông góc với $ OI $. Mặt khác, tam giác $SAB$ cũng cân tại $S$ nên và $ SI\perp AB. $ Do đó, $ AB $ vuông góc với $ SO. $
  Chứng minh tương tự có $ AC $ cũng vuông góc với $ SO. $ Từ đó suy ra $ SO $ vuông góc với mặt phẳng $ (ABC) $ hay $ O $ là hình chiếu của $ S $ lên mặt phẳng $ (ABC). $
Ví dụ 6. Cho hình chóp $ S.ABC $ có tam giác $ ABC $ vuông tại $ B $; cạnh bên $ SA $ vuông góc với đáy.

1. Chứng minh các mặt bên của hình chóp là các tam giác vuông.

2. Gọi $ H $ là hình chiếu vuông góc của $ A $ trên $ SB $, chứng minh đường thẳng $ AH $ vuông góc với mặt phẳng $ (SBC) $.

3. Gọi $ K $ là hình chiếu vuông góc của $ A $ lên $ SC, $ chứng minh đường thẳng $ SC $ vuông góc với mặt phẳng $ (AHK). $

4. Gọi $ I $ là giao điểm của $ BC $ và $ HK, $ chứng minh đường thẳng $ AI $ vuông góc với mặt phẳng $ (SAC). $

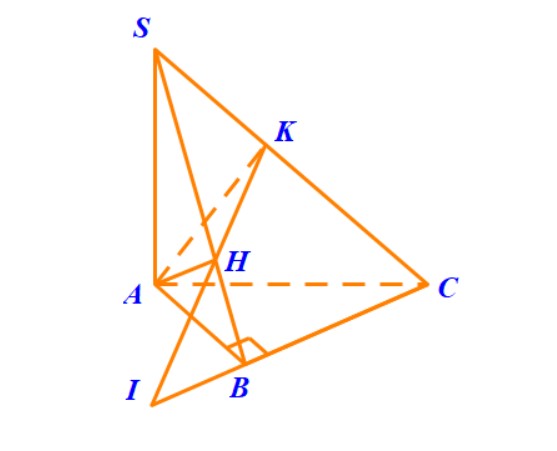
Hướng dẫn.

1. Vì \( SA \) vuông góc với đáy \( (ABC) \) nên \( SA \) vuông góc với \( AB,AC \). Do đó, các tam giác \( SAB, SAC \) vuông tại \( A \).

Để chứng minh tam giác \( SBC \) vuông, ta chứng minh \( BC\perp SB \) bằng cách chỉ ra \( BC \) vuông góc với mặt phẳng \( (SAB) \). Thật vậy, chúng ta có
$$ \begin{cases}
BC\perp AB\\
BC\perp SA\\
AB, SA \text{ cắt nhau}\\
AB, SA \subset (SAB)
\end{cases} $$

2. Theo chứng minh ở phần trước, có \( BC\perp (SAB) \) nên suy ra \( BC\perp AH \). Như vậy, ta có
$$ \begin{cases}
AH\perp SB\\AH\perp BC\\
BC, SB \text{ cắt nhau và nằm trong } (SBC)
\end{cases} $$ Suy ra đường thẳng \( AH \) vuông góc với mặt phẳng \( (SBC) \).

3. Chỉ ra \( SC \) vuông góc với hai đường thẳng cắt nhau của mặt phẳng \( (AHK) \) là \( AH \) và \( AK \).

4. Chỉ ra \( AI \) vuông góc với hai đường thẳng cắt nhau của mặt phẳng \( (SAC) \) là \( SA \) và \( SC \).

Ví dụ 7. Cho hình chóp $ S.ABC $, biết $ SA = SB = SC = a,$ $\widehat{ASB} = 60^\circ,$ $\widehat{BSC} = 90^\circ, $ $\widehat{CSA} = 120^\circ $. Gọi $ H $ là trung điểm $ AC $. Chứng minh $ SH $ vuông góc với mặt phẳng $ (ABC) $.

Hướng dẫn. Tam giác $ SAB $ đều nên $ AB = SA = a $. Tam giác $ SBC $ vuông tại $ S $ nên có $$ BC = \sqrt{SB^2 + SC^2} = a\sqrt{2}.$$ Tam giác $ SAC $ có $$ AC =\sqrt{SA^2 + SC^2 – 2SA.SC.\cos60^\circ}= a\sqrt{3}.$$ Từ đó suy ra tam giác $ ABC $ vuông tại $ B $. Vì $ H $ là trung điểm $ AC $ nên $ HA = HB = HC $, mà $ SA = SB = SC $ nên đường thẳng $ SH$ vuông góc với $(ABC) $.

Ví dụ 8. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác đều cạnh $ 2a $; cạnh bên $ SA $ vuông góc với đáy; $ SA = a\sqrt{3} $. Gọi $ E, F $ lần lượt là trung điểm của $ BC $ và $ SE $. Chứng minh hai đường thẳng $ AF $ và $ SC $ vuông góc với nhau.
Gợi ý. Chỉ ra tam giác $ SAE $ vuông cân tại $ A $.

Ví dụ 9. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $; cạnh bên $ SA $ vuông góc với đáy và $ SA = a\sqrt{2}$. Gọi $ M, N $ lần lượt là hình chiếu của $ A $ trên $ SB $ và $ SD $, chứng minh đường thẳng $ SC $ vuông góc với mặt phẳng $ (AMN) $. Gọi $ K $ là giao điểm của $ SC $ và $ (AMN) $. Chứng minh $ AK $ và $ MN $ vuông góc với nhau và tính diện tích tứ giác $ AMKN $.

Ví dụ 10. [Đề thi ĐH Khối B năm 2002] Cho hình lập phương $ ABCD.A’B’C’D’ $. Gọi $ M, N, P $ lần lượt là trung điểm của $ BB’,CD,A’D’ $. Chứng minh đường thẳng $ MP $ vuông góc với $ C’N $.

Ví dụ 11. Cho tứ diện $ OABC $ có $ OA, OB, OC $ đôi một vuông góc với nhau. Gọi $ H $ là hình chiếu vuông góc của điểm $ O $ trên mặt phẳng $ (ABC) $. Chứng minh rằng đường thẳng $ BC $ vuông góc với mặt phẳng $ (OAH) $. Chứng minh $ H $ là trực tâm tam giác $ ABC $ và tính độ dài $ OH $ theo $ OA,OB,OC. $ Chứng minh tam giác $ABC$ là tam giác nhọn.

Ví dụ 12. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $. Mặt bên $ SAB $ là tam giác đều còn $ SAD $ là tam giác vuông cân đỉnh $ S $. Gọi $ I, J $ lần lượt là trung điểm của $ AB $ và $ CD $. Tính các cạnh của tam giác $ SIJ $ và chứng minh rằng $ SI $ vuông góc với $ (SCD), SJ $ vuông góc với $ (SAB) $. Gọi $ H $ là hình chiếu vuông góc của $ S $ trên $ IJ $. Chứng minh rằng $ SH $ vuông góc $ AC $. Gọi $ M $ là một điểm thuộc đường thẳng $ CD $ sao cho đường thẳng $ BM $ vuông góc với $ SA $. Tính độ dài đoạn $ AM $ theo $ a $.

Đáp số. $SI=\frac{a}{2},\frac{a\sqrt{3}}{2} $; $\frac{a\sqrt{5}}{2}. $

3. Video bài giảng đường thẳng vuông góc với mặt phẳng

https://www.youtube.com/watch?v=aE-Ow2I5b7Q

https://www.youtube.com/watch?v=dKQiFn55Yzs

https://www.youtube.com/watch?v=LEcaaqpsCg4
02/06/2020
Cách tìm giao tuyến của hai mặt phẳng
Hướng dẫn cách tìm giao tuyến của hai mặt phẳng

Xem thêm
- Thiết diện là gì và các phương pháp tìm thiết diện
- Tìm giao điểm của đường thẳng và mặt phẳng
Chúng ta thừa nhận một kết quả sau của hình học không gian:

Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa. Tập hợp các điểm chung đó của hai mặt phẳng tạo thành một đường thẳng, được gọi là giao tuyến của hai mặt phẳng này.

Do đó, phương pháp chung để tìm giao tuyến của hai mặt phẳng phân biệt là ta chỉ ra hai điểm chung của chúng, và đường thẳng đi qua hai điểm chung đó chính là giao tuyến cần tìm.

1. Phương pháp xác định giao tuyến của hai mặt phẳng

Để xác định giao tuyến của hai mặt phẳng $(\alpha)$ và $ (\beta) $, chúng ta xét các khả năng sau:
- Nếu nhìn thấy ngay hai điểm chung $ A $ và $ B $ của hai mặt phẳng $(\alpha)$ và $ (\beta) $.
  Kết luận đường thẳng $ AB $ chính là giao tuyến cần tìm.
- Nếu chỉ chỉ tìm được ngay một điểm chung $ S $ của mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $. Lúc này, ta xét ba khả năng:
  - Hai mặt phẳng $(\alpha),(\beta)$ theo thứ tự chứa hai đường thẳng $d_1,d_2$ mà $d_1$ và $d_2$ cắt nhau tại $ I $ thì $ SI $ chính là giao tuyến cần tìm.
Đối với các em học sinh lớp 11 đầu năm thì chưa học đến quan hệ song song trong không gian nên sử dụng các kết quả trên là đủ. Sau khi các em học sang phần đường thẳng và mặt phẳng song song, hoặc các em học sinh lớp 12 thì sẽ sử dụng thêm các kết quả sau:
- - Hai mặt phẳng $(\alpha),(\beta)$ theo thứ tự chứa hai đường thẳng $d_1,d_2$ mà $d_1$ và $d_2$ song song với nhau thì giao tuyến cần tìm là đường thẳng $d$ đi qua $ S $ đồng thời song song với cả $ d_1,d_2. $
- - Nếu mặt phẳng $(\alpha)$ chứa đường thẳng $a$ mà $ a$ lại song song với $(\beta) $ thì giao tuyến cần tìm là đường thẳng $d$ đi qua $ S $ đồng thời song song với đường thẳng $ a. $
Đặc biệt, nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
Một số lưu ý.
- Cho mặt phẳng $ (ABC) $ thì các điểm $ A,B,C $ thuộc mặt phẳng $(ABC);$ các đường thẳng $ AB,AC,BC $ nằm trong mặt phẳng $ (ABC)$, và do đó mọi điểm thuộc những đường thẳng này đều thuộc mặt phẳng $ (ABC). $
- Hai đường thẳng chỉ cắt nhau được nếu chúng cùng thuộc một mặt phẳng nào đó, nên khi gọi giao điểm của hai đường thẳng ta phải xét trong một mặt phẳng cụ thể.
- Để tìm điểm chung của hai mặt phẳng ta chú ý tới tên gọi của chúng.
- Thường phải mở rộng mặt phẳng, tức là kéo dài các đường thẳng trong mặt phẳng đó.
2. Một số ví dụ tìm giao tuyến của 2 mp

Ví dụ 1. Cho tứ diện $ABCD$ có $ I $ là trung điểm của $ BD. $ Gọi $ E,F $ lần lượt là trọng tâm tam giác $ ABD$ và $CBD$. Tìm giao tuyến của hai mặt phẳng $ (IEF) $ và $ (ABC). $

Hướng dẫn.

Rõ ràng $E$ là trọng tâm của tam giác $ABD$ nên $E$ phải nằm trên đường thẳng $AI$. Suy ra, điểm $A$ thuộc vào đường thẳng $IE$. Tương tự, có điểm $F$ thuộc vào đường thẳng $CI$.
- Như vậy, chúng ta có: $$ \begin{cases} A\in (ABC)\\ A\in IE \subset (IEF) \end{cases}$$ hay $A$ là một điểm chung của hai mặt phẳng $ (IEF) $ và $ (ABC). $
- Tương tự, các em cũng chỉ ra được $C$ là một điểm chung nữa của hai mặt phẳng $ (IEF) $ và $ (ABC). $
Do đó, giao tuyến của hai mặt phẳng $ (IEF) $ và $ (ABC)$ là đường thẳng $AC$.

Ví dụ 2. Cho hình chóp $ S.ABCD $. Đáy $ABCD$ có $ AB $ cắt $ CD $ tại $ E$, $AC$ cắt $ BD $ tại $ F. $ Xác định giao tuyến của hai mặt phẳng:
1. $ (SAB) $ và $(SAC)$,
2. $ (SAB) $ và $ (SCD)$,
3. $(SAD)$ và $(SBC)$,
4. $(SAC) $ và $ (SBD) $,
5. $ (SEF) $ và $ (SAD)$,
Hướng dẫn.
1. Dễ thấy hai mặt phẳng $ (SAB) $ và $(SAC)$ cắt nhau theo giao tuyến là đường thẳng $SA$.
2. Ta thấy ngay $ (SAB) $ và $ (SCD)$ có một điểm chung là $S$. Để tìm điểm chung thứ hai, chúng ta dựa vào đề bài $ AB $ cắt $ CD $ tại $ E$. Tức là có $$\begin{cases} E\in AB\subset (SAB)\\ E\in CD\subset (SCD) \end{cases}$$. Như vậy $E$ là một điểm chung nữa của hai mặt phẳng $ (SAB) $ và $ (SCD)$.
  Tóm lại, giao tuyến của hai mặt phẳng $ (SAB) $ và $ (SCD)$ là đường thẳng $SE$.
3. Tương tự ý 2, các em tìm được giao tuyến của $(SAD)$ và $(SBC)$ là đường thẳng $SF$.
4. Giao tuyến của $(SAC) $ và $ (SBD) $ là đường thẳng $SO$, trong đó $O$ là giao điểm của $AC$ và $BD$.
5. $ (SEF) $ và $ (SAD)$ chính là đường thẳng $SF$.
Ví dụ 3. Cho tứ diện $ABCD$ có $ M $ thuộc miền trong tam giác $ ABC $. Xác định giao tuyến của mặt phẳng $ (ADM) $ và mặt phẳng $ (BCD) $.

Hướng dẫn.

Đầu tiên, chúng ta thấy ngay một điểm chung của hai mặt phẳng $ (ADM) $ và $ (BCD) $ là điểm $D$. Như vậy, nhiệm vụ của chúng ta là đi tìm một điểm chung nữa của hai mặt phẳng này.

Trong mặt phẳng $(ABC)$, kéo dài $AM$ cắt $BC$ tại $N$. Ta thấy $$\begin{cases} N\in BC \subset (BCD)\\ N\in AM\subset (ADM)\end{cases}$$ nên $N$ chính là một điểm chung nữa của hai mặt phẳng $ (ADM) $ và $ (BCD) $.

Tóm lại, giao tuyến của hai mặt phẳng $ (ADM) $ và $ (BCD) $ là đường thẳng $DN$.

Ví dụ 4. Cho bốn điểm $A, B, C, D$ không thuộc cùng một mặt phẳng. Trên các đoạn thẳng $AB, AC, BD$ lấy lần lượt các điểm $M, N, P$ sao cho $MN$ không song song với $BC$. Tìm giao tuyến của $(BCD)$ và $(MNP)$.

Hướng dẫn.

Vì P ∈ BD mà BD ⊂ (SBD) ⇒ P là một điểm chung của hai mặt phẳng (MNP) và (SBD).

Chúng ta cần tìm thêm một điểm chung nữa. Vì MN không song song với BC nên kẻ đường thẳng MN cắt đường thẳng BC tại I.

Khi đó,
- I ∈ MN mà MN ⊂ (MNP) ⇒ I ∈ (MNP)
- I ∈ BC mà BC ⊂ (SBC) ⇒ I ∈ (SBC)
Do vậy, I là một điểm chung của hai mặt phẳng (SBC) và (MNP).

Vậy, PI là giao tuyến của hai mặt phẳng (SBC) và (MNP).

Ví dụ 5. Cho tứ diện $ABCD$ có $ M $ thuộc miền trong tam giác $ ABC$, $N $ thuộc miền trong tam giác $ ABD$. Xác định giao tuyến của mặt phẳng $ (BMN) $ và mặt phẳng $ (ACD) $.

Hướng dẫn.

Trong mặt phẳng $(ABC)$, kéo dài $BM$ cắt $AC$ tại $P$ thì ta có:
- $P\in MB$ mà $MB$ nằm trong mặt phẳng $(BMN)$ nên $P$ cũng thuộc mặt phẳng $(BMN)$;
- $P\in AC$ mà $AC$ nằm trong mặt phẳng $(ACD)$ nên $P$ cũng thuộc mặt phẳng $(ACD)$;
Như vậy, $P$ là một điểm chung của hai mặt phẳng $ (BMN) $ và $ (ACD) $.

Tương tự, trong mặt phẳng $(ABD)$ kéo dài $BN$ cắt $AD$ tại $Q$ thì cũng chỉ ra được $Q$ là một điểm chung của hai mặt phẳng $ (BMN) $ và $ (ACD) $.

Tóm lại, giao tuyến của hai mặt phẳng $ (BMN) $ và $ (ACD) $ là đường thẳng $PQ$.

Ví dụ 6. Cho tứ diện $ABCD$ có $ M $ thuộc miền trong tam giác $ ABD,N $ thuộc miền trong tam giác $ ACD. $ Xác định giao tuyến của mặt phẳng $ (AMN) $ và mặt phẳng $ (BCD) $; mặt phẳng $ (DMN) $ và $ (ABC) $.

Hướng dẫn.

Ví dụ 7. Cho tứ diện $ABCD$ có $ I,J $ lần lượt là trung điểm của $ AC,BC. $ Lấy $ K $ thuộc $ BD $ sao cho $ KD<KB. $ Tìm giao tuyến của hai mặt phẳng $ (IJK) $ và $ (ACD),(IJK) $ và $ (ABD). $

Hướng dẫn.

Ví dụ 8. Cho tứ diện $ABCD$ có $ I,J $ lần lượt là trung điểm của $ AD,BC. $ Tìm giao tuyến của hai mặt phẳng $ (IBC) $ và $ (JAD). $ Gọi $ M,N $ là hai điểm trên cạnh $ AB,AC. $ Xác định giao tuyến của $ (IBC) $ và $ (DMN). $

Hướng dẫn.

Ví dụ 9. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm $BC,CD,SC $. Tìm giao tuyến của mặt phẳng $ (MNP) $ với các mặt phẳng $ (ABCD),(SAB),(SAD)$ và $ (SAC) $.

Hướng dẫn.

Ví dụ 10. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành tâm $ O. $ Gọi $ M,N,P $ lần lượt là trung điểm $BC,CD,SO $. Tìm giao tuyến của mặt phẳng $ (MNP) $ với các mặt phẳng $ (SAB),(SAD),(SBC) $ và $ (SCD)$.

Hướng dẫn.
01/06/2020
Tìm giao điểm của đường thẳng và mặt phẳng
Cách tìm giao điểm của đường thẳng và mặt phẳng
- Cách tìm giao tuyến của hai mặt phẳng
- Thiết diện là gì và các phương pháp tìm thiết diện
Bài toán. Trong không gian cho đường thẳng $a$ và mặt phẳng $(P)$. Tìm giao điểm (nếu có) của đường thẳng \(a\) và mặt phẳng \((P)\).

Phương pháp. Để tìm giao điểm của đường thẳng $a$ và mặt phẳng $(P)$ ta làm như sau:
- Nếu mặt phẳng $(P)$ chứa đường thẳng $ b $ mà $ b $ cắt đường thẳng $a$ tại $ M $ thì $ M $ chính là giao điểm cần tìm.
- Nếu chưa nhìn thấy đường thẳng nào trong mặt phẳng $(P)$ mà cắt đường thẳng $a$, thì ta thực hiện các bước sau:
  - Chọn một mặt phẳng $(Q)$ nào đó chứa đường thẳng $a$.
  - Xác định giao tuyến $ b $ của mặt phẳng $(P)$ và mặt phẳng $(Q)$.
  - Giao điểm $M$ của $ a $ và $ b $ chính là giao điểm cần tìm.
30/05/2020