Sự đồng biến nghịch biến của hàm số

1. Khái niệm sự đồng biến nghịch biến của hàm số

Để có kế hoạch, định hướng đúng đắn trong cuộc sống nhiều khi chúng ta phải biết được tốc độ tăng trưởng của một đại lượng nào đó, ví dụ, thị trường chứng khoán TQ mới bị khủng hoảng, suy thoái mà nếu theo dõi các bảng tin thời sự, tin tài chính ta sẽ thấy chỉ số của các sàn giao dịch được mô tả bằng các đường gấp khúc; theo chiều từ trái qua phải, nếu hướng lên là tăng, hướng xuống là giảm… (hoặc các biểu đồ giá vàng, USD, theo dõi nhiệt độ của các bệnh nhân, lượng mưa của một địa điểm, tốc độ tăng trưởng GDP, nợ công của VN…)

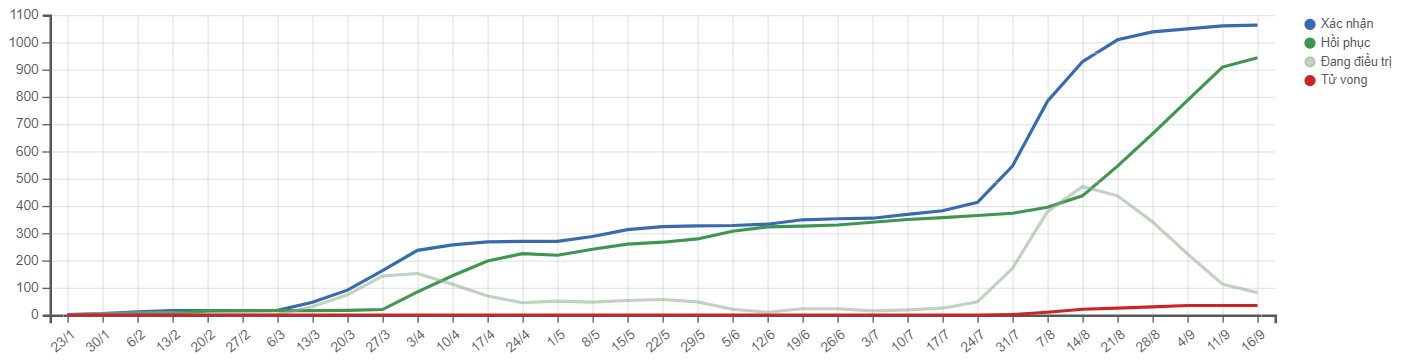
• Hàm số $ y=f(x) $ được gọi là tăng (đồng biến) trên $ \mathbb{K} $ nếu với mọi $ x_1,x_2\in \mathbb{K} $: $$x_1<x_2 \Leftrightarrow f(x_1)<f(x_2) $$
• Hàm số $ y=f(x) $ được gọi là giảm (nghịch biến) trên $ \mathbb{K} $ nếu với mọi $ x_1,x_2\in \mathbb{K} $: $$x_1<x_2 \Leftrightarrow f(x_1)>f(x_2) $$

2. Định lý về tính đơn điệu của hàm số

2.1. Mối quan hệ giữa đạo hàm và tính đồng biến nghịch biến của hàm số

Cho hàm số $ y=f(x) $ có đạo hàm trên $ \mathbb{K} $:

• Nếu $ f'(x)>0 $ với mọi $ x $ thuộc $ \mathbb{K} $ thì hàm số $ f(x) $ đồng biến trên $ \mathbb{K}. $
• Nếu $ f'(x)<0 $ với mọi $ x $ thuộc $ \mathbb{K} $ thì hàm số $ f(x) $ nghịch biến biến trên $ \mathbb{K}. $
• Nếu $ f'(x)=0 $ với mọi $ x $ thuộc $ \mathbb{K} $ thì hàm số $ f(x) $ không đổi (là hàm hằng) trên $ \mathbb{K}. $

Em nào quên cách tính đạo hàm của hàm số, có thể xem lại tại Tính đạo hàm của hàm số

Ví dụ 1. Chứng minh rằng hàm số $ y=3x+1 $ luôn đồng biến trên $ \mathbb{R}. $

Ví dụ 2. Chứng minh rằng hàm số $ y=-x^3-5x $ nghịch biến trên $ \mathbb{R}. $

Ví dụ 3. Chứng minh rằng hàm số $ y = 2x + \cos x $ luôn đồng biến trên $ \mathbb{R}. $

Ví dụ 4. Khảo sát sự biến thiên của hàm số $ y=x^2-3x+1 $.

Ví dụ 5. Tìm các khoảng đơn điệu của hàm số: $ y = -x^3 + 3x^2 $, $ y = \frac{{x + 1}}{{2x-3}} $?

Ví dụ 6. Tìm các khoảng đồng biến nghịch biến của hàm số $ y=\frac{4}{3}x^3-2x^2+x-3. $

Hướng dẫn. Bảng biến thiên của hàm số như hình vẽ sau:

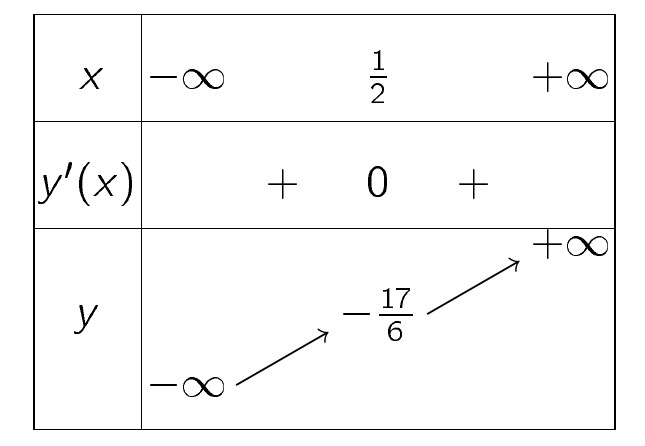
Như vậy, hàm số đồng biến trên mỗi khoảng $ (-\infty,\frac{1}{2}) $ và $ (\frac{1}{2},+\infty) $. Nhưng tại $ x=\frac{1}{2} $ hàm số liên tục, nên ta có thể gộp lại, kết luận rằng hàm số đồng biến trên toàn bộ tập $ \mathbb{R}. $

Chú ý. 

• Cho hàm số $ y=f(x) $ có đạo hàm trên $ \mathbb{K} $:
  • Nếu $ f'(x)\geqslant 0 $ với mọi $ x $ thuộc $ \mathbb{K} $ và dấu đẳng thức chỉ xảy ra tại hữu hạn điểm thì hàm số $ f(x) $ đồng biến trên $ \mathbb{K}. $
  • Nếu $ f'(x)\leqslant 0 $ với mọi $ x $ thuộc $ \mathbb{K} $ và dấu đẳng thức chỉ xảy ra tại hữu hạn điểm thì hàm số $ f(x) $ nghịch biến biến trên $ \mathbb{K}. $
• Lưu ý, nếu hàm số $f(x)$ xác định và liên tục trên đoạn $ [a,b] $ thì hàm số đồng biến trên đoạn $ [a,b] $ khi và chỉ khi hàm số đồng biến trên khoảng $ (a,b) $, tức là chỉ cần điều kiện $f'(x)\geqslant 0 $ với mọi $ x\in (a,b). $

Ví dụ 7. Chứng minh rằng hàm số $ y=\sqrt{3x+1} $ luôn đồng biến trên tập xác định.

• Tập xác định $ \mathbb{D}=[-\frac{1}{3},+\infty) $.
• Ta có, đạo hàm của hàm số là $$ y’=\frac{3}{2\sqrt{3x+1}} >0,\;\forall x\in (-\frac{1}{3},+\infty) $$
• Mà hàm số liên tục trên $ [-\frac{1}{3},+\infty) $ nên hàm số luôn đồng biến trên $ [-\frac{1}{3},+\infty) $.

Ví dụ 8. Tìm các khoảng đồng biến nghịch biến của hàm số $ y=\sqrt{1-x^2} $.

Hướng dẫn. Chúng ta lập được bảng biến thiên như hình vẽ sau:

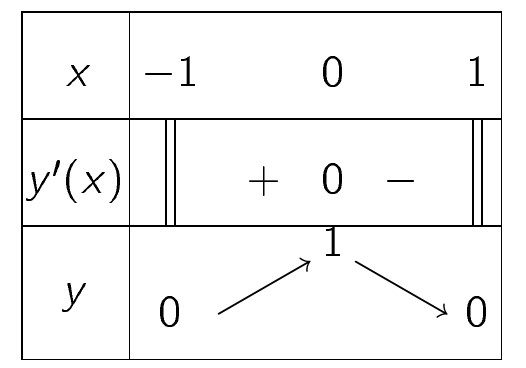
Căn cứ vào bảng biến thiên ta có, hàm số $ y=\sqrt{1-x^2} $ đồng biến trên khoảng $ (-1,0) $ và nghịch biến trên khoảng $ (0,1) $.

3. Các dạng toán đồng biến nghịch biến của hàm số

3.1. Tìm khoảng đơn điệu của hàm số

Bài toán. Tìm khoảng đơn điệu của hàm số $f(x)$ (tức là tìm các khoảng mà hàm số đồng biến, hàm số nghịch biến).

• Bước 1. Tìm tập xác định.
• Bước 2. Tính đạo hàm $f'(x)$ và lập bảng xét dấu của nó.
• Bước 3. Căn cứ vào bảng xét dấu để kết luận.

Dạng toán này đã xét kỹ ở phần 2, nên ở đây O2 Education xin đề nghị một ví dụ.

Ví dụ. Tìm các khoảng đồng biến, nghịch biến của hàm số:

1. $y=3x^{3}+2x^{2}-5x+2$
2. $y=x+\frac{1}{x} $
3. $ y=\sqrt{2x-1} $
4. $y=\sqrt{x^{2}+2x-3}$

3.2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số bằng lập bảng biến thiên

Trước tiên ta phải hiểu thế nào là giá trị lớn nhất, giá trị nhỏ nhất của một hàm số.

Xét hàm số $ y=f(x) $ xác định trên tập $ \mathbb{K} $.

• Nếu $ f(x)\leqslant M $ với mọi $ x\in \mathbb{K} $ và tồn tại $ x_0 $ thuộc $ \mathbb{K} $ sao cho $ f(x_0)=M $ thì $ M $ được gọi là giá trị lớn nhất\index{giá trị lớn nhất} của hàm số trên $ \mathbb{K}. $ Kí hiệu là $ \max\limits_{x\in \mathbb{K}}f(x) $.
• Nếu $ f(x)\geqslant m $ với mọi $ x\in \mathbb{K} $ và tồn tại $ x_0 $ thuộc $ \mathbb{K} $ sao cho $ f(x_0)=m $ thì $ m $ được gọi là giá trị nhỏ nhất\index{giá trị nhỏ nhất} của hàm số trên $ \mathbb{K}. $ Kí hiệu là $ \min\limits_{x\in \mathbb{K}}f(x) $.

Bài toán. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $ y=f(x) $ trên tập $ \mathbb{K}. $

Phương pháp. Ta thực hiện ba bước sau.

• Lập bảng biến thiên của hàm số trên tập $ \mathbb{K} $
• Tính các giá trị đầu và cuối mũi tên (có thể phải sử dụng giới hạn)
• Căn cứ vào bảng biến thiên để kết luận.

Ví dụ 1. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $ y=3x+5 $ trên đoạn $ [2;7] $

Ví dụ 2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $ f(x)=x+\frac{4}{x} $ trên đoạn $ [1,3]. $

Ví dụ 3. [DB2015] Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $ f(x)=x^3 +3x^2-9x+3 $ trên đoạn $ [0,2] $.

Đáp số $ \max\limits_{x\in[0,2]}f(x)=f(2)=5,\min \limits_{x\in[0,2]}f(x)=f(1)=-2 $.

Ví dụ 4. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:

• $ f(x)=1+8x-x^2 $ trên $ [-1,3] $
• $ g(x) = {x^3} – 3{x^{2 }} +1 $ trên ${\left[ { – 2,3} \right]}$
• $ h(x) = x – 5 + \frac{1}{x} $ trên $\left( {0, + \infty } \right) $

Ví dụ 5. [B2003] Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $ f(x) = x + \sqrt {4 – {x^2}} $

3.3. Tìm điều kiện để hàm số đơn điệu

Bài toán. Tìm điều kiện của tham số $ m $ để hàm số $ y=f(x) $ đồng biến trên $ \mathbb{K}. $

Phương pháp. Ta thực hiện các bước sau:

1. Tìm tập xác định và tính đạo hàm của hàm số.
2. Khẳng định: Hàm số $ y=f(x) $ đồng biến trên $ \mathbb{K} \Leftrightarrow f'(x) \geqslant 0 $ với mọi $ x\in \mathbb{K}. $
3. Xét các tình huống:
   • Nếu $ \mathbb{K} $ là $ \mathbb{R} $ và $ f'(x) $ là tam thức bậc hai thì sử dụng \emph{định lí về dấu tam thức bậc hai}.
   • Nếu cô lập được tham số $ m $ đưa điều kiện $ f'(x) \geqslant 0, \forall x\in \mathbb{K} $ về một trong hai điều kiện:
     • $ m\geqslant g(x), \forall x\in \mathbb{K} \Leftrightarrow m\geqslant \max\limits_{x\in \mathbb{K}} g(x) $
     • $ m\leqslant g(x), \forall x\in \mathbb{K} \Leftrightarrow m\leqslant \min\limits_{x\in \mathbb{K}} g(x) $
   • Các tình huống còn lại, ta lập bảng biến thiên và biện luận.

Tương tự đối với bài toán tìm điều kiện để hàm số $ y=f(x) $ nghịch biến trên $ \mathbb{K}. $

Ví dụ 1. Tìm $ m $ để hàm số $ y = -x^3 + (m – 1)x^2 – (m – 1)x + 9 $ luôn nghịch biến trên $ \mathbb{R}. $

• Tập xác định $\mathbb{D}=\mathbb{R}. $
• Đạo hàm $ y’=-3x^2+2(m-1)x-m+1 $ có $ \Delta’=m^2-5m+4. $
• Hàm số luôn nghịch biến trên $ \mathbb{R} \Leftrightarrow y’\leqslant 0 $ với mọi $ x\in \mathbb{R} $ khi và chỉ khi\[ \begin{cases} a<0\\ \Delta’\leqslant 0 \end{cases} \Leftrightarrow m\in [1,4]\]
  Vậy với $ m\in [1,4] $ thì hàm số đã cho luôn nghịch biến trên $ \mathbb{R}. $

Ví dụ 2. Tìm $ m $ để hàm số $y={{x}^{3}}-3\left( 2m+1 \right){{x}^{2}}+\left( 12m+5 \right)x+2$ luôn đồng biến trên tập xác định.

Hướng dẫn. Đạo hàm $ y’ $ có $ \Delta=36{{m}^{2}}-6=6\left( 6{{m}^{2}}-1 \right)$. Đáp số $-\frac{1}{\sqrt{6}}\leqslant m\leqslant \frac{1}{\sqrt{6}}$.

Ví dụ 3. Tìm $ m $ để hàm số $ y = mx^3 + (3 – m)x^2 + 2x + 2 $ luôn đồng biến trên $ \mathbb{R}. $

Hướng dẫn. Tập xác định $\mathbb{D}=\mathbb{R}. $

Ta xét hai trường hợp:

• Khi $ m=0 $ thì $ y=3x^2+2x+2 $ là một parabol nên không thể luôn đồng biến trên $ \mathbb{R}. $
• Khi $ m\ne0 $ thì $ y’=3mx^2+2(3-m)x+2 $ có $ \Delta’=m^2-12m+9. $ Do đó, hàm số luôn đồng biến trên $ \mathbb{R} $ khi và chỉ khi \[ \begin{cases} a>0\\\Delta’\leqslant 0 \end{cases} \Leftrightarrow 6-3\sqrt{3}\leqslant m\leqslant 6+3\sqrt{3}\]
  \end{itemize}
  Vậy với $ 6-3\sqrt{3}\leqslant m\leqslant 6+3\sqrt{3} $ thì hàm số đã cho luôn đồng biến trên $ \mathbb{R}. $

Ví dụ 4. Cho hàm số $ y=\frac{1-m}{3}{{x}^{3}}-2\left( 2-m \right){{x}^{2}}+2\left( 2-m \right)x+5 $.

1. Tìm $ m $ để hàm số luôn đồng biến trên tập xác định.
2. Tìm $ m $ để hàm số luôn nghịch biến trên tập xác định.

Chú ý dấu bằng trong điều kiện $ y’\geqslant 0 $ hoặc $ y’\leqslant 0 $, cụ thể ta đi xét hai ví dụ sau:

Ví dụ 5. Tìm $ m $ để hàm số $ y=\frac{mx-2}{x+m-3} $ nghịch biến trên mỗi khoảng xác định.

Hướng dẫn.

• Tập xác định $ \mathbb{D}=\mathbb{R}\setminus \{3-m\}. $ Đạo hàm $ y’=\frac{m^2-3m+2}{(x+m-3)^2} $.
• Hàm số đã cho nghịch biến trên mỗi khoảng xác định khi và chỉ khi $$ y'<0, \forall x\in \mathbb{D} \Leftrightarrow m^2-3m+2<0 \Leftrightarrow 1<m<2$$
  Vậy với $ m\in (1; 2) $ thì hàm số đã cho luôn nghịch biến trên mỗi khoảng xác định.

Ví dụ 6. Tìm $ m $ để hàm số $y=\frac{mx+4}{x+m}$ nghịch biến trong khoảng $\left( -\infty ;-1 \right)$.

Hướng dẫn. Có $ y’=\frac{{{m}^{2}}-4}{{{(x+m)}^{2}}}$ nên hàm số nghịch biến trong khoảng $\left( -\infty ;-1 \right)$ khi và chỉ khi
$$\begin{cases}
{{m}^{2}}-4<0 \\
\left( -\infty ;-1 \right) \subset (-\infty,m)
\end{cases} \Leftrightarrow \begin{cases}
-2<m<2 \\
-m\geqslant -1
\end{cases} \Leftrightarrow -2<m\leqslant 1$$
Vậy với $ -2<m\leqslant 1 $ thì hàm số đã cho nghịch biến trong $ (-\infty,-1). $

Ví dụ 7. Tìm $ m $ để hàm số $y = – \frac{1}{3}{x^3} + {x^2} + \left( {m + 3} \right)x+5$ đồng biến trên $ [1;3] $.

Hướng dẫn.

• Tập xác định: $ \mathbb{D}=\mathbb{R}. $
• Đạo hàm: $ y’= -x^2+2x+m+3$
• Hàm số đã cho đồng biến trên $ [1;3] $ khi và chỉ khi
  \begin{align*}
  y’&\geqslant 0,\;\forall x\in[1;3]\\
  \Leftrightarrow -x^2+2x+m+3&\geqslant 0,\;\forall x\in[1;3]\\
  \Leftrightarrow m&\geqslant x^2-2x-3,\;\forall x\in[1;3]\\
  \Leftrightarrow m&\geqslant \max\limits_{x\in[1;3]}(x^2-2x-3)
  \end{align*}
  Xét hàm số $ f(x)= x^2-2x-3$ trên $ [1;3] $ ta có bảng biến thiên sau:

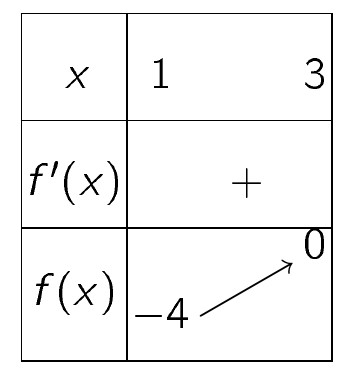
Suy ra $ \max\limits_{x\in[1;3]}f(x)=0 $ và do đó điều kiện cần tìm là $m \geqslant 0. $

Ví dụ 8. [A2013] Tìm $ m $ để hàm số $ y = -x^3+3x^2+3mx-1 $ nghịch biến trên $ \left( {0;+\infty} \right) $.

Hướng dẫn. Hàm số nghịch biến trên $ \left( {0;+\infty} \right) $ khi và chỉ khi $ y’\leqslant 0,\forall x\in \left( {0;+\infty} \right)$ khi và chỉ khi
\begin{align*}
-3x^2+6x+3m&\geqslant 0,\forall x\in \left( {0;+\infty} \right) \\
\Leftrightarrow m&\leqslant x^2-2x, \forall x\in \left( {0;+\infty} \right)\\
\Leftrightarrow m&\leqslant x^2-2x, \forall x\in \left[{0;+\infty} \right) \text{ (vì đạo hàm liên tục trên $ \left[{0;+\infty} \right) $) }\\
\Leftrightarrow m&\leqslant \min\limits_{x\in[0,+\infty)}\left( x^2-2x\right)
\end{align*}
Xét hàm số $ f(x)=x^2-2x $ trên $ \left[ {0;+\infty} \right) $ có $ f'(x)=2x-2; f'(x)=0\Leftrightarrow x=1. $ \\
Ta có bảng biên thiên như sau:

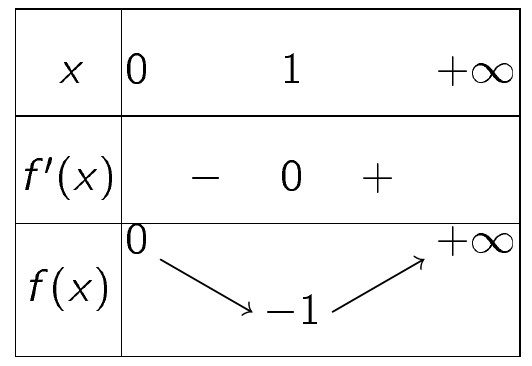
Dựa vào bảng biến thiên suy ra $ \min\limits_{x\in[0,+\infty)}f(x)=-1. $ Do đó, $ m\leqslant -1. $

Chú ý rằng, khi cô lập $ m, $ nếu phải chia cho biểu thức chứa $ x $ ta phải xét xem biểu thức đó âm hay dương trên tập đang xét! Cụ thể qua hai ví dụ sau đây.

Ví dụ 9. Tìm $ m $ để hàm số $y = – \frac{1}{3}{x^3} + \left( {m – 1} \right){x^2} + \left( {m + 3} \right)x – 4$ đồng biến trên $ [0,3] $.

Ví dụ 10. Tìm $ m $ để hàm số $y = – \frac{1}{3}{x^3} + \left( {m – 1} \right){x^2} + \left( {m + 3} \right)x – 4$ đồng biến trên $ [-4,-1] $.

Ví dụ 11. Cho hàm số $ y=x^4-2(m-1)x^2+m-2. $ Tìm $ m $ để hàm số đồng biến trên $ (1,3)? $

Xem thêm Tìm m để hàm số đồng biến trên các khoảng