Bài toán xác định góc giữa hai mặt phẳng trong không gian là một dạng toán quan trọng xuất hiện trong các đề thi THPTQG, thi học kì 2 lớp 11. Ngoài tính góc giữa 2 mặt phẳng thì các em cần thành thạo Cách tính góc giữa đường thẳng và mặt phẳng.
Một số dạng toán hình học không gian quan trọng mà các em có thể ôn tập:
- Cách chứng minh đường thẳng vuông góc với mặt phẳng
- Cách tính khoảng cách từ một điểm đến một mặt phẳng
- Khoảng cách giữa hai đường thẳng chéo nhau trong không gian
1. Góc giữa hai mặt phẳng trong không gian
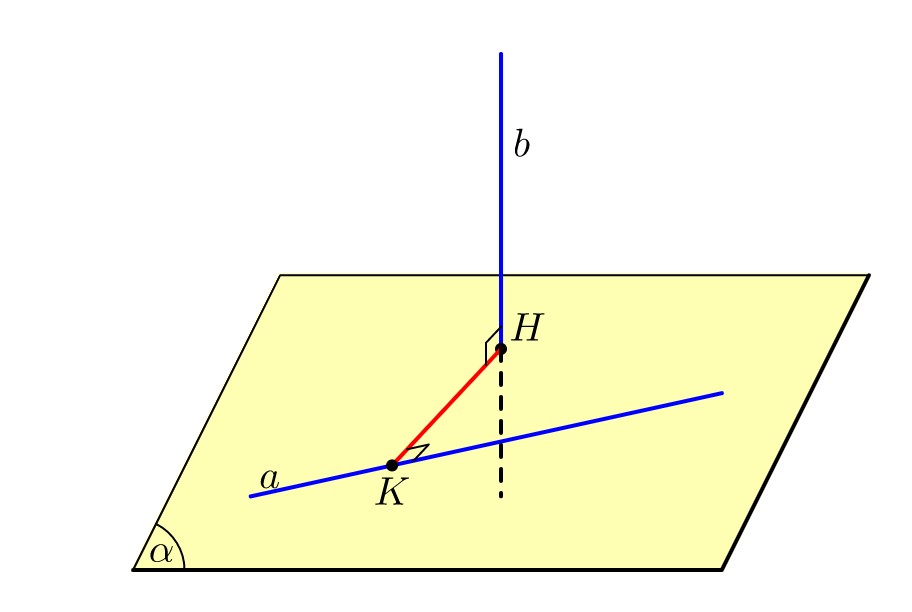
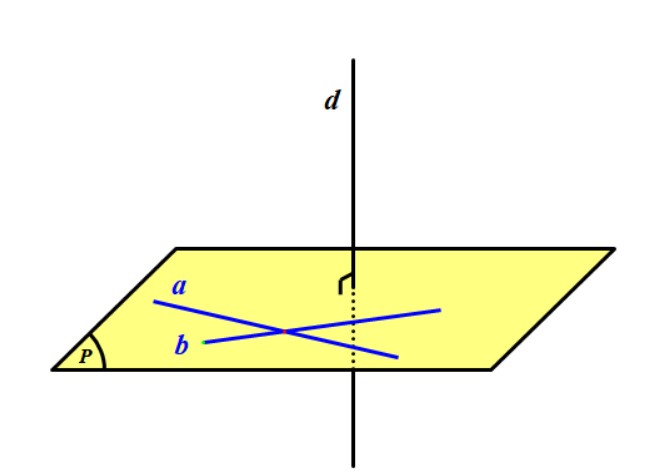
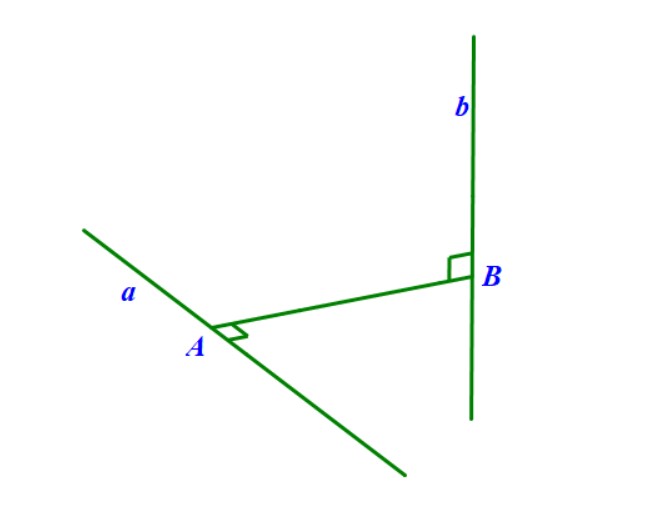
Góc giữa 2 mặt phẳng trong không gian bằng góc được tạo bởi hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.
Chú ý rằng góc giữa hai mặt phẳng có số đo từ $ 0^\circ $ đến $ 90^\circ. $
Nếu hai mặt phẳng song song hoặc trùng nhau thì góc giữa chúng bằng $ 0^\circ. $ Trái lại, hai mặt phẳng phải cắt nhau theo giao tuyến là một đường thẳng nào đó, giả sử là $ \Delta $, thì ta có ba cách như dưới đây.
Bài toán. Xác định góc giữa hai mặt phẳng \((P)\) và \((Q)\) trong không gian.
1.1. Sử dụng định nghĩa góc giữa hai mặt phẳng trong không gian.
Tìm hai đường thẳng $ a $ và $ b $ lần lượt vuông góc với hai mặt phẳng $(P)$ và $ (Q) $. Góc giữa hai mặt phẳng $(P)$ và $ (Q) $ chính bằng góc giữa hai đường thẳng $ a $ và $ b $.
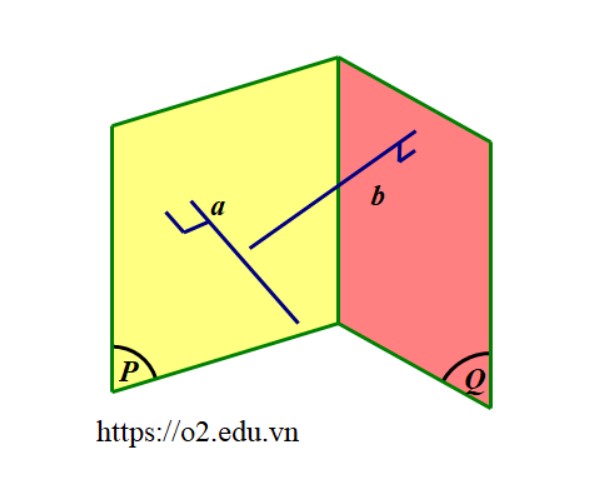
Vì chúng ta được quyền lựa chọn các đường thẳng $ a $ và $ b $ nên ta thường chọn sao cho hai đường thẳng này cắt nhau, để việc tính góc giữa chúng dễ dàng hơn.
1.2. Xác định góc giữa hai mặt phẳng bằng cách sử dụng giao tuyến
- Xác định giao tuyến $ \Delta $ của hai mặt phẳng $ (P)$ và $(Q) $.
- Tìm mặt phẳng $\left( R\right)$ vuông góc với giao tuyến $\Delta $.
- Lần lượt tìm các giao tuyến $ a $ và $ b $ của mặt phẳng $\left( R\right)$ với hai mặt phẳng $ (P)$ và $(Q) $.
- Tính góc giữa hai đường thẳng $ a $ và $ b $, đây chính là góc giữa hai mặt phẳng $ (P) $ và $ (Q) $.

Nhận xét. Thay vì tìm một mặt phẳng $(R)$ vuông góc với giao tuyến $ \Delta $, ta có thể đi tìm một điểm $ I $ nào đó trên $ \Delta $. Sau đó, từ điểm $ I $ này lần lượt dựng hai đường thẳng $ a $ và $ b $ nằm trong từng mặt phẳng rồi tính góc giữa chúng.

1.3. Tính góc giữa 2 mp bằng công thức diện tích hình chiếu
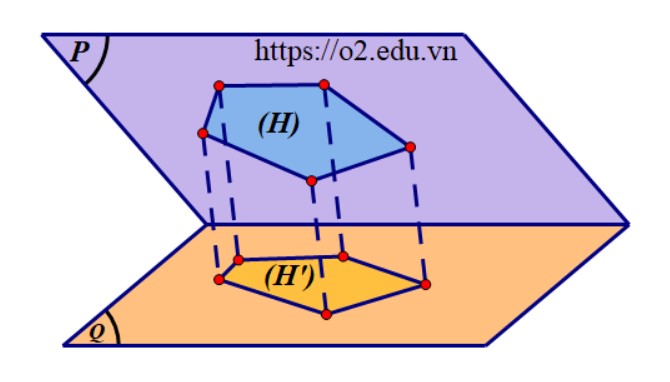
Giả sử góc giữa hai mặt phẳng $(P)$ và $ (Q) $ bằng $ \varphi $. Lấy trong mặt phẳng $(P)$ một đa giác $ (H) $ có diện tích $ S $, hình chiếu vuông góc của đa giác $ (H) $ lên mặt phẳng $(Q)$ là đa giác $ (H’) $ có diện tích $ S’ $. Khi đó ta luôn có công thức
\[ S’=S\cos\varphi. \]
2. Ví dụ tính góc giữa 2 mặt phẳng trong không gian
Nếu bài viết hữu ích, bạn có thể tặng tôi 1 cốc cafe vào số tài khoản Agribank 3205215033513. Xin cảm ơn!
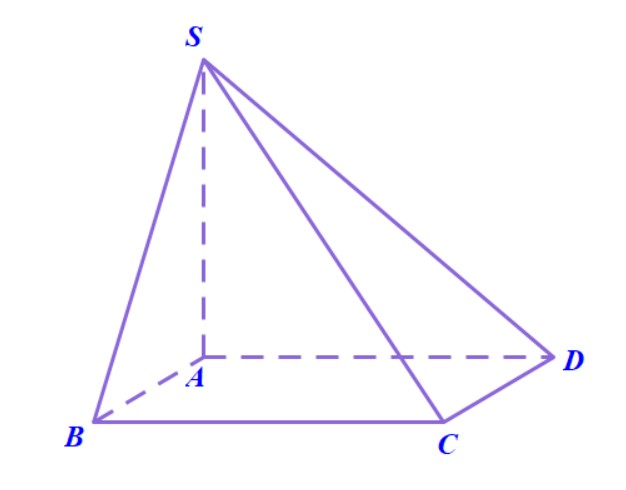
Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $ a $. Cạnh $ SA=a\sqrt{3} $ và vuông góc với đáy. Tính góc giữa hai mặt phẳng $ (SBC) $ và $ (ABCD), $ góc giữa mặt phẳng $ (SBD) $ và mặt phẳng $ (ABCD). $

Hướng dẫn. Để tính góc giữa hai mặt phẳng $ (SBC) $ và $ (ABCD)$, chúng ta sử dụng cách thứ 2.
- Giao tuyến của hai mặt phẳng $ (SBC) $ và $ (ABCD)$ chính là $BC$.
- Bây giờ, ta cần tìm (nếu chưa có sẵn thì chúng ta sẽ tự vẽ thêm) một mặt phẳng vuông góc với giao tuyến $BC$ này. Bạn nào phát hiện ra đó chính là mặt phẳng \( (SAB) \) thì tốt, nếu chưa thì chú ý hai điều sau:
- Muốn có một mặt phẳng vuông góc với \( BC \) thì cần tìm mặt phẳng nào chứa hai đường thẳng cắt nhau và cùng vuông góc với \( BC \).
- Đường thẳng \( BC \) đang vuông góc với những đường thẳng nào (chính là \( SA \) và \( AB \)).
- Bước tiếp theo, sau khi có mặt phẳng \( (SAB) \) rồi, chúng ta sẽ tìm giao tuyến của nó với hai mặt phẳng ban đầu, chính là các đường thẳng \( AB \) và \( SB \)
- Cuối cùng, chúng ta đi tính góc giữa hai đường thẳng \( AB \) và \( SB \), chính là góc \( SBA \), các em hãy tự tính xem góc này bằng bao nhiêu.
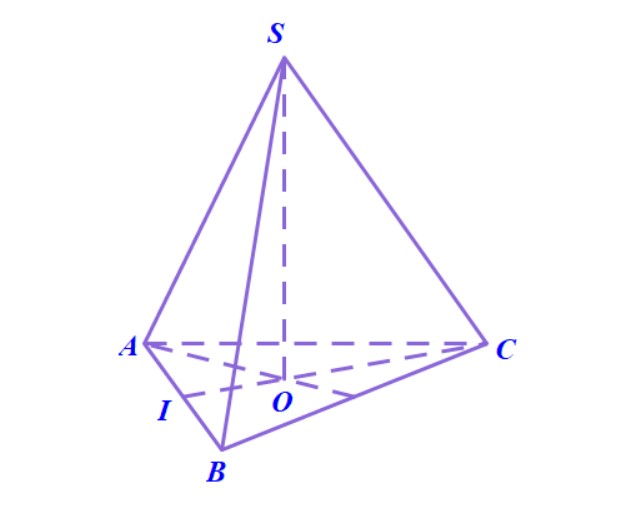
Để tính góc giữa hai mặt phẳng $ (SBD) $ và $ (ABCD)$, các em hãy thực hiện đúng các bước như trên. Gợi ý, góc giữa hai mặt phẳng này chính bằng góc $SOA$.
Nếu thấy bài viết hữu ích, bạn có thể ủng hộ chúng tôi bằng cách bấm vào các banner quảng cáo. Xin cảm ơn.
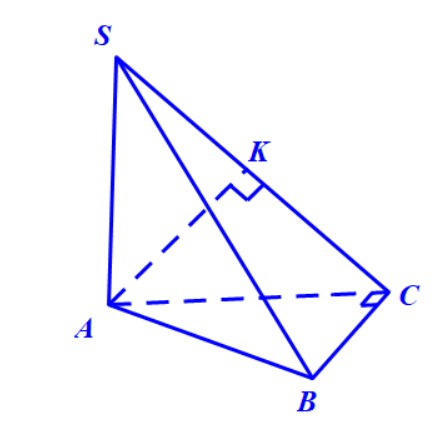
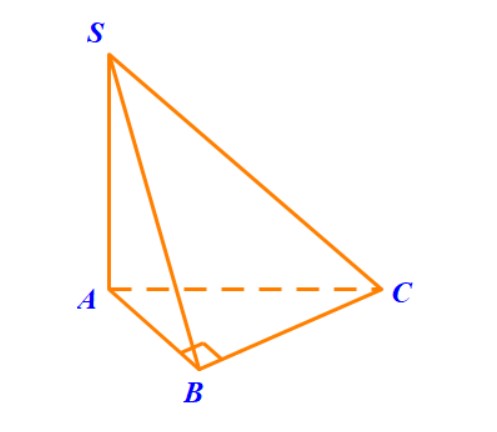
Ví dụ 2. Cho hình chóp $ S.ABC, $ có đáy $ ABC $ là tam giác vuông cân với $ BA = BC = a $; cạnh $ SA $ vuông góc với đáy và $ SA = a $. Gọi $ E, F $ lần lượt là trung điểm của các cạnh $ AB $ và $ AC. $
1. Tính góc giữa hai mặt phẳng $ (ABC) $ và $ (SBC). $
2. Tính góc giữa hai mặt phẳng $ (SEF) $ và $ (SBC). $
3. Tính góc giữa hai mặt phẳng $ (SAC) $ và $ (SBC). $
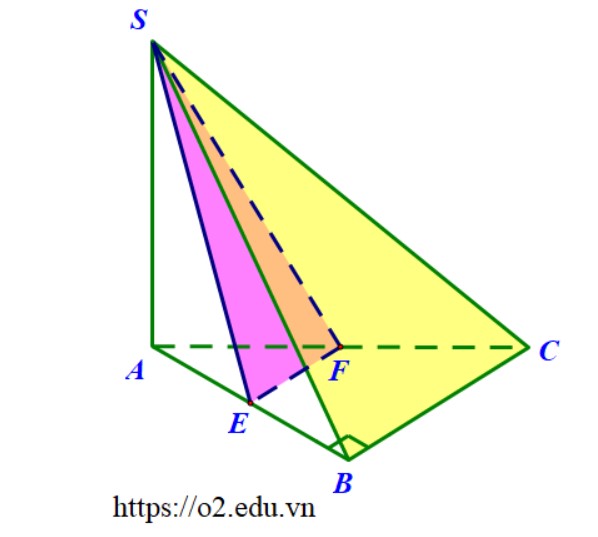
Hướng dẫn.
1. Góc giữa hai mặt phẳng $ (ABC) $ và $ (SBC) $ chính bằng góc $SBA$.
2. Giao tuyến của hai mặt phẳng $ (SEF) $ và $ (SBC) $ là đường thẳng \( d \) đi qua điểm \( S \) và song song với \( BC \). Do đó, chúng ta tìm một mặt phẳng vuông góc với giao tuyến \( d \) thì cũng chính là đi tìm một mặt phẳng vuông góc với đường thẳng \( BC \). Và, nhận thấy luôn mặt phẳng \( (SAB) \) vuông góc với \( BC \). Sau đó đi xác định giao tuyến của mặt phẳng $(SAB)$ với hai mặt phẳng ban đầu khá dễ dàng. Góc giữa hai mặt phẳng chính bằng góc \( BSE \) và đáp số $\cos({(SEF),(SBC)})=\frac{3}{\sqrt{10}}$.
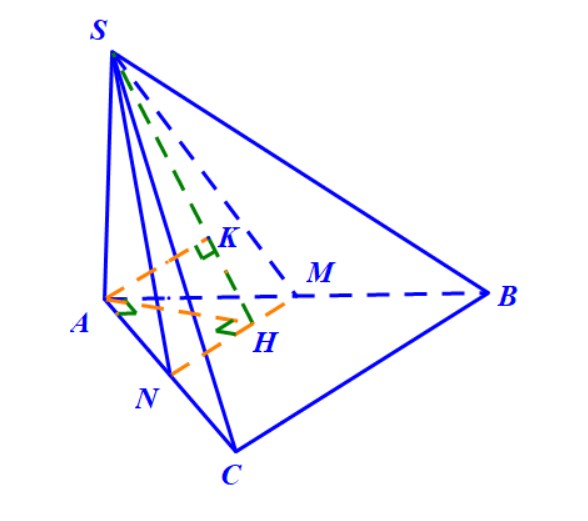
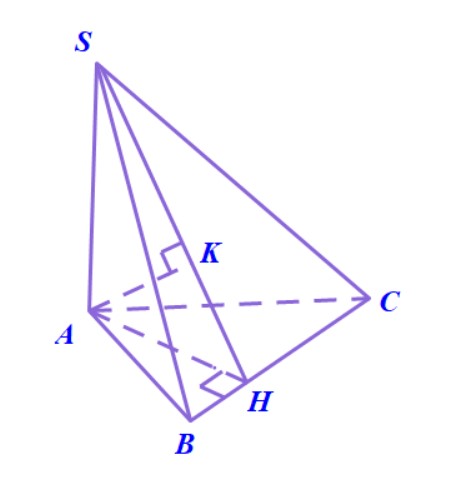
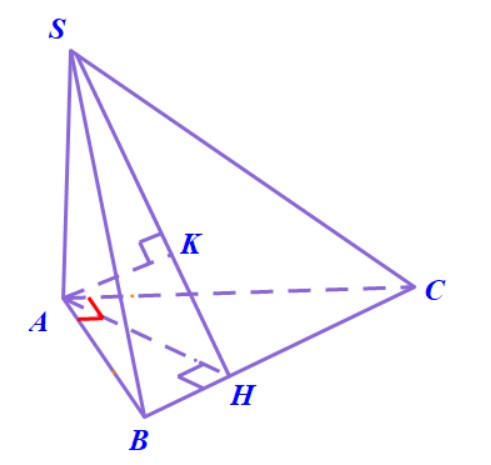
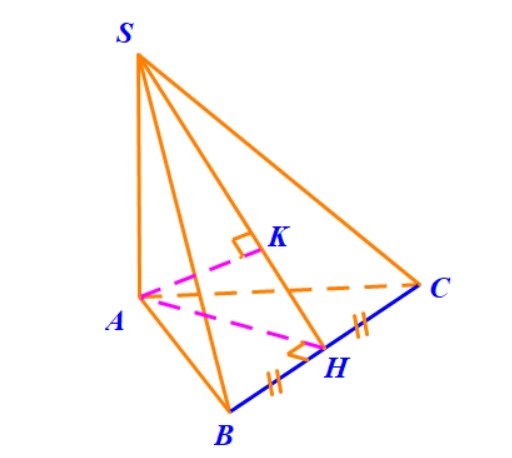
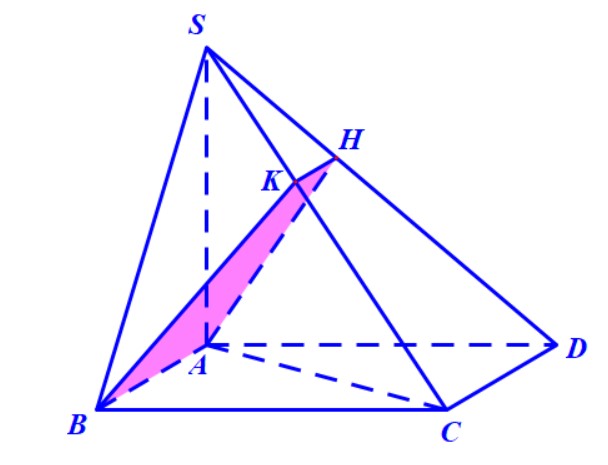
3. Để tính góc giữa hai mặt phẳng $ (SAC) $ và $ (SBC)$, chúng ta có thể làm theo cách dựng mặt phẳng vuông góc với giao tuyến $SC$ của chúng. Tuy nhiên, cách này không phải bạn nào cũng biết cách tạo ra một mặt phẳng thỏa mãn yêu cầu đó, nên ở đây thầy hướng dẫn theo cách sử dụng công thức diện tích hình chiếu.
Trong mặt phẳng \( (SBC) \) chúng ta chọn một đa giác mà dễ dàng tính được diện tích, chọn luôn tam giác \( SBC \). Đây là tam giác vuông tại \( B \) nên diện tích tính bởi $$ S_{SBC}=\frac{1}{2}SB\cdot BC $$ Tiếp theo, tìm hình chiếu của tam giác này lên mặt phẳng \( (SAC) \). Chúng ta có ngay hình chiếu vuông góc của \( C \) và \( S \) thì trùng với chính chúng luôn, nên chỉ cần tìm hình chiếu vuông góc của điểm \( B \) là đủ.
Phát hiện được trung điểm \( F \) của \( AC \) chính là hình chiếu vuông góc của điểm \( B \) lên mặt phẳng \( (SAC) \) (hãy thử giải thích tại sao, nếu không được thì mời các em để lại bình luận dưới bài viết, thầy sẽ hướng dẫn).
Như vậy, hình chiếu vuông góc của tam giác \( SBC \) lên mặt phẳng \( (SAC) \) chính là tam giác \( SCF \), tam giác này có diện tích \( S_{SCF}= \frac{1}{2}SA\cdot FC\). Theo công thức diện tích hình chiếu thì $$ S_{SCF}=S_{SBC}\cdot \cos\varphi $$ Thay số vào tìm được, $\left( {(SAC),(SBC)} \right)= 60^\circ$.
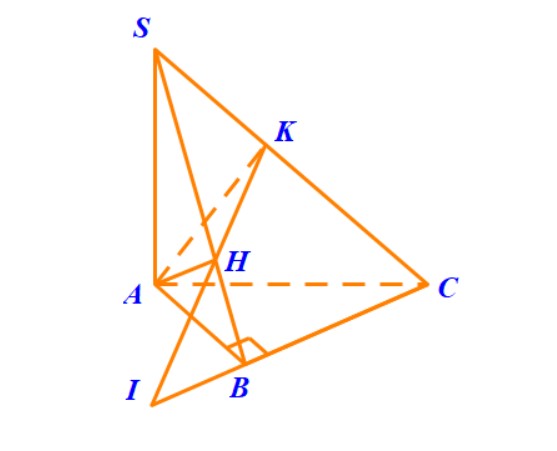
Nếu vẫn sử dụng cách dựng mặt phẳng vuông góc với giao tuyến \( SC \), thầy gợi ý là lần lượt gọi \( H,K \) là hình chiếu vuông góc của \( A \) lên \( SB,SC \) thì chứng minh được mặt phẳng \( (AHK) \) vuông góc với \( SC \). Góc giữa hai mặt phẳng cần tính chính bằng góc \( AKH \).
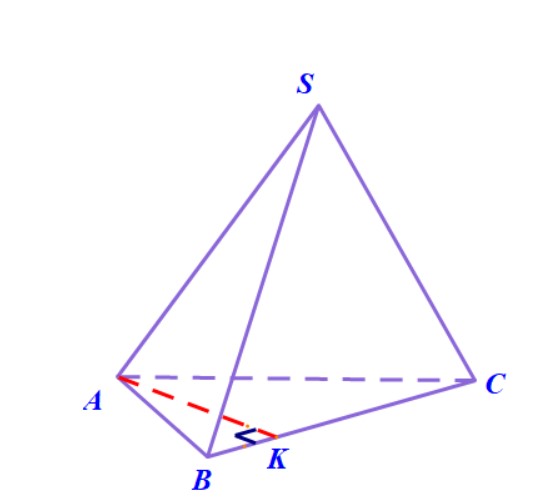
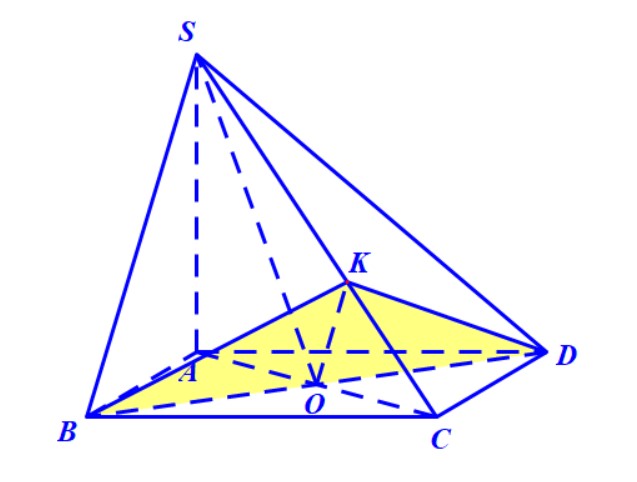
Ví dụ 3. Cho hình chóp $ S.ABCD $ có đáy là hình vuông $ ABCD $ cạnh bằng $ a $, tâm của đáy là điểm $ O $. Cạnh bên $ SA $ vuông góc với đáy $(ABCD)$. Tính độ dài cạnh $ SA $ theo $ a $ để số đo của góc giữa hai mặt phẳng $ (SCB) $ và $ (SCD) $ bằng $ 60^\circ $.
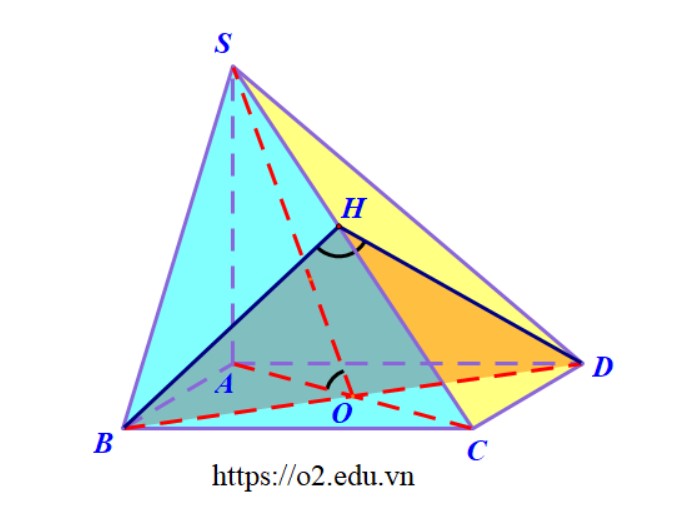
Hướng dẫn. Dễ thấy giao tuyến của hai mặt phẳng $ (SCB) $ và $ (SCD) $ là đường thẳng \( SC \).
Bây giờ, chúng ta cần tìm một mặt phẳng vuông góc với \( SC \). Trong tam giác \( SBC \) kẻ đường cao \( BH \) xuống cạnh \( SC \) thì chứng minh được \( DH \) cũng là đường cao của tam giác \( SCD \).
Suy ra \( SC \) vuông góc với mặt phẳng \( BHD \) và góc giữa hai mặt phẳng $ (SCB) $ và $ (SCD) $ chính là góc giữa \( BH \) và \( DH \). Tuy nhiên, không thể khẳng định được là góc \( \widehat{BHD} \) vì có thể góc này là góc tù. Tóm lại, chúng ta phải xét hai trường hợp:
- \( \left((SCB),(SCD)\right) =\widehat{BHD} \) tức là \(\widehat{BHD}= 60^\circ \)
- \( \left((SCB),(SCD)\right)=180^\circ – \widehat{BHD} \) tức là \(\widehat{BHD}= 120^\circ \)
Lần lượt xét hai trường hợp này, thấy trường hợp \(\widehat{BHD}= 120^\circ \) thỏa mãn yêu cầu và tìm được đáp số $ SA = a. $
Ví dụ 4. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh $ SA $ vuông góc với đáy và $SA = a\sqrt{3}$. Tính góc giữa các cặp mặt phẳng sau:
1. $ (SBC) $ và $ (ABC) $
2. $ (SBD) $ và $ (ABD) $
3. $ (SAB) $ và $ (SCD) $
Hướng dẫn. $ 60^\circ, \arctan\sqrt{6},30^\circ.$
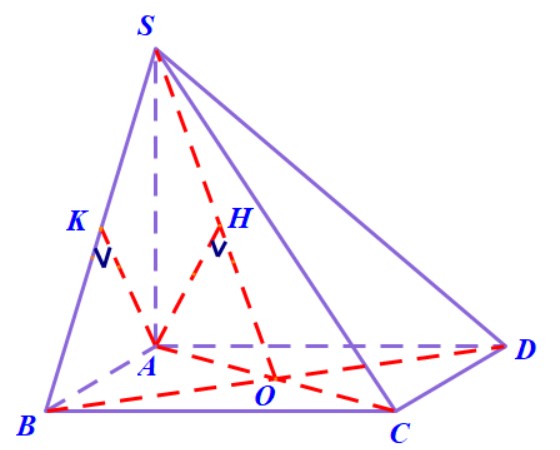
Ví dụ 5. Cho hình chóp $ S.ABCD $, có đáy $ ABCD $ là nửa lục giác đều nội tiếp đường tròn đường kính $ AB = 2a; $ cạnh $ SA $ vuông góc với đáy và $SA = a\sqrt{3}$.
1. Tính góc giữa hai mặt phẳng $ (SAD) $ và $ (SBC). $
2. Tính góc giữa hai mặt phẳng $ (SBC) $ và $ (SCD). $
Hướng dẫn. Sử dụng công thức diện tích hình chiếu (đơn giản) hoặc tính trực tiếp (phức tạp). Đáp số
Ví dụ 6. Cho hình thoi $ ABCD $ cạnh $ a $, tâm $O, OB = \frac{a\sqrt{3}}{3}; SA\perp (ABCD)$ và $SO = \frac{a\sqrt{6}}{3}$. Chứng minh góc $\widehat{ASC}$ vuông. Chứng minh hai mặt phẳng $ (SAB) $ và $ (SAD) $ vuông góc. Tính góc giữa hai mặt phẳng $ (SBC) $ và $ (ABC). $
Hướng dẫn. $ ({(SBC),(ABC)})=60^\circ. $
Ví dụ 7. Cho hình chóp $ S.ABCD $ có $ SA\perp (ABCD) $ và $SA = a\sqrt{2}$, đáy $ ABCD $ là hình thang vuông tại $ A $ và $ D $ với $ AB = 2a, AD = DC = a $. Tính góc giữa các cặp mặt phẳng: $ (SBC) $ và $ (ABC);(SAB)$ và $ (SBC);(SBC) $ và $ (SCD). $
Hướng dẫn. $45^\circ,60^\circ,\arccos\frac{\sqrt{6}}{3}$.
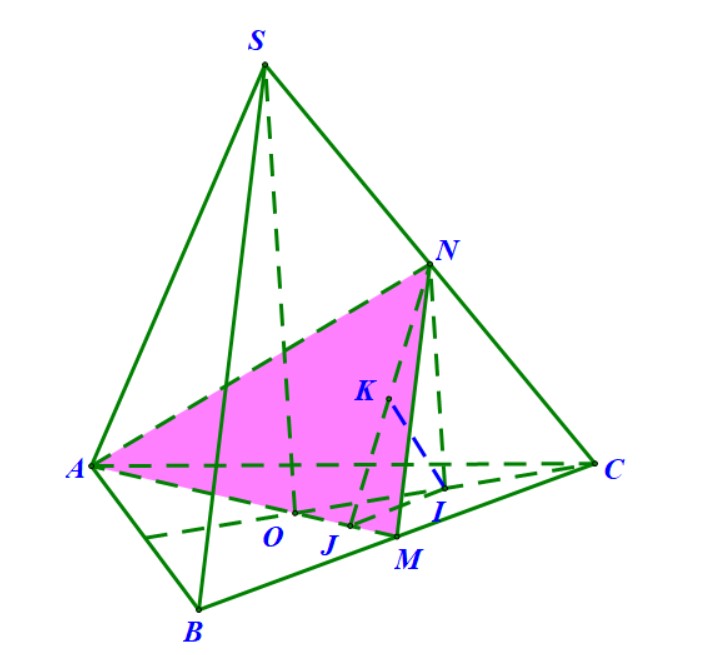
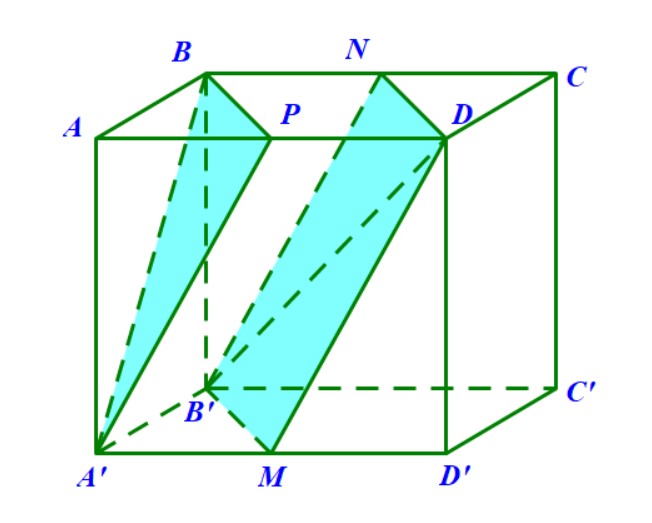
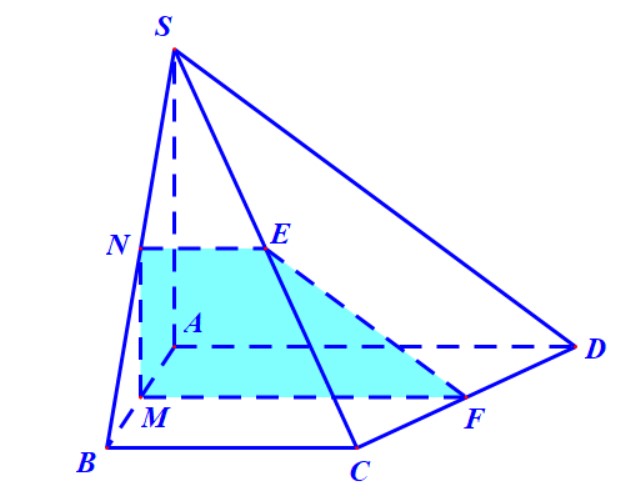
Ví dụ 8. Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \( a \), cạnh bên \( SA = a \) và vuông góc với đáy. Gọi \( M; N \) lần lượt là trung điểm \( SB \) và \( SD \). Tính \( \sin \) của góc giữa hai mặt phẳng \( (AMN) \) và \( (SBD) \).
Ví dụ 9. Cho hình chóp \(S.ABCD\) có đáy là hình vuông cạnh \( a \), cạnh bên \( SA = a \) và vuông góc với đáy. Gọi \( E\) và \(F \) lần lượt là trung điểm \( SB \) và \( SD \). Tính cosin của góc giữa hai mặt phẳng \( (AEF) \) và \( (ABCD) \).
3. Bài tập tính góc giữa hai mặt phẳng trong không gian
Bài 1. Cho hình chóp $S.ABCD$ đáy là hình vuông tâm $O$ cạnh $a.$ Cạnh $ SA = a$ và vuông góc với đáy.
1. Chứng minh rằng mặt phẳng $(SAB)$ vuông góc với mặt phẳng $(SAD)$; $(SBC)$ vuông góc với $(SAB)$; $(SCD)$ vuông góc với $(SAD)$; $(SAC)$ vuông góc $(SBD)$.
2. Gọi $AI, AJ$ lần lượt là đường cao của các tam giác $SAB, SAC$, chứng minh rằng $(SCD)$ vuông góc với $(AIJ)$. Tính góc giữa hai mặt phẳng $(SBC) $ và $(ABCD)$; $(SBD) $ và $(ABCD)$.
Bài 2. Cho hình vuông $ABCD$ cạnh $a$ có $I, J$ lần lượt là trung điểm $AB, CD$. Trên đường thẳng vuông góc với mặt phẳng $(ABCD)$ tại $I$ lấy điểm $S$. Chứng minh rằng $BC\perp (SAB), CD\perp (SIJ)$; $(SAB)\perp (SBC), (SAB)\perp (SIJ)$. Gọi $M$ là trung điểm $BC$, chứng minh $(SIM)\perp (SBD)$. Giả sử $SI = a$, tính góc giữa hai mặt phẳng $(SCD)$ và $(ABCD)$.
Bài 3. Cho hình chóp đều $S.ABCD$, $O$ là tâm $ABCD$. Gọi $I$ là trung điểm $AB$, cho $SA = a, AB = a.$ Chứng minh rằng $(SAC)\perp (SBD)$, $(SOI)\perp (ABCD)$; $(SIO)\perp (SCD)$. Gọi $OJ$ là đường cao của tam giác $SOI$, chứng minh $OJ\perp SB$. Gọi $BK$ là đường cao của tam giác $SBC$, chứng minh rằng $(SCD) \perp (BDK)$. Tính góc giữa mặt bên và mặt đáy.
Bài 4. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật. Mặt bên $(SAB)$ vuông góc với đáy $(ABCD)$. Cho $AB = a, AD = a\sqrt{2}$. Chứng minh rằng $SA\perp (ABCD), (SAD)\perp (SCD)$. Gọi $AH$ là đường cao của…, chứng minh $AH\perp (SBC)$, $(SBC)\perp (AHC)$; $DH\perp SB$. Tính góc giữa $(SAC)$ và $(SAD)$.
Bài 5. Cho hình chóp $S.ABCD$ đáy là hình vuông cạnh bằng $a$ tâm là điểm $O$. Cạnh $ SA = a$ và vuông góc với đáy. Chứng minh rằng các mặt bên hình chóp là các tam giác vuông. Chứng minh $BD$ vuông góc với $SC$. Tính góc giữa $SC $ và $(ABCD)$, góc giữa hai mặt phẳng $(SBD)$ và $(ABCD)$. Tính góc giữa mặt phẳng $(SCD) $ và mặt phẳng $(ABCD)$. Tính diện tích hình chiếu của tam giác $ SCD$ trên $(ABCD)$.
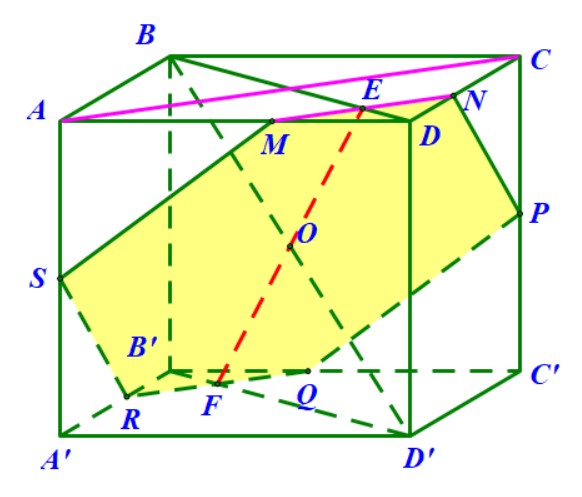

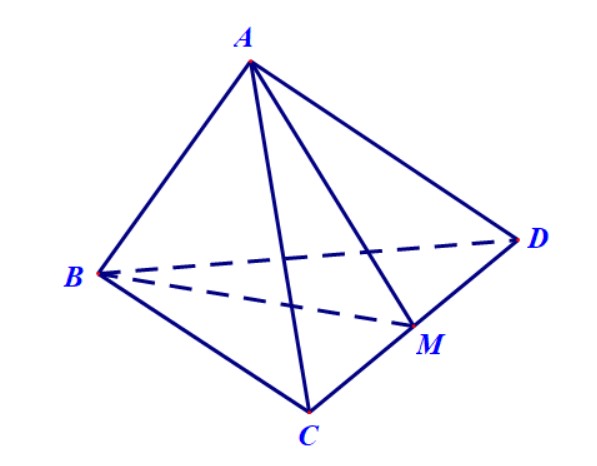
 Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).
Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).





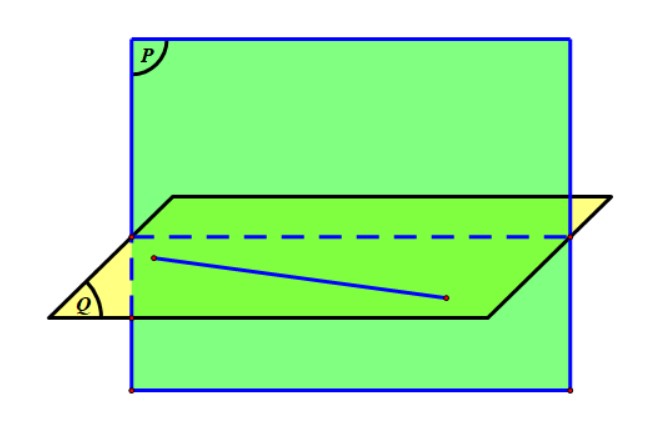
 Trong thực tế, việc tạo ra mặt phẳng \((P)\) song song với đường thẳng $a$ thường được thực hiện bằng cách, dựng hoặc tìm một đường thẳng $a’$ nào đó song song với $a$ và cắt đường thẳng $b$. Lúc này, mặt phẳng \((P)\) chính là mặt phẳng xác định bởi hai đường thẳng cắt nhau \(a’\) và \(b\). Và, việc tính khoảng cách tiếp tục quy về
Trong thực tế, việc tạo ra mặt phẳng \((P)\) song song với đường thẳng $a$ thường được thực hiện bằng cách, dựng hoặc tìm một đường thẳng $a’$ nào đó song song với $a$ và cắt đường thẳng $b$. Lúc này, mặt phẳng \((P)\) chính là mặt phẳng xác định bởi hai đường thẳng cắt nhau \(a’\) và \(b\). Và, việc tính khoảng cách tiếp tục quy về