HỆ THỨC LƯỢNG TRONG TAM GIÁC LỚP 10

I. TÓM TẮT KIẾN THỨC HỆ THỨC LƯỢNG TRONG TAM GIÁC LỚP 10

1. Các ký hiệu

Trong một tam giác $ABC$ thì chúng ta thường kí hiệu:

• $ A, B, C $: là các góc đỉnh $ A, B, C $
• $ a, b, c $: là độ dài các cạnh đối diện với các đỉnh $ A, B, C $
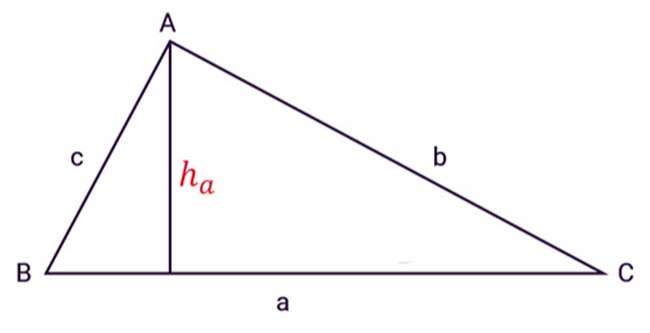
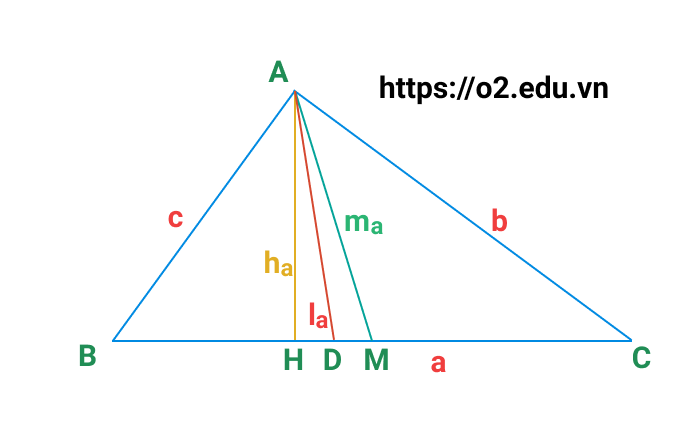
• $ h_a, h_b, h_c $: là độ dài các đường cao hạ từ các đỉnh $ A, B, C $
• $ m_a, m_b, m_c $: là độ dài các đường trung tuyến kẻ từ $ A, B, C $
• $ l_a, l_b, l_c $: là độ dài các đường phân giác trong kẻ từ $ A, B, C $
• $ R $: là bán kính đường tròn ngoại tiếp tam giác $ABC$
• $ r $: là bán kính đường tròn nội tiếp tam giác $ABC$
• $p=\frac{1}{2}(a+b+c)$ là nửa chu vi tam giác $ABC$
• $ S $: là diện tích tam giác $ABC$

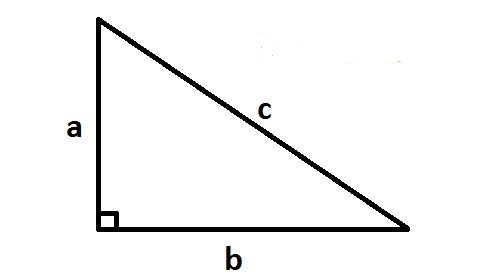
2. Các hệ thức lượng trong tam giác vuông

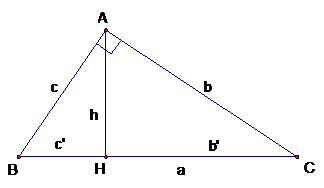
Trong tam giác vuông $ABC$. Gọi $b’, c’$ là độ dài các hình chiếu các cạnh góc vuông lên cạnh huyền ta có các hệ thức:

1. ${{b}^{2}}=a.{{b}’}$
2. ${{c}^{2}}=a.{{c}’}$
3. ${{a}^{2}}={{b}^{2}}+{{c}^{2}}$
4. ${{h}^{2}}={{b}’}.{{c}’}$
5. $\frac{1}{{{h}^{2}}}=\frac{1}{{{b}^{2}}}+\frac{1}{{{c}^{2}}}$
6. $a.h=b.c$
7. $b=a.\sin B=a.\cos C$
8. $c=a.\sin C=a.\cos B$
9. $b=c.\tan B=c.\cot C$
10. $c=b.\tan C=b.\cot B$

3. Các hệ thức lượng trong tam giác thường

Định lý hàm số CÔSIN:

Trong tam giác $ABC$ ta luôn có:

1. ${{a}^{2}}={{b}^{2}}+{{c}^{2}}-2bc\cos A $
2. ${{b}^{2}}={{c}^{2}}+{{a}^{2}}-2ca\cos B $
3. ${{c}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\cos C $

Ghi nhớ: Trong một tam giác, bình phương mỗi cạnh bằng tổng bình phương hai cạnh kia trừ đi hai lần tích hai cạnh ấy với côsin của góc xen giữa chúng.

Hệ quả: Trong tam giác $ABC$ ta luôn có:

1. $\cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$,
2. $\cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}$,
3.   $\cos C=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}$.

Định lý hàm số SIN:

Trong tam giác $ABC$ ta có: $$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$

Hệ quả: Với mọi tam giác $ABC$, ta có: $$a=2R\sin A;b=2R\sin B;c=2R\sin C$$

Ghi nhớ: Trong một tam giác, tỷ số giữa một cạnh của tam giác và sin của góc đối diện với cạnh đó bằng đường kính đường tròn ngoại tiếp tam giác.

Định lý về đường trung tuyến:

Trong tam giác $ABC$ ta có:\begin{align} m_{a}^{2}=\frac{{{b}^{2}}+{{c}^{2}}}{2}-\frac{{{a}^{2}}}{4} \\ m_{b}^{2}=\frac{{{a}^{2}}+{{c}^{2}}}{2}-\frac{{{b}^{2}}}{4} \\ m_{c}^{2}=\frac{{{a}^{2}}+{{b}^{2}}}{2}-\frac{{{c}^{2}}}{4} \\ \end{align}

Định lý về diện tích tam giác:

Diện tích tam giác $ABC$ được tính theo các công thức sau:

1. $S=\frac{1}{2}a{{h}_{a}}=\frac{1}{2}b{{h}_{b}}=\frac{1}{2}c{{h}_{c}} $
2. $S=\frac{1}{2}ab\sin A=\frac{1}{2}ac\sin B=\frac{1}{2}bc\sin A $
3. $S=\frac{abc}{4R} $
4. $S=pr $
5. $S=\sqrt{p(p-a)(p-b)(p-c)}$

Định lý về đường phân giác:

$${{l}_{a}}=\frac{2bc.\cos \frac{A}{2}}{b+c};{{l}_{b}}=\frac{2ac.\cos \frac{B}{2}}{a+c};{{l}_{c}}=\frac{2ab\cos \frac{C}{2}}{a+b}$$

II. CÁC DẠNG TOÁN HỆ THỨC LƯỢNG TRONG TAM GIÁC

Dạng 1: CHỨNG MINH ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC

Để chứng minh đẳng thức lượng giác $A=B$ ta có thể thực hiện theo một trong các phương pháp sau:

• Phương pháp 1: Biến đổi vế này thành vế kia.
• Phương pháp 2: Xuất phát từ một một hệ thức đúng đã biết để suy ra đẳng thức cần chứng minh.

VÍ DỤ MINH HỌA

Ví dụ 1: Cho tam giác $ABC$. Chứng minh các đẳng thức sau:

1. $\sin A+\sin B+\sin C=4.\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}$
2. ${{\sin }^{2}}A+{{\sin }^{2}}B+{{\sin }^{2}}C=2+2\cos A.\cos B.\cos C$

Ví dụ 2: Cho tam giác $ABC$. Chứng minh các đẳng thức sau:

1. $\tan A+\tan B+\tan C=\tan A.\tan B.\tan C$ ($\Delta $ABC không vuông)
2. $\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}=1$

Dạng 2: CHỨNG MINH BẤT ĐẲNG THỨC LƯỢNG GIÁC TRONG TAM GIÁC

Bất đẳng thức trong tam giác:

Nếu a, b, c là ba cạnh của một tam giác thì:

• $a > 0, b > 0, c > 0$
• $\left| b-c \right|<a<b+c$
• $\left| c-a \right|<b<c+a$
• $\left| a-b \right|<c<a+b$
• $a>b>c\Leftrightarrow A>B>C$

Các bất đẳng thức cơ bản: Mời các bạn xem trong bài Các bất đẳng thức thường sử dụng

Để chứng minh đẳng thức lượng giác $A<B$ ta có thể thực hiện theo một trong các phương pháp sau:

• Phương pháp 1: Biến đổi bất đẳng thức cần chứng minh đến đến một bất đẳng thức hiển nhiên đúng.
• Phương pháp 2: Sử dụng các bất đẳng thức cơ bản đã biết (Cô si, BCS,…) để suy ra bất đẳng thức cần chứng minh.

VÍ DỤ MINH HỌA:

Ví dụ 1: Cho tam giác $ABC$. Chứng minh rằng:  $$\sin \frac{A}{2}.\sin \frac{B}{2}.\sin \frac{C}{2}\le \frac{1}{8}$$

Ví dụ 2: Cho tam giác $ABC$. Chứng minh rằng:

1. $\cos \frac{A}{2}+\cos \frac{B}{2}+\cos \frac{C}{2}\le \frac{3\sqrt{3}}{2}$
2. $\sin A+\sin B+\sin C\le \frac{3\sqrt{3}}{2}$
3. $\tan \frac{A}{2}+\tan \frac{B}{2}+\tan \frac{C}{2}\ge \sqrt{3}$

Ví dụ 3: Cho tam giác $ABC$. Chứng minh rằng:

1. $\cos \frac{A}{2}.\cos \frac{B}{2}.\cos \frac{C}{2}\le \frac{3\sqrt{3}}{8}$
2. $\tan A+\tan B+\tan C\ge 3\sqrt{3}$
3. $\tan \frac{A}{2}.\tan \frac{B}{2}.\tan \frac{C}{2}\le \frac{1}{3\sqrt{3}}$

Dạng 3: NHẬN DẠNG TAM GIÁC

Phương pháp:

1. Sử dụng các phép biến đổi tương đương hoặc hệ quả để biến đổi các điều kiện của đề bài thành một đẳng thức mà từ đó ta dể dàng kết luận được tính chất của tam giác (vuông, cân, đều…)
2. Chứng minh bất đẳng thức $A\ge B$ hoặc $A\le B$ để tìm điều kiện xảy ra dấu bằng trong các bất đẳng thức đó là tam giác đã cho phải vuông, cân, đều,…

VÍ DỤ MINH HỌA:

Ví dụ 1: Tam giác ABC có $\frac{\sin A+\cos B}{\sin B+\cos A}=\tan A$. Chứng minh rằng $\Delta $ABC vuông.

Ví dụ 2: Chứng minh rằng nếu $\Delta ABC$ thỏa mãn điều kiện $\cos 2A+\cos 2B+\cos 2C+1=0$ thì tam giác đó là tam giác vuông

Ví dụ 3: Chứng minh rằng nếu tam giác $ABC$ thoả mãn một trong các điều kiện sau là tam giác cân:

1. $\tan A+\tan B=2.\cot \frac{C}{2}$
2. $\frac{\sin A+\sin B+\sin C}{\sin A+\sin B-\sin C}=\cot \frac{A}{2}.\cot \frac{C}{2}$

Ví dụ 4: Chứng minh rằng nếu tam giác $ABC$ thoả mãn một trong các điều kiện sau là tam giác đều

1. $\cos A.\cos B.\cos C=\frac{1}{8}$
2. $\frac{\cos \frac{A}{2}}{1+\cos A}+\frac{\cos \frac{B}{2}}{1+\cos B}+\frac{\cos \frac{C}{2}}{1+\cos C}=\sqrt{3}$
3. $\cos A+\cos B+\cos C=\sin \frac{A}{2}+\sin \frac{B}{2}+\sin \frac{C}{2}$
4. $\frac{1}{\cos A}+\frac{1}{\cos B}+\frac{1}{\cos C}=\frac{1}{\sin \frac{A}{2}}+\frac{1}{\sin \frac{B}{2}}+\frac{1}{\sin \frac{C}{2}}$

Ví dụ 5: Xác định dạng của tam giác $ABC$ biết:

1. $a+b=\tan \frac{C}{2}(a.\tan A+b.\tan B)$
2. $\frac{b}{\cos B}+\frac{c}{\cos C}=\frac{a}{\sin B.\sin C}$
3. $\cos B+\cos C=\frac{b+c}{a}$
4. $\frac{a.\cos A+b.\cos B+c.\cos C}{a+b+c}=\frac{1}{2}$

Ví dụ 6: Hãy tính các góc của tam giác $ABC$ nếu trong tam giác đó ta có: $${{\sin }^{2}}A+{{\sin }^{2}}B+{{\sin }^{2}}C=\frac{9}{4}+3\cos C+{{\cos }^{2}}C$$

Ví dụ 7: Tính các góc của tam giác $ABC$ biết rằng: $$\begin{cases} 4p(p-a)\le bc \\

\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}=\frac{2\sqrt{3}-3}{8} \end{cases}$$ trong đó BC = a, AB = c, $p=\frac{a+b+c}{2}$.