• 

  Tìm hai số khi biết hai hiệu số

  Tìm hai số khi biết hai hiệu số

  Bài toán Tìm hai số khi biết hai hiệu số là một trong những dạng toán thường gặp trong kì thi HSG.  Để tìm được hai số, chúng ta sử dụng phương pháp khử.

  Xem thêm các dạng toán tìm 2 số ở tiểu học:

  • Tìm hai số khi biết tổng và hiệu của hai số đó lớp 4
  • Tìm hai số khi biết tổng và tỉ số của hai số
  • Tìm hai số khi biết hiệu và tỉ số của hai số

  1. Phương pháp tìm hai số khi biết hai hiệu số

  Chúng ta tiến hành các bước sau:

  • Bước 1. Tìm được hai hiệu số (Hai hiệu số này thuộc hai đại lượng khác nhau.)
  • Bước 2. Tìm mối liên hệ giữa hai hiệu số vừa tìm được. Từ đó, đặt phép chia thích hợp để tìm giá trị của một đơn vị thuộc đại lượng thứ

  2. Ví dụ tìm 2 số khi biết hiệu 2 số

  Ví dụ 1. Để chuẩn bị cho năm học mới, hai bạn An và Bình rủ nhau đi mua sắm sách vở. An mua 15 quyển vở, Bình mua nhiều hơn hơn An 5 quyển vở cùng loại và phải trả nhiều hơn An 20.000 đồng. Hỏi mỗi bạn phải trả bao nhiêu tiền mua vở?

  Phân tích. 

  • Bình mua nhiều hơn An 5 quyển vở là hiệu số thứ nhất.
  • Bình phải trả nhiều 20.000 đồng là hiệu số thứ hai.
  • 20.000 đồng này chính là giá tiền của 5 quyển vở, từ đó chúng ta tìm được giá tiền của 1 quyển vở.
  • Từ giá tiền của 1 quyển vở, chúng ta tìm được số tiền mỗi bạn phải trả.

  Lời giải.

  Giá tiền một quyển vở là:

  20.000 : 5 = 4.000 (đồng)

  Số tiền bạn An mua hết là:

  4.000 x 15 = 60.000 (đồng)

  Số tiền bạn Bình mua hết là:

  60.000 + 20.000 = 80.000 (đồng)

  Đáp số: Bình: 60.000 đồng, An:  80.000 đồng.

  Ví dụ 2. Một hiệu sách, lần thứ nhất bán được 27 quyển vở. Lần thứ hai bán được 40 quyển vở cùng loại và thu được nhiều tiền hơn lần trước 52.000 đồng. Hỏi mỗi lần bán hiệu sách nhận bao nhiêu tiền?

  Lời giải

  Số quyển vở lần sau bán nhiều hơn làn trước là:

  40 – 27 = 13 (quyển)

  Giá tiền một quyển vở là:

  52.000 : 13 = 4.000 (đồng)

  Số tiền hiệu sách nhận được khi bán lần thứ hai là:

  4.000 x 40 = 160.000 (đồng)

  Số tiền hiệu sách nhận được khi bán lần thứ nhất là:

  160.000 – 52.000 = 108.000 (đồng)

  Đáp số: Lần thứ nhất: 108.000 đồng; Lần thứ hai:   160.000 đồng

  Ví dụ 3. Một vườn ươm bán cây, lần thứ nhất bán 10 cây phượng và 8 cây xà cừ được tất cả 64.000 đồng. Lần thứ hai bán 7 cây phượng và 8 cây xà cừ được tất cả 52.000 đồng. Tính giá tiền một cây phượng, một cây xà cừ?

  Lời giải

  Ta có: 10 cây phượng + 8 cây xà cừ = 64.000 đồng

  7 cây phượng + 8 cây xà cừ = 52.000 đồng

  Ta thấy, trong hai lần bán, số cây xà là như nhau nên 3 cây phượng con có giá là:

  64.000 – 52.000 = 12.000 (đồng)

  Suy ra, giá tiền một cây phượng là:

  12.000 : 3 = 4.000 (đồng).

  Mua 10 cây phượng hết số tiền là:

  4.000 x 10 = 40.000 (đồng)

  Mua 8 cây xà cừ hết số tiền là:

  64.000 – 40.000 = 24.000 (đồng)

  Giá tiền một cây xà cừ là:

  24.000 : 8 = 3.000 (đồng)

  Đáp số: Phượng: 4.000 đồng; Xà cừ:    3.000 đồng

  Ví dụ 4. Bà chia kẹo cho các cháu. Nếu bà chia cho mỗi cháu 5 cái kẹo thì bà còn thừa 3 cái kẹo. Nếu bà chia cho mỗi cháu 7 cái kẹo thì bà thiếu mất 9 cái kẹo. Hỏi bà chia kẹo cho mấy cháu và bà có bao nhiêu cái kẹo?

  Lời giải.

  Mỗi cháu chia 7 kẹo nhiều hơn mỗi cháu 2 kẹo là:

  7-5 = 2 (cái kẹo)

  Số kẹo chia đủ cho mỗi cháu 7 các nhiều hơn số kẹo chia cho mỗi cháu 5 cái là

  3+9 =12 (cái kẹo)

  Số cháu được bà chia kẹo là:

  12: 2= 6 (cháu)

  Số kẹo bà có là

  5×6 + 3= 33 (cái)

  Đáp số: 6 cháu và 33 cái kẹo

  Ví dụ 5. Chị chia đào cho các em, nếu cho mỗi em 3 quả, thì thừa 2 quả. Nếu chia mỗi em 4 quả thì thiếu 2 quả. Hỏi có bao nhiêu quả đào và bao nhiêu em được chia tào ?

  Lời giải:

  Vì nếu mỗi người được 3 quả thì thừa 2 quả, mỗi người 4 quả thì thiếu 2 quả, nên ta có sơ đồ:

  

  Nhìn vào sơ đồ, ta thấy số quả đào đủ để chia cho mỗi em 4 quả nhiều hơn số đào đủ chia cho mỗi em 3 quả là:

  2 + 2 = 4 (quả)

  Khi chia cho mỗi em 4 quả thì nhiều hơn khi chia cho mỗi em 3 quả là

  4 – 3 = 1 (quả)

  Do đó, số em được chia đào là:

  4 : 1 = 4 (em)

  Số đào là:

  3 x 4 + 2 = 14 (quả)

  03/03/2021

• 

  Tìm hai số khi biết tổng và tỉ số của hai số

  Tìm hai số khi biết tổng và tỉ số của hai số

  Dạng toán Tìm hai số khi biết tổng và tỉ số của hai sốđó thường xuất hiện trong các đề thi, đề kiểm tra của chương trình toán lớp 5, toán lớp 4. Dưới đây, chúng tôi xin giới thiệu phương pháp giải dạng toán tìm 2 số biết tổng  tỉ của chúng và các ví dụ mẫu.

  Xem thêm: Tìm hai số khi biết hiệu và tỉ số của hai số

  1. Cách giải bài toán tìm hai số khi biết tổng và tỉ số của hai số

  1.1. Phương pháp giải dạng toán tìm 2 số khi biết tổng và tỉ

  • Bước 1. Vẽ sơ đồ theo dữ kiện bài ra.
  • Bước 2. Tìm tổng số phần bằng nhau
  • Bước 3. Tìm số bé và số lớn (có thể tìm số lớn trước hoặc tìm số bé trước) bằng công thức

  Số bé = (Tổng : số phần bằng nhau) x số phần của số bé (hoặc tổng – số lớn)
  Số lớn = (Tổng: số phần bằng nhau) x số phần của số lớn (hoặc tổng – số bé)

  • Bước 4. Kết luận đáp số(Học sinh có thể tiến hành thêm bước thử lại để kiểm chứng kết quả)

  

  1.2. Các trường hợp đặc biệt tìm hai số khi biết tổng và tỉ số

  Đề bài nhiều bài toán lại không cho dữ kiện đầy đủ về tổng và tỉ số mà có thể cho dữ kiện như sau:

  • Thiếu (ẩn) tổng (Cho biết tỉ số, không cho biết tổng số)
  • Thiếu (ẩn) tỉ (Cho biết tổng số, không cho biết tỉ số)
  • Cho dữ kiện thêm, bớt số, tạo tổng (tỉ) mới tìm số ban đầu.

  Với những bài toán cho dữ kiện như vậy, cần tiến hành thêm một bước chuyển về bài toán cơ bản.

  2. Ví dụ mẫu và bài tập tìm 2 số biết tổng và tỉ

  2.1. Tìm hai số biết tổng và tỉ cơ bản

  Đối với dạng bài này, chúng ta so sánh giá trị của số lớn với giá trị của số bé.

  Ví dụ 1. Hai bạn Minh và Khôi có 25 quyển vở. Số vở của Minh bằng  số vở của Khôi. Hỏi mỗi bạn có bao nhiêu quyển vở?

  Bước 1: Học sinh đọc đề toán.

  Bước 2: Phân tích – tóm tắt bài toán.

  • Bài toán cho biết gì? (Minh và Khôi có 25 quyển vở, số vở của Minh bằng   số vở của Khôi).
  • Bài toán hỏi gì? (Bài toán yêu cầu tìm số vở của Minh và số vở của Khôi)
  • Bài toán thuộc dạng toán gì đã được học? (Bài toán thuộc dạng “Tìm hai số khi biết tổng và tỉ số của hai số đó”)

  Bước 3: Tìm cách giải bài toán:

  Tóm tắt bài toán bằng sơ đồ đoạn thẳng:

  

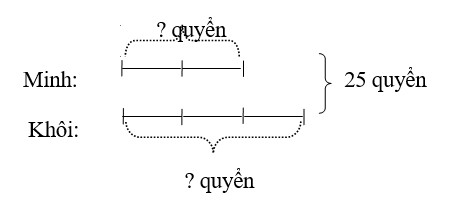
  Theo sơ đồ tổng số phần bằng nhau là:

  2 + 3 = 5 (phần)

  Giá trị của một phần là:

  25 : 5 = 5 (quyển)

  Số vở của bạn Minh là:

  5 x 2 = 10 (quyển)

  Số vở của bạn Khôi là:

  5 x 3 = 15 (quyển)

  hoặc: 25 – 10 = 15 (quyển)

                                                Đáp số: Minh: 10 quyển vở;

                                                                          Khôi: 15 quyển vở.

   

  Ví dụ 2. Tuổi Mẹ và An 36 tuổi. tuổi mẹ bằng 7/2 tuổi An. Hỏi mỗi người bao nhiêu tuổi?

  Hướng dẫn.

  • Tóm tắt bài toán bằng sơ đồ đoạn thẳng như sau:

  

  • Tổng số phần bằng nhau:

  7 + 2 = 9 (phần)

  • Giá trị một phần:

  36: 9 = 4 (tuổi)

  • Số tuổi của mẹ:

  4 x 7 = 28(tuổi)

  • Số tuổi của An:

  4 x 2 = 8(tuổi)

  Đáp số: mẹ 28 tuổi; An 8 tuổi.

  Ví dụ 3.  Đặt đề toán và giải bài toán theo sơ đồ sau.

  

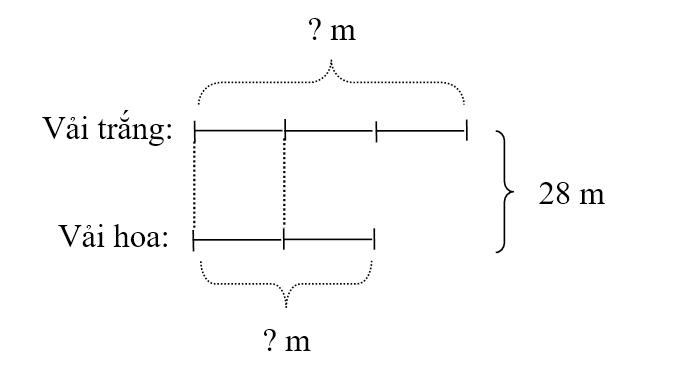
  Hướng dẫn học sinh dựa vào sơ đồ để xác định được dạng toán và đặt đề toán.

  • Bài toán yêu cầu chúng ta làm gì? (Bài toán yêu cầu nêu đề bài toán rồi giải theo sơ đồ).
  • Quan sát sơ đồ và cho biết bài toán thuộc dạng toán gì? (Bài toán thuộc dạng tìm hai số khi biết tổng và tỉ số của hai số đó).
  • Tổng của hai số là bao nhiêu? (Tổng của hai số là 28m)
  • Tỉ số của hai số là bao nhiêu? (Tỉ số của hai số là )
  • Giáo viên yêu cầu học sinh dựa vào sơ đồ đặt đề toán.

  Đặt đề toán. Một cửa hàng đã bán 28m vải, trong đó số vải hoa bằng  số vải trắng. Hỏi cửa hàng đó đã bán được bao nhiêu mét vải mỗi loại?

  Giải bài toán.

  • Xác định được tổng và tỉ số đã cho.
  • Xác định được hai số phải tìm là số nào?

  2.2. Dạng toán tổng (ẩn) – tỉ:

  Ví dụ 4. Hình chữ nhật có chu vi là 200m. Chiều dài bằng 3/2 chiều rộng. tính diện tích của hình chữ nhật?

  Sơ đồ số phần bằng nhau:

  

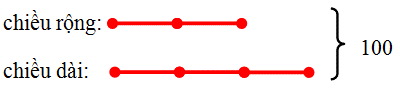
  Tổng chiều dài và chiều rộng:

  200: 2 = 100 (m)

  Tổng số phần bằng nhau:

  3 + 2 = 5 (phần)

  Giá trị một phần:

  100: 5 = 20 (m)

  Chiều dài của hình chữ nhật:

  20 x 3 = 60 (m)

  Chiều rộng của hình chữ nhật:

  20 x 3 = 40 (m)

  Diện tích của hình chữ nhật:

  60 x 40 = 2 400 (m²)

  Đáp số: 2 400 (m²).

  2.3. Dạng toán tổng – tỉ (ẩn):

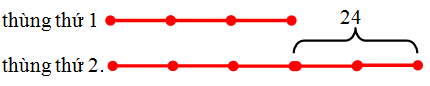
  Ví dụ 5. Có hai thùng đựng 96 lít dầu. 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai. Hỏi mỗi thùng đựng bao nhiêu lít dầu?

  Lời giải.

  Ta có: “5 lần thùng thứ nhất bằng 3 lần thùng thứ hai” nghĩa là “Thùng thứ nhất bằng 3/5 thùng thứ hai”. Do đó, nếu thùng thứ nhất biểu diễn bởi 3 đoạn thẳng bằng nhau thì thùng thứ 2 biểu diễn bởi 5 đoạn thẳng bằng nhau. Sơ đồ số phần bằng nhau:

  

   

  Tổng số phần bằng nhau:

  3 + 5 = 8 (phần)

  Giá trị một phần:

  96: 8 = 12 (lít)

  Số lít dầu thùng thứ nhất đựng:

  12 x 3 = 36 (lít)

  Số lít dầu thùng thứ hai đựng:

  12 x 5 = 60 (lít)

  Đáp số: 36 (lít); 60 (lít).

  2.4. Dạng toán tổng (ẩn) – tỉ (ẩn):

  Ví dụ 6. Tìm hai số tự nhiên, biết trung bình cộng của chúng là 120 và 1/3 số thứ nhất bằng 1/7 số thứ hai.

  Hướng dẫn. Để giải được bài toán này, các em học sinh cần xem lại CÁC BÀI TOÁN VỀ TRUNG BÌNH CỘNG LỚP 4

  Lời giải.

  Trung bình cộng của hai số là 120 nên suy ra tổng của hai số là:

  120 x 2 = 240

  “1/3 số thứ nhất bằng 1/7 số thứ hai” nghĩa là “số thứ nhất bằng 3/7 số thứ hai”. Từ đó, chúng ta có sơ đồ sau:

  

  Tổng số phần bằng nhau là:

  3 + 7 = 10 (phần)

  Như vậy, 10 phần này có tổng giá trị là 240 nên suy ra giá trị của một phần là:

  240: 10 = 24

  Số thứ nhất là:

  24 x 3 = 72

  Số thứ hai là:

  24 x 7 = 168

  Đáp số: 72 và 168.

  3. Bài tập tìm hai số khi biết tổng và tỉ

  Bài 1: Tổng của hai số bằng số lớn nhất của số có hai chữ số. Tỉ số của hai số đó là 4/5. Tìm hai số đó.

  Bài 2: Một hình chữ nhật có chu vi là 350m, chiều rộng bằng 3/4 chiều dài. Tìm chiều dài, chiều rộng của hình chữ nhật đó?

  Bài 3. Một sợi dây dài 28m được cắt thành hai đoạn, đoạn thứ nhất dài gấp 3 lần đoạn dây thứ hai. Hỏi mỗi đoạn dài bao nhiêu mét?

  Bài 4. Tổng của hai số là 72. Tìm hai số đó, biết rằng nếu số lớn giảm 5 lần thì được số bé.

  Bài 5: Tổng của hai số là 96. Tỉ số của hai số đó là 3/5. Tìm hai số đó?

  Bài 6: Minh và Khôi có 25 quyển vở. Số vở của Minh bằng 2/3 số vở của Khôi. Hỏi mỗi bạn có bao nhiêu quyển vở

  Bài 7: Tổng của hai số là 333. Tỉ của hai số là 2/7. Tìm hai số đó.

  Bài 8: Hai kho chứa 125 tấn thóc. Số thóc ở kho thứ nhất bằng 3/2 số thóc ở kho thứ 2. Hỏi mỗi kho chứa bao nhiêu tấn thóc?

  Bài 9: Một miếng vườn hình chữ nhật, có chu vi 200 m, chiều dài gấp 3 lần chiều rộng.  Tính diện tích miếng vườn?

  Bài 10: Miếng đất hình chữ nhật có chu vi 240m, chiều rộng bằng 2/3 chiều dài. Tính diện tích hình chữ nhật đó.

  Bài 11: Tìm 2 số. Biết tổng của chúng bằng 48, nếu lấy số lớn chia cho số bé thì được thương là 3.

  Bài 12: Tìm 2 số, biết tổng của chúng bằng số bé nhất có 3 chữ số. Nếu lấy số này chia cho số kia ta được thương là 4.

  Bài 13: Tổng 2 số bằng số lớn nhất có 4 chữ số. Nếu lấy số lớn chia cho số bé ta được thương là 10. Tìm 2 số đó.

  Bài 14: Một trường tiểu học có tất cả 567 học sinh. Biết rằng với 5 học sinh nam thì có 2 học sinh nữ. Hỏi trường tiểu học đó có bao nhiêu học sinh nam? Bao nhiêu học sinh nữ?

  Bài 15: Tìm số tự nhiên. Biết rằng khi ta thêm vào bên phải số đó 1 chữ số 0 thì ta được số mới và tổng của số mới và số cũ là 297.

  Bài 16: Trung bình cộng của 2 số là 440. Nếu ta thêm 1 chữ số 0 vào bên phải số bé thì ta được số lớn. Tìm 2 số đó.

  Bài 17: Tìm số tự nhiên. Biết rằng nếu ta thêm vào bên phải của số đó một chữ số 2 thì ta được số mới. Tổng của số mới và số cũ là 519.

  Bài 18: Tìm hai số có tổng là 107. Biết rằng nếu xoá đi chữ số 8 ở hàng đơn vị của số lớn ta được số bé.

  Bài 19: Tìm số tự nhiên. Biết rằng khi viết thêm vào bên phải số đó số 52 ta được số mới. Tổng của số mới và số đó bằng 5304.

  Bài 20: Trung bình cộng của 3 số là 85. Nếu thêm 1 chữ số 0 vào bên phải số thứ hai thì được số thứ nhất, nếu gấp 4 lần số thứ hai thì được số thứ ba. Tìm 3 số đó.

  Bài 21: Tổng 2 số bằng 385. Một trong hai số có số tận cùng bằng chữ số 0, nếu xóa chữ số 0 đó thì ta được 2 số bằng nhau. Tìm hai số đó.

  Bài 22: Hai số có tổng là 1/4 và thương cũng là 1/4. Tìm 2 số đó.

  Bài 23: Bính và Đinh có hai thửa ruộng, tổng diện tích của hai thửa ruộng đó là 780 m². Nếu chuyển 1/6 diện tích ruộng của Bính sang cho Đinh thì diện tích của hai thửa sẽ bằng nhau. Tính diện tích của mỗi thửa ruộng bằng mét vuông.

  Bài 24: Lớp 5A và lớp 5B nhận chăm sóc hai thửa ruộng có tổng diện tích là 1560 m2. Nếu lấy 1/4 diện tích thửa ruộng của lớp 5A chuyển sang cho lớp 5B chăm sóc thì diện tích chăm sóc của hai lớp bằng nhau. Tính diện tích của mỗi thửa ruộng.

  Bài 25: Hai hầm đông lạnh chưa 180 tấn tôm. Nếu người ta chuyển 2/7 khối lượng tôm ở hầm thứ nhất sang hầm thứ hai, thì khối lượng tôm ở hai hầm bằng nhau.  Hỏi mỗi hầm chứa bao nhiêu tấn tôm?

  Bài 26: Đội tuyển bóng đá mi ni của huyện A tham dự hội khỏe Phù Đổng cấp tỉnh gồm các bạn học sinh lớp 4 và lớp 5. Dự định số bạn tham gia đội tuyển bóng đá đang học lớp 4 chiếm 1/5 của cả đội. Nhưng do một bạn đang học lớp 4 không tham gia được mà thay bởi một bạn đang học lớp 5, khi đó số bạn đang học lớp 4 tham gia chỉ bằng 1/10 số thành viên của cả đội. Tính tổng số thành viên của cả đôi bóng đá mi ni?

  Bài 27: Đội tuyển của trường A tham gia Hội khoẻ Phù Đổng cấp huyện gồm các bạn học sinh nam và học sinh nữ. Dự định số bạn nữ tham gia đội tuyển chiếm 1/4 số nam  nhưng do điều kiện thay bởi một bạn nữ bằng một bạn nam. Khi đó số bạn nữ chiếm 1/5 số nam. Tính xem đội tuyển của trường A đi dự hội thao bao nhiêu học sinh?

  Bài 28: Đội tuyển trường em tham gia Hội khỏe Phù Đổng cấp huyện, ban đầu số nữ bằng 2/3 số nam. Sau khi xét theo yêu cầu thay thế một bạn nữ bằng một bạn nam vì thế số nữ lúc này bằng 3/4 số nam. Hỏi đội tuyển trường em có bao nhiêu bạn?

  Bài 29: Một tủ sách có hai ngăn. Số sách ở ngăn dưới gấp 3 lần số sách ngăn trên. Nếu chuyển 10 quyển sách ở ngăn trên xuống ngăn dưới thì số sách ngăn dưới gấp 7 lần ngăn trên. Tính số sách mỗi ngăn.

  Bài 30: Lúc đầu số vịt dưới ao nhiều gấp 5 lần số vịt trên bờ. Nhưng sau khi có 3 con vịt từ trên bờ nhảy xuống ao bơi lội thì số vịt dưới ao nhiều gấp 8 lần số vịt trên bờ. Hỏi cả đàn có bao nhiêu con?

  Bài 31: Một hình chữ nhật có chiều rộng bằng 2/5 chiều dài. Nếu thêm vào chiều rộng 4 m và đồng thời bớt chiều dài 4 m thì lúc đó chiều rộng bằng 2/3 chiều dài. Tính diện tích của hình chữ nhật đó.

  Bài 32: Cuối học kì I lớp 5A có số học sinh giỏi bằng 3/7 số học sinh còn lại của lớp. Cuối năm học sinh lớp 5A có thêm 4 học sinh giỏi nên tổng số học sinh giỏi bằng  2/3 số học sinh còn lại của lớp. Hỏi lớp 5 A có bao nhiêu học sinh?

  Bài 33: Một giá sách gồm hai ngăn: Số sách ngăn dưới bằng 6/5 số sách ngăn trên. Nếu xếp 15 quyển sách mới mua vào ngăn trên thì lúc đó số sách ở ngăn dưới bằng 12/11 số sách ngăn trên. Hỏi lúc đầu ở mỗi ngăn có bao nhiêu quyển sách?

  Bài 34: Số gà mái nhiều gấp 6 lần số gà trống. Sau đó mua thêm  5 con gà trống nữa nên bây giờ số gà trống bằng 1/4 số gà mái. Hỏi lúc đầu có bao nhiêu con gà mái, gà trống?

  Bài 35: Một cửa hàng nhập về một số xe máy. Người bán hàng lấy ra trưng bày để bán 1/8 số xe nhập về, số xe còn lại bỏ trong kho. Sau khi bán 3 chiếc xe ở quầy trưng bày thì người chủ quầy nhận thấy số xe ở trong kho nhiều gấp 10 lần số xe còn lại ở quầy trưng bày xe. Hỏi cửa hàng lúc đầu nhập về bao nhiêu chiếc xe máy?

  Bài 36: Để chuẩn bị tham gia Hội khỏe Phù Đổng cấp tỉnh, huyện em đã thành lập đội tuyển tham dự trong đó số nữ bằng 2/3 số nam. Sau khi đội được bổ sung 20 nữ và 15 nam nên lúc này số nữ bằng 4/5 số nam. Tính xem đội tuyển của huyện tham gia Hội khỏe Phù đổng cấp tỉnh có tất cả bao nhiêu bận động viên tham gia?

  Bài 37: Trong đợt thi tuyển chọn học sinh đi tham dự giao lưu Toán Tuổi thơ lần thứ Tư của tỉnh A, trong đó số học sinh nữ bằng 2/3 số học sinh nam. Nếu có thêm 10 học sinh nam tham gia dự thi thì số nữ lúc này bằng 3/5 số học sinh nam. Hỏi có bao nhiêu học sinh tham gia thi tuyển?

  Bài 38: Tủ sách thư viện trường em có hai ngăn: Ngăn thứ nhất có số sách bằng 2/3 số sách thứ hai. Nếu xếp thêm vào ngăn thứ nhất 80 cuốn và ngăn thứ hai 40 cuốn thì số sách ngăn thứ nhất bằng 3/4 số sách ngăn thứ hai. Hỏi ban đầu mỗi ngăn tủ có bao nhiêu cuốn sách?

  Bài 39:: Tí có một số bi không quá 80 viên, trong đó số bi đỏ gấp 5 lần số bi xanh. Nếu Tí có thêm 3 viên bi xanh nữa thì số bi đỏ gấp 4 lần số bi xanh. Hỏi lúc đầu Tí có mấy viên bi đỏ, mấy viên bi xanh?

  Bài 40: Tuổi của con hiện nay bằng 1/2 hiệu tuổi của bố và tuổi con. Bốn năm trước, tuổi con bằng 1/3 hiệu tuổi của bố và tuổi con. Hỏi khi tuổi con bằng 1/4 hiệu tuổi của bố và tuổi của con thì tuổi của mỗi người là bao nhiêu?

  Bài 41: Tìm hai số biết rằng tổng của chúng gấp 5 lần hiệu của chúng và tích của chúng là 4008. Tìm hiệu của chúng.

  Bài 42: Một hình bình hành có diện tích 216 cm2 và chiều cao là 12cm. Nếu tăng chiều cao gấp 2 lần và giảm chiều dài đi 6cm thì diện tích hình mới sẽ thay đổi như thế nào so với diện tích hình bình hành ban đầu?

  Bài 43: Người bán hàng có một bao gạo, lần đầu bán 3kg, lần sau bán 1/3 số gạo còn lại thì còn 18kg. Hỏi lúc đầu bao gạo nặng bao nhiêu kg?

  Bài 44: Tổng số tuổi hiện nay của hai cha con là 50 tuổi. Năm năm sau tuổi cha sẽ gấp 3 lần tuổi con. Tính tuổi mỗi người hiện nay?

  Bài 45: Chú Tuân đến chơi nhà chú Hùng. Chú Hùng và cô Lan cùng ngồi tiếp chuyện. Chú Hùng nói với chú Tuân: “Ngày hai chúng mình đi bộ đội thì tuổi cô Lan bằng 1/3 tuổi tôi thế mà đến bây giờ tổng số tuổi của hai anh em tôi đã là 48 tuổi và tuổi cô Lan đúng bằng tuổi tôi ngày tôi đi bộ đội.” Bạn tính xem cô Lan năm nay bao nhiêu tuổi?

  Bài 46: Nhân dịp tết cửa hàng có nhận về một số hộp mứt. Vì quầy chật nên người bán hàng chỉ để 1/10  số hộp mứt ở quầy, số còn lại đem cất vào trong. Sau khi  bán 4 hộp ở quầy thì số hộp cất đi gấp 15 lần số hộp còn lại ở ngoài quầy. Hỏi lúc đầu cửa hàng nhận về bao nhiêu hộp mứt?

  Bài 47: Một con mèo đuổi bắt một con chuột cách nó 3m. Mỗi bước con mèo nhảy được 8dm, con chuột nhảy được 3dm. Hỏi sau bao nhiêu bước thì mèo bắt được chuột?

  Bài 48: Hiện nay tuổi bố gấp 7 lần tuổi con. Sau 10 năm nữa tuổi bố gấp 3 lần tuổi con. Tính tuổi mỗi người hiện nay.

  Bài 49: Một chiều mùa hè hai cha con dạo chơi trên bãi biển. Trong cuộc dạo chơi đó có 997 lần bước chân hai cha con ngang hàng nhau. Hỏi quãng đường hai cha con đã đi dài bao nhiêu mét? (Biết trung bình một bước của con là 4dm, của cha là 5dm)

  Bài 50: Bố hơn con 30 tuổi, biết 1/2 tuổi con bằng 1/8 tuổi bố và bằng 1/14 tuổi ông. Tính tuổi mỗi người hiện nay.

  Bài 51: Trước đây 4 năm tuổi mẹ gấp 6 lần tuổi con, sau 10 năm nữa thì tỉ số tuổi giữa hai mẹ con là 8/3. Tính tuổi mỗi người hiện nay.

  Bài 52: Hiện nay tuổi anh gấp 3 lần tuổi em. Sau 14 năm nữa tỉ số tuổi giữa hai anh em là 5/4. Tính tuổi mỗi người hiện nay.

  Bài 53: Tết trồng cây, ba bạn Hạ, Thu, Đông cùng đi trồng cây. Số cây của bạn Đông trồng được ít hơn số cây của bạn Hạ và bạn Thu là 8 cây, số cây của bạn Hạ trồng được bằng 3/5 số cây của bạn Thu. Biết số cây của ba bạn, Hạ, Thu, Đông trồng được là 40 cây. Tính số cây của mỗi bạn đã trồng.

  Bài 54: Tháng 9, số học sinh trường tiểu học Kim Đồng được điểm 10 bằng 1/6 số học sinh còn lại của trường. Tháng 10 số học sinh đạt điểm 10 bằng 1/3 số học sinh còn lại của trường. Biết rằng tháng 10 số học sinh đạt điểm 10 nhiều hơn số học sinh tháng 9 đạt điểm 10 là 60 bạn. Hỏi toàn trường có bao hiêu học sinh?

  Bài 55: Có hai tấm bia hình vuông, Tấm bìa nhỏ có số đo cạnh bằng nửa số đo cạnh của tấm bia hình vuông lớn. Người ta cắt tấm bia có số đo cạnh lớn hơn thành các  hình vuông nhỏ. Rồi người ta ghép tất cả các hình lại với nhau thành một hình vuông, thì hình vuông mới có diện tích là 180 cm². Tính số đo cạnh của mỗi hình ban đầu.

  Bài 56: Cho phân số có tổng của tử số và mẫu số là 3345. Biết 2 lần mẫu số bằng 3 lần tử số. Tìm phân số đó?

  Bài 57: Một cửa hàng đã bán được 49kg gạo, trong đó số gạo nếp bằng 2/5 số gạo tẻ. Hỏi cửa hàng đó đã bắn bao nhiêu ki-lô-gam gạo?

  Bài 58: Tỉ của hai số là 3/4. Tổng của hai số đó là 658. Tìm hai số đó

  Bài 59: Chu vi hình chữ nhật là 630 cm, chiều dài gấp rưỡi chiều rộng. Tìm chiều dài, chiều rộng của hình đó.

  Bài 60: Buổi sáng và buồi chiều cửa hàng bán được 24 xe đạp. Số xe bán buổi sáng gấp đôi số xe bán buổi chiều. Hỏi buổi mỗi cửa hàng bán được  bao nhiêu xe đạp?

  Bài 61: Hai túi gạo cân nặng 54kg. Túi thứ nhất cân nặng bằng 4/5 túi thứ hai. Hỏi mỗi túi cân nặng bao nhiêu ki-lô-gam?

  Bài 62: Hình vuông có cạnh 3m. Hình chữ nhật có chiều rộng 3m, chiều dài 5m. Tìm tỉ số của diện tích hình vuông và diện tích hình chữ nhật.

  Bài 63: Tổng của hai số là 40. Tỉ của hai số là 3/5. Tìm hai số đó

  Bài 64: Có tất cả 35 con gà. Trong đó số gà trống bằng 2/3 số gà mái. Hỏi số gà trống và số gà mái là bao nhiêu?

  Bài 65: Tổng hai số là 888. Tỉ hai số đó là 5/3. Tìm hai số đó

  Bài 66: Hai kho gạo chứa 121 tấn gạo, trong đó số gạo ở kho thứ nhất bằng 3/8 số gạo ở kho thứ hai. Hỏi mỗi kho gạo chứa bao nhiêu tấn gạo?

  Bài 67: Lớp 4A có 30 học sinh. Lớp 4B có 35 học sinh. Nhà trường phát cho cả hai lớp 260 cuốn vở. Hỏi mỗi lớp được bao nhiêu cuốn vở? (Mỗi học sinh được số vở như nhau)

  Bài 68: Cả đàn trâu, bò có 24 con. Số trâu nhiều gấp 3 lần số bò. Tính số trâu, số bò.

  Bài 69: Có tất cả 18kg gạo. Trong đó số gạo tẻ bằng một nửa số gạo nếp. Hỏi số gạo mỗi loại?

  Bài 70: Thời gian từ đầu tháng đến ngày sinh của mẹ gấp ba lần khoảng thời gian từ sau ngày sinh của mẹ đến cuối tháng. Hỏi mẹ sinh ngày nào, tháng nào?

  Bài 71: Chu vi hình bình hành ABCD bằng 20cm. Biết rằng cạnh AB dài gấp rưỡi cạnh BC. Hãy tính độ dài các cạnh của hình bình hành.

  Bài 72: Thời gian từ đầu ngày đến bây giờ bằng một nửa thời gian bây giờ đến cuối ngày. Hỏi bây giờ là mấy giờ?

  Bài 73: Tổng của hai số là 36. Tỉ số của hai số đó là 5/4 Tìm số lớn.

  Bài 74: Một lớp có 35 học sinh, trong đó số học sinh nữ bằng 3/4 số học sinh nam. Tính số học sinh nữ của lớp đó.

  Bài 75: Chu vi một mảnh vườn hình chữ nhật là 144m, chiều rộng bằng 2/7 chiều dài. Tính chiều rộng mảnh đất đó.

  Bài 76: Tổng của hai số là 135. Nếu số lớn thêm 5 đơn vị và giữ nguyên số bé thì số bé bằng 2/3 số lớn. Tìm số lớn ban đầu.

  Bài 77: Tổng của hai số là 84. Nếu số bé giảm 7 đơn vị và giữ nguyên số lớn thì được số bé mới bằng 3/4 số lớn. Tìm số bé ban đầu.

  Bài 78: Tổng của hai số là số lớn nhất có ba chữ số. Tỉ của hai số là 5/4. Tìm số lớn, số bé.

  Bài 79: Hai thùng đựng tất cả 112 lít nước mắm. Nếu đổ từ thùng thứ nhất sang thùng thứ hai 7 lít thì số mắm ở thùng thứ hai bằng 5/3 số mắm ở thùng thứ nhất. Hỏi lúc đầu thùng thứ nhất có bao nhiêu lít nước mắm.

  Bài 80: Bác An và bác Bình làm được tất cả 108 sản phầm. Trong đó bác An làm việc trong 5 giờ, bác Bình làm việc trong 7 giờ và mức làm việc của mỗi người như nhau. Hỏi mỗi bác làm được bao nhiêu sản phẩm?

  Bài 81: Hiện nay tổng tuổi của 2 mẹ con là 35 tuổi. Tuổi con bằng 2/5 tuổi mẹ. Tính tuổi con cách đây 2 năm.

  Bài 82: Hiện nay tổng tuổi của 2 bố con là 50 tuổi. Tuổi bố gấp 4 lần tuổi con. Tính tuổi bố sau 5 năm.

  Bài 83: Hiện nay tổng tuổi của 2 mẹ con là 36 tuổi. Sau 3 năm nữa tuổi con bằng 1/5 tuổi mẹ. Tính tuổi mẹ hiện nay.

  Bài 84: Hiện nay tổng tuổi của hai chị em là 16 tuổi. Trước đây 2 năm tuổi chị gấp 3 lần tuổi em. Tính tuổi em trước đây 2 năm.

  Bài 85: Chu vi của cái chiếu hoa hình chữ nhật là 7m 2dm. Tính diện tích của cái chiều đó. (Biết chiều rộng bằng 4/5 chiều dài)

  Bài 86: Trung bình cộng của hai số là 35. Số thứ nhất bằng 2/3 số thứ hai. Tìm hai số đó

  Bài 87: Cho một số tự nhiên có hàng đơn vị là 9. Nếu xóa đi chữ số 9 đó thì được số mới mà tổng số mới và số ban đầu là 34 362. Tìm số tự nhiên đã cho.

  Bài 88: Trong phong trào kế hoạch nhỏ, lớp 4A và lớp 4B góp được 50kg giấy vụn. Tìm số giấy vụn của mỗi lớp, biết rằng 4/7 số giấy vụn của lớp 4A bằng 8/11 số giấy vụn của lớp 4B.

  Bài 89: Tìm số tự nhiên, biết rằng nếu viết thêm chữ số 6 vào bên phải số đó thì ta được số mới mà tổng số mới và số phải tìm là 13 591.

  Bài 90: Hình chữ nhật có chu vi 64cm. Nếu giảm chiều rộng 2cm, thêm chiều dài 2cm thì được hình chữ nhật mới có chiều dài gấp 3 lần chiều rộng. Tính chiều dài và chiều rộng hình chữ nhật ban đầu.

  Bài 91: Một chiếc đồng hồ cứ 30 phút chạy nhanh 2 phú. Lúc 6 giờ sáng người ta lấy lại giờ nhưng không chỉnh lại đồng hồ nên nó vẫn chạy nhanh. Hỏi khi đồng hồ chỉ 16giờ 40phút thì khi đó là mấy giờ đúng?

  Bài 92: Chu vi của một hình chữ nhật là 84 m. Chiều rộng bằng 3/4 chiều dài. Tìm diện tích của hình chữ nhật đó.

  Bài 93: Một người có 1 tạ rưỡi gạo gồm gạo nếp và gạo tẻ. Sau khi bán 15kg gạo nếp và 35kg gạo tẻ thì còn lại số gạo nếp bằng 2/3 số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?

  Bài 94: Trung bình cộng của 3 số là 75. Nếu thêm 1 chữ số 0 vào bên phải số thứ hai thì được số thứ nhất. Tính số thứ 2 biết rằng số đó kém số thứ ba 4 lần.

  Bài 95: Cho phân số 9/11. Tìm một số tự nhiên để khi cộng số đó vào cả tử số và mẫu số thì được phân số có giá trị là 5/6.

  02/03/2021

• 

  Tìm hai số khi biết hiệu và tỉ số của hai số

  Tìm hai số khi biết hiệu và tỉ số của hai số

  Cùng với bài toán Tìm hai số khi biết tổng và tỉ số của hai số thì bài toán Tìm hai số khi biết hiệu và tỉ số của hai số là những dạng toán quan trọng của chương trình toán tiểu học.

  1. Phương pháp giải dạng toán tìm hai số khi biết hiệu và tỉ

  Để giải bài toán tìm hai số khi biết hiệu và tỉ số của hai số, chúng ta thực hiện các bước sau:

  1. Vẽ sơ đồ đoạn thẳng biểu diễn cho hai số
  2. Tìm hiệu số phần bằng nhau
  3. Tìm số bé bằng công thức
  4. Tìm số lớn bằng công thức

  Có thể tóm tắt các bước giải bài toán tìm 2 số khi biết hiệu và tỉ số của chúng như sau:

   

  

  Tuy nhiên, trong nhiều bài toán, đề bài không cho dữ kiện đầy đủ về hiệu và tỉ số mà có thể cho dữ kiện như sau:

  • Chỉ cho biết tỉ số, không có biết hiệu số
  • Cho biết hiệu số, không cho biết tỉ số
  • Cho dữ kiện thêm, bớt số, tạo hiệu (tỉ) mới tìm số ban đầu

  Với những bài toán này, chúng ta cần tiến hành tìm hiệu, tìm tỉ để chuyển về bài toán cơ bản ở trên.

  Xem thêm TOÁN 4: DẠNG TOÁN TÌM PHÂN SỐ CỦA MỘT SỐ

  2. Các dạng toán tìm hai số biết hiệu và tỉ số của hai số

  2.1. Dạng toán hiệu – tỉ cơ bản:

  Ví dụ 1. Hiệu của hai số là 24. Tỉ số của hai số đó 

• Theo sơ đồ, hiệu số phần bằng nhau là:

5 – 3 = 2 (phần)

• Số bé là:

24 : 2 × 3 = 36

• Số lớn là:

36 + 24 = 60

                                    Đáp số: Số bé: 36; Số lớn: 60.

Ví dụ 2. Số thứ nhất kém số thứ hai là 123. Tỉ số của hai số đó là 

• Theo sơ đồ, hiệu số phần bằng nhau là:

5 – 2 = 3 (phần)

• Mà 3 phần này tương ứng với giá trị 123, nên giá trị của mỗi phần là:

123 : 3 =41

• Số thứ nhất chiếm 2 phần, mà mỗi phần có giá trị là 41 nên số thứ nhất là:

41 x 2 = 82

• Số thứ hai là:

82 + 123 = 205

Đáp số: Số thứ nhất: 82; Số thứ hai: 205.

Ví dụ 3. Tuổi của mẹ hơn tuổi An là 20 tuổi. Tuổi mẹ bằng 7/2 tuổi An.  Hỏi mỗi người bao nhiêu tuổi?

Hướng dẫn.

• Vì tuổi mẹ bằng 7/2 tuổi An, nên nếu biểu diễn tuổi của mẹ bằng 7 đoạn thẳng bằng nhau thì tuổi của An bằng 2 đoạn thẳng bằng nhau. Do đó, chúng ta có sơ đồ sau:
• 
• Theo sơ đồ, hiệu số phần bằng nhau là:   7 – 2 = 5 (phần)
• Số tuổi của An là:          (20 : 5) x 2 = 8 (tuổi)
• Số tuổi của mẹ An là:          8 + 20 = 28 (tuổi)

Đáp số: An 8 tuổi;   Mẹ 28 tuổi.

2.2. Dạng toán hiệu (ẩn) – tỉ

Dạng toán này đề bài không cho biết hiệu ngay, do đó chúng ta phải tìm cách tìm hiệu trước rồi mới đi tìm hiệu số phần bằng nhau và từ đó tìm được hai số.

Ví dụ 4. Hình chữ nhật có chiều dài bằng 3/2 chiều rộng. Nếu tăng chiều rộng thêm 20 m thì hình chữ nhật trở thành hình vuông. Tính diện tích của hình chữ nhật?

Lời giải.

• Vì chiều dài bằng 3/2 chiều rộng, nên nếu coi chiều rộng là 2 phần đoạn thẳng thì chiều dài là 3 phần. Theo đề bài ta có sơ đồ:
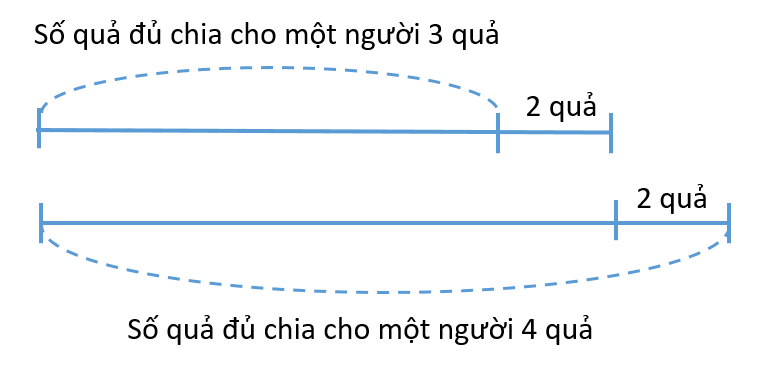
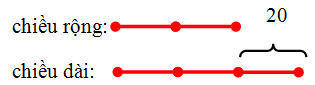• Nếu tăng chiều rộng thêm 20 m thì hình chữ nhật trở thành hình vuông, tức là khi đó chiều rộng sẽ dài bằng chiều dài. Hay nói cách khác, hiệu chiều dài và chiều rộng là 20 m.
• Theo sơ đồ, hiệu số phần bằng nhau là: 3 – 2 = 1 (phần)
• Chiều dài của hình chữ nhật là: 20 x 3 = 60 (m)
• Chiều rộng của hình chữ nhật là: 20 x 2 = 40 (m)
• Diện tích của hình chữ nhật là: 60 x 40 = 2 400 (m²)

Đáp số: 2 400 m²

2.3. Dạng toán hiệu – tỉ (ẩn)

Ví dụ 5. Có hai thùng dầu, thùng thứ nhất đựng ít thùng thứ hai 24 l dầu. Biết 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai. Hỏi mỗi thùng đựng bao nhiêu lít dầu?

Bài giải

• Đề bài chưa cho biết tỉ số, tuy nhiên lại cho biết “5 lần thùng I bằng 3 lần II”. Hay nói cách khác, tỉ số của thùng thứ nhất và thùng thứ hai là 3/5.
• Do đó, chúng ta có sơ đồ sau:

• Hiệu số phần bằng nhau là: 5 – 3 = 2 (phần)
• Số lít dầu thùng thứ nhất đựng là: (24: 2) x 3 = 36 (l)
• Số lít dầu thùng thứ hai đựng là: 36 + 24 = 60 (l)

Đáp số: 36 l dầu; 60 l dầu.

2.4. Dạng toán hiệu (ẩn) – tỉ (ẩn)

Ví dụ 6. Hiện nay, An 8 tuổi và chị Mai 28 tuổi. Sau bao nhiêu năm nữa thì 1/3 tuổi An bằng 1/7 tuổi chị Mai?

Lời giải.

• Theo đầu bài, ta có sơ đồ sau:

• Hiệu số tuổi của An và Mai luôn là: 28 – 8 = 20 (tuổi)
• Biết 1/3 tuổi của An bằng 1/7 tuổi của Mai nên suy ra tuổi của An bằng 3/7 tuổi của Mai.
• Hiệu số phần bằng nhau: 7 – 3 = 4 (phần)
• Số tuổi của An sau này là: (20:4) x 3 = 15 (tuổi)
• Số năm cần tìm là: 15 – 8 = 7 (năm)

Đáp số: 7 năm.

3. Bài tập tìm hai số khi biết hiệu và tỉ số của hai số

Bài 1. Tìm hai số biết tỉ số của chúng bằng  4/7 và nếu lấy số lớn trừ đi số bé thì được kết quả bằng 360.

Bài 2. An có nhiều hơn Bình 12 quyển vở. Tìm số vở của mỗi bạn. Biết rằng số vở của An gấp 4 lần số vở của Bình.

Bài 3. Hiện nay mẹ hơn con 28 tuổi. Biết rằng 3 năm sau tuổi của con bằng 3/7  tuổi mẹ. Hỏi hiện nay mỗi người bao nhiêu tuổi?

Bài 4. Tìm hai số có tỉ số  là 1/9, biết rằng số lớn là số có ba chữ số và nếu xóa chữ số 4 ở hàng trăm của số lớn thì được số bé.

Bài 5. Số thứ nhất bằng  2/5  số thứ hai. Tìm hai số đó? Biết rằng nếu viết thêm vào số thứ nhất 120 đơn vị và bớt số thứ hai đi 243 đơn vị thì hai số bằng nhau.

Bài 6. Một HCN có chiều rộng bằng 2/5 chiều dài. Tính chu vi và diện tích của HCN đó biết nếu chiều rộng thêm 21cm và giữ nguyên chiều dài thì HCN đó trở thành hình vuông.

Bài 7. Mảnh đất   hình chữ nhật có chiều rộng bằng  3/5 chiều dài. Biết rằng nếu giảm chiều dài 9 m và tăng chiều rộng thêm 7 m thì mảnh đất có dạng hình vuông. Tính diện tích mảnh đất hình chữ nhật đó?

Bài 8: Lớp 4A trồng ít hơn lớp 4B 18 cây. Biết 7 lần số cây lớp 4A trồng được  bằng 5 lần số cây lớp 4B trồng được. Hỏi mỗi lớp trồng được bao nhiêu cây?

Bài 9. Tùng có nhiều hơn Bình 20 viên bi. Biết 15 lần số bi của Bình bằng 5 lần số bi của Tùng. Hỏi mỗi lớp trồng được bao nhiêu cây?

Bài 10. Lớp 4A có 1/3 số HS nam bằng 1/5 số HS nữ. Biết số HS nữ hơn số HS nam là 10 bạn. Tìm số HS nam, số HS nữ?

Bài 11. Một nửa số thóc ở kho A bằng 1/3 số thóc ở kho B. Biết rằng số thóc ở kho B nhiều hơn số thóc ở kho A là 17350kg. Mỗi kho có bao nhiêu ki-lô-gam thóc?

Bài 12.  Tìm hai số có hiệu bằng 216, biết rằng nếu thêm một chữ số 0 vào bên phải số bé thì được số lớn.

Bài 13. Hiệu của hai số bằng 393, biết rằng nếu xoá chữ số cuối  của số lớn thì được số bé.

B14. Tìm hai số có hiệu bằng 516, biết rằng nếu lấy số lớn chia cho số bé thì được thương bằng 4.

Bài 15*. Tìm hai số có hiệu bằng 165, biết rằng nếu lấy số lớn chia cho số bé thì được thương là 7 và có số dư là 3.

Bài 16. Hiện nay bố 32 tuổi, em 5 tuổi. Hỏi bao nhiêu năm nữa tuổi của bố gấp 5 lần tuổi của con.

Bài 17. Mẹ sinh con khi 24 tuổi. Biết hiện nay tuổi mẹ gấp 4 lần tuổi con. Tính tuổi mẹ sau 2 năm nữa.

Bài 18. Nếu viết thêm chữ số 3 vào bên trái số đó ta được một số mới có 3 chữ số gấp 5 lần số đã cho. Số đã cho là bao nhiêu?

Bài 19.  Viết thêm chữ số 8 vào bên phải số tự nhiên có 3 chữ số thì số đó tăng 2312 đơn vị. Tìm số có 3 chữ số đó.

Bài 20*. Hiện nay tuổi mẹ gấp 4 lần tuổi con, trước đây 6 năm tuổi mẹ gấp 13 lần tuổi con. Hỏi hiện nay mẹ bao nhiêu tuổi? Con bao nhiêu tuổi? (đ/s 32 và 8)

Bài 21*. Lừa và Ngựa cùng chở hàng. Ngựa nói: “Nếu anh chở giúp tôi 2 bao hàng thì 2 chúng ta chở bằng nhau”. Lừa nói lại với Ngựa: “Còn nếu anh chở giúp  tôi 2 bao hàng thì anh sẽ chở gấp 5 lần tôi”. Hỏi mỗi con chở bao nhiêu bao hàng? (đ/s: 4 và 8)