TỔNG HỢP BÀI TẬP VECTƠ LỚP 10
BÀI TẬP VECTƠ LỚP 10: Chứng minh các đẳng thức vectơ
Ví dụ 1. Cho 6 điểm $A, B, C, D, E, F$. Chứng minh rằng: (bằng nhiều cách khác nhau)
- $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$
- $\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{DB}$
- $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}$
Ví dụ 2. Cho tam giác $ABC$ với $M, N, P$ là trung điểm các cạnh $AB, BC, CA$. Chứng minh rằng:
- $\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\overrightarrow{O}$
- $\overrightarrow{AN}=\overrightarrow{AM}+\overrightarrow{AP}$
- $\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{O}$
Ví dụ 3. (Hệ thức về trung điểm) Cho hai điểm $A, B$.
- Cho $M$ là trung điểm $A, B$. Chứng minh rằng với điểm $I$ bất kì ta có: $$\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IM}$$
- Với điểm $N$ sao cho $\overrightarrow{NA}=-2\overrightarrow{NB}$. Chứng minh rằng với $I$ bất kì: ta có $$\overrightarrow{IA}+2\overrightarrow{IB}=3\overrightarrow{IN}$$
- Với điểm $P$ sao cho $\overrightarrow{PA}=3\overrightarrow{PB}$. Chứng minh rằng với $I$ bất kì ta có $$\overrightarrow{IA}-3\overrightarrow{IB}=-2\overrightarrow{IP}$$
Ví dụ 3. (Hệ thức về trọng tâm) Cho tam giác $ABC$ và $G$ là trọng tâm của tam giác.
- Chứng minh rằng $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\overrightarrow{O}$. Với $I$ bất kì ta có: $$\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=3\overrightarrow{IG}$$
- Điểm $M$ thuộc đoạn $AG$ và $MG=\frac{1}{4}GA$. Chứng minh rằng:$$2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{O}$$
- Với $I$ bất kì, chứng minh rằng $$2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=4\overrightarrow{IM}$$
- Cho hai tam giác $ABC$ và DEF có trọng tâm là $G$ và $G’$. Chứng minh rằng: $$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CE}=3\overrightarrow{GG’}$$ Tìm điều kiện để hai tam giác có cùng trọng tâm.
Ví dụ 4. (Hệ thức về hình bình hành) Cho hình bình hành $ABCD$ tâm $O$.
- Chứng minh rằng: $\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=\overrightarrow{O}$
- Với $I$ bất kì $\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=4\overrightarrow{IO}$
Ví dụ 5. (Tứ giác bất kì) Cho tứ giác $ABCD$. Gọi $M, N$ là trung điểm của $AB$ và $CD$. Chứng minh rằng:
- $\overrightarrow{AD}+\overrightarrow{BC}=2\overrightarrow{MN}$
- $\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{MN}$
- Tìm vị trí điểm $I$ sao cho $$\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{O}$$
- Với điểm $M$ bất kì, Chứng minh rằng: $$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MI}$$
Ví dụ 6. (Khái niệm trọng tâm của hệ $n$ điểm và tâm tỉ cự của hệ $n$ điểm) Cho $n$ điểm ${{A}_{1}},{{A}_{2}},…,{{A}_{n}}$.
- Gọi $G$ là điểm thoả mãn $$\overrightarrow{G{{A}_{1}}}+\overrightarrow{G{{A}_{2}}}+…+\overrightarrow{G{{A}_{n}}}=\overrightarrow{O}.$$ Chứng minh rằng với điểm $M$ bất kì ta luôn có$$\overrightarrow{M{{A}_{1}}}+\overrightarrow{M{{A}_{2}}}+…+\overrightarrow{M{{A}_{n}}}=n\overrightarrow{MG}.$$
- Gọi $I$ là điểm thoả mãn ${{n}_{1}}\overrightarrow{IA_1}+n_2\overrightarrow{G{{A}_{2}}}+…+{{n}_{n}}\overrightarrow{G{{A}_{n}}}=\overrightarrow{O}$. Chứng minh rằng với $M$ bất kì: $${{n}_{1}}\overrightarrow{M{{A}_{1}}}+{{n}_{2}}\overrightarrow{M{{A}_{2}}}+…+{{n}_{n}}\overrightarrow{M{{A}_{n}}}=({{n}_{1}}+..+{{n}_{n}})\overrightarrow{MG}$$
Ví dụ 7.
- Cho lục giác đều $ABCDEF$. Chứng minh rằng hai tam giác $ACE$ và $BDF$ cùng trọng tâm.
- Cho lục giác $ABCDEF$. Gọi $M, N, P, Q, R, S$ lần lượt là trung điểm của $AB, CD, EF, BC, DE, FA$. Chứng minh rằng hai tam giác $MNP$ và $QRS$ cùng trọng tâm.
- Cho hai tam giác $ABC$ và $A’,B’,C’$ là các điểm thuộc $BC, CA, AB$ sao cho:$$\overrightarrow{{{A}’}B}=k\overrightarrow{{{A}’}C},\overrightarrow{{{B}’}C}=k\overrightarrow{{{B}’}A},\overrightarrow{{{C}’}A}=k\overrightarrow{{{C}’}B}$$ và $k\ne 1$. Chứng minh rằng hai tam giác $ABC$ và $A’B’C’$ cùng trọng tâm.
- Cho tứ giác lồi $ABCD$. Gọi $M, N, P, Q$ là trung điểm $AB, BC, CD, DA$. Chứng minh rằng hai tam giác $ANP$ và $CMQ$ cùng trọng tâm.
Ví dụ 8. (Một số đẳng thức về trực tâm, trọng tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp)
Cho tam giác $ABC$ có $G, H, O, I$ lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp. Chứng minh rằng:
- $3\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$
- $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$
- $2\overrightarrow{HO}=\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}$
- $a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{O}$
- $\tan A\overrightarrow{HA}+\tan B\overrightarrow{HB}+\tan C\overrightarrow{HC}=\overrightarrow{O}$
- Gọi $M$ là điểm bất kì nằm trong tam giác $ABC$. Chứng minh rằng: ${{S}_{BCM}}\overrightarrow{IA}+{{S}_{ACM}}\overrightarrow{IB}+{{S}_{ABM}}\overrightarrow{IC}=\overrightarrow{O}$ ($M$ nằm ngoài thì không còn đúng).
Ví dụ 9. (Nhấn mạnh bài toán và mở rộng ra nhiều trường hợp). Cho tam giác $ABC$. Gọi $M$ là trung điểm $AB$ và $N$ là một điểm trên cạnh $AC$ sao cho $NC = 2NA$. Gọi $K$ là trung điểm $MN$.
- Chứng minh rằng: $\overrightarrow{AK}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$.
- $D$ là trung điểm $BC$. Chứng minh rằng: $\overrightarrow{KD}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$
BÀI TẬP VECTƠ LỚP 10: Biểu diễn véc tơ
Ví dụ 1. Cho tam giác $ABC$ và $G$ là trọng tâm. Lấy $B_1$ đối xứng với $B$ qua $G$. $M$ là trung điểm $BC$. Hãy biểu diễn các véc tơ $\overrightarrow{AM}$, $\overrightarrow{AG},\overrightarrow{BC},\overrightarrow{C{{B}_{1}}},\overrightarrow{A{{B}_{1}}},\overrightarrow{M{{B}_{1}}}$ qua hai véc tơ $\overrightarrow{AB},\overrightarrow{AC}$.
Ví dụ 2. Cho tam giác $ABC$, gọi $I$ là điểm trên cạnh $BC$ sao cho $2CI = 3BI$ và $J$ thuộc $BC$ kéo dài sao cho $5JB = 2JC$.
- Tính $\overrightarrow{AI},\overrightarrow{AJ}$ theo hai véc tơ $\overrightarrow{AB},\overrightarrow{AC}$. Từ đó biểu diễn $\overrightarrow{AB},\overrightarrow{AC}$ theo $\overrightarrow{AI},\overrightarrow{AJ}$.
- Gọi $G$ là trọng tâm tam giác. Tính $\overrightarrow{AG}$ theo $\overrightarrow{AI},\overrightarrow{AJ}$.
BÀI TẬP VECTƠ LỚP 10: Chứng minh 3 điểm thẳng hàng
Phương pháp: Ba điểm $A, B, C$ thẳng hàng khi và chỉ khi $\overrightarrow{AB}=k\overrightarrow{AC}$.
Lưu ý: $\overrightarrow{AB}=m\overrightarrow{x}+n\overrightarrow{y},\overrightarrow{AC}=km\overrightarrow{x}+kn\overrightarrow{y}$ thì $\overrightarrow{AB}=k\overrightarrow{AC}$
Ví dụ 1. Cho tam giác $ABC$ và $M, N$ lần lượt là trung điểm $AB, AC$.
- Gọi $P, Q$ là trung điểm $MN$ và $BC$. Chứng minh $A, P, Q$ thẳng hàng.
- Gọi $E, F$ thoả mãn: $\overrightarrow{ME}=\frac{1}{3}\overrightarrow{MN}$, $\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC}$. Chứng minh $A, E, F$ thẳng hàng.
Ví dụ 2. Cho tam giác $ABC$, có $E$ là trung điểm $AB$ và $F$ thuộc đoạn $AC$ thoả mãn $AF = 2FC$.
- Gọi $M$ là trung điểm $BC$ và $I$ là điểm thoả mãn $4EI = 3FI$. Chứng minh $A, M, I$ thẳng hàng.
- Lấy $N$ thuộc $BC$ sao cho $BN = 2 NC$ và $J$ thuộc $EF$ sao cho $2EJ = 3JF$. Chứng minh $A, J, N$ thẳng hàng.
- Lấy điểm $K$ là trung điểm $EF$. Tìm $P$ thuộc $BC$ sao cho $A, K, P$ thẳng hàng.
Xem thêm tại Chứng minh thẳng hàng bằng vectơ
Ví dụ 3. Cho tam giác $ABC$ và M, N, P là các điểm thoả mãn: $\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{O}$, $\overrightarrow{AN}=3\overrightarrow{NC}$, $\overrightarrow{PB}+\overrightarrow{PA}=\overrightarrow{O}$. Chứng minh rằng: $M, N, P$ thẳng hàng.
Hướng dẫn. $\overrightarrow{MP}=\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA},\text{ }\overrightarrow{MN}=\frac{1}{2}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{CA}$.
Ví dụ 4. Cho tam giác $ABC$ và $L, M, N$ thoả mãn $\overrightarrow{LB}=2\overrightarrow{LC},$$\overrightarrow{MC}=\frac{-1}{2}\overrightarrow{MA}$, $\overrightarrow{NB}+\overrightarrow{NA}=\overrightarrow{O}$. Chứng minh $L, M, N$ thẳng hàng.
Ví dụ 5. Cho tam giác $ABC$ với $G$ là trọng tâm. $I, J$ thoả mãn: $2\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{O}$, $2\overrightarrow{JA}+5\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{O}$.
- Chứng minh rằng: $M, N, J$ thẳng hàng với $M, N$ là trung điểm $AB$ và $BC$.
- Chứng minh rằng $J$ là trung điểm $BI$.
- Gọi $E$ là điểm thuộc $AB$ và thoả mãn $\overrightarrow{AE}=k\overrightarrow{AB}$. Xác định $k$ để $C, E, J$ thẳng hàng.
Ví dụ 6. Cho tam giác $ABC$. Gọi $I, J$ là hai điểm thoả mãn: $\overrightarrow{IA}=2\overrightarrow{IB}, 3\overrightarrow{JA}+2\overrightarrow{JC}=\overrightarrow{O}$. Chứng minh đường thẳng $IJ$ đi qua $G$.
BÀI TẬP VECTƠ LỚP 10: Xác định điểm thoả mãn một đẳng thức vectơ
Đặt Vấn đề: Cho hai điểm $A, B, C$ cố định.
- Nếu $\overrightarrow{PB}+\overrightarrow{PA}=\overrightarrow{O}$ thì $P$ là trung điểm của $AB$.
- Nếu $\overrightarrow{PB}+\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{O}$ thì $P$ là trọng tâm tam giác $ABC$.
- Nếu $P$ là một điểm thoã mãn một đẳng thức véc tơ khác thì có xác định được vị trí của $P$ hay không?
Ví dụ 1. Cho hai điểm $A,B$. Xác định vị trí điểm $I$ thoả mãn: $\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{O}$.
Nhận xét. Với hai điểm $A, B$ cho trước luôn xác định được điểm $I$ thoả mãn: $$m\overrightarrow{IA}+n\overrightarrow{IB}=\overrightarrow{O}$$ Với điểm O bất kì ta có: $\overrightarrow{OI}=\frac{m}{m+n}\overrightarrow{OA}+\frac{n}{m+n}\overrightarrow{OB}$.
Ví dụ 2. Bài toán 3 điểm. Cho 3 điểm $A, B, C$. Tìm vị trí điểm $M$ sao cho:
- $\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}$
- $2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{O}$
- $\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{O}$
- $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{O}$
- $\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{O}$
- $\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{O}$
BÀI TẬP VECTƠ LỚP 10: Tìm quĩ tích thoả mãn một đẳng thức véc tơ
Một số quĩ tích cơ bản:
- $\left| \overrightarrow{MA} \right|=\left| \overrightarrow{MB} \right|$ thì $M$ nằm trên đường trung trực của $AB$.
- $\left| \overrightarrow{MC} \right|=k\left| \overrightarrow{AB} \right|$, với $A, B, C$ cố định thì $M$ nằm trên đường tròn tâm $C$ bán kính $k.AB$.
- $\overrightarrow{AM}=k\overrightarrow{BC}$ với $A, B, C$ cho trước:
- $k > 0$ thì $M$ nằm trên nửa đường thẳng qua $A$ và song song với $BC$ và theo hướng $\overrightarrow{BC}$.
- $k< 0$
- $k$ bất kì.
Dạng 1. (Bài toán hai điểm)
Ví dụ 1. Cho hai điểm $A,B$ cố định. Tìm quĩ tích điểm $M$ sao cho:
- $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=2\left| \overrightarrow{AB} \right|$
- $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=\left| \overrightarrow{AB} \right|$
- $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=2\left| \overrightarrow{MA} \right|$
- $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=\left| \overrightarrow{MA} \right|$
- $\left| 2\overrightarrow{MA}+\overrightarrow{MB} \right|=\left| \overrightarrow{MA}-\overrightarrow{MB} \right|$
Dạng 2. (Bài toán 3 điểm)
Ví dụ 2. Cho tam giác $ABC$. Tìm quĩ tích điểm $M$ sao cho:
- $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right|=\frac{3}{2}\left| \overrightarrow{MB}+\overrightarrow{MC} \right|$
- $\left| \overrightarrow{MA}+\overrightarrow{AC} \right|=\left| \overrightarrow{MA}-\overrightarrow{MB} \right|$
- $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|=\left| \overrightarrow{MB}-\overrightarrow{MC} \right|$
- $\left| 3\overrightarrow{MA}+2\overrightarrow{MB}-2\overrightarrow{MC} \right|=\left| \overrightarrow{MB}-\overrightarrow{MC} \right|$
Ví dụ 3. Tìm quĩ tích điểm $M$ sao cho:
- $\overrightarrow{MA}+k\overrightarrow{MB}-k\overrightarrow{MC}=\overrightarrow{O}$
- $k\overrightarrow{MA}+\overrightarrow{MB}=k\overrightarrow{MC}$
- $(1-k)\overrightarrow{MA}+\overrightarrow{MB}-k\overrightarrow{MC}=\overrightarrow{O}$
BÀI TẬP VECTƠ LỚP 10: Một số bài toán về khoảng cách
Ví dụ 1 Cho hai điểm $A, B$ và đường thẳng $d$. Tìm vị trí điểm $M$ trên $d$ sao cho độ dài các véc tơ sau nhỏ nhất?
- $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|$
- $\left| \overrightarrow{MA}+2\overrightarrow{MB} \right|$
- $\left| 3\overrightarrow{MA}-\overrightarrow{MB} \right|$
- $\left| 3\overrightarrow{MA}+2\overrightarrow{MB} \right|$
- $\left| 2\overrightarrow{MA}-3\overrightarrow{MB} \right|$
Ví dụ 2. Cho tam giác $ABC$ và đường thẳng $d$. Tìm vị trí điểm $M$ trên $d$ sao cho độ dài các véc tơ sau nhỏ nhất.
- $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right|$
- $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|$
- $\left| 3\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right|$
- $\left| \overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC} \right|$
Ví dụ 3. Cho tứ giác $ABCD$ và đường thẳng $d$. Tìm vị trí điểm $M$ trên $d$ sao cho độ dài các véc tơ sau nhỏ nhất.
- $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD} \right|$
- $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}+2\overrightarrow{MD} \right|$
- $\left| 3\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-\overrightarrow{MD} \right|$
- $\left| \overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}-\overrightarrow{MD} \right|$
- $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+2\overrightarrow{AB} \right|$
BÀI TẬP VECTƠ LỚP 10: Chứng minh đường thẳng đi qua một điểm cố định
Ví dụ 1. (Bài toán 2 điểm) Cho hai điểm $A, B$ cố định. Hai điểm $M, N$ di động. Chứng minh rằng đường thẳng $MN$ luôn đi qua một điểm cố định nếu:
- Với $I$ là trung điểm $AB$ thì: $$\overrightarrow{MB}+\overrightarrow{MA}=2\overrightarrow{MI}$$
- Nếu $M, I, N$ thẳng hàng thì khi đó: $\overrightarrow{MN}=k\overrightarrow{MA}+k\overrightarrow{MB}$, hay nói cách khác là đường thẳng $MN$ đi qua điểm $I$ cố định.
Từ đó dẫn dắt vào bài toán bằng cách thay điểm $I$ bằng điểm bất kì:
- $\overrightarrow{MN}=\overrightarrow{MA}+2\overrightarrow{MB}$
- $\overrightarrow{MN}=\overrightarrow{MA}-2\overrightarrow{MB}$
- $\overrightarrow{MN}=-\overrightarrow{MA}+2\overrightarrow{MB}$
- $\overrightarrow{MN}=3\overrightarrow{MA}+2\overrightarrow{MB}$
Ví dụ 2. (Bài toán 3 điểm). Cho tam giác $ABC$ và điểm $M$ trong mặt phẳng. Chứng minh rằng đường thẳng $MN$ luôn đi qua một điểm cố định nếu (Xác định vị trí điểm cố định và điểm $N$ trong mỗi trường hợp)
- $\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MA}=\overrightarrow{MN}$
- $2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MN}$
- $\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MN}$
- $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{MN}$
- $\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{MN}$
- $\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{MN}$


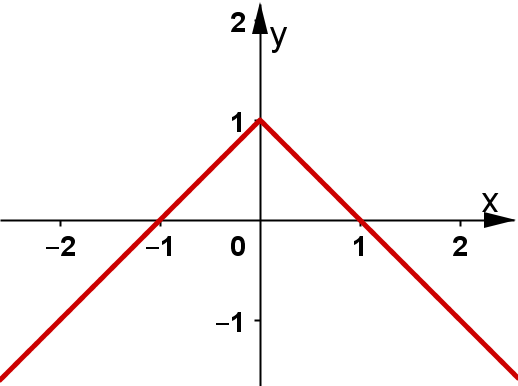
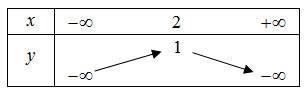 A. $ y=-{{x}^{2}}+4x-3.$
A. $ y=-{{x}^{2}}+4x-3.$