100 BÀI TOÁN LUYỆN HỌC SINH GIỎI LỚP 2
Xin giới thiệu với thầy cô và các em học sinh 100 đề toán dành cho học sinh giỏi lớp 2. Tải file PDF để in xin mời xem ở cuối bài viết.
Bài 1: Từ 3 chữ số 3, 5, 6. Em hãy viết tất cả các số có hai chữ số có thể được.

Bài 2: Hãy viết các số có hai chữ số sao cho mỗi số chỉ có 1 chữ số 5.

Bài 3: Từ 3 số 4, 7, 9 em hãy viết tất cả các số có hai chữ số khác nhau (Ở mỗi số không có hai chữ số giống nhau )

Bài 4: Số x có bao nhiêu chữ số biết
a) x bé hơn 100.
b) x đứng liền sau một số có hai chữ số.

Bài 5: Viết số thích hợp vào ô trống (theo mẫu)
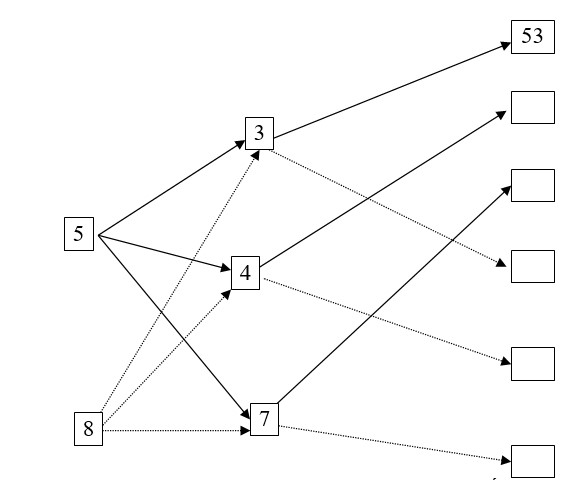
Bài 6: Hình vẽ sau đây có bao nhiêu hình tứ giác , viết tên các hình tứ giác đó?
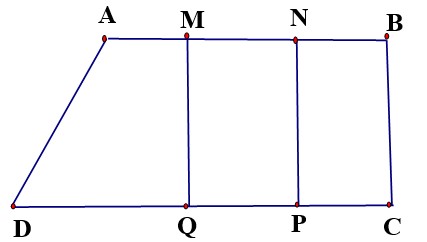
Bài 7: Hình vẽ sau có bao nhiêu hình chữ nhật? Viết tên các hình chữ nhật đó.
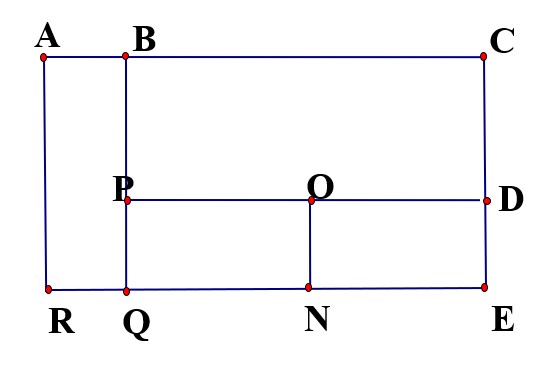
Bài 8: Hình vẽ sau có bao nhiêu hình vuông, bao nhiêu hình tam giác?
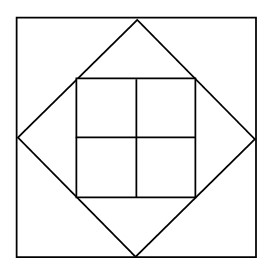
Bài 9: Bao gạo thứ nhất nặng 26 kg, bao gạo thứ 2 nặng hơn bao gạo thứ nhất 15 kg . Hỏi cả hai bao gạo nặng bao nhiêu kg?

Bài 10: Hãy cho biết có bao nhiêu số tự nhiên lớn hơn 24 và nhỏ hơn 79?
Trả lời: Có tất cả ………….. số tự nhiên lớn hơn 24 và nhỏ hơn 79.
Bài 11. Hãy cho biết từ số 26 đến số 78 có tất cả bao nhiêu số tự nhiên?
Trả lời: Có…………………….số tự nhiên lớn hơn 24 và nhỏ hơn 79.
Bài 12. Hãy cho biết có bao nhiêu số tự nhiên từ số 36 đến số 93?
Trả lời: Có………………..số tự nhiên từ số 36 đến số 93.
Bài 13: Thùng thứ nhất đựng 32 lít dầu, thùng thứ 2 đựng ít hơn thùng thứ nhất 9 lít dầu . Hỏi cả hai thùng đựng được bao nhiêu lít dầu?
Bài 14: Một cửa hàng có 68 kg đường . Sau một ngày bán hàng còn lại 18 kg đường . Hỏi cửa hàng đã bán hết bao nhiêu kg đường?
Bài 15: Số lớn nhất có hai chữ số mà tổng các chữ số của nó bằng 9 là số………………………
Bài 16: Số bé nhất có hai chữ số mà hiệu hai chữ số của số đó bằng 4 là số…………………………
Bài 17: Một cửa hàng bán được 45 kg gạo trong ngày đầu, còn lại 28 kg gạo sau ngày thứ nhất. Sau ngày thứ hai còn lại 2 kg gạo . Hỏi lúc ban đầu cửa hàng có bao nhiêu kg gạo? Cả hai ngày cửa hàng đã bán được bao nhiêu kg gạo?
Bài 18: Có một cân đĩa và hai quả cân loại 1kg và 5 kg . Làm thế nào cân được 4 kg gạo qua một lần cân?
Bài 19: Thứ 5 tuần này là ngày 8 tháng 7. Hỏi thứ 5 tuần trước là ngày nào?
Bài 20: Thứ sáu tuần này là ngày 16 tháng 9 . Hỏi thứ 7 tuần sau là ngày nào?
Bài 21: Hồng muốn biết sinh nhật của mình 15 tháng 6 là ngày thứ mấy .Bạn Mai lại cho biết ngày 7 tháng 6 là ngày thứ 3. Em hãy giúp bạn Hồng biết ngày sinh nhật của bạn là ngày thứ mấy?
Bài 22: An có 12 viên bi . Bình có nhiều hơn An 9 viên bi . Chung có ít hơn Bình 6 viên bi . Hỏi cả ba bạn có bao nhiêu viên bi?
Bài 23: Hình vẽ sau đây có bao nhiêu đoạn thẳng, bao nhiêu tam giác, bao nhiêu tứ giác, kể tên các hình đó?
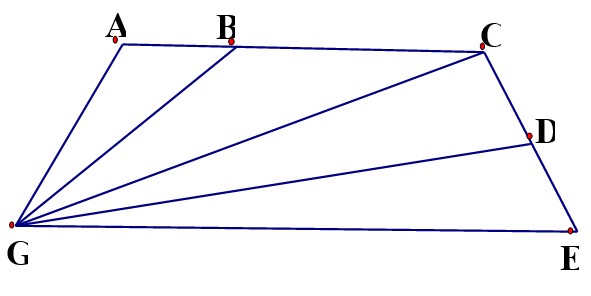
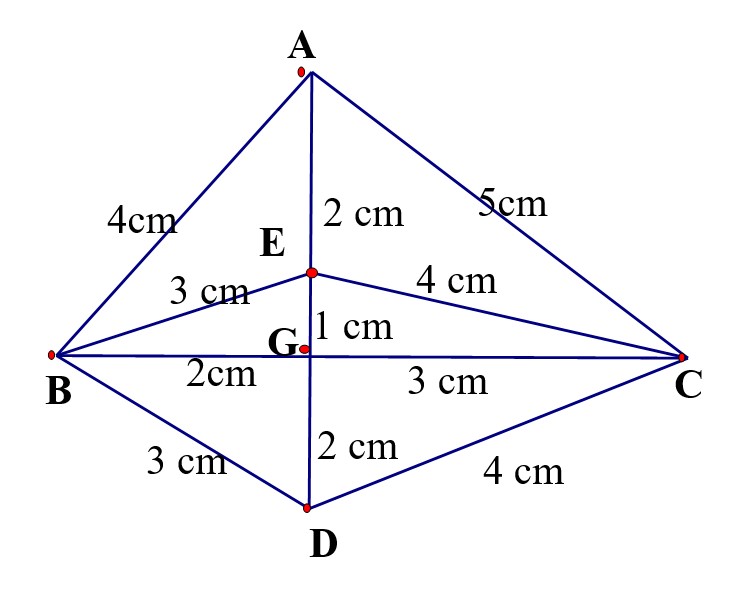
Bài 24: Cho hình vẽ sau đây.
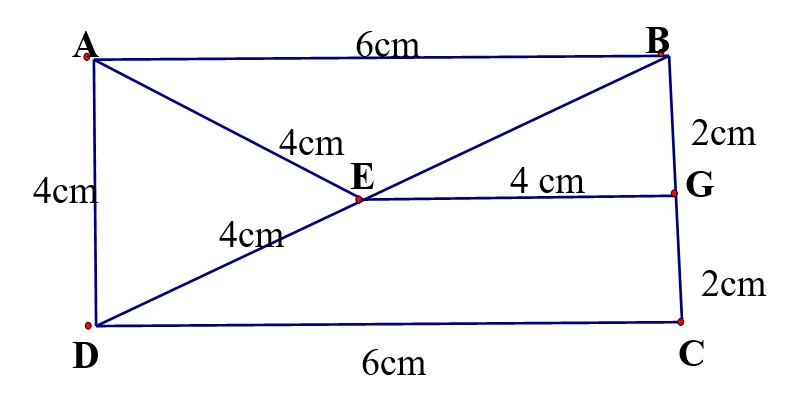
- Chu vi tam giác BEG là: …………………………………………………..
- Chu vi tam giác AED là: …………………………………………………..
- Chu vi tứ giác ABGE là: …………………………………………………..
- Chu vi tứ giác DEGC là: ………………………………………………………………………………………………………………………..
- Độ dài đường gấp khúc ABCDEG là: ………………………………………………………………………………………………………………………..
- Độ dài đường gấp khúc AEDCGE là: ………………………………………………………………………………………………………………………..
Bài 25: Bạn An có 9 viên bi. Nếu An cho Bình 4 viên bi thì Bình có 10 viên bi. Hỏi cả hai bạn có bao nhiêu viên bi?
Bài 26: Dũng có 1 số bi xanh và đỏ. Biết rằng số bi của Dũng ít hơn 10 viên. Trong đó số bi đỏ hơn số bi xanh 7 viên. Hỏi Dũng có bao nhiêu bi xanh, bao nhiêu bi đỏ?
Bài 27: Lan có 4 bìa xanh và đỏ, số bìa xanh ít hơn số bìa đỏ. Hỏi Lan có bao nhiêu tấm bìa xanh, bao nhiêu tấm bìa đỏ?
Bài 28: Minh có 18 viên bi, nếu Minh cho Bình 3 viên thì Bình có nhiều hơn Minh 3 viên bi. Hỏi Bình có bao nhiêu viên bi?
Bài tập 29: Có ba thúng xoài, thúng thứ nhất ít hơn thúng thứ hai 6 quả, thúng thứ ba nhiều hơn thúng thứ hai 5 quả. biết thúng thứ nhất có 12 quả. Hỏi
a) Thúng nào có nhiều xoài nhất?
b) Cả ba thúng có bao nhiêu quả xoài?
Bài 30: Số lớn nhất có hai chữ số khác nhau là số……………..
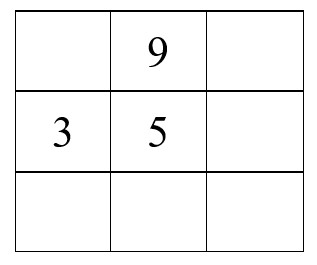
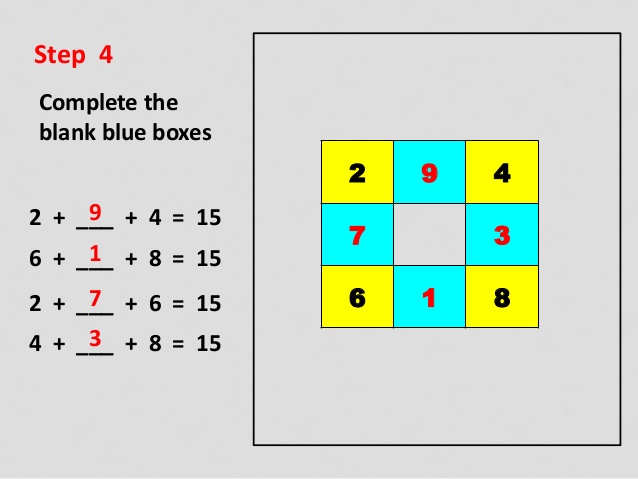
Bài 31: Điền các số vào ô trống sao cho có đủ các số từ 1 đến 9 sao cho tổng các số trong mỗi hàng, trong mỗi cột đều bằng 15.
Bài 32: Hình vẽ bên dưới có…….. đoạn thẳng.
Kể tên các đoạn thẳng: …………………………………………………………………………………………………
Hình vẽ bên trên có……..hình tam giác. Tính chu vi mỗi tam giác.
Bài 33: Hình vẽ dưới đây:

- Có……. tứ giác
- Có………..hình chữ nhật
- Có………..hình vuông
Bài 34: Một cửa hàng ngày thứ nhất bán được 66 gói kẹo, ngày thứ nhất bán hơn ngày thứ hai 14 gói kẹo. Hỏi ngày thứ hai cửa hàng bán được bao nhiêu gói kẹo.
Bài 35: Lan có nhiều hơn Huệ 8 bông hoa, Hồng có nhiều hơn Lan 4 bông hoa. Hỏi Hồng có nhiều hơn Huệ bao nhiêu bông hoa?
Bài 36: Khánh có 18 quyển truyện. Nếu Khánh cho Hoà 2 quyển truyện thì Hoà có 19 quyển truyện. Hỏi Khánh và Hoà ai nhiều truyện hơn.
Bài 37: Hộp thứ nhất có 78 viên kẹo, hộp thứ hai có ít hơn hộp thứ nhất 16 viên kẹo. Hỏi cả hai hộp có bao nhiêu viên kẹo?
Bài 38: Có hai đàn vịt, đàn vịt thứ nhất có 95 con, đàn vịt thứ nhất nhiều hơn đàn vịt thứ hai 32 con. Hỏi cả hai đàn vịt có bao nhiêu con?
Bài 39: Đoạn thẳng MN dài 45 cm, đoạn thẳng PQ ngắn hơn đoạn thẳng MN 14 cm. Hỏi đoạn thẳng PQ dài bao nhiêu cm?
Bài 40: Đặt một đề toán sau rồi giải.
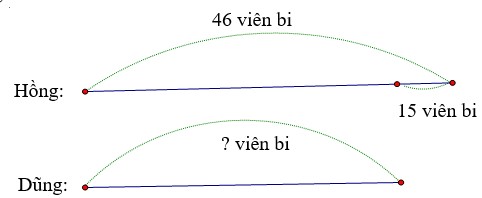
Tóm tắt:
Bài 41: Một cửa hàng ngày thứ nhất bán được 25 chiếc xe đạp, ngày thứ nhất bán ít hơn ngày thứ hai 8 chiếc xe đạp. Hỏi cả hai ngày cửa hàng bán được bao nhiêu chiếc xe đạp?
Bài 42: Nam có ít hơn Bảo 8 viên bi. Hùng cho Nam thêm 3 viên bi. Hỏi Bảo còn nhiều hơn Nam bao nhiêu viên bi?
Bài 43: Hùng cân nặng 22 kg. Hoàng cân nặng 24 kg. Hậu cân nặng 23 kg. Hỏi
- Bạn nào cân nặng nhất?
- Hùng và Hoàng cân nặng bao nhiêu kg?
- Cả ba bạn cân nặng bao nhiêu kg?
Bài 44: Có 1 cân đĩa, người ta đặt lên đĩa cân thứ nhất 3 kg, đĩa thứ hai đặt túi đường và quả cân 1 kg thì cân thăng bằng. Hỏi túi đường nặng bao nhiêu kg?
Bài 45: Bao gạo và bao đường cân nặng 86 kg. Bao gạo cân nặng 42 kg. Hỏi bao nào nặng hơn và nặng hơn bao kia bao nhiêu kg?
Bài 46: Một thùng nước mắm có 36 lít. Sau khi rót ra bán thùng còn lại 12 lít. Hỏi số mắm đã bán được và số mắm còn lại trong thùng số mắm nào nhiều hơn và nhiều hơn bao nhiêu?
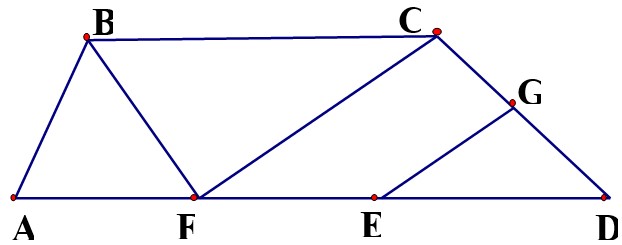
Bài 47: Hình vẽ dưới đây có bao nhiêu tam giác, bao nhiêu tứ giác? Kể tên các tam giác, tứ giác đó.
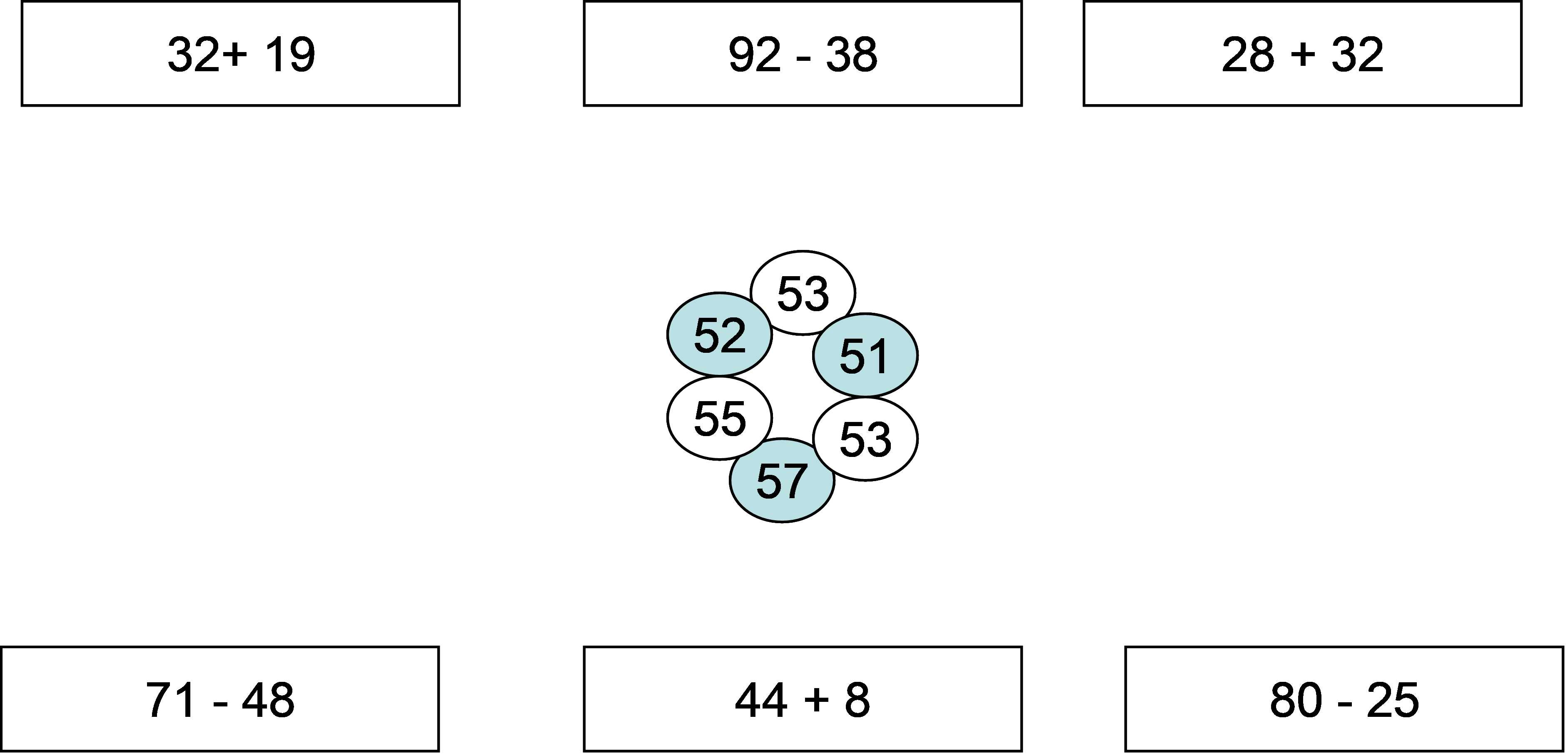
Bài 48: Nối phép tính với các số thích hợp
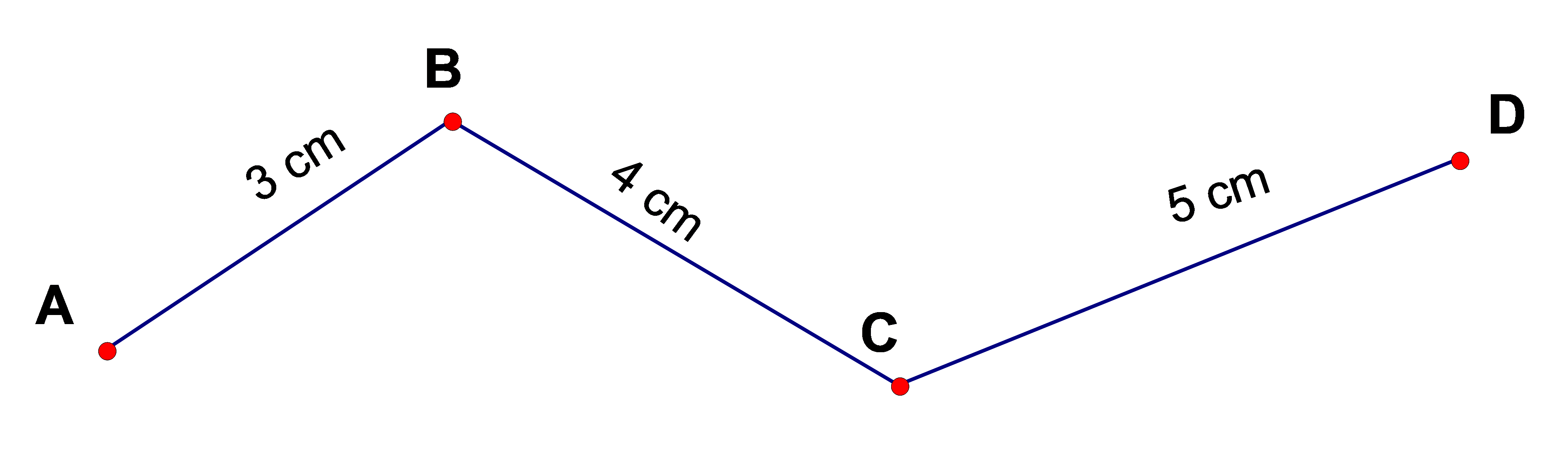
Bài 49: Tính độ dài đường gấp khúc ABCD.
Bài 50: Độ dài đường gấp khúc ABCD có tổng độ dài của hai đoạn thẳng AB và BC bằng 36 cm, đoạn thẳng CD dài 25 cm. Tính độ dài đường gấp khúc ABCD?
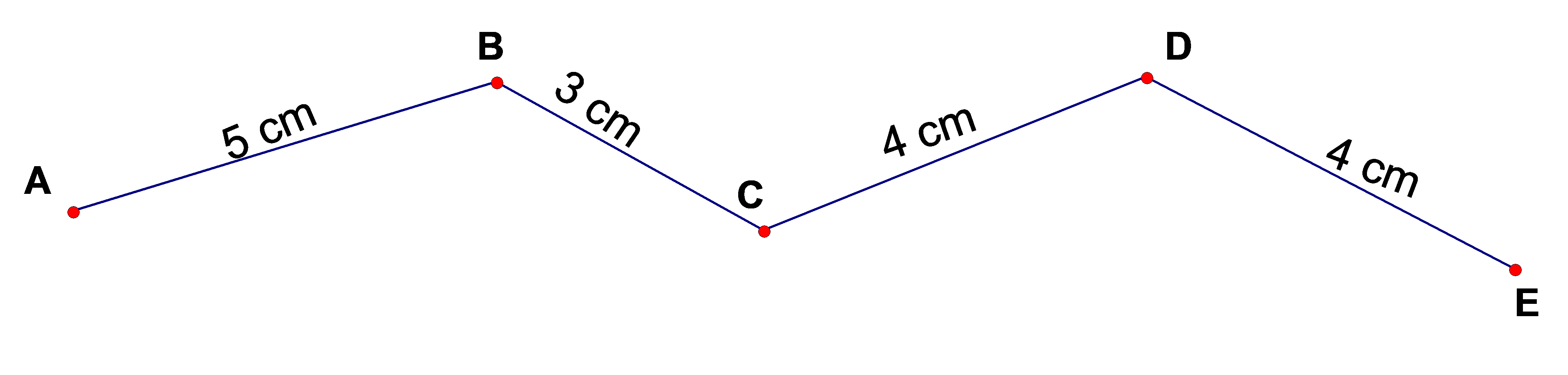
Bài 51: Con kiến vàng bò từ A đến C, con kiến đen bò từ C đến E. Hỏi con kiến nào bò được đoạn đường dài hơn?
Bài 52: Hai đường gấp khúc ABC và MNP có độ dài bằng nhau, đoạn thẳng AB dài hơn đoạn thẳng MN. Hãy so sánh độ dài đoạn thẳng BC và đoạn thẳng NP.
Bài 53: Tam giác ABC có cạnh AB dài 14 cm, cạnh BC dài 18 cm, cạnh CA dài 22 cm. Tính chu vi tam giác ABC.
Bài 54: Tính chu vi tứ giác MNPQ có độ dài các cạnh lần lượt là 15 cm, 2 dm3cm, 20 cm, 3 dm?
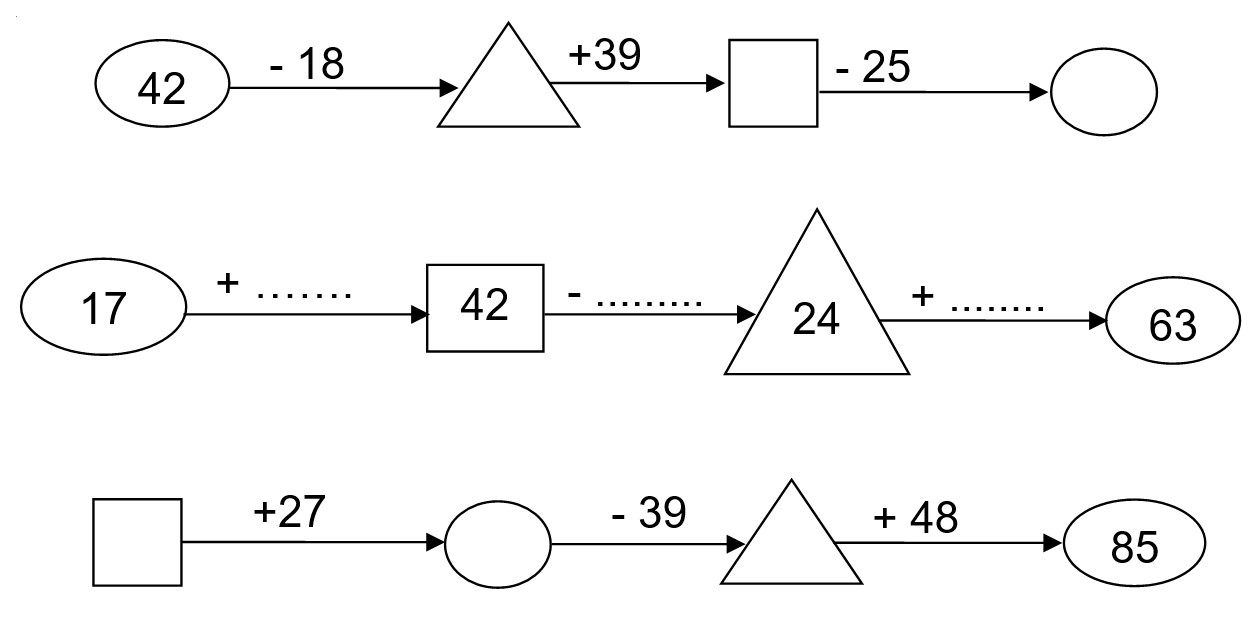
Bài 55: Điền sốthích hợp
Bài 56: Tính
- 15 + 67 -11 = 98 -69 + 7 =
- 82 -46 + 12 = 59 + 17 -28 =
Bài 57: Đặt tính và tính
15 + 7 57 + 29 87 -29 56 – 47 46 + 54 100 -34
Bài 58: Tìm x biết:
x + 12 = 71 17 + x = 32 34 -x = 15 x -34 = 15
Bài 59: Một cửa hàng ngày thứ nhất bán được 25 thùng sữa, ngày thứ nhất bán ít hơn ngày thứ hai 8 thùng sữa.
- Hỏi ngày thứ hai của hàng đó bán được bao nhiêu thùng sữa?
- Hỏi cả hai ngày cửa hàng bán được bao nhiêu thùng sữa?
Bài 60: Trong hình vẽ bên dưới.
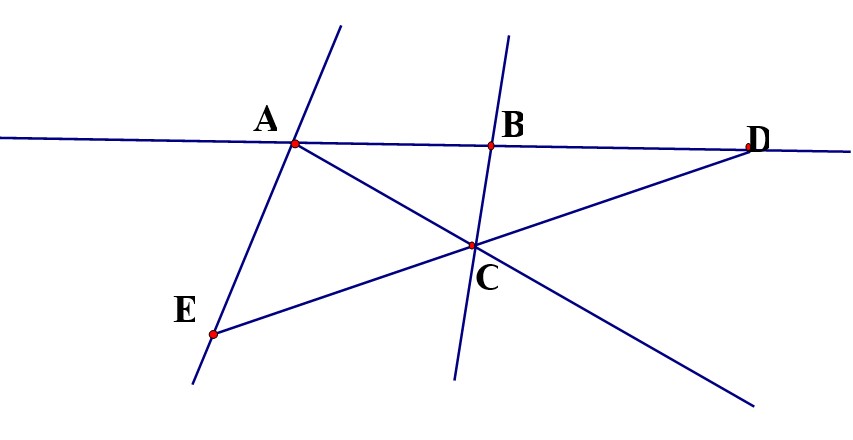
- Có:…………………..đoạn thẳng. Đó là các đoạn thẳng……………………………………………………………………………………………………………………………………….
- Có……………………đường thẳng. Đó là các đường thẳng:……………………………………………………………………………………………………………………………………..
- Có ba điểm thẳng hàng là:………………………………………………………………………………….
Bài 61: Từ 4 chữ số: 0 ; 1; 2; 3 em hãy viết tất cả các số có hai chữ số khác nhau.
Bài 62:Cho số a có hai chữ số
- Nếu chữ số hàng chục bớt đi 2 thì số a giảm đi bao nhiêu đơn vị?
- Nếu chữ số hàng chục tăng thêm 1 và chữ số hàng đơn vị giảm đi 2 thì số a tăng thêm bao nhiêu đơn vị?
Bài 63:
- Tìm những số lớn hơn 35 mà chữ số hàng chục của nó bé hơn 4
- Tìm những số có hai chữ số bé hơn 24 mà chữ số hàng đơn vị của nó lớn hơn 4
Bài 64: Viết tất cả những số có hai chữ số mà tổng hai chữ số của nó bằng 12
Bài 65: Viết tất cả những số có hai chữ số mà hiệu hai chữ số của nó 5
Bài 66: Viết các số có hai chữ số biết tổng hai chữ số của nó bằng số lớn nhất có 1 chữ số và hiệu hai chữ số của nó bằng 3.
Bài 67: Hai số có hiệu bằng 14, nếu thêm vào số trừ 3 đơn vị và giữ nguyên số bị trừ thì hiệu mới bằng bao nhiêu?
Bài 68: Tổng của hai số sẽ thay đổi như thế nào nếu mỗi số hạng cùng tăng thêm 25 đơn vị?
Bài 69: Tìm 1 số biết số lớn nhất có hai chữ số trừ đi số đó thì được kết quả là 35?
Bài 70: Số 45 thay đổi như thế nào nếu:
- Xoá bỏ chữ số 5
- Thay đổi vị trí chữ số 4 và chữ số 5
- Tăng chữ số hàng chục thêm 2
Bài 71: Để đánh các trang của cuốn sách dày 15 trang cần dùng bao nhiêu chữ số để đánh
Bài 72: Nga dùng 20 chữ số để viết các số liền nhau thành 1 dãy số 0;1;2;3;…;a. Hỏi a là số nào?
Bài 73: Viết thêm 4 số vào dãy sau:
- 3 ; 6 ; 9 ; …………………………….
- 39 ; 35 ; 31 ; …………………………
Bài 74: Tìm x
- a) 14 -x = 14 -2 c) 46 < x -45 < 49
- b) 52 + 4 > x + 52 d) x -8 < 3
Bài 75: Tính nhanh
- a) 11 + 28 + 24 + 16 + 12 + 9
- b) 75 -13 -17 + 25
Bài 76: Ngày đầu cửa hàng bán được 15 kg đường. Ngày sau bán hơn ngày đầu 5 kg đường. Cửa hàng còn lại 40 kg đường. Hỏi
- Ngày sau bán được bao nhiêu kg đường
- Trước khi bán cửa hàng có tất cả bao nhiêu kg đường
Bài 77: Mai cao hơn Hoa 2 cm. Bình thấp hơn Mai 3 cm. Hỏi ai cao nhất? Ai thấp nhất. Hoa cao hơn Bình mấy cm?
Bài 78: Mẹ để hai đĩa cam bằng nhau trên bàn. Lan lấy 3 quả từ đĩa bên phải bỏ sang đĩa bên trái. Hỏi bây giờ đĩa bên nào nhiều cam hơn và nhiều hơn mấy quả cam?
Bài 79: Lan có 20 cái kẹo, Hà có 14 cái kẹo. Hỏi Lan phải cho Hà mấy cái kẹo để só kẹo hai bạn bằng nhau.
Bài 80: Lan hơn Huệ 4 quyển vở. Huệ lại tặng Lan 3 quyển vở. Hỏi bây giờ ai nhiều vở jơn và nhiều hơn mấy quyển.
Bài 81: Thu hơn Lan 7 nhãn vở. Lan lại cho Thu 5 nhãn vở. Hỏi bây giờ ai có nhiều nhãn vở hơn và nhiều hơn mấy nhãn vở.
Bài 82: Trong chuồng có cả gà và thỏ. Bạn Hoa đếm được tất cả có 8 cái chân. Em hãy đoán xem trong chuồng có mấy con gà? mấy con thỏ?
Bài 83: Từ can 10 lít dầu em muốn rót sang can 3 lít và can 2 lít. Hỏi có thể rót đầy được mấy can 2 lít? mấy can 3 lít?
Bài 84: Có 9 lít nước mắm đựng vào các can loại 2 lít và 3 lít. Hỏi có bao nhiêu can 2 lít? bao nhiêu can 3 lít?
Bài 85: Có 17 lít nước đựng trong các can 5 lít và 2 lít. Hỏi có mấy can 5 lít? mấy can 2 lít?
Bài 86: Dũng có 1 số bi xanh và đỏ. Biết rằng số bi của Dũng bé hơn 10. Số bi đỏ hơn số bi xanh là 7 viên. Hỏi Dũng có mấy bi xanh? mấy bi đỏ?
Bài 87: Tổng số bút chì màu và đen của Lan bé hơn 9. Số bút màu hơn số bút đen là 6 cái. Hỏi Lan có mấy bút đen? mấy bút màu?
Bài 88: Vừa gà vừa chó đếm được 10 cái chân. Biết số gà nhiều hơn số chó. Hỏi có bao nhiêu gà? Bao nhiêu con chó?
Bài 89: Có 13 lít dầu đựng vào các can 3 lít và 2 lít. Biết số can 3 lít nhiều hơn số can 2 lít. Hỏi có mấy can 2 lít? Mấy can 3 lít?
Bài 90 : Vừa gà vừa thỏ đếm được 14 cái chân. Biết số thỏ nhiều hơn số gà. Hỏi có mấy con thỏ? Mấy con gà?
Bài 91: Hoà câu được tổng số cá ít hơn 11, gồm cá rô và cá giếc. Số cá rô hơn cá giếc là 8 con. Hỏi có mấy con cá rô? Mấy con cá giếc?
Bài 92: Lan câu được tổng số cá ít hơn 12, gồm cá trôi và cá rô. Số cá trôi hơn cá rô là 9 con. Hỏi có bao nhiêu con cá trôi? bao nhiêu con cá rô?
Bài 93: Con ngỗng và con gà cộng lại bằng con ngan và con vịt cộng lại. Con ngỗng nặng bằng hai con vịt. Hỏi giữa con gà và con ngan con nào nặng hơn? Có thể nói chắc chắn con ngan nặng bằng hai con gà không?
Bài 94: Cô giáo chấm bài toán của bốn bạn Hoà, Bình, Hải, Tú thì có hai điểm 10, có một điểm 9 và một điểm 7. Hoà được điểm cao hơn Bình nhưng lại thấp hơn Hải. Hỏi mỗi bạn được mấy điểm?
Bài 95: Ba bạn đi câu cá. Trong giỏ câu được 3 con cá rô và chừng ấy con cá giếc. Số cá trê ít hơn cá giếc nhưng lại nhiều hơn cá quả. Hỏi ba bạn câu được mấy con cá?
Bài 96: Có 9 lít dầu em muốn rót vào can 5 lít và can 2 lít. Hỏi em có thể rót đầy được mấy can 5 lít và mấy can 2 lít?
Bài 97: Cả gà và chó đếm được 12 cái chân. Biết số gà nhiều hơn số chó. Hỏi có mấy con gà? Mấy con chó?
Bài 98: Lan có 1 số tờ giấy mầu xanh và đổ. Biết rằng tổng số giấy mầu của lan bé hơn 13. Số giấy mầu đỏ hơn giấy mầu xanh là 10 tờ. Hởi Lan có mấy tờ giấy mầu xanh? Mấy tờ giấy mầu đỏ?
Bài 99: Hà, Lan, Thu có 7 cái bút. Lan có nhiều hơn Hà nhưng ít hơn Thu. Hỏi mỗi bạn có mấy cái bút?
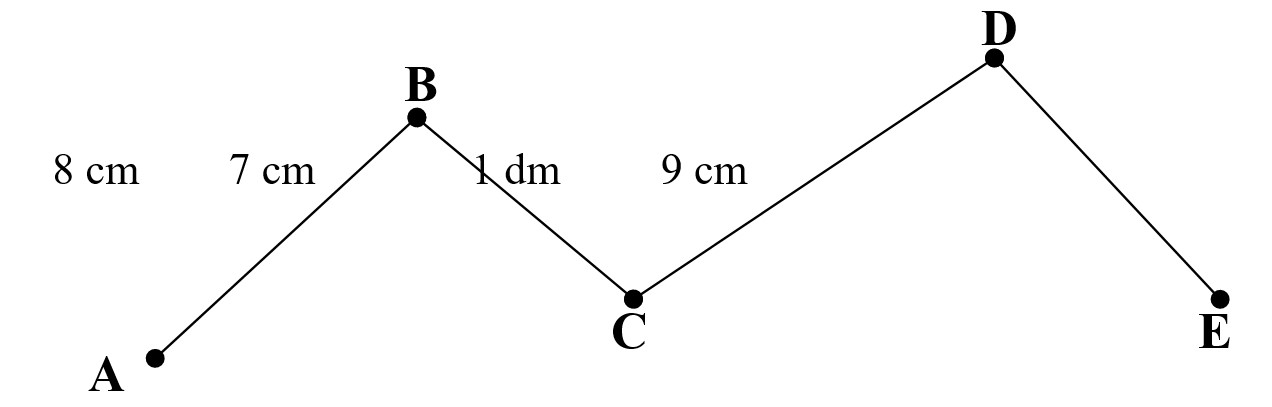
Bài 100: Tính độ dài đường gấp khúc ABCDE:



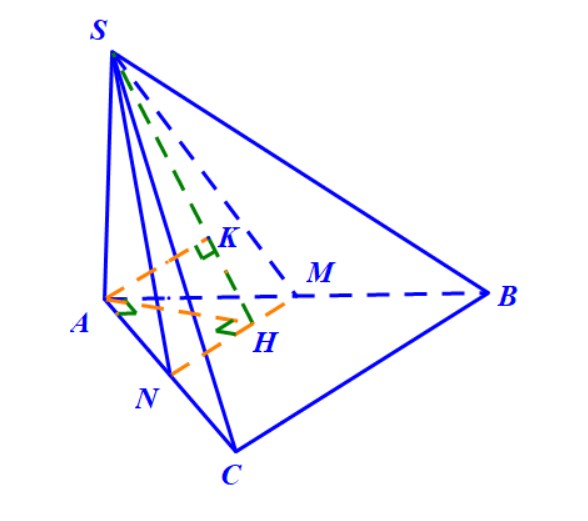
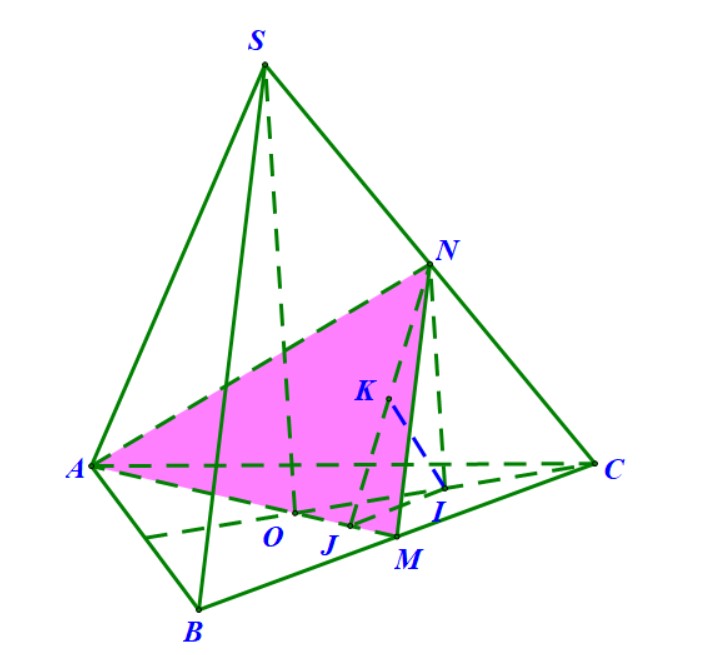
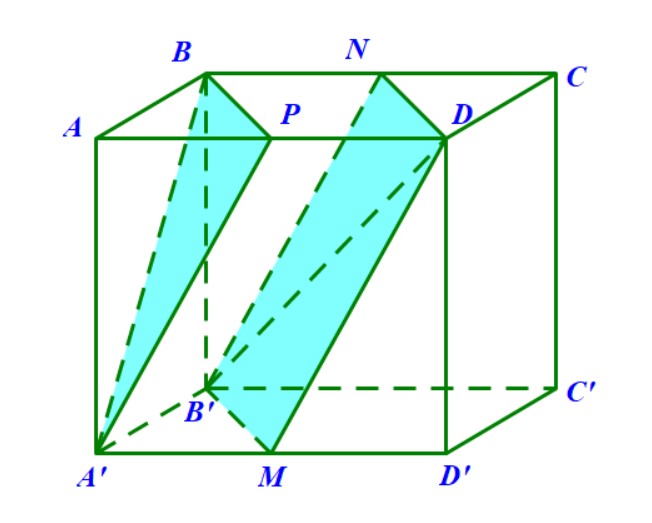
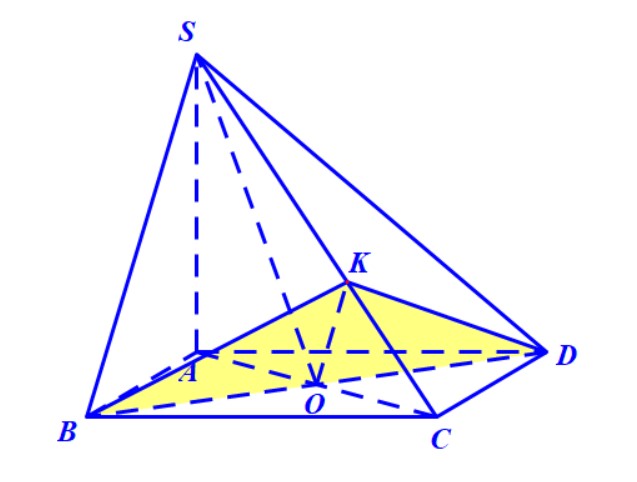
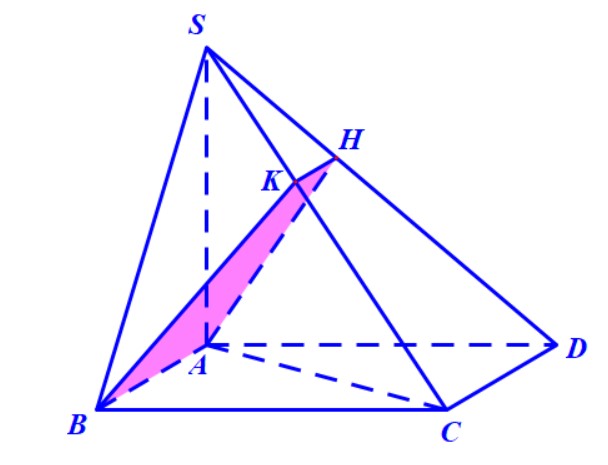
 Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).
Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).


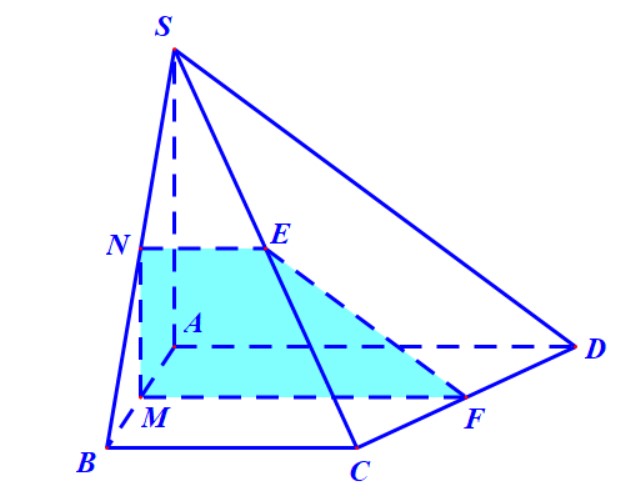


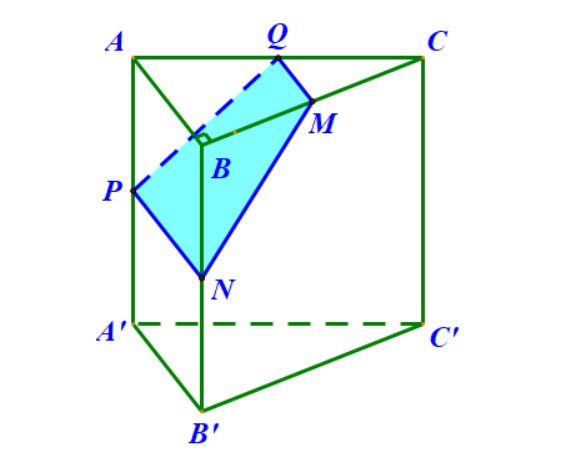




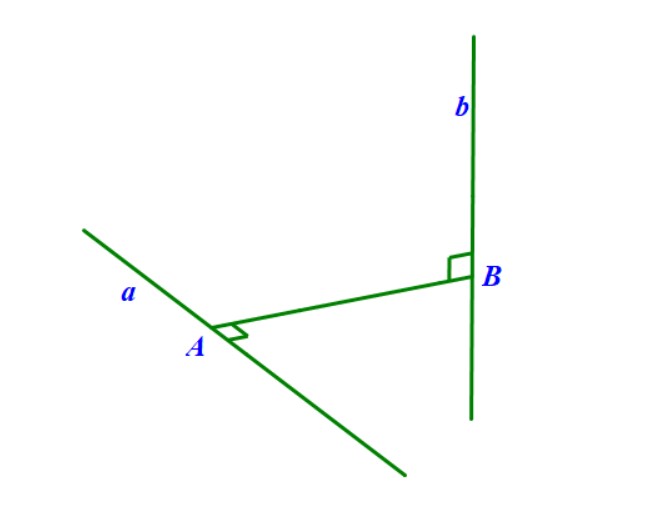
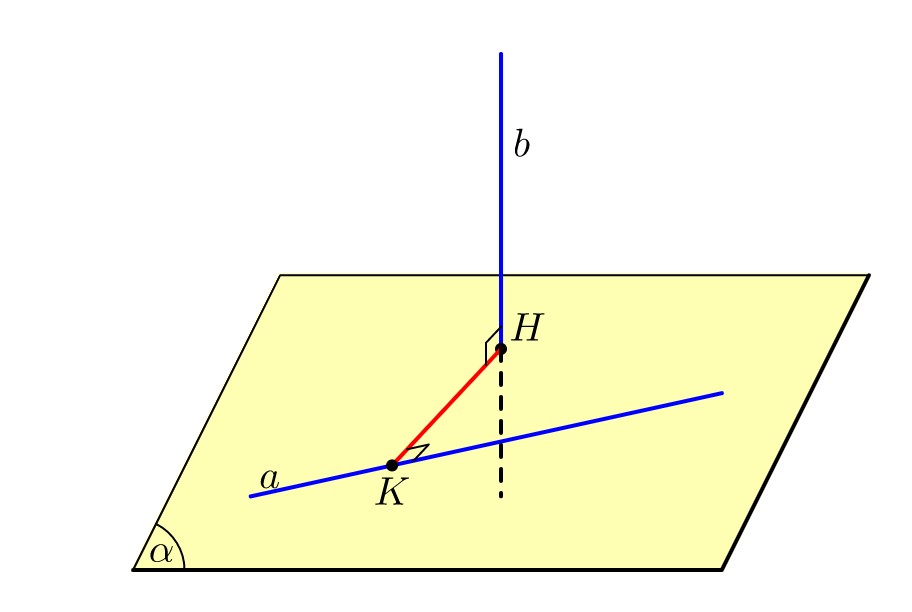
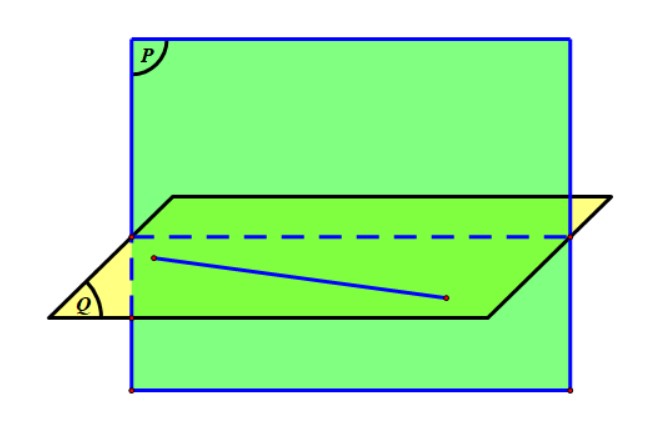
 Trong thực tế, việc tạo ra mặt phẳng \((P)\) song song với đường thẳng $a$ thường được thực hiện bằng cách, dựng hoặc tìm một đường thẳng $a’$ nào đó song song với $a$ và cắt đường thẳng $b$. Lúc này, mặt phẳng \((P)\) chính là mặt phẳng xác định bởi hai đường thẳng cắt nhau \(a’\) và \(b\). Và, việc tính khoảng cách tiếp tục quy về
Trong thực tế, việc tạo ra mặt phẳng \((P)\) song song với đường thẳng $a$ thường được thực hiện bằng cách, dựng hoặc tìm một đường thẳng $a’$ nào đó song song với $a$ và cắt đường thẳng $b$. Lúc này, mặt phẳng \((P)\) chính là mặt phẳng xác định bởi hai đường thẳng cắt nhau \(a’\) và \(b\). Và, việc tính khoảng cách tiếp tục quy về