Category: Hình học

Trực tâm là gì?

Trực tâm là gì?

Trực tâm là giao điểm của 3 đường cao trong một tam giác. Đường cao trong tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.

Trực tâm là gì?

Chúng ta xuất phát từ định lí sau:

Trong một tam giác có 3 đường cao. Ba đường này cùng đi qua một điểm, điểm này gọi là trực tâm của tam giác.

Đường cao của tam giác là gì? Đường cao của một tam giác chính là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện. Cạnh đối diện này thường được gọi là đáy tương ứng với mỗi đường cao.

Giả sử cho tam giác ABC có ba đường cao lần lượt là AM, BN, CP. Gọi H là là giao điểm của ba đường cao này thì H là trực tâm của tam giác ABC.

Cách xác định trực tâm của một tam giác

Như vậy, trực tâm của tam giác là điểm giao nhau của ba đường cao trong tam giác.

Tuy nhiên để xác định trực tâm trong tam giác chúng ta chỉ cần vẽ hai đường cao của tam giác ta đã có thể xác định được trực tâm của tam giác. Chẳng hạn, trong tam giác ABC ta chỉ cần vẽ hai đường cao AF và BE. Hai đường cao này cắt nhau tại H thì H chính là trực tâm của tam giác ABC. Khi đó, chúng ta có vẽ đường cao từ đỉnh C của tam giác thì đường cao đó cũng sẽ đi qua điểm H.

Đối với các loại tam giác thông thường như tam giác nhọn tam giác tù hay tam giác cân tam giác đều thì ta đều có cách xác định trực tâm giống nhau. Từ hai đỉnh của tam giác ta kẻ hai đường cao của tam giác đến hai cạnh đối diện. Hai cạnh đó giao nhau tại điểm nào thì điểm đó chính là trực tâm của tam giác. Và đường cao còn lại chắc chắn cũng đi qua trực tâm của tam giác dù ta không cần vẽ nó.

Tuy nhiên đối với tam giác vuông thì việc xác định đường cao có khác một chút. Tam giác vuông có hai cạnh góc vuông chính là hai đường cao của tam giác vì hai cạnh vuông góc với nhau. Chính vì vậy trực tâm của tam giác vuông trùng với đỉnh của góc vuông.

Đối với tam giác nhọn thì trực tâm của nó nằm bên trong tam giác, tam giác vuông thì trực tâm trùng với đỉnh góc vuông, tam giác tù thì trực tâm nằm bên ngoài tam giác (xem hình vẽ).

Trực tâm của tam giác đều

Trong một tam giác đều thì trực tâm, trọng tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của nó đều trùng nhau.

Trong hình sau thì O vừa là trọng tâm, vừa là trực tâm, vừa là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của tam giác đều ABC.

21/01/2022
Các quy tắc biểu diễn hình trong không gian
Các quy tắc biểu diễn hình trong không gian

Để vẽ hình biểu diễn của các hình không gian, chúng ta sử dụng các quy tắc biểu diễn hình trong không gian sau:
- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng;
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau;
- Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa điểm và đường thẳng;
- Đường nhìn thấy vẽ nét liền, đường bị che khuất vẽ nét đứt;
- Trên cùng một đường thẳng hoặc trên hai đường thẳng song song thì tỉ lệ về độ dài được giữ nguyên, do đó, ta cần vẽ chính xác trung điểm của các đoạn thẳng.
Một số hình biểu diễn thường gặp
- Các hình tam giác thường, tam giác đều, tam giác vuông đều vẽ thành một tam giác tù như dưới đây:
- Các hình bình hành, hình vuông, hình chữ nhật, hình thoi đều vẽ thành một hình bình hành:
- Hình thang có thể vẽ như hình dưới đây:
- Hình thang vuông có thể vẽ như hình dưới đây:
Hình chóp có đáy là tam giác

Hình chóp có đáy là tứ giác

Hình tứ diện

Hình chóp có đáy là hình vuông, hình bình hành, hình chữ nhật, hình thoi

Hình lăng trụ tam giác, tứ giác

Hình hộp
16/01/2022
Chứng minh ba đường thẳng đồng quy trong không gian
Chứng minh ba đường thẳng đồng quy trong không gian

Nhờ việc sử dụng định lí về giao tuyến của ba mặt phẳng phân biệt trong không gian hoặc đồng quy, hoặc đôi một so sánh nên trong không gian để chứng minh ba đường thẳng a, b, c đồng quy ta có thể làm như sau:
- Tìm giao điểm I của hai trong ba đường thẳng đã cho, chẳng hạn a và b;
- Giả sử c là giao tuyến của hai mặt phẳng (α) và (β) nào đó lần lượt chứa đường thẳng a và đường thẳng b;
- Chứng minh rằng I là điểm chung của (α) và (β), tức là I phải thuộc vào giao tuyến c;
- Kết luận: a, b, c đồng quy tại O.
Xem thêm Cách chứng minh thẳng hàng trong hình học không gian

Ví dụ. Cho tứ diện ABCD. Gọi M; N lần lượt là trung điểm của AB và CD. Mặt phẳng (P) qua MN và cắt AD; BC lần lượt tại P và Q. Biết MP cắt NQ tại I. Chứng minh rằng MP, NQ và BD đồng quy tại I.

Lời giải

Ta có: (ABD) ∩ (BCD) = BD

Lại có I ∈ MP ⊂ (ABD) và I ∈ NQ ⊂ (BCD) nên I là điểm chung của hai mặt phẳng (ABD) và (BCD). Nói cách khác, I thuộc vào giao tuyến của hai mặt phẳng (ABD) và (BCD).

Do đó, I ∈ BD hay ba đường thẳng MP, NQ và BD đồng quy tại I.

Bài 1. Cho tứ diện ABCD mặt phẳng(P) không chứa AB và CD cắt các cạnh AC, BC, AD lần lượt tại M, N, R, S.
1. Chứng minh 3 đường thẳng AB, MN, RS đồng qui.
2. Chứng minh 3 đường thẳng CD, MS, NR đồng qui
Bài 2. Cho tứ diện ABCD. M, N lần lượt là trung điểm BC, BD. Các điểm P và S lần lượt thuộc AD, AC sao cho AR= AD:3 ; AS= AC:3. CMR ba đường thẳng AB, MS, NR đồng qui.

Bài 3. Cho hình thang ABCD (AB// CD) điểm S nằm ngoài mặt phẳng chứa ABCD. Gọi M, N lần lượt là trung điểm của SC, SD. Gọi I là giao điểm của AD và BC, J là giao điểm của AN và BM. Gọi O là giao điểm của AC và BD. CMR : SO, AM, BN đồng qui.
16/01/2022
Hình chóp, hình lăng trụ, hình hộp là gì?
Hình chóp, hình lăng trụ, hình hộp là gì?

Hình chóp, hình lăng trụ, hình hộp là những hình cơ bản trong hình học không gian. Đa số các bài toán ở cấp THPT đều làm việc trên các hình này. Để có thể giải quyết được các bài toán không gian, bước đầu chúng ta ta phải hiểu được thế nào là hình chóp, hình lăng trụ hay hình hộp.

Xem thêm 38+ tài liệu hình học không gian 11 hay nhất

1. Hình chóp

Hình chóp là gì?

Cho đa giác $A_1A_2A_3… A_n$ nằm trong mặt phẳng $(P)$ và một điểm $S$ nằm ngoài mặt phẳng $(P)$. Nối $S$ với các đỉnh của đa giác ta được $n$ miền tam giác $SA_1A_2, SA_2A_3,…, SA_nA_1$. Hình tạo bởi $n$ tam giác đó và đa giác $A_1A_2A_3… A_n$ gọi là hình chóp và kí hiệu là $S.A_1A_2A_3… A_n$.

Trong đó:
- $S$ được goi là đỉnh của hình chóp;
- $A_1A_2A_3… A_n$ là mặt đáy của hình chóp;
- $SA_1, SA_2,…, SA_n$ là các cạnh bên của hình chóp;
- A1A2, A2A3,…, AnA1 là các cạnh đáy của hình chiếu;
- Các miền tam giác $SA_1A_2, SA_2A_3,…, SA_nA_1$ là mặt bên của hình chóp.
Cách gọi tên hình chóp bằng tên của đỉnh và mặt đáy, ví dụ như hình vẽ sau là hình chóp $S.ABCDE$ hoặc cụ thể hơn là hình chóp ngũ giác $S.ABCDE$
- Đường cao của hình chóp là đường vuông góc kẻ từ đỉnh của hình chóp đến mặt đáy.
Xem thêm Các phương pháp tính thể tích khối chóp

Hình tứ diện

Cho bốn điểm A, B, C, D không đồng phẳng. Hình gồm bốn tam giác ABC, BCD, CDA, ABD gọi là tứ diện ABCD.
- A, B, C, D là các đỉnh của tứ diện;
- AB, BC, CD, CA là các cạnh bên của tứ diện;
- Các tam giác ABC, BCD, CDA, ABD là các mặt bên của tứ diện;
- Hai cạnh không đi qua một đỉnh được gọi là hai cạnh đối nhau;
- Đỉnh không nằm trên một mặt được gọi là đỉnh đối diện với mặt đó.
Hình chóp và hình tứ diện đều có 4 đỉnh, 4 mặt và 6 cạnh như nhau, nhưng hình chóp có phân biệt mặt bên và mặt đáy, trong khi hình tứ diện thì không quy ước gọi đâu là mặt đáy, đâu là mặt bên.

Hình chóp đều
- Định nghĩa: Hình chóp đều là hình chóp có các cạnh bên bằng nhau và mặt đáy là một đa giác đều.
- Tính chất: Trong hình chóp đều, chân đường cao của hình chóp trùng với tâm đường tròn ngoại tiếp đa giác đáy.
Hình chóp đều có đáy lần lượt là tam giác đều, hình vuông (tứ giác đều) và lục giác đều

Như vậy, từ định nghĩa suy ra:
- Hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và chân đường cao của nó trùng với tâm của đa giác đáy.
- Hình chóp là hình chóp đều khi và chỉ khi đáy của nó là đa giác đều và các cạnh bên tạo với mặt đáy các góc bằng nhau.
2. Hình chóp cụt

Hình chóp cụt

Hình chóp cụt đều

Cho hình chóp cụt đều $S.A_1A_2…A_n$. Một mặt phẳng $(P)$ song song với mặt đáy cắt các cạnh bên $SA_1, SA_2,…,SA_n$ lần lượt tại $A’_1, A’_2,…, A’_n$. Phần hình nằm giữa đáy và mặt phẳng $(P)$ gọi là hình chóp đều.
- Đa giác $A_1A_2A_3… A_n$ và thiết diện $A’_1A’_2A’_3… A’_n$ gọi là hai mặt đáy;
- Các hình thang cân $A_1A’_1A’_2A_2,…, A_nA’_nA’_1A_1$ là các mặt bên;
- Đoạn thẳng nối hai tâm O và O’ của hai đáy gọi là đường cao của hình chóp cụt đều.
3. Hình lăng trụ

Hình lăng trụ là gì?

Hình hợp bởi các hình bình hành $A_1A’_1A’_2A_2,A_2A_3A’_3A’_2…, A_nA’_nA’_1A_1$ và hai miền đa giác $A_1A_2A_3… A_n; A’_1A’_2A’_3… A’_n$ nằm trong hai mặt phẳng song song đươc goi là hình lăng trụ.
- Các hình bình hành $A_1A’_1A’_2A_2,A_2A_3A’_3A’_2…, A_nA’_nA’_1A_1$ là các mặt bên;
- Hai miền đa giác $A_1A_2A_3… A_n; A’_1A’_2A’_3… A’_n$ là hai mặt đáy (hai hình đa giác này bằng nhau);
- Các đoạn thẳng $A_1A’_1,…, A_nA’_n$ là các cạnh bên;
- Các đoạn thẳng $A_1A_2,A’_1A’_2,…, A_nA_1, A’_nA’_1$ là các cạnh đáy của hình lăng trụ.
Ký hiệu hình lăng trụ: $A_1A_2…A_n.A’_1A’_2…A’_n$.

Gọi tên lăng trụ theo tên các đa giác đáy: Lăng trụ tam giác (có đáy là tam giác), lăng trụ tứ giác (có đáy là tứ giác),…

Hình lăng trụ đứng
- Hình lăng trụ đứng là hình lăng trụ có các cạnh bên vuông góc với mặt đáy.
- Nhận xét: Các mặt bên của hình lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy.
Hình lăng trụ đều
- Hình lăng trụ đều là hình lăng trụ đứng có đáy là đa giác đều.
- Nhận xét: Các mặt bên của hình lăng trụ đều là các hình chữ nhật bằng nhau. Ngoài ra, hình lăng trụ đều có các tính chất của hình lăng trụ đứng.
4. Hình hộp

Hình hộp là gì?

Hình lăng trụ tứ giác có đáy là hình bình hành được gọi là hình hộp.

Nhận xét:
- Sáu mặt (bốn mặt bên và hai mặt đáy) đều là những hình bình hành.
- Mỗi mặt có một mặt song song với nó, hai mặt như thế gọi là hai mặt đối diện.
Hình hộp đứng
- Hình hộp đứng là hình lăng trụ đứng có đáy là hình bình hành.
- Nhận xét: Trong hình hộp đứng có bốn mặt bên là hình chữ nhật.
Hình hộp chữ nhật

Hình hộp chữ nhật là hình hộp đứng có đáy là hình chữ nhật.

Nhận xét: Tất cả sáu mặt của hình hộp chữ nhật đều là hình chữ nhật.

Hình lập phương

Hình lập phương là hình hộp có tất cả sáu mặt là hình vuông. (Các hình vuông này bằng nhau).
14/01/2022
Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng trong không gian

1. Góc giữa hai đường thẳng trong không gian là gì?

Trong không gian cho 2 đường thẳng a, b bất kỳ. Từ một điểm O nào đó ta vẽ 2 đường thẳng a’, b’ lần lượt song song với a và b. Ta nhận thấy rằng khi điểm O thay đổi thì góc giữa 2 đường thẳng a và b không thay đổi.

Định nghĩa: Góc giữa hai đường thẳng trong không gian là góc giữa 2 đường thẳng cùng đi qua một điểm và lần lượt song song với hai đường thẳng đã cho.

Xem thêm:
- Cách tính góc giữa đường thẳng và mặt phẳng lớp 11
- Cách tính góc giữa hai mặt phẳng trong không gian
2. Cách xác định góc giữa hai đường thẳng

Ngoài việc làm như trong định nghĩa, để xác định góc giữa 2 đường thẳng a và b ta có thể lấy điểm O thuộc một trong hai đường thẳng đó rồi vẽ một đường thẳng qua O và song song với đường thẳng còn lại.

Hoặc ta có thể sử dụng tích vô hướng:
- Nếu \(\overrightarrow{u}\) là vecto chỉ phương của đường thẳng a và \(\overrightarrow{v}\) là vecto chỉ phương của đường thẳng b và \(\left( \overrightarrow{u};\overrightarrow{v} \right)=\alpha \) thì góc giữa 2 đường thẳng a và b bằng \(\alpha \) nếu \(0\le \alpha \le 90^\circ \) và bằng \(180^\circ -\alpha \) nếu \(90^\circ <\alpha \le 180^\circ \).
- Nếu 2 đường thẳng a và b song song hoặc trùng nhau thì góc giữa chúng bằng \(0^\circ \). Góc giữa 2 đường thẳng là góc có số đo \(0\le \alpha \le 90^\circ \).
3. Cách tính góc giữa hai đường thẳng

Để tính được góc giữa hai đường thẳng trong không gian, nếu xác định (dựng) được góc giữa hai đường thẳng trong không gian và gắn chúng vào một tam giác cụ thể thì có thể sử dụng các hệ thức lượng trong tam giác để tìm số đo của góc đó:
- Định lý hàm số cosin trong tam giác ABC: \(\cos \widehat{BAC}=\frac{A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}}}{2.AB.AC}\)
- Tương tự ta có: \(\cos \widehat{ABC}=\frac{B{{A}^{2}}+B{{C}^{2}}-A{{C}^{2}}}{2.BA.BC}\) và \(\cos \widehat{ACB}=\frac{C{{A}^{2}}+C{{B}^{2}}-A{{B}^{2}}}{2.CA.CB}\)
  Chú ý: \(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC\cos \widehat{BAC}=\frac{1}{2}\left( A{{B}^{2}}+A{{C}^{2}}-B{{C}^{2}} \right)\)
Ngoài ra, để tính góc giữa hai véc-tơ \(\vec{u}, \vec{v} \) chúng ta sử dụng định nghĩa tích vô hướng: \[\vec{u} . \vec{v} = |\vec{u}|.|\vec{v}|.\cos\left( \overrightarrow{u};\overrightarrow{v} \right)\].

Tính góc giữa hai đường thẳng AB và CD ta tính góc giữa hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\) dựa vào công thức \(\cos \left( \overrightarrow{AB};\overrightarrow{CD} \right)=\frac{\overrightarrow{AB}.\overrightarrow{CD}}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{CD} \right|}\Rightarrow \cos \left( AB;CD \right)=\frac{\left| \overrightarrow{AB}.\overrightarrow{CD} \right|}{\left| \overrightarrow{AB} \right|.\left| \overrightarrow{CD} \right|}\) từ đó suy ra góc giữa hai đường thẳng AB và CD.

4. Bài tập góc giữa hai đường thẳng trong không gian

Ví dụ 1. Cho hình lập phương $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có cạnh là $a$. Tính góc giữa các cặp đường thẳng sau đây:
1. AB và A’D’.
2. AD và A’C’.
3. BC’ và B’D’.
Lời giải.
1. Ta có $A^{\prime} D^{\prime} / / A D$ nên $\left(A B, A^{\prime} D^{\prime}\right)=(A B, A D)=\widehat{B A D}=90^{\circ}$.
2. Ta có $A^{\prime} C^{\prime} / / A C$ nên $\left(A D, A^{\prime} C^{\prime}\right)=(A D, A C)=\widehat{D A C}=45^{\circ}$.
3. Ta có $B^{\prime} D^{\prime} / / B D$ nên $\left(B C^{\prime}, B^{\prime} D^{\prime}\right)=\left(B C^{\prime}, B D\right)=\widehat{D B C^{\prime}}$.
  Ta có $B D=B C^{\prime}=C^{\prime} D=A B \sqrt{2}$ nên $\triangle B D C^{\prime}$ dều, suy ra $\widehat{D B C^{\prime}}=60^{\circ}$.
  Vậy $\left(B C^{\prime}, B^{\prime} D^{\prime}\right)=60^{\circ}$.
Ví dụ 2. Cho hình chóp $S . A B C$ có $S A=S B=S C=A B=A C=a \sqrt{2}$ và $B C=2 a$. Tính góc giữa hai đường thẳng $A C$ và $S B$.

Lời giải.

Ta có $S A B$ và $S A C$ là tam giác đều, $A B C$ và $S B C$ là tam giác vuông cân cạnh huyền $B C$.
Gọi $M, N, P$ lần lượt là trung điểm của $S A, A B, B C$, ta có $M N / / S B, N P / / A C$ nên $(A C, S B)=(N P, M N)$.

\begin{aligned}
&M N=\frac{S B}{2}=\frac{a \sqrt{2}}{2}, N P=\frac{A C}{2}=\frac{a \sqrt{2}}{2} . \\
&A P=S P=\frac{B C}{2}=a, S A=a \sqrt{2}
\end{aligned}

Ví dụ 3. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, \(SA\bot \left( ABC \right)\) và \(SA=a\sqrt{3}\). Gọi M, N lần lượt là trung điểm của AB và SC. Tính cosin góc giữa hai đường thẳng AN và CM.

Cách 1: Dựng hình bình hành AMCE suy ra \(AM=CE=\frac{a}{2}\).

Khi đó \(AE//CM\Rightarrow \left( \widehat{AE;CM} \right)=\left( \widehat{AN;AE} \right)=\varphi .\)

Mặt khác \(SC=\sqrt{S{{A}^{2}}+A{{C}^{2}}}=2a\Rightarrow \) độ dài đường trung tuyến AN là \(AN=\frac{SC}{2}=a.AE=CM=\frac{a\sqrt{3}}{2}.\)

Do \(\Delta ABC\) đều nên \(CM\bot AM\Rightarrow \) AMCE là hình chữ nhật.

Khi đó \(CE\bot AE\) mà \(CE\bot SA\Rightarrow CE\bot \left( SAE \right)\Rightarrow CE\bot SE.\)

\(\Delta SEC\) vuông tại E có đường trung tuyến \(EN=\frac{1}{2}SC=a.\)

Ta có: \(\cos \widehat{NAE}=\frac{A{{N}^{2}}+A{{E}^{2}}-N{{E}^{2}}}{2.AN.AE}=\frac{\sqrt{3}}{4}>0\Rightarrow \cos \varphi =\frac{\sqrt{3}}{4}.\)

Cách 2: Ta có: \(\overrightarrow{AN}=\frac{1}{2}\left( \overrightarrow{AS}+\overrightarrow{AC} \right);\overrightarrow{CM}=\overrightarrow{AM}-\overrightarrow{AC}=\frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC}.\)

Khi đó \(\overrightarrow{AN}.\overrightarrow{CM}=\frac{1}{2}\left( \overrightarrow{AS}+\overrightarrow{AC} \right)\left( \frac{1}{2}\overrightarrow{AB}-\overrightarrow{AC} \right)=\frac{1}{4}\overrightarrow{AB}.\overrightarrow{AC}-\frac{1}{2}A{{C}^{2}}=\frac{1}{4}{{a}^{2}}\cos 60{}^\circ -\frac{{{a}^{2}}}{2}=\frac{-3{{a}^{2}}}{8}.\)

Lại có: \(AN=\frac{SC}{2}=a;CM=\frac{a\sqrt{3}}{2}\Rightarrow \cos \varphi =\frac{\left| \frac{-3{{a}^{2}}}{8} \right|}{a.\frac{a\sqrt{3}}{2}}=\frac{\sqrt{3}}{4}.\)

Bình luận: Dựa vào hai cách làm trên ta thấy rằng, trong một số trường hợp, việc sử dụng công cụ vectơ để tính góc giữa hai đường thẳng giúp bài toán trở nên dễ ràng hơn rất nhiều!.

Ví dụ 4. Cho hình chóp S.ABC có \(SA=SB=SC=AB=a;AC=a\sqrt{2}\) và \(BC=a\sqrt{3}\). Tính cosin góc giữa hai đường thẳng SC và AB.

Cách 1: Gọi M, N, P lần lượt là trung điểm của SA, SB và AC. Khi đó \(\left\{ \begin{align}

& MP//SC \\

& N//AB \\

\end{align} \right.\Rightarrow \left( \widehat{SC;AB} \right)=\left( \widehat{MP;MN} \right).\)

Ta có: \(MN=\frac{AB}{2}=\frac{a}{2};MP=\frac{SC}{2}=\frac{a}{2}.\)

Mặt khác \(\Delta SAC\) vuông tại S \(\Rightarrow SP=\frac{AC}{2}=\frac{a\sqrt{2}}{2}.\)

\(B{{P}^{2}}=\frac{B{{A}^{2}}+B{{C}^{2}}}{2}-\frac{A{{C}^{2}}}{4}=\frac{3}{2}{{a}^{2}}\Rightarrow BP=\frac{a\sqrt{6}}{2}.\)

Suy ra \(P{{N}^{2}}=\frac{P{{S}^{2}}+P{{B}^{2}}}{2}-\frac{S{{B}^{2}}}{4}=\frac{3{{a}^{2}}}{4}\Rightarrow NP=\frac{a\sqrt{3}}{2}.\)

Khi đó \(\cos \widehat{NMP}=\frac{M{{N}^{2}}+M{{P}^{2}}-N{{P}^{2}}}{2.MN.MP}=-\frac{1}{2}\Rightarrow \widehat{NMP}=120{}^\circ \Rightarrow \varphi =\left( \widehat{SC;AB} \right)=60{}^\circ .\)

Cách 2: Ta có: \(\overrightarrow{AB}=\overrightarrow{SB}-\overrightarrow{SA}\Rightarrow \overrightarrow{AB}.\overrightarrow{SC}=\left( \overrightarrow{SB}-\overrightarrow{SA} \right).\overrightarrow{SC}=\overrightarrow{SB}.\overrightarrow{SC}-\overrightarrow{SA}.\overrightarrow{SC}\)

\(=\frac{1}{2}\left( S{{B}^{2}}+S{{C}^{2}}-A{{C}^{2}} \right)-\frac{1}{2}\left( S{{A}^{2}}+S{{C}^{2}}-A{{B}^{2}} \right)=-\frac{{{a}^{2}}}{2}.\)

Suy ra \(\cos \left( SC;AB \right)=\frac{\left| \frac{-{{a}^{2}}}{2} \right|}{a.a}=\frac{1}{2}\Rightarrow \left( SC;AB \right)=60{}^\circ .\)
05/01/2022
Bài tập giá trị lượng giác của góc từ 0 đến 180°
Bài tập giá trị lượng giác của góc từ 0 đến 180°

Để làm được các bài tập giá trị lượng giác của góc từ 0 đến 180°, các em học sinh cần khi nắm vững định nghĩa và các công thức trong bài Giá trị lượng giác của góc từ 0 đến 180 độ.

Bài 1. Cho $\sin x =\frac{5}{13}\left(90^{\circ}<x<180^{\circ}\right)$. Tính các giá trị lượng giác còn lại.

Hướng dẫn. Từ đẳng thức $\sin^2x+\cos^2x=1$ ta suy ra $$\cos ^{2} x =1-\sin ^{2} x =1-\frac{25}{169}=\frac{144}{169}$$ Mặt khác, $90^{\circ}<x<180^{\circ}$ nên $\cos x <0$. Do đó, $$\cos x=-\frac{12}{13}$$
Từ đó tính được $\tan x=\frac{5}{13} \cdot-\frac{13}{12}=-\frac{5}{12}, \cot x=-\frac{12}{5}$.

Bài 2. Biết $\cot 15^\circ=2+\sqrt{3}$. Tính các giá trị lượng giác còn lại của góc $15^{\circ}$.

Hướng dẫn. Dễ dàng có ngay $$\tan 15^{\circ}=\frac{1}{2+\sqrt{3}}=2-\sqrt{3} $$ Để tính $\cos 15^\circ$, chúng ta sử dụng hằng đẳng thức $$1+\tan^2 x = \frac{1}{\cos^2x}$$

Ta có $$\frac{1}{\cos ^{2} 15^{\circ}}=1+\tan ^{2} 15^{\circ}=4(2-\sqrt{3}) $$ Suy ra $$\cos ^{2} 15^\circ=\frac{1}{4(2-\sqrt{3})}=\frac{2+\sqrt{3}}{4} $$ Lưu ý rằng $15^\circ$ là góc nhọn nên $$\cos 15^\circ=\frac{\sqrt{2+\sqrt{3}}}{2} $$ Cuối cùng, ta tính $$\sin 15^\circ=\tan 15^\circ \cdot \cos 15^\circ=\frac{\sqrt{2-\sqrt{3}}}{2}$$

Bài 3. Cho $\tan \alpha=3$. Tính:
1. $\frac{2 \sin \alpha+3 \cos \alpha}{4 \sin \alpha-11 \cos \alpha}$
2. $\frac{3 \sin \alpha-2 \cos \alpha}{\sin ^{3} \alpha-17 \cos ^{3} \alpha}$
Hướng dẫn.
1. Chia hai vế cho $\cos\alpha $ ta được $$\frac{2 \sin \alpha+3 \cos \alpha}{4 \sin \alpha-11 \cos \alpha}=\frac{2 \tan \alpha+3}{4 \tan \alpha-11}=11$$
2. Chia hai vế cho $\cos^3\alpha $ ta được \begin{align} \frac{3 \sin \alpha-2 \cos \alpha}{\sin ^{3} \alpha-17 \cos ^{3} \alpha}&=\frac{3 \tan \alpha-2}{\tan ^{3} \alpha-17} \cdot \frac{1}{\cos ^{2} \alpha}\\
  &=\frac{3 \tan \alpha-2}{\tan ^{3} \alpha-17}\left(1+\tan ^{2} \alpha\right)=7\end{align}
Bài 4. Cho tana $+$ cota $={m}$, hãy tính theo ${m}$:
1. $\tan ^{2} {a}+\cot ^{2} {a}$
2. $\tan ^{3} {a}+\cot ^{3} {a}$
3. $\mid \tan a- \cot a \mid$
Hướng dẫn.
1. $ \tan ^{2} {a}+\cot ^{2} {a}=(\tan {a}+\cot a)^{2}-2 \tan a \cdot \cot a={m}^{2}-2$
2. $\tan ^{3} {a}+\cot ^{3} {a}=(\tan {a}+\cot {a})^{3}-3 \tan a \cdot \cot {a}(\tan {a}+\cot {a})={m}^{3}-3 {m}$
3. $|\tan a-\cot a|=\sqrt{(\tan a+\cot a)^{2}-2 \tan a \cot a}=\sqrt{m^{2}-2}$
Bài 5. Cho $\sin a +\cos a=m$, hãy tính theo $m$ các biểu thức sau:
1. $\sin a \cos a$
2. $ |\sin a – \cos a |$
3. $\sin ^{3} a+\cos ^{3} a$
4. $\sin ^{4} a+\cos ^{4} a$
Bài 6. Chứng minh rằng:
1. $\frac{\tan ^{2} a-\sin ^{2} a}{\cot ^{2} a-\cos ^{2} a}=\tan ^{6} a$
2. $\sin ^{2} a\tan^{2} a+4 \sin ^{2} a-\tan ^{2} a+3 \cos ^{2} a=3$
3. $\frac{\sin a+\cos a}{\cos ^{3} a}=1+\tan a+\tan ^{2} a+\tan ^{3} a $
Bài 7. Chứng minh các đẳng thức sau:
1. $ \cos ^{4} x-\sin ^{4} x=2 \cos ^{2} x-1$
2. $\cot ^{2} x-\cos ^{2} x=\cos ^{2} x \cdot \cot ^{2} x$
3. $\tan ^{2} x-\sin ^{2} x=\tan ^{2} x \cdot \sin ^{2} x$
4. $(\sin x+\cos x)^{2}+(\sin x-\cos x)^{2}=2$
Bài 8. Rút gọn các biểu thức sau:
1. $2\left(\sin ^{6} x+\cos ^{6} x\right)-3\left(\sin ^{4} x+\cos ^{4} x\right) $
2. $2 \cos ^{4} x-\sin ^{4} x+\sin ^{2} x \cos ^{2} x+3 \sin ^{2} x $
3. $\left(\sin ^{4} x+\cos ^{4} x-1\right)\left(\tan ^{2} x+\cot ^{2} x+2\right) $
12/11/2021
100 bài tập khối nón, khối trụ, khối cầu VDC

100 bài tập khối nón, khối trụ, khối cầu VDC

Bài tập khối nón khối trụ khối cầu có lời giải

Câu 1. Cắt hình nón $\left( N \right)$ bằng một mặt phẳng đi qua trục của hình nón được thiết diện là một tam giác vuông cân có diện tích bằng \(4\). Thể tích của khối nón được giới hạn bởi hình nón đã cho bằng

A. \(\frac{8\pi }{3}\).
B. \(\frac{32\pi }{3}\).
C. \(8\pi \).
D. \(64\pi \).

Lời giải. Chọn A

Gọi tam giác \(SAB\) vuông cân tại S là thiết diện của hình nón cắt bởi mặt phẳng.

Ta có \(S{}_{\Delta SAB}=\frac{1}{2}S{{A}^{2}}=4\Rightarrow SA=2\sqrt{2}\Rightarrow AB=4\).

Khi đó bán kính đáy của hình nón \(r=\frac{AB}{2}=2\) và \(SO=r=2\).

Vậy thể tích của khối nón được giới hạn bởi hình nón đã cho là:

\(V=\frac{1}{3}\pi {{r}^{2}}h=\frac{8\pi }{3}\).

Câu 2. Cho hình trụ có hai đáy là hai hình tròn \(\left( O;R \right)\) và \(\left( {O}’;R \right)\). \(AB\) là một dây cung của đường tròn \(\left( O;R \right)\) sao cho tam giác \({O}’AB\) là tam giác đều và mặt phẳng \(\left( {O}’AB \right)\) tạo với mặt phẳng chứa đường tròn \(\left( O;R \right)\) một góc \(60{}^\circ \). Tính theo \(R\) thể tích \(V\) của khối trụ đã cho.

A.\(V=\frac{\pi \sqrt{7}{{R}^{3}}}{7}\).
B. \(V=\frac{3\pi \sqrt{5}{{R}^{3}}}{5}\).
C. \(V=\frac{\pi \sqrt{5}{{R}^{3}}}{5}\).
D. \(V=\frac{3\pi \sqrt{7}{{R}^{3}}}{7}\).

Lời giải. Chọn D

Đặt độ dài cạnh $AB=x$ $\left( x>0 \right)$ và \(M\) là trung điểm \(AB\).

Vì tam giác ${O}’AB$ đều nên ${O}’A={O}’B=AB=x$$\Rightarrow {O}’M=\frac{x\sqrt{3}}{2}$.

Vì mặt phẳng \(\left( {O}’AB \right)\) tạo với mặt phẳng chứa đường tròn \(\left( O;R \right)\) góc \(60{}^\circ \) nên $\widehat{{O}’MO}=60{}^\circ $.

Xét tam giác ${O}’OM$ vuông tại \(O\) ta có: $\cos \widehat{{O}’MO}=\frac{OM}{{O}’M}$. Suy ra

$\cos 60{}^\circ =\frac{OM}{\frac{x\sqrt{3}}{2}}\Leftrightarrow OM=\frac{x\sqrt{3}}{4}$

Xét tam giác $OAM$vuông ở \(M\) có: $O{{A}^{2}}=O{{M}^{2}}+A{{M}^{2}}$ nên

${{R}^{2}}={{\left( \frac{x\sqrt{3}}{4} \right)}^{2}}+{{\left( \frac{x}{2} \right)}^{2}}\Leftrightarrow {{R}^{2}}=\frac{7}{16}{{x}^{2}}\Rightarrow x=\frac{4\sqrt{7}}{7}R$

Do đó: ${O}’M=\frac{x\sqrt{3}}{2}=\frac{2\sqrt{21}}{7}R$ và $OM=\frac{x\sqrt{3}}{4}=\frac{\sqrt{21}}{7}R$. Vì vậy, ta có

$O{O}’=\sqrt{{O}'{{M}^{2}}-O{{M}^{2}}}=\frac{3\sqrt{7}}{7}R$.

Vậy thể tích khối trụ là $V=\pi {{R}^{2}}.h=\pi {{R}^{2}}.\frac{3\sqrt{7}}{7}R\Rightarrow V=\frac{3\pi \sqrt{7}{{R}^{3}}}{7}$.

Câu 3. Một hình trụ có chiều cao bằng $10$ và bán kính mặt đáy bằng $5$. Một mặt phẳng song song với trục của hình trụ và cách trục một khoảng bằng 2 cắt hình trụ theo thiết diện có diện tích bằng

A. $40\pi $.
B. $80\pi $.
C. $100\pi $.
D. $50\pi $.

Lời giải. Chọn B

Thiết diện là hình chữ nhật và giả sử là $ABCD$ như hình vẽ.

Gọi $M$là trung điểm $AB$. Ta có: $\left\{ {\begin{array}{*{20}{c}} {AD = OO’ = 10}\\ {OB = 5,OM = 3} \end{array}} \right. \Rightarrow MB = \sqrt {O{B^2} – O{M^2}} = 4 \Rightarrow AB = 8$.

Suy ra, diện tích thiết diện bằng: ${S_{ABCD}} = AD.AB = 10.8 = 80 \Rightarrow $Chọn B

Câu 4. Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy bằng $a$, cạnh bên bằng $2a$. Khoảng cách từ $A$ đến mặt phẳng $\left( SBC \right)$bằng

A. $\frac{a\sqrt{165}}{45}$.
B. $\frac{a\sqrt{165}}{15}$.
C. $\frac{2a\sqrt{165}}{15}$.
D. $\frac{a\sqrt{165}}{30}$.

Lời giải.Chọn B

Gọi $G$ là trọng tâm tam giác $ABC$. Do hình chóp $S.ABC$ đều nên $SO\bot \left( ABC \right)$

$SO=\sqrt{S{{A}^{2}}-A{{O}^{2}}}=\sqrt{4{{a}^{2}}-{{\left( \frac{a\sqrt{3}}{3} \right)}^{2}}}=\frac{a\sqrt{33}}{3}$; $GM=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}$

$d\left( A,\left( SBC \right) \right)=3d\left( G,\left( SBC \right) \right)=\frac{3SG.GM}{\sqrt{S{{G}^{2}}+G{{M}^{2}}}}$ $=\frac{a\sqrt{165}}{15}$.

Câu 5. Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O đến AB bằng 2 và $SAO = {30^0}$; $SAB = {60^0}$. Tính diện tích xung quanh hình nón?

A. $4\pi \sqrt 3 $
B. $\frac{{3\pi \sqrt 2 }}{4}$
C. $2\pi \sqrt 3 $
D. $3\pi \sqrt 2 $

Lời giải. Chọn A

Gọi I là trung điểm của AB thì $OI \bot AB;SI \bot AB;OI = 2$

Lại có $\left\{ {\begin{array}{*{20}{c}}

{AO = SA.\cos SAO = SA.\frac{{\sqrt 3 }}{2}}\\

{AI = SA.\cos SAI = \frac{{SA}}{2}}

\end{array}} \right.$

Từ đó ta có $\frac{{AI}}{{AO}} = \frac{1}{{\sqrt 3 }}$. Mặt khác $\frac{{AI}}{{AO}} = \cos IAO \Rightarrow \sin IAO = \frac{{\sqrt 6 }}{3} = \frac{2}{{OA}} \Rightarrow OA = \sqrt 6 $

Mà $SA = \frac{{OA}}{{\cos 30}} = \sqrt 6 .\frac{2}{{\sqrt 3 }} = 2\sqrt 2 $

Diện tích xung quanh cần tính là: ${S_{xq}} = \pi .OA.SA = 4\pi \sqrt 3 $

Download bài tập khối nón khối trụ khối cầu file word

Các câu còn lại, mời thầy cô và các em download tại đây 100 bai tap khoi non khoi tru khoi cau o2.edu.vn

01/11/2021
TỔNG HỢP BÀI TẬP VECTƠ LỚP 10
TỔNG HỢP BÀI TẬP VECTƠ LỚP 10

BÀI TẬP VECTƠ LỚP 10: Chứng minh các đẳng thức vectơ

Ví dụ 1. Cho 6 điểm $A, B, C, D, E, F$. Chứng minh rằng: (bằng nhiều cách khác nhau)
1. $\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}$
2. $\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}+\overrightarrow{DB}$
3. $\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}$
Ví dụ 2. Cho tam giác $ABC$ với $M, N, P$ là trung điểm các cạnh $AB, BC, CA$. Chứng minh rằng:
1. $\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\overrightarrow{O}$
2. $\overrightarrow{AN}=\overrightarrow{AM}+\overrightarrow{AP}$
3. $\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\overrightarrow{O}$
Ví dụ 3. (Hệ thức về trung điểm) Cho hai điểm $A, B$.
1. Cho $M$ là trung điểm $A, B$. Chứng minh rằng với điểm $I$ bất kì ta có: $$\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IM}$$
2. Với điểm $N$ sao cho $\overrightarrow{NA}=-2\overrightarrow{NB}$. Chứng minh rằng với $I$ bất kì: ta có $$\overrightarrow{IA}+2\overrightarrow{IB}=3\overrightarrow{IN}$$
3. Với điểm $P$ sao cho $\overrightarrow{PA}=3\overrightarrow{PB}$. Chứng minh rằng với $I$ bất kì ta có $$\overrightarrow{IA}-3\overrightarrow{IB}=-2\overrightarrow{IP}$$
Ví dụ 3. (Hệ thức về trọng tâm) Cho tam giác $ABC$ và $G$ là trọng tâm của tam giác.
1. Chứng minh rằng $\overrightarrow{AG}+\overrightarrow{BG}+\overrightarrow{CG}=\overrightarrow{O}$. Với $I$ bất kì ta có: $$\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=3\overrightarrow{IG}$$
2. Điểm $M$ thuộc đoạn $AG$ và $MG=\frac{1}{4}GA$. Chứng minh rằng:$$2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{O}$$
3. Với $I$ bất kì, chứng minh rằng $$2\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=4\overrightarrow{IM}$$
4. Cho hai tam giác $ABC$ và DEF có trọng tâm là $G$ và $G’$. Chứng minh rằng: $$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CE}=3\overrightarrow{GG’}$$ Tìm điều kiện để hai tam giác có cùng trọng tâm.
Ví dụ 4. (Hệ thức về hình bình hành) Cho hình bình hành $ABCD$ tâm $O$.
1. Chứng minh rằng: $\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=\overrightarrow{O}$
2. Với $I$ bất kì $\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=4\overrightarrow{IO}$
Ví dụ 5. (Tứ giác bất kì) Cho tứ giác $ABCD$. Gọi $M, N$ là trung điểm của $AB$ và $CD$. Chứng minh rằng:
1. $\overrightarrow{AD}+\overrightarrow{BC}=2\overrightarrow{MN}$
2. $\overrightarrow{AC}+\overrightarrow{BD}=2\overrightarrow{MN}$
3. Tìm vị trí điểm $I$ sao cho $$\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{O}$$
4. Với điểm $M$ bất kì, Chứng minh rằng: $$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=4\overrightarrow{MI}$$
Ví dụ 6. (Khái niệm trọng tâm của hệ $n$ điểm và tâm tỉ cự của hệ $n$ điểm) Cho $n$ điểm ${{A}_{1}},{{A}_{2}},…,{{A}_{n}}$.
1. Gọi $G$ là điểm thoả mãn $$\overrightarrow{G{{A}_{1}}}+\overrightarrow{G{{A}_{2}}}+…+\overrightarrow{G{{A}_{n}}}=\overrightarrow{O}.$$ Chứng minh rằng với điểm $M$ bất kì ta luôn có$$\overrightarrow{M{{A}_{1}}}+\overrightarrow{M{{A}_{2}}}+…+\overrightarrow{M{{A}_{n}}}=n\overrightarrow{MG}.$$
2. Gọi $I$ là điểm thoả mãn ${{n}_{1}}\overrightarrow{IA_1}+n_2\overrightarrow{G{{A}_{2}}}+…+{{n}_{n}}\overrightarrow{G{{A}_{n}}}=\overrightarrow{O}$. Chứng minh rằng với $M$ bất kì: $${{n}_{1}}\overrightarrow{M{{A}_{1}}}+{{n}_{2}}\overrightarrow{M{{A}_{2}}}+…+{{n}_{n}}\overrightarrow{M{{A}_{n}}}=({{n}_{1}}+..+{{n}_{n}})\overrightarrow{MG}$$
Ví dụ 7.
1. Cho lục giác đều $ABCDEF$. Chứng minh rằng hai tam giác $ACE$ và $BDF$ cùng trọng tâm.
2. Cho lục giác $ABCDEF$. Gọi $M, N, P, Q, R, S$ lần lượt là trung điểm của $AB, CD, EF, BC, DE, FA$. Chứng minh rằng hai tam giác $MNP$ và $QRS$ cùng trọng tâm.
3. Cho hai tam giác $ABC$ và $A’,B’,C’$ là các điểm thuộc $BC, CA, AB$ sao cho:$$\overrightarrow{{{A}’}B}=k\overrightarrow{{{A}’}C},\overrightarrow{{{B}’}C}=k\overrightarrow{{{B}’}A},\overrightarrow{{{C}’}A}=k\overrightarrow{{{C}’}B}$$ và $k\ne 1$. Chứng minh rằng hai tam giác $ABC$ và $A’B’C’$ cùng trọng tâm.
4. Cho tứ giác lồi $ABCD$. Gọi $M, N, P, Q$ là trung điểm $AB, BC, CD, DA$. Chứng minh rằng hai tam giác $ANP$ và $CMQ$ cùng trọng tâm.
Ví dụ 8. (Một số đẳng thức về trực tâm, trọng tâm, tâm đường tròn ngoại tiếp, tâm đường tròn nội tiếp)

Cho tam giác $ABC$ có $G, H, O, I$ lần lượt là trọng tâm, trực tâm, tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp. Chứng minh rằng:
1. $3\overrightarrow{OG}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$
2. $\overrightarrow{OH}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$
3. $2\overrightarrow{HO}=\overrightarrow{HA}+\overrightarrow{HB}+\overrightarrow{HC}$
4. $a\overrightarrow{IA}+b\overrightarrow{IB}+c\overrightarrow{IC}=\overrightarrow{O}$
5. $\tan A\overrightarrow{HA}+\tan B\overrightarrow{HB}+\tan C\overrightarrow{HC}=\overrightarrow{O}$
6. Gọi $M$ là điểm bất kì nằm trong tam giác $ABC$. Chứng minh rằng: ${{S}_{BCM}}\overrightarrow{IA}+{{S}_{ACM}}\overrightarrow{IB}+{{S}_{ABM}}\overrightarrow{IC}=\overrightarrow{O}$ ($M$ nằm ngoài thì không còn đúng).
Ví dụ 9. (Nhấn mạnh bài toán và mở rộng ra nhiều trường hợp). Cho tam giác $ABC$. Gọi $M$ là trung điểm $AB$ và $N$ là một điểm trên cạnh $AC$ sao cho $NC = 2NA$. Gọi $K$ là trung điểm $MN$.
1. Chứng minh rằng: $\overrightarrow{AK}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}$.
2. $D$ là trung điểm $BC$. Chứng minh rằng: $\overrightarrow{KD}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$
BÀI TẬP VECTƠ LỚP 10: Biểu diễn véc tơ

Ví dụ 1. Cho tam giác $ABC$ và $G$ là trọng tâm. Lấy $B_1$ đối xứng với $B$ qua $G$. $M$ là trung điểm $BC$. Hãy biểu diễn các véc tơ $\overrightarrow{AM}$, $\overrightarrow{AG},\overrightarrow{BC},\overrightarrow{C{{B}_{1}}},\overrightarrow{A{{B}_{1}}},\overrightarrow{M{{B}_{1}}}$ qua hai véc tơ $\overrightarrow{AB},\overrightarrow{AC}$.

Ví dụ 2. Cho tam giác $ABC$, gọi $I$ là điểm trên cạnh $BC$ sao cho $2CI = 3BI$ và $J$ thuộc $BC$ kéo dài sao cho $5JB = 2JC$.
1. Tính $\overrightarrow{AI},\overrightarrow{AJ}$ theo hai véc tơ $\overrightarrow{AB},\overrightarrow{AC}$. Từ đó biểu diễn $\overrightarrow{AB},\overrightarrow{AC}$ theo $\overrightarrow{AI},\overrightarrow{AJ}$.
2. Gọi $G$ là trọng tâm tam giác. Tính $\overrightarrow{AG}$ theo $\overrightarrow{AI},\overrightarrow{AJ}$.
BÀI TẬP VECTƠ LỚP 10: Chứng minh 3 điểm thẳng hàng

Phương pháp: Ba điểm $A, B, C$ thẳng hàng khi và chỉ khi $\overrightarrow{AB}=k\overrightarrow{AC}$.

Lưu ý: $\overrightarrow{AB}=m\overrightarrow{x}+n\overrightarrow{y},\overrightarrow{AC}=km\overrightarrow{x}+kn\overrightarrow{y}$ thì $\overrightarrow{AB}=k\overrightarrow{AC}$

Ví dụ 1. Cho tam giác $ABC$ và $M, N$ lần lượt là trung điểm $AB, AC$.
1. Gọi $P, Q$ là trung điểm $MN$ và $BC$. Chứng minh $A, P, Q$ thẳng hàng.
2. Gọi $E, F$ thoả mãn: $\overrightarrow{ME}=\frac{1}{3}\overrightarrow{MN}$, $\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC}$. Chứng minh $A, E, F$ thẳng hàng.
Ví dụ 2. Cho tam giác $ABC$, có $E$ là trung điểm $AB$ và $F$ thuộc đoạn $AC$ thoả mãn $AF = 2FC$.
1. Gọi $M$ là trung điểm $BC$ và $I$ là điểm thoả mãn $4EI = 3FI$. Chứng minh $A, M, I$ thẳng hàng.
2. Lấy $N$ thuộc $BC$ sao cho $BN = 2 NC$ và $J$ thuộc $EF$ sao cho $2EJ = 3JF$. Chứng minh $A, J, N$ thẳng hàng.
3. Lấy điểm $K$ là trung điểm $EF$. Tìm $P$ thuộc $BC$ sao cho $A, K, P$ thẳng hàng.
Xem thêm tại Chứng minh thẳng hàng bằng vectơ

Ví dụ 3. Cho tam giác $ABC$ và M, N, P là các điểm thoả mãn: $\overrightarrow{MB}-3\overrightarrow{MC}=\overrightarrow{O}$, $\overrightarrow{AN}=3\overrightarrow{NC}$, $\overrightarrow{PB}+\overrightarrow{PA}=\overrightarrow{O}$. Chứng minh rằng: $M, N, P$ thẳng hàng.

Hướng dẫn. $\overrightarrow{MP}=\overrightarrow{CB}+\frac{1}{2}\overrightarrow{CA},\text{ }\overrightarrow{MN}=\frac{1}{2}\overrightarrow{CB}+\frac{1}{4}\overrightarrow{CA}$.

Ví dụ 4. Cho tam giác $ABC$ và $L, M, N$ thoả mãn $\overrightarrow{LB}=2\overrightarrow{LC},$$\overrightarrow{MC}=\frac{-1}{2}\overrightarrow{MA}$, $\overrightarrow{NB}+\overrightarrow{NA}=\overrightarrow{O}$. Chứng minh $L, M, N$ thẳng hàng.

Ví dụ 5. Cho tam giác $ABC$ với $G$ là trọng tâm. $I, J$ thoả mãn: $2\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{O}$, $2\overrightarrow{JA}+5\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{O}$.
1. Chứng minh rằng: $M, N, J$ thẳng hàng với $M, N$ là trung điểm $AB$ và $BC$.
2. Chứng minh rằng $J$ là trung điểm $BI$.
3. Gọi $E$ là điểm thuộc $AB$ và thoả mãn $\overrightarrow{AE}=k\overrightarrow{AB}$. Xác định $k$ để $C, E, J$ thẳng hàng.
Ví dụ 6. Cho tam giác $ABC$. Gọi $I, J$ là hai điểm thoả mãn: $\overrightarrow{IA}=2\overrightarrow{IB}, 3\overrightarrow{JA}+2\overrightarrow{JC}=\overrightarrow{O}$. Chứng minh đường thẳng $IJ$ đi qua $G$.

BÀI TẬP VECTƠ LỚP 10: Xác định điểm thoả mãn một đẳng thức vectơ

Đặt Vấn đề: Cho hai điểm $A, B, C$ cố định.
1. Nếu $\overrightarrow{PB}+\overrightarrow{PA}=\overrightarrow{O}$ thì $P$ là trung điểm của $AB$.
2. Nếu $\overrightarrow{PB}+\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{O}$ thì $P$ là trọng tâm tam giác $ABC$.
3. Nếu $P$ là một điểm thoã mãn một đẳng thức véc tơ khác thì có xác định được vị trí của $P$ hay không?
Ví dụ 1. Cho hai điểm $A,B$. Xác định vị trí điểm $I$ thoả mãn: $\overrightarrow{IA}+2\overrightarrow{IB}=\overrightarrow{O}$.

Nhận xét. Với hai điểm $A, B$ cho trước luôn xác định được điểm $I$ thoả mãn: $$m\overrightarrow{IA}+n\overrightarrow{IB}=\overrightarrow{O}$$ Với điểm O bất kì ta có: $\overrightarrow{OI}=\frac{m}{m+n}\overrightarrow{OA}+\frac{n}{m+n}\overrightarrow{OB}$.

Ví dụ 2. Bài toán 3 điểm. Cho 3 điểm $A, B, C$. Tìm vị trí điểm $M$ sao cho:
1. $\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{AB}$
2. $2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{O}$
3. $\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{O}$
4. $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{O}$
5. $\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{O}$
6. $\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{O}$
BÀI TẬP VECTƠ LỚP 10: Tìm quĩ tích thoả mãn một đẳng thức véc tơ

Một số quĩ tích cơ bản:
1. $\left| \overrightarrow{MA} \right|=\left| \overrightarrow{MB} \right|$ thì $M$ nằm trên đường trung trực của $AB$.
2. $\left| \overrightarrow{MC} \right|=k\left| \overrightarrow{AB} \right|$, với $A, B, C$ cố định thì $M$ nằm trên đường tròn tâm $C$ bán kính $k.AB$.
3. $\overrightarrow{AM}=k\overrightarrow{BC}$ với $A, B, C$ cho trước:
  - $k > 0$ thì $M$ nằm trên nửa đường thẳng qua $A$ và song song với $BC$ và theo hướng $\overrightarrow{BC}$.
  - $k< 0$
  - $k$ bất kì.
Dạng 1. (Bài toán hai điểm)

Ví dụ 1. Cho hai điểm $A,B$ cố định. Tìm quĩ tích điểm $M$ sao cho:
1. $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=2\left| \overrightarrow{AB} \right|$
2. $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=\left| \overrightarrow{AB} \right|$
3. $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=2\left| \overrightarrow{MA} \right|$
4. $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|=\left| \overrightarrow{MA} \right|$
5. $\left| 2\overrightarrow{MA}+\overrightarrow{MB} \right|=\left| \overrightarrow{MA}-\overrightarrow{MB} \right|$
Dạng 2. (Bài toán 3 điểm)

Ví dụ 2. Cho tam giác $ABC$. Tìm quĩ tích điểm $M$ sao cho:
1. $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right|=\frac{3}{2}\left| \overrightarrow{MB}+\overrightarrow{MC} \right|$
2. $\left| \overrightarrow{MA}+\overrightarrow{AC} \right|=\left| \overrightarrow{MA}-\overrightarrow{MB} \right|$
3. $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|=\left| \overrightarrow{MB}-\overrightarrow{MC} \right|$
4. $\left| 3\overrightarrow{MA}+2\overrightarrow{MB}-2\overrightarrow{MC} \right|=\left| \overrightarrow{MB}-\overrightarrow{MC} \right|$
Ví dụ 3. Tìm quĩ tích điểm $M$ sao cho:
1. $\overrightarrow{MA}+k\overrightarrow{MB}-k\overrightarrow{MC}=\overrightarrow{O}$
2. $k\overrightarrow{MA}+\overrightarrow{MB}=k\overrightarrow{MC}$
3. $(1-k)\overrightarrow{MA}+\overrightarrow{MB}-k\overrightarrow{MC}=\overrightarrow{O}$
BÀI TẬP VECTƠ LỚP 10: Một số bài toán về khoảng cách

Ví dụ 1 Cho hai điểm $A, B$ và đường thẳng $d$. Tìm vị trí điểm $M$ trên $d$ sao cho độ dài các véc tơ sau nhỏ nhất?
1. $\left| \overrightarrow{MA}+\overrightarrow{MB} \right|$
2. $\left| \overrightarrow{MA}+2\overrightarrow{MB} \right|$
3. $\left| 3\overrightarrow{MA}-\overrightarrow{MB} \right|$
4. $\left| 3\overrightarrow{MA}+2\overrightarrow{MB} \right|$
5. $\left| 2\overrightarrow{MA}-3\overrightarrow{MB} \right|$
Ví dụ 2. Cho tam giác $ABC$ và đường thẳng $d$. Tìm vị trí điểm $M$ trên $d$ sao cho độ dài các véc tơ sau nhỏ nhất.
1. $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right|$
2. $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC} \right|$
3. $\left| 3\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC} \right|$
4. $\left| \overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC} \right|$
Ví dụ 3. Cho tứ giác $ABCD$ và đường thẳng $d$. Tìm vị trí điểm $M$ trên $d$ sao cho độ dài các véc tơ sau nhỏ nhất.
1. $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD} \right|$
2. $\left| \overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}+2\overrightarrow{MD} \right|$
3. $\left| 3\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}-\overrightarrow{MD} \right|$
4. $\left| \overrightarrow{MA}-2\overrightarrow{MB}+\overrightarrow{MC}-\overrightarrow{MD} \right|$
5. $\left| \overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+2\overrightarrow{AB} \right|$
BÀI TẬP VECTƠ LỚP 10: Chứng minh đường thẳng đi qua một điểm cố định

Ví dụ 1. (Bài toán 2 điểm) Cho hai điểm $A, B$ cố định. Hai điểm $M, N$ di động. Chứng minh rằng đường thẳng $MN$ luôn đi qua một điểm cố định nếu:
- Với $I$ là trung điểm $AB$ thì: $$\overrightarrow{MB}+\overrightarrow{MA}=2\overrightarrow{MI}$$
- Nếu $M, I, N$ thẳng hàng thì khi đó: $\overrightarrow{MN}=k\overrightarrow{MA}+k\overrightarrow{MB}$, hay nói cách khác là đường thẳng $MN$ đi qua điểm $I$ cố định.
Từ đó dẫn dắt vào bài toán bằng cách thay điểm $I$ bằng điểm bất kì:
1. $\overrightarrow{MN}=\overrightarrow{MA}+2\overrightarrow{MB}$
2. $\overrightarrow{MN}=\overrightarrow{MA}-2\overrightarrow{MB}$
3. $\overrightarrow{MN}=-\overrightarrow{MA}+2\overrightarrow{MB}$
4. $\overrightarrow{MN}=3\overrightarrow{MA}+2\overrightarrow{MB}$
Ví dụ 2. (Bài toán 3 điểm). Cho tam giác $ABC$ và điểm $M$ trong mặt phẳng. Chứng minh rằng đường thẳng $MN$ luôn đi qua một điểm cố định nếu (Xác định vị trí điểm cố định và điểm $N$ trong mỗi trường hợp)
1. $\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MA}=\overrightarrow{MN}$
2. $2\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MN}$
3. $\overrightarrow{MA}+2\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MN}$
4. $\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC}=\overrightarrow{MN}$
5. $\overrightarrow{MA}+\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{MN}$
6. $\overrightarrow{MA}+2\overrightarrow{MB}-\overrightarrow{MC}=\overrightarrow{MN}$
03/10/2021
Phương pháp so sánh thể tích
Phương pháp so sánh thể tích

Để tính thể tích của một khối chóp, khối lăng trụ chúng ta có thể tính trực tiếp bằng cách xác định diện tích đáy và chiều cao như trong bài Tính thể tích khối chóp. Tuy nhiên, có một cách rất hiệu quả để tính thể tích của khối chóp, khối lăng trụ, khối đa diện mà đề bài yêu cầu là so sánh chúng với các khối có thể tích dễ dàng tính được.

1. Lý thuyết Phương pháp so sánh thể tích

Từ công thức tính thể tích khối chóp, ta thấy thể tích của khối chóp không đổi khi:
- Đáy cố định, đỉnh của hình chóp di chuyển trên một mặt phẳng hoặc một đường thẳng song song với đáy.
- Đỉnh của hình chóp cố định, đáy của hình chóp biến đổi trên một mặt phẳng cố định thành những đa giác tương đương (tức là những đa giác có cùng diện tích).
Do đó, khi tính thể tích khối chóp, chúng ta thường sử dụng các kết quả:
- Hai khối chóp có chung đáy thì ta đi so sánh vị trí của hai đỉnh.
- Hai khối chóp có chung đỉnh thì ta đi so sánh diện tích của hai đáy.
- Sử dụng công thức tỉ số thể tích.
2. Ví dụ Phương pháp so sánh thể tích

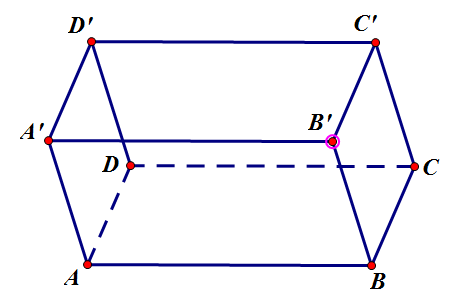
Ví dụ 1. Chia khối lăng trụ $ABC.A’B’C’$ thành ba khối tứ diện bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$. Hãy kể tên ba khối tứ diện đó và chứng tỏ rằng chúng có cùng thể tích.

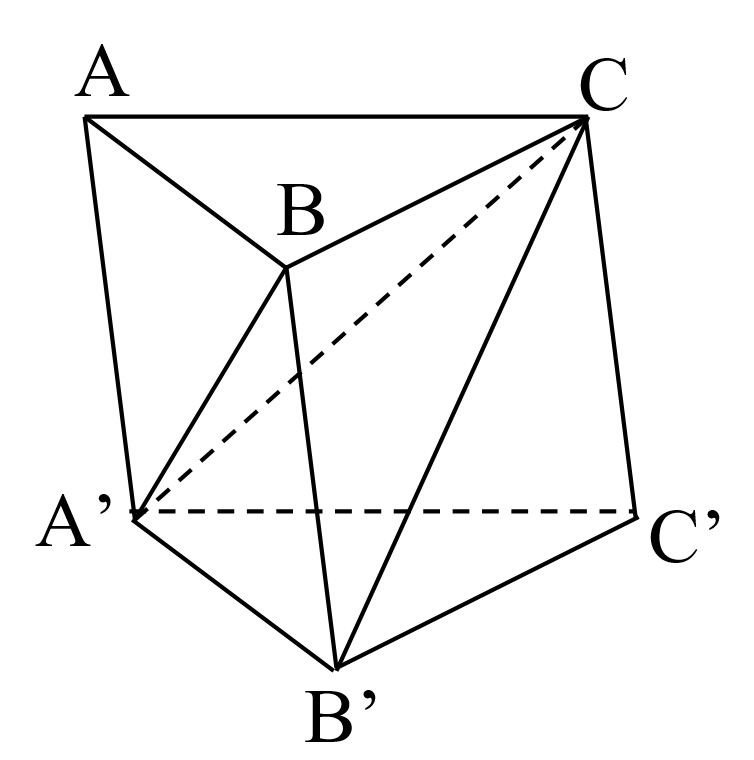
Lời giải
- Chia khối lăng trụ $ABC.A’B’C’$ bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$ thành ba khối tứ diện: $CC’A’B’$, $CBA’B’$, $CABA’$.
- Xét hai hình chóp $C.ABA’$ và $C.BA’B’$ có cùng độ dài đường cao là khoảng cách từ $C$ tới mặt phẳng $(ABB’A’)$ và đáy là các tam giác $ABA’$, $BB’A’$ là hai tam giác cùng diện tích (cùng bằng một nửa diện tích của hình bình hành $ABB’A’$). Vậy \[{{V}_{C.{ABA}}}={{V}_{C.{BA}B’}}\] hay \[{{V}_{{CABA}}}={{V}_{{CBA}B’}}\]
- Ta có: $BB’//(ACC’A’)$ nên suy ra $d(B; (ACC’A’))=d(B’; (ACC’A’))$ hay $$d(B; (ACA’))=d(B’; (CC’A’)).$$
- Lại có $ACA’$ và $CC’A’$ la hai tam giác có cùng diện tích nên \[V_{B.ACA’}=V_{B’.CC’A}\] hay \[V_{CABA’}=V_{CC’AB’}\]
Từ đó suy ra điều phải chứng minh.

Ví dụ 2. [CĐ2011] Cho hình chóp $ S.ABC $ có đáy là tam giác vuông cân tại $ B, AB=a,SA $ vuông góc với đáy. Góc giữa hai mặt phẳng $ (SBC) $ và $ (ABC) $ bằng $ 30^\circ. $ Gọi $ M,N $ lần lượt là trung điểm $ SC,AB $. Tính thể tích các khối chóp $ S.ABM, S.BMN. $

Hướng dẫn. Chỉ ra $ \widehat{SBA}=30^\circ $ và $ V_{S.ABM}=\frac{1}{2}V_{S.ABC} =\frac{a^3\sqrt{3}}{36}. $

Ví dụ 3. Cho hình chóp $ S.ABC $ có đáy là $ \Delta ABC $ vuông cân ở $ B$, $AC=a\sqrt{2},SA\perp\left( ABC \right), SA=a $. Gọi $ G $ là trọng tâm của $ \Delta SBC $, mặt phẳng $ \left( \alpha \right) $ đi qua $ AG $ và song song với $ BC $ cắt $ SC,SB $ lần lượt tại $ M,N $. Tính thể tích khối chóp $ S.AMN $?

Hướng dẫn. Tính được $ V_{S.ABC}=\frac{{{a}^{3}}}{6}. $ Ta có \[ \frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=\frac{4}{9} \] Suy ra $ {{V}_{S.AMN}}=\frac{4}{9}.{{V}_{S.ABC}}=\frac{4}{9}.\frac{{{a}^{3}}}{6}=\frac{2{{a}^{3}}}{27}. $

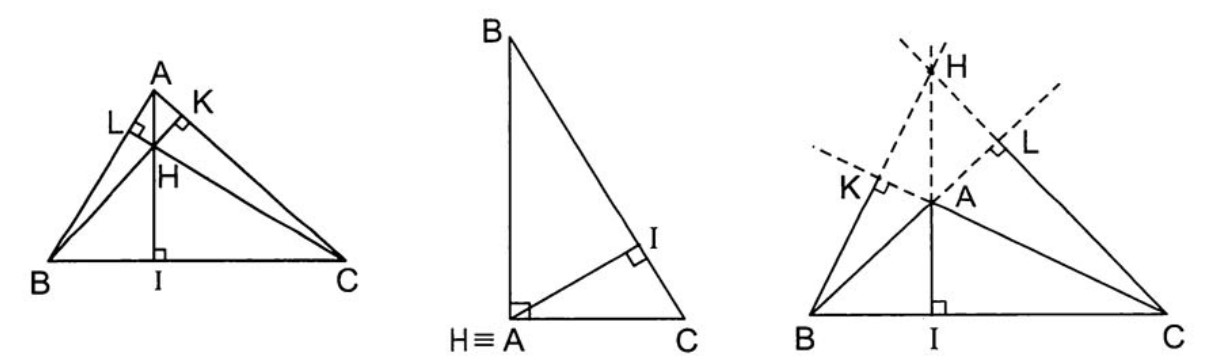
Ví dụ 4. [D2006] Cho hình chóp $ S.ABC $ có đáy là $ \Delta ABC $ đều cạnh $ a $ và $ SA\perp \left( ABC \right), SA=2a $. Gọi $ H,K $ lần lượt là hình chiếu vuông góc của điểm $ A $ lần lượt lên cạnh $ SB,SC $. Tính thể tích khối $ A.BCKH $ theo $ a $.

Hướng dẫn. Tính ngay được \[{{V}_{S.ABC}}=\frac{1}{3}.{{S}_{\Delta ABC}}.SA=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.2a=\frac{{{a}^{3}}\sqrt{3}}{6}\] Mặt khác lại có \[\frac{{{V}_{S.AHK}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SH}{SB}.\frac{SK}{SC}=\frac{SH.SB}{S{{B}^{2}}}.\frac{SK.SC}{S{{C}^{2}}}=\frac{16}{25}\] Suy ra \[ {{V}_{A.BCKH}}={{V}_{S.ABC}}-{{V}_{S.AHK}}=\frac{9}{25}.{{V}_{S.ABC}}=\frac{3{{a}^{3}}\sqrt{3}}{50} \]

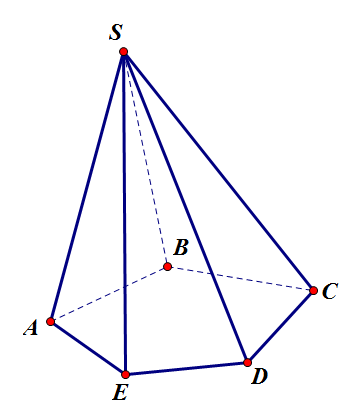
Ví dụ 5. Cho hình chóp tứ giác đều $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh bên tạo với đáy một góc $ 60^\circ $. Gọi $ M $ là trung điểm $ SC $. Mặt phẳng đi qua $ AM $ và song song với $ BD $, cắt $ SB $ tại $ E $ và cắt $ SD $ tại $ F $. Tính thể tích khối chóp $ S.AEMF $.

Hướng dẫn. $ {{V}_{SAMF}}=\frac{1}{3}{{V}_{SACD}}=\frac{1}{6}{{V}_{S.ABCD}}=\frac{{{a}^{3}}\sqrt{6}}{36}\Rightarrow {{V}_{S.AEMF}}=2.\frac{{{a}^{3}}\sqrt{6}}{36}=\frac{{{a}^{3}}\sqrt{6}}{18} $

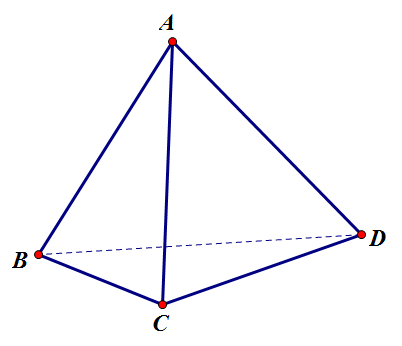
Ví dụ 6. Cho hình chóp $S.ABC$ có các góc $ \widehat{ASB}=\widehat{BSC}=\widehat{CSA}=60^\circ $. Độ dài các cạnh $ SA,SB,SC $ lần lượt là $ a,b,c $. Tính thể tích khối chóp $ S.ABC. $

Hướng dẫn.
Trên các cạnh $ SB,SC $ lần lượt lấy $ B’,C’ $ sao cho $ SB’=SC’=SA=a $. Như vậy, hình chóp $S.AB’C’$ là một tứ diện đều cạnh bằng $ a $ nên có thể tích \[ V_{SAB’C’}=\frac{a^3\sqrt{2}}{12}. \] Mặt khác, theo tỉ số thể tích thì
\[ \frac{V_{S.ABC}}{V_{S.AB’C’}}=\frac{SA}{SA}\cdot\frac{SB}{SB’}\cdot\frac{SC}{SC’}=\frac{bc}{a^2}\]
Do đó, thể tích khối chóp cần tìm là \[ V_{S.ABC}=\frac{abc\sqrt{2}}{12}. \]

Ví dụ 7. [CĐ2008] Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$?

Hướng dẫn. Vì $MS=MA$ nên $ d\left(A,(MNP) \right)=d\left(S,(MNP) \right)$. Do đó $ V_{A.MNP}=V_{S.MNP} $. Mặt khác \[\frac{{{V}_{S.MNP}}}{{{V}_{S.ABP}}}=\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SP}=\frac{1}{4}\]
Từ đó tìm được $ {{V}_{A.MNP}}=\frac{{{a}^{3}}\sqrt{6}}{48}. $

3. Bài tập sử dụng Phương pháp so sánh thể tích

Bài 1. [CĐ2009] Cho hình chóp tứ giác đều $ S.ABCD $ có $ AB=a,SA=a\sqrt{2} $. Gọi $ M,N,P $ lần lượt là trung điểm của các cạnh $ SA,SB,CD $. Chứng minh rằng đường thẳng $ MN $ vuông góc với đường thẳng $ SP $. Tính theo $ a $ thể tích khối tứ diện $ AMNP $.

Hướng dẫn. Vì $ MN\parallel CD $ mà $ CD\perp SP $ nên $ MN\perp SP. $ Ta có $ V_{AMNP}=\frac{1}{4}V_{ABSP}= \frac{1}{8}V_{S.ABCD}$. Đáp số. $ V=\frac{a^3\sqrt{6}}{48} $

Bài 2. Cho tứ diện đều $ ABCD $ có cạnh $ a $. Lấy các điểm $ B’,C’ $ trên $ AB $ và $ AC $ sao cho $ AB’=\frac{a}{2},AC’=\frac{2a}{3} $. Tính thể tích khối tứ diện $ AB’C’D $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{2}}{36} $.

Bài 3. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a, SC\perp(ABCD) $ cho $ SA=a\sqrt{3} $. Gọi $ H $ là hình chiếu của $ C $ lên $ SB,K $ là trung điểm của $ SD. $ Tính thể tích khối chóp $ S.ABCD $ và khối chóp $ C.BDKH? $

Hướng dẫn. Xét tam giác vuông $ SCB $ có $ SH.SB=SC^2 $ nên $ \frac{SH}{SB}=\frac{SC^2}{SB^2}=\frac{2}{3}. $ Suy ra \[ \frac{V_{S.CKH}}{V_{S.CDB}}=\frac{SC}{SC}.\frac{SK}{SD}.\frac{SH}{SB}=\frac{1}{3} \] Do đó, $ V_{C.BDKH}=\frac{2}{3}V_{S.CBD}=\frac{1}{3}V_{S.ABCD} $

Đáp số. $ V_{S.ABCD}=\frac{a^3\sqrt{2}}{3}$, $V_{C.BDKH}=\frac{a^3\sqrt{2}}{9}. $

Bài 4. Cho hình chóp $ S.ABCD $ có đáy là hình chữ nhật với $ AB=a,\,AD=2a, $ cạnh $ SA $ vuông góc với đáy, cạnh $ SB $ tạo với mặt đáy một góc $ {{60}^{\circ }} $. Trên cạnh $ SA $ lấy điểm $ M $ sao cho $ AM=\frac{a\sqrt{3}}{3} $. Mặt phẳng $ (BCM) $ cắt cạnh $ SD $ tại $ N $. Tính thể tích khối chóp $ S.BCMN? $

Hướng dẫn. $ {{V}_{S.BCMN}}={{V}_{SMBC}}+{{V}_{SMNC}}=\frac{5}{9}{{V}_{S.ABCD}}=\frac{5}{9}.\frac{1}{3}.SA.{{S}_{ABCD}}=\frac{10\sqrt{3}}{27}{{a}^{3}} $

Bài 5. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh bên $ SA $ vuông góc với đáy và $ SA = a $. Gọi $ M $ là một điểm trên cạnh $ SA $ sao cho $ AM = x $. Mặt phẳng $ (MBC) $ cắt $ SD $ tại $ N $. Tính thể tích khối đa diện $ ABCDMN $ theo $ a $ và $ x $.

Đáp số. $ V=\frac{ax.(3a-x)}{6} $

Bài 6. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác đều cạnh $ a\sqrt{3} $, đường cao $ SA=a $. Mặt phẳng qua điểm $ A $ và vuông góc với $ SB $ tại $ H $ và cắt $ SC $ tại $ K $. Tính thể tích hình chóp $ S.AHK $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{3}}{40} $.

Bài 7. Cho hình chóp $ S.ABCD $ có $ ABCD $ là hình bình hành, $ M $ thuộc cạnh $ SA $ và $ \frac{SM}{SA}=x $. Tìm $ x $ để mặt phẳng $ (MBC) $ chia hình chóp thành hai phần có thể tích bằng nhau?

Hướng dẫn. Mặt phẳng $ (MBC) $ cắt $ (SAD) $ theo giao tuyến $ MN\parallel AD. $ Phân chia $ V_{S.MNBC} =V_{S.MBC}+V_{S.MNC} $ để so sánh.

Đáp số. $ x=\frac{-1+\sqrt{5}}{2} $

Bài 8. [DB B2006] Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thoi cạnh $ a $ và góc $ \widehat{BAD}={{60}^\circ} $. Biết rằng $ SA\perp \left( ABCD \right),SA=a $. Gọi $ C’ $ là trung điểm của cạnh $ SC $. Mặt phẳng $ \left( P \right) $ đi qua $ AC’ $ và song song với $ BD $, cắt các cạnh $ SB,SD $ lần lượt tại $ B’ $ và $ D’ $. Tính thể tích khối chóp $ S.ABC’D’ $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{3}}{18} $.

Bài 9. Cho hình chóp $ S.ABCD $ có thể tích là $ V.$ Tứ giác $ ABCD $ là hình bình hành, $ M $ là trung điểm của $ BC $ và $ G $ là trọng tâm tam giác $ SCD $. Tính thể tích tứ diện $ SAMG? $

Hướng dẫn. So sánh thể tích hình chóp $ S.AMG $ với thể tích hình chóp $ S.AMN $ bằng cách coi $ \Delta SAM $ làm đáy chung.

Đáp số. $ V_{SAMG}=\frac{1}{4}V $

Bài 10. Cho hình chóp $ S.ABCD $ có thể tích là $ V.$ Tứ giác $ ABCD $ là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ BC,CD,SD $. Tính thể tích tứ diện $ AMNP? $

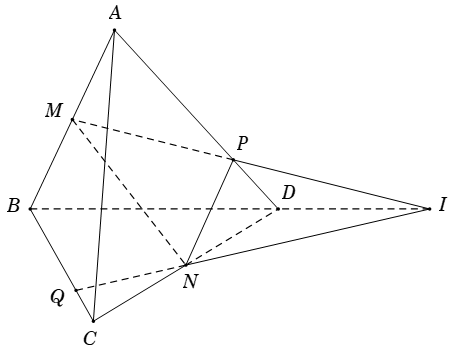
Bài 11. Cho hình chóp $ S.ABC $ có điểm $ M\in SA,N\in SB $ sao cho $ \frac{SM}{MA}=\frac{1}{2},\frac{SN}{NB}=2. $ Gọi $ (\alpha) $ là mặt phẳng qua $ MN $ và song song với $ SC $. Mặt phẳng này cắt $ AC $ tại $ E,BC $ tại $ F. $
1. Chứng minh rằng $ AB,MN,EF $ đồng quy, gọi điểm này là $ I, $ tính tỉ số $ \frac{BI}{BA}? $
2. Mặt phẳng $ (\alpha) $ chia hình chóp thành hai phần. Tính tỉ số thể tích của hai phần này?
Hướng dẫn. Gọi $ L $ là trung điểm của $ SN. $

Đáp số. $ \frac{BI}{BA}=\frac{1}{3},\frac{V_1}{V_2}=\frac{4}{5}. $
24/09/2021