Category: TOÁN HỌC

Cách tính góc giữa hai vectơ trong mặt phẳng
Cách tính góc giữa hai vectơ trong mặt phẳng

1. Cách xác định góc giữa hai vectơ trong mặt phẳng

Cho hai véc-tơ $ \vec{a}$ và $\vec{b}$ đều khác $ \vec{0}$. Từ một điểm $ O$ bất kỳ, dựng $ \overrightarrow{OA}=\vec{a}$ và $ \overrightarrow{OB}=\vec{b}$ thì góc $ \widehat{AOB}$ được gọi là góc giữa hai véc-tơ $ \vec{a}$ và $\vec{b}$, kí hiệu là $ \left(\vec{a},\vec{b}\right)$.

Nhận xét.
- Trong định nghĩa thì điểm $ O$ được lấy tuỳ ý. Tuy nhiên, trong lúc giải toán ta có thể chọn O trùng với điểm gốc của vectơ $ \overrightarrow{a}$ hoặc $ \overrightarrow{b}$ cho đơn giản.
- Hiểu một cách đơn giản, để xác định góc giữa hai véc-tơ ta thay thế hai vectơ đã cho bởi hai vecto mới có chung điểm gốc.
2. Tính chất góc giữa hai véc-tơ trong mặt phẳng
- Góc giữa hai vecto bất kì luôn nằm trong đoạn từ $ 0^\circ $ đến $180^\circ$.
- Góc giữa hai véc tơ bằng $0^\circ$ khi và chỉ khi hai véc tơ đó cùng chiều.
- Góc giữa hai véc tơ bằng $180^\circ$ khi và chỉ khi hai véc tơ đó ngược chiều.
- Góc giữa hai véc tơ bằng $90^\circ$ khi và chỉ khi hai véc tơ đó vuông góc.
3. Bài tập xác định góc giữa hai vectơ trong mặt phẳng

Ví dụ 1. Cho tam giác đều $ $ABC$ có$ $ $H$$ là trung điểm $ $BC$$ Tính góc giữa các cặp vectơ sau:
1. $ \overrightarrow{AH}$ và $ \overrightarrow{BC}$;
2. $ \overrightarrow{AB}$ và $ \overrightarrow{AC}$;
3. $ \overrightarrow{AB}$ và $ \overrightarrow{CA}$;
4. $ \overrightarrow{AB} $ và $ \overrightarrow{AH}$;
5. $ \overrightarrow{AB} $ và $ \overrightarrow{HA}$;
6. $ \overrightarrow{AB}$ và $ \overrightarrow{BC}$.
Ví dụ 2. Cho tam giác $ABC$ vuông tại $A$, cạnh $AB=3,AC=4$. Tính góc giữa các cặp vectơ:
1. $ \overrightarrow{AB}, \overrightarrow{AC}$;
2. $ \overrightarrow{AB}, \overrightarrow{BC}$.
Ví dụ 3. Cho hình vuông $ABCD$, tính góc giữa các véc-tơ:
1. $ \overrightarrow{AB},\overrightarrow{AD}$;
2. $ \overrightarrow{AC},\overrightarrow{BD}$;
3. $ \overrightarrow{AB},\overrightarrow{CB}$;
4. $ \overrightarrow{AD},\overrightarrow{DC}$.
01/12/2020
Tích vô hướng của hai vectơ
Toán 10: Tích vô hướng của hai vectơ

1. Tích vô hướng của hai vectơ là gì?

1.1. Định nghĩa tích vô hướng của hai vectơ

Cho hai véc-tơ $ \vec{a}$ và $\vec{b}$ đều khác $ \vec{0}$. Tích vô hướng của hai véc-tơ $ \vec{a}$ và $\vec{b}$, kí hiệu là $ \vec{a}\cdot \vec{b}$ là một số, được xác định bởi $$ \vec{a}\cdot \vec{b} = \left|\vec{a}\right |\cdot \left|\vec{b} \right|\cdot \cos (\vec{a},\vec{b}) .$$

Quy ước, nếu $ \vec{a}=\vec{0}$ hoặc $ \vec{b}=\vec{0}$ thì $ \vec{a}\cdot \vec{b} =0.$

Xem lại cách xác định góc giữa hai véc-tơ: Góc giữa hai vectơ trong mặt phẳng.

Hai véc-tơ vuông góc với nhau khi và chỉ khi tích vô hướng của chúng bằng $0$.

Tích vô hướng chính là công trong Vật lý. Cho một lực có độ lớn $F$ tác động lên vật làm vật di chuyển được quãng đường $s=OO’$. Lực $F$ hợp với hướng chuyển động $OO’$ một góc là $\phi$ thì công mà lực $F$ sinh ra có độ lớn là $$A=F.s.\cos\phi.$$

1.2. Tính chất của tích vô hướng

Với ba véc-tơ $ \vec{a},\vec{b},\vec{c}$ bất kỳ và một số thực $ k$, ta luôn có
- $ \vec{a}\cdot \vec{b}=\vec{b}\cdot\vec{a}$ (tính chất giao hoán);
- $ \vec{a}(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$ (tính chất phân phối);
- $ (k\vec{a})\cdot\vec{b}=k(\vec{a}\cdot\vec{b})$.
1.3. Biểu thức tọa độ của tích vô hướng

Trong mặt phẳng tọa độ $Oxy$ với hệ trục $ (O;\vec{i},\vec{j})$ cho hai véc-tơ $ \vec{a}=(x;y)$ và $ \vec{b}=(x’;y’)$ thì ta có $$ \vec{a}\cdot\vec{b}=xx’+yy’. $$

Hai véc-tơ $ \vec{a}=(x;y)$ và $ \vec{b}=(x’;y’)$ khi và chỉ khi $xx’+yy’=0$.

1.4. Ứng dụng của tích vô hướng 2 vecto
- Độ dài của $ \vec{a}(x;y)$ được tính bởi công thức $$ |\vec{a}|=\sqrt{x^2+y^2}.$$
- Góc giữa hai vectơ $ \vec{a}=(x;y)$ và $ \vec{b}=(x’;y’)$ có $$ \cos\left(\vec{a},\vec{b}\right)=\frac{\vec{a}\cdot\vec{b}}{|\vec{a}|\cdot|\vec{b}|}=\frac{xx’+yy’}{\sqrt{x^2+y^2}\cdot\sqrt{x’^2+y’^2}}.$$
- Khoảng cách giữa hai điểm $ A(x_A;y_A)$ và $ B(x_B;y_B)$ được tính bởi công thức $$ AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}.$$
1.5. Công thức hình chiếu
- Nếu hai điểm $ A’,B’ $ lần lượt là hình chiếu vuông góc của $ A,B $ lên đường thẳng $ CD, $ thì ta luôn có \[ \overrightarrow{AB}\cdot\overrightarrow{CD}=\overrightarrow{A’B’}\cdot\overrightarrow{CD} \]
- Ngược lại, nếu hai điểm $ C’,D’ $ lần lượt là hình chiếu vuông góc của $ C,D $ lên đường thẳng $ AB $ thì
  \[ \overrightarrow{AB}\cdot\overrightarrow{CD}=\overrightarrow{AB}\cdot\overrightarrow{C’D’} \]
2. Các dạng toán tích vô hướng của hai vectơ

2.1. Tính tích vô hướng bằng định nghĩa

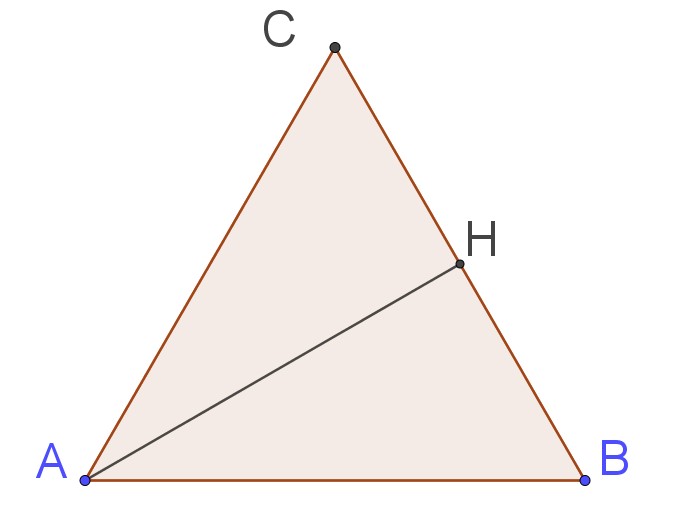
Ví dụ 1. Cho tam giác $ABC$ đều, cạnh bằng $ a $ và đường cao $ AH $. Tính các tích vô hướng:
- $ \overrightarrow{AB}\cdot\overrightarrow{AC}$;
- $(2\overrightarrow{AB})\cdot(3\overrightarrow{HC})$;
- $ (\overrightarrow{AB}-\overrightarrow{AC})(2\overrightarrow{AB}+\overrightarrow{BC}). $
Ví dụ 2. Cho tam giác đều $ ABC $ có cạnh bằng $ 3a. $ Lấy hai điểm $ M,N $ thuộc đoạn $ AC $ sao cho $ AM=MN=NC $. Tính các tích vô hướng:
- $ \overrightarrow{AB}\cdot\overrightarrow{AC}$;
- $\overrightarrow{AC}\cdot\overrightarrow{CB}$;
- $\overrightarrow{BM}\cdot\overrightarrow{BN} $.
Hướng dẫn.
- Ta có: $ \overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cos\widehat{BAC}=3a\cdot 3a\cdot\cos60^\circ=\frac{9a^2}{2}.$
- Dựng $ \overrightarrow{CE}=\overrightarrow{AC} $ thì $\left(\overrightarrow{AC},\overrightarrow{CB}\right)=\left(\overrightarrow{CE},\overrightarrow{CB}\right)=\widehat{BCE}=120^\circ. $ Từ đó tính được, $\overrightarrow{AC}\cdot\overrightarrow{CB}=-\frac{9a^2}{2}$.
- Để tính tích vô hướng còn lại, ta phân tích các véctơ sử dụng quy tắc ba điểm như sau: \begin{align*}\overrightarrow{BM}\cdot\overrightarrow{BN}&=\left(\overrightarrow{AM}-\overrightarrow{AB}\right)\left(\overrightarrow{AN}-\overrightarrow{AB}\right)\\ &=\overrightarrow{AM}\cdot\overrightarrow{AN}-\overrightarrow{AB}\cdot\overrightarrow{AM}-\overrightarrow{AB}\cdot\overrightarrow{AN}+\overrightarrow{AB}^2 \end{align*}
  Thay số vào các tích vô hướng trên, được đáp số $ \frac{13a^2}{2} $.
Khi tính các tích vô hướng ta thường có hai hướng, tính trực tiếp bằng định nghĩa, hoặc phân tích thành các véctơ có mối liên hệ đặc biệt với nhau (vuông góc, cùng hướng hoặc ngược hướng với nhau). Hãy xem ví dụ sau để rõ hơn về ý tưởng này.

Ví dụ 3. Cho hình vuông $ ABCD $ cạnh bằng $ a $ có $ M, N $ lần lượt là trung điểm của $ BC $ và $ CD $. Tính các tích vô hướng:
- $ \overrightarrow{AB}\cdot\overrightarrow{AM}$;
- $\overrightarrow{AM}\cdot\overrightarrow{AN}. $
Hướng dẫn.
- Ta có $ \overrightarrow{AB}\cdot\overrightarrow{AM}=\overrightarrow{AB}\left(\overrightarrow{AB}+\overrightarrow{BM}\right)=\overrightarrow{AB}^2+\overrightarrow{AB}\cdot\overrightarrow{BM}=a^2. $
- Tương tự, cũng có $ \overrightarrow{AM}\cdot\overrightarrow{AN}=\left( \overrightarrow{AB}+\overrightarrow{BM}\right)\left(\overrightarrow{AD}+\overrightarrow{DN}\right)=…=a^2. $
Ví dụ 4. Cho hình vuông $ ABCD $ cạnh bằng $ a $ và $ M $ là một điểm nằm trên đường tròn ngoại tiếp hình vuông. Tính các tích vô hướng:
- $ \left( \overrightarrow{AB}+\overrightarrow{AD} \right) \cdot\left(\overrightarrow{BD}+\overrightarrow{BC} \right) $;
- $ \left( 2\overrightarrow{AB}-\overrightarrow{AD} \right) \cdot \left( 2\overrightarrow{AC}+\overrightarrow{AB} \right) $;
- $ \overrightarrow{MA}\cdot\overrightarrow{MB}+\overrightarrow{MC}\cdot\overrightarrow{MD} $.
Ví dụ 5. Cho hai điểm $ A,B $ cố định và $ k $ là hằng số. Tìm tập hợp các điểm $ M $ thỏa mãn $$ \overrightarrow{MA}\cdot\overrightarrow{MB}=k. $$

Hướng dẫn. Gọi $ I $ là trung điểm $ AB $, ta có: \begin{align}
\overrightarrow{MA}\cdot\overrightarrow{MB}&= \left(\overrightarrow{MI}+\overrightarrow{IA}\right) \left(\overrightarrow{MI}+\overrightarrow{IB}\right)\\
&= \left(\overrightarrow{MI}+\overrightarrow{IA}\right) \left(\overrightarrow{MI}-\overrightarrow{IA}\right)\\
&=MI^2-IA^2
\end{align} Do đó, $ MI^2=k+IA^2 $, nên có các khả năng:
- Nếu $ k+IA^2 <0 $, tập hợp điểm $ M $ là tập rỗng.
- Nếu $ k+IA^2=0 $, tập hợp điểm $ M $ là điểm $ I $.
- Nếu $ k+IA^2 >0 $, tập hợp điểm $ M $ là một đường tròn tâm $ I, $ bán kính $ R=\sqrt{k+IA^2} $.
Như vậy, tùy thuộc vào số $ k $ mà tập hợp điểm $ M $ là các tập khác nhau như trên.

Ví dụ 6. Cho hai véctơ $ \overrightarrow{OA},\overrightarrow{OB} $, gọi $ B’ $ là hình chiếu vuông góc của điểm $ B $ lên đường thẳng $ OA $. Chứng minh rằng $ \overrightarrow{OA}\cdot\overrightarrow{OB}= \overrightarrow{OA}\cdot\overrightarrow{OB’}$.

Hướng dẫn. Chúng ta xét hai trường hợp:
- Hai điểm $A$ và $ B’ $ nằm ở cùng một phía so với điểm $ O. $ Khi đó, $ \cos\widehat{AOB}=\cos\widehat{BOB’} $ nên:
  \begin{align}
  \overrightarrow{OA}\cdot\overrightarrow{OB}&=OA\cdot OB\cdot\cos\widehat{AOB}\\
  &=OA\cdot OB’\\
  &=OA\cdot OB’\cdot\cos0^\circ\\
  &=\overrightarrow{OA}\cdot\overrightarrow{OB’}
  \end{align}
- Hai điểm $A$ và $ B’ $ nằm hai phía so với điểm $ O. $ Khi đó, $ \cos\widehat{AOB}=-\cos\widehat{BOB’} $ nên:
  \begin{align}
  \overrightarrow{OA}\cdot\overrightarrow{OB}&=OA\cdot OB\cdot\cos\widehat{AOB}\\
  &=-OA\cdot OB\cdot\cos\widehat{AOB’}\\
  &=-OA\cdot OB’\\
  &=OA\cdot OB’\cdot\cos180^\circ\\
  &=\overrightarrow{OA}\cdot\overrightarrow{OB’}
  \end{align}
Như vậy, trong cả hai trường hợp, ta đều có $ \overrightarrow{OA}\cdot\overrightarrow{OB}= \overrightarrow{OA}\cdot\overrightarrow{OB’}$.

Ví dụ 7. Cho đường tròn tâm $ I, $ bán kính $ R $ và một điểm $ M $ bất kỳ. Một đường thẳng qua $ M $ cắt đường tròn tại hai điểm $ A,B $. Chứng minh rằng giá trị của biểu thức $ P=\overrightarrow{MA}\cdot\overrightarrow{MB} $ không đổi.

Hướng dẫn. Kẻ đường kính $ BB’ $ thì ta có $ A $ là hình chiếu của $ B’ $ lên $ MB $. Áp dụng công thức hình chiếu trong ví dụ trên, ta có: \begin{align}
P&=\overrightarrow{MA}\cdot\overrightarrow{MB}\\
&=\overrightarrow{MB}\cdot\overrightarrow{MB’}\\
&=\left(\overrightarrow{MI}+\overrightarrow{IB}\right)\left(\overrightarrow{MI}+\overrightarrow{IB’}\right)
\end{align} Nhưng $ \overrightarrow{IB}=-\overrightarrow{IB’}$, nên suy ra $$P= \left(\overrightarrow{MI}+\overrightarrow{IB}\right)\left(\overrightarrow{MI}-\overrightarrow{IB}\right)=MI^2-IB^2=MI^2-R^2 $$, đây là một đại lượng không đổi.

Ví dụ 8. Cho tam giác $ABC$ vuông tại $ A $ và $ \overrightarrow{AB}\cdot\overrightarrow{CB}=4, \overrightarrow{AC}\cdot\overrightarrow{BC}=9 $. Tính độ dài ba cạnh của tam giác.

Hướng dẫn. Ta có $ A $ là hình chiếu vuông góc của $ C $ lên đường thẳng $ AB $, do đó: \[ 4=\overrightarrow{AB}\cdot\overrightarrow{CB}=\overrightarrow{AB}\cdot\overrightarrow{AB}=AB^2 \] Suy ra $ AB=2. $ Tương tự có $ AC=3, $ và sử dụng Pytago được $ BC=\sqrt{13}. $

Ví dụ 9. Cho hình thang vuông $ ABCD $, đường cao $ AB = 2a $, đáy lớn $ BC = 3a $, đáy nhỏ $ AD = a $.
- Tính các tích vô hướng $ \overrightarrow{AB}\cdot\overrightarrow{CD},\overrightarrow{BD}\cdot\overrightarrow{BC},\overrightarrow{AC}\cdot\overrightarrow{BD} $.
- Gọi $ I $ là trung điểm của $ CD, $ tính góc $ \left(\overrightarrow{AI},\overrightarrow{BD}\right) $.
Hướng dẫn. Sử dụng công thức hình chiếu hoặc phân tích theo hai véctơ vuông góc với nhau là $ \overrightarrow{AB},\overrightarrow{AD}. $

Ví dụ 10. Cho hình vuông $ ABCD $ cạnh bằng $ a $ và điểm $ M $ thuộc cạnh $ AB $ sao cho $ AM=\frac{a}{3}. $ Tính giá trị lượng giác $ \cos\widehat{CMD} $.

2.2. Chứng minh đẳng thức bằng tích vô hướng

Ví dụ 1. Cho tam giác $ABC$ có trọng tâm $ G $ và $ M $ là một điểm nằm trên đường thẳng đi qua $ G $ đồng thời vuông góc với $ BC. $ Chứng minh rằng $$\left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\cdot\overrightarrow{BC}=0. $$ Hướng dẫn. Ta có $ \left(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right)\cdot\overrightarrow{BC}=3\overrightarrow{MG}\cdot\overrightarrow{BC}=0. $

Ví dụ 2. Cho hình vuông $ ABCD $ tâm là $ O $, cạnh bằng $ a $. Chứng minh rằng với mọi điểm $ M $ ta luôn có:
\[ MA^2+MB^2+MC^2+MD^2=4MO^2+2a^2 \] Hướng dẫn. Ta có: $$ MA^2=\overrightarrow{MA}^2=\left(\overrightarrow{MO}+\overrightarrow{OA}\right)^2=MO^2+OA^2+2\overrightarrow{MO}\cdot\overrightarrow{OA}. $$ Làm tương tự đối với $ MB,MC,MD $ và cộng từng vế các đẳng thức này được: \begin{align}
MA^2+MB^2+MC^2+MD^2&=4MO^2+4OA^2+2\overrightarrow{MO}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}+\overrightarrow{OD}\right)\\
&=4MO^2+2a^2
\end{align} Vì $ \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}+\overrightarrow{OD}=\vec{0}. $

2.3. Chứng minh hai đường thẳng vuông góc

Ví dụ 1. Chứng minh rằng với bốn điểm phân biệt $ A,B,C,D $ bất kì, ta luôn có, $ AB $ vuông góc với $ CD $ khi và chỉ khi
\[ AC^2-AD^2=BC^2-BD^2 \]
Hướng dẫn. Áp dụng công thức $ \vec{a}^2=|\vec{a}|^2 $, ta có:
\begin{align*}
AC^2-AD^2&=BC^2-BD^2\\
\Leftrightarrow \overrightarrow{AC}^2-\overrightarrow{AD}^2&=\overrightarrow{BC}^2-\overrightarrow{BD}^2\\
\Leftrightarrow \left(\overrightarrow{AC}-\overrightarrow{AD}\right)\left(\overrightarrow{AC}+\overrightarrow{AD}\right)&=\left(\overrightarrow{BC}-\overrightarrow{BD}\right)\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\\
\Leftrightarrow \overrightarrow{DC}\left(\overrightarrow{AC}+\overrightarrow{AD}\right)&=\overrightarrow{DC}\left(\overrightarrow{BC}+\overrightarrow{BD}\right)\\
\Leftrightarrow \overrightarrow{DC}\left(\overrightarrow{AC}+\overrightarrow{AD}-\overrightarrow{BC}-\overrightarrow{BD}\right)&=0\\
\Leftrightarrow 2\overrightarrow{DC}\cdot\overrightarrow{AB}&=0
\end{align*} Điều này xảy ra, khi và chỉ khi hai đường thẳng $ AB $ và $ CD $ vuông góc với nhau.

Chú ý rằng, ở bước thứ ba, ta không được “chia” hai vế cho $ \overrightarrow{DC} $.

2.4. Biểu thức tọa độ của tích vô hướng

Ví dụ 1. Cho tam giác $ ABC$ với $ A(-1 ;-1 ) , B(3 ;1) , C(6 ; 0)$. Tính chu vi tam giác $ABC$ và tìm số đo góc $ B$.

Ví dụ 2. Trong mặt phẳng tọa độ cho hai điểm $ A(-3,2),B(4,3). $ Tìm tọa độ điểm $M$ thuộc trục $ Ox $ sao cho tam giác $ MAB $ vuông tại $ M. $

Hướng dẫn. $ M(3,0) $ hoặc $ M(-2,0) $

Ví dụ 3. Trong mặt phẳng tọa độ cho tam giác $ABC$ có $A(1;2),B(5;3)$ và $C(-2;-2)$.
- Tính chu vi tam giác $ABC$;
- Tính số đo các góc của tam giác $ABC$;
- Tìm tọa độ trọng tâm, trực tâm, tâm đường tròn ngoại tiếp tam giác $ABC$.
Ví dụ 4. [B03] Cho tam giác $ ABC $ vuông cân tại điểm $A$. Biết $ M(1,-1) $ là trung điểm cạnh $ BC $ và $ G(2/3,0) $ là trọng tâm tam giác $ ABC $. Tìm tọa độ các đỉnh của tam giác.

Hướng dẫn.
- Gọi $ A(x_A,y_A) $ thì $ \overrightarrow{AG}=2\overrightarrow{GM} \Leftrightarrow A(0,2).$
- Gọi $ B(x_B,y_B) $ thì vì $ M $ là trung điểm $ BC $ nên $ C(2-x_B,-2-y_B) $ do đó tính được $$ \overrightarrow{AB},\overrightarrow{AC}. $$
- Mặt khác, có tam giác $ ABC $ vuông cân tại $A$ khi và chỉ khi $$\begin{cases} \overrightarrow{AB}.\overrightarrow{AC}=0 \\ AB=AC \end{cases}$$ Giải hệ này tìm được $B(4,0)$ hoặc $ B(-2,2) .$ Từ đó tìm được $ C(-2,2) $ hoặc $ C(4,0). $
Ví dụ 5. Trong mặt phẳng toạ độ $ Oxy, $ cho tam giác $ ABC $ có các đỉnh $ A(-1, 0), B (4, 0), C(0,m) $ với $ m\ne 0 $. Tìm tọa độ trọng tâm $ G $ của tam giác $ ABC $ theo $ m $. Xác định $ m $ để tam giác $ GAB $ vuông tại $ G. $

Hướng dẫn. Đáp số $ m=\pm3\sqrt{6} $.

Ví dụ 6. Cho $ A(0,2),B(-\sqrt{3},-1). $ Tìm tọa độ trực tâm và tâm đường tròn ngoại tiếp tam giác $ OAB. $

Hướng dẫn.
- Có $ H $ là trực tâm tam giác $OAB$ khi và chỉ khi $$\begin{cases} \overrightarrow{AB}.\overrightarrow{OH}=0\\ \overrightarrow{AH}.\overrightarrow{OB}=0 \end{cases} $$ Giải hệ này tìm được đáp số $H(\sqrt{3},-1).$
- Ta có $ I $ là tâm đường tròn ngoại tiếp tam giác $ OAB $ khi và chỉ khi $$IA=IB=IO$$ Giải hệ này tìm được đáp số $I(-\sqrt{3},1)$.
Ví dụ 7. Cho tứ giác $ABCD$ có $A( 2 ; 1) , B(0 ; -3 ), C(6 ; -6 ), D(8 ; -2 )$. Tính diện tích tứ giác $ABCD$.

Hướng dẫn. Chỉ ta tứ giác $ABCD$ là hình chữ nhật nên diện tích được tính bằng công thức $$S=\frac{1}{2} AB\cdot AD.$$

3. Bài tập tích vô hướng của hai vectơ

Bài 1. Cho hình vuông ABCD cạnh $a$. Tính $\overrightarrow{AB}\cdot \overrightarrow{AD}$ và $\overrightarrow{AB}\cdot \overrightarrow{AC}$.

Bài 2. Cho tam giác $ABC$ có $\widehat{A}=90^\circ;\widehat{B}=60^\circ$ và $AB=a$. Tính các tích vô hướng $\overrightarrow{AB}\cdot \overrightarrow{AC};\overrightarrow{CA}\cdot \overrightarrow{CB}$ và $\overrightarrow{AC}\cdot \overrightarrow{CB}$.

Bài 3. Cho tam giác $ABC$ vuông cân tại A có $AB=AC=a$. Tính $\overrightarrow{AB}\cdot \overrightarrow{AC};\;\overrightarrow{BA}\cdot \overrightarrow{BC}$ và $\overrightarrow{AB}\cdot \overrightarrow{BC}$.

Bài 4. Cho tam giác $ABC$ đều cạnh $a$. Tính $\overrightarrow{AB}\cdot \overrightarrow{AC}$ và $\overrightarrow{BC}\cdot \overrightarrow{AB}$.

Bài 5. Trong mặt phẳng $ Oxy $ cho $A=(4;6),B(1;4)$ và $C(7;\frac{3}{2})$.
- Chứng minh tam giác $ABC$ vuông tại $ A $.
- Tính độ dài các cạnh $AB,AC,BC$.
Bài 6. Tính góc giữa hai vec tơ $\overrightarrow{a}$ và $\overrightarrow{b}$ trong các trường hợp sau
- $\overrightarrow{a}=(1;-2)$ và $\overrightarrow{b}=(-1;-3)$.
- $\overrightarrow{a}=(3;-4)$ và $\overrightarrow{b}=(4;3)$.
- $\overrightarrow{a}=(2;5)$ và $\overrightarrow{b}=(3;-7)$.
Bài 7. Cho hình vuông $ ABCD $. Gọi $ M,N $ lần lượt là trung điểm của $ BC,CD $. Chứng minh rằng $ AM $ vuông góc với $ BN. $

Bài 8. Cho hình thang vuông $ ABCD $ với đường cao $ AD=h $ và hai đáy $ AB=a,CD=b $.
- Tìm điều kiện của $ a,b $ và $ h $ để $ AC $ vuông góc với $ BD $.
- Gọi $ M $ là trung điểm của $ BC $. Tìm điều kiện của $ a $ và $ b $ để $ AM $ vuông góc với $ BD. $
Bài 9. Chứng minh rằng với bốn điểm $ A,B,C,D $ bất kỳ ta có
\[ \overrightarrow{AB}\cdot \overrightarrow{CD}+\overrightarrow{AC}\cdot\overrightarrow{DB}+\overrightarrow{AD}\cdot\overrightarrow{BC}=\vec{0} \]Suy ra ba đường cao của tam giác đồng quy.

Bài 10. Cho tam giác $ABC$, trên các cạnh $ AB,CD $, ta dựng ra phía ngoài các tam giác $ ABE,ACF $ vuông cân tại $ A $. Gọi $ I $ là trung điểm của $ BC $. Chứng minh rằng $ AI $ vuông góc với $ EF $.

Bài 11. Cho tam giác $ABC$ nội tiếp đường tròn tâm $ O $. Gọi $ BH,CK $ là các đường cao của tam giác. Chứng minh rằng $ OA $ vuông góc với $ HK $.

Bài 12. Cho tam giác $ABC$ cân tại $ A $ với $ O $ là tâm đường tròn ngoại tiếp. Gọi $ D $ là trung điểm của $ AB $ và $ E $ là trọng tâm của tam giác $ ACD $. Chứng minh rằng $ OE $ vuông góc với $ CD $.

Bài 13. Cho tam giác $ABC$ nội tiếp đường tròn tâm $ O $ và một điểm $ H $. Chứng minh rằng $ H $ là trực tâm của tam giác $ ABC $ khi và chỉ khi $ \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH} $.

Bài 14. Cho tứ giác lồi $ ABCD $ với $ O $ là giao điểm của hai đường chéo. Gọi $ H,K $ tương ứng là trực tâm của các tam giác $ OAB,OCD $. Gọi $ I,J $ tương ứng là trung điểm của $ BC,DA $. Chứng minh rằng $ HK $ vuông góc với $ IJ $.

Bài 15. Cho tứ giác nội tiếp $ ABCD $ với $ I $ là giao điểm của hai đường chéo. Gọi $ E,F $ lần lượt là trung điểm của $ AB,BC $. Chứng minh rằng $ IE $ vuông góc với $ CD $ khi và chỉ khi $ IF $ vuông góc với $ AD $.

Bài 16. Cho góc vuông $ xSy $ và đường tròn $ (O) $ cắt $ Sx $ tại $ A,B $ và $ Sy $ tại $ C,D $. Chứng minh rằng trung tuyến vẽ từ $ S $ của tam giác $ SAC $ vuông góc với $ BD $.

Bài 17. Trong mặt phẳng $ Oxy $ cho hai điểm $A(2;4)$ và $B(1;1)$. Tìm tọa độ điểm $ C $ sao cho tam giác $ABC$ là tam giác vuông cân tại $ B $.

Bài 18. Cho tam giác $ABC$ biết $A(1;-1),B(5;-3)$ và $C(2;0)$.
- Tính chu vi và nhận dạng tam giác $ABC$.
- Tìm tọa độ điểm M biết $\overrightarrow{CM}=2\overrightarrow{AB}-3\overrightarrow{AC}$.
- Tìm tâm và bán kính đường tròn ngoại tiếp tam giác $ABC$.
Bài 19. Trong mặt phẳng $Oxy$ cho 4 điểm $A,B,C,D$ với $A(-1;1) ,B(0;2) ,C(3;1)$ và $D(0;-2)$. Chứng minh rằng $ABCD$ là hình thang cân

Bài 20. Trong mặt phẳng $Oxy$ cho 4 điểm $A(3;4) ,B(4;1) ,C(2;- 3) ,D(-1;6)$. Chứng minh rằng $ABCD$ là tứ giác nội tiếp.

Bài 21. Cho hình vuông $ ABCD $. Gọi $ M,N $ lần lượt là trung điểm của $ BC,CD $. Chứng minh rằng $ AM $ vuông góc với $ BN. $

Bài 22. Cho hình thang vuông $ ABCD $ với đường cao $ AD=h $ và hai đáy $ AB=a,CD=b $.
- Tìm điều kiện của $ a,b $ và $ h $ để $ AC $ vuông góc với $ BD $.
- Gọi $ M $ là trung điểm của $ BC $. Tìm điều kiện của $ a $ và $ b $ để $ AM $ vuông góc với $ BD. $
Bài 23. Cho tam giác $ABC$. Với điểm $ M $ tùy ý, chứng minh rằng
$$\overrightarrow{MA}\cdot \overrightarrow{BC}+\overrightarrow{MB}\cdot \overrightarrow{CA}+\overrightarrow{MC}\cdot \overrightarrow{AB}=0$$

Bài 24. Cho $ O $ là trung điểm của đoạn thẳng $ AB $ và $ M $ là một điểm tùy ý. Chứng minh rằng $\overrightarrow{MA}\cdot \overrightarrow{MB}=OM^2 – OA^2$.

Bài 25. Cho tam giác $ABC$ có ba đường trung tuyến là $ AD, BE, CF $. Chứng minh rằng $\overrightarrow{BC}\cdot \overrightarrow{AD}+\overrightarrow{CA}\cdot \overrightarrow{BE}+\overrightarrow{AB}\cdot \overrightarrow{CF}=0$.

Bài 26. Cho hình chữ nhật $ ABCD $ có $AB=a$ và $AD=a\sqrt{2}$. Gọi $ K $ là trung điểm của cạnh $ AD $. Chứng minh $BK\perp AC$.

Bài 27. Cho tam giác $ABC$ cân tại $ A $. Gọi $ H $ là trung điểm của cạnh $ BC $, $ D $ là hình chiếu vuông góc của $ H $ trên cạnh $ AC, M $ là trung điểm của đoạn $ HD $. Chứng minh $AM\perp BD$.

Bài 28. Cho tam giác $ABC$. Gọi $ H $ là trực tâm của tam giác và $ M $ là trung điểm của $ BC $. Chứng minh $\overrightarrow{MH}\cdot \overrightarrow{MA}=\frac{1}{4}BC^2$.

Bài 29. Cho tứ giác $ ABCD $ có hai đường chéo $ AC $ và $ BD $ vuông góc với nhau và cắt nhau tại $ M $. Gọi $ P $ là trung điểm của $ AD $. Chứng minh
$$MP\perp BC \Leftrightarrow \overrightarrow{MA}\cdot \overrightarrow{MC}=\overrightarrow{MB}\cdot \overrightarrow{MD}$$

Bài 30. Chứng minh rằng với bốn điểm $ A,B,C,D $ bất kỳ ta có
\[ \overrightarrow{AB}\cdot \overrightarrow{CD}+\overrightarrow{AC}\cdot\overrightarrow{DB}+\overrightarrow{AD}\cdot\overrightarrow{BC}=\vec{0}. \] Từ đó chứng minh ba đường cao của một tam giác đồng quy.

Bài 31. Cho tam giác $ABC$, trên các cạnh $ AB,CD $, ta dựng ra phía ngoài các tam giác $ ABE,ACF $ vuông cân tại $ A $. Gọi $ I $ là trung điểm của $ BC $. Chứng minh rằng $ AI $ vuông góc với $ EF $.

Bài 32. Cho tam giác $ABC$ nội tiếp đường tròn tâm $ O $. Gọi $ BH,CK $ là các đường cao của tam giác. Chứng minh rằng $ OA $ vuông góc với $ HK $.

Bài 33. Cho tam giác $ABC$ cân tại $ A $ với $ O $ là tâm đường tròn ngoại tiếp. Gọi $ D $ là trung điểm của $ AB $ và $ E $ là trọng tâm của tam giác $ ACD $. Chứng minh rằng $ OE $ vuông góc với $ CD $.

Bài 34. Cho tam giác $ABC$ nội tiếp đường tròn tâm $ O $ và một điểm $ H $. Chứng minh rằng $ H $ là trực tâm của tam giác $ ABC $ khi và chỉ khi $ \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{OH} $.

Bài 35. Cho tứ giác lồi $ ABCD $ với $ O $ là giao điểm của hai đường chéo. Gọi $ H,K $ tương ứng là trực tâm của các tam giác $ OAB,OCD $. Gọi $ I,J $ tương ứng là trung điểm của $ BC,DA $. Chứng minh rằng $ HK $ vuông góc với $ IJ $.

Bài 36. Cho tứ giác nội tiếp $ ABCD $ với $ I $ là giao điểm của hai đường chéo. Gọi $ E,F $ lần lượt là trung điểm của $ AB,BC $. Chứng minh rằng $ IE $ vuông góc với $ CD $ khi và chỉ khi $ IF $ vuông góc với $ AD $.

Bài 37. Cho góc vuông $ xSy $ và đường tròn $ (O) $ cắt $ Sx $ tại $ A,B $ và $ Sy $ tại $ C,D $. Chứng minh rằng trung tuyến vẽ từ $ S $ của tam giác $ SAC $ vuông góc với $ BD $.

Bài 38. Cho tam giác không cân $ ABC $. Hỏi tam giác này phải thỏa mãn điều kiện gì để đường thẳng Euler của nó vuông góc với trung tuyến qua $ A $?

Bài 39. Qua trung điểm các cạnh của một tứ giác lồi kẻ các đường thẳng vuông góc với cạnh đối diện. Chứng minh rằng nếu ba trong số các đường đó đồng quy thì cả bốn đường thẳng đồng quy.

Bài 40. Trong mặt phẳng cho $ n $ điểm phân biệt $ A_1,A_2,…,A_n $, và $ n $ số thực khác không $ \lambda_1,\lambda_2,…,\lambda_n $ sao cho $ A_iA_j^2=\lambda_i+\lambda_j $. Chứng minh rằng $ n \leqslant 4 $ và nếu $ n=4 $ thì $ \frac{1}{\lambda_1}+\frac{1}{\lambda_2}+\frac{1}{\lambda_3}+\frac{1}{\lambda_4}=0 $.

Xem thêm Bài tập tích vô hướng của hai vectơ
01/12/2020
Giá trị lượng giác của góc từ 0 đến 180 độ
Toán 10 – Giá trị lượng giác của góc từ 0 đến 180 độ

1. Giá trị lượng giác của một góc từ 0 đến 180⁰

1.1. Nửa đường tròn đơn vị
- Trong mặt phẳng tọa độ $Oxy$, nửa đường tròn đơn vị là nửa đường tròn có tâm $ O(0;0)$, bán kính bằng $ 1$ và đi qua các điểm $ A(1;0), B(0;1), A'(-1;0)$.
1.2. Giá trị lượng giác của một góc từ $0^\circ$ đến $180^\circ$
- Với mỗi góc $0^\circ \leqslant \alpha \leqslant 180^\circ$ thì có đúng một điểm $ M$ trên nửa đường tròn đơn vị sao cho $ \widehat{AOM}=\alpha$. Ngược lại, với mỗi điểm $ M$ trên nửa đường tròn đơn vị thì tồn tại đúng một góc $0^\circ \leqslant \alpha \leqslant 180^\circ$ sao cho $ \widehat{AOM}=\alpha$.
- Giả sử điểm $ M$ có tọa độ $ M(x_0;y_0)$ thì chúng ta định nghĩa:
  - $ \sin \alpha =y_0$;
  - $ \cos \alpha = x_0$;
  - $ \tan \alpha =\frac{y_0}{x_0}=\frac{\sin x}{\cos x}$ nếu $ x_0\ne 0$;
  - $ \cot \alpha =\frac{x_0}{y_0}=\frac{\cos x}{\sin x}$ nếu $ y_0\ne 0$.
Trục hoành – trục nằm ngang – còn được gọi là trục cos, trục tung – trục thẳng đứng – còn được gọi là trục sin.

1.3. Tính chất của giá trị lượng giác
- Nếu $ a+b=180^\circ$ (hai góc bù nhau) thì \begin{align} \sin a =\sin b,\\ \cos a = -\cos b,\\ \tan a =-\tan b, \\ \cot a =-\cot b.\end{align}
- Các hệ thức lượng giác cơ bản:
  - $ \sin^2x+\cos^2x =1$
  - $ \tan x =\frac{\sin x}{\cos x}$
  - $ \cot x =\frac{\cos x}{\sin x}$
  - $ \tan x \cdot \cot x =1$
1.4. Giá trị lượng giác của các góc đặc biệt

2. Bài tập giá trị lượng giác của một góc từ 0° đến 180°

Bài 1. Cho $\cos \alpha=-\frac{2}{3}$. Tính $\sin \alpha;\tan \alpha$ và $\cot \alpha$.

Bài 2. Cho góc $\alpha$ biết $0^\circ < \alpha < 90^\circ $ và $\tan \alpha =3$. Tính $\sin \alpha$ và $\cos \alpha$.

Bài 3. Cho $\sin \alpha =\frac{3}{4}$ với $90^\circ <\alpha < 180^\circ$. Tính $\cos \alpha$ và $\tan \alpha$.

Bài 4. Cho $\cos \alpha=-\frac{\sqrt{2}}{4}$. Tính $\sin \alpha;\tan \alpha$ và $\cot \alpha$.

Bài 5. Cho góc $\alpha$ biết $0^\circ < \alpha < 90^\circ $ và $\tan \alpha = 2\sqrt{2}$. Tính $\sin \alpha$ và $\cos \alpha$.

Bài 6. Biết $\tan \alpha = \sqrt{2}$. Tính giá trị của biểu thức $$A=\frac{3\sin \alpha -\cos \alpha}{2\sin \alpha+\cos \alpha}$$

Bài 7. Biết $\tan \alpha = \sqrt{2}$. Tính giá trị của biểu thức $$T=\frac{\sin \alpha -\cos \alpha}{\sin^3 \alpha+3\cos^3 \alpha+2\sin \alpha}$$

Bài 8. Biết $\sin \alpha = \frac{2}{3}$. Tính giá trị của biểu thức $$B=\frac{\cot \alpha -\tan \alpha}{\cot \alpha+2\tan \alpha}$$

Bài 9. Cho $0^\circ \leqslant \alpha \leqslant 180^\circ$. Chứng minh rằng:
1. $(\sin \alpha +\cos \alpha)^2=1+2\sin \alpha\cos \alpha$.
2. $(\sin \alpha -\cos \alpha)^2=1-2\sin \alpha\cos \alpha$.
3. $\sin^4 \alpha +\cos^4 \alpha=1-2 \sin^2 \alpha\cos^2 \alpha$.
4. $\sin^4 \alpha -\cos^4 \alpha=2\sin^2 \alpha -1$.
5. $\sin^6 \alpha+\cos^6 \alpha = 1-3\sin^2 \alpha\cos^2 \alpha$.
6. $\sin \alpha\cos\alpha (1+\tan \alpha)(1+\cot\alpha)=1+2\sin \alpha\cos \alpha$.
Bài 10. Chứng minh rằng các biểu thức sau đây không phụ thuộc $\alpha$
- $A=(\sin \alpha+\cos \alpha)^2+(\sin \alpha -\cos \alpha)^2$.
- $B=\sin^4 \alpha-\cos^4 \alpha -2\sin^2 \alpha +1$.
Xem thêm Bài tập giá trị lượng giác của góc từ 0 đến 180°
01/12/2020
Giải và biện luận phương trình ax+b=0
Giải và biện luận phương trình ax+b=0

Giải và biện luận phương trình bậc nhất $ax+b=0$ là một dạng toán quan trọng giúp học sinh rèn luyện khả năng lập luận, tư duy logic.

Xem thêm Toán 10 – Biện luận hệ phương trình, hệ bất phương trình bằng đồ thị

1. Giải và biện luận phương trình ax+b=0

Để giải và biện luận phương trình $ax+b=0$, ta xét hai trường hợp:
- Trường hợp 1. Nếu $ a\ne 0$ thì phương trình đã cho là phương trình bậc nhất nên có nghiệm duy nhất $$ x=-\frac{b}{a}.$$
- Trường hợp 2. Nếu $ a = 0$ thì phương trình đã cho trở thành $ 0x+b=0$, lúc này:
  - Nếu $ b=0$ thì phương trình đã cho có tập nghiệm là $ \mathbb{R};$
  - Nếu $ b\ne 0$ thì phương trình đã cho vô nghiệm.
Bảng tóm tắt cách giải và biện luận phương trình $ax+b=0$

Chú ý khi giải và biện luận phương trình bậc nhất:
- Biến đổi để đưa phương trình đã cho về đúng dạng $ax+b=0$ trước khi xét các trường hợp.
- Nếu phương trình đã cho có điều kiện thì cần kiểm tra nghiệm tìm được có thỏa mãn điều kiện hay không rồi mới kết luận.
2. Ví dụ giải và biện luận phương trình ax+b=0

Ví dụ 1. Giải và biện luận phương trình $ mx+2-m=0$.

Chúng ta xét hai trường hợp:
- Trường hợp 1. Nếu $ m=0$, phương trình đã cho trở thành $$ 0x+2=0 $$ Rõ ràng phương trình này vô nghiệm, nên phương trình đã cho vô nghiệm.
- Trường hợp 2. Nếu $ m\ne 0$, phương trình đã cho là phương trình bậc nhất, nên nó có nghiệm duy nhất $ \displaystyle x=\frac{m-2}{m}.$
Vậy, $ m=0$ thì phương trình đã cho vô nghiệm; $ m\ne 0$ thì phương trình đã cho có nghiệm duy nhất.

Ví dụ 2. Giải và biện luận phương trình $ (m-2)x+2-m=0$.

Chúng ta xét hai trường hợp:
- Trường hợp 1. $ m-2=0$ hay $ m=2$ thì phương trình đã cho trở thành $$ 0x+0=0 $$ Rõ ràng phương trình này có tập nghiệm là $ \mathbb{R}$ nên phương trình đã cho cũng có tập nghiệm là $ \mathbb{R}$.
- Trường hợp 2. $ m\ne 2$, phương trình đã cho là phương trình bậc nhất, nên nó có nghiệm duy nhất $ \displaystyle x=\frac{m-2}{m-2}=-1.$
Vậy, $ m=2$ thì phương trình đã cho có tập nghiệm là $ \mathbb{R}$; $ m\ne 2$ thì phương trình đã cho có nghiệm duy nhất $ x=-1$.

Ví dụ 3. Giải và biện luận phương trình $ mx+(2-3m)x+5=0$.

Hướng dẫn. Trước tiên chúng ta biến đổi phương trình đã cho về dạng $ ax+b=0$. Có, phương trình đã cho tương đương với $$ (2-2m)x+5=0 $$ Chúng ta xét hai trường hợp:
- Trường hợp 1. $ 2-2m=0$ hay $ m=1$ thì phương trình đã cho trở thành $$ 0x+5=0 $$ Phương trình này vô nghiệm, nên phương trình đã cho vô nghiệm.
- Trường hợp 2. $ m\ne 1$, phương trình đã cho là phương trình bậc nhất, nên nó có nghiệm duy nhất $ \displaystyle x=\frac{-5}{2-2m}.$
Vậy, $ m=1$ thì phương trình đã cho vô nghiệm; $ m\ne 1$ thì phương trình đã cho có nghiệm duy nhất $ x=\frac{-5}{2-2m}$.

Ví dụ 4. Giải và biện luận phương trình $ \frac{5x-m}{x-1}=0$.

Hướng dẫn. Trước tiên chúng ta tìm điều kiện xác định của phương trình, sau đó biến đổi đưa phương trình về dạng quen thuộc $ ax+b=0.$
- Điều kiện xác định: $ x\ne 1$. Với điều kiện đó, phương trình đã cho tương đương với $$ 5x-m=0 $$
- Phương trình này có nghiệm $ x=\frac{m}{5}$. Tuy nhiên đây chưa phải nghiệm của phương trình đã cho vì cần có điều kiện $ x\ne 1$. Do đó chúng ta xét hai trường hợp:
  - Trường hợp 1. Nếu $ \frac{m}{5}=1$ hay $ m=5$ thì phương trình đã cho vô nghiệm.
  - Trường hợp 2. Nếu $ m\ne 5$ thì phương trình đã cho có nghiệm duy nhất $ x=\frac{m}{5}.$
Tóm lại, $ m=5$ thì phương trình đã cho vô nghiệm; $ m\ne 5$ thì phương trình đã cho có nghiệm duy nhất $ x=\frac{m}{5}.$

Ví dụ 5. Giải và biện luận phương trình $$ \frac{mx+2m}{x-3}=0 $$

Ví dụ 6. Giải và biện luận phương trình $$ \frac{(m+1)x+2m}{x^2-4}=0 $$

Ví dụ 7. Giải và biện luận phương trình $$ \frac{x+2-m}{\sqrt{x-4}}=0 $$

Ví dụ 8. Tìm $m$ để phương trình $ (x-1)(x-3m)=0$ có hai nghiệm phân biệt.

Ví dụ 9. Tìm $m$ để phương trình $ \sqrt{x-3}(x+5-m)=0$ có hai nghiệm phân biệt.

Ví dụ 10. Tìm $m$ để phương trình $ (3-m)x+9-m^3=0$ có tập nghiệm là $ \mathbb{R}$.

Ví dụ 11. Tìm $m$ để phương trình $ (3-m)x+9-m^3=0$ vô nghiệm.

Ví dụ 12. Tìm $m$ để phương trình $ \frac{(3-m)x+3}{x-5}=0$ vô nghiệm.

3. Bài tập giải và biện luận phương trình bậc nhất

Bài 1. Giải và biện luận các phương trình sau theo tham số $m$:
1. $mx = 3$
2. $( m -2) x = m -2$
3. $(2 m -1) x = 5m +3$
4. $( m ^2-1) x =2 m +2$
5. $m ( x -2)=x +1$
6. $( m -1) x =2 x + m -3$
7. $( m +1)( x -2)=3 m -1$
8. $( m -1)( x +1)= m ^{2}-1$
9. $( m -3) x = m ( m -1)-6$
10. $(2 m -3) x = m (2 m -5)+3$
09/11/2020
Phương pháp tìm thiết diện bằng phép chiếu xuyên tâm
Phương pháp tìm thiết diện bằng phép chiếu xuyên tâm

Khi mà học sinh chưa được học về quan hệ song song trong không gian thì bài toán xác định thiết diện của hình chóp khi cắt bởi một mặt phẳng khá hạn chế. Lúc đó, để giải quyết các bài toán mà đáy là hình bình hành, hình thoi, hình chữ nhật… chúng ta phải sử dụng đến phương pháp phép chiếu xuyên tâm (còn được gọi là Phương pháp đường gióng – đường dóng).

Xem thêm:
- Thiết diện là gì và các phương pháp tìm thiết diện
- Xác định thiết diện sử dụng quan hệ vuông góc trong không gian
1. Phép chiếu xuyên tâm là gì?

Phép chiếu xuyên tâm (còn được gọi là phép phối cảnh, tiếng Anh: inner projection) được giới thiệu ngay từ lớp 8, trong chương trình công nghệ – vẽ kỹ thuật.

Trong không gian, cho một điểm S và một mặt phẳng (P) không đi qua S. Quy tắc biến mỗi điểm M trong không gian thành điểm M’ là giao điểm của mặt phẳng (P) và đường thẳng SM được gọi là phép chiếu xuyên tâm (tâm S) xuống mặt phẳng (P).
- Trong phép chiếu này, các điểm M nằm trong mặt phẳng (Q) đi qua S và song song với (P) thì không có ảnh. Trong chương trình vẽ kỹ thuật, để cho mọi điểm trong không gian đều có ảnh, người ta bổ sung cho (P) một đường thẳng ở vô tận, coi như giao của (P) và (Q).
- Nếu ta hạn chế chỉ xét phép chiếu trên một mặt (R) nào đó trong không gian thì phép chiếu xuyên tâm nói trên gọi là phép chiếu xuyên tâm (tâm S) từ mặt (R) xuống mặt phẳng (P).
- Phép chiếu xuyên tâm bảo toàn tỉ số kép.
2. Các ví dụ xác định thiết diện bằng phép chiếu xuyên tâm

Bài toán. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $(\alpha)$.

Phương pháp phép chiếu xuyên tâm (Inner Projection Method)
- Chọn một tam giác trên mặt phẳng $(\alpha)$, gọi là tam giác cơ sở và xác định hình chiếu của tam giác cơ sở đó lên mặt đáy qua phép chiếu xuyên tâm với tâm là đỉnh của hình chóp.
- Xác định các giao điểm của tam giác hình chiếu với các cạnh, đường chéo của đáy.
- Dựa vào quan hệ liên thuộc, tìm các điểm trên mặt phẳng $(\alpha)$ tương ứng với các điểm ở dưới mặt đáy.
Ví dụ 1. Cho hình chóp $S.ABCD$ có $ C’ $ là một điểm trên cạnh $ SC. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABC’). $

Hướng dẫn.
- Rõ ràng vì đáy là một tứ giác bất kỳ, nên có nhiều khả năng kéo dài các cạnh đáy chúng sẽ không thể cắt nhau. Do đó ta không thể sử dụng phương pháp giao tuyến gốc.
- Trong mặt phẳng $(ABC’)$, ta chọn một tam giác làm tam giác cơ sở, chính là tam giác $ABC’$ luôn. Ta tìm ảnh của nó qua phép chiếu xuyên tâm $S$ lên mặt phẳng đáy, chính là tam giác $ABC$.
- Tiếp theo, ta xác định giao điểm của tam giác $ABC$ này với các cạnh và đường chéo của đáy. Ta tìm thấy $ O$ là giao điểm của $AC$ và $BD $.
  Lưu ý rằng, điểm $O$ trên mặt phẳng đáy, mà $ O$ thuộc vào cạnh $ AC$, cạnh $ AC$ lại là ảnh của cạnh $ AC’$ qua phép chiếu. Điều này chứng tỏ phải có một điểm nào đó (tạm đặt tên là $ I$), mà qua phép chiếu thì tạo thành điểm $ O$. Mục đích của ta là đi tìm điểm $ I$ này.
- Trong mặt phẳng $ (SAC) $ giao điểm của $SO$ và $AC’ $ chính là điểm $I$ nói trên. Lúc này, mặt phẳng $ (ABC,)$ xuất hiện một đường thẳng mới là đường thẳng $ BI$, mà đường thẳng này có thể cắt được $ SD.$
- Trong mặt phẳng $ (SBD) $ gọi $ D’$ là giao điểm của $BI$ và $ SD. $
- Dễ dàng chỉ ra thiết diện cần tìm là tứ giác $ ABC’D’. $
Ví dụ 2. Cho hình chóp $S.ABCD$ có ba điểm $ M,N,P $ lần lượt thuộc $ SA,SB,SC. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (MNP). $

Ví dụ 3. Cho hình chóp $S.ABCD$ có $ M $ là một điểm thuộc miền trong tam giác $ SCD. $ Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM). $

Ví dụ 4. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành và $ M $ là trung điểm $ SB. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (AMD). $

Ví dụ 5. Cho hình chóp $S.ABCD$ có $ M $ là một điểm thuộc miền trong tam giác $ SCD. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM). $
Hướng dẫn.
Trong mặt phẳng $ (SCD) $ gọi $ E=SM\cap CD, $ trong mặt phẳng $ (ABCD) $ gọi $ F=AC\cap BE, $ trong mặt phẳng $ (SBE) $ gọi $ I=BM\cap SF, $ trong mặt phẳng $ (SAC) $ gọi $ N=AI\cap SC, $ trong mặt phẳng $ (SCD) $ gọi $ H=MN\cap SD. $ Thiết diện là tứ giác $ ABNH. $

3. Bài tập tìm thiết diện sử dụng phép chiếu xuyên tâm
06/11/2020
Xác định thiết diện bằng phương pháp giao tuyến gốc
Xác định thiết diện bằng phương pháp giao tuyến gốc

Để xác định thiết diện của một hình chóp khi cắt bởi một mặt phẳng, chúng ta có hai phương pháp là phương pháp xác định thiết diện bằng giao tuyến gốc và xác định thiết diện bằng phép chiếu xuyên tâm. Bài viết này xin trình bày chi tiết phương pháp giao tuyến gốc và các ví dụ vận dụng.

1. Phương pháp giao tuyến gốc là gì?

Bài toán. Xác định thiết diện của một hình chóp khi cắt bởi mặt phẳng $(\alpha)$.

Phương pháp giao tuyến gốc (Trace method).
- Xác định giao tuyến $ d $ của mặt phẳng $(\alpha)$ với một mặt $ \mathcal{H} $ của hình chóp (thường là với mặt đáy).
- Tìm các giao điểm của giao tuyến $ d $ với các cạnh, đường chéo của mặt $ \mathcal{H} $.
- Dựa vào các giao điểm này và giao tuyến $ d, $ tìm tiếp các giao tuyến của mặt phẳng $(\alpha)$ với những mặt còn lại của hình chóp.
2. Ví dụ tìm thiết diện bằng phương pháp giao tuyến gốc

Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy không là hình thang. Giả sử $ M $ là một điểm trên $ SD $, xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM).$

Hướng dẫn.
- Rõ ràng rằng giao tuyến của mặt phẳng $ (ABM)$ với mặt đáy $ (ABCD)$ là đường thẳng $AB$, nên chúng ta lựa chọn đường thẳng $AB$ làm giao tuyến gốc.
- Tiếp theo, ta xác định các giao điểm của đường thẳng $AB$ với các cạnh của đáy, nếu không được thì sẽ sử dụng đến giao điểm với đường chéo. Vì tứ giác $ ABCD$ không là hình thang nên kéo dài hai đường thẳng $ AB$ và $ CD$ thì chúng sẽ cắt nhau, giả sử là điểm $ I$.
- Lúc này, đường thẳng $ IM$ nằm trong mặt phẳng $ (SCD)$ nên nó sẽ cắt được đường thẳng $ SC$, giả sử cắt tại điểm $ N$.
- Rõ ràng, mặt phẳng $ (ABM)$ lần lượt cắt các mặt của hình chóp $S.ABCD$ theo các giao tuyến tạo thành một tứ giác là $ AMNB$ nên thiết diện chính là tứ giác $ AMNB.$
Ví dụ 2. Cho tứ diện $ ABCD $ có $ M,N $ là trung điểm của $ AB,CD. $ Giả sử $ P $ là một điểm nằm trên cạnh $ AD $ nhưng không là trung điểm. Xác định thiết diện của mặt phẳng $ (MNP) $ và tứ diện.

Ví dụ 3. Cho tứ diện $ ABCD $ có $ I,J $ lần lượt là trọng tâm các tam giác $ ABC $ và $ ACD. $ Trên cạnh $ AB $ lấy điểm $ K $ sao cho $ AK>BK. $ Xác định thiết diện của tứ diện khi cắt bởi mặt phẳng $ (IJK). $

Ví dụ 4. Cho hình chóp $ S.ABCD $ có điểm $ M $ là trung điểm $ SC,N $ là một điểm trên cạnh $ SD $ sao cho $ SN<DN. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ AMN $.

Ví dụ 5. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ BC,CD $ và $ SA. $ Xác định thiết diện của hình chóp và mặt phẳng $ (MNP) $.

Ví dụ 6. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ CD,BC $ và $ SB. $ Xác định thiết diện của hình chóp và mặt phẳng $ (MNP) $.

Hướng dẫn. Trong mặt phẳng $ (ABCD) $ gọi $ E,F $ lần lượt là giao điểm của $ MN $ với $ AB $ và $ AD. $ Trong mặt phẳng $ (SAB) $ gọi $ Q=PE\cap SA, $ trong mặt phẳng $ (SAD) $ gọi $ R=QF\cap SD. $ Thiết diện là ngũ giác $ MNPQR. $

Ví dụ 7. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $ O. $ Gọi $ M,N $ lần lượt là trung điểm của $ BC,CD. $ Trên đoạn $ SO $ lấy điểm $ P $ sao cho $ SP>OP. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (MNP)$.

Hướng dẫn. Trong mặt phẳng $ (ABCD) $ gọi $ E,F,G $ lần lượt là giao điểm của $ MN $ với $ AB,AD,AC. $ Trong mặt phẳng $ (SAC) $ gọi $ J= GP\cap SA, $ trong $ (SAB) $ gọi $ K=JE\cap SB, $ trong $ (SAD) $ gọi $ I=JF\cap SD. $ Thiết diện là ngũ giác $ MNIJK. $

Ví dụ 8. Cho hình chóp $ S.ABCD $ có $ G $ là trọng tâm tam giác $ SCD $ và $ M $ là trung điểm cạnh $ SD. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (AGM)$.

Ví dụ 9. Cho hình chóp $S.ABCD$ có $ G $ là trọng tâm tam giác $ SCD, H$ là một điểm thuộc cạnh $ SA $ sao cho $ SH>AH. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (CGH). $

Hướng dẫn. Gọi $ M $ là trung điểm $ SD,E=HM\cap AD,K=CE\cap AB. $ Thiết diện là tứ giác $ CMHK. $

Ví dụ 10. Cho hình chóp $S.ABCD$ có $ G $ là trọng tâm tam giác $ SCD, H$ là một điểm thuộc cạnh $ SA $ sao cho $ SH<AH. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (CGH). $

Hướng dẫn. Gọi $ M $ là trung điểm $ SD,E=HM\cap AD,F=CE\cap AB,K=HF\cap SB. $ Thiết diện là tứ giác $ CMHK. $
06/11/2020
Toán 9 – Giải bài toán bằng cách lập hệ phương trình
Giải bài toán bằng cách lập hệ phương trình lớp 9

Giải bài toán bằng cách lập hệ phương trình lớp 9 là một dạng toán quan trọng, thường xuyên xuất hiện trong các đề thi học kì, bài kiểm tra, đề thi tuyển sinh vào lớp 10. Để giải được dạng toán lập hệ phương trình ở lớp 9, học sinh cần nắm được 2 cách giải hệ phương trình bậc nhất là phương pháp cộng đại số và phương pháp thế. Ngoài ra, kỹ năng quan trọng là cách đặt ẩn và biểu thị mối quan hệ giữa các ẩn để có được một hệ phương trình.

1. Phương pháp giải bài toán bằng cách lập hệ phương trình

Cách giải một bài toán bằng cách lập hệ phương trình, chúng ta thực hiện các bước sau:
- Bước 1: Lập hệ phương trình.
  - Biểu diễn hai đại lượng phù hợp bằng ẩn số $x$ và $y$ (thường đặt ẩn số là những đại lượng đề bài yêu cầu cần tìm, ví dụ yêu cầu tính chiều dài và chiều rộng của mảnh vườn thì chúng ta sẽ đặt $x$ là chiều dải mảnh vườn, $y$ là chiều rộng mảnh vườn…). Sau đó, đặt đơn vị và điều kiện của ẩn một cách thích hợp (ví dụ độ dài, thời gian hoàn thành công việc thì không thể là số âm…).
  - Biểu thị các đại lượng chưa biết còn lại qua ẩn.
  - Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng và thành lập hệ hai ẩn từ các phương trình vừa tìm.
- Bước 2: Giải hệ phương trình nói trên.
- Bước 3: Kiểm tra nghiệm tìm được thỏa mãn điều kiện của bài toán và nêu kết luận của bài toán.
2. Các dạng toán giải bài toán bằng cách lập hệ phương trình thường gặp:

Dạng 1: Chuyển động (trên đường bộ, trên đường sông có tính đến dòng nước chảy)

Đối với dạng toán này, cần chú ý đến điều kiện của ẩn:
- Nếu gọi $x$ là vận tốc của chuyển động thì điều kiện là $x>0$.
- Đặt thời gian chuyển động là $y$ thì điều kiện là $y \ge 0$.
- Một số công thức:
  - Quãng đường bằng vận tốc nhân thời gian, s=v.t;
  - Vận tốc khi nước đứng yên = vận tốc riêng;
  - Vận tốc xuôi dòng = vận tốc riêng + vận tốc dòng nước;
  - Vận tốc ngược dòng = vận tốc riêng – vận tốc dòng nước.
- Nếu hai xe đi ngược chiều nhau cùng xuất phát khi gặp nhau lần đầu:
  - Thời gian hai xe đi được là như nhau,
  - Tổng quãng đường 2 xe đi được bằng đúng quãng đường cần đi của 2 xe.
- Cách đổi đơn vị thời gian, vận tốc:
  - 1 h (1 giờ) = 60 phút.
  - 1 (m/s) = 3,6 (km/h), vì 1 m = 1/1000 km và 1 s = 1/3600 giờ.
  - 1 (km/h) = 5/18 (m/s).
Ví dụ 1. Hai thị xã A và B cách nhau 90 km. Một chiếc ô-tô khởi hành từ A và một xe máy khởi hành từ B cùng một lúc ngược chiều nhau. Sau khi gặp nhau ô-tô chạy thêm 30 phút nữa thì đến B, còn xe máy chạy thêm 2 giờ nữa mới đến A. Tìm vận tốc của mỗi xe.

Hướng dẫn. Gọi vận tốc của ô-tô và xe máy lần lượt là $x$ và $y$ (đơn vị km/h, điều kiện $x > 0, y > 0$). Giả sử hai xe gặp nhau tại C. Do ô-tô đi hết quãng đường BC trong 30 phút (bằng 0,5 giờ) và xe máy đi hết quãng đường CA trong 2 giờ nên ta có:
- Quãng đường AC dài $2y$ (km), quãng đường BC dài $0,5x$ (km).
- Thời gian ôtô đi hết quãng đường AC là $\frac{2y}{x}$ (km/h).
- Thời gian xe máy đi trên quãng đường BC là $0,5\frac{x}{y}$ (km/h).
- Do tổng quãng đường AB dài 90km và thời gian hai xe từ lúc xuất phát tới C bằng nhau nên ta có hệ phương trình \[\begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {0,5x + 2y = 90}\\ {\frac{{0,5x}}{y} = \frac{{2y}}{x}} \end{array}} \right.\\ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {0,5x + 2y = 90}\\ {{x^2} = 4{y^2}} \end{array}} \right. \end{array}\] Vì \( x,y>0 \) nên từ phương trình \( {{x^2} = 4{y^2}} \) suy ra $x = 2y$. Thay vào phương trình còn lại của hệ, ta được $$3y = 90 \Leftrightarrow y = 30$$ Suy ra, $x = 60$ (thỏa mãn điều kiện $x, y > 0$).
- Vậy, vận tốc của ôtô là 60km/h và vận tốc của xe máy là 30km/h.
Dạng 2: Toán làm chung – làm riêng (Bài toán vòi nước)

Ví dụ 1. Hai vòi nước cùng chảy đầy một bẻ không có nước trong 3h 45ph . Nếu chảy riêng rẽ , mỗi vòi phải chảy trong bao lâu mới đầy bể? biết rằng vòi chảy sau lâu hơn vòi trước 4 h.

Hướng dẫn.
- Gọi thời gian vòi đầu chảy chảy một mình đầy bể là x (điều kiện x > 0 , x tính bằng giờ)
- Gọi thời gian vòi sau chảy chảy một mình đầy bể là y (điều kiện y > 4 , y tính bằng giờ)
- Suy ra, trong 1 giờ vòi đầu chảy được $\frac{1}{x}$ bể, vòi sau chảy được $\frac{1}{y}$ bể.
- Sau 1 giờ, cả hai vòi chảy được
$\frac{1}{x}+\frac{1}{y}$ bể
- Hai vòi cùng chảy thì đầy bể trong 3h 45ph = 15/4 h, nên trong 1 giờ thì cả hai vòi chảy được
$1 : \frac{15}{4} = \frac{4}{15} $ bể.
- Suy ra, ta có phương trình
$\frac{1}{x}+\frac{1}{y} = \frac{4}{15}$
- Mặt khác, nếu chảy một mình thì vòi sau chảy lâu hơn vòi trước 4 giờ tức là $y – x = 4$ nên ta có hệ phương trình $$\begin{cases} \frac{1}{x}+\frac{1}{y} = \frac{4}{15}\\ y – x = 4 \end{cases}$$
- Giải hệ phương trình này tìm được $x=6,y=10$.
- Vậy, vòi đầu chảy một mình đầy bể trong 6 h; vòi sau chảy một mình đầy bể trong 10 h.
Ví dụ 2. Hai vòi nước cùng chảy vào một cái bể không có nước thì trong 5 giờ sẽ đầy bể. Nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được $\frac{2}{3}$ bể nước. Hỏi nếu mỗi vòi chảy một mình thì trong bao lâu mới đầy bể.

Hướng dẫn.
- Gọi thời gian vòi thứ nhất chảy một mình đầy bể là $x$ (giờ), thời gian vòi thứ hai chảy một mình đầy bể là $y$ (giờ). Điều kiện x, y>5.
- Suy ra, trong 1 giờ vòi đầu chảy được $\frac{1}{x}$ bể, vòi sau chảy được $\frac{1}{y}$ bể. Sau 1 giờ, cả hai vòi chảy được
$\frac{1}{x}+\frac{1}{y}$ bể
- Mà theo đề bài, cả hai vòi nước cùng chảy vào bể không có nước thì trong 5 giờ sẽ đầy bể nên trong một giờ cả hai vòi chảy được $\frac{1}{5}$ bể. Do đó ta có phương trình $$\frac{1}{x}+\frac{1}{y}=\frac{1}{5}$$
- Mặt khác, nếu vòi thứ nhất chảy trong 3 giờ và vòi thứ 2 chảy trong 4 giờ thì được $\frac{2}{3}$ bể nên ta
  có phương trình $$3.\frac{1}{x}+4.\frac{1}{y}=\frac{2}{3}$$
- Do đó, ta có hệ phương trình $$\begin{cases} \frac{1}{x}+\frac{1}{y}=\frac{1}{5}\\ \frac{3}{x}+\frac{4}{y}=\frac{2}{3} \end{cases}.$$
- Giải hệ phương trình này tìm được $x=7,5$ và $y=15$ (thỏa mãn điều kiện).
- Vậy thời gian vòi thứ nhất chảy một mình đầy bể là 7,5 giờ, thời gian vòi thứ hai chảy một mình đầy bể là 15 giờ.
Ví dụ 3. Lớp 9A và lớp 9B cùng lao động tổng vệ sinh sân trường thì sau 6 giờ sẽ hoàn thành xong công việc. Nếu làm riêng thì lớp 9A mất nhiều thời gian hơn lớp 9B là 5 giờ mới hoàn thành xong công việc. Hỏi nếu làm riêng, mỗi lớp cần bao nhiêu thời gian để hoàn thành xong công việc?

Hướng dẫn.
- Gọi thời gian lớp 9A, 9B hoàn thành xong công việc là $x$ (giờ) và $y$ (giờ), điều kiện $x>5,y>0$.
- Trong 1 giờ, lớp 9A làm được: $\frac{1}{x}$ (công việc), lớp 9B làm được $\frac{1}{y}$ (công việc). Nên trong 1 giờ, cả 2 lớp làm được
$\frac{1}{x}+\frac{1}{y}$ công việc.
- Mà theo đề bài, cả hai lớp cùng lao động tổng vệ sinh sân trường thì sau 6 giờ sẽ hoàn thành xong công việc nên ta có phương trình $$\frac{1}{x}+\frac{1}{y}=\frac{1}{6}$$
- Nếu làm riêng thì lớp 9A mất nhiều thời gian hơn lớp 9B là 5 giờ mới hoàn thành xong công việc. Tức là $x-y=5$.
- Do đó, ta có hệ phương trình $$\begin{cases} \frac{1}{x}+\frac{1}{y} = \frac{1}{6}\\ x-y=5 \end{cases}$$
- Giải hệ phương trình này bằng phương pháp thế, tìm được $y=-3$ (loại) hoặc $y=10$ (thỏa mãn). Từ đó tìm được $x=15$.
Dạng 3: Toán liên quan đến tỉ lệ phần trăm.

Chú ý cách tính tỉ lệ phần trăm.

Ví dụ 1. Theo kế hoạch hai tổ sản xuất 600 sản phẩm trong một thời gian nhất định. Do áp dụng kĩ thuật mới nên tổ I đã vượt mức 18% và tổ II đã vượt mức 21%. Vì vậy trong thời gian quy định họ đã hoàn thành vượt mức 120 sản phẩm. Hỏi số sản phẩm
được giao của mỗi tổ theo kế hoạch?

Hướng dẫn.
- Gọi $x,y$ là số sản phẩm của tổ I, II theo kế hoạch, điều kiện x, y nguyên dương và x < 600; y < 600.
- Theo kế hoạch hai tổ sản xuất 600 sản phẩm nên ta có phương trình: $$x+y=600.$$
- Số sản phẩm tăng thêm của tổ I là: $ \frac{18}{100} x$ sản phẩm. Số sản phẩm tăng của tổ II là: $ \frac{18}{100} y$ sản phẩm.
- Do số sản phẩm của hai tổ vượt mức 120 (sản phẩm) nên ta có phương trình $$\frac{18}{100}x + \frac{21}{100}y = 120. $$
- Từ đó ta có hệ phương trình $$\left\{\begin{array}{l} x+y=600 \\ \frac{18}{100} x+\frac{21}{100} y=120 \end{array}\right.$$
- Giải hệ này tìm được $x=200, y=400$ (thỏa mãn điều kiện).
Ví dụ 3. Trong tháng giêng hai tổ sản xuất được 720 chi tiết máy. Trong tháng hai, tổ I vượt mức 15%, tổ II vượt mức 12% nên sản xuất được 819 chi tiết máy. Tính xem trong tháng giêng mỗi tổ sản xuất được bao nhiêu chi tiết máy?

Hướng dẫn.

Ví dụ 4. Năm ngoái tổng số dân của hai tỉnh A và B là 4 triệu người. Dân số tỉnh A năm nay tăng 1,2%, còn tỉnh B tăng 1,1%. Tổng số dân của cả hai tỉnh năm nay là 4 045 000 người. Tính số dân của mỗi tỉnh năm ngoái và năm nay?

Hướng dẫn.

Dạng 4: Toán có nội dung hình học.
- Khi đặt ẩn là độ dài các đoạn thẳng, độ dài các cạnh thì điều kiện của ẩn là không âm.
- Diện tích hình chữ nhật $S = x.y$, với $ x$ là chiều rộng; $y$ là chiều dài.
- Diện tích tam giác $S=\frac{1}{2}a.h_a$ với $a$ là độ dài một cạnh tam giác và $h_a$ là chiều cao ứng với cạnh đó.
- Định lý Pitago trong tam giác vuông với độ dài cạnh huyền là $c$, độ dài hai cạnh góc vuông là $a,b$ thì $$a^2+b^2=c^2.$$
Ví dụ 1. Một mảnh vườn hình chữ nhật có chu vi 34 m. Nếu tăng chiều dài thêm 3 m và tăng chiều rộng thêm 2 m thì diện tích tăng thêm 45m². Hãy tính chiều dài, chiều rộng của mảnh vườn.

Hướng dẫn.
- Gọi chiều rộng và chiều dài của mảnh vườn là lần lượt là $x$ và $y$ (đơn vị m, điều kiện $x > 0, y > 0$).
- Theo đề bài ta có, chu vi hình chữ nhật là: $$2(x + y) = 34$$
- Khi tăng chiều dài thêm 3 m và tăng chiều rộng thêm 2 m thì ta được một hình chữ nhật mới có chiều dài $(y + 3)$ m, chiều rộng $(x +2)$ m nên có diện tích là $(x + 2)(y + 3)$.
- Do hình chữ nhật mới có diện tích tăng thêm 45 m² nên ta có phương trình: $$(x+2)(y+3)= xy + 45 $$ Từ đó, ta có hệ phương trình: \[\left\{ \begin{array}{l} 2\left( {x{\rm{ }} + {\rm{ }}y} \right){\rm{ }} = {\rm{ }}34\\ \left( {x + 2} \right)\left( {y + 3} \right) = {\rm{ }}xy{\rm{ }} + {\rm{ }}45 \end{array} \right.\] Giải hệ phương trình này tìm được $x=5$ và $y=12$.
- Vậy, hình chữ nhật đã cho có chiều dài $12$ m và chiều rộng $5$ m.
Ví dụ 2. Cho một hình chữ nhật. Nếu tăng chiều dài lên 10 m, tăng chiều rộng lên 5 m thì diện tích tăng 500 m². Nếu giảm chiều dài 15 m và giảm chiều rộng 9 m thì diện tích giảm 600 m². Tính chiều dài, chiều rộng ban đầu.

Hướng dẫn.

Ví dụ 3. Cho một tam giác vuông. Nếu tăng các cạnh góc vuông lên 2 cm và 3 cm thì diện tích tam giác tăng 50 cm². Nếu giảm cả hai cạnh đi 2 cm thì diện tích sẽ giảm đi 32 cm². Tính hai cạnh góc vuông.

Hướng dẫn.

Dạng 5: Toán về tìm số.
- - Số có hai, chữ số được ký hiệu là $\overline{ab} $, điều kiện $1 \le q \le 9; 0\le b \le 9; a,b \in \mathbb{N}$.
  - Giá trị của số: $\overline{ab} = 10a+b$.
  - Số có ba, chữ số được ký hiệu là $\overline{abc}$ thì $\overline{abc} = 100a +10b + c$, điều kiện $1 \le q \le 9; 0\le b,c \le 9; a,b,c \in \mathbb{N}$.
  - Tổng hai số $x; y$ là: $x+ y$.
  - Tổng bình phương hai số $x, y$ là: $x^2+y^2$.
  - Bình phương của tổng hai số $x, y$ là: $(x+y)^2$.
  - Tổng nghịch đảo hai số $x, y$ là: $\frac{1}{x}+\frac{1}{y}$.
Ví dụ 1. Cho số tự nhiên có hai chữ số, tổng của chữ số hàng chục và chữ số hàng đơn vị bằng 14. Nếu đổi chữ số hàng chục và chữ số hàng đơn vị cho nhau thì được sốmới lớn hơn số đã cho 18 đơn vị. Tìm số đã cho.

Hướng dẫn.
- Gọi chữ số số cần tìm là $\overline{xy}$, điều kiện $x ,y\in \mathbb{N}, 0 < x \le 9, 0 \le y \le 9$.
- Tổng chữ số hàng chục và chữ số hàng đơn vị bằng 14 nên có phương trình: $$x+y=14.$$
- Đổi chữ số hàng chục và chữ số hàng đơn vị cho nhau thì được số mới lớn hơn số đã cho 18 đơn vị nên có phương trình: $\overline{yx}-\overline{xy}=18$ hay chính là $$10y+x-(10x+y)=18$$
- Do đó, ta có hệ phương trình $$\begin{cases} x+y=14 \\ 10y+x-(10x+y)=18 \end{cases}$$
- Giải hệ này, tìm được $x=6,y=8$ (thỏa mãn điều kiện) nên số cần tìm là $68$.
Ví dụ 2. Tìm một số tự nhiên có hai chữ số. Biết rằng chữ số hàng đơn vị hơn chữ số hàng chục là 5 đơn vị và khi viết chữ số 1 xen vào giữa hai chữ số của số đó thì ta được số mới lớn hơn số đó là 280 đơn vị .

Hướng dẫn.
- Gọi chữ số hàng chục là $a$, chữ số hàng đơn vị là $b$, điều kiện $a,b\in \mathbb{N}; 1\le a\le 9; 0\le b\le 9$.
- Số cần tìm là $\overline{ab}$ có giá trị $\overline{ab}=10a+b$.
- Ta có chữ số hàng đơn vị hơn chữ số hàng chục là 5 đơn vị nên ta có phương trình: $$ b-a=5$$
- Lại có, khi viết chữ số 1 xen vào giữa hai chữ số của số đó thì ta được số mới là $\overline{a1b}$ có giá trị $\overline{a1b}=100a+10+b$.
- Do số mới lớn hơn số ban đầu là 280 đơn vị nên ta có phương trình: $$100a+10+b-(10a+b)=280$$
- Ta có hệ phương trình $$\left\{\begin{array}{l} -a+b=5 \\ (100 a+10+b)-(10 a+b)=280\end{array}\right.$$
- Giải hệ này, tìm được $a=3,b=8$ đều thỏa mãn điều kiện nên số cần tìm là $38$.
Ví dụ 3. Tìm một số tự nhiên có hai chữ số, tổng các chữ số bằng 11, nếu đổi chỗ hai chữ số hàng chục và hàng đơn vị cho nhau thì số đó tăng thêm 27 đơn vị.

Hướng dẫn.

Ví dụ 4. Tìm một số có hai chữ số, biết rằng số đó gấp 7 lần chữ số hàng đơn vị của nó và nếu số cần tìm chia cho tổng các chữ số của nó thì được thương là 4 và số dư là 3.

Hướng dẫn.

3. Bài tập giải bài toán bằng cách lập hệ phương trình

Bài 1. Nếu tử số của một phân số được tăng gấp đôi và mẫu số thêm 8 thì giá trị của phân số bằng $\frac{1}{4}$. Nếu tử số thêm 7 và mẫu số tăng gấp 3 thì giá trị phân số bằng $\frac{5}{24}$. Tìm phân số đó.

Bài 2. Nếu thêm 4 vào tử và mẫu của một phân số thì giá trị của phân số giảm 1. Nếu bớt 1 vào cả tử và mẫu, phân số tăng $\frac{3}{2}$. Tìm phân số đó.

Bài 3: Tìm hai số có tổng bằng $31$ và có hiệu bằng $9$.

Bài 4: Tìm một số tự nhiên có hai chữ số. Biết rằng số đó gấp bảy lần chữ số hàng đơn vị và nếu đem số đó chia cho tổng các chữ số của nó thì được thương là $4$ và dư là $3$.

Bài 5: Một người đi xe đạp từ A đến B gồm đoạn lên dốc AC và đoạn xuống dốc CB. Thời gian đi AB là 4 giờ 20 phút, thời gian về BA là 4 giờ. Biết vận tốc lên dốc là 10 km/h và vận tốc xuống dốc là 15 km/h. Tính AC, CB.

Bài 6: Hai ôtô khởi hành cùng một lúc trên quãng đường từ A đến B dài 120 km. Mỗi giờ ôtô thứ nhất chạy nhanh hơn ôtô thứ hai là 10 km nên đến B trước ôtô thứ hai là 2/5 giờ. Tính vận tốc của mỗi ôtô?

Bài 7: Lúc 7 h, một người đi xe máy khởi hành từ A với vận tốc 40 km/h. Sau đó, lúc 8h30’ một người khác cũng đi xe máy từ A đuổi theo với vận tốc 60 km/h. Hỏi hai người gặp nhau lúc mấy giờ?

Bài 8: Một tàu thủy chạy trên khúc sông dài 80 km, cả đi lẫn về mất 8h20’. Tính vận tốc của tàu thủy khi nước yên lặng, biết rằng vận tốc của dòng nước là 4 km/h.

Bài 9: Hai ca nô cùng khởi hành từ hai bến A và B cách nhau 85 km đi ngược chiều nhau. Sau 1 giờ 40 phút thì gặp nhau. Tính vận tốc riêng của mỗi ca nô, biết rằng vận tốc ca nô đi xuôi lớn hơn vận tốc ca nô đi ngược 9km/h và vận tốc dòng nước là 3 km/h.

Bài 10: Một ca nô xuôi từ bến A đến bến B với vận tốc trung bình 30 km/h, sau đó lại ngược từ B trở về A. Thời gian đi xuôi ít hơn thời gian đi ngược là 40 phút. Tính khoảng cách giữa hai bến A và B, biết rằng vận tốc dòng nước là 3 km/h và vận tốc riêng của ca nô không đổi.

Bài 11: Một canô chạy trên sông trong 8 giờ, xuôi dòng 81km và ngược dòng 105km. Một lần khác cũng trên dòng sông đó, canô này chạy trong 4 giờ,xuôi dòng 54km và ngược dòng 42km. Hãy tính vận tốc khi xuôi dòng và vận tốc khi ngược dòng của ca nô, biết vận tốc dòng nước và vận tốc riêng của ca nô không đổi.

Bài 12: Một ô tô dự định đi từ A đến B trong một thời gian đã định. Nếu ô tô tằng vận tốc thêm 3km/h thì đến B sớm hơn 2 giờ. Nếu ô tô giảm vận tốc đi 3km/h thì sẽ đến B chậm hơn 3 giờ. Tính quãng đường AB.

Bài 13: Để hoàn thành một công việc, hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ hai được điều đi làm việc khác, tổ một đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ làm xong công việc đó?

Bài 14: Theo kế hoạch hai tổ sản xuất 600 sản phẩm. Do áp dụng kĩ thuật mới nên tổ I đã vượt mức 18% và tổ II đã vượt mức 21%. Vì vậy trong thời gian quy định họ đã hoàn thành vượt mức 120 sản phẩm. Hỏi số sản phẩm được giao của mỗi tổ theo kế hoạch?

Bài 15: Hai đội công nhân cùng làm chung một công việc. Thời gian để đội I làm một mình xong công việc ít hơn thời gian đội II làm một mình xong công việc đó là 4 giờ. Tổng thời gian này gấp 4,5 lần thời gian hai đội cùng làm chung để xong công việc đó. Hỏi mỗi đội nếu làm một mình thì phải bao lâu mới làm xong công việc?

Bài 16: Một khu vườn hình chữ nhật có chiều dài bằng 7/4 chiều rộng và có diện tích bằng 1792m2. Tính chu vi của khu vườn ấy.

Bài 17: Có hai loại dung dịch chứa cùng một thứ axit, loại thứ nhất chứa 30% axit, loại thứ hai chứa 5% axit. Muốn có 50 lit dung dịch chứa 10% axit thì cần phải trộn lẫn bao nhiêu lít dung dịch của mỗi loại?

Bài 18: Giải hệ phương trình $$\left\{ \begin{array}{l} \left( {3x – 1} \right)\left( {2y + 3} \right) = \left( {2x – 1} \right)\left( {3y + 4} \right)\\ {x^2} – {y^2} = 2x – 5 \end{array} \right.$$

Bài 19: Giải phương trình: $\left| {x + 1} \right| + 2\left| {x – 1} \right| = x + 2 + \left| x \right| + 2\left| {x – 2} \right|$.

Bài 20: Với giá trị nào của $k$, hệ phương trình sau có nghiệm $$\left\{ \begin{array}{l} x + \left( {1 + k} \right)y = 0\\ \left( {1 – k} \right)x + ky = 1 + k \end{array} \right.$$
02/11/2020
Cách chứng minh đường thẳng song song với mặt phẳng
Phương pháp chứng minh đường thẳng song song với mặt phẳng

Thành thạo cách chứng minh đường thẳng song song với mặt phẳng sẽ giúp các em học sinh có thể chứng minh được hai mặt phẳng song song với nhau.

Xem thêm 3 cách chứng minh hai mặt phẳng song song

1. Vị trí tương đối của đường thẳng và mặt phẳng

Trong không gian, xét một đường thẳng $d$ và mặt phẳng $(\alpha)$ thì có ba khả năng về vị trí giữa chúng:
- Đường thẳng $d$ cắt $ (\alpha) $: có một điểm chung.
- Đường thẳng $d$ nằm trên $ (\alpha) $: có vô số điểm chung.
- Đường thẳng $ d $ song song $ (\alpha) $: không có điểm chung.
Định nghĩa đường thẳng và mặt phẳng song song.

Đường thẳng và mặt phẳng được gọi là song song nếu chúng không có điểm chung.

Tính chất của đường thẳng và mặt phẳng song song.
- Nếu một đường thẳng không nằm trên mặt phẳng mà song song với một đường thẳng của mặt phẳng đó thì đường thẳng đã cho song song với mặt phẳng đó. $$ \begin{cases} d\not\subset (\alpha)\\ d\parallel a\\ a\subset (\alpha) \end{cases} \Rightarrow d \parallel (\alpha)$$
- Nếu mặt phẳng $(\alpha)$ chứa đường thẳng $d$ mà $ d\parallel(\beta) $ thì giao tuyến của hai mặt phẳng $(\alpha)$ và $ (\beta) $ cũng song song với đường thẳng $ d. $ $$ \begin{cases} d \subset (\alpha)\\ d \parallel (\beta)\\ b=(\alpha) \cap (\beta) \end{cases} \Rightarrow d \parallel b$$
  Đặc biệt, nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó. $$ \begin{cases} (P) \parallel a\\ (Q) \parallel a\\ \Delta=(P) \cap (Q) \end{cases} \Rightarrow a \parallel \Delta$$
- Cho hai đường thẳng chéo nhau thì có duy nhất mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
2. Phương pháp chứng minh đường thẳng song song với mặt phẳng

Để chứng minh đường thẳng song song với mặt phẳng ta chứng minh đường thẳng đó không nằm trên mặt phẳng đã cho và song song với một đường thẳng của mặt phẳng đó.

3. Ví dụ cách đường thẳng song song với mặt phẳng

Ví dụ 1. Cho hình chóp $S.ABCD$ có $ M,N $ lần lượt là trung điểm của $ SA$ và $SB. $ Chứng minh rằng $ MN\parallel(ABCD). $

Hướng dẫn. Vì $ MN $ là đường trung bình trong tam giác $ SAB $ nên $ MN\parallel AB. $ Như vậy ta có \[ \begin{cases}
MN\not\subset (ABCD)\\ MN\parallel AB\subset (ABCD) \end{cases} \] Suy ra $ MN\parallel(ABCD). $

Ví dụ 2. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành. Gọi $ M,N $ lần lượt là trung điểm của $ AB,CD $. Chứng minh rằng $ MN\parallel(SBC),MN\parallel(SAD). $ Gọi $ P $ là trung điểm $ SA, $ chứng minh rằng $ SB,SC $ cùng song song với mặt phẳng $ (MNP). $ Gọi $ G_1,G_2 $ lần lượt là trọng tâm tam giác $ ABC $ và $ SBC. $ Chứng minh rằng $ G_1G_2\parallel(SAB).$

Hướng dẫn. Gọi $ O $ là tâm hình bình hành thì $ SC\parallel PO. $ Gọi $ I $ là trung điểm $ BC $ và xét tam giác $ SAI $ có $ G_1G_2\parallel SA. $

Ví dụ 3. Cho tứ diện $ABCD$ có $ G $ là trọng tâm tam giác $ ABD. $ Lấy điểm $ M $ thuộc cạnh $ BC $ sao cho $ MB=2MC. $ Chứng minh rằng $ MG\parallel (ACD) $.

Hướng dẫn. Kéo dài $ BG $ cắt $ AD $ tại $ E $ thì $ (BMG)\cap(ACD)=CE. $ Đi chứng minh $ MG\parallel CE $ và suy ra điều phải chứng minh.

Ví dụ 4. Cho hai hình bình hành $ ABCD $ và $ ABEF $ không đồng phẳng. Chứng minh rằng bốn điểm $ C, D, E, F $ đồng phẳng. Gọi $ O, I $ là tâm các hình bình hành $ ABCD, ABEF $. Chứng minh rằng $ OI\parallel (BCE), OI \parallel (ADF). $ Gọi $ M, N $ lần lượt là trọng tâm tam giác $ ABD, ABF $. Chứng minh rằng $ MN\parallel (CDFE) $.

Hướng dẫn. Chỉ ra $ MN\parallel DF $ nên….

Ví dụ 5. Hai hình bình hành $ ABCD,ABEF $ có chung cạnh $ AB $ và không đồng phẳng. Trên các cạnh $ AD, BE $ lần lượt lấy các điểm $ M, N $ sao cho $\frac{AM}{AD}=\frac{BN}{BE}$. Chứng minh đường thẳng $ MN $ song song với mặt phẳng $ (CDFE) $.

Hướng dẫn. Trên $ CE $ lấy điểm $ P $ sao cho $ \frac{CP}{CE}=\frac{BN}{BE} $. Chứng minh tứ giác $ DMNP $ là hình bình hành. Từ đó suy ra $ MN\parallel DP $ và có điều phải chứng minh.

Ví dụ 6. Cho hình chóp $ S.ABCD $ có $ ABCD $ là hình bình hành, $ G $ là trọng tâm của tam giác $ SAB $ và $ E $ là điểm trên cạnh $ AD $ sao cho $ DE = 2EA $. Chứng minh rằng $ GE\parallel(SCD)$.

Hướng dẫn. Gọi $ H $ là trọng tâm tam giác $ SCD $ thì chứng minh được $ GE\parallel HD. $

4. Bài tập chứng minh đường thẳng song song với mặt phẳng

Bài 1. Cho hình chóp $S.ABCD$ đáy là hình bình hành. Gọi $M, N, P$ lần lượt là trung điểm $AB, CD, SA.$ Chứng minh: $MN \parallel (SBC); MN \parallel (SAD)$; $SB \parallel (MNP); SC \parallel (MNP)$. Gọi $I, J$ là trọng tâm tam giác $ ACD,SCD $. Chứng minh: $IJ \parallel (SAB), IJ \parallel (SAD), IJ \parallel (SAC).$

Bài 2. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O.$ Gọi $I, J$ là trung điểm $BC, SC$ và $ K\in SD$ sao cho $KD=2SK.$ Chứng minh: $OJ \parallel (SAD), OJ \parallel (SAB) $; $IO \parallel (SCD), IJ \parallel (SBD)$. Gọi $M$ là giao điểm của $AI$ và $BD$. Chứng minh: $MK \parallel (SBC)$.

Bài 3. Cho hình chóp $S.ABCD$ có đáy là hình thoi tâm $O$ và $M, N, P$ là trung điểm $SB, SO, OD.$ Chứng minh: $MN \parallel (ABCD), MO \parallel (SCD)$; $NP \parallel (SAD),$ tứ giác $ NPOM$ là hình gì? Gọi $I\in SD$ sao cho $SD = 4ID$. Chứng minh $PI \parallel (SBC), PI \parallel (SAB)$.
01/11/2020
3 cách chứng minh hai mặt phẳng song song
3 cách chứng minh hai mặt phẳng song song trong không gian

Để biết cách chứng minh hai mặt phẳng song song, chúng ta cần phải xem thế nào là hai mặt phẳng song song, và từ đó sẽ có các phương pháp chứng minh 2 mặt phẳng song song trong không gian.

1. Thế nào là hai mặt phẳng song song?

1.1. Vị trí tương đối của hai mặt phẳng.

Trong không gian, cho hai mặt phẳng $(\alpha)$ và $ (\beta) $ thì có ba khả năng về vị trí của chúng:
- Mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $ trùng nhau. Khi đó, hai mặt phẳng có vô số điểm chung.
- Mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $ cắt nhau theo giao tuyến là một đường thẳng. Khi đó, hai mặt phẳng có vô số điểm chung.
- Mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $ song song. Khi đó, hai mặt phẳng không có điểm chung.
Từ đó, người ta định nghĩa hai mặt phẳng song song như sau:

Hai mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung

1.2. Định lý về hai mặt phẳng song song
- Nếu một mặt phẳng chứa hai đường thẳng cắt nhau mà cả hai đường thẳng này song song với mặt phẳng còn lại thì hai mặt phẳng đó song song với nhau.
Xem thêm: Cách chứng minh đường thẳng song song với mặt phẳng.
- Nếu một mặt phẳng chứa hai đường thẳng cắt nhau mà hai đường thẳng này lần lượt song song với hai đường thẳng của mặt phẳng còn lại thì hai mặt phẳng đó song song với nhau.
1.3. Tính chất hai mặt phẳng song song
- Cho hai mặt phẳng song song, mọi đường thẳng nằm trên mặt phẳng thứ nhất đều song song với mặt phẳng thứ hai.
- Hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau.
- Hai mặt phẳng song song bị cắt bởi mặt phẳng thứ ba thì hai giao tuyến song song với nhau.
- Định lý Thales trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
1.4. Hình lăng trụ, hình chóp cụt
- Hình lăng trụ là hình gồm có hai đáy là hai đa giác bằng nhau đồng thời nằm trên hai mặt phẳng song song và các mặt bên là các hình bình hành.
- Hình lăng trụ có đáy là hình bình hành thì gọi là hình hộp. Như vậy, hình hộp là hình có tất cả các mặt đều là hình bình hành.
- Cắt hình chóp bởi một mặt phẳng song song với đáy thu được một hình chóp mới và một hình chóp cụt.
2. Cách chứng minh hai mặt phẳng song song

Phương pháp chứng minh hai mặt phẳng song song: Để chứng minh hai mặt phẳng song song chúng ta có thể sử dụng một trong ba cách:
- Chỉ ra trong mặt phẳng thứ nhất chứa hai đường thẳng cắt nhau, mà hai đường thẳng này lần lượt song song với mặt phẳng thứ hai.
- Chỉ ra trong mặt phẳng thứ nhất chứa hai đường thẳng cắt nhau, mà hai đường thẳng này lần lượt song song với hai đường thẳng của mặt phẳng thứ hai.
- Chứng minh chúng cùng song song với một mặt phẳng thứ ba.
3. Ví dụ về cách chứng minh hai mặt phẳng song song

Ví dụ 1. Cho hai hình bình hành $ ABCD $ và $ ABEF $ nằm trong hai mặt phẳng khác nhau.
1. Chứng minh rằng $ (ADF)\parallel(BCE) $;
2. Gọi $ I,J,K $ là trung điểm của các cạnh $ AB,CD,EF $. Chứng minh rằng $ (DIK)\parallel(JBE) $.
Ví dụ 2. Cho tứ diện $ ABCD $ có $ M,N,P $ lần lượt là trọng tâm của các tam giác $ ABC, ABD, ACD $. Chứng minh rằng $ (MNP)\parallel(BCD) $.

Ví dụ 3. Cho hình bình hành $ ABCD.$ Từ $ A $ và $ C $ kẻ hai tia $ Ax $ và $ Cy $ song song, cùng chiều và không nằm trong mặt phẳng $ (ABCD). $ Chứng minh mặt phẳng $ (BAx)\parallel (DCy). $

Ví dụ 4. Cho hình chóp $ S.ABCD $ với $ ABCD $ là hình bình hành. Gọi $ I $ là trung điểm của $ SD. $
1. Xác định giao điểm $K$ của $BI $ và $(SAC)$.
2. Trên $ IC $ lấy điểm $ H $ sao cho $ HC=2HI $. Chứng minh $ KH\parallel(SAD)$.
3. Gọi $ N $ là điểm trên $ SI $ sao cho $ SN=2NI $. Chứng minh $ (KHN)\parallel(SBC) $.
4. Dựng thiết diện của hình chóp với mặt phẳng $ (KHN). $
Hướng dẫn. Chỉ ra $ K $ là trọng tâm tam giác $ SBD. $

Ví dụ 5. Cho lăng trụ tam giác $ ABC.A’B’C’ $ có $ I ,K ,G $ lần lượt là trọng tâm của các tam giác $ ABC, A’B’C’ $ và $ ACC’ $. Chứng minh rằng: $ (IKG) \parallel (BB’C’C), (A’KG)\parallel(AIB’) $.

Hướng dẫn. Gọi $ M,N $ lần lượt là trung điểm của $ BC $ và $ B’C’ $ thì mặt phẳng $ (A’KG) $ chính là mặt phẳng $ (A’CN) $, còn mặt phẳng $ (AIB’) $ chính là mặt phẳng $ (AMB’). $ Hai mặt phẳng này song song vì có $ AM\parallel A’N $ và $ B’M\parallel CN. $

4. Bài tập chứng minh 2 mặt phẳng song song

Bài 1. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O$. Gọi $M, N, P, Q$ là trung điểm $SA, SD, AB, ON.$ Chứng minh: $(OMN) \parallel (SBC)$. Chứng minh: $PQ \parallel (SBC)$.

Bài 2. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O$. Gọi $M, N, P$ là trung điểm $SA, CD, AD.$ Chứng minh $(OMN) \parallel (SBC)$. Gọi $I$ là điểm trên $MP$. Chứng minh: $OI \parallel (SCD)$.

Bài 3. Cho hình chóp $S.ABCD$, đáy là hình bình hành. Gọi $M, N, P, Q$ là trung điểm $BC, AB, SB, AD.$ Chứng minh $(MNP) \parallel (SAC)$, $PQ \parallel (SCD)$. Gọi $I$ là giao điểm $AM$ và $BD, JSA$ sao cho $AJ = 2JS$, chứng minh $IJ \parallel (SBC)$. Gọi $K$ là một điểm trên $AC$, tìm giao tuyến $(SKM)$ và $(MNC)$.

Bài 4. Cho hình chóp $S.ABCD$ đáy là hình bình hành. Gọi $I, J, G, P, Q$ là trung điểm $DC, AB, SB, BG, BI.$ Chứng minh $(IJG) \parallel (SAD)$, $PQ \parallel (SAD)$. Tìm giao tuyến của $(SAC)$ và $(IJG)$; $(ACG)$ và $(SAD)$.

Bài 5. Cho hai hình bình hành $ABCD$ và $ABEF$ không đồng phẳng. Gọi $I, J, K$ là trung điểm $AB, CD, EF.$ Chứng minh $(ADF) \parallel (BCE)$; $(DIK) \parallel (JBE)$.
31/10/2020