100 ĐỀ THI HỌC SINH GIỎI TIN HỌC – ĐỀ THI TIN HỌC TRẺ
Bài 1: Viết chương trình nhập vào tọa độ tâm I(a;b) và bán kính r của một đường tròn (a, b, r là các số nguyên). Sau đó nhập vào một điểm A(x, y) bất kì và kiểm tra xem nó có thuộc đường tròn hay không?
Bài 2: Viết chương trình tính tích xy (với x, y là hai số thực có độ lớn tùy ý).
Bài 3: Tìm tất cả các chữ số có ba chữ số, sao cho tổng các lập phương của các chữ số thì bằng chính số đó.
Bài 4: Nhập 3 loại tiền và số tiền cần đổi. Hãy tìm tất cả các tổ hợp có được của 3 loại tiền trên cho số tiền vừa nhập.
Bài 5: Viết chương trình giải bài toán cổ sau:
Trăm trâu trăm cỏ
Trâu đứng ăn năm
Trâu nằm ăn ba
Trâu già ba con một bó.
Hỏi có bao nhiêu con mỗi loại?
Bài 6: Lập tam giác PASCAL, dùng chương trình con.
Bài 7: Viết các chương trình con tính diện tích tam giác, tròn, vuông, chữ nhật trong một chương trình. Sau đó hỏi chọn một trong các phương án tính diện tích bằng cách chọn trong bảng chọn lệnh sau:
- Không làm gì hết và trở về màn hình soạn thảo.
- Tính diện tích hình vuông
- Tính diện tích hình tròn
- Tính diện tích tam giác
- Tính diện tích hình chữ nhật
Bài 8: Viết chương trình nhập vào một dãy số nguyên có n phần tử. In ra màn hình phần tử nhỏ nhất, phần tử lớn nhất và giá trị trung bình của danh sách ra màn hình.
Bài 9: Viết chương trình nhập vào một dãy số nguyên có n phần tử.
- Đưa những phần tử lẻ ra đầu danh sách, những phần tử chẵn về cuối danh sách và in kết quả ra màn hình.
- Sắp xếp các phần tử lẻ đầu danh sách theo thứ tứ tăng dần, sắp xếp các phần tử chẵn cuối danh sách theo thứ tự giảm dần. In danh sách ra màn hình.
Bài 10: Viết chương trình nhập vào một chuỗi kí tự, sau đó nhập vào một kí tự bất kì và đếm số lần của nó trong chuỗi đã nhập.
Bài 11: Viết chương trình nhập vào một chuỗi ký tự. Kiểm tra xem nó có đối xứng hay không (Ví dụ: Chuỗi đối xứng RADAR, MADAM).
Bài 12: Viết chương trình nhập vào họ tên của một người. Sau đó in chuỗi họ tên ra màn hình với các ký tự đầu đổi thành chữ hoa, toàn bộ chuỗi họ và tên đổi thành chữ hoa.
Bài 13: Viết chương trình nhập vào một dãy số nguyên có n phần tử.
- Sắp xếp dãy theo thứ tự tăng dần và in kết quả ra màn hình.
- Nhập vào một số
x bất kì, đếm số lần xuất hiện của nó trong dãy trên.
- In ra màn hình số phần tử nhỏ hơn hoặc bằng
x.
- In ra màn hình số phần tử lớn hơn
x.
Bài 14: Sử dụng lệnh lặp để tính tổng của 11 số hạng đầu tiên
S = 100 + 105 + 110 +...
Bài 15: Tìm số P, biết rằng
P/4 = 1 - 1/3 + 1/5 - 1/7 +...
Với độ chính xác: |1/2n-1| < 10^-5
Bài 16: Cho một dãy số nguyên A(i) với i=1,...N. Viết chương trình:
- Tính và in ra trung bình cộng cuả các số dương trong dãy.
- Đếm xem có bao nhiêu số chia hết cho
3.
- In ra vị trí các số bằng
0 (nếu có) trong dãy đã cho.
Bài 17: Viết chương trình tìm các số có 3 chữ số mà tổng lập phương các chữ số của nó bằng chính nó (các số Amstrong).
Bài 18: Nhập một số thực x rồi tính
S = 1 + x/1! + x^2/2! + x^3/3! +...+ x^n/n!
với độ chính xác | x^n/n! | < 10^-5.
Bài 19: Dãy Fibonaxi được định nghĩa như sau:
A1=A2=1, An=A(n-1) + A(n-2) với n>=2.
Hãy:
- Nhập một số
n và in ra n số Fibonaxi đầu tiên.
- Nhập một số
n và in ra các số Fibonaxi nhỏ hơn hoặc bằng n.
Bài 20: Cho một dãy số. Viết chương trình:
- Gom tất cả các số chia hết cho
7 về đầu dãy và tất cả các số chia hết cho 5 vể cuối dãy.
- Sắp xếp phần số đã gom theo thứ tự tăng dần.
Bài 21: Cho một dãy số. Hãy viết chương trình Tìm phần tử nhỏ nhất và phần tử nhỏ thứ hai. Hãy cho biết vị trí đầu tiên của phần tử lớn nhất.
Bài 22: Cho một dãy ký tự. Hãy viết chương trình tách dãy trên thành hai nửa, nửa đầu gồm các số, nửa sau là các chữ cái. Sắp xếp nửa đầu giảm dần, nửa sau tăng dần.
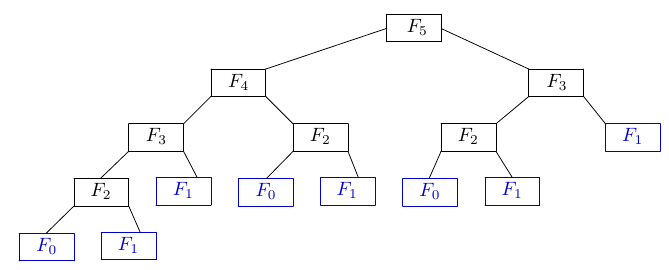
Bài 23: Xét dãy các xâu F1, F2,... Fn trong đó:
F1 = 'A'; F2 = 'B'; Fk+1 = Fk + F(k-1) với k=>2
Ví dụ:
F1 = 'A'
F2 = 'B'
F3 = 'BA'
F4 = 'BAB'
F5 = 'BABBA'
F6 = 'BABBABAB'...
Cho xâu S độ dài không quá 25, chỉ bao gồm các kí tự 'A' và 'B'. Yêu cầu:
- Hãy xác định số lần xuất hiện xâu
S trong xâu Fn, n<=35. Chú ý: Hai lần xuất hiện của S trong Fn không nhất thiết phải là các xâu rời nhau hoàn toàn.
- Dữ liệu vào: Đọc từ file văn bản FIBISTR.INP có cấu trúc như sau: Gồm nhiều dòng, mỗi dòng gồm
n và S. Giữa n và S có đúng 1 dấu cách. Dữ liệu vào là chuẩn, không cần kiểm tra.
- Dữ liệu ra: Ghi ra file văn bản FIBISTR.OUT có cấu trúc như sau: Gồm nhiều dòng, mỗi dòng dữ liệu ứng với một dòng kết quả ra.
Bài 24: SỐ PHẢN NGUYÊN TỐ. Một số tự nhiên n được gọi là số phản nguyên tố nếu nó có nhiều ước số nhất trong n số tự nhiên đầu tiên.
Yêu cầu: Cho số K không vượt quá 10000. Ghi ra số phản nguyên tố lớn nhất nhỏ hơn hoặc bằng K.
Dữ liệu vào: Đọc từ file văn bản OPNT.INP có cấu trúc như sau:
- Dòng đầu tiên là số
M (1<M<=100) là số lượng các số cần tìm số phản nguyên tố lớn nhất của nó.
- M dòng tiếp theo là các số K1,K2,..KM
Dữ liệu ra: Ghi ra file văn bản SOPNT.OUT có cấu trúc như sau:
- Gồm
M dòng.
- Dòng thứ
i (1<=i<=M) là số phản nguyên tố lớn nhất nhỏ hơn hoặc bằng Ki.
Bài 25: Ngồi nhà quá rỗi, Sơn có ý tưởng dùng các que diêm tạo thành các số hập phân. Một cách đại diện cho 10 chữ số thập phân như sau:

Cho N que diêm, Sơn có thể tạo ra một loạt các chữ số. Sơn kinh gạc phát hiện ra số nhỏ nhất và lớn nhất trong số đó có thể tạo được bằng cách sử dụng tất cả các que diêm của Sơn.
Yêu cầu: Xác định số nhỏ nhất và lớn nhất mà Sơn có thể tạo ra.
Dữ liệu vào: Đọc từ file văn bản MATCH.INP có cấu trúc như sau:
- Dòng đầu tiên là số test K (1<K<=100)
- K dòng tiếp theo, mỗi test gồm một dòng chứa số nguyên n (2<=n<=100) là số que diêm
Bài 26: Dãy số được gọi là dãy số đối xứng nếu đọc các phần tử của dãy số này từ trái sang phải hay đọc ngược lại đều được cùng kết quả. Ví dụ: 1, 2, 1 hoặc 1, 2, 2, 1 là các dãy số đối xứng.
Dãy số P được gọi là dãy số con của dãy số A nếu các phần tử thuộc P có mặt liên tiếp trong dãy số A với thứ tự không đổi. Ví dụ: 2, 1, 3 là dãy số con của 1, 2, 2, 1, 3.
Cho dãy số tự nhiên A gồm n phần tử a1, a2, a3…an (ai <35000, 5<n<100)
Yêu cầu: Hãy viết phương trình tìm dãy số P là dãy số con đối xứng dài nhất của dãy số A.
Dữ liệu vào: Nhập vào số tự nhiên n và n phần tử của dãy số A.
Kết quả: Xuất ra màn hình kết quả vừa tìm được
Ví dụ:
Dữ liệu vào: (nhập từ bàn phím)
N=5 1 2 2 1
Kết quả: (xuất ra màn hình)
A: 1 2 2 1 2
Bài 27: Xâu s1 có độ dài m và s2 có độ dài n ( m,n là hai số tự nhiên; n,m<250). Biết rằng s1,s2 chỉ chứa các kí tự ‘A’…’Z’.
Yêu cầu: Hãy viết phương trình tìm xâu con chung dài nhất của xâu s1 và s2.
Dữ liệu vào: Nhập từ bàn phím 2 xâu s1 và s2.
Kết quả: Xuất ra màn hình xâu con chung của 2 xâ s1 và s2.
Ví dụ:
Dữ liệu vào: kết quả: ABBA
S1:ABBABC
S2:ABABBA
Bài 28: Cho xâu S có độ dài N (N<100). Xâu S chỉ chứa các k tự số ‘0’…’9’.
Yêu cầu: Hãy viết chương trình tìm xâu S1 bằng cách hoán vị các k tự số trong xâu S sao cho xâu S1 có giá trị nhỏ nhất lớn hơn S.
Đữ liệu vào: Cho trong tệp tin so.inp, gồm 1 dòng ghi xâu S.
Kết quả: Ghi trong tập tin so.out, gồm 1 dòng ghi kết quả vừa tìm được.
Ví dụ:
Dữ liệu vào: (So.inp) Kết quả: (so.out)
‘1234’ ‘1324’
Bài 29: Viết chương tìm ước số chung lớn nhất của hai số nguyên a và b khác 0, với a, b được nhập từ bàn phím.
Bài 30: Viết chương trình nhập vào một mảng gồm n phần tử (n<=100). Kiểm tra và in ra màn hình các số là số nguyên tố sắp xếp theo thứ tự tăng dần.
Bài 31: Cho số tự nhiên N (N<=50). Hãy viết chương trình thực hiện:
- Nhập số N, sau đó nhập N số nguyên từ bàn phím. thứ tự của các số gọi là chỉ số.
- Hãy tính trong dãy số trên có bào nhiêu số dương chẵn.
- Tìm (các) chỉ số của giá trị âm lớn nhất của dãy số nếu có.
- Tìm tất cả các dãy con dài nhất các số khác không cùng dấu.
Bài 32: Nhập vào từ bàn phím một số N nguyên dương (N<=5000).
- Hãy phân tích N thành tổng của hai số nguyên tố (nếu được) và thông báo không được nếu không có phương án nào.
- Nếu N thoả mãn câu a, hãy đưa càng nhiều càng tốt các phương án phân tích (2 phương án có cùng các số hạng chỉ coi là một)
Bài 33: Cho trước một dãy số bao gồm toàn các số 0 và 1. Dãy này có độ dài nhỏ hơn 255.
- Viết chương trình nhập dãy số trên từ bàn phím. Các số được nhập liên tiếp từ bàn phím, quá trình nhập dữ liệu kết thúc nhấn phím <Enter>. Nếu việc nhập dữ liệu sai trên màn hình kết quả “Bạn đã nhập sai, đề nghị nhập lại” và cho phép nhập lại ngay dữ liệu.
- Một dãy con đúng của dãy trên được gọi là một dãy con liên tục bất kỳ của dãy trên bao gồm các số hạng giống nhau. Hãy tính độ dài lớn nhất của một dãy con đúng của dãy trên.
- Một dãy con đúng bậc 1 của dãy trên được coi là một dãy con liên tục bất kỳ của dãy trên bao gồm toàn các số hạng giống nhau ngoại trừ 1 phần tử. Hãy tính độ dài lớn nhất của một dãy con đúng bậc 1 của dãy trên.
Bài 34: Cho số nguyên N trong phạm vi từ 1000 đến 999999. Cần xác định số này có phải là thông tin về một ngày tháng có trong thế kỷ 21 không. (Thế kỷ 21 bắt đầu từ 1 tháng 1 năm 2001 và kết thúc vào ngày 31 tháng 12 năm 3000. Biết rằng 2 chữ số cuối của N là chỉ hai chữ số cuối của năm, các chữ số còn lại (ở đầu) xác định ngày và tháng.
Ví dụ:
1111 tương ứng với 1 tháng 1 năm 2011;
21290 tương ứng với 2 tháng 12 năm 2090 hoặc 21 tháng 2 năm 2090;
131192 tương ứng với 13 tháng 11 năm 2092;
32392 Không phải là thông tin về một ngày tháng nào cả;
311198 Không phải là thông tin về một ngày tháng nào cả;
29205 Không phải là thông tin về một ngày tháng nào cả;
Dữ liệu: Nhập vào số N từ bàn phím.
Kết quả: Đưa ra màn hình các ngày tháng năm tương ứng với N hoặc thông báo là KHONG nếu N không phải là thông tin về một ngày tháng nào cả.
Ví dụ:
| Giá trị của N |
Thông báo ra màn hình tương ứng |
| 1111
21290
29205 |
1-1-2011
2-12-2090 HOAC 21-2-2090
KHONG |
Bài 35: Cho dãy số nguyên a1, a2,…, an (n <= 1000).
Hãy tìm cách thực hiện một số ít nhất phép đổi chỗ hai số hạng bất kỳ của dãy để thu được dãy số mà số lẻ đứng ở vị trí lẻ, số chẵn đứng ở vị trí chẵn.
Dữ liệu: Vào từ file văn bản DAYSO.INP:
- Dòng đầu tiên chứa số nguyên dương n;
- Dòng thứ i trong số n dòng tiếp theo chứa số hạng ai của dãy đã cho (-32767 à 32767, i = 1, 2,…, n).
Kết quả: ghi ra file văn bản DAYSO.OUT:
- Dòng đầu tiên ghi số lượng phép đổi chỗ cần thực hiện k (qui ước k = -1, nếu không thể biến đổi được dãy đã cho thành dãy thoả mãn yêu cầu đầu bài);
- Nếu k > 0, thì dòng thứ j trong số k dòng tiếp theo ghi chỉ số của hai số hạng cần đổi chỗ cho nhau ở lần đổi chỗ thứ j ( j =1, 2,…, k).
Ví dụ:
| DAYSO.INP |
DAYSO.OUT |
|
DAYSO.INP |
DAYSO.OUT |
| 6
1
2
3
4
6
5 |
1
5 6 |
|
4
1
3
2
5 |
-1 |
Bài 36: Một nhóm gồm n bạn học sinh của một lớp tham gia một câu lạc bộ tin học vào dịp nghỉ hè. Biết rằng khoảng thời gian mà bạn thứ i có mặt tại câu lạc bộ là [ai, bi] (ai<bi tương ứng là các thời điểm đến và rời khỏi câu lạc bộ). Cô giáo chủ nhiệm lớp muốn tới thăm các bạn trong nhóm này. Hãy giúp cô giáo chủ nhiệm xác định thời điểm đến câu lạc bộ sao cho tại thời điểm đó cô giáo có thể gặp được nhiều bạn trong nhóm nhất.
Dữ liệu: Vào từ file văn bản MEETING.INP:
- Dòng đầu tiên ghi số nguyên dương n (n <= 1000);
- Dòng thứ i trong số n dòng tiếp theo ghi 2 số nguyên không âm ai, bi, i = 1, 2,…, n.
Kết quả: Ghi ra file văn bản MEETING.OUT:
- Dòng đầu tiên ghi số nguyên dương k là số lượng bạn đang có mặt ở câu lạc bộ tại thời điểm cô giáo đến;
- Trong k dòng tiếp theo ghi chỉ số của k bạn có mặt ở câu lạc bộ tại thời điểm cô giáo đến, mỗi dòng ghi một chỉ số của một bạn.
Ví dụ:
| MEETING.INP |
MEETING.OUT |
|
MEETING.INP |
MEETING.OUT |
| 6
1 2
2 3
2 5
5 7
6 7
9 11 |
3
1
2
3 |
|
5
1 2
3 5
7 9
11 15
17 21 |
1
1 |
Bài 37: Ứng với mỗi số tự nhiên x, ta có số tự nhiên f(x) bằng tổng bình phương các chữ số của x. Từ x ta xây dựng dãy (Xn) như sau:
X1 = x ; X2 = f(X1) ; X3 = f(X2) ; …; Xi = f(Xi – 1) với 1 <= I <= n
Ví dụ:
x = 12 ta có dãy: 12; 5; 25; 29; 85; 89; 145; 42; 20; 4; 16; 37; 58; 89
x = 4 ta có dãy: 4; 16; 37; 58; 89; 145; 42; 20; 4
Viết chương trình nhập vào từ bàn phím số tự nhiên x và in ra màn hình dãy (Xn)
Dữ liệu vào: Số tự nhiên x.
Dữ liệu ra: In ra màn hình dãy (Xn)
Bài 38: Tạo một dãy gồm n (3 < n < 20) số nguyên nhận các giá trị ngẫu nhiên từ 1 đến 99. Xuất dãy và xuất ra vị trí các số nguyên tố của dãy.
Dữ liệu vào: Số nguyên n có giới hạn theo đề.
Kết quả ra: Mảng a ngẫu nhiên và vị trí các số nguyên tố trong mảng.
Ví dụ:
| Dữ liệu vào |
Dữ liệu ra |
| 19
|
So phan tu cua mang: 19
Mang a la:
74 98 69 94 5 11 11 50 21 61 89 73 14 19 55 31 71 50 1
Vi tri cac so nguyen to co trong a la: 5 6 7 10 11 12 14 16 17 |
Lưu ý: số 1 không phải là số nguyên tố
Bài 39: Viết chương trình in ra màn hình các số từ x đến y là số chẵn và chia hết cho 3. với x, y nhập từ bàn phím? Đếm xem có tất cả bao nhiêu số?
Dữ liệu vào: Số nguyên x và y (x < y).
Kết quả ra: Các số chẵn chia hết cho 3 trong phạm vi từ x đến y và đếm có bao nhiêu số.
Ví dụ:
| Dữ liệu vào |
Dữ liệu ra |
| 3
40 |
12 18 24 30 36
Co tat ca: 6 so |
Các bài từ 40 đến 64 sau đây lấy từ 100 đề Toán Tin (Tin học & Nhà trường)
Bài 65: Bạn Huy không tập trung tư tưởng trong giờ toán vì vậy thầy giáo cho thêm bài tập về nhà rèn luyện khả năng tập trung tư tưởng và tính cẩn thận chu đáo. Nội dung bài tập là cho n xâu chỉ bao gồm các ký tự la tinh thường và chữ số. Đoạn các ký tự số liên tục tạo thành một số nguyên. Ở mỗi đoạn ký tự số liên tục Huy phải trích ra số lớn nhất có thể, sắp xếp các số nhận được từ các xâu đã cho và đưa ra theo thứ tự không giảm, mỗi số được đưa ra dưới dạng không có các số 0 không có nghĩa.
Ví dụ, với n = 1 và xâu là 01a2b3456cde478 dãy số cần đưa ra là 1, 2, 478, 3456.
Yêu cầu: Cho số nguyên n (1 ≤ n ≤ 100) và n xâu, mỗi xâu có độ dài không quá 100. Hãy đưa ra dãy số nhận được đã sắp xếp theo thứ tự không giảm, mỗi số trên một dòng.
Dữ liệu: Vào từ file văn bản numbers.inp:
Dòng đầu tiên chứa số nguyên n,
Mỗi dòng trong n dòng sau chứa một xâu chỉ gồm các ký tự la tinh thường và số.
Dữ liệu đảm bảo có không quá 500 số được tách ra.
Kết quả: Đưa ra file văn bản NUMBERS.OUT dãy số nhận được đã sắp xếp theo thứ tự không giảm, mỗi số trên một dòng.
Ví dụ:
| numbers.inp |
|
numbers.out |
| 4
43silos0
zita002
le2sim
231233 |
|
0
2
2
43
231233 |
Bài 66: Hãy viết chương trình đổi tờ giấy bạc có mệnh giá n (Việt Nam đồng) ra ba loại giấy bạc có mệnh giá 500, 200, 100 (Việt Nam đồng) sao cho số tờ gấy bạc phải sử dụng là ít nhất (n được nhập từ bàn phím).
Bài 67: Tuổi của cha hiện nay là b tuổi, tuổi của con là c tuổi (b-c > 0 và b, c là các số nguyên dương). Hãy viết chương trình (với b, c được nhập từ bàn phím) để kiểm tra xem tuổi cha có gấp đôi tuổi con hay không? Nếu đúng thì đưa ra màn hình thông báo “hiện nay tuổi cha gấp đôi tuổi con”; trường hợp ngược lại, hãy tính số năm n (trước đó hoặc sau đó) tuổi cha gấp đôi tuổi con và đưa ra màn hình thông báo “n năm trước đây tuổi cha gấp đôi tuổi con” hay “sau n năm tuổi cha sẽ gấp đôi tuổi con”.
Bài 68: Hàng tháng, các hộ dân sử dụng điện đều nhận được một hóa đơn thanh toán tiền điện. Giá tiền điện phải trả được tính như sau:
- 100 số đầu tiên, mỗi số phải trả 550 đồng,
- Từ số 101 đến số 150, mỗi số phải trả 1100 đồng,
- Từ số 151 đến số 200, mỗi số phải trả 1470 đồng,
- Từ số 201 trở đi, mỗi số phải trả 1600 đồng.
Số tiền điện mà mỗi hộ dân phải trả ở hóa đơn là tổng số tiền điện mà người đó đã sử dụng với 10% thuế VAT. Hãy viết chương trình tính số tiền điện mà người tiêu dùng phải trả trong tháng với a là số KW điện mà người tiêu dùng đã sử dụng và được nhập từ bàn phím.
Bài 69: Nhập vào số tự nhiên n (0 < n < 10) và hai mảng số nguyên A, B có n phần tử đại diện cho hai tập hợp theo yêu cầu không có hai phần tử trùng nhau trong cùng một tập hợp. (Do đó, trong quá trình nhập nếu phần tử vừa nhập vào đã có trong mảng thì không bổ sung vào mảng). In ra màn hình tập hợp A, tập hợp B và các phần tử là giao của hai tập hợp A và B.
Bài 70:
- Nhập một dãy số nguyên có n phần tử (0< n <= 100)
- Sắp xếp dãy vừa nhập theo thứ tự tăng dần, in ra màn hình dãy đã sắp thứ tự
- Tìm trên dãy đã sắp xếp có phần tử x hay không, với x được nhập từ bàn phím.
Bài 71: Cho đa thức bậc n:
A = anxn + an-1xn-1+…+ a1x + a0
Trong đó an, an-1,…a1,a0 là các hệ số nguyên có giá trị tuyệt đối không quá 100.
Biết rằng phương trình A = 0 nếu có nghiệm nguyên thì nghiệm nguyên đó chỉ có thể là ước số của hệ số a0.
Yêu cầu: Hãy tìm tất cả các nghiệm nguyên (nếu có) của phương trình A = 0.
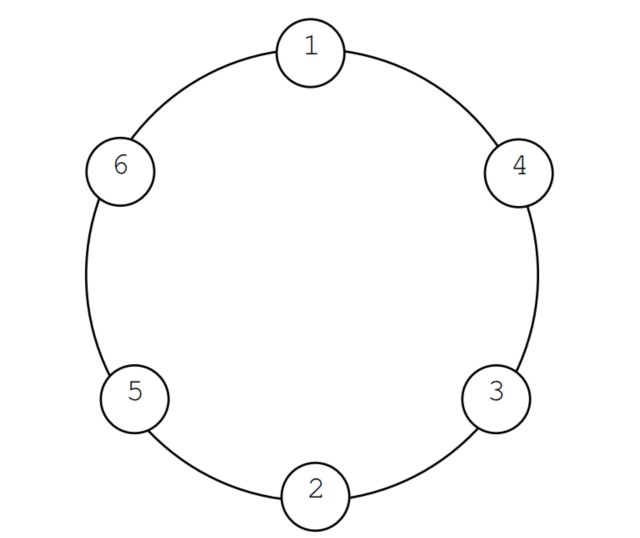
Bài 72: Kỳ thi học sinh giỏi năm học 2008-2009 của tỉnh Bà Rịa-Vũng Tàu có 8 đội tuyển dự thi đến từ các huyện (TX, TP), số thứ tự các huyện được đánh số lần lượt từ 1 đến 8 là Vũng Tàu, Bà Rịa, Tân Thành, Châu Đức, Xuyên Mộc, Đất Đỏ, Long Điền, Côn Đảo. Mỗi thí sinh dự thi có một số báo danh duy nhất (là một số nguyên dương), mỗi đội tuyển của huyện tối đa 90 thí sinh. Sau khi thi xong Sở Giáo dục- Đào tạo tổ chức cho các thí sinh giao lưu với nhau, Ban tổ chức sắp xếp các thí sinh đứng thành một vòng tròn, để tạo điều kiện cho các thí sinh trong tỉnh được giao lưu với nhau Ban tổ chức yêu cầu các thí sinh cùng huyện không đứng gần nhau, các thí sinh thuộc 2 huyện có số thứ tự liền kề cũng không được đứng gần nhau.
Yêu cầu: Hãy giúp Ban tổ chức chỉ ra một cách xếp thỏa mãn yêu cầu trên
Dữ liệu vào: file ‘pupil.inp’
Gồm có 8 dòng, dòng thứ i chứa các số báo danh của các thí sinh huyện thứ i, các số báo danh cách nhau ít nhất một dấu cách.
Dữ liệu ra: file ‘pupil.out’
(Mô tả cách xếp n thí sinh theo yêu cầu trên một vòng tròn, ta có thể mô tả trên một đường thẳng, trong đó thí sinh đầu và thí sinh cuối đứng gần nhau trên vòng tròn)
Gồm n dòng (n là tổng số thí sinh), mỗi dòng là số báo danh của thí sinh. Trong trường hợp không có cách nào thỏa mãn yêu cầu thì ghi là -1
Ví dụ
| Pupil.inp |
|
Pupil.out |
| 1 2 3
4 5 6
7 8 9
10 11 12
13 14 15
16 17 18
19 20 21
22 23 |
|
1
22
16
7
17
23
2
18
8
3
9
10
4
11
5
12
6
13
19
14
20
15
21 |
Bài 73: Nhập vào một số tự nhiên N với (0 < N ≤ 65535). Hãy cho biết chữ số lớn nhất của số tự nhiên vừa nhập. Hãy in đảo ngược số N.
Ví dụ: N=6548. Chữ số lớn nhất là: 8. Số in ngược là: 8456.
Bài 74: Nhập vào một số tự nhiên N với (0 < N ≤ 65535), phân tích số vừa nhập thành các thừa số nguyên tố, nếu số vừa nhập là số nguyên tố thì chỉ thông báo ra màn hình đây là số nguyên tố.
Ví dụ:
- Nếu số vừa nhập là 300, thì in ra màn hình 300 = 2. 2. 3. 5. 5
- Nếu số vừa nhập là 307, thì in ra màn hình “307 là số nguyên tố”
Bài 75: Tìm tất cả các số nguyên dương x, y, z thỏa mãn phương trình: ax + by + cz = n; trong đó a, b, c, n là các số nguyên dương (a, b, c ≤ 65535; n ≤ 2.147.483.647)
Yêu cầu kỹ thuật:
- Kiểm tra việc nhập dữ liệu thỏa mãn yêu cầu của đề bài. Nếu người sử dụng nhập sai thì thông báo nhập sai và hỏi người dùng có muốn nhập lại hay không, nếu không thì kết thúc chương trình.
- Không được dùng quá 2 vòng lặp lồng nhau và điều kiện dừng của mỗi vòng lặp không được vượt quá ngưỡng mà từ đó ta biết chắc chắn phương trình không có nghiệm.
- Nếu phương trình có nghiệm thì liệt kê có thứ tự các bộ nghiệm của phương trình theo dạng sau:
Giả sử phương trình có dạng 15x + 28y + 24z = 454, ta in ra màn hình như sau:
STT x y x
1 10 10 1
2 14 7 2
Ngược lại không thì thông báo phương trình không có nghiệm.
Bài 76: Một số có tổng các ước nhỏ hơn nó bằng chính nó được gọi là số hoàn chỉnh.
Ví dụ: 6 có các ước nhỏ hơn nó là 1, 2, 3. Tổng là 1 + 2 + 3 = 6.
Viết chương trình xét xem một số n được nhập từ bàn phím có phải là số hoàn chỉnh không.
Bài 77: Viết chương trình tìm các số hoàn chỉnh nhỏ hơn n (Với n được nhập từ bàn phím).
Bài 78: Dãy Fibonacy có hai phần tử đầu là 1, 1. Các phần tử sau bằng tổng hai phần tử đứng ngay trước nó:
1, 1, 2, 3, 5, 8, 13, 21,…
Viết chương trình in ra dãy Fibonacy có phần tử lớn nhất nhỏ hơn n?
Bài 79: Viết chương trình nhập n số, xoá số thứ k trong n số vừa nhập. In ra n-1 số còn lại.
Bài 80: Viết chương trình cho phép nhập một dãy gồm n số nguyên. Nhập thêm một số và chèn thêm vào dãy sau phần tử k.
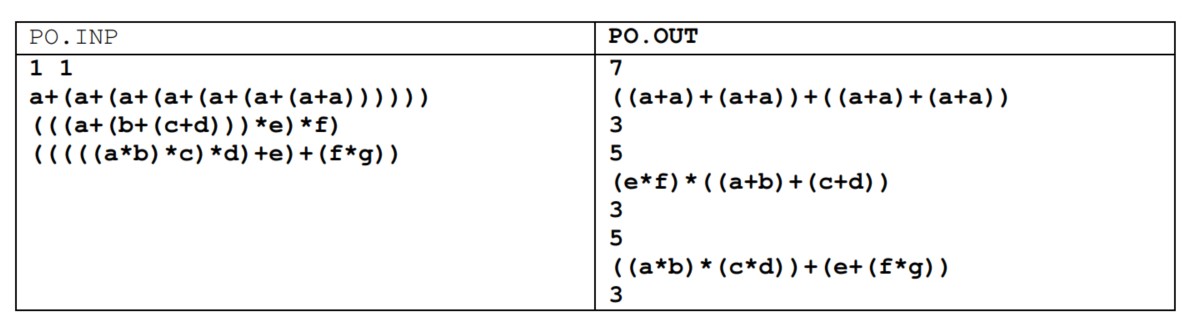
Bài 81: Viết chương trình in ra màn hình tam giác Pascal. Ví dụ, với n=4 sẽ in ra hình sau:
1 1
1 2 1
1 3 3 1
1 4 6 4 1
Hàng thứ n được xác định từ hàng n-1:
- Phần tử đầu tiên và phần tử cuối cùng đều bằng 1.
- Phần tử thứ 2 là tổng của phần tử thứ nhất và thứ 2 của hàng n-1
- Phần tử thứ k của hàng thứ n là tổng của phần tử thứ k-1 và k của hàng thứ n-1.
Bài 82: Viết chương trình tính giai thừa của số n (Viết là n!). Với yêu cầu:
- Nếu người dùng nhập số n < 0 thì yêu cầu nhập lại.
- Sử dụng chương trình con để tính giai thừa của một số.
Bài 83: Viết chương trình cho phép cộng hai phân số.
Bài 84: Nhập vào một số nguyên dương n. Hãy in ra số nguyên tố nhỏ nhất lớn hơn n. VD: Nhập n = 10. Kết quả in ra số 11.
Bài 85: Tìm các số tự nhiên nhỏ hơn hoặc bằng n mà sau khi làm phép phân tích ra thừa số nguyên tố có nhiều nhân tử nhất. Ví dụ n=9. Các số có nhiều nhân tử nhất sau khi làm phép phân tích là: 8 = 2.2.2
Viết chương trình cho phép phân tích một số ra thừa số nguyên tố và ghi kết quả dưới dạng tích các lũy thừa. Ví dụ: 300 = 2^2.3.5^2
Bài 86: Mọi số tự nhiên đều có thể viết được dưới dạng tổng của hai số nguyên tố. Viết chương trình thực hiện tách một số tự nhiên thành tổng của hai số nguyên tố.
Bài 87: Hai số tự nhiên A, B được coi là hữu nghị nếu như số này bằng tổng các ước số của số kia và ngược lại. Lập trình tìm và in ra màn hình các cặp số hữu nghị trong phạm vi từ 1 đến 10000. (Lưu ý, số 1 được coi là ước số của mọi số còn mỗi số không được coi là ước số của chính nó).
Bài 88: Cho dãy số gồm n số. Tìm dãy con lớn nhất các phần tử tăng (giảm) dần.
Bài 89: Cho dãy số gồm n số. Tìm dãy con lớn nhất các phần tử có cùng dấu, (đan dấu).
Bài 90: Cho dãy gồm n số. Tìm dãy con lớn nhất đơn điệu (liên tục tăng, giảm hoặc giảm, tăng).
Bài 91: Cho dãy số gồm n số nguyên. Tìm dãy con có tổng lớn nhất
Hướng dẫn. Sử dụng kỹ thuật vét cạn các dãy con, dùng hàm tính tổng dãy con để kiểm tra.
Bài 92: Gọi abcd là một số có 4 chữ số. Hãy lập chương trình tìm tất cả các số có 4 chữ số thỏa mãn biểu thức: abcd=(ab + cd)^2. Ví dụ 2025=(20 + 25)^2.
Bài 93: Viết chương trình cho nhập hai số tự nhiên N và k. Hãy cho biết chữ số thứ k tính từ trái sang phải trong số N là chữ số nào? Nếu k lớn hơn độ dài của N hoặc k bằng 0 thì thông báo không tìm được.
Bài 94: Một số được gọi là số bậc thang nếu biểu diễn thập phân của nó có nhiều hơn một chữ số đồng thời theo chiều từ trái qua phải, chữ số đứng sau không nhỏ hơn chữ số đứng trước. Viết chương trình in ra các số bậc thang trong đoạn [n1, n2] với n1, n2 được nhập từ bàn phím.
Bài 95: Viết chương trình cho phép đổi một số từ cơ số 10 sang cơ số bất kỳ.
Thuật toán:
- Dùng mảng CS để lưu các chữ số.
- Lặp khi n <> việc: Chia n cho s lấy phần dư. Lấy phần dư làm chỉ số để lấy và lưu chữ số. Gán n = n div s.
Chú ý chữ số lấy sau sẽ nằm trước.
Bài 96: Viết chương trình cho phép đổi một số từ cơ số bất kỳ sang cơ số 10.
Bài 97: Năm 1973, nhà Toán học Neil Sloan đưa ra khái niệm độ bền của một số nguyên không âm N như sau:
- Nếu
N có một chữ số thì độ bền của N bằng 0.
- Nếu
N có từ hai chữ số trở lên thì độ bền của N bằng độ bền của số nguyên là tích các chữ số của N cộng 1.
Cho N từ 0 đến 2.000.000.000, tìm số bé hơn N có độ bền lớn nhất.
Ví dụ
| Persist.inp |
Persist.out |
Giải thích |
| 100 |
77 |
Doben(77)=Doben(49)+1=Doben(36)+1+1=Doben(18)+1+1+1=Doben(8)+1+1+1+1=0+1+1+1+1=4 |
Hướng dẫn.
- Để tìm độ bền một số cần một hàm
TICH(n) tính tích các chữ số của n.
- Cho
d = 0. Lặp lại điều kiện n >9 việc tăng d lên 1 thay n = TICH(n).