Quy hoạch động là gì?
Quy hoạch động (Dynamic Programming) là kĩ thuật được được dùng khi có một công thức truy hồi và một (hoặc một vài) trạng thái bắt đầu. Một bài toán được tính bởi các bài toán nhỏ hơn đã tìm ra trước đó, một kĩ thuật giải quyết các bài toán khi có thể giải quyết bài toán đó bằng cách sử dụng lại các bài toán nhỏ hơn đã được giải quyết và lưu lại kết quả.

1. Quy hoạch động là gì?
Theo thầy Lê Minh Hoàng thì
Các thuật toán đệ quy có ưu điểm dễ cài đặt, tuy nhiên do bản chất của quá trình đệ quy, các chương trình này thường kéo theo những đòi hỏi lớn về không gian bộ nhớ và một khối lượng tính toán khổng lồ. Quy hoạch động (Dynamic programming) là một kỹ thuật nhằm đơn giản hóa việc tính toán các công thức truy hồi bằng cách lưu trữ toàn bộ hay một phần kết quả tính toán tại mỗi bước với mục đích sử dụng lại.
Dynamic Programming = Solving Recurrence + Memoization
Hiểu đơn giản, QUY HOẠCH ĐỘNG = GIẢI QUYẾT TRUY HỒI + GHI NHỚ KẾT QUẢ. Quy hoạch động có độ phức tạp đa thức nên sẽ chạy nhanh hơn quay lui và vét cạn.

2. Khi nào thì dùng Quy hoạch động?
Không có một quy tắc chung nào để cho biết một bài toán có giải được bằng quy hoạch động hay không. Tuy nhiên, nếu bài toán có hai tính chất sau thì bạn có thể nghĩ tới quy hoạch động:
- Có một hệ thức truy hồi. Tức là, bài toán lớn có thể giải quyết dựa vào các bài toán con lồng nhau. Chẳng hạn số Fibonacci
f(n)được tính dựa vào hai số thứf(n-1)vàf(n-2). - Một hoặc nhiều bài toán con đã được giải quyết (biết trạng thái). Ví dụ đối với bài toán tìm số Fibonacci thì số
f(0)vàf(1)là đã biết trước.
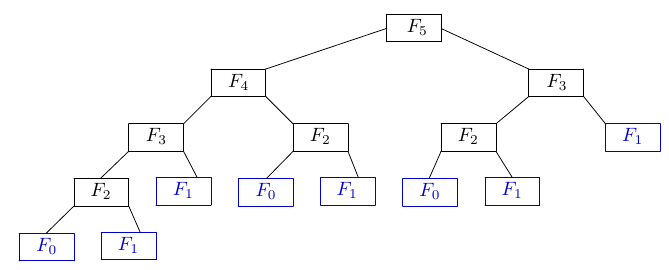
Nghe có vẻ giống như đệ quy, một bài toán lớn được chia nhỏ thành các bài toán con lồng nhau. Nhưng, phương pháp quy hoạch động sẽ lưu kết quả của bài toán con này, và khi được gọi, nó sẽ không cần phải tính lại, do đó làm giảm thời gian tính toán.
Ví dụ, đối với bài toán tìm số Fibonacci thứ n, nếu sử dụng đệ quy đơn thuần, chúng ta rất nhiều bài toán con sẽ được tính đi tính lại, điển hình là các số fib(0) và fib(1).

def fib(n):
if n <= 1:
return n
return fib(n -1) + fib(n - 2)
Nếu sử dụng quy hoạch động, mỗi bài toán con fib(i) sẽ được lưu lại trước khi tính những bài toán con lớn hơn. Nhờ đó, mà việc tính toán giảm đi đáng kể, mỗi bài toán con chỉ cần tính đúng một lần.
def fib(n):
dp = [0] * (n + 1)
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
Như vậy, vấn đề mấu chốt ở đây là gì?
Đệ quy chỉ đơn giản là gọi lại chính nó. Quy hoạch động là một cách để giải quyết các vấn đề có cấu trúc cụ thể (cấu trúc con tối ưu) trong đó một vấn đề có thể được chia thành các vấn đề con tương tự như bài toán ban đầu.
Ghi nhớ kết quả là một cách để tối ưu hóa các thuật toán quy hoạch động dựa trên đệ quy. Và, chúng ta không phải giải quyết bài toán con một lần nữa nếu chúng đã được giải quyết.

Rõ ràng người ta có thể gọi đệ quy để giải quyết một bài toán quy hoạch động, nhưng nó không cần thiết. Người ta có thể giải một bài toán quy hoạch động mà không cần đệ quy (chẳng hạn trong bài tính số Fibonacci bằng quy hoạch động ở trên, chúng ta thấy không có lời gọi đệ quy nào cả).
3. Một số ví dụ về Quy hoạch động
Phân tích số nguyên dương
Cho số tự nhiên n ≤ 100. Hãy cho biết có bao nhiêu cách phân tích số n thành tổng của dãy các số nguyên dương, các cách phân tích là hoán vị của nhau chỉ tính là một cách. (Bài toán này được viết lại dựa theo sách của thầy Lê Minh Hoàng).
Ví dụ: n = 5 có 7 cách phân tích:
1. 5 = 1 + 1 + 1 + 1 + 1
2. 5 = 1 + 1 + 1 + 2
3. 5 = 1 + 1 + 3
4. 5 = 1 + 2 + 2
5. 5 = 1 + 4
6. 5 = 2 + 3
7. 5 = 5
Lưu ý: n = 0 vẫn coi là có 1 cách phân tích thành tổng các số nguyên dương, là tổng của dãy rỗng.

Để giải bài toán này, chúng ta có thể dùng phương pháp liệt kê tất cả các cách phân tích và đếm số cấu hình. Tuy nhiên, khi số cách phân tích tương đối lớn, phương pháp liệt kê tỏ ra khá chậm. Chẳng hạn với n = 100 có 190569292 cách phân tích.
Nhận xét:
Nếu gọi F[m, v] là số cách phân tích số v thành tổng các số nguyên dương nhỏ hơn hoặc bằng m thì khi đó, các cách phân tích số v thành tổng các số nguyên dương nhỏ hơn hoặc bằng m có thể chia làm hai loại:
- Loại 1: Không chứa số
mtrong phép phân tích, khi đó số cách phân tích loại này chính là số cách phân tích sốvthành tổng các số nguyên dương nhỏ hơnm, tức là số cách phân tích sốvthành tổng các số nguyên dương nhỏ hơn hoặc bằngm - 1và bằngF[m-1, v]. - Loại 2: Có chứa ít nhất một số
mtrong phép phân tích. Khi đó nếu trong các cách phân tích loại này ta bỏ đi sốmđó thì ta sẽ được các cách phân tích sốv - mthành tổng các số nguyên dương nhỏ hơn hoặc bằngm(Lưu ý, điều này chỉ đúng khi không tính lặp lại các hoán vị của một cách). Có nghĩa là về mặt số lượng, số các cách phân tích loại này bằngF[m, v - m].
Trong trường hợp m > v thì rõ ràng chỉ có các cách phân tích loại 1, còn trong trường hợp m ≤ v thì sẽ có cả các cách phân tích loại 1 và loại 2. Vì thế, công thức truy hồi là: $$F[m,v]=\begin{cases} F[m-1,v] &\text{ nếu } m>v\\ F[m-1,v] +F[m,v-m]&\text{ nếu } m \leqslant v \end{cases}$$

Tìm số lượng đồng xu
Cho $N$ đồng xu, giá trị của mỗi đồng là $V_0,V_1,…,V_{N−1}$, và số $S$. Tìm số lượng đồng xu nhỏ nhất để tổng giá trị của chúng bằng $S$ (số lượng đồng xu không giới hạn).
Với bài toán này, chúng ta cần xây dựng và giải các bài toán con lồng (gối) nhau. Với ví dụ của chúng ta, mỗi bài toán con dp(P) với P<= S là bài toán tìm số đồng xu nhỏ nhất để khối lượng của chúng là P. và dp(P) = k chính là số lượng đồng xu nhỏ nhất đó.
Chúng ta sẽ áp dụng phương pháp quy hoạch động bằng cách bắt đầu từ bài toán con dp(0) sau đó tiếp tục với các bài toán con lớn hơn. Lời giải của các bài toán con sẽ được xây dựng lần lượt cho đến chúng ta xây dựng đến bài toán dp(S) và đó chính là kết quả của bài toán lớn. Một điều cần lưu ý với kỹ thuật này là bài toán con tiếp theo sẽ không thể giải được nếu chúng ta chưa giải bài toán con trước đó.
Cuối cùng là phần khó nhất của mọi bài toán quy hoạch động, đó là trả lời câu hỏi: cấu trúc con tối ưu của bài toán này ở đâu. Hay nói một cách khác, làm thế nào để từ những bài toán nhỏ hơn có thể tổ hợp ra lời giải cho bài toán lớn. Với vị dụ kinh điển này, mọi thứ sẽ tương đối đơn giản, nhưng với những bài toán phức tạp hơn, chúng ta cần suy nghĩ và tính toán nhiều hơn.

Quay trở lại với bài toán của chúng ta. Giả sử P là tổng khối lượng của các đồng xu nặng lần lượt là V1, V2, ..., Vj. Để có được khối lượng P, chúng ta cần thêm vài đúng 1 đồng xu nặng U vào khối lượng Q sao cho Q + U = P. Tất nhiên, bài toán con dp(Q) chúng ta đã có lời giải nên chúng ta sẽ biết được cần bao nhiêu đồng xu cho dp(P). Và vì có nhiều đồng xu U (nhiều nhưng hữu hạn) nên chúng ta có thể cần đến nhiều bài toán con trước đó, và dp(p) là giá trị nhỏ nhất sau khi tổng hợp những bài toán con đó.
Ví dụ với n = 3, S = 11, W = [1, 3, 5].
- Bắt đầu với bài toán con
0ta códp(0) = 0 - Với bài toán con
1, có 1 đồng xu (nặng 1) có thể thêm vào từ0đồng xu nào cả. Vậydp(1) = dp(0) + 1 = 1. - Với bài toán con
2, cũng chỉ có 1 đồng xu (nặng 1) có thể thêm vào từ1đồng xu. Vậydp(2) = dp(1) + 1 = 2. - Với bài toán con
3, chúng ta có thể thêm 1 đồng xu 3 vào0đồng xu hoặc thêm 1 đồng xu 1 vào2đồng xu. Rõ ràng là cách đầu tiên cho kết quả nhỏ hơn. Vậydp(3) = min(dp(2) + 1, dp(0) + 1) = min(3, 1) = 1 - …
- Cứ tiếp tục như vậy cho đến bài toán
Schính là đáp án chúng ta cần tìm.
Về mặt cài đặt, quy hoạch động thường lưu kết quả vào một mảng. Trong ví dụ của chúng ta, mảng dp[0..S] sẽ lưu kết quả cho từng bài toán con. Nói cách khác, dp[P] = k nghĩa là cần ít nhất k đồng xu để có khối lượng là P Toàn bộ mảng này sẽ được tính bằng vòng lặp. Đoạn code sau mô tả toàn bộ quá trình này.
n, S = map(int, input().split())
w = list(map(int, input().split()))
dp = [0] * (S + 1)
dp[0] = 0
for P in range(1, S + 1):
dp[P] = min(dp[P - x] for x in w if x <= P) + 1
print(dp)
print(dp[S])
# Nếu đầu vào như sau: n = 3, S = 11, w = [1, 3, 5]
# Thì bảng lời giải cho các bài toán con sẽ lần lượt như sau:
# P = 0 |1 |2 |3 |4 |5 |6 |7 |8 |9 |10|11
# ------+--+--+--+--+--+--+--+--+--+--+--
# k = 0 |1 |2 |1 |2 |1 |2 |3 |2 |3 |2 |3Bạn có thể tham khảo thêm MỘT SỐ BÀI TOÁN QUY HOẠCH ĐỘNG ĐIỂN HÌNH



Leave a Reply