O₂ Education

Category: THCS

  • Cách tính diện tích tam giác

    Cách tính diện tích tam giác

    Cách tính diện tích tam giác

    Cách tính diện tích tam giác bất kì

    Để tính diện tích một tam giác bất kì, cách làm chung là ta lấy chiều cao nhân với độ dài cạnh đáy tương ứng và chia cho 2.

    Cách tính diện tích tam giác

    Ví dụ, trong hình trên thì diện tích tam giác ABC là $$S=\frac{1}{2} a. h_a$$

    Hoặc, có thể thay bằng $S=\frac{1}{2} b.h_b=\frac{1}{2} c. h_c$ với $h_a, h_b,h_c$ lần lượt là độ dài đường cao kẻ từ các đỉnh A, B, C của tam giác.

    Tính diện tích hình tam giác có độ dài đáy là 5m và chiều cao là 24dm.

    Giải: Chiều cao 24dm = 2,4m. Diện tích tam giác là $$S=\frac{1}{2} . 5. 2{,}4=6\, m^2$$

    Đối với các em học sinh lớp 10, có thể tham khảo thêm các cách tính diện tích tam giác HỆ THỨC LƯỢNG TRONG TAM GIÁC LỚP 10

    Cách tính diện tích tam giác vuông

    Cách tính diện tích tam giác 1

    Tam giác vuông hơi đặc biệt một chút, là các cạnh góc vuông cũng đồng thời là đường cao. Do đó, diện tích của tam giác vuông có thể tính bằng 1/2 tích độ dài hai cạnh góc vuông.

    Ví dụ, trong hình trên thì diện tích của tam giác là $$\frac{1}{2} a.b$$

    Công thức tính diện tích tam giác đều

    Cách tính diện tích tam giác 2

    Diện tích tam giác đều cạnh bằng a thì diện tích là $\frac{a^2\sqrt{3}}{4}$

    Cách tính diện tích tam giác cân

    Để tính diện tích tam giác cân, chúng ta thường kẻ đường cao ứng với cạnh đáy của tam giác cân.

  • Trung tuyến là gì?

    Trung tuyến là gì?

    Trung tuyến là gì?

    Trong hình học, trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện. Mỗi tam giác đều có ba trung tuyến. Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau.

    1. Đường trung tuyến là gì?

    Trong hình học, trung tuyến của một tam giác là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện.

    Mỗi tam giác có ba đường trung tuyến. Ba đường trung tuyến này cùng cắt nhau tại một điểm, điểm đó gọi là trọng tâm của tam giác.

    Ví dụ, trong hình sau thì tam giác ABC có ba đường trung tuyến là AM, BN và CP. Ba đường này đồng quy tại trọng tâm G của tam giác.

    trọng tâm là gì

    Đối với tam giác cân và tam giác đều, mỗi trung tuyến của tam giác chia đôi các góc ở đỉnh với hai cạnh kề có chiều dài bằng nhau. Khi đó, các đường trung tuyến đó đồng thời cũng là đường cao, đường phân giác của tam giác đó.

    2. Trung tuyến của tam giác vuông

    Trong tam giác vuông thì đường trung tuyến ứng với cạnh huyền có độ dài bằng nửa cạnh huyền. Ngược lại, một tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

    Trung tuyến của tam giác vuông

  • Trọng tâm là gì?

    Trọng tâm là gì?

    Trọng tâm là gì?

    Trọng tâm là gì?

    Mỗi tam giác có 3 đường trung tuyến, là đoạn thẳng nối từ đỉnh của tam giác đến trung điểm của cạnh đối diện. Ba đường trung tuyến này đồng quy tại một điểm (cùng cắt nhau tại một điểm). Điểm đó được gọi là trọng tâm của tam giác.

    Trọng tâm của tam giác là giao điểm của ba đường trung tuyến.

    trọng tâm là gì

    Tính chất của trọng tâm trong tam giác

    Khoảng cách từ trọng tâm của tam giác đến đỉnh bằng 2/3 độ dài đường trung tuyến ứng với đỉnh đó.

    Tam giác ABC, với các đường trung tuyến AM, BN, CP và trọng tâm G, ta có:

    • GA = 2/3 AM
    • GC = 2/3 GP
    • BG = 2/3 GN
    		 tính chất trọng tâm của tam giác

    Cách tìm trọng tâm tam giác

    Cách 1: Giao điểm 3 đường trung tuyến

    Xác định trọng tâm tam giác bằng cách lấy giao điểm của ba đường trung tuyến.

    Bước 1: Vẽ tam giác ABC, lần lượt xác định trung điểm của các cạnh AB, BC, CA.

    Bước 2: Nối lần lượt các đỉnh đến trung điểm của cạnh đối diện. Nối A với G, B với F, C với E.

    Bước 3: Giao điểm I của ba đường trung tuyến là AG, BF, CE là trọng tâm của tam giác ABC.

    Chú ý, trong thực tế chúng ta chỉ cần tìm giao điểm của hai đường trung tuyến là đủ.

    		 cách xác định trọng tâm của tam giác

    Cách 2: Tỉ lệ trên đường trung tuyến

    Xác định trọng tâm tam giác dựa trên tỉ lệ đường trung tuyến.

    Bước 1: Vẽ tam giác ABC, xác định trung điểm M của cạnh BC.

    Bước 2: Nối đỉnh A với trung điểm M, sau đó lấy điểm S sao cho AS = 2/3 AM.

    Theo tính chất trọng tâm tam giác thì điểm S chính là trọng tâm tam giác ABC.

    		 Trọng tâm là gì? 3
  • Trung điểm là gì?

    Trung điểm là gì?

    Trung điểm là gì?

    Trung điểm của đoạn thẳng là điểm nằm chính giữa đoạn thẳng đó, chia đoạn thẳng đó thành hai đoạn dài bằng nhau.

    Trung điểm là gì?

    Trung điểm là điểm nằm chính giữa đoạn thẳng và chia đoạn thẳng ra làm hai đoạn có độ dài bằng nhau.

    Ví dụ ta có đoạn thẳng AB, điểm C nằm trên AB và AC = CB. Vậy C chính là trung điểm của đoạn AB

    trung điểm là gì

    Tính chất trung điểm của đoạn thẳng

    Chia đoạn thẳng ra làm hai đoạn thẳng bằng nhau. Ví dụ: M là trung điểm của đoạn thẳng OP thì MO = MP.

    Trung điểm là gì? 4

    Đoạn thẳng nối đỉnh của một tam giác với trung điểm cạnh đối diện được gọi là đường trung tuyến. Giao điểm của ba đường trung tuyến của một tam giác gọi là trọng tâm của tam giác.

    Biểu thức tọa độ của trung điểm đoạn thẳng

    Công thức để xác định trung điểm của một đoạn thẳng trên một mặt phẳng tọa độ Oxy. Cho hai điểm $A(x_A, y_A)$ và $B(x_B, y_B)$ thì trung điểm $M$ của đoạn thẳng $AB$ có tọa độ là $$\displaystyle M\left({\frac {x_{1}+x_{2}}{2}},{\frac {y_{1}+y_{2}}{2}}\right).$$

  • Bài toán về năng suất

    Bài toán về năng suất

    Cách giải Bài toán về năng suất

    Năng suất là gì? Năng suất chính là khối lượng công việc làm trong một thời gian nhất định.

    Khi giải bài toán bằng cách lập phương trình dạng năng suất, ta cần phải nhớ:

    1. Bài toán về năng suất có 3 đại lượng: khối lượng công việc, năng suất và thời gian.
    2. Mối quan hệ giữa 3 đại lượng:
      • Khối lượng công việc = Năng suất x Thời gian
      • Năng suất = Khối lượng công việc : Thời gian
      • Thời gian = Khối lượng công việc : Năng suất
    3. Bài toán về công việc làm chung, làm riêng, hay vòi nước chảy chung, chảy riêng thì ta thường coi toàn bộ công việc là 1 đơn vị.
      • Suy ra năng suất là 1/ Thời gian.
      • Lập phương trình theo: Tổng các năng suất riêng = Năng suất chung.

    Ví dụ Bài toán về năng suất

    Bài toán 1. (Dạng toán công việc chung, công  việc riêng)

    Một đội máy kéo dự định mỗi ngày cày 40 ha. Khi thực hiện mỗi ngày cày được 52 ha, vì vậy  đội không những cày xong trước thời hạn 2 ngày mà còn cày  thêm được 4 ha nữa. Tính diện tích thửa ruộng mà đội phải cày theo kế hoạch.

    Lời Giải:

    Gọi diện tích mà đội phải cày theo kế hoạch là x, (ha), (  x> 0).

    Thời gian đội dự định cày là: $\frac{x}{40}$ (giờ).

    Diện tích mà đội thực cày là: (x + 4),  (ha).

    Thời gian mà đội thực cày là: $\frac{x+4}{52}$ (giờ).

    Vì khi thực hiện đội đẵ cày xong trước thời hạn 2 ngày do đó ta có phương trình: $\frac{x}{40}$ – $\frac{x+4}{52}$= 2.

    Giải phương trình trên ta được x= 360.

    Vậy diện tích mà đội dự định cày theo kế hoạch là: 360 ha.

    Bài toán 2. (Dạng toán công việc chung, công  việc riêng)

    Hai người thợ cùng làm một công việc trong 16 giờ thì xong. Nếu người thứ nhất làm trong 3 giờ, người thợ thứ hai làm trong 6 giờ thì học làm được 25% khối lượng công việc. Hỏi mỗi người thợ làm  một mình  công việc đó trong bao lâu.

    Lời Giải:

    Gọi thời gian để Người thứ nhất làm  một mình xong công việc là x, (giờ), x > 16.

    Gọi thời gian để Người thứ hai làm  một mình xong công việc là y, (giờ), y > 16.

    Trong 1 giờ Người thứ nhất và người thứ hai làm được khối lượng công việc tương ứng là: $\frac{1}{x}$, $\frac{1}{y}$ .

    Vì hai người làm chung trong 16 giờ thì xong KLCV do đó ta có phương trình (1) : $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{1}{16}$

    Sau 3 giờ Người thứ nhất làm được 3. $\frac{1}{x}$ (KLCV).

    Sau 6 giờ Người thứ hai làm được 6. $\frac{1}{y}$ (KLCV).

    Vì người thứ nhất làm trong 3 giờ, người thợ thứ hai làm trong 6 giờ thì học làm được 25% khối lượng công việc do đó ta có phương trình:  $\frac{3}{x}$ + $\frac{6}{y}$ = $\frac{1}{4}$.

    Theo bài ra ta có hệ phương trình: $$\left\{ \begin{align} & \frac{1}{x}+\frac{1}{y}=\frac{1}{16} \\ & \frac{3}{x}+\frac{6}{y}=\frac{1}{4}. \\ \end{align} \right.$$

    Giải hệ phương trình ta được: $\left\{ \begin{align}& x=24 \\& y=48 \\\end{align} \right.$

    Vậy thời gian để người thứ nhất làm  một mình xong công việc là: 24 (giờ).

    Thời gian để người thứ hai làm  một mình xong công việc là: 48 (giờ).

    Bài toán 3. (Dạng toán công việc chung, công  việc riêng)

    Hai tổ công nhân làm chung trong 12 giờ sẽ hoàn thành một công việc đã định. Họ làm chung với nhau trong 4 giờ thì tổ thứ nhất được điều đi làm công việc khác, tổ thứ hai làm một mình phần công việc còn lại trong 10 giờ. Hỏi tổ thứ hai nếu làm một mình thì sau  bao lâu sẽ hoàn thành công việc.

    Lời Giải:

    Gọi thời gian tổ hai làm một nmình hoàn thành công việc là x, (giờ), x> 12.

    Trong 1 giờ tổ hai làm được khối lượng công việc: $\frac{1}{x}$ (KLCV).

    Sau 4 giờ hai tổ đẵ là chung được khối lượng công việc là:  $\frac{4}{12}$ = $\frac{1}{3}$ (KLCV).

    Phần công việc còn lại tổ hai phải làm là: 1 – $\frac{1}{3}$ = $\frac{2}{3}$ (KLCV).

    Vì tổ hai hoàn thàmh khối lượng công việc còn lại trong 10 giờ nên ta có phương trình: $\frac{2}{3}$: x = 10.

    Giải PTBN ta được x= 15.    Vậy thời gian tổ hai làm  một mình hoàn thành khối lượng công việc là: 15 giờ.

    Bài toán 4. (Dạng toán công việc chung, công  việc riêng)

    Một đội công nhân hoàn thành một công việc với mức 420 ngày công. Hãy tính số công nhân của đội,  biết rằng nếu đội tăng thêm 5 người thì số ngày để hoàn thành công việc sẽ giảm đi 7 ngày.

    Lời Giải:

    Gọi số công nhân của đội là x, (người), x> 0, (nguyên dương).

    Số ngày hoàn thành công việc với x người là: $\frac{420}{x}$ (ngày).

    Số công nhân sau khi tăng 5 người là: x + 5.

    Số ngày hoàn thành công việc với x + 5  người là: $\frac{420}{x+5}$ (ngày).

    Vì nếu đội tăng thêm 5 người thì số ngày để hoàn thành công việc sẽ giảm đi 7 ngày do đó ta có phương trình:

    $\frac{420}{x} -\frac{420}{x+5}  = 7.$

    Giải phương trình bậc hai trên ta được hai nghiệm x1  = 15; x2 = – 20 (loại).

    Vậy số công nhân của đội là 15 người.

    Bài toán 5. (Dạng toán công việc chung, công  việc riêng)

    Hai đội xây dựng  cùng làm chung một công việc và dự đinh  xong trong 12 ngày. Họ cùng làm chung với nhau được 8 ngày thì đội  1  được điều động đi làm công việc khác, đội 2 tiếp tục làm. Do  cải tiến kỹ thuật,  năng suất tăng gấp đôi nên đội 2 đẵ làm xong phần việc còn lại trong 3,5 ngày. Hỏi mỗi đội làm một mình thì sau bao  nhiêu ngày sẽ  làm xong công việc nói trên (với năng suất bình thường).

    Lời Giải:

    Gọi thời gian để  đội I làm  một mình xong công việc là x, (ngày), x > 12.

    Gọi thời gian để đội II làm  một mình xong công việc là y, (ngày), y > 12.

    Trong 1 ngày đội  I và đội  II làm được khối lượng công việc tương ứng là: $\frac{1}{x}$, $\frac{1}{y}$ .

    Vì hai đội dự định làm chung trong 12 ngày  thì xong KLCV do đó ta có phương trình (1)  $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{1}{12}$

    Phần công việc hai đội làm chung trong  8 ngày là $\frac{8}{12}$ = $\frac{2}{3}$ (KLCV).

    Phần việc còn lại đội II phải làm là: $1 – \frac{2}{3} = \frac{1}{3}$ (KLCV).

    Vì năng suất tăng gấp đôi nên đội II  đẵ làm xong $\frac{1}{3}$  phần việc còn lại trong 3,5 ngày do ta có phương trình:$$\frac{1}{2}. \frac{1}{y} = \frac{1}{3}$$

    Theo bài ra ta có hệ phương trình: $$\left\{ \begin{align} & \frac{1}{x}+\frac{1}{y}=\frac{1}{12} \\ & \frac{7}{y}=\frac{1}{3}. \\ \end{align} \right.$$Giải hệ phương trình ta được: $\left\{ \begin{align}& x=28 \\& y=21 \\\end{align} \right.$

    Vậy thời gian để  đội I làm  một mình xong công việc là: 28 (ngày).

    Thời gian để  đội II làm  một mình xong công việc là: 21 (ngày).

    Bài toán 6. (Dạng toán công việc chung, công  việc riêng)

    Hải và Sơn  cùng làm một công việc trong 7 giờ 20 phút thì xong. Nếu Hải làm trong 5 giờ và  Sơn làm  trong 6 giờ thì cả hai làm được $\frac{3}{4}$  khối lượng công việc. Hỏi mỗi người làm  công  việc đó  trong mấy giờ thì  xong.

    Lời Giải:

    Gọi thời gian Hải làm một mình xong công việc là x (giờ), x > $\frac{22}{3}$.

    Gọi thời gian Sơn làm một mình xong công việc là y (giờ), y > $\frac{22}{3}$.

    Năng suất  của Hải và Sơn tính theo giờ là: $\frac{1}{x}$, $\frac{1}{y}$.

    Vì Hải và Sơn  cùng làm một công việc trong 7 giờ 20 phút thì xong do đó ta có phương trình: $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{3}{4}$.

    Sau 5 giờ Hải làm được KLCV là: 5. $\frac{1}{x}$; sau 6 giờ Sơn làm được KLCV là: 6. $\frac{1}{y}$.

    Vì Hải làm trong 5 giờ và  Sơn làm  trong 6 giờ thì cả hai làm được $\frac{3}{4}$ KLCV do đó ta có phương trình:$$\frac{5}{x} +\frac{6}{y} = \frac{3}{22}$$

    Theo bài ra ta có hệ phương trình: $$\left\{ \begin{align}& \frac{1}{x}+\frac{1}{y}=\frac{3}{22} \\ & \frac{5}{x}+\frac{6}{y}=\frac{3}{4}. \\ \end{align} \right.$$ Giải hệ phương trình ta được: $\left\{ \begin{align} & x=\frac{44}{3} \\ & y=\frac{44}{3} \\ \end{align} \right.$

    Vậy Hải làm công việc đó một mình trong:   44/3  giờ , Sơn làm công việc đó một mình trong:  44/3   giờ.

    Bài toán 7. (Dạng toán vòi nước chảy chung, chảy riêng)

    Hai vòi nước chảy chung vào một bể thì sau 4$\frac{4}{5}$ giờ đầy bể. Mỗi giờ lượng nước của vòi I chảy được bằng 1$\frac{1}{2}$ lượng nước chảy được  của vòi II. Hỏi  mỗi vòi chảy riêng thì trong bao  lâu đầy bể.

    Lời Giải:

    Gọi thời gian để vòi I chảy  một mình đầy bể là x, (giờ), x > $\frac{24}{5}$.

    Gọi thời gian để vòi II chảy  một mình đầy bể là y, (giờ), y > $\frac{24}{5}$.

    Trong 1 giờ vòi I và vòi II  chảy được lượng nước tương ứng là: $\frac{1}{x}$, $\frac{1}{y}$ (bể).

    Vì hai vòi cùng chảy sau $\frac{24}{5}$ thì đầy bể do đó ta có phương trình (1) :   $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{5}{24}$

    Vì trong 1 giờ lượng nước chảy được của vòi I bằng $\frac{2}{3}$ lượng nước chảy được của vòi II do đó ta có phương trình (2): $\frac{1}{x}$ = $\frac{3}{2}$. $\frac{1}{y}$    ;Theo bài ra ta có hệ phương trình:$$\left\{ \begin{align} & \frac{1}{x}+\frac{1}{y}=\frac{5}{24} \\ & \frac{1}{x}=\frac{3}{2}.\frac{1}{y}. \\ \end{align} \right.$$ Giải  hệ phương trình ta được: $\left\{ \begin{align} & x=8 \\ & y=12 \\ \end{align} \right.$

    Vậy vòi I chảy  một mình đầy bể trong 8 giờ, Vòi II chảy một mình đầy bể trong 12 giờ.

    Bài toán 8. (Dạng toán vòi nước chảy chung, chảy riêng)

    Một Máy bơm  muốn bơm đầy nước vào một bể chứa trong một  thời gian quy định thì mỗi giờ phải bơm  được 10m3. Sau khi bơm được $\frac{1}{3}$ dung tích bể chứa, người công nhân  vận hành cho máy bơm công xuất lớn hơn mỗi giờ bơm được 15 m3. Do đó bể được bơm đầy trước 48 phút so  với  thời  gian quy định. Tính dung tích của bể chứa.

    Lời Giải:

    Gọi dung tích của bể chứa là x, (m3), x > 0.

    Ta có thời gian dự định để bơ   m  đầy bể là: $\frac{x}{10}$  (giờ).

    Thời gian để bơm  $\frac{1}{3}$ bể  với công suất 10 m3/s là: $\frac{x}{30}$ (giờ).

    Thời gian để bơm  $\frac{2}{3}$ bể  còn lại với công suất 15 m3/s là: $\frac{2x}{45}$.

    Do công suất tăng khi bơm  $\frac{2}{3}$ bể  còn lại nên thời gian thời gian bơm đầy trước 48 phút so với quy định do đó ta có phương trình: $\frac{x}{10}$ – ($\frac{x}{30}$ + $\frac{2x}{45}$) = $\frac{4}{5}$    ; Giải PTBN ta được x = 36.      Vậy dung tích bể chứa là 36 m3.

    Bài toán 9. (Dạng toán vòi nước chảy chung, chảy riêng)

    Hai vòi  nước cùng chảy vào một bể sau 1 giờ 20 phút thì đầy bể. Nếu mở vòi thứ nhất chảy trong 10 phút và vòi thứ  hai chảy trong 12 phút thì đầy  $\frac{2}{15}$  bể. Hỏi nếu mỗi vòi chảy một mình thì bao lâu mới đầy bể.

    Lời Giải:

    Gọi thời gian để Vòi thứ nhất chảy  một mình đầy bể là x, (phút), x > 80.

    Gọi thời gian để Vòi thứ hai chảy  một mình đầy bể là y, (phút), y > 80.

    Công suất tính theo phút của  Vòi thứ nhất là: $\frac{1}{x}$ (Bể), vòi thứ hai là $\frac{1}{y}$  (Bể).

    Vì hai vòi cùng chảy sau 1 giờ 20 phút = 80 Phút, thì đầy bể do đó ta có phương trình (1) : $\frac{1}{x}$ + $\frac{1}{y}$ = $\frac{1}{80}$

    Sau 10 phút Vòi 1 chảy được: 10. $\frac{1}{x}$ (Bể).   ;Sau 12 phút Vòi  2 chảy  được: 12. $\frac{1}{y}$ (Bể)

    Vì nếu mở Vòi thứ nhất chảy trong 10 phút và Vòi thứ  hai chảy trong 12 phút thì đầy  $\frac{2}{15}$  bể do đó ta có phương trình: $\frac{10}{x}$ + $\frac{12}{y}$ = $\frac{2}{15}$. Theo bài ra ta có hệ phương trình: $$\left\{ \begin{align} & \frac{1}{x}+\frac{1}{y}=\frac{1}{80} \\ & \frac{10}{x}+\frac{12}{y}=\frac{2}{15} \\ \end{align} \right.$$ Giải hệ phương trình ta được: x= 120 phút, y = 240 phút.

    Vậy thời gian vòi 1 chảy đầy bể là 120 phút, vòi 2 là 240 phút.

  • Giải bài toán chuyển động lớp 9

    Giải bài toán chuyển động lớp 9

    Khi giải bài toán bằng cách lập hệ phương trình, chúng ta thường gặp các bài toán về chuyển động như chuyển động cùng chiều, chuyển động ngược chiều nhau, chuyển động xuôi dòng, chuyển động ngược dòng… Dưới đây là phương pháp giải bài toán chuyển động lớp 9.

    Cách giải bài toán chuyển động lớp 9

    • Toán chuyển động có 3 đại lượng: Quãng đường, Vận tốc, Thời gian.
    • Mối liên hệ của 3 đại lượng trên:
      • Quãng đường = Vận tốc x Thời gian
      • Vận tốc = Quãng đường : Thời gian
      • Thời gian = Quãng đường : Vận tốc
    • Các đơn vị của ba đại lượng phải phù hợp với nhau
      • Quãng đường tính bằng km, vận tốc km/h thì thời gian tính bằng giờ (h)
      • Quãng đường tính bằng m, vận tốc m/s thì thời gian tính bằng giây (s)

    Ví dụ toán chuyển động lớp 9

    Bài toán 1. (Dạng toán chuyển động)

    Một Ô tô đi từ A đến B cùng một lúc, Ô tô thứ hai đi từ  B về A  với vận tốc bằng $\frac{2}{3}$  vận tốc Ô tô thứ nhất. Sau 5 giờ chúng gặp nhau. Hỏi mỗi Ô tô đi cả quãng đường AB  mất bao lâu.

    Lời Giải

    • Gọi thời gian ô tô đi từ A đến B là $x$ (h), điều kiện $x>0$;
    • Ta có vận tốc Ô tô đi từ A đến B là : $\frac{AB}{x}$ (km/h);
    • Vận tốc  Ô tô đi từ B về A là: $\frac{2}{3}$ $\frac{AB}{x}$ (km/h);
    • Sau 5 giờ Ô tô đi từ A đến B đi được quãng đường là: $5. \frac{AB}{x}$ (km);
    • Sau 5 giờ Ô tô đi từ B đến A đi được quãng đường là: $5. \frac{2}{3}$. $\frac{AB}{x}$ (km);
    • Vì sau 5 giờ chúng gặp nhau do đó ta có phương trình: $5. \frac{AB}{x} + 5. \frac{2}{3}. \frac{AB}{x} = AB$;
    • Giải phương trình ta được: x = $\frac{25}{3}$.
    • Vậy thời gian Ô tô đi từ A đến B là $\frac{25}{3}$, thời gian Ô tô đi từ B đến A là $\frac{25}{2}$.

    Bài toán 2. (Dạng toán chuyển động)

    Một Ô tô du  lịch đi từ A đến C. Cùng lúc từ địa điểm B nằm trên đoạn AC có một Ô tô vận tải cùng đi đến C.  Sau 5 giờ hai Ô tô gặp nhau tại C. Hỏi Ô tô du lịch đi từ A đến B mất bao lâu ,  biết rằng  vận tốc  của Ô tô tải bằng $\frac{3}{5}$ vận tốc của Ô tô du lịch.

    Lời Giải

    • Gọi thời gian ô tô du lịch đi từ A đến B là $x$ (h). (điều kiện $0 < x< 5$).
    • Ta có thời gian ô tô du lịch đi từ B đến C là $(5 – x)$ (h).
    • Vận tốc xe ô tô du lịch là: $\frac{BC}{5-x}$ (km/h).
    • Ta có vận tốc xe tải là: $\frac{BC}{5}$ (km/ h).
    • Vì vận tốc  của Ô tô tải bằng $\frac{3}{5}$ vận tốc của Ô tô du lịch, nên ta có phương trình: $$\frac{BC}{5} =\frac{3}{5}.\frac{BC}{5-x}$$ Giải phương trình ta được: $x = 2$.
    • Vậy Ô tô du lịch đi từ A đến B mất 2 giờ.

    Bài toán 3 (Dạng toán chuyển động)

    Đường sông từ thành phố A đến thành phố B ngắn hơn đường bộ 10 km để đi từ thành phố A đến thành phố B  Ca nô đi hết 3  giờ 20  phút Ô tô  đi hết 2 giờ. Vận tốc Ca nô kém vận tốc Ô tô 17 km /h. Tính vận tốc  của Ca nô.

    Lời Giải

    • Gọi vận tốc của Ca nô  là $x$ (km/h). (điều kiện $x> 0$).
    • Ta có vận tốc của Ô tô là  $x + 17$  (km/h).
    • Ta có chiều dài quãng đường sông AB là: $\frac{10}{3}$x (km); chiều dài quãng đường bộ AB là: $2(x + 17)$ (km).
    • Vì đường sông từ thành phố A đến thành phố B ngắn hơn đường bộ 10 km do đó ta có phương trình $$2(x + 17) – \frac{10}{3}x =10$$ Giải phương trình này ta được $x = 18$.
    • Vậy vận tốc của Ca nô là: 18 km/h.

    Bài toán 4 (Dạng toán chuyển động)

    Một người  đi xe đạp từ tỉnh A đến tỉnh B cách nhau 50 km. Sau đó 1 giờ 30 phút một người đi  xe  máy cũng đi từ A và đến B  sớm hơn 1 giờ. Tính vận tốc  của  mỗi xe, biết rằng vận tốc xe máy gấp  2,5  lần  vân tốc xe đạp.

    Lời Giải

    Gọi vận tốc của người đi xe đạp  là x (km/h).(x> 0).

    Ta có vận tốc của người đi xe máy là 2,5 x  (km/h).

    Thời gian người đi xe đạp đi từ A đến B là $\frac{50}{x}$ (h); Thời gian người đi xe máy đi từ A đến B là $\frac{50}{2,5x}$ (h).

    Vì người đi xe máy đi sau  1 giờ 30 phút và đến B sớm hơn 1 giờ so với người đi xe đạp do đó ta có phương trình:$$\frac{50}{x} – \frac{50}{2,5x} = 2,5$$ Giải phương trình bậc nhất này ta được $x = 12$.

    Vậy vận tốc của người đi xe đạp là 12 km/h, vận tốc của người đi xe máy là 30 km/h.

    Bài toán 5 (Dạng toán chuyển động)

    Một người đi xe máy từ A đến B với  vân tốc trung bình 30 km / h. Khi  đến B  người đó nghỉ 20 phút  rồi quay trở về A  với vận tốc trung bình 25 km /h. Tính quãng đường AB,  biết thời gian cả đi và về là 5 giờ 50 phút.

    Lời Giải

    Gọi chiều dài của quãng đường AB là x (km).(x> 0).

    Thời gian người đi xe máy đi từ A đến B là $\frac{x}{30}$ (h); Thời gian người đi xe máy đi từ B đến A là $\frac{x}{25}$ (h)

    Vì người đi xe máy nghỉ tại B  20 phút và tổng thời gian cả đi và về là là 5 giờ 50 phút do đó ta có phương trình:$$\frac{x}{30} + \frac{x}{25}+ \frac{1}{3} = 5\frac{5}{6}$$ Giải phương trình này ta được $x = 75$.

    Vậy độ dài quãng đường AB là 75 km/h.

    Bài toán 6 (Dạng toán chuyển động)

    Một  Ô tô dự định đi từ tỉnh A đến tỉnh B với vận tốc trung  bình  40 km/ h. Lúc đầu ô tô đi với vận tốc đó, khi  còn 60 km nữa thì được nửa quãng đường AB, người lái xe tăng thêm vân tốc 10 km/h trên quãng đường  còn lại,  do đó Ô tô đến B sớm  hơn 1 giờ so với dự định. Tính quãng đường AB.

    Lời Giải

    Gọi chiều dài của quãng đường AB là x (km).(x> 0). (Ta chỉ xét quãng đường BC khi vận tốc thay đổi)

    Ta có thời gian dự định đi hết quãng đường BC là $\frac{\frac{x}{2}+60}{40}$ (h)

    Thời gian Ô tô thực đi trên quãng đường BC sau khi tăng vận tốc thêm 10 km/h là: $\frac{\frac{x}{2}+60}{50}$

    Vì sau khi người lái xe tăng thêm vân tốc 10 km/h trên quãng đường  còn lại,  do đó Ô tô đến B sớm  hơn 1 giờ so với dự định do đó ta có phương trình: $$\frac{\frac{x}{2}+60}{40}-\frac{\frac{x}{2}+60}{50}= 1$$ Giải PTBN ta được: $x = 280$.

    Vậy quãng đường AB dài 280 km.

    Bài toán 7 (Dạng toán chuyển động)

    Một  Ô tô dự định đi từ A đến B trong thời gian nhất định nếu xe chạy  với vận tốc 35 km/h thì đến  chậm mất 2 giờ. Nếu xe chạy với vận tốc 50 km/h thì đến sớm  hơn 1 giờ. Tính quãng đường AB và thời gian dự định đi lúc đầu.

    Lời Giải

    Gọi chiều dài của quãng đường AB là x (km).(x> 0).

    Thời gian xe chạy với vận tốc 35 km/h là $\frac{x}{35}$ (h); Thời gian xe chạy với vận tốc 50 km/h là $\frac{x}{50}$ (h).

    Theo bài ra ta có phương trình: $$\frac{x}{35} – 2 = \frac{x}{50} + 1$$ Giải phương trình này ta được $x = 350$ km.

    Vậy thời gian dự định là $\frac{350}{35}$ – 2 = 8 (giờ), Quãng đường AB là 350 km.

    Bài toán 8 (Dạng toán chuyển động)

    Hai vật chuyển động trên một đường tròn có đương kính 2m , xuất phát cùng một lúc từ cùng một điểm .  Nếu chúng chuyển động cùng chiều thì cứ 20 giây lại gặp nhau. Nếu chúng chuyển động ngược chiều thì cứ 4 giây lại gặp nhau. Tính vận tốc của  mỗi  vật.

    Lời Giải

    Gọi vận tốc của Vật I là $x$ (m/s). (điều kiện $x> 0$).

    Gọi vận tốc của Vật II là $y$ (m/s). (điều kiện $y> 0, x>y$).

    Sau 20 s hai vật chuyển động được quãng đường là $20x, 20y$ (m).

    Vì nếu chúng chuyển động cùng chiều thì cứ 20 giây lại gặp nhau do đó ta có phương trình: $$20x – 20y = 20\pi $$

    Sau 4 s hai vật chuyển động được quãng đường là $4x, 4y$ (m).

    Vì nếu chúng chuyển động ngược chiều thì cứ 4 giây lại gặp nhau do đó ta có phương trình: $$4x + 4y = 20$\pi $$

    Theo bài ra ta có hệ phương trình: $$\left\{ \begin{array} 20x-20y=20\pi  \\ 4x+4y=20\pi  \\ \end{array} \right.$$ Giải hệ PT ta được: $\left\{ \begin{array} x=3\pi  \\ y=2\pi  \\ \end{array} \right.$

    Vậy vận tốc của hai vật là: 3$\pi $ (m/s) và 2$\pi $ (m/s).

    Bài toán 9 (Dạng toán chuyển động)

    Một chiếc Thuyền khởi hành từ bến sông A, sau 5 giờ 20 phút một Ca nô  chạy từ bến sông A đuổi theo và gặp thuyền cách bến A 20 km. Hỏi  vận tốc của thuyền, biết rằng Ca nô chạy nhanh hơn Thuyền 12 km/h.

    Lời Giải

    Gọi vận tốc của của Thuyền là x (km/h).(x> 0).

    Ta có vận tốc của Ca nô là x + 12 (km/h).

    Thời gian Thuyền đi hết quãng đường 20 km là: $\frac{20}{x}$ (h).

    Thời gian Ca nô đi hết quãng đường 20 km là: $\frac{20}{x+12}$ (h).

    Vì sau 5 giờ 20 phút một Ca nô  chạy từ bến sông A đuổi theo và gặp thuyền cách bến A 20 km, do đó ta có phương trình: $$\frac{20}{x} – \frac{20}{x+12} = \frac{16}{3}$$ Giải phương trình bậc hai x2 + 12x – 45 =0 ta được x = 3 (TM).

    Vậy vận tốc của Ca nô là 15 km/h.

    Bài toán 10 (Dạng toán chuyển động)

    Quãng đường AB dài 270 km. Hai Ô tô khởi hành cùng một lúc đi từ A đến B. Ô tô thứ nhất chạy nhanh hơn Ô tô thứ  hai 12 km/h,  nên đến trước Ô tô thứ hai 40 phút. Tính vận tốc của mỗi Ô tô.

    Lời Giải

    Gọi vận tốc của Ô tô thứ nhất là x (km/h).(x> 12).

    Ta có vận tốc của Ô tô thứ hai là x – 12 (km/h).

    Thời gian Ô tô thứ nhất đi hết quãng đường AB là: $\frac{270}{x}$ (h).

    Thời gian Ô tô thứ  hai đi hết quãng đường AB là: $\frac{270}{x-12}$ (h).

    Vì  hai Ô tô cùng xuất phát và Ô tô thứ nhất đến B trước Ô tô thứ hai là 40 P nên ta có PT:$\frac{270}{x-12}$- $\frac{270}{x}$= $\frac{2}{3}$

    Giải PTBH ta được x= 6+12$\sqrt[{}]{34}$

    Vậy vận tốc của Ô tô thứ nhất 6+12$\sqrt[{}]{34}$km/h, Ô tô thứ hai là 12$\sqrt[{}]{34}$- 6  km/h.

    Bài toán 11 (Dạng toán chuyển động)

    Một Tàu thuỷ chạy trên một khúc sông dài 80 km, cả đi và  về mất 8 giờ 20 phút. Tính vận tốc của Tàu thuỷ khi nước yên lặng, biết rằng  vận tốc của  dòng  nước là 4 km/h.

    Lời Giải

    Gọi vận tốc của Tàu thuỷ khi nước yên lặng là x (km/h).(x> 4).

    Vận tốc Tàu thuỷ khi đi xuôi dòng: x + 4 (km/h).

    Vận tốc Tàu thuỷ khi đi ngược dòng: x – 4 (km/h).

    Thời gian Tàu thuỷ đi xuôi dòng là: $\frac{80}{x+4}$ (h), Thời gian Tàu thuỷ đi ngược dòng là: $\frac{80}{x-4}$ (h).

    Vì tổng thời gian cả xuôi dòng và ngược dòng là 8 giờ 20 phút do đo ta có phương trình:

    $\frac{80}{x+4}$ + $\frac{80}{x-4}$=$\frac{25}{3}$.

    Giải PTBH:  được: x = 20 (TM).

    Vậy vận tốc Tàu thuỷ khi nước yên lặng là: 20 km/h.

    Bài toán 12 (Dạng toán chuyển động)

    Hai Ca  nô khởi hành cùng một lúc và chạy từ bến sông A đến bến sông B Ca nô I chạy với vận tốc 20 km/h, Ca nô II chạy với vận tốc 24 km/h. Trên đường đi Ca nô II dừng lại 40 phút, sau đó tiếp tục chạy với vận tốc  như  cũ. Tính chiều dài quãng sông AB, biết rằng hai Ca nô đến B cùng một lúc.

    Lời Giải

    Gọi chiều dài quãng sông A B là x (km).(x> 0).

    Ta có thời gian Canô I  chạy từ A đến B là: $\frac{x}{20}$ (h), Ta có thời gian Canô II  chạy từ A đến B là: $\frac{x}{24}$ (h).

    Trên đường đi Ca nô II dừng lại 40 phút và cùng đến B do đó ta có phương trình: $\frac{x}{20}$ – $\frac{x}{24}$=  $\frac{2}{3}$

    Giải PTBN ta được x = 80 km.           Vậy quãng đường AB là 80km.

    Bài toán 13 (Dạng toán chuyển động)

    Hai Ô tô khởi hành cùng một lúc từ địa điểm  A đến địa điểm B dài 240 km. Mỗi giờ Ô tô thứ nhất chạy chanh hơn Ô tô thứ hai 12 km/h nên đến địa điểm B trước Ô tô thứ hai là 100 phút. Tính vận tốc  của mỗi Ô tô.

    Lời Giải

    Gọi vận tốc của Ô tô thứ hai là x (km/h).(x> 0).

    Ta có vận tốc của Ô tô thứ nhất là x + 12 km/h.

    Thời gian Ô tô thứ hai đi hết quãng đường AB là: $\frac{240}{x}$ (h).

    Thời gian Ô tô thứ nhất đi hết quãng đường AB là: $\frac{240}{x+12}$ (h).

    Vì Ô tô thứ nhất đến địa điểm B trước Ô tô thứ hai là 100 phút do đó ta có PT: $\frac{240}{x}$ – $\frac{240}{x+12}$ = $\frac{5}{3}$

    Giải PTBH ta được x= 36.               Vậy vận tốc của Ô tô thứ nhất 48 km/h, Ô tô thứ hai là 36 km/h.

    Bài toán 14 (Dạng toán chuyển động)

    Một Ca nô  xuôi dòng 42 km rồi ngước dòng trở lại 20 km  hết tổng cộng 5 giờ. Biết vận tốc của dòng chảy là 2 km/h. Tính vận tốc của Ca nô lúc dòng nước yên lặng.

    Lời Giải

    Gọi vận tốc của Ca nô khi nước yên lặng là x (km/h).(x> 2).

    Vận tốc Ca nô khi đi xuôi dòng: x + 2 (km/h).

    Vận tốc Ca nô khi đi xuôi dòng: x – 2 (km/h).

    Thời gian Ca nô đi xuôi dòng là: $\frac{42}{x+2}$ (h).

    Thời gian Ca nô đi ngược dòng là: $\frac{20}{x-2}$ (h).

    Vì tổng thời gian cả xuôi dòng và ngược dòng là 5 giờ do đó ta có phương trình:  $\frac{42}{x+2}$ + $\frac{20}{x-2}$= 5.

    Giải PTBH: 5x2 – 62x + 24 = 0   ta được: x = 12 (TM).       Vậy vận tốc Ca nô khi nước yên lặng là: 12 km/h.

    Bài toán 15 (Dạng toán chuyển động)

    Hai người đi xe đạp cùng xuất phát một lúc đi từ A đến B dài 30 km, vận tốc của họ hơn kém nhau 3 km/h nên đến B sớm  muộn hơn nhau 30 phút. Tính vận tốc của mỗi người.

    Lời Giải

    Gọi vận tốc của người đi chậm là x (km/h).(x> 0).

    Ta có vận tốc của người đi nhanh là x + 3 (km/h).

    Thời gian người đi nhanh từ A đến B là $\frac{30}{x+3}$ (h).

    Thời gian người đi chậm từ A đến B là $\frac{30}{x}$ (h).

    Vì hai người đến  B sớm, muộn hơn nhau 30 phút do đó ta có phương trình: $\frac{30}{x}$ – $\frac{30}{x+3}$ = $\frac{1}{2}$

    Giải PTBH:  x2 + 3x – 180 = 0  ta được x = 12 (TM)

    Vậy vận tốc của người đi nhanh là 15km/h, vận tốc của người đi chậm là:12 km/h.

    Bài toán 16 (Dạng toán chuyển động)

    Một người đi  từ tỉnh A đến tỉnh B cách nhau 78 km. sau đó 1 giờ người thứ hai đi từ tỉnh B đến tỉnh A hai người gặp  nhau tại địa điểm C cách B 36 km. Tính thời gian mỗi người đã đi từ lúc khởi hành đến lúc gặp nhau, biết vận tốc người thứ hai lớn hơn vận tốc người thứ nhất là 4 km/h.

    Lời Giải

    Gọi vận tốc của người đi từ A  là x (km/h).(x> 0).

    Thời gian người đi từ A, tính từ lúc khởi hành đến lúc gặp nhau là: $\frac{42}{x}$ (h).

    Vận tốc của người đi từ B  là x + 4 (km/h).

    Thời gian người đi từ B, tính từ lúc khởi hành đến lúc gặp nhau là: $\frac{36}{x+4}$ (h).

    Vì hai người gặp nhau tại C, người thứ hai đi sau người thứ nhất 1 giờ do đó ta có phương trình:$$\frac{42}{x} – \frac{36}{x+4}=1$$ Giải PTBH: x2 – 2x – 168 = 0    ta được x= 14 (TM).

    Vậy thời gian người đi từ A từ lúc khởi hành đến lúc gặp nhau là: 3 giờ.

    thời gian người đi từ B từ lúc khởi hành đến lúc gặp nhau là: 2 giờ.

    Bài toán 17 (Dạng toán chuyển động)

    Quãng đường AB  dài 120 km. Hai Ô tô khởi hành cùng một lúc đi từ A đến B,Ô tô thứ nhất chạy nhanh hơn Ô tô thứ hai là 10 km/h nên đến  B trước Ô tô thứ hai 24 phút. Tính vận tốc  mỗi xe.

    Lời Giải

    Gọi vận tốc của Ô tô thứ nhất là x (km/h).(x> 0).

    Ta có vận tốc của Ô tô thứ hai là x – 10 (km/h).

    `Thời  gian Ô tô thứ nhất đi hết quãng đường AB là:$\frac{120}{x}$ (h).

    Thời  gian Ô tô thứ hai hết quãng đường AB là:$\frac{120}{x-10}$ (h).

    Vì Ô tô thứ nhất chạy nhanh hơn Ô tô thứ hai là 10 km/h nên đến  B trước Ô tô thứ hai 24 phút do đó ta có phương trình: $$\frac{120}{x-10}- \frac{120}{x} =\frac{2}{5}$$ Giải PT BH: x2 – 10x – 300 = 0   ta được x= 60 (TM).        Vậy vận tốc  của Ô tô thứ nhất là : 60 km/h, vận tốc  của Ô tô thứ hai là : 50 km/h.

    Bài toán 18 (Dạng toán chuyển động)

    Một người dự định đi từ A đến B với thời gian đẵ định. Nếu người đó tăng vận  tốc thêm  10 km/h thì đến B sớm hơn dự định 1 giờ. Nếu người đó giảm vận tốc đi 10 km/h thì đến B muộn hơn dự định 2 giờ. Tính vận tốc, thời gian dự định đi và độ dài quãng đường  AB.

    Lời Giải :

    Gọi vận tốc dự định đi từ A đến B của người đó là x  (km/h).(x> 0).

    Gọi thời gian dự định đi từ A đến B của người đó là y  (h).(y> 0).

    Ta  có độ dài của quãng đường AB là x.y.

    Vì nếu người đó tăng vận  tốc thêm 10 km/h thì đến B sớm hơn dự định 1 giờ do đó ta có PT (1):

    (x + 10).(y-1) =xy.

    Vì nếu người đó giảm vận tốc đi 10 km/h thì đến B muộn hơn dự định 2 giờ do đó ta có PT (2)

    (x – 10).(y+2) =xy.

    Theo bài ra ta có hệ phương trình: $$\left\{ \begin{array}& (x+10)(y-1)=xy \\ & (x-10)(y+2)=xy \\ \end{array} \right.$$ Giải hệ phương trình ta được $\left\{ \begin{array} & x=30 \\ & y=4 \\ \end{array} \right.$

    Vậy vân tốc dự định là 30 km/h, thời gian dự định là 4 giờ, Quãng đường AB là 120 km.

    Bài toán 19 (Dạng toán chuyển động)

    Một Ca nô xuôi dòng 1 km và ngược dòng 1km hết tất cả 3,5 phút. Nếu Ca nô xuôi 20 km  và ngược 15 km thì hết 1 giờ. Tính vận tốc dòng nước và vận tốc riêng của Ca nô.

    Lời Giải :

    Gọi  vận tốc riêng của Ca nô là x (km/p), (x> 0).

    Gọi  vận tốc riêng của dòng nước  là y ; (km/p), (y> 0) ; (x> y).

    Ta có vận tốc của Ca nô khi đi xuôi dòng là  x+ y (km/phút), ngược dòng là x – y (km/phút).

    Thời gian Ca nô xuôi dòng 1 km là $\frac{1}{x+y}$ (P). Thời gian Ca nô ngược dòng 1 km là $\frac{1}{x-y}$ (P).

    Vì tổng thời gian xuôi dòng 1 km và ngược dòng 1km hết tất cả 3,5 phút do đó ta có phương trình (1) là

    $\frac{1}{x+y}$ + $\frac{1}{x-y}$ =3,5

    Vì tổngthời gian Ca nô xuôi dòng 20 km  và ngược 15 km thì hết 1 giờ do đó ta có phương trình (2)$$\frac{20}{x+y} + \frac{15}{x-y} =60$$Theo bài ra ta có hệ phương trình: $$\left\{ \begin{array}& \frac{1}{x+y}+\frac{1}{x-y}=3.5 \\ & \frac{20}{x+y}+\frac{15}{x-y}=60. \\

    \end{array} \right.$$ Giải hệ phương trình ta được $\left\{ \begin{array} & x=7/12 \\ & y=1/12 \\ \end{array} \right.$ Vậy vận tốc của dòng nước là:1/12 , Vận tốc riêng của Ca nô là:7/12

    Bài toán 20 (Dạng toán chuyển động)

    Bạn Hà dự định đi từ A đến B cách nhau 120 km trong một thời gian đẵ định. Sau khi 1 giờ, Hà nghỉ 10 phút, do đó để đến B đúng hẹn Hà phải tăng  vận tốc thêm  6 km/h. Tính vận tốc lúc đầu  của Hà.

    Lời Giải :

    Gọi vận tốc lúc đầu của Hà là x, (km/h), (x> 0);

    Thời gian Hà dự định đi từ A đến B là $\frac{120}{x}$ (giờ);

    Sau 1 giờ Hà đi được quãng đường là x km, quãng đường còn lại Hà phải đi là (120 – x);

    Thời gian Hà đi trên quãng đường còn lại (120 – x) là $\frac{120-x}{x+6}$ (giờ);

    Vì trên đường đi Hà nghỉ 10 phút, do đó để đến B đúng hẹn Hà phải tăng  vận tốc thêm  6 km/h nên ta có phương trình: $\frac{120}{x}$ = 1 + $\frac{1}{6}$ + $\frac{120-x}{x+6}$ , giải PT BH: x2 + 42x – 4320 = 0   ta được: x1 = 48, x2 = – 90 (loại).

    Vậy vận tốc lúc đầu của Hà là 48 km/h.

  • Toán 9 – Giải bài toán bằng cách lập phương trình

    Toán 9 – Giải bài toán bằng cách lập phương trình

    Dưới đây, O2 Education xin hướng dẫn cách giải bài toán bằng cách lập phương trình lớp 9. Bao gồm các dạng bài về chuyển động, hình học, năng suất, tính tuổi, thêm bớt số. Mời các em tham khảo thêm Giải bài toán bằng cách lập hệ phương trình.

    1. Các bước giải bài toán bằng cách lập phương trình

    Bước 1: Đọc hiểu đề bài để lập phương trình

    • Xác định đại lượng cần tìm, đại lượng đã cho và mối quan hệ giữa các đại lượng;
    • Chọn ẩn phù hợp, tìm điều kiện cho ẩn số đó;
    • Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết (chú ý cần đưa về sử dụng thống nhất cùng một đơn vị);
    • Lập phương trình biểu thị mối quan hệ giữa các đại lượng.

    Bước 2: Giải phương trình vừa lập

    Bước 3: Kiểm tra và kết luận

    • Kiểm tra nghiệm nào thoả mãn điều kiện của ẩn
    • Trả lời câu hỏi của đề bài

    Khó khăn bạn thường gặp phải khi giải bài toán bằng cách lập phương trình là bước 1. Bạn không biết biểu diễn các đại lượng chưa biết theo ẩn và theo các đại lượng đã biết khác.

    2. Các dạng toán giải bằng cách lập phương trình

    Các bài toán giải bằng cách lập phương trình có thể chia thành các dạng sau:

    • Dạng toán chuyển động. Mời các em xem trong bài Giải bài toán chuyển động lớp 9
    • Dạng toán liên quan tới các kiến thức hình học.
    • Dạng toán năng suất (công việc làm chung, làm riêng; chảy chung, chảy riêng của vòi nước). Mời các em xem chi tiết trong bài Bài toán về năng suất
    • Dạng toán tìm số.
    • Dạng toán sử dụng các các kiến thức về %.
    • Dạng toán sử dụng các kiến thức vật lý, hóa học.

    3. Bài tập giải bằng cách lập phương trình

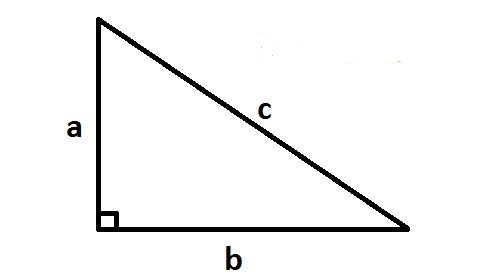
    Bài toán 21 (Dạng toán liên quan tới các kiến thức hình học)

    Tìm  hai cạnh của một tam giác vuông biết cạn huyền bằng 13 cm và tổng hai cạnh góc vuông bằng 17.

    Lời Giải :

    Gọi cạnh góc  vuông thứ nhất của tam giác là x (cm), (0< x < 17).

    Ta có cạnh góc vuông còn lại là: (17 – x), (cm).

    Vì cạnh huyền  của tam giác vuông là 13  do đó ta có phương trình:  x2 + (17 – x)2  = 132

    Giải PTBH: x2 – 17x + 60 = 0    ta được: x1 = 12, x2 = 5.

    Vậy độ dài các cạnh góc  vuông lần lượt là 12 cm, 5, cm.

    Bài toán 22 (Dạng toán liên quan tới các kiến thức hình học)

    Một khu vườn Hình chữ nhật có chu vi 280 m. Người ta làm  một lối đi xung quanh vườn (thuộc đất vườn) rộng 2 m, diện tích còn lại để trồng trọt là 4256 m2. Tính kích thước (các cạnh) của khu vườn đó

    Lời Giải :

    Gọi một cạnh của khu vườn là x, (m), x< 140.

    Ta có cạnh  còn lại của khu vườn là: (140 – x).

    Do lối xung quanh vườn rộng 2 m nên các kích thước các cạnh còn lại để trồng trọt là: (x – 4), (140 – x – 4) (m).

    Vì diện tích còn lại để trồng trọt là 4256 m2 do đó ta có phương trình: (x – 4). (140 – x – 4) = 4256.

    Giải PTBH: x2 – 140x + 4800 = 0    ta được x2  = 80, x2 = 60.    Vậy các cạnh của khu vườn HCN là 80 m, 60 m.

    Bài toán 23 (Dạng toán liên quan tới các kiến thức hình học)

    Một thửa ruộng hình chữ nhật có chu vi 250 m. Tính diện tích của thửa ruộng biết rằng nếu chiều dài giảm 3 lần và chiều rộng tăng 2 lần thì chu vi thửa ruộng không đổi.

    Lời Giải :

    Gọi chiều rộng và chiều dài của thửa ruộng hình chữ nhật lần lượt là x và y, (m), (0< x< y < 125).

    Vì chu vi thửa ruộng hình chữ nhật là 250 m do đó ta có phương trình: x + y = 125.

    Vì chiều dài giảm 3 lần và chiều rộng tăng 2 lần thì chu vi thửa ruộng không đổi do đó ta có phương trình:

    1. x + $\frac{y}{3}$ = 125. Theo bài ra ta có hệ phương trình: $\left\{ \begin{align}

    & x+y=125 \\

    & 2x+\frac{y}{3}=125 \\

    \end{align} \right.$  , giải hệ phương trình ta được $\left\{ \begin{align}

    & x=50 \\

    & y=75 \\

    \end{align} \right.$

    Vậy dịên tích của thửa ruộng HCN là; 50. 75 = 3750 m2.

    Bài toán 24 (Dạng toán liên quan tới các kiến thức hình học)

    Cho một tam giác vuông. Khi ta tăng mỗi cạnh góc vuông lên 2 cm  thì diện tích tăng 17 cm2. Nếu giảm các cạnh góc vuông đi một cạnh đi 3 cm một cạn 1 cm thì diện tích sẽ giảm đi 11cm2. Tìm  các cạnh của tam giác vuông đó.

    Lời Giải :

    Gọi các cạnh của tam giác vuông lần lượt là x, y; (cm), x, y > 3.

    Vì khi tăng mỗi cạnh góc vuông lên 2 cm  thì diện tích tăng 17 cm2 do đó ta có phương trình:

    $\frac{1}{2}$ (x+ 2) (y + 2) =  $\frac{1}{2}$ xy + 17.

    Vì nếu giảm các cạnh góc vuông đi một cạnh đi 3 cm một cạn 1 cm thì diện tích sẽ giảm đi 11cm2 do đó ta có phương trình: $\frac{1}{2}$ (x – 3) (y – 1) =  $\frac{1}{2}$ xy – 11.

    Theo bài ra ta có hệ phương trình: $\left\{ \begin{align}

    & x+y=15 \\

    & x-3y=25 \\

    \end{align} \right.$ , giải hệ phương trình ta được: $\left\{ \begin{align}

    & x=10 \\

    & y=5 \\

    \end{align} \right.$

    Vậy ta có các cạnh của tam giác là: 5, 10, 5$\sqrt[{}]{5}$ (cm).

     

    Bài toán 34 (Dạng toán tìm số)

    Tìm hai số biết tổng bằng 19 và tổng các bình phương của chúng bằng 185.

    Lời Giải:

    Gọi số thứ nhất là x, (0< x<19).

    Ta có số thứ hai là (  19 – x).

    Vì tổng các bình phương của chúng bằng 185  do đó ta có phương trình: x2 + (19 – x)2 = 185.

    Giải PTBH: x2 – 19x + 88 = 0    được:  x1= 11, x2  = 9.

    Vậy hai số phải tìm là 11 và 9.

    Bài toán 35 (Dạng toán tìm số)

    Tìm tất cả các số tự nhiên có hai chữ số, biết rằng chữ số hàng đơn vị  nhỏ hơn chữ số hàng  chục là 2 và tích của hai chữ số đó của nó luôn lớn hơn tổng hai chữ số của nó là 34.

    Lời Giải:

    Gọi chữ số phải tìm là $\overline{ab}$; 0 $\le $a,b $\le $9, a  # 0.

    Vì chữ số hàng đơn vị  nhỏ hơn chữ số hàng  chục là 2 do đó ta có phương trình: a – b = 2.

    Vì tích của hai chữ số đó của nó luôn lớn hơn tổng hai chữ số của nó là 34, do đó ta có phương trình:

    a.b – (a + b) = 34.

    Theo bài ra ta có hệ phương trình: $\left\{ \begin{align}

    & a-b=2 \\

    & a.b-(a+b)=34 \\

    \end{align} \right.$             ;Giải hệ phương trình ta được : $\left\{ \begin{align}

    & a=8 \\

    & b=6 \\

    \end{align} \right.$

    Vậy số phải tìm là 86.

    Bài toán 36 (Dạng toán tìm số)

    Trong dịp kỷ niệm 57 năm ngày thành lập nước CHXHCN Việt Nam 180 học sinh được điều về thăm quan diễu hành, người ta tính. Nếu dùng loại xe lớn chuyên chở một lượt hết số học sinh thì phải điều động ít hơn dùng loại xe nhỏ là 2  chiếc. Biết rằng mỗi ngế ngồi 1 học sinh và mỗi xe lớn nhiều hơn  xe nhỏ là 15 chỗ ngồi. Tính số xe lớn, nếu loại xe đó được huy động.

    Lời Giải:

    Gọi số Xe lớn là x (chiếc), x nguyên dương.

    Ta có số Xe nhỏ là: x + 2.

    Ta có số hoc sinh Xe lớn chở được là: $\frac{180}{x}$ (HS).

    Ta có số hoc sinh Xe nhỏ chở được là: $\frac{180}{x+2}$ (tấn).

    Vì mỗi Xe lớn chở được số học sinh nhiều hơn số Xe nhỏ là 15 học sịnh do đó ta có phương trình:

    $\frac{180}{x}$ – $\frac{180}{x+2}$ = 15  ;    Giải phương trình ta được x = 4;      Vậy số Xe lớn là 4 .

    Bài toán 37 (Dạng toán tìm số)

    Một đội xe phải chở 168 tấn thóc. Nếu tăng thêm 6 xe và chở thêm 12 tấn thóc thì mỗi xe xhở nhẹ hơn lúc đầu là 1 tấn. Hỏi lúc đầu mỗi đội có bao nhiêu xe.

    Lời Giải:

    Gọi số Xe lúc đầu lúc đầu của đội là x (chiếc),  x nguyên dương.

    Số thóc lúc đầu mỗi xe phải chở là : $\frac{168}{x}$ (tấn).

    Số Xe sau khi tăng thêm 6 xe là: (x + 6), (Chiếc).

    Sau khi tăng số xe thêm 6 , số thóc thêm 12 tấn thì số thóc mỗi xe cần phải chở là:$\frac{168+12}{x+6}$ (tấn).

    Vì số thóc mỗi xe chở nhẹ hơn 1 tấn sau khi tăng số xe và thêm 12 tấn do đó ta có phương trình:

    $\frac{168}{x}$ – $\frac{168+12}{x+6}$ = 1;     Giải  PTBH: x2 + 2x – 24 = 0    ta được: x = 24;   Vậy số xe lúc đầu của đội là 24 xe.

    Bài toán 38 (Dạng toán tìm số)

    Một phòng họp có 360 Ghế ngồi được xếp thành từng dãy và số Ghế của từng dãy đều như nhau. Nếu số dãy tăng thêm  1 và số Ghế của mỗi dãy tăng thêm 1, thì trong phòng có 400 Ghế. Hỏi trong phòng họp có bao nhiêu dãy Ghế, mỗi dãy có bao nhiêu ghế.

    Lời Giải:

    Gọi số dãy của ghế của phòng học là x (dãy), x nguyên dương.

    Ta có số người của từng dãy là: $\frac{360}{x}$ người.

    Số dãy ghế sau khi tăng thêm  1 dãy là: (x + 1).

    Số người sau khi tăng thêm  1  người trên dãy  là: $\frac{360}{x}$ + 1.

    Vì sau khi tăng số dãy tăng thêm  1 và số ghế của mỗi dãy tăng thêm 1, thì trong phòng có 400 Ghế do đó ta có phương trình: (x + 1) ($\frac{360}{x}$ + 1) = 400;        Giải PTBH ta được : x1 = 15, x2 = 24.

    Vậy  nếu số dãy là 15 thì số ghế trên dãy là 24…. 

    Bài toán 39 (Dạng toán tìm số)

    Cho một số có hai chữ số. Tìm số đó, biết rằng tổng hai chữ số của nó nhỏ hơn số đó 6 lần, nếu thêm  25  vào tích của hai chữ số đó sẽ được một số theo thứ tự ngược lạivới số đẵ cho.

    Lời Giải:

    Gọi chữ số phải tìm là   $\overline{xy}$;  x, y nguyên dương,  0 $\le $x,y $\le $9, x# 0.

    Vì tổng hai chữ số của nó nhỏ hơn số đó 6 lần do đó ta có phương trình: 6 (x + y) = $\overline{xy}$.

    Vì nếu thêm  25  vào tích của hai chữ số đó sẽ được một số theo thứ tự ngược lạivới số đẵ cho do đó ta có phương trình: $\overline{xy}$ + 25 =  $\overline{yx}$.

    Theo bài ra ta có hệ phương trình: $\left\{ \begin{align}

    & 6(x+y)=\overline{xy} \\

    & \overline{xy}+25=\overline{yx} \\

    \end{align} \right.$  ;  Giải hệ phương trình ta được $\left\{ \begin{align}

    & x=5 \\

    & y=4 \\

    \end{align} \right.$

    Vậy số phải tìm là 54.

    Bài toán 40 (Dạng toán sử dụng kiến thức %)

    Trong tháng đầu hai tổ công nhân sản xuất được 800  chi tiết máy. Sang tháng thứ hai tổ  vượt mức 15%, tổ II sản xuất vượt mức 20%, do đó cuối tháng cả hai tổ sản xuất được 945 chi tiết máy. Hỏi rằng trong tháng đầu, mỗi tổ công nhân sản xuất được bao nhiêu chi tiết máy.

    Lời Giải:

    Gọi số chi tiết sản xuất được trong tháng đầu  của Tổ I là x (x nguyên dương), x< 720.

    Gọi số chi tiết sản xuất được trong tháng đầu  của Tổ II là y (y nguyên dương), y< 720.

    Vì trong tháng đầu hai tổ sản xuất được 800 chi tiết máy do đó ta có phương  trình (1)

    x + y = 800

    Vì trong tháng thứ hai Tổ I  vượt mức 15%, Tổ II sản xuất vượt mức 12%, cả hai tổ sản xuất được 720 chi tiết máy do đó ta có phương trình (2) là: x + $\frac{15x}{100}$ + y + $\frac{20x}{100}$ = 945 $$Û $\frac{115}{100}$ x + $\frac{112}{100}$ y = 945

    Theo bài ra ta có hệ phương trình:    $\left\{ \begin{align}

    & x+y=800 \\

    & \frac{115}{100}x+\frac{112}{100}y=945 \\

    \end{align} \right.$; Giải hệ phương trình ta được: $\left\{ \begin{align}

    & x=300 \\

    & y=500 \\

    \end{align} \right.$

    Vậy trong tháng đầu tổ I sản xuất được 300 chi tiết máy, tổ II sản xuất được 500 chi tiết máy.

    Bài toán 41 (Dạng toán sử dụng kiến thức %)

    Năm ngoái dân số của hai tỉnh A và B là 4 triệu người. Dân số tỉnh A năm  nay tăng 1,2 % còn tỉnh B tăng 1,1 %, tổng dân số của hai tỉnh năm nay là 4 045 000 người. Tính dân số của mỗi tỉnh năm ngoái và năm  nay.

    Lời Giải:

    Gọi  dân số năm ngoái của tỉnh A là x (x nguyên dương), x<  4 triệu.

    Gọi  dân số năm ngoái của tỉnh B là y (y nguyên dương), y<  4 triệu

    Vì dân số  năm ngoái của hai tỉnh năm ngoái là 4 triệu do đó ta có phương  trình (1)

    x + y = 4

    Vì dân số năm nay của tỉnh A năm nay tăng 1,2%, tỉnh B tăng 1,1 % do đó ta có phương trình (2) là:

    $\frac{1,2x}{100}$ + $\frac{1,1y}{100}$ = 0, 045

    Theo bài ra ta có hệ phương trình: $\left\{ \begin{align}

    & x+y=4 \\

    & \frac{1,2x}{100}+\frac{1,1y}{100}=0,045 \\

    \end{align} \right.$    ;Giải hệ phương trình ta được: $\left\{ \begin{align}

    & x=1012000 \\

    & y=3033000 \\

    \end{align} \right.$

    Vậy dân số của tỉnh A năm nay là 1 012 000 người, tỉnh B là 3 033 000 người.

    Bài toán 42 (Dạng toán sử dụng kiến thức %)

    Trong tháng đầu, hai tổ công nhân sản xuất được 720  chi tiết máy. Sang tháng thứ hai tổ  vượt mức 15%, tổ II sản xuất vượt mức 12%, do đó cuối tháng cả hai tổ sản xuất được 819 chi tiết máy. Hỏi rằng trong tháng đầu, mỗi tổ công nhân sản xuất được bao nhiêu chi tiết máy.

    Lời Giải:

    Gọi số chi tiết sản xuất được trong tháng đầu  của tổ I là x (x nguyên dương), x< 720.

    Gọi số chi tiết sản xuất được trong tháng đầu  của tổ II là y (y nguyên dương), y< 720.

    Vì trong tháng đầu hai tổ sản xuất được 720 chi tiết máy do đó ta có phương  trình (1)

    x + y = 720

    Vì trong tháng thứ hai tổ I  vượt mức 15%, tổ II sản xuất vượt mức 12%, cả hai tổ sản xuất được 720 chi tiết máy do đó ta có phương trình (2) là: x + $\frac{15x}{100}$ + y + $\frac{12x}{100}$ = 819 $$Û $\frac{115}{100}$ x + $\frac{112}{100}$ y = 819

    Theo bài ra ta có hệ phương trình: $\left\{ \begin{align}

    & x+y=720 \\

    & \frac{115}{100}x+\frac{112}{100}y=819 \\

    \end{align} \right.$

    Giải hệ phương trình ta được: $\left\{ \begin{align}

    & x=420 \\

    & y=300 \\

    \end{align} \right.$

    Vậy trong tháng đầu tổ I sản xuất được 420 chi tiết máy, tổ II sản xuất được 300 chi tiết máy. 

    3. Bài tập giải bài toán bằng cách lập phương trình

    Bài toán 43  Một ô tô đi từ A đến B với một vận tốc xác định và trong một thời gian đã định. Nếu vận tốc ô tô giảm 10 km/ h thì thời gian tăng 45 phút. Nếu vận tốc ô tô tăng 10 km/ h thì thời gian giảm 30 phút. Tính vận tốc và thời gian dự định đi của ô tô.

    Bài toán 44  Hai xí nghiệp theo kế hoạch phải làm tổng cộng 360 dụng cụ. Thực tế, xí nghiệp I vượt mức kế hoạch 10%, xí nghiệp II vưượt mức kế hoạch 15%, do đó cả hai xí nghiệp đã làm đưược 404 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch.

    Bài toán 45  Một công nhân dự định làm 72 sản phẩm trong một thời gian đã định. Nhưng thực tế xí nghiệp lại giao 80 sản phẩm. Mặc dù ngưười đó mỗi giờ đã làm thêm một sản phẩm so với dự kiến, nhưưng thời gian hoàn thành công việc vẫn chậm so với dự định là 12 phút. Tính số sản phẩm dự kiến làm trong 1 giờ của ngưười đó. Biết mỗi giờ ngưười đó làm không quá 20 sản phẩm.

    Bài toán 46  Một xe khách và một xe du lịch khởi hành đồng thời từ A để đi đến B. Biết vận tốc của xe du lịch lớn hơn vận tốc xe khách là 20 km/h. Do đó nó đến B trưước xe khách 50 phút. Tính vận tốc mỗi xe, biết quãng đưường AB dài 100km

    Bài toán 47  Theo kế hoạch, một công nhân phải hoàn thành 60 sản phẩm trong thời gian nhất định. Nhưưng do cải tiến kĩ thuật nên mỗi giờ ngưười công nhân đó đã làm thêm đưược 2 sản phẩm. Vì vậy, chẳng những hoàn thành kế hoạch sớm hơn dự định 30 phút mà còn vưượt mức 3 sản phẩm. Hỏi theo kế hoạch, mỗi giờ ngưười đó phải làm bao nhiêu sản phẩm.

    Bài toán 48  Để hoàn thành một công việc, hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II đưược điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ xong công việc đó.

    Bài toán 49  Một khu vườn hình chữ nhật có chu vi bằng 48 m. Nếu tăng chiều rộng lên bốn lần và chiều dài lên ba lần thì chu vi của khu vườn sẽ là 162 m. Hãy tìm diện tích của khu vườn ban đầu.

    Bài toán 50  Một người đi xe máy từ A đến B. Vì có việc gấp phải đến B trước thời gian dự định là 45 phút nên người đó tăng vận tốc lên mỗi giờ 10 km. Tính vận tốc mà người đó dự định đi, biết quãng đường AB dài 90 km.

    Bài toán 51  Một đội công nhân hoàn thành một công việc với mức 420 ngày công thợ (nghĩa là nếu công việc đó chỉ có một người làm thì phải mất 420 ngày). Hãy tính số công nhân của đội biết rằng nếu đội tăng thêm 5 người thì số ngày để đội hoàn thành công việc sẽ giảm đi 7 ngày.  (trích Đề thi Tốt nghiệp THCS 1999 – 2000, tỉnh Vĩnh Phúc)

    Bài toán 52  Hai lớp 9A và 9B cùng tham gia lao động vệ sinh sân trường thì công việc hoàn thành sau 1 giờ 20 phút. Nếu mỗi lớp chia nhau làm nửa công việc thì thời gian hoàn tất là 3 giờ. Hỏi nếu mỗi lớp làm một mình thì phải mất bao nhiêu thời gian.

    Bài toán 53  Người ta muốn làm một chiếc thùng tôn hình trụ không có lắp có bán kính đáy là 25 cm, chiều cao của thùng là 60 cm. Hãy tính diện tích tôn cần dùng (không kể mép nối). Thùng tôn đó khi chứa đầy nước thì thể tích nước chứa trong thùng là bao nhiêu.

    Bài toán 54  Một tam giác có chiều cao bằng  cạnh đáy. Nếu tăng chiều cao thêm 3 dm, giảm cạnh đáy đi 2 dm thì diện tích của nó tăng thêm 12 dm2. Tính chiều cao và cạnh đáy của tam giác.

    (trích Đề thi tuyển sinh THPT 1999-2000, ngày 09- 07- 1999, tỉnh Vĩnh Phúc)

    Bài toán 55  Một đội xe vận tải phải vận chuyển 28 tấn hàng đến một địa điểm qui định. Vì trong đội có 2 xe phải điều đi làm việc khác nên mỗi xe phải chở thêm 0,7 tấn hàng nữa. Tính số xe của đội lúc đầu.

    (trích Đề thi tuyển sinh THPT 1999-2000, ngày 10- 07- 1999, tỉnh Vĩnh Phúc)

    Bài toán 56  Ba ô tô chở 100 tấn hàng tổng cộng hết 40 chuyến. Số chuyến thứ nhất chở gấp rưỡi số chuyến xe thứ hai. Mỗi chuyến, xe thứ nhất chở 2 tấn, xe thứ hai chở 2,5 tấn, xe thứ ba chở 3 tấn. Tính xem mỗi ô tô chở bao nhiêu chuyến.                                                 (trích Đề thi tuyển sinh THPT 2000-2001, ngày 02- 08- 2000, tỉnh Vĩnh Phúc)

    Bài toán 57  Ba chiếc bình có thể tích tổng cộng là 132 lít. Nếu đổ đầy nước vào bình thứ nhất rồi lấy nước đó đổ vào hai bình kia thì:

    Hoặc bình thứ ba đầy nước, còn bình thứ hai chỉ được một nửa bình.

    Hoặc bình thứ hai đầy nước, còn bình thứ ba chỉ được một phần ba bình.

    (Coi như trong quá trình đổ nước từ bình này sang bình kia lượng nước hao phí bằng không).

    Hãy xác định thể tích của mỗi bình.

    (trích Đề thi tuyển sinh THPT 2000-2001, ngày 03- 08- 2000, tỉnh Vĩnh Phúc) .

    Bài toán 58  Một người đi xe máy từ A tới B. Cùng một lúc một người khác cũng đi xe máy từ B tới A với vận tốc bằng  vận tốc của người thứ nhất. Sau 2 giờ hai người gặp nhau. Hỏi mỗi người đi cả quãng đường AB hết bao lâu?

    (trích Đề thi tuyển sinh THPT 2001-2002, ngày 22- 07- 2001, tỉnh Vĩnh Phúc)

    Bài toán 59 Một thửa ruộng hình chữ nhật có diện tích là 100 m2. Tính độ dài các cạnh của thửa ruộng. Biết rằng nếu tăng chiều rộng của thửa ruộng lên 2 m và giảm chiều dài của thửa ruộng đi 5 m thì diện tích của thửa ruộng sẽ tăng thêm 5 m2.                                    (trích Đề thi tuyển sinh THPT 2002-2003, ngày 03- 08- 2002, tỉnh Vĩnh Phúc)

    Bài toán 60 Tìm hai số biết rằng tổng của hai số đó bằng 17 đơn vị. Nếu số thứ nhất tăng thêm 3 đơn vị, số thứ hai tăng thêm 2 đơn vị thì tích của chúng bằng 105 đơn vị.

    (trích Đề thi tuyển sinh THPT 2003-2004, ngày 14- 07- 2003, tỉnh Vĩnh Phúc)

    Bài toán 61 Một ca nô ngược dòng từ bến A đến bến B với vận tốc 20 km/h, sau đó lại xuôi từ bến B trở về bến A. Thời gian ca nô ngược dòng từ A đến B nhiều hơn thời gian ca nô xuôi dòng từ B trở về A là 2 giờ 40 phút. Tính khoảng cách giữa hai bến A và B. Biết vận tốc dòng nước là 5 km/h, vận tốc riêng của ca nô lúc xuôi dòng và lúc ngược dòng bằng nhau.                        (trích Đề thi tuyển sinh THPT 2003-2004, ngày 15- 07- 2003, tỉnh Vĩnh Phúc)

    Bài toán 62 Người ta dự kiến trồng 300 cây trong một thời gian đã định. Do điều kiện thuận lợi nên mỗi ngày trồng được nhiều hơn 5 cây so với dự kiến, vì vậy đã trồng xong 300 cây ấy trước 3 ngày. Hỏi dự kiến ban đầu mỗi ngày trồng bao nhiêu cây? (Giả sử số cây dự kiến trồng mỗi ngày là bằng nhau).

    (trích Đề thi tuyển sinh THPT 2004-2005, ngày 29- 06- 2004, tỉnh Vĩnh Phúc)

    Bài toán 63 Một khu vườn hình chữ nhật, chiều dài lớn hơn chiều rộng 5 m, diện tích bằng 300 m2. Tính chiều dài và chiều rộng của khu vườn.

    (trích Đề thi tuyển sinh THPT 2004-2005, ngày 30- 06- 2004, tỉnh Vĩnh Phúc)

    Bài toán 64 Cho một hình chữ nhật. Nếu tăng độ dài mỗi cạnh của nó lên 1 cm thì diện tích của hình chữ nhật sẽ tăng thêm 13 cm2. Nếu giảm chiều dài đi 2 cm, chiều rộng đi 1 cm thì diện tích của hình chữ nhật sẽ giảm 15 cm2. Tính chiều dài và chiều rộng của hình chữ nhật đã cho.

    (trích Đề thi tuyển sinh THPT 2005-2006, ngày 06- 07- 2005, tỉnh Vĩnh Phúc)

    Bài toán 65  Một mảnh đất hình chữ nhật có chu vi 80 m. Nếu tăng chiều dài thêm 3 m, chiều rộng thêm 5 m thì diện tích của mảnh đất tăng thêm 195 m2. Tính chiều dài, chiều rộng của mảnh đất.

    Bài toán 66 Hai xe máy khởi hành cùng một lúc từ hai tỉnh A và B cách nhau 90 km, đi ngược chiều và gặp nhau sau 1,2 giờ (xe thứ nhất khởi hành từ A, xe thứ hai khởi hành từ B). Tìm vận tốc của mỗi xe. Biết rằng thời gian để xe thứ nhất đi hết quãng đường AB ít hơn thời gian để xe thứ hai đi hết quãng đường AB là 1 giờ.

    (trích Đề thi tuyển sinh THPT 2005-2006, ngày 07- 07- 2005, tỉnh Vĩnh Phúc)

    Bài toán 67 Một xe lửa đi từ ga Hà Nội vào ga Trị Bình (Quảng Ngãi). Sau đó 1 giờ, một xe lửa khác đi từ ga Trị Bình ra ga Hà Nội với vận tốc lớn hơn vận tốc của xe thứ nhất là 5 km/h. Hai xe gặp nhau tại một ga ở chính giữa quãng đường. Tìm vận tốc của mỗi xe lửa, biết quãng đường sắt Hà Nội- Trị Bình dài 900km

    (trích đề thi tốt nghiệp THCS tỉnh Bà Rịa- Vũng Tàu, năm 2004 – 2005)

    Bài toán 68 Theo kế hoạch hai tổ sản xuất 600 sản phẩm trong một thời gian nhất định. Do áp dụng kĩ thuật mới nên tổ I đã vượt mức 18% và tổ II đã vượt mức 21%. Vì vậy trong thời gian quy định họ đã hoàn thành vượt mức 120 sản phẩm. Hỏi số sản phẩm được giao của mỗi tổ theo kế hoạch?

    (trích đề thi tốt nghiệp THCS  thành phố Hà Nội, năm 2002- 2003)

    Bài toán 69 Hai ôtô khởi hành cùng một lúc trên quãng đường từ A đến B dài120 km. Mỗi giờ ôtô thứ nhất chạy nhanh hơn ôtô thứ hai là 10 km nên đến B trước ôtô thứ hai là  giờ. Tính vận tốc của mỗi ôtô?

    (trích đề thi tốt nghiệp THCS  tỉnh Bắc Giang, năm 2002- 2003)

    Bài toán 70 Một ca nô xuôi dòng từ bến sông A đến bến sông B cách nhau 24 km; cùng lúc đó, cũng từ A về B một bè nứa trôi với vận tốc dòng nước là 4 km/h. Khi đến B ca nô quay lại ngay và gặp bè nứa tại địa điểm C cách A là 8 km. Tính vận tốc thực của ca nô                                                   (trích ĐTTS THPT tỉnh Bắc Giang, năm 2003- 2004)

    Bài toán 71 Có 3 đội xây dựng cùng làm chung một công việc. Làm chung được 4 ngày thì đội III được điều động làm việc khác, 2 đội còn lại cùng làm thêm 12 ngày nữa thì hoàn thành công việc. Biết rằng năng suất của đội I cao hơn năng suất của đội II; năng suất của đội III là trung bình cộng của năng suất đội I và năng suất đội II; và nếu mỗi đội làm một mình một phần ba công việc thì phải mất tất cả 37 ngày mới xong. Hỏi nếu mỗi đội làm một mình thì bao nhiêu ngày xong công việc trên.        (trích ĐTTS THPT năng khiếu ĐHQG TP. Hồ Chí Minh, năm 2003- 2004)

    Bài toán 72 Một khu vườn hình chữ nhật có chiều dài bằng  chiều rộng và có diện tích bằng 1792 m2. Tính chu vi của khu vườn ấy.                                                               (trích tốt nghiệp THCS TP. Hồ Chí Minh, năm 2003- 2004)

    Bài toán 73 Cùng một thời điểm, một chiếc ôtô XA xuất phát từ thành phố A về hướng thành phố B và một chiếc khác XB xuất phát từ thành phố B về hướng thành phố A. Chúng chuyển động với vận tốc riêng không đổi và gặp nhau lần đầu tại một điểm cách A là 20 km. Cả hai chiéc xe sau khi đến B và A tương ứng, lập tức quay trở lại và chúng gặp nhau lần thứ hai tại một điểm C. Biết thời gian xe XB đi từ C đến B là 10 phút và thời gian giữa hai lần gặp nhau là 1 giờ. Hãy tính vận tốc của từng chiếc ôtô.

    (trích ĐTTS THPT năng khiếu ĐHQG TP. Hồ Chí Minh, năm 2004- 2005)

    Bài toán 74 Để hoàn thành một công việc, hai tổ phải làm chung trong 6 giờ. Sau 2 giờ làm chung thì tổ II được điều đi làm việc khác, tổ I đã hoàn thành công việc còn lại trong 10 giờ. Hỏi nếu mỗi tổ làm riêng thì sau bao lâu sẽ làm xong công việc đó?

    (trích đề thi tốt nghiệp THCS TP. Hà Nội, năm 2003- 2004)

    Bài toán 75 Một xuồng máy xuôi dòng sông 30 km và ngược dòng 28 km hết một thời gian bằng thời gian mà xuồng đi 59,5 km trên mặt hồ yên lặng. Tính vận tốc của xuồng khi đi trên hồ biết rằng vận tốc của nước chảy trong sông là 3 km/h

    Bài toán 76 Nếu mở cả hai vòi nước chảy vào một bể cạn thì sau 2 giờ 55 phút bể đầy nước. Nếu mở riêng từng vòi thì vòi thứ nhất làm đầy bể nhanh hơn vòi thứ hai là 2 giờ. Hỏi nếu mở riêng từng vòi thì mỗi vòi chảy bao lâu đầy bể?

    Bài toán 77  Một mảnh vườn hình chữ nhật có diện tích là 720 m2, nếu tăng chiều dài thêm 6 m và giảm chiều rộng đi 4 m thì diện tích mảnh vườn không đổi. Tính các kích thước của mảnh vườn.

    (trích ĐTTS THPT 2005- 2006, tỉnh Thái Bình)

    Bài toán 78 Nếu hai vòi nước cùng chảy vào một cái bể không có nước thì sau 12 giờ bể đầy. Sau khi hai vòi cùng chảy 8 giờ thì người ta khoá vòi I, còn vòi II tiếp tục chảy. Do tăng công suất vòi II lên gấp đôi, nên vòi II đã chảy đầy phần còn lại của bể trong 3 giờ rưỡi. Hỏi nếu mỗi vòi chảy một mình với công suất bình thường thì phải bao lâu mới đầy bể?

    Bài toán 79 Một tam giác có chiều cao bằng  cạnh đáy. Nếu chiều cao giảm đi 2 dm và cạnh đáy tăng thêm 3 dm thì diện tích của nó giảm đi 14 dm2.

    Tính chiều cao và cạnh đáy của tam giác.

    Bài toán 80 Mội thửa ruộng hình chữ nhật có chu vi 250 m. Tính diện tích của thửa ruộng biết rằng nếu chiều dài giảm 3 lần và chiều rộng tăng 2 lần thì chu vi thửa ruộng vẫn không thay đổi.

    Bài toán 81 Nhà trường tổ chức cho 180 học sinh khối 9 đi tham quan di tích lịch sử. Người ta dự tính: Nếu dùng loại xe lớn chuyên chở một lượt hết số học sinh thì phải điều ít hơn nếu dùng loại xe nhỏ là hai chiếc. Biết rằng mỗi xe lớn có nhiều hơn mỗi xe nhỏ là 15 chỗ ngồi. Tính số xe lớn, nếu loại xe đó được huy động.

    Bài toán 82 Một xe máy đi từ A đến B trong một thời gian dự định. Nếu vận tốc tăng thêm 14 km/ giờ thì đến sớm 2 giờ, nếu giảm vận tốc đi 4 km/ giờ thì đến muộn 1 giờ.

    Tính vận tốc dự định và thời gian dự định.

    Bài toán 83 Một tàu thuỷ chạy trên khúc sông dài 120 km, cả đi và về mất 6 giờ 45 phút. Tính vận tốc của tàu thuỷ khi nước yên lặng, biết rằng vận tốc của dòng nước là 4 km/ h.

    Bài toán 84 Một ca nô đi xuôi dòng 48 km rồi đi ngược dòng 22 km. Biết rằng thời gian đi xuôi dòng lớn hơn thời gian đi ngược dòng là 1 giờ và vận tốc đi xuôi lớn hơn vận tốc đi ngược là 5 km/h. Tính vận tốc ca nô lúc đi ngược dòng.                                                    (trích ĐTTS THPT chuyên Nguyễn Bỉnh Khiêm 2005 – 2006, tỉnh Vĩnh Long)

    Bài toán 85  Một xe ô tô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn 10 km thì đến nơi sớm hơn dự định 3 giờ, nếu xe chạy chậm lại mỗi giờ 10 km thì đến nơi chậm nhất 5 giờ.

    Tính vận tốc của xe lúc đầu, thời gian dự định và chiều dài quãng đường AB.                   

    Bài toán 86  Hai đội bóng bàn của hai trường phổ thông thi đấu với nhau. Mỗi cầu thủ của đội này phải thi đấu với mỗi cầu thủ của đội kia một trận. Biết rầng tổng số trận đấu bằng 4 lần tổng số cầu thủ của hai đội và số cầu thủ của ít nhất một trong hai đội là số lẻ. Hỏi mỗi đội có bao nhiêu cầu thủ?

    Bài toán 87  Một thửa ruộng hình chữ nhật, nếu tăng chiều dài thêm 2m, chiều rộng thêm 3 m thì diện tích tăng thêm 100 m2. Nếu giảm cả chiều dài lẫn chiều rộng đi 2 m thì diện tích giảm đi 68 m2. Tính diện tích của thửa ruộng đó.

    Bài toán 88  Ba xe ô tô chở 118 tấn hàng tổng cộng hết 50 chuyến. Số chuyến xe thứ nhất chở gấp rưỡi số chuyến xe thứ hai. Mỗi chuyến xe thứ nhất chở 2,5 tấn, xe thứ ba chở 3 tấn. Hỏi mỗi ô tô chở mấy chuyến.

    Bài toán 89  Ba ca nô cùng rời bến sông A một lúc để đến B. Ca nô thứ 2 mỗi giờ đi kém ca nô thứ nhất 3 km nhưng hơn ca nô thứ ba 3km nên đến B sau ca nô thứ nhất 2 giờ, nhưng trước ca nô thứ ba là 3 giờ. Tính chiều dài quãng sông AB.

    Bài toán 90  Một bè lứa trôi tự do (trôi theo vận tốc dòng nước) và một ca nô đồng thời rời bến A để suôi dòng sông. Ca nô suôi dòng được 96 km thì quay ngay lại A. Cả đi lẫn về hết 14 giờ. Trên đường quay về A khi còn cách A là 24 km thì ca nô gặp chiếc bè lứa nói trên. Tính vận tốc của ca nô và vận tốc của dòng nước.

    Bài toán 91  Ba vòi nước A, B, C được bắc cùng vào một bể chứa. Các vòi chảy được một lượng nước bằng thể tích của bể theo thời gian chảy được ghi trong các trường hợp sau:

    a)Vòi A : 2giờ và vòi B : 1giờ 30 phút;

    b)Vòi A : 1giờ và vòi C : 4 giờ;

    c)Vòi B : 3 giờ và vòi C : 2 giờ.

    Tính thời gian để riêng từng vòi chảy được một lượng bằng thể tích của bể.

    Bài toán 92  Có 2 hộp đựng bi, nếu lấy từ hộp thứ nhất một số bi bằng số bi có trong hộp thứ hai rồi bỏ vào hộp thứ hai, rồi lại lấy từ hộp thứ hai một số bi bằng số bi còn lại trong hộp thứ nhất và bỏ vào hộp thứ nhất, cuối cùng lấy từ hộp thứ nhất một số bi bằng số bi còn lại trong hộp thứ hai và bỏ vào hộp thứ hai. Khi đó số bi trong mỗi hộp đều là 16 viên. Hỏi lúc đầu mỗi hộp có bao nhiêu viên bi?

    Bài toán 93  Ba chiếc bình có thể tích tổng cộng là 120 lít. Nếu đổ đầy nước vào bình thứ nhất rồi rót vào hai bình kia thì hoặc bình thứ ba đầy nước, còn bình thứ hai chỉ được thể tích của nó, hoặc bình thứ hai đầy nước còn bình thứ ba chỉ được thể tích của nó. Hãy xác định thể tích của mỗi bình.

    Bài toán 94  Hai máy cày có công suất khác nhau cùng làm việc đã cày được  cánh đồng trong 15 giờ. Nếu máy thứ nhất cày 12 giờ, máy thứ hai cày trong 20 giờ thì cả hai máy cày được 20% cánh đồng. Hỏi nếu mỗi máy làm việc riêng thì sẽ cày song cánh đồng trong bao lâu?

    Bài toán 95  Hai người cùng làm một công việc như theo cách sau:

    Người thứ nhất làm trong thời gian mà người thứ hai làm một mình xong công vịêc đó.

    Tiếp đó người thứ hai làm trong  thời gian mà người thứ nhất một mình làm xong công việc đó.

    Như vậy cả hai người làm được  công việc.

    Tìm thời gian mà mỗi người làm một mình xong công việc đó, biết rằng nếu cả hai người cùng làm thì 3 giờ 36 phút xong công việc đó.

    Bài toán 96  Đem một số có hai chữ số nhân với tổng các chữ số của nó thì được 405.

    Nếu lấy số được viết bởi hai chữ số ấy nhưng theo thứ tự ngược lại nhân với tổng các chữ số của nó thì được 468. Hãy tìm số có hai chữ số đó.

    Bài toán 97  Một đoàn học sinh tổ chức đi thăm quan bằng ô tô. Người ta nhận thấy rằng nếu mỗi xe chỉ trở 22 học sinh thì còn thừa 1 học sinh. Nếu bớt đi một ô tô thì có thể phân phối đều các học sinh trên các ô tô còn lại. Hỏi lúc đầu có bao nhiêu ô tô và có bao nhiêu học sinh đi thăm quan, biết rằng mỗi ô tô chỉ chở được không quá 32 học sinh.

    Bài toán 98  Một hình chữ nhật có diện tích 1200 m2. Tính các kích thước của vườn đó, biết rằng nếu tăng chiều dài thêm 5 m và giảm chiều rộng đi 10 m thì diện tích của vườn giảm đi 300m2.

    Bài toán 99  Một thửa ruộng hình tam giác có diện tích 180m2. Tính cạnh đáy của thửa ruộng đó, biết rằng nếu tăng cạnh đáy thêm 4 m và giảm chiều cao tương ứng đi 1 m thì diện tích của nó không đổi.

    Bài toán 100  Hai công nhân nếu làm chung thì hoàn tyhành một công việc trong 4 ngày. Người thứ nhất làm một nửa công việc, sau đó người thứ hai làm nốt nửa công việc còn lại thì toàn bộ công việc sẽ được hoàn thành trong 9 ngày. Hỏi nễu mỗi người làm riêng thì sẽ hoàn thành công việc đó trong bao nhiêu ngày.

    Bài toán 101  Một phòng họp có 100 người được sắp xếp ngồi đều trên các ghế. Nếu có thêm 44 người thì phải kê thêm hai dãy ghế và mỗi dãy ghế phải xếp thêm hai người nữa. Hỏi lúc đầu trong phòng họp có bao nhiêu dãy ghế?

    Bài toán 102  Lúc 6h30 phút một người đi xe máy từ A đến B dài 75km với vận tốc định trước. Đến B người đó nghỉ lại 20 phút rồi quay trở về A với vận tốc lớn hơn vận tốc dự định là 5km/h. Người đó về đến A lúc 12 giờ 20 phút. Tính vận tốc dự dịnh của người đi xe máy.

    Bài toán 103  Hai bến sông A và B cách nhau 40 km. Cùng một lúc một chiếc ca nô xuôi dòng từ A đến B và một chiếc bè cũng trôi từ A đến B với vận tốc 3km/h. Sau khi đến B, ca nô quay về A ngay và gặp chiếc bè ở một địa điểm cách A là 8km. Tính vận tốc của ca nô.

    Bài toán 104  Người ta trộn 4 kg chất lỏng loại I với 3 kg chất lỏng loại II thì được một hỗn hợp có khối lượng riêng là 700kg/m3. Biết rằng khối lượng riêng của chất lỏng loại I lớn hơn khối lượng riêng của chất lỏng loại II là 200kg/m3. Tính khối lượng riêng của mỗi chất lỏng.

    Bài toán 105  Một hợp kim gồm đồng và kẽm trong đó có 5 gam kẽm. Nếu thêm 15 gam kẽm vào hợp kim này thì được một hợp kim mới mà trong hợp kim đó lượng đồng đã giảm so với lúc đầu là 30%. Tìm khối lượng ban đầu của hợp kim.

    Bài toán 106  Số đường chéo của một đa giác lồi là 230. Tính số cạnh của đa giác này.

    Bài toán 107  Một ca nô dự định đi từ A đến B trong thời gian đã định. Nếu vận tốc ca nô tăng 3km/h thì đến nơi sớm hai giờ. Nếu vận tốc ca nô giảm 3km/h thì đến nơi chậm 3 giờ. Tính chiều dài khúc sông AB.

    Bài toán 108  Tính các kích thước của một hình chữ nhật biết rằng nếu tăng chiều dài 3m, giảm chiều rộng 2 m thì diện tích không đổi; nếu giảm chiều dài3 m, tăng chiều rộng 3 m thì diện tích không đổi.

    Bài toán 109  Một công nhân phải làm một số dụng cụ trong một thời gian. Nếu mỗi ngày tăng 3 dụng cụ thì hoàn thành sớm 2 ngày, nếu mỗi ngày làm giảm 3 dụng cụ thì thời gian phải kéo dài 3 ngày. Tính số dụng cụ được giao.

    Bài toán 110  Để sửa chữa một quãng đường, cần huy động một số người làm trong một số ngày. Nếu bổ sung thêm 3 người thì thời gian hoàn thành rút được 2 ngày. Nếu rút bớt 3 người thì thời gian hoàn thành phải kéo dài thêm 3 ngày. Tính số người dự định huy động và số ngày dự định hoàn thành công việc.

    Bài toán 111  Trong một trang sách, nếu tăng thêm 3 dòng, mỗi dòng bớt 2 chữ thì số chữ của trang không đổi; nếu bớt đi 3 dòng, mỗi dòng tăng thêm 3 chữ thì số chữ của trang cũng không đổi. Tính số chữ trong trang sách.

    Bài toán 112  Một câu lạc bộ có một số ghế quy định.

    Nếu thêm 3 hàng ghế thì mỗi hàng bớt được 2 ghế.

    Nếu bớt đi ba hàng thì mỗi hàng phải thêm 3 ghế.

    Tính số ghế của câu lạc bộ.

    Bài toán 113  Một phòng họp có một số dãy ghế, tổng cộng 40 chỗ. Do phải xếp 55 chỗ nên người ta kê thêm 1 dãy ghế và mỗi dãy xếp thêm 1 chỗ. Hỏi lúc đầu có mấy dãy ghế trong phòng?

    Bài toán 114  Có ba thùng đựng nước.

    • Lần thứ nhất, người ta đổ ở thùng I sang hai thùng kia một số nước bằng số nước ở mỗi thùng đó đang có.
    • Lần thứ hai,  người ta đổ ở thùng II sang hai thùng kia một số nước gấp đôi số nước ở mỗi thùng đó đang có.
    • Lần thứ  ba, người ta đổ ở thùng III sang hai thùng kia một số nước bằng số nước ở mỗi thùng đó đang có.
    • Cuối cùng mỗi thùng đều có 24 lít nước. Tính số nước ở mỗi thùng có lúc đầu.

    Bài toán 115  Một hình vườn hình chữ nhật có chu vi 450 m. Nếu giảm chiều dài đi  chiều dài cũ, tăng chiều rộng lên  chiều rộng cũ thì chu vi hình chữ nhật không đổi. Tính chiều dài và chiều rộng của vườn.

    Bài toán 116  Một vườn hình chữ nhật có chiều dài hơn chiều rộng 20 m, diện tích 3500 m2. Tính độ dài hàng rào xung quanh vườn biết rằng người ta chừa ra 1 m để làm cổng ra vào.

    Bài toán 117  Một tuyến đường sắt có một số ga, mỗi ga có một loại vé đến từng ga còn lại. Biết rằng có tất cả 210 loại vé. Hỏi tuyến đường ấy có bao nhiêu ga?

    Bài toán 118  Hai trường A và B của một thị trấn có 210 học sinh thi đỗ hết lớp 9, đạt tỷ lệ trúng tuyển 84%.

    Tính riêng thì trường A đỗ 80%, trường B đỗ 90%.

    Tính xem mỗi trường có bao nhiêu học sinh lớp 9 dự thi?

    Bài toán 119  Dân số của một thành phố hiện nay là 408 040 người, hàng năm dân số tăng 1%. Hỏi hai năm trước đây, dân số thành phố là bao nhiêu?

    Bài toán 120  Mức sản xuất của một xí nghiệp cách đây hai năm là 75000 dụng cụ một năm, hiện nay là 90750 dụng cụ một năm. Hỏi năm sau xí nghiệp làm tăng hơn năm trước bao nhiêu phần trăm?

    Bài toán 121  Quãng đường AB gồm một đoạn lên dốc dài 4 km, đoạn xuống dốc dài 5 km. Một người đi xe đạp từ A đến B hết 40 phút và đi từ B về A hết 41 phút (vận tốc lên dốc lúc đi và về như nhau, vận tốc xuống dốc lúc đi và về như nhau). Tính vận tốc lúc lên dốc và lúc xuống dốc.

    Bài toán 122  Một ca nô xuôi khúc sông dài 40 km rồi ngược khúc sông ấy hết 4 giờ rưỡi. Biết thời gian ca nô xuôi 5 km bằng thời gian ngược 4km .

    Tính vận tốc dòng nước.

    Bài toán 123  Một ca nô đi xuôi dòng 45 km rồi ngược dòng 18 km.

    Biết rằng thời gian xuôi lâu hơn thời gian ngược 1giờ và vận tốc xuôi lớn hơn vận tốc ngược là 6 km/h.

    Tính vận tốc của ca nô lúc ngược dòng.

    Bài toán 124  Một người đi xe đạp từ A đến B đường dài 78 km. Sau đó một giờ, người thứ hai đi từ B đến A. Hai người gặp nhau tại C cách B là 36 km. Tính thời gian mỗi người đã đi từ lúc khởi hành đến lúc gặp nhau biết rằng vận tốc người thứ hai lớn hơn vận tốc người thứ nhất là 4 km/h.

    Bài toán 125  Hai công nhân phải làm một số dụng cụ bằng nhau trong cùng một. Người thứ nhất mỗi giờ làm tăng thêm 2 dụng cụ nên hoàn thành công việc trước thời hạn 2 giờ. Người thứ hai mỗi giờ làm tăng 4 dụng cụ nên không những hoàn thành công việc trước thời hạn 3 giờ mà còn làm thêm 6 chiếc nữa. Tính số dụng cụ mỗi người được giao.

    Bài toán 126  Vào thế kỷ thứ III trước Công Nguyên, vua xứ Xiracut giao cho Acsimét kiểm tra xem chiếc mũ bằng vàng của nhà vua có bị pha thêm bạc hay không. Chiếc mũ có trọng lượng 5 Niutơn (theo đơn vị hiện nay), nhúng trong nước thì trọng lượng giảm 0,3 Niutơn. Biết rằng khi cân trong nước, vàng giảm  trọng lượng, bạc giảm  trọng lượng. Hỏi chiếc mũ chứa bao nhiêu gam vàng, bao nhiêu gam bạc?

    Vật có khối lượng 100 gam thì có trọng lượng 1 Niutơn).

    Bài toán 127  Có hai loại quặng chứa 75% sắt và 50% sắt. Tính khối lượng của mỗi loại quặng đem trộn để được 25 tấn quặng chứa 66% sắt.

    Bài toán 128  Hai máy cày làm việc trên một cánh đồng. Nếu cả hai máy cùng cày thì 10 ngày xong công việc. Nhưng thực tế hai máy chỉ cùng làm việc 7 ngày đầu, sau đó máy thứ nhất đi cày nơi khác, máy thứ hai làm tiếp 9 ngày nữa thì xong. Hỏi mỗi máy làm việc một mình thì trong bao lâu cày xong cả cánh đồng?

     Bài toán 129 Tìm số có ba chữ số sao cho chia nó cho 11, ta được thương bằng tổng các chữ số của số bị chia.

    Bài toán 130  Tìm số có bốn chữ số biết rằng chữ số hàng nghìn và hàng trăm giống nhau, chữ số hàng chục và hàng đơn vị giống nhau, số phải tìm có thể viết được thành một tích của ba thừa số, mỗi thừa số gồm hai chữ số giống nhau.

    Bài toán 131  Tìm số chính phương có bốn chữ số biết rằng nếu mỗi chữ số giảm đi 1 ta được một số mới cũng là số chính phương.

    Bài toán 132  Nếu thêm 3 vào mỗi chữ số của một số chính phương có bốn chữ số (mỗi chữ số của số chính phương này đều nhỏ hơn 7) ta được một số chính phương mới. Tìm hai số chính phương đó.

    Bài toán 133  Tìm ba số tự nhiên sao cho tổng các nghịch đảo của chúng bằng 2.

    Bài toán 134  Tìm ba số tự nhiên sao cho tổng các nghịch đảo của chúng bằng1.

    Bài toán 135 Tuổi hai anh em cộng lại bằng 21. Tuổi anh hiện nay gấp đôi tuổi em lúc anh bằng tuổi em hiện nay. Tính tuổi mỗi người hiện nay.

    Bài toán 136  Một xí nghiệp dự định điều một số xe để chuyển 120 tạ hàng. Nếu mỗi xe chở thêm 1 tạ so với dự định thì số xe giảm đi 4 chiếc. Tính số xe dự định điều động.

    Bài toán 137  Có hai đội công nhân, mỗi đội phải sửa 10 km đường. Thời gian đội I làm nhiều hơn đội II là 1 ngày. Trong một ngày, mỗi đội làm được bao nhiêu kilômét biết rằng cả hai đội làm được 4,5 km trong một ngày.

    Bài toán 138  Một sân hình chữ nhật có diện tích 720 m2. Nếu tăng chiều dài 6 m, giảm chiều rộng 4 m thì diện tích không đổi. Tính các kích thước của sân.

    Bài toán 139  Một tấm sắt có chu vi 96 cm. Người ta cắt ra ở mỗi góc một hình vuông cạnh 4 cm rồi gấp lên thành một hình hộp chữ nhật không nắp có thể tích 768 cm3. Tính kích thước của tấm sắt.

    Bài toán 140  Hai đội thuỷ lợi cùng đào một con mương. Nếu mỗi đội làm một mình cả con mương thì thời gian tổng cộng hai đội phải làm là 25 giờ. Nếu hai đội cùng làm thì công việc hoàn thành trong 6 giờ. Tính xem mỗi đội làm một mình xong cả con mương trong bao lâu?

    Bài toán 141  Tìm hai số tự nhiên biết tổng của chúng bàng 59, hai lần số này bé hơn ba lần số kia là 7. Tìm hai số đó.

    Bài toán 142  Tìm hai số biết rằng bốn lần số thứ hai cộng với năm lần số thứ nhất bằng 18040, và ba lần số số thứ nhất hơn hai lần số thứ hai là 2002.

  • Trực tâm là gì?

    Trực tâm là gì?

    Trực tâm là gì?

    Trực tâm là giao điểm của 3 đường cao trong một tam giác. Đường cao trong tam giác là đoạn vuông góc kẻ từ một đỉnh đến cạnh đối diện. Cạnh đối diện này được gọi là đáy ứng với đường cao. Độ dài của đường cao là khoảng cách giữa đỉnh và đáy.

    Trực tâm là gì?

    Chúng ta xuất phát từ định lí sau:

    Trong một tam giác có 3 đường cao. Ba đường này cùng đi qua một điểm, điểm này gọi là trực tâm của tam giác.

    Đường cao của tam giác là gì? Đường cao của một tam giác chính là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện. Cạnh đối diện này thường được gọi là đáy tương ứng với mỗi đường cao.

    Giả sử cho tam giác ABC có ba đường cao lần lượt là AM, BN, CP. Gọi H là là giao điểm của ba đường cao này thì H là trực tâm của tam giác ABC.

    Trực tâm là gì? trực tâm của tam giác là gì?

    Cách xác định trực tâm của một tam giác

    Như vậy, trực tâm của tam giác là điểm giao nhau của ba đường cao trong tam giác.

    Tuy nhiên để xác định trực tâm trong tam giác chúng ta chỉ cần vẽ hai đường cao của tam giác ta đã có thể xác định được trực tâm của tam giác. Chẳng hạn, trong tam giác ABC ta chỉ cần vẽ hai đường cao AF và BE. Hai đường cao này cắt nhau tại H thì H chính là trực tâm của tam giác ABC. Khi đó, chúng ta có vẽ đường cao từ đỉnh C của tam giác thì đường cao đó cũng sẽ đi qua điểm H.

    Trực tâm là gì? 5

    Đối với các loại tam giác thông thường như tam giác nhọn tam giác tù hay tam giác cân tam giác đều thì ta đều có cách xác định trực tâm giống nhau. Từ hai đỉnh của tam giác ta kẻ hai đường cao của tam giác đến hai cạnh đối diện. Hai cạnh đó giao nhau tại điểm nào thì điểm đó chính là trực tâm của tam giác. Và đường cao còn lại chắc chắn cũng đi qua trực tâm của tam giác dù ta không cần vẽ nó.

    Tuy nhiên đối với tam giác vuông thì việc xác định đường cao có khác một chút. Tam giác vuông có hai cạnh góc vuông chính là hai đường cao của tam giác vì hai cạnh vuông góc với nhau. Chính vì vậy trực tâm của tam giác vuông trùng với đỉnh của góc vuông.

    Đối với tam giác nhọn thì trực tâm của nó nằm bên trong tam giác, tam giác vuông thì trực tâm trùng với đỉnh góc vuông, tam giác tù thì trực tâm nằm bên ngoài tam giác (xem hình vẽ).

    Trực tâm là gì? 6

    Trực tâm của tam giác đều

    Trong một tam giác đều thì trực tâm, trọng tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của nó đều trùng nhau.

    Trong hình sau thì O vừa là trọng tâm, vừa là trực tâm, vừa là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của tam giác đều ABC.

    Trực tâm là gì? 7

  • Tỉ lệ nghịch là gì?

    Tỉ lệ nghịch là gì?

    Tỉ lệ nghịch là mối tương quan giữa hai đại lượng, mà nếu tăng đại lượng này bao nhiêu lần thì đại lượng kia giảm bấy nhiêu lần.

    Nói cách khác, nếu $a$ là đại lượng thứ nhất, thì đại lượng tỉ lệ nghịch với $a$ là nghịch đảo – có hệ số – của $a$ (tức là $k/a$), và $k$ là một hằng số dương nào đó.

    Khi giá trị của một đại lượng tăng lên so với sự giảm của đại lượng khác hoặc ngược lại, thì chúng được cho là tỷ lệ nghịch.  Nó có nghĩa là hai đại lượng hoạt động trái ngược nhau về bản chất. Ví dụ, tốc độ và thời gian tỷ lệ nghịch với nhau. Khi bạn tăng tốc độ, thời gian sẽ giảm xuống. Các thuật ngữ khác được sử dụng ở đây cho loại tỷ lệ này là tỷ lệ nghịch hoặc thay đổi tỷ lệ nghịch hoặc biến thiên nghịch đảo hoặc tỷ lệ tương hỗ.

    tỉ lệ thuận là gì, tỉ lệ nghịch là gì

    Hai đại lượng tỉ lệ nghịch $x$ và $y$ liên hệ với nhau bởi công thức $y=\frac{a}{x}$ hay $xy=a$ (với $a$ là một số khác $0$) thì ta nói $y$ tỉ lệ nghịch với $x$ theo hệ số tỉ lệ $a$.

    Ví dụ: Nếu $y=\frac{4}{x}$ thì $y$ tỉ lệ nghịch với $x$ theo hệ số tỉ lệ là $4$.

    Chú ý: Khi $y$ tỉ lệ nghịch với $x$ theo hệ số tỉ lệ $a$, ta cũng nói $x$ tỉ lệ nghịch với $y$ theo hệ số tỉ lệ $a$.

    Tính chất của tỉ lệ nghịch

    Tích của một giá trị bất kì của đại lượng này với giá trị tương ứng của đại lượng kia luôn là một hằng số (bằng hệ số tỉ lệ) $$x_1 y_1=x_2 y_2=x_3 y_3 = … = a$$

    Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia $$\frac{x_1}{x_2}=\frac{y_2}{y_1}, \frac{x_1}{x_3} = \frac{y_3}{y_1},…$$

    Ví dụ tỉ lệ nghịch

    Ví dụ 1. Hai đại lượng $x$ và $y$ có tỉ lệ nghịch với nhau hay không, nếu:

    $x$ 1 2 4 5 8
    $y$ 120 60 30 24 15

    Hướng dẫn.

    Để kiểm tra hai số $x$ và $y$ có tỉ lệ nghịch với nhau hay không, chúng ta kiểm tra xem tích $xy$ có luôn là một hằng số hay không.

    Ta có: $$x y = 1 \times 120 = 2 \times 60 = 4 \times 30 = 5 \times 24 = 8 \times 15 = 120$$

    Theo tính chất của đại lượng tỉ lệ nghịch thì $x$ và $y$ trong trường hợp này là hai đại lượng tỉ lệ nghịch.

    Ví dụ 2. Hai đại lượng $x$ và $y$ có tỉ lệ nghịch với nhau hay không, nếu:

    $x$ 1 3 4 5 6
    $y$ 30 20 15 12,5 10

    Hướng dẫn. Ta có $$x y = 1 \times 30 \ne  3 \times 60$$ Suy ra $x$ và $y$ trong trường hợp này không là hai đại lượng tỉ lệ nghịch.

    Các bài toán tỉ lệ nghịch

    Đối với các bài tập tỉ lệ thuận, mời các em xem trong bài viết Đại lượng tỉ lệ thuận là gì?

    Bài 1. Để làm xong một công việc thì 21 công nhân cần làm trong 15 ngày. Do cải tiến kĩ thuật nên năng suất lao động của mỗi công nhân tăng thêm 25%. Hỏi 18 công nhân phải cần bao nhiêu ngày để làm xong công việc trên.

    Bài 2. Có ba tủ sách đựng tất cả 2250 cuốn. Nếu chuyển 100 cuốn từ tủ 1 sang tủ 3 thì số sách tủ 1, tủ 2, tủ 3 tỉ lệ với 16, 15 và 14. Hỏi trước khi chuyển mỗi tủ có bao nhiêu cuốn sách.

    Bài 3. Một bể nước hình chữ nhật có chiều rộng và chiều dài tỉ lệ với 4 và 5, chiều rộng và chiều cao tỉ lệ với 5 và 4, thể tích của bể là 64m3. Tính chiều rộng, chiều dài, chiều cao của bể.

    Bài 4. Một trường có ba lớp 7 biết rằng $\displaystyle \frac{2}{3}$ học sinh lớp 7A bằng số học sinh lớp 7B và bằng $\displaystyle \frac{4}{5}$ số học sinh lớp 7C. Lớp 7C có số học sinh ít hơn tổng số học sinh hai lớp kia là 57 bạn. Tính số học sinh mỗi lớp.

    Bài 5. Ba bạn A, B, C theo thứ tự học lớp 8, 7, 6 và có điểm tổng kết học kì I là 8,0; 8,4; 7,2. Nhà trường dùng 85 cái bút để phát thưởng cho ba bạn trên, biết rằng số bút được thưởng tỉ lệ nghịch với lớp học và tỉ lệ thuận với điểm trung bình. Tính số bút mà mỗi bạn được thưởng ?

    Bài 6. Nếu cộng lần lượt độ dài từng hai đường cao của tam giác thì tỉ lệ các kết quả là 5:7:8. Tính tỉ lệ ba cạnh của tam giác đó.

    Bài 7. Nhờ thi đua một nhà máy đó hoàn thành kế hoạch cả năm. Khối lượng sản phẩm thực hiện của ba quý đầu tỉ lệ với $\displaystyle 2\frac{1}{10}$; $2\frac{1}{4}$; $2\frac{2}{5}$. Còn quý IV thực hiện được 28% kế hoạch cả năm. Hỏi cả năm nhà máy sản xuất được bao nhiêu tấn hàng nếu quý IV hơn quý I là 84 tấn.

    Bài 8. Gạo được chứa trong ba kho theo tỉ lệ \displaystyle 1,3 : 2\frac{1}{2} : 1\frac{1}{5}. Gạo trong kho thứ hai nhiều hơn trong kho thứ nhất là 43,2 tấn. Sau một tháng người ta tiêu thụ hết ở kho thứ nhất 40%, ở kho thứ hai 30% và kho thứ ba 25% của số gạo trong kho. Hỏi trong một tháng đó tiêu thụ hết bao nhiêu tấn gạo?

    Bài 9. Một nhà máy chia 1500kg thóc cho ba đội sản xuất tỉ lệ với số người của mỗi đội. Biết rằng số người của đội thứ hai bằng trung bình cộng số người của đội thứ nhất và đội thứ ba. Đội thứ nhất lĩnh nhiều hơn đội thứ ba là 300kg. Hỏi mỗi đội được lĩnh bao nhiêu kg thóc?

    Bài 10. Cùng một lúc: Một ô tô đi từ A đến B với vận tốc 40 km/h, một ô tô khác đi từ B về A với vận tốc 50 km/h, một xe đạp đi C về B với vận tốc 15 km/h ( C nằm giữa A và B ). Hỏi sau bao lâu thì xe đạp ở chính giữa hai ô tô. Biết rằng quãng đường AB là 102 km, quãng đường AC là 41 km.