100 Bài tập phương pháp tọa độ trong mặt phẳng
Xem thêm Toán 10 – Biện luận hệ phương trình, hệ bất phương trình bằng đồ thị
1. Hệ trục tọa độ trong mặt phẳng
Hệ trục tọa độ và tọa độ của điểm, tọa độ của vecto
- Hệ trục tọa độ Descartes trong mặt phẳng. Hệ trục gồm hai đường thẳng $ x’Ox,y’Oy $ vuông góc với nhau; trên các đường thẳng đó chọn lần lượt các véc-tơ đơn vị $ \vec{i},\vec{j}. $
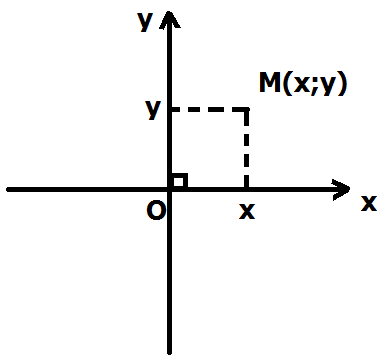
- Tọa độ của một điểm: \[ M(x,y) \Leftrightarrow \overrightarrow{OM}=x\vec{i}+y\vec{j}\]
- Tọa độ của một véc-tơ: \[ \vec{v}=(x,y) \Leftrightarrow \vec{v}=x\vec{i}+y\vec{j}\]
- Các phép toán và công thức. Cho ba điểm $ A(x_A,y_A) ,B(x_B,y_B)$, và các véc-tơ $\vec{v}_1(x_1,y_1),$ $\vec{v}_2(x_2,y_2) $ thì ta có:
- Hai véc-tơ bằng nhau $ \vec{v}_1=\vec{v}_2 \Leftrightarrow \begin{cases} x_1=x_2\\y_1=y_2\end{cases}$
- Tọa độ của $ \overrightarrow{AB}=(x_B-x_A,y_B-y_A) $
- Trung điểm $ M $ của $ AB $ có tọa độ $ M(\frac{x_A+x_B}{2},\frac{y_A+y_B}{2}) $
- Trọng tâm $ G $ của tam giác $ABC$ có tọa độ $ G(\frac{x_A+x_B+x_C}{3},\frac{y_A+y_B+y_C}{3}) $
- Phép cộng, trừ các véc-tơ $ \vec{v}_1\pm \vec{v}_2= (x_1\pm x_2,y_1\pm y_2)$
- Nhân véc-tơ với một số $ k\vec{v}_1=(kx_1,kx_2) $ với mọi số thực $ k. $
- Điểm chia đoạn thẳng \[ \overrightarrow{MA}+\lambda \overrightarrow{MB}=\vec{0} \Leftrightarrow \begin{cases}
x_M=\frac{x_A+\lambda x_B}{1+\lambda}\\
x_M=\frac{y_A+\lambda y_B}{1+\lambda}
\end{cases}\] Đặc biệt khi $ \lambda=-1 $ thì $ M $ là trung điểm của $ AB. $ - Hai véc-tơ cùng phương: $ \vec{v}_1 $ và $ \vec{v}_2 $ cùng phương $ \Leftrightarrow \vec{v}_1=k \vec{v}_2. $ Có thể sử dụng điều kiện $ \frac{x_1 }{x_2}=\frac{y_1}{y_2} $, với quy ước rằng mẫu bằng không thì tử bằng không.
Tích vô hướng của hai véc-tơ.
Cho hai véc-tơ $\vec{v}_1(x_1,y_1),\vec{v}_2(x_2,y_2) $ thì ta có:
- Định nghĩa. $ \vec{v}_1\cdot \vec{v}_2= |\vec{v}_1|\cdot |\vec{v}_2|\cdot \cos(\vec{v}_1,\vec{v}_2)$
- Biểu thức tọa độ: $ \vec{v}_1\cdot \vec{v}_2= x_1 x_2+y_1 y_2 $
- Hệ quả:
- $ \vec{v}_1\perp \vec{v}_2 \Leftrightarrow \vec{v}_1\cdot \vec{v}_2= 0 $
- $ |\vec{v}_1|= \sqrt{x_1^2+y_1 ^2},\; AB=|\overrightarrow{AB}|=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
- $\displaystyle \cos(\vec{v}_1,\vec{v}_2)=\frac{\vec{v}_1\cdot \vec{v}_2}{|\vec{v}_1|\cdot |\vec{v}_2|}=\frac{\text{tích vô hướng}}{\text{tích độ dài}} $
Bài 1. Trong mặt phẳng tọa độ $ Oxy, $ cho điểm $ M(x, y). $ Tìm tọa độ các điểm:
- $ M_1 $ đối xứng với $ M $ qua $ Ox. $
- $ M_2 $ đối xứng với $ M $ qua $ Oy $
- $ M_3 $ đối xứng với $ M $ qua gốc tọa độ $ O. $
Bài 2. Cho ba điểm $ A(2,5),B(1,1),C(3,3). $ Tìm tọa độ của điểm $D$ sao cho $ABCD$ là hình bình hành. Tìm tọa độ tâm $ I $ của hình bình hành đó?
Đáp số $ D(4,7),I(5/2,4) $
Bài 3. Cho hình bình hành $ ABDC $ có $ A(-1, 3), B(2, 4), C(0, 1) $. Tìm tọa độ đỉnh $ D. $
Bài 4. Cho tam giác $ ABC $ có các điểm $ M(1, 0), N(2, 2), P(-1, 3) $ lần lượt là trung điểm của các cạnh $ BC, CA, AB. $ Tìm tọa độ các đỉnh của tam giác.
Bài 5. Cho $ A(3, 4), B(2, 5). $ Tìm $ x $ để điểm $ C(-7, x) $ thuộc đường thẳng $ AB $.
Bài 6. Trong mặt phẳng tọa độ $Oxy$, thực hiện các yêu cầu sau:
- Cho ba điểm $ A(-1, 1), B(1, 3), C(-2, 0). $ Chứng minh ba điểm $ A, B, C $ thẳng hàng.
- Cho $ A(-1, 8), B(1, 6), C(3, 4). $ Chứng minh ba điểm $ A, B, C $ thẳng hàng.
- Cho $ A(1, 1), B(3, 2), C(m + 4, 2m + 1). $ Tìm $ m $ để ba điểm $ A, B, C $ thẳng hàng
- Cho bốn điểm $ A(0, 1), B(1, 3), C(2, 7), D(0, 3). $ Chứng minh đường thẳng $ AB $ và $ CD $ song song.
- Cho bốn điểm $ A(-2, -3), B(3, 7), C(0, 3), D(-4, -5). $ Chứng minh rằng hai đường thẳng $ AB $ và $ CD $ song song.
Bài 7. Cho tam giác $ ABC $ với $ A (3, 2), B (- 11, 0), C (5, 4). $ Tìm tọa độ trọng tâm $ G $ của tam giác $ ABC. $
Bài 8. Cho $\Delta ABC $ có $ A (1, – 1), B (5, – 3) $ đỉnh $ C $ thuộc $ Oy $ và trọng tâm $ G $ thuộc $ Ox. $ Tìm tọa độ đỉnh $ C. $
Bài 9. Cho $ A (- 2, 1), B (4, 5). $ Tìm tọa độ trung điểm $ I $ của đoạn thẳng $ AB $ và tìm tọa độ của điểm $ C $ sao cho tứ giác $ OACB $ là hình bình hành với $ O $ là gốc tọa độ.
Bài 10. Trong mặt phẳng tọa độ $ Oxy $ cho ba điểm $ A(-1, 3), B(4, 2), C(3, 5). $
- Chứng minh rằng ba điểm $ A, B, C $ không thẳng hàng.
- Tìm tọa độ điểm $ D $ sao cho $ \overrightarrow{AD}=-3\overrightarrow{BC}. $
- Tìm tọa độ điểm $ E $ sao cho $ O $ là trọng tâm của tam giác $ ABE. $
Bài 11. Trong mặt phẳng tọa độ $ Oxy $ cho $ A(3,4),B(-1,2),I(4,-1). $ Xác định tọa độ các điểm $ C, D $ sao cho tứ giác $ ABCD $ là hình bình hành với $ I $ là trung điểm cạnh $ CD. $ Tìm tọa độ tâm $ O $ của hình bình hành $ ABCD. $
Đáp số. $C(2,-2),D(6,0)$
Bài 12. Trong hệ trục $ Oxy $ cho điểm $ A(-1, 2) $ và $ B(4, 5). $
- Tìm tọa độ của diểm $ A’ $ đối xứng của $ A $ qua $ Ox. $
- Tìm tọa độ của $ M $ trên $ Ox $ sao cho $ A’,M ,B $ thẳng hàng.
Hướng dẫn. Điểm $ A(-1, 2) $ thì đối xứng của $ A $ qua $ Ox $ là $ A(-1 , -2). $
Điểm $ M $ trên $ Ox $ nên có tọa độ dạng $ M(x_0, 0). $ Từ $ \overrightarrow{A’B} $ và $ \overrightarrow{A’M} $ cùng phương tìm được $ x_0=3/7. $
Bài 13. [Đề thi Toán khối D năm 2010] Trong mặt phẳng toạ độ $ Oxy, $ cho tam giác $ ABC $ có đỉnh $ A(3,-7), $ trực tâm là $ H(3,-1), $ tâm đường tròn ngoại tiếp là $ I(-2,0) $. Xác định toạ độ đỉnh $ C $, biết $ C $ có hoành độ dương.
Đáp số. $ C(-2+\sqrt{65},3) $
2. Phương trình đường thẳng
Phương trình đường thẳng
- Phương trình tổng quát của đường thẳng $\Delta$ đi qua $M(x_{0},y_{0})$ và có một véc-tơ pháp tuyến $\vec{n}(a,b)$:
\[ ax+by-(ax_{0}+by_{0})=0 \] - Phương trình tham số} của đường thẳng $\Delta$ đi qua $M(x_{0},y_{0})$ và có một véc-tơ chỉ phương $\vec{u}(a,b)$ là:\[
\begin{cases} x =x_{0}+at\\ y =y_{0}+bt \end{cases}, (t\in \mathbb{R})
\] - Phương trình chính tắc} của đường thẳng đi qua $ M(x_0,y_0) $ và có véc-tơ chỉ phương $ \vec{u}(a,b) $ mà $ ab\ne0 $ là $$\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}$$
- Đường thẳng đi qua điểm $M(x_{0},y_{0})$ và cóhệ số góc} $k$ có phương trình: $$y-y_{0}=k(x-x_{0})$$
- Véctơ chỉ phương và véc-tơ pháp tuyến vuông góc với nhau, do đó nếu véc-tơ pháp tuyến là $\vec{n}=(a,b)$ thì có thể chọn véc-tơ chỉ phương $\vec{u}=(-b,a)$ hoặc $\vec{u}=(b,-a);$ và ngược lại.
- Hai đường thẳng song song thì có cùng các véc-tơ chỉ phương, cùng các véc-tơ pháp tuyến, hai đường thẳng vuông góc thì véc-tơ chỉ phương của đường thẳng này là véc-tơ pháp tuyến của đường thẳng kia và ngược lại. Tức là, nếu đường thẳng $\Delta$ có phương trình: $ax+by+c=0$ thì đường thẳng $\Delta’$
- vuông góc với $\Delta$ là $\Delta’:-bx+ay+c’=0$ hoặc $\Delta’:bx-ay+c’=0$.
- song song với $\Delta$ là $\Delta’:ax+by+c’=0$ với $ c\ne c’. $
- Đường thẳng cắt hai trục tọa độ tại $A(a,0)$ và $B(0,b)$ có phương trình:
$$\frac{x}{a}+\frac{y}{b}=1$$ Phương trình này được gọi là phương trình đoạn chắn. - Lấy một điểm thuộc đường thẳng ta có thể rút tọa độ $ x $ theo $ y $ hoặc ngược lại, nếu cần thì chuyển về phương trình tham số.
Góc – Khoảng cách
- Khoảng cách từ điểm $ M(x_0,y_0) $ đến đường thẳng $ \Delta:ax+by+c=0 $ là $$ d(M,\Delta)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
- Góc giữa hai véc-tơ $ \vec{a},\vec{b} $ có $\cos(\vec{a},\vec{b})=\frac{\vec{a}.\vec{b}}{|\vec{a}|.|\vec{b}|}=\frac{\text{tích vô hướng}}{\text{tích độ dài}} $
- Góc giữa hai đường thẳng\footnote{Bằng trị tuyệt đối của tích vô hướng chia tích độ dài các véc-tơ pháp tuyến của hai đường thẳng.} $ \Delta $ và $ \Delta’ $ có $$\cos(\Delta,\Delta’)=|\cos(\vec{n},\vec{n’})|=\frac{|\vec{n}.\vec{n’}|}{|\vec{n}|.|\vec{n’}|}$$
2.1. Các bài tập cơ bản viết phương trình tham số, phương trình tổng quát của đường thẳng
Bài 1. Cho $\Delta ABC$ với $A(3,2),B(1,1),C(5,6)$.
- Viết phương trình tổng quát các cạnh của $\Delta ABC$.
- Viết phương trình tổng quát của đường cao $AH$, đường trung tuyến$AM$.
Bài 2. Viết phương trình đường thẳng $d$ biết nó
- Đi qua giao điểm của 2 đường thẳng $d_{1}:2x-3y-15=0,d_{2}:x-12y+3=0$ và $d$ đi qua điểm $A(2,0)$.
- Đi qua giao điểm của 2 đường thẳng $d_{1}:3x-5y+2=0,d_{2}:5x-2y+4=0$ và song song với đường thẳng $d_{3}:2x-y+4=0$.
- Đi qua giao điểm của 2 đường thẳng $d_{1}:2x-3y+5=0,d_{2}:x-2y-3=0$ và vuông góc với đường thẳng $d_{3}:x-7y-1=0.$
Bài 3. Tìm $m$ để hai đường thẳng: $x+(2m-3)y-3=0$ và $\begin{cases} x & =1-t\\ y & =2-t \end{cases}$ vuông góc với nhau.
Bài 4. Lập phương trình tổng quát của 3 đường trung trực và 3 cạnh của $\Delta ABC$ biết các trung điểm của $BC,CA$ và $AB$ là $M(4,2),N(0,-1),P(1,4).$
Bài 5. Cho đường thẳng $d:3x+4y-12=0$.
- Tìm hình chiếu vuông góc $H$ của gốc $O$ trên $d$.
- Tìm điểm đối xứng $O’$ của gốc $O$ qua $d$.
- Viết phương trình đường thẳng $d’$ đối xứng của $d$ qua $O$.
Bài 6. Cho tam giác $ ABC $ có trung điểm $ M $ của $ AB $ có tọa độ $ (- 1/2, 0) $, đường cao$ CH $ với $ H(- 1, 1) $, đường cao $ BK $ với $ K(1 , 3) $ và biết $ B $ có hoành độ dương.
- Viết phương trình $ AB $.
- Tìm tọa độ $ B, A $ và $ C $.
Hướng dẫn. Đường thẳng $AB$ đi qua $H$ và $M$ nên có phương trình $ 2x+y+1=0. $
Điểm $ B\in AB $ nên có tọa độ dạng $ B(b,-1-2b). $ Có $A$ đối xứng với $B$ qua $M\Leftrightarrow A(-1-b,1+2b).$ Mà $ \overrightarrow{AK}.\overrightarrow{BK}=0 \Leftrightarrow b=1.$ Từ đó tìm được $ A(-2,3),B(1,-3) $ và $ C(3,3) $.
2.2. Sử dụng điểm thuộc đường thẳng (tham số hóa)
Bài 1. Trong mặt phẳng tọa độ $Oxy$ cho các điểm $ A(1,0),B(-2,4),C(-1,4),D(3,5) $ và đường thẳng $ d:3x-y-5=0 $. Tìm điểm $ M $ trên $ d $ sao cho hai tam giác $ MAB, MCD $ có diện tích bằng nhau.
Hướng dẫn. Phương trình đường thẳng $AB:4x+3y-4=0,$ đường thẳng $ CD:x-4y-17=0. $
Vì $ M\in d $ nên có tọa độ dạng $ M(t,3t-5). $ Do đó $ d(M,AB)=…, d(M,CD)=… $
Bài 2. Trong mặt phẳng tọa độ $Oxy$, cho đường thẳng $ d:x-3y-6=0 $ và điểm $ N(3,4) $. Tìm tọa độ điểm $ M $ thuộc đường thẳng $ d $ sao cho tam giác $ OMN $ có diện tích bằng $ \frac{15}{2}. $
Hướng dẫn. Đáp số $ M(3,-1) $ và $ M(-7,-\frac{13}{3}) $.
Bài 3. Cho tam giác $ ABC $ có diện tích bằng 2. Biết tọa độ $ A(1,0), B(0,2) $ và trung điểm $ I $ của $ AC $ nằm trên đường thẳng $ y = x $. Tìm toạ độ đỉnh $ C $.
Hướng dẫn. Vì $ I $ thuộc đường thẳng $ y=x $ nên có tọa độ dạng $ I(t,t) $. Từ $ I $ là trung điểm $ AC $ suy ra $ C(2t-1,2t) $.
Mặt khác, từ $ S_{\Delta ABC}=\frac{1}{2}AB.d(C,AB)=2 $ suy ra $ d(C,AB)= $
Bài 4. Cho tam giác $ ABC $ có trung điểm của $ AB $ là $ I(1 , 3) , $ trung điểm $ AC $ là $ J(- 3, 1) $. Điểm $ A $ thuộc trục $ Oy $ và đường $ BC $ qua gốc tọa độ $ O $. Tìm tọa độ điểm $ A $, phương trình $ BC $ và đường cao vẽ từ $ B $.
Hướng dẫn. Vì $A$ thuộc trục $ Oy $ nên có tọa độ $ A(0,a), $ suy ra $ B(2,6-a) $ và $ C(-6,2-a). $ Ta có đường thẳng $BC$ đi qua $O\Leftrightarrow \overrightarrow{OB},\overrightarrow{OC} $ cùng phương $ \Leftrightarrow a=5. $
Bài 5. Trong mặt phẳng toạ độ $ Oxy $, cho hai đường thẳng $ d_1:x+y-3=0,d_2:x+y-9=0 $ và điểm $ A(1, 4) $. Tìm điểm $ B\in d_1,C\in d_2 $ sao cho tam giác $ ABC $ vuông cân tại $A$.
Hướng dẫn. Gọi $ B(b,3-b) $ và $ C(c,9-c). $ Lập hệ, từ phương trình $ \overrightarrow{AB}.\overrightarrow{AC}=0 $ rút ra $ b-1=\frac{(b+1)(5-c)}{c-1} $ thay vào phương trình còn lại được $ (b+1)^2=(c-1)^2 $. Đáp số $ B(2,1),C(4,5) $ hoặc $ B(-2,5),C(2,7). $
Bài 6. Trong hệ tọa độ $Oxy,$ cho hình thoi $ABCD$ cạnh $AC$ có phương trình là: $x+7y-31=0,$ hai đỉnh $ B,D $ lần lượt thuộc các đường thẳng $ d_1:x+y-8=0,d_2:x-2y+3=0 $. Tìm tọa độ các đỉnh của hình thoi biết rằng diện tích hình thoi bằng 75 và đỉnh $ A $ có hoành độ âm.
Hướng dẫn. Đáp số $A(-11,6),B(0,8),C(10,3),D(-1,1).$
Bài 7. Trong mặt phẳng tọa độ $ Oxy $ cho điểm $ A(1,1) $ và đường thẳng $ \Delta:2x+3y+4=0. $Tìm tọa độ điểm $ B $ thuộc $ \Delta $ sao cho đường thẳng $ AB $ và $ \Delta $ hợp với nhau góc $ 45^\circ $.
Đáp số. $ B(-\frac{32}{13},\frac{4}{13}),B(\frac{22}{13},-\frac{32}{13}) $
Bài 8 .Cho đường thẳng $ \Delta:x-2y-2=0$ và hai điểm điểm $A(-1,2),B(3,4).$ Tìm điểm $ M\in \Delta $ sao cho $ 2MA^2+MB^2 $ đạt giá trị nhỏ nhất.
Hướng dẫn. Sử dụng hàm số. Đáp số $ M(\frac{26}{15},-\frac{2}{15}) $
Bài 9. Cho điểm $ C(2,-5) $ và đường thẳng $ \Delta:3x-4y+4=0. $ Tìm trên $ \Delta $ hai điểm $ A,B $ đối xứng nhau qua $ I(2,\frac{5}{2}) $ sao cho diện tích tam giác $ ABC $ bằng 15.
Hướng dẫn. $(0,1),(4,4).$
Bài 10. Trong mặt phẳng toạ độ $ Oxy $, cho đường thẳng $ d:2x-y+3=0 $ và hai điểm $ A(1,0),B(2,1). $ Tìm điểm $ M $ trên $ d $ sao cho $ MA + MB $ nhỏ nhất.
Hướng dẫn. Nhận xét $ A,B $ nằm cùng phía so với đường thẳng $ d$. Tìm được $ A'(-3,2) $ đối xứng với $ A $ qua $d$ và phương trình $ A’B:x+5y-7=0. $
Ta có $ MA+MB= MA’+MB\ge A’B $ nên $ MA+MB $ nhỏ nhất $ \Leftrightarrow M,A’,B $ thẳng hàng hay $ M $ là giao điểm của $ A’B $ với $ d. $ Đáp số $ M(-\frac{8}{11},\frac{17}{11}). $
2.3. Sử dụng véc-tơ pháp tuyến
Bài 1. Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $ d:x-\sqrt{3} y-2=0,$ điểm $ A(1,\sqrt{3}) $ và điểm $ B $ không thuộc đường thẳng $ d. $ Lập phương trình đường thẳng $AB$ biết khoảng cách từ điểm $B$ đến giao điểm của đường thẳng $ d$ và $ AB $ bằng hai lần khoảng cách từ $ B $ đến $ d. $
Hướng dẫn. Gọi $ C $ là giao điểm của $ d $ và $ AB, H $ là hình chiếu của $ B $ lên $ d$ thì $\sin(d,AB)=\frac{BH}{BC}=\frac{1}{2}. $
Bài 2. [HVKTQS 2001] Tam giác $ ABC $ cân đỉnh $ A $, cạnh đáy $ BC $ có phương trình $x-3y-1=0$, cạnh bên $ AB $ có phương trình $x-y-5=0$, đường thẳng $ AC $ đi qua điểm $M(-4;1)$. Tìm toạ độ đỉnh $ C? $
Hướng dẫn. Giả sử đường thẳng $ AC $ có một vectơ pháp tuyến $\overrightarrow{n}\left( a,b \right)$, dùng điều kiện $\cos \left( AB,BC \right)=\cos \left( AC,BC \right)$, lập được phương trình hai ẩn: $7{{a}^{2}}-{{b}^{2}}+6ab=0$.
Suy ra phương trình $ AC: x+7y-3=0$ (Chú ý loại trường hợp song song với $ AB $). Từ đó tìm được toạ độ điểm $C\left( \frac{8}{5};\frac{1}{5} \right)$
2.4. Sử dụng phương trình đoạn chắn
Bài 1. Viết phương trình đường thẳng qua $ M(3 , 2) $ và cắt tia $ Ox $ tại $ A $, tia $ Oy $ tại $ B $ sao cho
- $ OA + OB = 12 $;
- tạo với hai trục một tam giác có diện tích là 12.
Hướng dẫn. 1. $ x +3y-9 =0, 2x+y-8=0. $ 2. $ 2x+3y-12=0. $
Bài 2. Cho điểm $ M(3 , 3) $. Viết phương trình đường thẳng $ \Delta $ cắt $ Ox $ và $ Oy $ tại $ A $ và $ B $ sao cho tam giác $ MAB $ vuông tại $ M $ và $ AB $ qua điểm $ I(2 , 1) $.
Hướng dẫn. Gọi tọa độ $ A(a,0),B(0,b) $ với $ ab\ne0 $ thì $ \overrightarrow{MA}.\overrightarrow{MB}=0 \Leftrightarrow a+b=6. $ Mặt khác phương trình đường thẳng $ AB: \frac{x}{a}+\frac{y}{b}=1,$ mà $ I(2,1)\in AB \Leftrightarrow a+2b=ab. $
Từ đó tìm được $a=4, b=2 $ hoặc $ a=3,b=3. $
Bài 3. Trên mặt phẳng $Oxy$ cho điểm $A(2,-2)$. Viết phương trình đường thẳng $\Delta$ đi qua điểm $M(3,1)$ và cắt trục $Ox,Oy$ tại $B$ và $C$ sao cho tam giác $ABC$ cân.
Hướng dẫn. $\frac{x}{2}+\frac{y}{-2}=1$
Bài 4. Cho điểm $ M(9 , 4) $. Viết phương trình đường thẳng $ \Delta $ qua $ M $, cắt hai tia $ Ox $ và tia $ Oy $ tại $ A $ và $ B $ sao cho tam giác $ OAB $ có diện tích nhỏ nhất.
Hướng dẫn. Gọi tọa độ $ A(a,0),B(0,b) $ với $ a,b>0 $ thì phương trình đường thẳng $ \Delta $ cần tìm là $ \frac{x}{a}+\frac{y}{b}=1 $. Đường thẳng $\Delta$ qua $ M(9,4) \Leftrightarrow \frac{9}{a}+\frac{4}{b}=1.$ Áp dụng Cauchy có \[ 1=\frac{9}{a}+\frac{4}{b}\ge 2\sqrt{\frac{36}{ab}}=\frac{12}{\sqrt{ab}} \] Suy ra $ \sqrt{ab}\ge 12\Rightarrow S_{\Delta OAB}=\frac{1}{2}ab\ge 72 $.
Vậy tam giác $ OAB $ có diện tích nhỏ nhất là 72 khi $ \frac{9}{a}=\frac{4}{b}=\frac{1}{2} \Leftrightarrow a=18,b=8. $ Khi đó phương trình đường thẳng $\Delta$ là $ 4x+9y-72=0. $
Bài 5. Trong mặt phẳng tọa độ $Oxy$ cho điểm $ M(1,2) $. Viết phương trình đường thẳng $ d $ đi qua $M$ và cắt các trục $Ox,Oy$ lần lượt tại $ A, B $ khác $ O $ sao cho $ \frac{9}{OA^2}+\frac{4}{OB^2} $ nhỏ nhất.
Hướng dẫn. Sử dụng Bunhia. Đáp số $ 2x+9y-20=0. $
2.5. Các bài toán liên quan đến tam giác
Bài 1. Cho tam giác $ ABC $ có $ A(2;2) $. Hai đường cao xuất phát từ đỉnh $ B $ và $ C $ lần lượt có phương trình là: $9x-3y-4=0;x+y-2=0$. Viết phương trình đường các cạnh và tính diện tích của tam giác.
Bài 2. Lập phương trình các cạnh của $\Delta ABC$ nếu cho $B(-4,5)$ và hai đường cao của tam giác có phương trình: $5x+3y-4=0$và $3x+8y+13=0.$
Bài 3. Viết phương trình các cạnh của tam giác $ ABC $ có đỉnh $ C(4,-1) $, đường cao và trung tuyến kẻ từ đỉnh $ A $ có phương trình lần lượt là ${{d}_{1}}:2x-3y+12=0$ và ${{d}_{2}}:2x+3y=0$.
Bài 4. Trong mặt phẳng $ Oxy $ cho $ \Delta ABC $ có $ A(2,1). $ Đường cao qua đỉnh $ B $ có phương trình $ x-3y-7=0. $ Đường trung tuyến qua đỉnh $ C $ có phương trình $ x+y+1=0. $ Xác định tọa độ $ B $ và $ C. $ Tính diện tích tam giác $ ABC $.
Hướng dẫn. $ C(4,-5), B(1,-2), S=6. $
Bài 5. Cho tam giác $ABC$ có đường cao $ BH:x+2y-3=0, $ trung tuyến $ AM:3x+3y-8=0. $ Cạnh $ BC $ đi qua $ N(3,-2) $ và $ C $ thuộc đường thẳng $ d:x-y+2=0. $ Tìm tọa độ các đỉnh của tam giác.
Hướng dẫn. Gọi tọa độ $ B(3-2b,b) $ và $ C(c,c+2) $ và biểu diễn tọa độ $ M $ theo $ b,c. $ Mà $ M\in AM $ nên $ 3b-6c+1=0. $ Từ $ B,N,C $ thẳng hàng tìm được $ 3bc+5b+2c-6=0. $ Từ đó tìm được tọa độ $ B,C. $
Bài 6. [ĐHBK 1994] Phương trình hai cạnh của một tam giác trong mặt phẳng toạ độ là: ${{d}_{1}}:5x-2y+6=0$ và ${{d}_{2}}:4x+7y-21=0$. Viết phương trình cạnh thứ ba biết rằng trực tâm của tam giác trùng với gốc toạ độ.
Bài 7. Cho tam giác $ABC$ có $ A(1,5). $ Điểm $ B $ nằm trên đường thẳng $ d_1:2x+y+1=0 $ và chân đường cao hạ từ đỉnh $ B $ xuống $ AC $ nằm trên đường thẳng $ d_2:2x+y-8=0. $ Biết $ M(3,0) $ là trung điểm của $ BC. $ Tìm tọa độ các đỉnh $ B,C$.
Hướng dẫn. Gọi $ B(m,-2m-1) $ và $ H(n,8-2n) $ suy ra $ C(6-m,2m+1). $ Từ $ A,H,C $ thẳng hàng tìm được $ m=11-6n. $ Mặt khác $ AH\perp BH $ nên tìm được $ n=2 $ hoặc $ n=\frac{52}{35}. $
Bài 8. Cho $\Delta ABC$ có trọng tâm $G(-2,-1)$ và các cạnh $AB:4x+y+15=0$, $AC:2x+5y+3=0$
- Tìm đỉnh $A$ và trung điểm $M$ của cạnh $BC$.
- Tìm đỉnh $B$ và viết phương trình đường thẳng $BC$.
Bài 9. Cho tam giác $ ABC $ có đỉnh $ A(-1;-3) $, đường trung trực của đoạn $ AB $ là: $ 3x+2y-4=0 $. Trọng tâm $ G(4;-2) $. Tìm tọa độ $ B, C $.
Hướng dẫn. $ B(5;1),C(8;-4). $
Bài 10. Cho tam giác $ ABC $ có đỉnh $ A $ thuộc $ d: x-4y-2=0. $ Cạnh $ BC $ song song với đường thẳng $d$, đường cao $ BH:x+y+3=0 $ và $ M(1;1) $ là trung điểm của $ AC $. Tìm tọa độ của các đỉnh $ A, B, C $.
Hướng dẫn. $ A\left( { – \frac{2}{3}; – \frac{2}{3}} \right),B(-4;2),C(\frac{8}{3},\frac{8}{3}) $.
Bài 11. Trong mặt phẳng $ Oxy, $ cho các điểm $ A(1,0),B(-2,4),C(-1,4),D(3,5) $ và đường thẳng $ d:3x-y-5=0. $ Tìm điểm $ M $ trên $ d $ sao cho hai tam giác $ MAB, MCD $ có diện tích bằng nhau.
Hướng dẫn. $ M(8,9) $ hoặc $ M(\frac{11}{12},-\frac{27}{12}) $
Bài 12. Cho hình tam giác $ ABC $ có diện tích bằng 2. Biết $ A(1,0),B(0,2) $ và trung điểm $ I $ của $ AC $nằm trên đường thẳng $ d:y=x. $ Tìm toạ độ đỉnh $ C. $
Hướng dẫn. $ C(\frac{1+\pm \sqrt{3}}{2},\frac{1+\pm \sqrt{3}}{2}) $
Bài 13. Cho tam giác $ ABC $ với $ A(1,1),B(-2,5) $ và đỉnh $ C $ nằm trên đường thẳng $ x-4=0,$ trọng tâm $ G $ của tam giác nằm trên đường thẳng $ 2x-3y+6=0. $ Tính diện tích tam giác $ ABC $.
Hướng dẫn. $S=\frac{15}{2} $
Bài 14. Cho tam giác $ ABC $ có $ A(2,-1),B(1,-2), $ trọng tâm $ G $ nằm trên đường thẳng $ d:x+y-2=0.$ Tìm tọa độ tỉnh $ C $ biết diện tích tam giác bằng $ \frac{27}{2}. $
Hướng dẫn. $ C(-6,12),C(\frac{38}{3},-\frac{20}{3}) $
Bài 15. Cho tam giác $ABC$ có $ C(-1,-1) $; phương trình cạnh $ AB:x+2y-5=0 $ và $ AB=\sqrt{5}. $ Trọng tâm $ G $ của tam giác $ABC$ thuộc đường thẳng $d:x+y-2=0$ . Xác định tọa độ các đỉnh còn lại của tam giác?
Hướng dẫn. Gọi $ A(5-2a,a) $ và $ B(5-2b,b) $ thuộc $ AB $ thì từ $ AB^2=5 $ suy ra $ a-b=\pm1. $ Suy ra tọa độ trọng tâm $ G $. Mà $ G\in d $ nên tìm được Hướng dẫn.
Bài 16. Cho tam giác $ ABC $ có trọng tâm $ G (1; 1) $, đường cao từ đỉnh $ A $ có phương trình $ d:2x – y + 1 = 0 $. Các đỉnh $ B $ và $ C $ thuộc đường thẳng $ d’: x + 2y – 1 = 0 $. Xác định tọa độ các đỉnh của tam giác biết tam giác $ ABC $ có diện tích bằng 6.
Hướng dẫn. Gọi $ M $ là trung điểm $ BC $ và $ A(a,2a+1) $ thì từ $ \overrightarrow{AG}=2\overrightarrow{GM} $ có $ M(\frac{3-a}{2},1-a) $. Mà $ M\in d’ $ nên tìm được $ A(1;2) $ và $ M(1;0). $ Gọi $ H $ là giao điểm của $ d $ và $ d’ $ thì $ H(-\frac{1}{5},\frac{3}{5}) $ do đó $ AH=\frac{6}{\sqrt{5}} $. Từ diện tích bằng $ 6 $ tìm được $ MB=MC=\sqrt{5}. $
Đáp số $ B(-1,1),C(3,-1) $ và $ B(3,-1),C(-1,1) $.
Bài 17. Cho tam giác $ ABC $ biết $ A(5,2). $ Phương trình đường trung trực cạnh $ BC, $ đường trung tuyến $ CC’ $ lần lượt là $ x+y-6=0,2x-y+3=0. $ Tìm tọa độ các đỉnh của tam giác $ ABC. $
Hướng dẫn. $ B(37,88),C(-20,-31). $
Bài 18. Trong mặt phẳng với hệ toạ độ $ Oxy, $ hãy viết phương trình các cạnh của tam giác $ ABC $ biết trực tâm $ H(1,0), $ chân đường cao hạ từ đỉnh $ B $ là $ K (0,2), $ trung điểm cạnh $ AB $ là $ M (3,1). $
Hướng dẫn. $ AB:3x-y-8=0,BC:3x+4y+2=0 $
Bài 19. Cho tam giác $ ABC $ có phương trình cạnh $ AB:x-y-2=0, $ phương trình cạnh $ AC:x+2y-5=0. $ Biết trọng tâm của tam giác là $ G(3,2). $Viết phương trình cạnh $ BC. $
Hướng dẫn. $ B(5,3),C(1,2)… $
Bài 20. Cho tam giác $ ABC $ biết $ A(1,-1),B(2,1), $ diện tích bằng $ \frac{11}{2} $ và trọng tâm $ G $ thuộc đường thẳng $ d:3x+y-4=0. $ Tìm tọa độ đỉnh $ C. $
Hướng dẫn. $C(1,0)\vee C(\frac{17}{5},-\frac{26}{5})$
Bài 21. Tam giác $ ABC $ có $ AB=\sqrt{5}, C(-1,-1), AB:x+2y-3=0, $ trọng tâm $ G $ thuộc đường thẳng $ x+y-2=0. $ Xác định tọa độ $ A,B? $
Hướng dẫn. $ (6,\frac{-3}{2}) $ và $ (4,\frac{-1}{2}) $
Bài 22. Cho tam giác $ ABC $ có $ A(2,-3),B(3,-2), $ diện tích bằng $ \frac{3}{2} $ và trọng tâm thuộc đường thẳng $ \Delta:3x-y-8=0. $ Tìm tọa độ đỉnh $ C. $
Hướng dẫn. Giả sử $ G(t,3t-8). $ Từ tọa độ trung điểm $ M $ của $ AB $ suy ra $ C(2t-5,9t-19)… $ Đáp số $C(\frac{-7\pm6\sqrt{5}}{3},-7\pm9\sqrt{5}) $
Bài 23. Viết phương trình các cạnh của tam giác $ ABC $ biết $ B(2,-1) $ đường cao và đường phân giác trong qua đỉnh $ A, C $ lần lượt là $ d_1:3x-4y+27=0,d_2:x+2y-5=0. $
Hướng dẫn. $ BC:4x+3y-7=0, AC:y-3=0 $ hoặc $ AC:4x+3y-5=0,AB:… $
Bài 24. Cho tam giác $ ABC $ có $ A(1,-2), $ đường cao $ CH:x-y+1=0, $ phân giác trong $ BN:2x+y+5=0. $ Tìm tọa độ các đỉnh $ B,C $ và tính diện tích tam giác?
Hướng dẫn. $B(-4,3)),C(-\frac{13}{4},-\frac{9}{4}), S=\frac{9\sqrt{10}}{4}. $
Bài 25. Cho tam giác $ABC$ vuông tại $ A $ có $ B $ và $ C $ đối xứng nhau qua gốc tọa độ $ O. $ Đường phân giác trong góc $ \widehat{B} $ có phương trình $ d:x+2y-5=0. $ Tìm tọa độ các đỉnh của tam giác biết $ AC $ đi qua $ K(6,2). $
Hướng dẫn. Gọi $ B(5-2b,b) $ thì $ C(2b-5,-b) .$ Gọi $ I $ đối xứng với $ O $ qua đường phân giác thì $ I(2,4) $ và $ I\in AB. $ Từ $ AB\perp AC $ tìm được $ b=1 $ hoặc $ b=5. $
Bài 26. Cho tam giác $ABC$ có đường cao hạ từ $ A $ là $ x-2y=0, $ đường phân giác trong góc $ \widehat{A} $ là $ x-y+1=0. $ Biết $ M(1,0) $ nằm trên $ AB $ và diện tích tam giác $ABC$ là $ \frac{180}{7} $. Tìm tọa độ các đỉnh của tam giác.
Hướng dẫn. Tìm được ngay $ A(-2,-1) $ và $ AB:x-3y-1=0 $. Gọi $ N $ là điểm đối xứng với $ M $ qua đường phân giác thì $ N(-1,2) $ và $ N\in AC. $ Từ đó tìm được $ AC:3x-y+5=0. $ Gọi $ B(3m+1,m) $ và $ C(n,3n+5) $ thì từ $ AH\perp BC $ suy ra $ 5n-7m+3=0. $ Kết hợp với diện tích tam giác $ABC$ bằng $ \frac{180}{7} $ suy ra $ m=\frac{8}{7} $ hoặc $ m=-\frac{22}{7} $.
Bài 27. Cho tam giác $ ABC $ cân tại $ A, $ biết phương trình đường thẳng $ AB, BC $ lần lượt là: $ x+2y-5=0,3x-y+7=0. $ Viết phương trình đường thẳng $ AC, $ biết rằng $ AC $ đi qua điểm $ F(1,-3). $
Hướng dẫn. $x+8y+23=0,4x+7y+25=0.$
Bài 28. Cho tam giác $ABC$ cân tại $ A $ và phương trình các cạnh $ AB,BC $ lần lượt là $ 7x-y+17=0,x-3y-9=0. $ Viết phương trình đường cao hạ từ $ C $ biết $ M(2,-1) $ thuộc đường thẳng $ AC. $
Hướng dẫn. Gọi véctơ pháp tuyến của $ AB $ là $ \vec{n}(a,b) $. Đáp số $ x+7y+11=0. $
Bài 29. Trong mặt phẳng với hệ toạ độ vuông góc $Oxy$, cho tam giác $ABC$ cân tại $A$. Biết phương trình các đường thẳng $AB$, $BC$ theo thứ tự là \[(d_1): 2x + y -1 = 0, (d_2): x + 4y + 3 = 0.\] Lập phương trình đường cao qua đỉnh $B $ của tam giác $ABC$.
Hướng dẫn. $31x +22y – 9 = 0$.
Bài 30. Cho tam giác $ABC$ cân tại $A$, biết $AB:x + 3y + 5 = 0 $, $BC: x – y + 1 = 0$, đường thẳng $AC$ đi qua điểm $M(3;0)$. Tìm toạ độ các đỉnh $A$, $B$, $C$.
Hướng dẫn. $A(4;-3)$, $B(-2;-1)$, $C(2;3)$.
Bài 31. Cho tam giác $ ABC $ cân tại $ A $, phương trình cạnh $ BC $ là $ d:2x – y + 3 = 0 $. Điểm $ I (-2; -1) $ là trung điểm cạnh $ BC $, điểm $ E (4; 1) $ nằm trên cạnh $ AB $. Tìm tọa độ các đỉnh của tam giác biết diện tích tam giác $ ABC $ bằng 90.
Hướng dẫn. Chỉ ra $ AI $ vừa là đường cao vừa là phân giác, có phương trình $ AI: x+2y+4=0.$ Qua $ E $ kẻ đường thẳng vuông góc với $ AI $ và cắt $ AI $ tại $ F, $ cắt $ AC $ tại $ M. $ Viết được phương trình $ EM, $ từ đó tìm được $ M(0,7) $. Gọi $ B(b,2b+3) $ thì $ C(-4-b,5-2b) $. Tam giác $ABC$ cân tại $ A $ nên $ \cos(BE,BC)=\cos(MC,BC) $. Tìm được $ b=1 $ và $ b=4. $ Với mỗi trường hợp của $ b $ tìm được tọa độ $ C,A $ tương ứng.
Bài 32. Cho tam giác $ ABC $ cân tại $ A $, có trực tâm $ H (-3; 2) $. Gọi $ D, E $ là chân đường cao hạ từ $ B $ và $ C $. Điểm $ A $ thuộc đường thẳng $ d:x – 3y – 3 = 0 $, điểm $ F (-2; 3) $ thuộc đường thẳng $ DE $ và $ HD = 2 $. Tìm tọa độ đỉnh $ A $.
Hướng dẫn. Có $ HD=2 $ nên $ (x_D+3)^2+(y_D-2)^2=4. $ Lấy $ A(3a+3,a) $ thì từ $ AD\perp DH $ nên có $ (x_D-3a-3)(x_D+3)+(y_D-a)(y_D-2)=0. $ Từ hai phương trình này tìm được $ (6+3a)x_D+(a-2)y_D+7a+18=0 $. Tương tự, có $ (6+3a)x_E+(a-2)y_E+7a+18=0 $ nên phương trình $ DE $ có dạng $ (6+3a)x+(a-2)y+7a+18=0 $. Mà $ F\in DE $ nên tìm được $ a=0. $ Đáp số $ A(3,0) $.
Bài 33. Trong mặt phẳng với hệ trục tọa độ $ Oxy, $ cho tam giác $ ABC $ cân tại $ A $ có $ AB:3x+2y-7=0 $ và $ BC:2x-y=0. $ Lập phương trình đường thẳng chứa đường cao $ BH $ của $ \Delta ABC. $
Bài 34. Trong mặt phẳng với hệ tọa độ $ Oxy, $ cho tam giác $ ABC $ có trực tâm $H(3,0).$ Biết $M(1,1)$ và $N(4,4)$ lần lượt là trung điểm của hai cạnh $AB, AC.$ Tìm tọa độ các đỉnh của tam giác $ABC.$
Đáp số. $ A(-1,4),B(3,-2),C(9,4) $ hoặc $ A(\frac{5}{2},\frac{1}{2}), B(\frac{-1}{2},\frac{3}{2}), C(\frac{11}{2},\frac{15}{2}). $
Bài 35. Tam giác $ ABC $ có $ B(2,-1), $ đường cao và đường phân giác kẻ từ $ A,C $ lần lượt là $ 3x-4y+27=0, x+2y-5=0. $ Viết phương trình các cạnh của tam giác.
Hướng dẫn. $ A(-5,3) $ và $ AB:4x+7y-1=0. $
Bài 36. [Đề thi thử SGD Bắc Ninh 2014] Cho tam giác $ ABC $ cân tại $ A(6,6), $ đường thẳng $ \Delta:x+y-4=0 $ đi qua trung điểm hai cạnh $ AB,AC. $ Điểm $ E(1,-3) $ nằm trên đường cao đi qua đỉnh $ C. $ Tìm tọa độ $ B,C? $ Bắc Ninh K.B NC 2014
Hướng dẫn. Gọi được $ H(-2,-2) $ đối xứng với $ A $ qua $ \Delta $ thì $ H $ là trung điểm $ BC. $ Suy ra $ BC:x+y+4=0. $ Giả sử $ B(t,-4-t) $ thì $ C(-4-t,t). $ Từ $ \overrightarrow{AB}.\overrightarrow{CE} $ tìm được $ B(0,-4), C(-4,0) $ hoặc $ B(-6,2),C(2,-6). $
Bài 37. Tam giác $ ABC $ có $ A(1,5) $, trọng tâm $ G(1,3) $ và trực tâm $ H(-23,17). $ Tìm tọa độ $ B,C $ biết $ x_B>x_C. $
Hướng dẫn. Gọi $ M $ là trung điểm $ BC $, tìm được $ M(1,2). $ Kẻ đường kính $ AD $ thì tứ giác $ BHCD $ là hình bình hành, suy ra $ D(25,-13). $ Gọi $ I $ là tâm đường tròn, suy ra $ I(13,-4). BC:2x-y=0.$ Đặt $ B(b,2b), C(c,2c). $ Có $ IA=IB=IC $ tìm được $ B(4,8), C(-2,-4). $ Đáp số $B(4,8), C(-2,-4).$
Bài 38. Tam giác $ABC$ có $ A(-1,-3) $, trực tâm $ H(1,-1) $ và tâm đường tròn ngoại tiếp là $ I(2,-1). $ Tìm tọa độ các đỉnh của tam giác.
Hướng dẫn. Gọi $ D $ là điểm đối xứng với $ A $ qua $ I $ thì $ AD $ là đường kính của đường tròn $ (I). $ Chỉ ra $ BHCD $ là hình bình hành và tìm được $ BC:x+y-2=0. $
Bài 39. [Đề thi thử trường chuyên Vĩnh Phúc] Cho tam giác $ ABC $ vuông cân tại $ A, $ điểm $ A $ có hoành độ dương và nằm trên đường thẳng $ \Delta:x-4y+6=0, BC: 2x-y-7=0, M(-1,1)\in AC.$ Tìm tọa độ các đỉnh của tam giác.
Hướng dẫn. Giả sử điểm $A(4a-6,a)\in \Delta.$ Có $ \cos (\overrightarrow{MA},\vec{u}_{BC})=\cos 45^\circ, $ tìm được $ A(2,2). $ Viết phương trình $ AC, $ tìm được tọa độ điểm $ C(5,3). $ Từ $ \overrightarrow{AB}.\overrightarrow{AC}=0 $ và $ B\in BC $ tìm được $ B(3,-1). $
Bài 40. [Đề thi thử Đặng Thúc Hứa năm 2014] Cho tam giác $ ABC $ vuông tại điểm $A$. Lấy điểm $M$ thuộc đoạn $ AC $ sao cho $ AB=3AM. $ Đường tròn tâm $ I $ đường kính $ CM $ cắt $ BM $ tại $ D. $ Phương trình $ CD:x-3y-6=0. $ Xác định tọa độ các đỉnh tam giác $ ABC $ biết $ N(\frac{4}{3},0)\in BC $ và điểm $ C $ có hoành độ dương.
Hướng dẫn. Có $\cos \widehat{ACD}= \cos \widehat{ABM}=\frac{3}{\sqrt{10}}. $ Giả sử $ C(3t+6,t) $ thì $ \cos \widehat{ACD}=\cos (\overrightarrow{IC},\vec{u}_{CD}) $ tìm được $C(3,-1). $ Viết phương trình đường thẳng $ BC,BM $ suy ra tọa độ $B(-2,2)$. Viết phương trình $ AB, CN $ suy ra tọa độ $ A(-2,-1). $
Bài 41. [Đề thi thử trường SPHN Lần 4 năm 2014] Cho $ C(6,0) $ và đường thẳng $ d:3x-y-10=0, \Delta:3x+3y-16=0 $ lần lượt là phân giác trong góc $ \widehat{A} $ và đường thẳng vuông góc với $ AC. $ Biết $ AC>AB $ và ba đường thẳng $ \Delta,d, $ trung trực của $ BC $ đồng quy. Tìm tọa độ điểm $B$.
Hướng dẫn. Giả sử giao điểm của $ d$ và $ \Delta $ là $ I. $ Gọi $ E $ đối xứng với $ B $ qua $ d $ thì $ E $ thuộc đoạn $ AC $ và $ IB=IE=IC $ nên $ \Delta $ là trung trực của $ CE. $ Gọi $ H=\Delta\cap AC, $ tìm được $ H(\frac{17}{3},-\frac{1}{3}). $ Suy ra $ E(\frac{16}{3},-\frac{2}{3}). $ Đáp số $ B(\frac{4}{3},\frac{2}{3}). $
Bài 42. [Đề thi thử trường Chuyên Lào Cai năm 2015] Trong mặt phẳng với hệ tọa độ $ Oxy, $ cho tam giác $ ABC $ có trực tâm $ H(5,5), $ phương trình đường thẳng $ BC:x+y-8=0. $ Biết đường tròn ngoại tiếp tam giác $ ABC $ đi qua hai điểm $ M(7,3),N(4,2). $ Tính diện tích tam giác $ ABC. $
Hướng dẫn. Tìm được $ H'(3,3) $ là điểm đối xứng với $ H $ qua $ BC $ thì $ H’ $ nằm trên đường tròn ngoại tiếp tam giác $ ABC. $ Như vậy, đường tròn ngoại tiếp tam giác $ ABC $ đi qua ba điểm $ M,N,H’. $ Do đó phương trình đường tròn ngoại tiếp là $ x^2+y^2-10x-8y+36=0. $ Từ đó tìm được $ A(6,6) $ và $ B,C $ có tọa độ $ (3,5),(6,2). $ Diện tích $S=6.$
Bài 43. Cho tam giác $ABC$ có trực tâm $ H(2,2) $; tâm đường tròn ngoại tiếp $ I(1,2) $ và trung điểm của $ BC $ là $ M(\frac{5}{2},\frac{5}{2}). $ Tìm tọa độ các đỉnh của tam giác biết $ x_B>x_C. $
Hướng dẫn. Gọi $ G $ là trọng tâm tam giác $ABC$ thì $ 2\overrightarrow{HI}=3\overrightarrow{HG} $. Từ đó tìm được $ G(\frac{4}{3},2) $ và $ A(-1,1) $. Đáp số $ B(3,1) $ và $ C(2,4). $
Bài 44. Viết phương trình các cạnh của tam giác $ABC$ biết rằng $B(2; -7)$ và nếu $ 3x + y + 11 = 0$ và $x + 2y + 7 = 0$ lần lượt là phương trình đường cao và đường trung tuyến của tam giác kẻ từ các đỉnh khác nhau.
(Find the equations of the sides of a triangle having $B(2; -7)$ as a vertex, if $3x + y + 11 = 0$ and $x + 2y + 7 = 0$ are the respective equations of an altitude and a median drawn from diferrent vertices.)
Hướng dẫn. $x – 3y – 23 = 0$, $ 7x + 9y + 19 = 0$, $ 4x + 3y + 13 = 0$.
Bài 45. Cho tam giác $ABC$, biết phương trình cạnh $AB$, phương trình đường phân giác trong $BE$, phương trình đường phân giác trong $CE$ lần lượt có phương trình $$3x – 4y – 2 = 0, x – y – 1 = 0, 11x + 3y + 10 = 0.$$ Viết phương trình hai cạnh $BC$ và $AC$.
Hướng dẫn. $BC: 4x – 3y – 5 = 0$, $AC: 5x + 12y + 27 = 0$.
Bài 46. Viết phương trình các cạnh của tam giác $ABC$ biết rằng $A(-3; 3)$ và phương trình các đường phân giác trong $B$ và $C$ của tam giác lần lượt là $ x – 2y + 1 = 0$, $x + y + 3 = 0$.
Hướng dẫn. $AB: 2x + y – 3 = 0$, $AC: x – y – 3 = 0$, $BC: 4x – y + 3 = 0$.
Bài 47. Viết phương trình các cạnh của tam giác $ABC $ biết rằng $B(2; -1)$ và nếu $3x – 4y + 27 = 0 $ và $x + 2y – 5 = 0$ lần lượt là phương trình đường cao và đường phân giác trong của tam giác kẻ từ các đỉnh khác nhau.
(Find the equations of the sides of a triangle having $B(2; -1)$ as a vertex, if $3x – 4y + 27 = 0 $ and $x + 2y – 5 = 0$ are the respective equations of an altitude and an angle bisector drawn from diferrent vertices.)
Hướng dẫn. $4x + 7y – 1 = 0$, $y – 3 = 0$, $4x + 3y – 5 = 0$.
Bài 48. Viết phương trình các cạnh của tam giác $ABC$ biết rằng $A(3; – 1) $ và nếu $x – 4y +10 = 0$ và $6x + 10y – 59 = 0$ lần lượt là phương trình đường phân giác trong và đường trung tuyến của tam giác kẻ từ các đỉnh khác nhau.
(Find the equations of the sides of a triangle having $A(3; – 1) $ as a vertex, if $x – 4y +10 = 0$ and $6x + 10y – 59 = 0$ are the respective equations of an angle bisector and a median drawn from diferrent vertices.)
Hướng dẫn. $2x + 9y – 65 = 0$, $6x – 7y – 25 = 0$, $18x + 13y – 41 = 0.$
Bài 49. Viết phương trình đường thẳng $\Delta$ đi qua điểm $C(-5;4)$, biết rằng $\Delta$ cắt hai đường thẳng $d_1:x + 2y + 1 = 0$ và $d_2:x+2y – 1=0$ lần lượt tại tại $A$ và $B$ sao cho độ dài đoạn thẳng $AB$ bằng 5.
Hướng dẫn. $3x + 4y -1=0$ và $7x + 24y – 61 = 0.$
Bài 50. Cho tam giác $ABC$ có đỉnh $A(0;4)$, trọng tâm $G\left(\frac{4}{3}; \frac{2}{3}\right)$ và trực tâm trùng với gốc toạ độ. Tìm toạ độ các đỉnh $B$ và $C$ và diện tích của tam giác $ABC$, biết rằng hoành độ điểm $B$ nhỏ hơn hoành độ điểm $C$.
Hướng dẫn. $B(-1;-1)$, $C(5;-1)$, $S_{ABC} = 15$.
Bài 51. Cho tam giác $ABC$ có $AB = \sqrt{2}$ và $G(1;1)$ là trọng tâm; đỉnh $C$ ở trên trục hoành và hai đỉnh $A$, $B$ ở trên đường thẳng $\Delta: x – y + 1 = 0$. Tìm toạ độ các đỉnh $A$, $B$, $C$.
Hướng dẫn. $A(0;1)$, $B(1;2)$, $C(2;0)$ hoặc $A(1;2)$, $B(0;1)$, $C(2;0)$.
Bài 52. Cho tam giác $ABC$ có phương trình đường cao và đường trung tuyến kẻ từ đỉnh $A$ lần lượt có phương trình $$
x – 2y – 13 = 0 \text{ và } 13x -6y – 9 = 0.$$ Tìm toạ độ các đỉnh $B$ và $C$ biết toạ độ tâm đường tròn ngoại tiếp của tam giác $ABC$ là $I(-5; 1)$.
Hướng dẫn. $(4;3)$ và $(2;7)$.
Bài 53. Cho tam giác $ABC$ vuông tại $A$, có đỉnh $C(-3;1)$, đường trung trực của cạnh $BC$ có phương trình $7x + y – 5 = 0$. Tìm toạ độ nguyên của đỉnh $A$ biết diện tích của tam giác $ABC$ bằng 10.
Đáp số. $A(-2; 4)$.
Bài 54. Cho tam giác $ABC$ có $A(0;6)$, tâm đường tròn ngoại tiếp tam giác $ABC$ là $K(4;3)$, đường cao kẻ từ $A$ đi qua điểm $I(2;2)$ và độ dài cạnh $BC = 4\sqrt{5}$. Tìm toạ độ các đỉnh $B$ và $C$, biết rằng góc $A$ là góc tù.
Hướng dẫn. $B(-1;3)$ và $C(7;7)$ hay ngược lại.
Bài 55. Cho tam giác $ABC$ có phương trình đường trung tuyến và phân giác trong cùng kẻ từ đỉnh $B$ lần lượt là $$(d_1): 2x + y – 3 = 0, (d_2): x + y – 2 = 0.$$ Điểm $M$ thuộc đường thẳng $AB$, đường thẳng r ngoại tiếp tam giác $ABC$ có bán kính bằng $\sqrt{5}$. Biết đỉnh $A$ có hoành độ dương, xác định toạ độ các đỉnh của tam giác $ABC$.
Hướng dẫn. $A(3; 1)$, $B(1;1)$, $C(1;- 3)$.
Bài 56. Cho tam giác $ABC$ có trực tâm $H(1;-1)$, điểm $E(-1;2)$ là trung điểm của cạnh $AC$ và phương trình cạnh $BC$ là $2x -y + 1 = 0$. Xác định toạ độ các đỉnh của tam giác $ABC$.
Hướng dẫn. $A(-3;1)$, $B(0;1)$, $C(1;3)$.
Bài 57. Cho điểm $M(2;3)$. Viết phương trình đường thẳng $\Delta$ lần lượt cắt các trục $Ox$, $Oy$ tại $A$, $B$ sao cho tam giác $MAB$ vuông cân tại $A$.
Hướng dẫn. $x – 3y – 3 = 0$, $5x + 3y + 15=0.$
Bài 58. Cho điểm $M(2;1)$ và đường thẳng $(d): x – y = 0$. Viết phương trình đường thẳng $\Delta$ lần lượt cắt trục $Ox$ và $(d)$ tại $A$, $B$ sao cho tam giác $MAB$ vuông cân tại $M$.
Hướng dẫn. $x + y – 2 = 0$, $3x + y – 12=0.$
Bài 59. Viết phương trình của đường thẳng $\Delta$ đi qua gốc toạ độ và tạo với hai đường thẳng $(d_1): x – y + 12 = 0$ và $(d_2): 2x + y + 9 = 0$ một tam giác có diện tích là 1.5 đơn vị diện tích. (Write the equations of the line passing through the origin and forming, together with the line $(d_1): x – y + 12 = 0$ and $(d_2): 2x + y + 9 = 0$ a triangle of an equal to 1.5 square units.)
Hướng dẫn.
- Gọi phương trình $\Delta$ có dạng $y = kx$.
- Đường thẳng $\Delta$ cắt $(d_1)$ tại $A\left(\frac{12}{k-1}; \frac{12k}{k – 1}\right)$ và cắt cắt $(d_2)$ tại $B\left(\frac{-9}{k + 2}; \frac{-9k}{k + 2}\right)$; $(d_1)$ cắt $(d_2)$ tại điểm $C(-7; 5)$.
- Diện tích tam giác $ABC$ là $S = \frac{3}{2}\left\vert\frac{(7k + 5)^2}{(k – 1)(k + 2)}\right\vert$.
- Giải phương trình $S = \frac{3}{2}$, ta được $k = -\frac{1}{2}$ và $k = -\frac{23}{25}$.
- Đáp số $x + 2y = 0$, $23x + 25y = 0$.
Bài 60. Cho tam giác $ABC$ cân tại $A$, điểm $M\left(2; \frac{5}{2}\right)$ là trung điểm của cạnh $AB$, $B(1;0)$. Tìm toạ độ các đỉnh $A$ và $C$ biết rằng diện tích của tam giác $ABC$ bằng 10 (đ.v.d.t) và toạ độ các đỉnh $A$ và $C$ là các số nguyên.
Hướng dẫn. $A(3;5)$, $C(5;0)$; hoặc $A(5; 0)$, $C(3;5)$ hoặc $A(3;5)$, $C(1;10)$ hoặc $A(1;10)$, $C(3;5)$.
Bài 61. Cho tam giác $ABC$ có diện tích bằng 24 và phương trình các đường trung tuyến kẻ từ các đỉnh $A$, $B$, $C$ lần lượt là $$\Delta_1: x – y +2 = 0, \Delta_2: 5x – y – 2 = 0, \Delta_3: x + 3y – 10 = 0. $$ Tìm toạ độ các đỉnh của tam giác $ABC$.
Hướng dẫn.
- Gọi $A(x_1; x_1 + 2)$, $B(x_2; 5x_2 – 2)$. Điểm $G(1;3)$ là trọng tâm tam giác $ABC$, nên tìm được toạ độ điểm $C$ theo $x_1$ và $x_2$.
- Tìm $x_1$, $x_2$ từ các điều kiện $C$ thuộc trung tuyến $\Delta_3$ và tam giác $ABC$ có diện tích bằng 24.
- Đáp số $A(5;7)$, $B(0;-2)$, $C(-2;4)$ hoặc $A(-3; -1)$, $B(2; 8)$, $C(4; 2)$.
2.6. Hình chữ nhật
Bài 1. Cho hình chữ nhật $ ABCD $ có $ AD=2AB $ và $ A(1,5). $ Phương trình đường chéo $ BD:3x+4y-13=0. $ Tìm tọa độ các đỉnh hình chữ nhật biết điểm $ B $ có hoành độ âm.
Hướng dẫn. Gọi véctơ pháp tuyến của $ AB $ và sử dụng $ \cos\widehat{ABD}=\frac{1}{\sqrt{5}} $. Đáp số $ B(-1,4). $
Bài 2. Cho hình chữ nhật $ ABCD $ có phương trình đường thẳng $ AB:x-2y+1=0, $ phương trình đường thẳng $ BD:x-7y+14=0, $ đường thẳng $ AC $ đi qua $ M(2,1). $ Tìm toạ độ các đỉnh của hình chữ nhật.
Hướng dẫn. Tìm được $ B(\frac{21}{5},\frac{13}{5}) $ và viết phương trình $ BC. $ Có $ \widehat{(AC,BD)}=\widehat{BID}=2\widehat{ABD}=2\widehat{(AB,BD)}, $ suy ra $ AC:17x-31y-3=0 $ hoặc $ AC:x+y-3=0. $
Bài 3. Cho hình chữ nhật $ ABCD $ có cạnh $ AB:x-2y-1=0, $ đường chéo $ BD:x-7y+14=0 $ và đường chéo $ AC $ đi qua điểm $ M(2,1). $ Tìm toạ độ các đỉnh của hình chữ nhật.
Hướng dẫn. Sử dụng $ \cos(AB,AC)=\cos(AB,BD). $ Đáp số $ B(7,3),C(6,5),A(1,0),D(0,2) $ hoặc…
Bài 4. Trong mặt phẳng tọa độ $ Oxy $ cho hình chữ nhật $ ABCD $ có tâm $ I(\frac{1}{2},0). $ Đường thẳng $ AB $ có phương trình $ x-2y+2=0,AB=2AD $ và hoành độ điểm $ A $ âm. Tìm tọa độ các đỉnh.
Hướng dẫn. Gọi $ H $ là hình chiếu của $ I $ lên $ AB $ thì $ AH=2IH… $ Đáp số. $A(-2,0),B(2,2),C(3,0),D(-1,-2).$
Bài 5. Cho hình chữ nhật $ ABCD, $ có diện tích bằng 12, tâm $ I $ là giao điểm của hai đường thẳng $ d_1:x-y-3=0,d_2:x+y-6=0. $ Trung điểm của một cạnh là giao điểm của $ d_1 $ với trục $ Ox. $ Tìm toạ độ các đỉnh của hình chữ nhật.
Hướng dẫn. Chú ý rằng $ d_1 $ song song với hai cạnh của hình chữ nhật. Đáp số $A(3,1),D(4,-1),C(7,2),B(11,4)$ hoặc $ A(4,-1),D(2,1),C(5,4),B(13,2) $.
Bài 6. Cho hình chữ nhật $ ABCD $ có diện tích bằng $ 6 $. Phương trình đường thẳng chứa đường chéo $ BD $ là $ d:2x + y – 11 = 0 $, đường thẳng $ AB $ đi qua điểm $ M (4; 2) $, đường thẳng $ BC $ đi qua điểm $ N (8; 4) $. Xác định tọa độ các đỉnh của hình chữ nhật biết các điểm $ B,D $ đều có hoành độ lớn hơn 4.
Hướng dẫn. Gọi $ B(b,11-2b) $ thì từ $ AB\perp BC $ tìm được $ B(5,1) $. Suy ra phương trình $ AB:x+y-6=0,AC: x-y-4=0.$ Gọi $ A(a,6-a) $ và $ C(c,c-4) $ thì tâm hình chữ nhật là $ I(\frac{a+c}{2},\frac{c-a+2}{2}) $. Vì $I\in BD $ nên $ 3c+a-20=0. $ Ta có $ AB=\sqrt{2}|a-5| $ và $ BC=\sqrt{2}|c-5| $ nên $ 2|a-5|.|c-5|=6. $ Từ đó tìm được đáp số $ A(8,-2),C(4,0),D(7,-3). $
Bài 7. Cho hình chữ nhật $ ABCD $ có diện tích bằng 10, phương trình đường thẳng chứa cạnh $ AD $ là $ 3x – y = 0 $. Lấy điểm $ M $ đối xứng với $ D $ qua $ C $ và đường thẳng $ BM $ có phương trình $ 2x + y-10 = 0 $. Xác định tọa độ các đỉnh của hình chữ nhật biết đỉnh $ B $ có hoành độ dương.
Hướng dẫn. Gọi $ N $ là giao điểm của $ BM $ và $ AD $ thì $ N(2,6). $ Gọi $ D(d,3d) $ và $ B(b,10-2b) $ với $ b>0. $ Vì $ A $ là trung điểm $ ND $ nên $ A(\frac{d+2}{2},\frac{3d+6}{2}) .$ Vì $ B $ là trung điểm $ MN $ nên $ M(2b-2,14-4b) $ mà $ C $ là trung điểm $ MD $ nên $ C(\frac{2b-2+d}{2},\frac{14-4b+3d}{2}). $ Mặt khác $ AB\perp AD $ nên có phương trình $ b+d=4. $ Từ diện tích bằng 10 tìm được đáp số $ A(1,3),B(4,2),C(3,-1),D(0,0) $.
Bài 8. Cho hình chữ nhật $ ABCD $ có $ AD=2AB. $ Gọi $ M,N $ là trung điểm $ AD,BC. $ Lấy $ K $ thuộc $ MN $ sao cho $ N $ là trung điểm $ MK. $ Tìm tọa độ $ A,B,C,D $ biết $ K(-5,1),AC:2x+y-3=0 $ và điểm $ A $ có tung độ dương.
Hướng dẫn. Gọi $ I $ là tâm hình chữ nhật thì $ \cos \widehat{MIA}=\frac{1}{\sqrt{5}.} $ Từ đó tìm được phương trình $ MK$ suy ra tọa độ $ I$ suy ra tọa độ $ M$ suy ra…
Bài 9. Cho hình chữ nhật $ ABCD $ có đỉnh $ C $ thuộc đường thẳng $d:x+3y+7=0$ và $ A(1,5). $ Lấy $ M $ thuộc tia đối của $ CD $ sao cho $ MC=2BC. $ Gọi $ N $ là hình chiếu của $ B $ lên $ MD. $ Xác định tọa độ $ B,C $ biết $ N(-\frac{5}{2},\frac{1}{2}). $
Hướng dẫn. Gọi $ C(-3c-7,c) $ thì tâm hình chữ nhật là $ I\left(\frac{-3c-6}{2},\frac{c+5}{2}\right).$ Tam giác $ DNB $ vuông tại $ N $ nên $ IN=IB=ID=IA $. Từ đó tìm được $ C(2,-3). $ Gọi $ B(m,n) $ thì từ $ AB\perp BC $ được phương trình $$ (m-1)(m-2)+(n-5)(n+3)=0 $$ Từ $ \overrightarrow{CM}=2\overrightarrow{BC} $ suy ra $ M(6-2m,-9-2n)$. Mà $ MN\perp BN $ nên được phương trình $$ \left(m+\frac{5}{2}\right)\left(\frac{17}{2}-2m\right)+\left(n-\frac{1}{2} \right)\left(-\frac{19}{2}-2n\right)=0 $$ Giải hệ tìm được $ m,n… $
Bài 10. Cho hình chữ nhật $ABCD$ có phân giác trong góc $ \widehat{ABC} $ đi qua trung điểm $ M $ của $ AD. $ Phương trình đường thẳng $ BM:x-y+2=0. $ Điểm $ D $ thuộc đường thẳng $ d:x+y-9=0 $ và $ E(-1,2) $ là điểm thuộc đường thẳng $ AB. $ Tìm tọa độ các đỉnh hình chữ nhật biết điểm $ B $ có hoành độ âm.
Hướng dẫn. Chỉ ra tam giác $ ABM $ vuông cân tại $ A $. Gọi véctơ pháp tuyến của $ AB $ là $ \vec{n}(a,b) $ và tìm được $ ab=0 $. Từ đó tìm được $ B(-1,1). $ Gọi $ A(-1,m) $ và $ D(n,9-n) $ thì trung điểm của $ AD $ là $ M(\frac{n-1}{2},\frac{9-n+m}{2}) $ thuộc $ BM. $ Suy ra phương trình $ 2n-m-6=0. $ Kết hợp với $ \overrightarrow{AD}\perp \overrightarrow{AB} $ được hệ. Đáp số $ A(-1,4),C(5,1),D(5,4). $
Bài 11. Cho hình chữ nhật $ABCD$ biết phương trình cạnh $BC$ là $x + 2y – 4 = 0$, phương trình đường chéo $BD$ là $3x + y – 7 = 0$, đường chéo $AC$ đi qua điểm $M(-5;2)$. Tìm toạ độ các đỉnh của hình chữ nhật $ABCD$.
Hướng dẫn. $A(4;5)$, $B(2;1)$, $C(-2; 3)$, $D(0; 7)$.
Bài 12. Cho hình chữ nhật $ABCD$ có diện tích bằng 12, tâm $I$ là giao điểm của hai đường thẳng $$d_1: x – y – 3 = 0, d_2: x + y – 6 = 0.$$ Trung điểm của một cạnh là giao điểm của đường thẳng $d_1$ với trục $Ox$. Tìm toạ độ các đỉnh của hình chữ nhật $ABCD$.
Hướng dẫn. $(2;1)$, $(5;4)$, $(7;2)$, $(4;-1)$.
Bài 13. Cho hình chữ nhật $ABCD$ có diện tích bằng 12, tâm $I\left(\frac{9}{2}; \frac{3}{2}\right)$ và trung điểm của cạnh $AD$ là $M(3;0)$. Xác định toạ độ các đỉnh của hình chữ nhật $ABCD$.
Hướng dẫn. $(2;1)$, $(5;4)$, $(7;2)$, $(4;-1)$.
Bài 14. Trong mặt phẳng với hệ toạ độ $Oxy$, cho hình chữ nhật $ABCD$ có điểm $I(6;2)$ là giao điểm của hai đường chéo $AC$ và $BD$. Điểm $M(1;5)$ thuộc đường thẳng $AB$ và trung điểm $E$ của cạnh $CD$ thuộc đường thẳng $\Delta:x+y-5=0$. Viết phương trình đường thẳng $AB$.
Hướng dẫn. $AB:y-5=0$ hoặc $AB: x – 4y + 19 = 0.$
2.7. Hình vuông
Bài 1. [Đề thi khối A năm 2005] Cho hai đường thẳng $ d_1:x-y=0, d_2:2x+y-1=0. $ Tìm tọa độ các đỉnh hình vuông $ ABCD $ biết rằng đỉnh $ A $ thuộc $ d_1 $ đỉnh $ C $ thuộc $ d_2 $và các đỉnh $ B, D $ thuộc trục hoành.
Hướng dẫn. Nhận xét $ BD $ trùng với $ Ox. $ Gọi $ A(t,t)\in d_1. $ Vì $ A,C $ đối xứng nhau qua $ BD $ nên $ C(t,-t). $ Mà $ C\in d_2 $ nên tìm được $ C(1,-1) $ và $ A(1,1). $ Gọi trung điểm của $ AC $ là $ I(1,0). $ Vì $ I $ là tâm hình vuông nên $ IB=ID=IA=1. $ Đáp số $ B(0,0),D(2,0) $ hoặc $ D(0,0),B(2,0). $
Bài 2. Cho hình vuông có đỉnh $ (-4,5) $ và một đường chéo có phương trình $ 7x-y+8=0. $ Viết phương trình các cạnh hình vuông.
Hướng dẫn. $3x-4y+32=0,4x+3y+1=0…$
Bài 3. [Đề thi thử trường Cổ Loa năm 2015] Cho hình vuông $ ABCD $ có $ M $ là trung điểm $ BC, N $ thuộc đoạn $ AC $ sao cho $ AC=4AN. $ Đường thẳng $ MN $ có phương trình $ 3x-y-4=0 $ và $ D(5,1). $ Tìm tọa độ điểm $ B $ biết điểm $ M $ có tung độ dương.
Hướng dẫn. Kẻ $ NH\perp BC, NK\perp DC. $ Chứng minh $ \Delta DNK=\Delta MNH $ từ đó suy ra $ \Delta DNM $ vuông cân tại $ N. $ Suy ra phương trình $ DN:x+3y-8=0. $ Do đó $ N(2,2). $ Ta có $ M\in MN $ nên $ M(m,3m-4) $ mà $ DN=MN $ nên tìm được $ M(3,5). $ Gọi $ P=MN\cap AD $ thì $ \overrightarrow{MN}=3\overrightarrow{NP} $ suy ra $ P(\frac{5}{3},1). $ Chứng minh $ \overrightarrow{DP}=\frac{5}{6}\overrightarrow{DA}. $ Suy ra tọa độ $ B(1,5).$
Bài 4. [Đề thi thử THPT Can Lộc 2014] Trong mặt phẳng tọa độ $ Oxy, $ cho hình vuông $ ABCD. $ Trên các cạnh $ AD, AB $ lấy hai điểm $ E $ và $ F $ sao cho $ AE = AF. $ Gọi $ H $ là hình chiếu vuông góc của $ A $ lên $ BE. $ Tìm tọa độ của $ C $ biết $ C $ thuộc đường thẳng $ d: x -2y + 1 = 0 $ và tọa độ $ F(2, 0), H(1, -1). $
Hướng dẫn. Gọi $ M $ là giao điểm của $ AH $ và $ CD. $ Ta có $ \widehat{ABE}=\widehat{DAM} $ nên hai tam giác $ ABE $ và $ ADM $ bằng nhau. Do đó $ DM = AE = AF, $ suy ra $ BCMF $ là hình chữ nhật. Gọi $ I $ là tâm hình chữ nhật $ BCMF. $ Trong tam giác vuông $ MHB $ ta có $ BM=2HM $ mà $ BM=CF $ nên tam giác $ CHF $ vuông tại $ H. $ Đáp số $C(-\frac{1}{3},\frac{1}{3}).$
Bài 5. Cho hình vuông $ ABCD $ có tâm $ I $, điểm $ K (0; 2) $thuộc đoạn $ IA $. Giả sử $ M $ và $ N $ lần lượt là trung điểm của cạnh $ AB,CD $ và cùng nằm trên đường thẳng $ d:x – 1 = 0 $. Điểm $ Q $ là giao của $ KM $ với $ BC $. Xác định tọa độ các đỉnh của hình vuông $ ABCD $ biết điểm $ H (4; 8) $ thuộc đường thẳng $ NQ $.
Hướng dẫn. Gọi véctơ pháp tuyến của $ AC $ là $ \vec{n}(a,b) $ thì từ $ \widehat{AIM}=45^\circ $ tìm được $ a=\pm b. $ Sau đó xét hai trường hợp.
Bài 6. Cho hình vuông $ABCD$ có $M$ là trung điểm cạnh $BC$, đường thẳng $DM$ có phương trình $x – y – 2 = 0$, điểm $C(3;-3)$, điểm $A$ thuộc đường thẳng $(d): 3x + y – 2 = 0$. Tìm toạ độ các đỉnh $A$, $B$, $D$.
Hướng dẫn. Đáp số $A(-1; 5)$, $B(-3;-1)$, $D(5;3)$.
2.8. Tứ giác khác
Bài 1. Cho hình thang cân $ ABCD $ có $ CD = 2AB $, phương trình hai đường chéo $ AC $ và $ BD $ lần lượt là $ x + y – 4 = 0$ và $ x – y – 2 = 0 $. Biết rằng tọa độ hai điểm $ A $ và $ B $ đều dương và diện tích hình thang bằng 36. Tìm tọa độ các đỉnh hình thang.
Hướng dẫn. Từ diện tích hình thang bằng 36 tìm được $AC=BD=6\sqrt{2}. $ Hai tam giác $ AIB $ và $ CID $ đồng dạng nên tìm được $ IA=IB=\frac{1}{3}AC=2\sqrt{2}. $ Lấy $ A(a,4-a) $ và $ B(b,b-2) $ lập hai phương trình tìm được $ A(1,3) $ và $ B(5,3). $ Từ đó tìm được $ C(7,-3) $ và $ D(-1,-3). $
Bài 2. Cho hình thang cân $ ABCD $ có diện tích bằng $ \frac{45}{2}, $ đáy lớn $ CD $ có phương trình $ x-3y-3=0. $ Biết hai đường chéo $ AC,BD $ vuông góc với nhau và cắt nhau tại $ I(2,3). $ Viết phương trình đường thẳng $ BC $ biết điểm $ C $ có hoành độ dương.
Hướng dẫn. Từ tam giác $ ICD $ vuông cân tại $ I $ tìm được $ IC=\sqrt{20}. $ Gọi $ C(3c+3,c) $ thì $ IC^2=10 $ nên $ C(6,1) $. Suy ra phương trình $ BD:2x-y-1=0 $ và tọa độ $ D(0,-1) $. Đặt $ IA+IB=x $ và biểu diễn diện tích hình thang theo $ x $ là $ \frac{1}{2}x^2+2x\sqrt{5}+10=\frac{45}{2} $. Từ đó tìm được $ x=\sqrt{5}. $ Đáp số $ BC:4x+3y-27=0. $
Bài 3. Cho hình thang $ ABCD $ có diện tích bằng $ \frac{45}{8}. $ Phương trình hai cạnh đáy là $ AB:x-3y+1=0 $ và $ CD:2x-6y+17=0 $. Hai cạnh $ AD,BC $ cắt nhau tại $ K(2,6) $, hai đường chéo cắt nhau tại $ I(1,\frac{7}{3}) $. Xác định tọa độ các đỉnh của hình thang.
Hướng dẫn. Từ diện tích hình thang bằng $ \frac{45}{8} $ suy ra $ AB+CD=\frac{3\sqrt{10}}{2}. $ Từ các tam giác đồng dạng, suy ra $ AB=2CD=\sqrt{10}. $ Suy ra $ CD $ là đường trung bình của tam giác $ KAB. $ Gọi giao điểm của $ KI $ và $ AB,CD $ là $ M,N $ thì $ M,N $ là trung điểm $ AB,CD. $ Tìm được $ M(\frac{1}{2},\frac{1}{2}) $ và đáp số $ A(2,1),B(-1,0),C(2,\frac{7}{2}),D(\frac{1}{2},3). $
Bài 4. Cho hình thoi $ ABCD $ có tâm $ I (3;3) $ và $ AC= 2BD $. Điểm $ M(2,\frac{4}{3}) $ thuộc đường thẳng $ AB $, điểm $ N(3,\frac{13}{3}) $ thuộc đường thẳng $ CD $. Viết phương trình đường chéo $ BD $ biết điểm $ B $ có hoành độ nhỏ hơn 3.
Hướng dẫn. Lấy $ P $ đối xứng với $ N $ qua tâm $ I $ thì $ P\in AB. $ Đáp số $ BD:7x-y-18=0. $
Bài 5. Cho hình thoi $ ABCD $ có $ BD:x-y=0. $ Đường thẳng $ AB $ đi qua $ P(1,\sqrt{3}). $ Đường thẳng $ CD $ đi qua $ Q(-2,-2\sqrt{3}). $ Tìm tọa độ các đỉnh hình thoi biết $ AB=AC $ và $ B $ có hoành độ lớn hơn 1.
Hướng dẫn. Chỉ ra tam giác $ABC$ đều, do đó góc giữa $ AB $ và $ BD $ là $ 30^\circ. $ Gọi véctơ pháp tuyến của $ AB $ và tìm được $ B(2,2). $
Bài 6. Cho hình thang $ ABCD $ vuông ở $ A $ và $ B $. Có $ AD=\frac{1}{2} AB=\frac{1}{3} BC $. Gọi hình chiếu
vuông góc các trung điểm của $ AB $ và $ CD $ xuống đường thẳng $ AC $ là $ H $ và $ N $. Biết $HN=\frac{6}{\sqrt{13}}, C(2; 4)$. Đỉnh $ A $ thuộc đường thẳng $ 5x+4y-4=0 $, đường thẳng $ 8x-5y- 11=0 $ đi qua đỉnh $ B $. Xác định tọa độ các đỉnh $ A, B, D $.
Hướng dẫn. Đặt $ AD=a $. Gọi $ I,J $ là trung điểm của $ AB,CD $ và hình chiếu vuông góc của $ D $ xuống $ BC $ là $ E $. Ta có $$ \overrightarrow{AB}.\overrightarrow{BD}=-4a^2, \overrightarrow{BC}.\overrightarrow{BD}=3a^2$$
và \[ \overrightarrow{AC}.\overrightarrow{BD}=(\overrightarrow{AB}+\overrightarrow{BC})\overrightarrow{BD}=-a^2,\overrightarrow{AC}.\overrightarrow{IJ}=\overrightarrow{AC}.\frac{\overrightarrow{AC}+\overrightarrow{BD}}{2}=6a^2 \] Mặt khác $ \overrightarrow{AC}.\overrightarrow{IJ}=\overline{AC}.\overline{HN}=a\sqrt{13}HN=\frac{6a}{\sqrt{13}} $. Suy ra $ a=1, $ và $ BC=3,AC=\sqrt{13}. $ Từ đó tìm được đáp số $ A(0,1) $ hoặc $ A(-\frac{56}{41},\frac{111}{41}). $
Bài 7. Viết phương trình các cạnh của hình thang cân $ABCD$ biết rằng trung điểm của các cạnh đáy $AB$ và $CD$ lần lượt là $I(2;2)$ và $J(-4;6)$; hai điểm $M(4;-5)$ và $N(-5;7)$ lần lượt thuộc hai cạnh bên $AD$ và $BC$.
Hướng dẫn. $AB: 3x – 2y – 2 = 0$, $CD: 3x – 2y + 24 = 0$, $BC: 4x + 185y -1025 = 0$, $AD:150x + 121y + 5 = 0$
Bài 8. Cho hình bình hành $ABCD$ có $M$ là trung điểm của cạnh $BC$, $N$ là trung điểm của đoạn $MD$, $P$ là giao điểm của hai đường thẳng $AN$ và $CD$. Tìm toạ độ các đỉnh $C$ và $D$ biết rằng $A(1;2)$, $B(4;-1)$, $P(2;0)$.
Hướng dẫn. $D(0;2)$; $C(3;-1)$.
Bài 9. Cho hình thoi $MNPQ$ với các cạnh $MN$, $MQ$ lần lượt có phương trình $$x + 2y – 4 = 0 \text{ và } 2x + y – 2 = 0.
$$ Trung điểm một cạnh của hình thoi là $I(2;1)$. Viết phương trình cạnh $PQ$ của hình thoi.
Hướng dẫn. $x + 2y +2=0$ hoặc $x + 2y -10 = 0.$
Bài 10. Cho hình thoi $ABCD$, cạnh $BC$ có phương trình $x + 3y – 8 = 0$, đường chéo $AC$ có phương trình $2x + y + 4 = 0$ và điểm $M(-9; -1)$ thuộc đường thẳng $AD$. Viết phương trình các cạnh còn lại của hình thoi.
Hướng dẫn. $AD:x+3y + 12 = 0$, $CD: 3x – y + 16 = 0$ và $AB: 3x -y – 4 = 0.$
Bài 11. Trong mặt phẳng với hệ toạ độ $Oxy$, cho hình thoi $ABCD$ có hai cạnh $AB$, $CD$ lần lượt nằm trên hai đường thẳng
$$(d_1): x – 2y + 5 = 0, (d_2): x – 2y + 1 = 0.$$ Viết phương trình các đường thẳng $AD$ và $BC$, biết điểm $M(-3; 3)$ thuộc đường thẳng $AD$ và điểm $N(-1;4)$ thuộc đường thẳng $BC$.
Hướng dẫn. $BC: x + 2y – 7 = 0$, $AD:x + 2y – 3 = 0$ hoặc $BC: 11x – 2y +19 = 0$, $AD:11x – 2y + 39 = 0$.
Bài 12. Cho hình thoi $ABCD$ có $A(2;3)$, $\widehat{ABC} = 60^\circ$, phương trình đường thẳng $BD$ là $x – 2y + 2 = 0$. Xác định toạ độ các đỉnh $B$, $C$, $D$.
Bài 13. Viết phương trình các cạnh của hình thoi $ABCD$ biết rằng $A(-3;1)$, $B(5;7)$ và diện tích của hình thoi bằng $ 25 $.
3. Phương trình đường tròn
- Đường tròn $ (C) $ tâm $ I(a;b), $ bán kính $ R $ có phương trình \[ (x-a)^2+(y-b)^2=R^2 \]
- Khai triển ra ta được dạng sau \[ x^2+y^2-2ax-2by+c=0 \]
- Đường thẳng $\Delta$ tiếp xúc với đường tròn $ (I,R) $ khi và chỉ khi $$ d(I,\Delta)=R $$ hoặc $ \Delta $ vuông góc với bán kính tại tiếp điểm.
- Đường thẳng $\Delta$ cắt đường tròn $ (I,R) $ theo dây cung\index{độ dài dây cung} $ AB, $ gọi $ H $ là trung điểm $AB$ thì $ IH\perp AB $ và $ R^2=IH^2+AH^2. $
- Chỉ có bài toán lập phương trình đường tròn đi qua ba điểm thì gọi phương trình đường tròn rồi giải hệ ba ẩn, các bài toán còn lại ta đi tìm tọa độ tâm và bán kính.
3.1. Viết phương trình đường tròn
Bài 1. Cho hai đường thẳng $ \Delta:x+3y+8=0, \Delta’:3x-4y+10=0 $ và điểm $ A (-2,1). $ Viết phương trình đường tròn có tâm thuộc đường thẳng $ \Delta $ đi qua điểm $ A $ và tiếp xúc với đường thẳng $ \Delta’. $
Hướng dẫn. Gọi tọa độ tâm $ I $ của đường tròn $ (C). $ Đường thẳng $\Delta’$ tiếp xúc $(C) \Leftrightarrow d(I,\Delta’)=IA.$
Bài 2. [Đại học Thái nguyên 1998] Cho $ A(4,0), B(0,4) $. Viết phương trình đường tròn nội tiếp và ngoại tiếp tam giác $ AOB $.
Bài 3. Trong mặt phẳng toạ độ $ Oxy $ cho tam giác $ ABC, $ có điểm $ A(2,3) $ trọng tâm $ G(2,0). $ Hai đỉnh $ B $ và $ C $ lần lượt nằm trên hai đường thẳng $ d_1:x+y+5=0,d_2:x+2y-7=0. $ Viết phương trình đường tròn có tâm $ C $ và tiếp xúc với đường thẳng $ BG. $
Hướng dẫn. Tìm được $ B(-1,-4),C(5,1), BG:4x-3y-8=0. $ Suy ra $ R=d(C,BG). $ Đáp số $ (x-5)^2+(y-1)^2=\frac{169}{25}. $
Bài 4. [ĐHQGHN 1996] Cho đường tròn $(C):{{(x-1)}^{2}}+{{(y-2)}^{2}}=9$. Viết phương trình đường thẳng đi qua $ M(2;1) $ và cắt đường tròn $ (C) $ tại hai điểm $ A; B $ phân biệt sao cho $ M $ là trung điểm $ AB $.
Bài 5. Viết phương trình đường tròn đi qua hai điểm $ A(2,5),B(4,1) $ và tiếp xúc với đường thẳng có phương trình $\Delta: 3x-y+9=0. $
Hướng dẫn. Gọi tọa độ tâm $ I(a,b). $ Từ $ IA=IB $ và $ IA=d(I,\Delta) $ lập được hai phương trình…
Bài 6. Cho đường tròn $(C):x^2+y^2-2x+4y+2=0.$ Viết phương trình đường tròn $ (C’) $ có tâm $ M(5,1) $ và cắt $(C)$ tại $ A,B $ sao cho $ AB=\sqrt{3}. $
Hướng dẫn. Gọi $ H $ là giao điểm của $ AB $ và $ IM… $ Đáp số $ (x-5)^2+(y-1)^2=13. $
Bài 7. Cho tam giác $ ABC $ có diện tích bằng $\frac{3}{2}, A(2; -3), B(3;-2)$, trọng tâm của $ ABC $ nằm trên đường thẳng $ d: 3x-y-8 = 0 $. Viết phương trình đường tròn đi qua ba điểm $ A, B, C? $
Hướng dẫn. ${x^2} + {y^2} – \frac{{11}}{3}x + \frac{{11}}{3}y + \frac{{16}}{3} = 0,{x^2} + {y^2} – \frac{{91}}{3}x + \frac{{91}}{3}y + \frac{{416}}{3} = 0$
Bài 8. Trong mặt phẳng tọa độ $ Oxy, $ cho đường tròn $ (C) : x^2 + y^2 + 2x -4y-20 = 0 $ và điểm $ A(5,-6). $ Từ $ A $ vẽ các tiếp tuyến $ AB, AC $ với đường tròn $ (C) $ với $ B, C $ là các tiếp điểm. Viết phương trình đường tròn nội tiếp tam giác $ ABC. $
Bài 9. Cho tam giác $ ABC $ vuông tại $ A $ với $ B(-3,0),C(3,0). $ Biết tâm $ I $ của đường tròn nội tiếp $ \Delta ABC $ thuộc đường thẳng $ d:y = x. $ Viết phương trình đường tròn nội tiếp tam giác $ ABC $ biết $ I $ có tung độ dương.
3.2. Phương trình tiếp tuyến của đường tròn
Bài 1. Trong mặt phẳng $ Oxy $ cho $ A( 2;-1), B( -2;2) $. Viết phương trình đường tròn đường kính $ AB. $ Viết phương trình tiếp tuyến với đường tròn tại $ A. $
Hướng dẫn. $ x^2 + {{(y-\frac{1}{2})}^{2}}=\frac{25}{4},-4x +3y + 11 = 0$
Bài 2. Viết phương trình tiếp tuyến của đường tròn $ (C): x^2 +y^2 -6x +2y = 0 $ vuông góc với đường thẳng $ 3x – y +6 = 0 $.
Hướng dẫn.$ x +3y +10 = 0, x +3y -10 = 0 $
Bài 3. [ĐHTCKT 1997] Cho đường tròn $(C):{{(x-1)}^{2}}+{{(y-3)}^{2}}=4$ và điểm $ M(2;4) $.
- Viết phương trình đường thẳng đi qua $ M $ và cắt $ (C) $ tại hai điểm phân biệt $ A,B $ sao cho $ M $ là trung điểm $ AB $.
- Viết phương trình các tiếp tuyến của đường tròn đó biết tiếp tuyến có hệ số góc $ k = – 1 $.
Bài 4. Viết phương trình tiếp tuyến với đường tròn $ ( C): x^2 +y^2 – 6x +2y +6 = 0 $ biết tiếp tuyến đi qua điểm $ A(1;3). $
Hướng dẫn.$ x-1=0,3x +4y -15 = 0 $
Bài 5. [ĐHNT 1997] Cho đường tròn $(C):{{x}^{2}}+{{y}^{2}}+2x-4y-4=0$ và điểm $ A(3;5) $.
- Hãy viết phương trình các tiếp tuyến của đường tròn kẻ từ $ A $.
- Giả sử các tiếp tuyến tiếp xúc với $ (C) $ tại $ M $ và $ N $. Hãy tính độ dài $ MN $.
3.3. Các bài toán liên quan đến đường tròn
Bài 1. Trong mặt phẳng với hệ toạ độ $ Oxy, $ cho đường tròn $ (C):x^2+y^2+2x-8y-8=0. $ Viết phương trình đường thẳng song song với đường thẳng $ d:3x+y-2 =0 $ và cắt đường tròn theo một dây cung có độ dài bằng 6.
Hướng dẫn. $ 3x+y+19=0,3x+y-21=0. $
Bài 2. Cho điểm $ M(6,2) $ và đường tròn $ (C) : (x-1)^2 + (y-2)^2 = 5. $ Lập phương trình đường thẳng $ d $ đi qua $ M $ và cắt đường tròn $ (C) $ tại hai điểm $ A, B $ sao cho $ AB = \sqrt{10}. $
Hướng dẫn. Gọi $ H $ là hình chiếu của $ I $ lên $ AB $ thì $ IH^2=IA^2-AH^2=\frac{5}{2}. $ Giả sử véctơ pháp tuyến của $ d $ là $ \vec{n}(a,b) $ thì phương trình đường thẳng $ d$ là $ a(x-6)+b(y-2)=0. $ Từ $ d(I,d)=IH $ tìm được $ b=\pm 3a. $ Đáp số $x-3y=0, x+3y-12=0.$
Bài 3. Trong mặt phẳng toạ độ $ Oxy, $ cho điểm $ K(3,2) $ và đường tròn $ (C):x^2+y^2-2y-4y+1=0 $ có tâm là $ I. $ Tìm tọa độ điểm $ M\in(C) $ sao cho $ \widehat{IMK} = 60^\circ. $
Hướng dẫn. $ (C) $ có tâm $ I(1,2) $ và bán kính $ R=2. $ Có $ IK=2 $ nên tam giác $ IMK $ cân tại $ I. $ Do đó $ \widehat{IMK} = 60^\circ \Leftrightarrow \Delta IMK$ đều. Giả sử $ M(x_0,y_0) \in (C) $ thì $ (x_0-1)^2+(y_0-2)^2=4 $ và $ KM=2 \Leftrightarrow (x_0-3)^2+(y_0-2)^2=4. $ Từ đó tìm được $M(2,2+\sqrt{3}), M(2,2-\sqrt{3}).$
Bài 4. Trong mặt phẳng tọa độ $ Oxy, $ cho tam giác $ ABC $ cân tại $ A $ nội tiếp đường tròn $ (C):x^2+y^2+2x-4y + 1 = 0. $ Tìm tọa độ các đỉnh $ A, B, C $ biết điểm $ M(0, 1) $ là trung điểm cạnh $ AB $ và $ A $ có hoành độ dương.
Hướng dẫn. Có $ IM\perp AB $ nên viết được $ AB:x-y+1=0. $ Giả sử $ A(a,a+1) $ thì $ IA=2 $ nên tìm được $A(1,2),B(-1,0),C(-1,4).$
Bài 5. [Đề thi thử ĐH Vinh 2014] Cho tam giác $ ABC $ có $ A(3,3) $ và tâm đường tròn ngoại tiếp tam giác là $ I(2,1). $ Phân giác trong của góc $ \widehat{BAC} $ là $ x-y=0. $ Tìm tọa độ điểm $ B,C $ biết $ BC=\frac{8}{\sqrt{5}} $ và tam giác $ ABC $ nhọn.
Hướng dẫn.
- $ AD $ là phân giác trong nên $ AD $ cắt đường tròn tại $ E $ là điểm chính giữa cung $ BC \Rightarrow IE\perp BC. $
- $ E\in AD $ và $ IE=IA=R $ nên tìm được $ E(0,0) \Rightarrow BC:2x+y+m=0.$
- $ d(I,BC)=IH=\sqrt{IB^2-BH^2} $ từ đó tìm được $ m=-2 $ hoặc $ m=-8 $ (loại vì tam giác $ ABC $ nhọn nên $ I,A $ cùng phía so với $ BC$).
- Đáp số. $ (0,2) $ và $ (\frac{8}{5},-\frac{6}{5}). $
Bài 6. Trong mặt phẳng $ Oxy $ cho đường tròn $ (C) : x^2 + y^2 + 2x – 4y – 8 = 0 $ và đường thẳng $d: x-5y-2 = 0. $ Xác định tọa độ giao điểm $ A, B $ của đường tròn $ (C) $ và đường thẳng $ d $ (cho biết điểm $ A $ có hoành độ dương). Tìm tọa độ điểm $ C $ thuộc đường tròn $ (C) $ sao cho tam giác $ ABC $ vuông ở $ B. $
Bài 7. [Đề thi thử ĐH Vinh K.A] Trong mặt phẳng với hệ tọa độ $ Oxy, $ cho đường tròn $ (C):(x-2)^2+(y-1)^2=5 $ và đường thẳng $ d:x-3y-9=0. $ Từ điểm $ M $ thuộc $ d $ kẻ hai đường thẳng tiếp xúc với $ (C) $ lần lượt tại $ A $ và $ B. $ Tìm tọa độ điểm $ M $ sao cho độ dài $ AB $ nhỏ nhất.
Hướng dẫn.
- Đường tròn $(C)$ có tâm $ I(2,1) $ và bán kính $ R=\sqrt{5}. $ Vì $ d(I,d)>R $ nên $ d $ không cắt $(C)$.
- Giả sử $ (3m+9,m) \in d.$ Từ tính chất tiếp tuyến ta có $ MI\perp AB $ tại trung điểm $ H $ của $ AB. $ Tính được $ AH^2=R^2-\frac{R^4}{IM^2}. $ Từ đó có $ AB $ nhỏ nhất $ \Leftrightarrow IM $ nhỏ nhất khi $ m=-2. $
- Đáp số $ M(3,-2). $
Bài 8. [Đề thi thử Chuyên Hà Tĩnh 2014] Cho hai đường tròn: $ (C): x^2 + y^2 – 4x – 4y +4 = 0 $ và $ (C’): x^2 + y^2 – 16x +8y+ 28 = 0. $ Viết phương trình đường thẳng qua $ A(4,2) $ cắt các đường tròn trên theo các dây cung có độ dài bằng nhau.
Hướng dẫn. $ A(4,2), B(2,0) $ là các giao điểm của $ (C) $ và $ (C’). $ Có đường thẳng qua $ A, B $ có phương trình: $ x-y-2=0 $ là một trường hợp cần tìm. Gọi $ K $ là trung điểm $ II’ $ thì đường thẳng qua $ A $ và vuông góc với $ KA $ là một trường hợp nữa thỏa mãn yêu cầu. Đáp số $x-y-2=0, x-3y+2=0.$
Bài 9. [Đề thi khối A năm 2010] Trong mặt phẳng với hệ toạ độ $Oxy$, cho hai đường thẳng $d_1:\sqrt{3}x + y = 0$ và $d_2 :\sqrt{3}x – y = 0$. Gọi $(T)$ là đường tròn tiếp xúc với $d_1$ tại $A$, cắt $d_2$ tại hai điểm $B$ và $C$ sao cho tam giác $ABC$ vuông tại $B$. Viết phương trình của $(T)$, biết tam giác $ABC$ có diện tích bằng $\frac{\sqrt{3}}{2}$ và điểm $A$ có hoành độ dương.
Hướng dẫn. $\left(x + \frac{1}{2\sqrt{3}}\right)^2 + \left(y + \frac{3}{2}\right)^2 = 1$.
Bài 10. Cho đường tròn $\mathcal{(C)}: (x – 4)^2 + y^2 = 25$ và điểm $M(1;-1)$. Viết phương trình đường thẳng $\Delta$ đi qua điểm $M$ và cắt đường thẳng r $\mathcal{(C)}$ tại hai điểm $A$, $B$ sao cho $MA = 3MB$.
Hướng dẫn. $2x + y + 3 = 0,x + 2y + 1 = 0$.
Bài 11. Cho hai đường tròn $$ \mathcal{(C)}: (x – 1)^2 + (y + 2)^2 = 5 \text{ và } \mathcal{(C’)}: (x + 1)^2 + (y + 3)^2 = 9. $$ Viết phương trình đường thẳng $\Delta$ tiếp xúc với $\mathcal{(C)}$ và cắt $\mathcal{(C’)}$ tại hai điểm $A$, $B$ sao cho $AB = 4$.
Hướng dẫn. $x – 2y = 0$, $x – 2y – 10 = 0$ hoặc $x + y – 2 = 0$, $x + 7y – 6 = 0$.
Bài 12. Cho hai đường tròn \begin{equation*}
\mathcal{(C)}: (x – 1)^2 + y^2 = \frac{1}{2} \text{ và } \mathcal{(C’)}: (x – 2)^2 + (y – 2)^2 = 4.
\end{equation*} Viết phương trình đường thẳng $\Delta$ tiếp xúc với $\mathcal{(C)}$ và cắt $\mathcal{(C’)}$ tại hai điểm $A$, $B$ sao cho $AB = 2\sqrt{2}$.
Hướng dẫn. $x – y – 2 = 0$, $7x – y – 2 = 0$.
Bài 13. Cho tam giác $ABC$ nội tiếp trong đường tròn \begin{equation*}
\mathcal{(C)}: x^2 + y^2 -4x -2y – 8 = 0. \end{equation*} Đỉnh $A$ thuộc tia $Oy$, đường cao vẽ từ $C$ nằm trên đường thẳng $(d): x + 5y = 0$. Tìm toạ độ các đỉnh $A$, $B$, $C$ biết rằng đỉnh $C$ có hoành độ là một số nguyên.
Hướng dẫn. $A(0;4)$, $B(-1;-1)$, $C(5;-1)$
Bài 14. Cho đường tròn $\mathcal{(C)}: x^2 + y^2 -4x +2y – 15 = 0$. Gọi $I$ là tâm của $\mathcal{(C)}$. Đường thẳng $\Delta$ đi qua điểm $M(1;-3)$ cắt $\mathcal{(C)}$ tại hai điểm $A$, $B$. Viết phương trình đường thẳng $\Delta$, biết tam giác $IAB$ có diện tích bằng 8 và cạnh $AB$ có độ dài lớn nhất.
Hướng dẫn. $y + 3 = 0$, $4x + 3y + 5 = 0$
Bài 15. Cho đường tròn $\mathcal{(C)}: x^2 + y^2 – 2x – 6y + 6 = 0$ và điểm $M(-3;1)$. Gọi $A$ và $B$ là các tiếp điểm của các tiếp tuyến kẻ từ $M$ đến $\mathcal{(C)}$. Tìm toạ độ hình chiếu vuông góc $H$ của $M$ lên đường thẳng $AB$.
Hướng dẫn. $\left(\frac{1}{5}; \frac{13}{5}\right)$
Bài 16. [Đề dự bị 2, B, 2008] Trong mặt phẳng với hệ trục toạ độ $Oxy$, cho hai điểm $A(3;0)$ và $B(0;4)$. Chứng minh rằng đường tròn nội tiếp tam giác $OAB$ tiếp xúc với đường tròn đi qua trung điểm của các cạnh tam giác $OAB$.
Bài 17. Cho đường tròn $\mathcal{(C)}: x^2 + y^2 + 2x – 10y + 16 = 0$ và điểm $M(-2;3)$. Tìm toạ độ hai điểm $A$, $B$ thuộc $\mathcal{(C)}$ sao cho đường thẳng $AB$ đi qua điểm $M$ và đoạn thẳng $AB$ ngắn nhất.
Hướng dẫn. $(-4;4)$ và $(0;2)$
Bài 18. [B2006] Cho đường thẳng r $(C):x^2+y^2-2x-6y+6=0$ và điểm $M(-3;1)$. Gọi $T_1$ và $T_2$ là các tiếp điểm của các tiếp tuyến kẻ từ điểm $M$ đến $(C)$. Viết phương trình đường thẳng $T_1T_2$.
Hướng dẫn. $2x+y-3=0$
Bài 19. [Đề minh hoạ D2009] Trong mặt phẳng với hệ trục toạ độ $Oxy$, cho đường tròn $\mathcal{(C)}$ có phương trình $(x-4)^2 + y^2 = 4$ và điểm $E(4;1)$. Tìm toạ độ điểm $M$ trên trục tung sao cho từ $M$ kẻ được hai tiếp tuyến $MA$, $MB$ đến đường tròn $\mathcal{(C)}$ (với $A$, $B$ là các tiếp điểm) sao cho đường thẳng $AB$ qua đểm $E$.
Hướng dẫn. $M(0;4)$
Bài 20. (Đề minh hoạ A2009) Trong mặt phẳng với hệ tọa độ $Oxy$, cho đường tròn $\mathcal{(C)}$ có phương trình $x^2+y^2 – 6x + 5=0$. Tìm điểm $M$ thuộc trục tung sao cho qua $M$ kẻ được hai tiếp tuyến của $\mathcal{(C)}$ mà góc giữa hai tiếp tuyến đó bằng $60^\circ.$
Hướng dẫn. $M_1(0;\sqrt{7})$ và $M_2(0;-\sqrt{7})$
Bài 21. (Dự bị A2008) Trong mặt phẳng với hệ trục toạ độ $Oxy$, cho đường tròn $\mathcal{(C)}$ có phương trình $x^2 + y^2 = 1$. Tìm các giá trị thực của tham số $m$ để trên đường thẳng $y=m$ tồn tại đúng hai điểm mà từ mỗi điểm đó có thể kẻ được hai tiếp tuyến với $\mathcal{(C)}$ sao cho góc giữa hai tiếp tuyến đó bằng $60^\circ$.
Hướng dẫn. $-2 < m < -\frac{2}{\sqrt{3}}$ hoặc $\frac{2}{\sqrt{3}} < m <2.$
Bài 22. [D2007] Cho đường tròn $\mathcal{(C)}:(x-1)^2 + (y+2)^2 = 9$ và đường thẳng $d:3x-4y+m=0$. Tìm $m$ để trên $d$ có duy nhất một điểm $P$ mà từ đó có thể kẻ được hai tiếp tuyến $PA$, $PB$ tới $\mathcal{(C)}$ sao cho tam giác $PAB$ đều ($A$, $B$ là hai tiếp điểm).
Hướng dẫn. $m = 19$, $ m = -41$.
Bài 23. Cho đường tròn $\mathcal{(C)}: x^2 + y^2 +2x -4y – 20 = 0$ và điểm $A(5;-6)$. Từ $B$ vẽ các tiếp tuyến $AB$, $AC$ với đường tròn ($B$, $C$ là các tiếp điểm). Viết phương trình đường thẳng r nội tiếp tam giác $ABC$.
Hướng dẫn. $(x – 2)^2 + (y + 2)^2 = \frac{25}{4}$.
Bài 24. Cho đường tròn $\mathcal{(C)}: x^2 + y^2 -6x -10y + 9 = 0$ và đường thẳng $(d): x + 2y – 3 = 0$. Chứng minh rằng $(d)$ cắt $\mathcal{(C)}$ tại hai điểm phân biệt $A$, $B$. Tìm toạ độ điểm $M$ trên $\mathcal{(C)}$ sao cho tam giác $MAB$ cân tại $M$.
Hướng dẫn. $M_1(3 + \sqrt{5}; 5 + 2\sqrt{5})$, $M_2(3 – \sqrt{5}; 5 – 2\sqrt{5})$.
4. Bài tập tổng hợp
Bài 1. Trong mặt phẳng tọa độ $Oxy$ cho $ A(-1;1) $ và $ B(2;3) $. Chứng minh rằng ba điểm $ O,A,B $ không thẳng hàng và viết phương trình các cạnh của $ \Delta AOB $. Viết phương trình đường cao qua $ A $, phân giác trong qua $ A $ của $ \Delta AOB $. Tìm tọa độ trực tâm, tâm đường tròn ngoại tiếp, nội tiếp của $ \Delta AOB. $ Tìm tọa độ điểm $ A’ $ đối xứng với $ A $ qua đường thẳng $ BO $. Viết phương trình đường thẳng qua $ A $ và song song với $ BO $. Viết phương trình đường thẳng qua $ A $ tạo với $ BO $ góc $60^{\circ}$.
Bài 2. Cho tam giác $ ABC $ có $ M(2;1) $ là trung điểm cạnh $ AC $, điểm $ H(0;-3) $ là chân đường cao kẻ từ $ A $, điểm $ E(23;-2) $ thuộc đường thẳng chứa trung tuyến kẻ từ $ C $. Tìm tọa độ điểm $ B $ biết điểm $ A $ thuộc đường thẳng $ d:2x+3y-5=0 $ và điểm $ C $ có hoành độ dương.
Bài 3. Cho tam giác $ ABC $ có đỉnh $ A(3;3) $ tâm đường tròn ngoại tiếp $ I(2;1) $ phương trình đường phân giác trong góc $ \widehat{BAC} $ là $ x-y=0 $. Tìm tọa độ các đỉnh $ B, C $ biết rằng $ BC=8/\sqrt{5} $ và góc $ \widehat{BAC} $ nhọn.
Bài 4. Cho tam giác $ ABC $ có phương trình đường thẳng chứa đường cao kẻ từ $ B $ là $ x+3y-18=0 $, phương trình đường thẳng trung trực của đoạn thẳng $ BC $ là $ 3x+19y-279=0 $, đỉnh $ C $ thuộc đường thẳng $ d:2x-y+5=0 $. Tìm tọa độ đỉnh $ A $ biết rằng $ \widehat{BAC}=135^{\circ} $.
Bài 5. Cho hình vuông $ ABCD $. Gọi $ M $ là trung điểm của $ BC, N $ nằm trên cạnh $ CD $ sao cho $ CN=2ND $. Biết $ M=(\frac{11}{2};\frac{1}{2}) $ và $AN$ có phương trình $ 2x-y-3=0 $. Tìm tọa độ đỉnh $ A $.
Bài 6. Cho tam giác $ ABC $ có đường cao $ AH:3x+4y+10=0 $, phân giác trong $ BE:x-y+1=0 $. Điểm $ M(0;2) $ thuộc $ AB $ và cách $ C $ một khoảng $ \sqrt{2} $. Tính diện tích tam giác $ABC$.
Bài 7. Cho hình chữ nhật $ ABCD $ có diện tích bằng 12, tâm $ I(9/2;3/2) $, trung điểm của $ BC $ là $ M(3;0) $ và $ x_B>x_C $. Xác định tọa độ các đỉnh của nó.
Bài 8. Cho $ \Delta ABC $ có tâm đường tròn ngoại tiếp $ I(4;-1) $, đường cao và trung tuyến qua $ A $ có phương trình lần lượt là $ d_1:x+y-1=0,d_2:x+2y-1=0 $. Viết phương trình các đường thẳng chứa các cạnh của nó.
Bài 9. Cho hình chữ nhật $ ABCD $ trong mặt phẳng tọa độ $ Oxy $. Cạnh $ AB $ có phương trình là $ x-y+3=0 $. Điểm $ I(0;1) $ là giao điểm của $ AC $ và $ BD $. Tìm tọa độ các đỉnh $ A, B, C, D $ nếu $ AB=3AD $ và điểm $ A $ có hoành độ lớn hơn hoành độ của điểm $ B $.
Bài 10. Cho hình vuông $ MNPQ $. Biết $ MN,NP,PQ,QM $ lần lượt đi qua các điểm có tọa độ $ A(10;3),B(7;-2),C(-3;4),D(4;-7) $. Lập phương trình $ MN $.
Bài 11. Cho $ C(6;0), d:3x-y-10=0,\Delta:3x+3y-16=0 $. Tìm tọa độ đỉnh $ B $ của tam giác $ ABC $ biết $ AC>AB $, đường thẳng $ d $ chứa phân giác trong của góc $ A, \Delta\bot AC $ đồng thời ba đường thẳng $ \Delta,d $ và trung trực của $ BC $ đồng quy tại một điểm.
Bài 12. Cho $ \Delta ABC $ có đỉnh $ A(1;5) $, trọng tâm $ G(1;3) $, trực tâm $ H(-23;17) $. Tìm tọa độ $ B,C $ nếu $ x_B>x_C $.
Bài 13. Lập phương trình các cạnh của tam giác đều $ ABC $ biết $ A(3; -5) $ và trọng tâm $ G(1; 1) $.
Bài 14. Viết phương trình cạnh $ AB $ (đường thẳng $ AB $ có hệ số góc dương), $ AD $ của hình vuông $ ABCD $ biết tọa độ $ A(2; -1) $ và đường chéo $ BD: x+2y-5=0 $.
Bài 15. Trong mặt phẳng với hệ toạ độ $ Oxy $ cho hai điểm $ A(1;-1) $ và $ B(4;3) $. Tìm toạ độ các điểm $ C $ và $ D $ sao cho tứ giác $ ABCD $ là hình vuông.











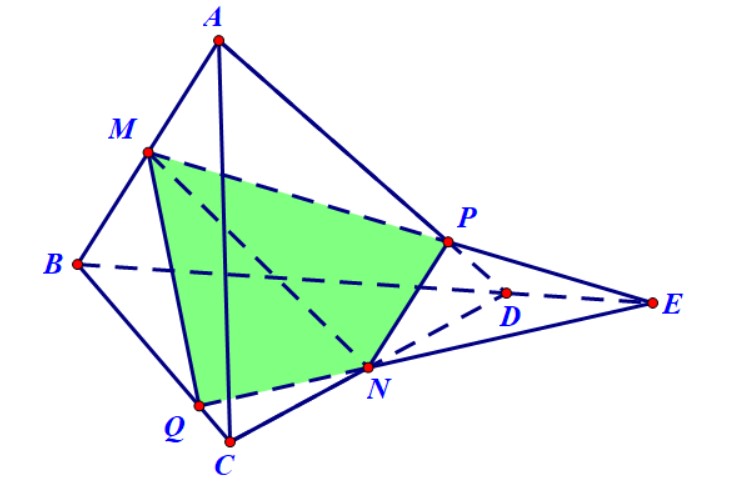
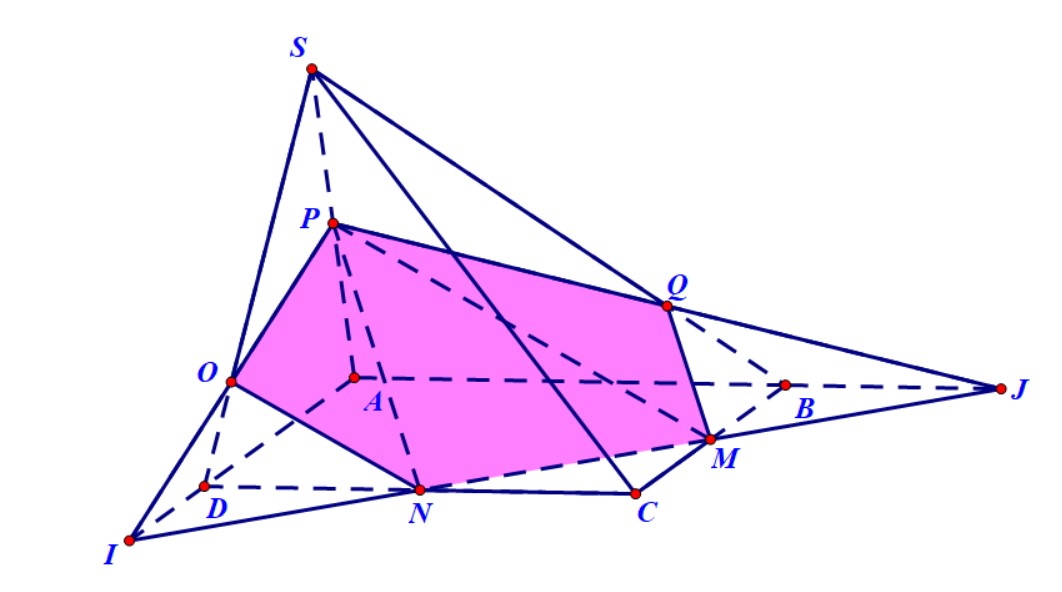
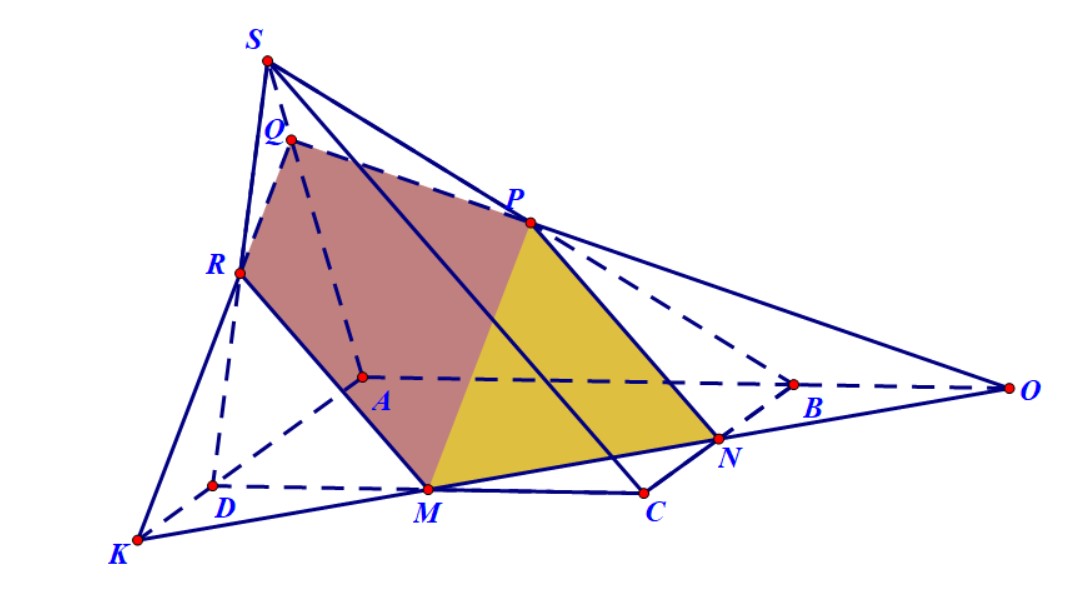
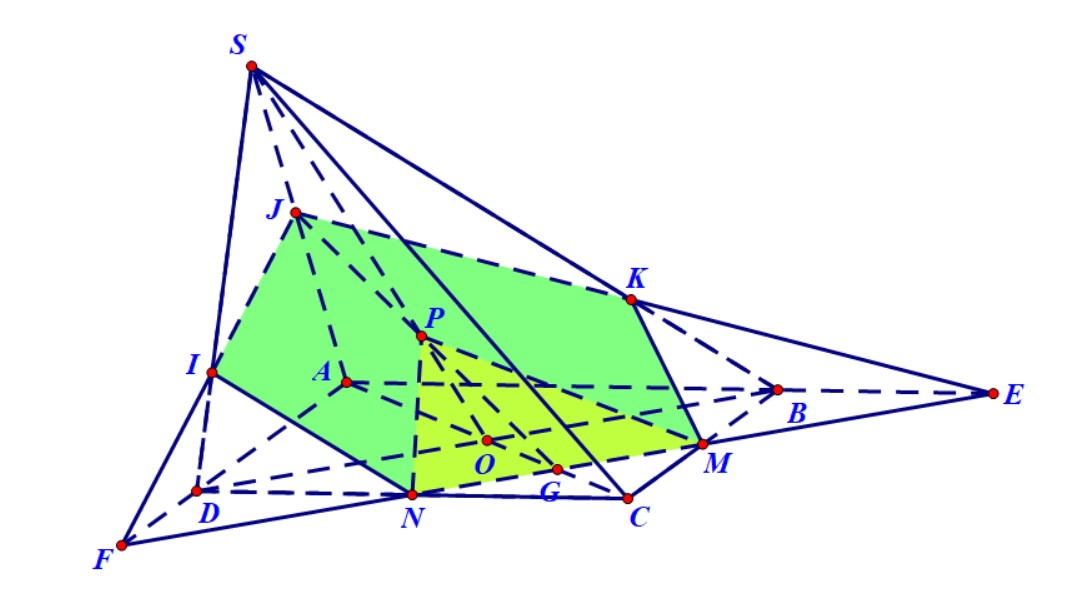
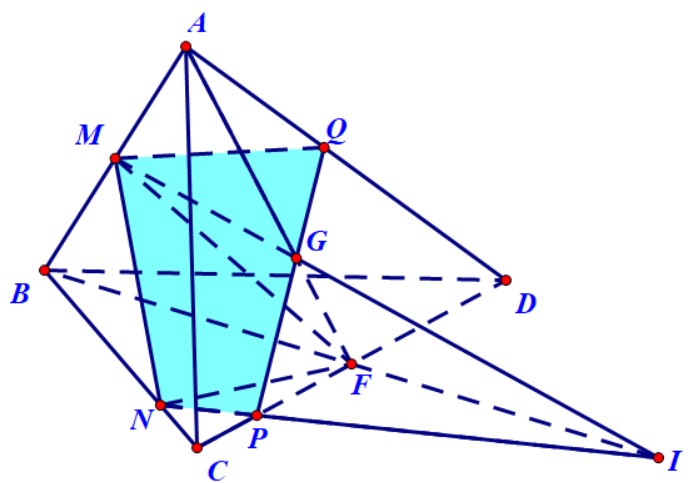
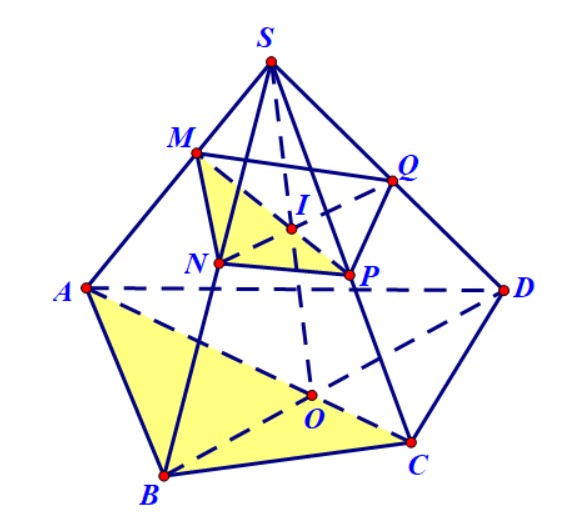
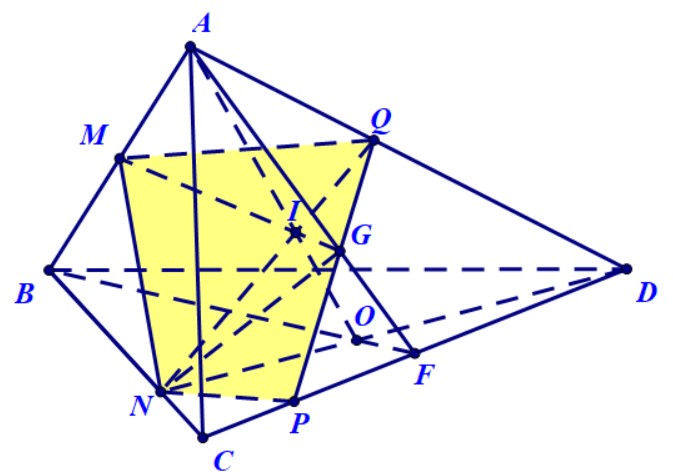
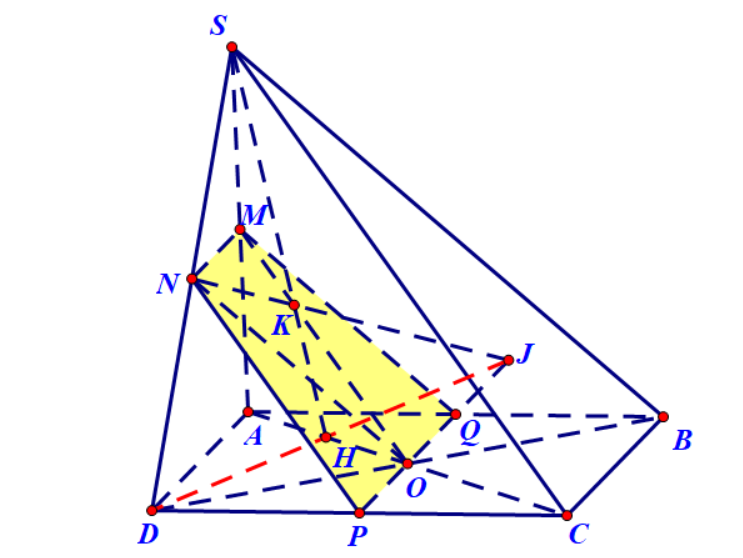
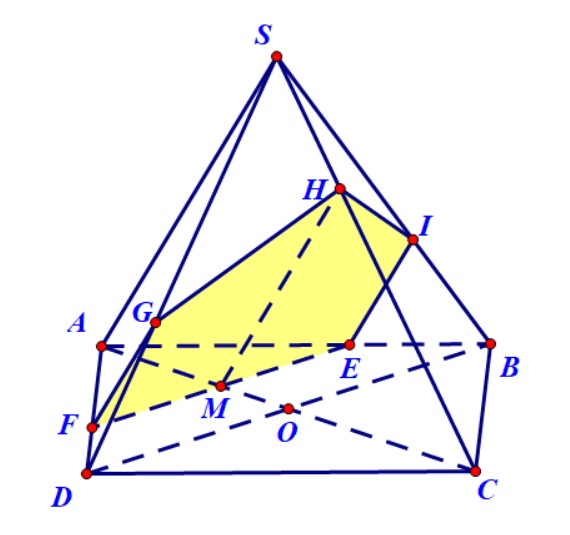
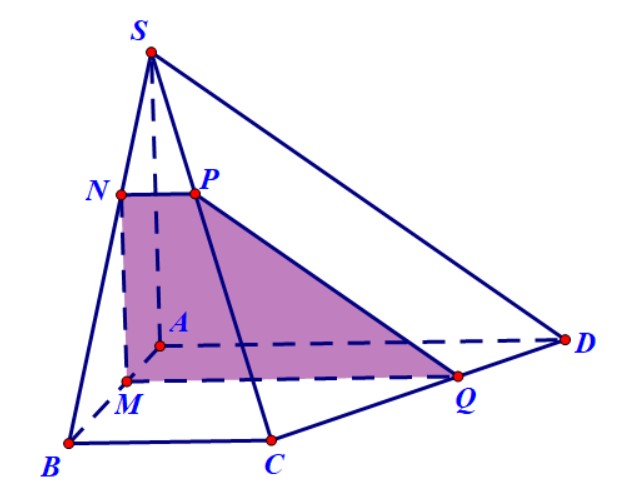
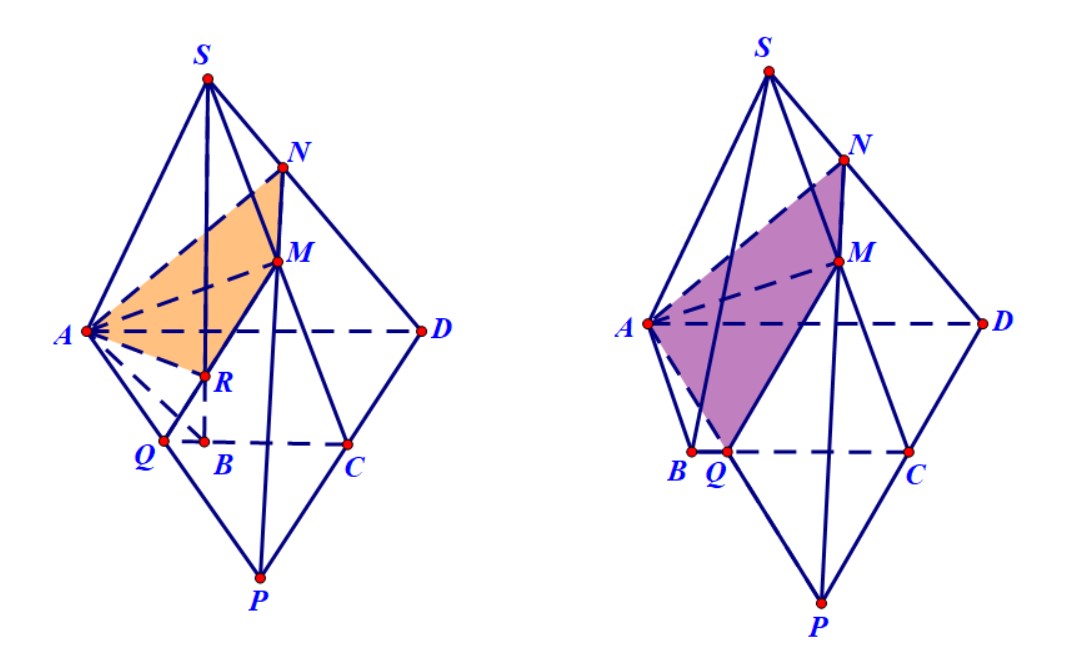 Ví dụ 4. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M,N,P$ lần lượt là trung điểm của $BC,CD$ và $SA$. Xác định thiết diện của hình chóp và mặt phẳng $\left( {MNP} \right)$.
Ví dụ 4. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M,N,P$ lần lượt là trung điểm của $BC,CD$ và $SA$. Xác định thiết diện của hình chóp và mặt phẳng $\left( {MNP} \right)$.