1000 Bài Tổ hợp Xác suất có lời giải
O2 Education xin giới thiệu cùng thầy cô và các em học sinh 1000 bài tập tổ hợp xác suất có lời giải. Các bài toán được chúng tôi sưu tầm từ các đề thi HSG, đề thi ĐHCĐ, đề thi tốt nghiệp, đề thi THPTQG và đề thi thử của các trường trên cả nước.
Các đề bài được chúng tôi cập nhật thường xuyên, một số câu hỏi do chưa có thời gian nên chúng tôi sẽ bổ sung lời giải sau.
Mời thầy cô và các em học sinh xem thêm
Câu 1. [SGD Hà Nam 2018] Xếp ngẫu nhiên 3 quả cầu màu đỏ khác nhau và 3 quả cầu màu xanh giống hệt nhau vào một giá chứa đồ nằm ngang có 7 ô trống, mỗi quả cầu được xếp vào một ô. Xác suất để 3 quả cầu màu đỏ xếp cạnh nhau và 3 quả cầu màu xanh xếp cạnh nhau bằng bao nhiêu?
Hướng dẫn. Phép thử chính là việc “chọn 3 trong 7 vị trí để sắp xếp các quả cầu màu đỏ khác nhau, rồi chọn 3 trong bốn vị trí còn lại để đặt các quả cầu màu xanh giống nhau”, nên không gian mẫu có số phần tử là
\[ n(\Omega)=A^3_7\cdot C^3_4 \] Gọi $ A $ là biến cố “3 quả cầu màu đỏ xếp cạnh nhau và 3 quả cầu màu xanh xếp cạnh nhau”. Khi đó, ta coi “3 quả cầu màu xanh xếp cạnh nhau” chỉ là 1 phần tử, và “3 quả cầu màu đỏ xếp cạnh nhau” cũng là một phần tử. Bài toán trở thành sắp xếp hai phần tử khác nhau này vào hai trong ba vị trí, nên có $ A^2_3 $ cách. Tuy nhiên, vì các quả cầu màu đỏ khác nhau nên khi hoán vị chúng, ta được các kết quả khác nhau. Do đó, số phần tử thuận lợi của biến cố $ A $ là \[ n(A)=A^2_3\cdot 3! \] Từ đó tìm được xác suất $ P=\frac{3}{70}. $
Câu 2. [SGD Nam Định 2018] Một nhóm có 7 học sinh trong đó có 3 nam và 4 nữ. Hỏi có bao nhiêu cách xếp các học sinh trên thành một hàng ngang sao cho các học sinh nữ đứng cạnh nhau?
Hướng dẫn. Coi như bốn học sinh nữ ngồi chung một ghế, còn ba học sinh nam mỗi em ngồi một ghế. Ta thực hiện hai bước như sau:
- Sắp xếp 4 học sinh nữ vào một ghế, có $ 4!=24$ cách.
- Sắp xếp bốn chiếc ghế, một chiếc của nhóm học sinh nữ và ba chiếc của ba học sinh nam, có $ 4!=24$ cách.
Theo quy tắc nhân, có tất cả $ 24\cdot 24=576$ cách.
Câu 3. [SGD Thanh Hóa 2019] Gọi $ S $ là tập hợp tất cả các số tự nhiên có bốn chữ số đôi một khác nhau được chọn từ các chữ số$ 1,2,3,4,5,6,7,8,9. $ Lấy ngẫu nhiên một số thuộc $ S $. Tính xác suất để lấy được một số chia hết cho $ 11 $ và tổng bốn chữ số của nó cũng chia hết cho $ 11 $.
Hướng dẫn. Không gian mẫu có $ \mathrm{A}^4_9=3024 $ phần tử. Giả sử số cần lập là $ \overline{abcd}$ thì ta có \begin{align}
\overline{abcd}&=1000a+100b+10c+d\\
& =\left(1001a+99b+11c\right) -a+b-c+d
\end{align} Chú ý rằng $ \left(1001a+99b+11c\right) $ chia hết cho $ 11 $ nên $ \overline{abcd} $ chia hết cho $ 11 $ khi và chỉ khi $ \left(-a+b-c+d\right) $ phải chia hết cho $ 11 $.
Nhưng theo giả thiết thì $ a+b+c+d $ cũng chia hết cho $ 11 $. Từ đây suy ra cả $ a+c $ và $ b+d $ cùng chia hết cho $ 11. $
Mà, các cặp có tổng chia hết cho $ 11 $ là $(2 ; 9),(3 ; 8),(4 ; 7) ;(5 ; 6)$. Suy ra, số phần tử thuận lợi là $$n(A)=4 \cdot 3 \cdot 2 ! \cdot 2 !=48$$ Từ đó tìm được xác suất là $ \frac{1}{63}. $
Câu 4. Từ các chữ số $ 1,2,3,4,5,6,7,8,9 $ có thể lập được bao nhiêu nhiêu số tự nhiên có 5 chữ số dạng $ \overline{{a_1}{a_2}{a_3}{a_4}{a_5}} $ sao cho $ a_1<a_2<a_3<a_4<a_5. $
Hướng dẫn. Rõ ràng, với mỗi cách lấy ra $ 5 $ chữ số bất kì từ $ 9 $ chữ số đã cho, chúng ta chỉ có duy nhất một cách sắp xếp chúng theo thứ tự từ nhỏ đến lớn, tức là không tính các hoán vị của $ 5 $ chữ số này. Đương nhiên, mỗi cách sắp xếp đó ta thu được một số thỏa mãn yêu cầu. Do đó, có tất cả \[ \mathrm{C}^5_9=126 \] số tự nhiên thỏa mãn yêu cầu.
Câu 5. Từ các chữ số $ 0,1,2,3,4,5,6,7 $ có thể lập được bao nhiêu nhiêu số tự nhiên có 5 chữ số dạng $ \overline{{a_1}{a_2}{a_3}{a_4}{a_5}} $ sao cho $ a_1<a_2<a_3<a_4<a_5. $
Hướng dẫn. Nhận xét rằng $ a_1 $ phải là số bé nhất và khác $ 0, $ nên bài toán tương đương với việc lập số từ tập gồm $ 7 $ chữ số $ 1,2,3,4,5,6,7 $. Với mỗi cách lấy ra $ 5 $ chữ số bất kì từ $ 7 $ chữ số đã cho, chúng ta chỉ có duy nhất một cách sắp xếp chúng theo thứ tự từ nhỏ đến lớn, tức là không tính các hoán vị của $ 5 $ chữ số này. Đương nhiên, mỗi cách sắp xếp đó ta thu được một số thỏa mãn yêu cầu. Do đó, có tất cả \[ \mathrm{C}^5_7=21 \] số tự nhiên thỏa mãn yêu cầu.
Câu 6. [Chuyên Thái Nguyên Lần 1 năm 2019] Gọi $ S $ là tập hợp các số tự nhiên có ba chữ số, các chữ số không nhất thiết khác nhau, được lập từ các chữ số $ 0; 1; 2; 3; 4; 5; 6; 7; 8; 9 $. Chọn ngẫu nhiên một số $ \overline{abc} $ từ $ S $. Tính xác suất để số được chọn thỏa mãn $ a \leqslant b \leqslant c. $
Hướng dẫn. Tập $ S $ gồm các số từ $ 100 $ đến $ 999 $ nên có $ 900 $ phần tử. Phép thử là chọn một số tự nhiên từ tập $ S $ nên số phần tử của không gian mẫu là \[ |\Omega|=\mathrm{C}^1_{900}=900 \] Gọi $ A $ là biến cố cần tính xác suất, đặt $ b’=b+1, c’=c+2 $ thì yêu cầu bài toán tương đương với việc chọn ra ba số $ 1 \leqslant a < b'<c’ \leqslant 11 $ rồi sắp xếp ba số này theo thứ tự từ bé đến lớn, nên số phần tử thuận lợi là \[ |A|= \mathrm{C}^3_{11}=165\] Xác suất cần tìm là $ \mathrm{P}(A)=\frac{165}{900}=\frac{11}{60}. $
Bài tập trên cũng có thể làm bằng cách chia bốn trường hợp, $ a<b<c, a=b<c, a<b=c $ và $ a=b=c. $
Câu 7. [Chuyên Vĩnh Phúc — L3 2019] Chọn ngẫu nhiên một số tự nhiên có $ 4 $ chữ số. Tính xác suất để số được chọn có dạng $ \overline{abcd} $, trong đó $ 1 \leqslant a \leqslant b \leqslant c \leqslant d \leqslant 9 $.
Hướng dẫn. Có tất cả $ 9000$ số tự nhiên có bốn chữ số. Phép thử là “chọn một số tự nhiên từ $ 9000$ số tự nhiên có bốn chữ số”, nên số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^1_{9000}=9000. $$ Sử dụng tính chất của hai số tự nhiên, $ m \leqslant n \Leftrightarrow m < n+1$, chúng ta có điều kiện $ 1 \leqslant a \leqslant b \leqslant c \leqslant d \leqslant 9 $ tương đương với
\[ 1 \leqslant a < b+1<c+2<d+3 \leqslant 12. \] Đặt $ a’=a, b’=b+1, c’=c+2, d’=d+3 $ thì yêu cầu bài toán trở thành lấy bốn số tự nhiên khác nhau $ a’,b’,c’,d’ $ từ các số $ 1,2,3,\dots,12 $ và sắp xếp chúng theo một thứ tự duy nhất từ nhỏ đến lớn, tức là không tính các hoán vị. Do đó, số cách chọn là
\[ \mathrm{C}^4_{12}=495. \] Xác suất cần tìm là $$ \mathrm{P}=\frac{495}{9000}\approx 0.055 $$
Câu 8. [SGD Nam Định — HK2 2018] Chọn ngẫu nhiên một số tự nhiên có năm chữ số. Tính xác suất để số được chọn có dạng $ \overline{abcde} $ sao cho $ 1 \leqslant a \leqslant b \leqslant c \leqslant d \leqslant e \leqslant 9. $
Hướng dẫn. Không gian mẫu có số phần tử là \[ \big|\Omega\big| = 9\cdot 10^4=90000.\] Sử dụng tính chất của hai số tự nhiên, $ m \leqslant n \Leftrightarrow m < n+1$, chúng ta có điều kiện $ 1 \leqslant a \leqslant b \leqslant c \leqslant d \leqslant e \leqslant 9 $ tương đương với \[ 1 \leqslant a < b+1<c+2<d+3<e+4 \leqslant 13. \] Đặt $ a’=a, b’=b+1, c’=c+2, d’=d+3, e’=e+4 $ thì yêu cầu bài toán trở thành lấy năm số tự nhiên khác nhau $ a’,b’,c’,d’,e’ $ từ các số $ 1,2,3,\dots,13 $ và sắp xếp chúng theo một thứ tự duy nhất từ nhỏ đến lớn, tức là không tính các hoán vị. Do đó, số cách chọn là \[ \mathrm{C}^5_{13}=1287. \] Xác suất cần tìm là $ \mathrm{P}(A)=\frac{143}{10000}. $
Câu 9. [Chuyên Quang Trung — Bình Phước 2018] Cho $ A $ là tập hợp gồm các số tự nhiên có $ 9 $ chữ số đôi một khác nhau. Chọn ngẫu nhiên một số từ tập $ A $. Tính xác suất để số được chọn có các chữ số $ 0; 1; 2; 3; 4 $ mà các chữ số $ 1; 2; 3; 4 $ sắp theo thứ tự tăng dần.
Hướng dẫn. Tập $ A $ có tất cả $ 9\cdot \mathrm{A}^8_9=3265920 $ số. Phép thử là “chọn ngẫu nhiên một số từ $ 2903040 $ số của tập $ A $”, nên số phần tử của không gian mẫu là \[ \big|\Omega\big| =\mathrm{C}^1_{3265920}=3265920.\] Giả sử có một bảng gồm một hàng có $ 9 $ ô trống cạnh nhau, để tạo thành một số tự nhiên có $ 9 $ chữ số ta lần lượt lựa chọn và viết các chữ số trong các chữ số từ $ 0 $ đến $ 9 $ vào các ô trống này.
Gọi $ E $ là biến cố cần tính xác suất. Biến cố $ E $ xảy ra, ta phải thực hiện các bước sau:
- Chọn một trong tám ô trống, vì ô đầu tiên không thể là $ 0 $, để viết chữ số $ 0 $; có $ 8 $ cách.
- Chọn bốn trong tám ô trống còn lại, và viết các chữ số $ 1,2,3,4 $ theo thứ tự từ trái qua phải vào các ô trống đó; có tất cả $ \mathrm{C}^4_8 $ cách.
- Chọn bốn trong năm chữ số $ 5,6,7,8,9 $, và sắp xếp các hoán vị của chúng vào bốn ô trống còn lại; có $ \mathrm{A}^4_5 $ cách.
Theo quy tắc nhân, số phần tử thuận lợi cho biến cố $ E $ là \[ \big|E\big| =8\cdot \mathrm{C}^4_8\cdot \mathrm{A}^4_5=67200.\] Xác suất cần tìm là $ \mathrm{P}=\frac{67200}{3265920}=\frac{5}{243}. $
Câu 10. [Cụm trường chuyên đồng bằng sông Hồng L1 2019] Có bao nhiêu số tự nhiên chẵn có $ 5 $ chữ số đôi một khác nhau, sao cho mỗi số đó nhất thiết phải có mặt chữ số $ 0 $.
Hướng dẫn. Gọi số tự nhiên cần lập là $ \overline{abcde} $ trong đó $ a\ne0,e $ chẵn và phải có mặt chữ số $ 0 $. Ta xét hai trường hợp:
- Nếu $ e=0 $ thì $ e $ chỉ có một cách chọn. Tiếp theo ta chọn 4 chữ số từ 9 chữ số $ 1,2,\dots,9 $ và sắp xếp vào bốn vị trí còn lại, có $ \mathrm{A}^4_9 $ cách. Trường hợp này có tất cả $ 1\cdot \mathrm{A}^4_9=3024 $ số.
- Nếu $ e\ne 0 $ thì $ e $ có 4 cách chọn, từ các chữ số $ 2,4,6,8 $. Tiếp theo, ta chọn vị trí cho chữ số $ 0 $, có 3 cách vì không thể ở vị trí của $ a $ hoặc $ e $. Cuối cùng, ta chọn 3 chữ số từ 8 chữ số còn lại và sắp xếp vào ba vị trí còn lại, có $ \mathrm{A}^3_8 $ cách. Trường hợp này có tất cả $ 4\cdot 3\cdot \mathrm{A}^3_8= 4032 $ số.
Theo quy tắc cộng, có tất cả $ 3024+4032=7056 $ số tự nhiên thỏa mãn yêu cầu.
Câu 11. [Nguyễn Thị Minh Khai — Hà Tĩnh L1 2019] Gọi $ S $ là tập hợp các số tự nhiên có chín chữ số được lập từ các chữ số $ 1,2,3,4,5 $. Lấy ngẫu nhiên một số từ tập $ S $. Tính xác suất để lây được số thỏa mãn điều kiện: các chữ số $ 1,2,3,4 $ có mặt đúng hai lần; chữ số $ 5 $ có mặt đúng một lần và các chữ số lẻ nằm ở vị trí lẻ, tính từ trái qua phải.
Hướng dẫn. Tập $ S$ có tất cả $ 5^9=1953125$ phần tử. Số phần tử của không gian mẫu là $$ |\Omega|= \mathrm{C}^1_{1953125}=1953125$$ Gọi $ A$ là biến cố lấy được số thỏa mãn yêu cầu. Để biến cố $ A$ xảy ra chúng ta thực hiện các bước sau:
- Chọn vị trí cho chữ số $ 5$, vì $ 5$ là số lẻ nên chỉ có thể chọn các vị trí thứ nhất, thứ ba, thứ năm, thứ bảy và thứ chín. Tóm lại, có $ 5$ cách chọn vị trí cho chữ số $ 5$.
- Sắp xếp hai chữ số $ 1$ và hai chữ số $ 3$ vào bốn vị trí lẻ còn lại, số cách sắp xếp là $$ \frac{4!}{2!\cdot 2!} =6$$
- Sắp xếp hai chữ số $ 2$ và hai chữ số $ 4$ vào bốn vị trí chẵn, số cách sắp xếp là $$ \frac{4!}{2!\cdot 2!} =6$$
Suy ra, số phần tử thuận lợi cho $ A$ là $$ 5\cdot 6\cdot 6 =180 $$ Xác suất cần tìm là $$ \mathrm{P}(A)=\frac{180}{5^9}. $$
Câu 12. Có bao nhiêu số có $ 10 $ chữ số được tạo thành từ ba chữ số $ 1,2,3 $ sao cho hai chữ số bất kỳ nào đứng cạnh nhau đều hơn kém nhau một đơn vị.
Hướng dẫn. Nhận xét rằng hai số hơn kém nhau $ 1 $ đơn vị thì tính chẵn lẻ đối lập nhau. Trong ba chữ số $ 1,2,3 $ thì chỉ có $ 2 $ là số chẵn. Do đó, gọi các số thỏa mãn điều kiện đề bài có dạng $ \overline{a_1a_2a_3…a_{10}} $ thì ta xét hai trường hợp:
- Chữ số $ 2 $ chiếm các vị trí chẵn $ a_2,a_4,…,a_{10} $. Lúc này, điền các chữ số $ 1 $ hoặc $ 3 $ vào các vị trí lẻ thì có $ 2^5=32 $ cách, nên có tất cả $ 32 $ số.
- Chữ số $ 2 $ chiếm các vị trí lẻ $ a_1,a_3,…,a_9 $. Và, ta viết các chữ số $ 1 $ hoặc $ 3 $ vào các vị trí chẵn thì có $ 2^5=32 $ cách, nên có tất cả $ 32 $ số.
Theo quy tắc cộng, có tất cả $ 64 $ số thỏa mãn điều kiện đề bài.
Câu 13. [Lê Văn Thịnh — Bắc Ninh 2019] Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán.
Hướng dẫn. Phép thử là “lấy ngẫu nhiên 3 quyển sách từ 9 quyển sách” nên số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^3_9=84 $$ Vì đề bài xuất hiện cụm từ ít nhất, nên chúng ta sử dụng biến cố đối. Giả sử $ A$ là biến cố “trong ba quyển sách lấy ra có ít nhất một quyển là toán” thì $ \overline{A}$ là biến cố “trong ba quyển sách lấy ra có không có sách toán”.
Biến cố $ \overline{A}$ xảy ra khi và chỉ khi lấy được 3 quyển chỉ gồm sách lý và hóa. Số phần tử thuận lợi của biến cố $ \overline{A}$ là $$ \mathrm{C}^3_5 =10$$ Xác suất cần tìm là \begin{align}
\mathrm{P}(A)&=1-\mathrm{P}(\overline{A})\\
&=1-\frac{10}{84}=\frac{37}{42}
\end{align}
Câu 14. [Chuyên Bắc Giang 2/2019] Lớp 11A có 2 tổ. Tổ I có 5 bạn nam, 3 bạn nữ và tổ II có 4 bạn nam, 4 bạn nữ. Lấy ngẫu nhiên mỗi tổ 2 bạn đi lao động. Tính xác suất để trong các bạn đi lao động có đúng 3 bạn nữ.
Hướng dẫn. Phép thử: “Lấy ngẫu nhiên mỗi tổ 2 bạn đi lao động”, tức là lấy từ tổ I hai bạn và tổ II hai bạn. Số phần tử của không gian mẫu là $$ |\Omega|= \mathrm{C}^2_8\cdot \mathrm{C}^2_8=784.$$ Để trong các bạn đi lao động có đúng 3 bạn nữ, chúng ta xét hai trường hợp:
- Chọn từ tổ I hai bạn nữ và tổ II một nam một nữ. Số cách chọn là $$ \mathrm{C}^2_{3}\cdot \mathrm{C}^1_4\cdot \mathrm{C}^1_4=48 $$
- Chọn từ tổ I một nam một nữ và tổ hai hai bạn nữ. Số cách chọn là $$ \mathrm{C}^1_5\cdot \mathrm{C}^1_3\cdot \mathrm{C}^2_{4}=90 $$
Theo quy tắc cộng, có tất cả $ 48+90=138$ cách chọn.
Xác suất cần tính là $$ \mathrm{P}=\frac{138}{784}=\frac{69}{392}$$
Câu 15. [Chuyên Bắc Ninh L1 2019] Có 7 bông hồng đỏ, 8 bông hồng vàng và 10 bông hồng trắng, các bông hồng khác nhau từng đôi một. Hỏi có bao nhiêu cách lấy 3 bông hồng có đủ ba màu.
Hướng dẫn. Lấy 3 bông hồng có đủ ba màu đồng nghĩa với lấy được 1 bông hồng đỏ, 1 bông hồng trắng và 1 bông hồng vàng. Số cách lấy thỏa mãn yêu cầu là $$ \mathrm{C}^1_7\cdot \mathrm{C}^1_8\cdot \mathrm{C}^1_{10}=560. $$
Câu 16. [Chuyên Bắc Ninh L1 2019] Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp đó. Gọi P là xác suất để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng bao nhiêu?
Hướng dẫn. Phép thử là “Lấy ngẫu nhiên $ 4$ thẻ từ $ 11$ thẻ”. Suy ra không gian mẫu có số phần tử là $$ |\Omega|=\mathrm{C}^4_{11}=330.$$ Trong $ 11$ tấm thẻ, có $ 6$ ghi số lẻ là $\{1,3,5,7,9,11\}$ và $ 5$ thẻ ghi số chẵn là $ \{2,4,6,8,10\}$.
Để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ thì ta có các trường hợp sau:
- Chọn 1 thẻ lẻ và 3 thẻ chẵn. Số cách chọn là $$ \mathrm{C}^1_6\cdot \mathrm{C}^3_{5}=60 $$
- Chọn 3 thẻ lẻ và 1 thẻ chẵn. Số cách chọn là $$ \mathrm{C}^3_6\cdot \mathrm{C}^1_{5}=100 $$
Theo quy tắc cộng, số phần tử thuận lợi là $$ 60+100=160 $$ Xác suất cần tìm là $ \mathrm{P}=\frac{160}{330}=\frac{16}{33}$.
Câu 17. [THTT 2/2019] Tại Giải vô địch bóng đá AFF Suzuki Cup 2019 có 10 đội tuyển tham dự, trong đó có đội tuyển Việt Nam và đội tuyển Malaysia. Ở vòng bảng, Ban tổ chức chia ngẫu nhiên 10 đội thành 2 bảng, bảng A và bảng B, mỗi bảng có 5 đội. Giả sử khả năng xếp mỗi đội vào mỗi bảng là như nhau. Tính xác suất đề đội tuyển Việt Nam và đội tuyển Malaysia được xếp trong cùng một bảng.
Hướng dẫn. Không gian mẫu có số phần tử là $$ \mathrm{C}^5_{10}\cdot \mathrm{C}^5_5=252.$$ Để xếp được đội Việt Nam và Malaysia ở cùng một bảng ta thực hiện hai bước:
- Chọn một bảng, có thể là bảng A hoặc bảng B, để xếp hai đội Việt Nam và Malaysia thì có 2 cách chọn. Khi đó, ở bảng này còn thiếu 3 đội nữa, nên có $ \mathrm{C}^3_8 $ cách chọn 3 đội từ 8 đội còn lại cho đủ 5 đội của bảng đó.
- Tiếp theo, đương nhiên chỉ có $ \mathrm{C}^5_5 $ cách chọn 5 đội vào bảng còn lại.
Theo quy tắc nhân, có $ 2\cdot \mathrm{C}^3_8\cdot \mathrm{C}^5_5=112 $ cách. Do đó, xác suất cần tìm là \[ \mathrm{P}=\frac{112}{252}=\frac{4}{9}. \]
Câu 18. [Cụm trường chuyên đồng bằng sông Hồng L1 2019] Giải bóng chuyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội của Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm ở hai bảng khác nhau bằng bao nhiêu?
Hướng dẫn. Số phần tử của không gian mẫu là \[ |\Omega|=\mathrm{C}^4_8\cdot \mathrm{C}^4_4=70. \] Ở đây không có sự phân biệt giữa hai bảng, tức là không nói rõ bảng A và bảng B chẳng hạn, nên ta xét bảng thứ nhất.
- Chọn một trong hai đội của Việt Nam vào bảng này, có $ \mathrm{C}^1_2 $ cách. Chọn tiếp ba trong sáu đội nước ngoài để xếp vào bảng đó, có $ \mathrm{C}^3_6 $ cách. Theo quy tắc nhân, bước này có $ \mathrm{C}^1_2\cdot \mathrm{C}^3_6=40 $ cách.
- Xếp bốn đội còn lại vào bảng thứ hai, có 1 cách duy nhất.
Như vậy, số phần tử thuận lợi của không gian mẫu là $ 40\cdot 1=40 $. Xác suất cần tìm là \[ \mathrm{P}=\frac{40}{70}=\frac{4}{7}. \]
Câu 19. [HSG 12 Bắc Giang năm học 2015-2016] Một công ty nhận được 30 hồ sơ của 30 người muốn xin việc vào công ty, trong đó có 15 người biết tiếng Anh, 8 người biết tiếng Pháp và 14 người không biết tiếng Anh và tiếng Pháp. Công ty cần tuyển 5 người biết ít nhất tiếng Anh hoặc tiếng Pháp. Tính xác suất để trong 5 người được chọn có 3 người biết cả tiếng Anh và tiếng Pháp.
Hướng dẫn. Số người biết cả hai tiếng Anh và Pháp là \[ 15+8+14-30=7. \] Phép thử: “Chọn 5 người trong 16 người không phân biệt nhiệm vụ” nên không gian mẫu có số phần tử là \[ |\Omega|=\mathrm{C}^5_{16}=4368. \]
Gọi $ A $ là biến cố “trong 5 người được chọn có 3 người biết cả tiếng Anh và tiếng Pháp” thì $ A $ xảy ra khi và chỉ khi:
- Chọn được 3 người biết cả tiếng Anh và tiếng Pháp, 2 người chỉ biết tiếng Anh và 0 người chỉ biết tiếng Pháp. Trường hợp này có $\mathrm{C}^3_7\cdot \mathrm{C}^2_8\cdot \mathrm{C}^0_1 $ cách chọn.
- Chọn được 3 người biết cả tiếng Anh và tiếng Pháp, 1 người chỉ biết tiếng Anh và 1 người chỉ biết tiếng Pháp. Trường hợp này có $ \mathrm{C}^3_7\cdot \mathrm{C}^1_8\cdot \mathrm{C}^1_1 $ cách chọn.
Suy ra, số phần tử thuận lợi cho $ A $ là \[ |A|=\mathrm{C}^3_7\cdot \mathrm{C}^2_8\cdot \mathrm{C}^0_1 + \mathrm{C}^3_7\cdot \mathrm{C}^1_8\cdot \mathrm{C}^1_1 = 1260.\] Xác suất cần tìm là $ \mathrm{P}(A)=\frac{1260}{4268}=\frac{15}{52}. $
Câu 20. [HSG Nghệ An lớp 11 năm học 2016 – 2017] Thầy X có 15 cuốn sách gồm 4 cuốn sách Văn, 5 cuốn sách Sử và 6 cuốn sách Địa. Các cuốn sách đôi một khác nhau. Thầy X chọn ngẫu nhiên 8 cuốn sách để làm phần thưởng cho một học sinh. Tính xác suất để số cuốn sách còn lại của thầy X có đủ 3 môn.
Hướng dẫn. Phép thử: “Chọn ngẫu nhiên 8 cuốn sách trong 15 cuốn sách” nên số phần tử của không gian mẫu là\[ |\Omega|=\mathrm{C}^8_{15}=6435. \] Gọi $ A $ là biến cố “Số cuốn sách còn lại của thầy X có đủ 3 môn”. Suy ra $ \overline{A} $ là biến cố “Số cuốn sách còn lại của thầy X không có đủ 3 môn”. Vì số cuốn sách mỗi môn đều ít hơn 7, nên nếu còn lại 7 cuốn sách thì phải gồm từ 2 môn trở lên. Do đó, biến cố $ \overline{A} $ xảy ra có 3 trường hợp:
- 7 cuốn sách còn lại chỉ có Văn và Sử. Số cách chọn là $ \mathrm{C}^7_9. $
- 7 cuốn sách còn lại chỉ có Văn và Địa. Số cách chọn là $ \mathrm{C}^7_{10}. $
- 7 cuốn sách còn lại chỉ có Địa và Sử. Số cách chọn là $ \mathrm{C}^7_{11}. $
Suy ra, số phần tử thuận lợi cho $ \overline{A} $ là \[ |\overline{A}|=\mathrm{C}^7_9+\mathrm{C}^7_{10}+\mathrm{C}^7_{11}=486. \] Xác suất cần tìm là \[ \mathrm{P}(A)=1-P(\overline{A})=1-\frac{486}{6435}=\frac{661}{715}. \]
Câu 21. [A Hải Hậu — Nam Định L1 2019] Trong một buổi dạ hội có 10 thành viên nam và 12 thành viên nữ, trong đó có 2 cặp vợ chồng. Ban tổ chức muốn chọn ra 7 đôi, mỗi đôi gồm 1 nam và 1 nữ để tham gia trò chơi. Tính xác suất để trong 7 đôi đó, có đúng một đôi là cặp vợ chồng. Biết rằng trong trò chơi, người vợ có thể ghép đôi với một người khác chồng mình và người chồng có thể ghép đôi với một người khác vợ mình.
Hướng dẫn. Để chọn ra 7 đôi, mỗi đôi gồm 1 nam và 1 nữ ta thực hiện các bước:
- Chọn ra 7 nam từ 10 nam, có $ \mathrm{C}^7_{10} $ cách.
- Chọn ra 7 nữ từ 12 nữ, có $ \mathrm{C}^7_{12} $ cách.
- Sắp xếp thành 7 đôi, có $ 7! $ cách.
Do đó, không gian mẫu có $ \mathrm{C}^7_{10} \cdot \mathrm{C}^7_{12}\cdot 7!$ phần tử.
Để chọn được 7 đôi sao cho có đúng 1 đôi là cặp vợ chồng, ta thực hiện như sau:
- Chọn ra 1 đôi là vợ chồng trong 2 cặp vợ chồng, có $ \mathrm{C}^1_2 $ cách.
- Chọn ra 6 đôi từ 9 nam và 11 nữ còn lại, có $ \mathrm{C}^6_{9} \cdot \mathrm{C}^6_{11}\cdot 6! $. Nhưng trong số những cách này đã bao gồm cả những cách có cả hai đôi là vợ chồng, do đó phải trừ đi $ \mathrm{C}^1_1\cdot \mathrm{C}^5_{8} \cdot \mathrm{C}^5_{10}\cdot 5!$. Như vậy, bước này có $ \mathrm{C}^6_{9} \cdot \mathrm{C}^6_{11}\cdot 6! – C^1_1\cdot \mathrm{C}^5_{8} \cdot \mathrm{C}^5_{10}\cdot 5!$ cách.
Theo quy tắc nhân, có tất cả \[ \mathrm{C}^1_2\left(\mathrm{C}^6_{9} \cdot \mathrm{C}^6_{11}\cdot 6! – C^1_1\cdot \mathrm{C}^5_{8} \cdot \mathrm{C}^5_{10}\cdot 5!\right). \] Xác suất cần tìm là
\[ \mathrm{P}= \frac{\mathrm{C}^1_2\left(\mathrm{C}^6_{9} \cdot \mathrm{C}^6_{11}\cdot 6! – C^1_1\cdot \mathrm{C}^5_{8} \cdot \mathrm{C}^5_{10}\cdot 5!\right) }{\mathrm{C}^7_{10} \cdot \mathrm{C}^7_{12}\cdot 7!}=\frac{217}{1980}.\]
Câu 22. [Lương Thế Vinh — HN L1 2019] Cho đa giác đều có $ 2018 $ đỉnh. Hỏi có bao nhiêu hình chữ nhật có $ 4 $ đỉnh là các đỉnh của đa giác đã cho?
Hướng dẫn. Vì đa giác đều nên có tâm đường tròn ngoại tiếp, giả sử là tâm $ O $, nó có $ 2018 $ đỉnh thì có $ 1009 $ đường chéo đi qua $ O $. Cứ $ 2 $ trong số $ 1009 $ đường chéo này thì sẽ tạo thành một hình chữ nhật, đo đó có tất cả $ \mathrm{C}^2_{1009} $ hình chữ nhật.
Câu 23. Cho đa giác đều $ 54 $ cạnh. Gọi $ S $ là tập hợp các tứ giác tạo thành có 4 đỉnh lấy từ các đỉnh của đa giác đều. Chọn ngẫu nhiên một phần tử của $ S $. Xác suất để chọn được một hình chữ nhật là bao nhiêu?
Hướng dẫn. Đa giác đều có $ 54 $ cạnh thì có $ 54 $ đỉnh. Mỗi tứ giác có 4 đỉnh lấy từ các đỉnh của đa giác đều là một tổ hợp chập 4 của 54 phần tử, nên số phần tử của tập $ S $ là $$ \mathrm{C}^4_{54}=316251 $$ Phép thử là “chọn một tứ giác trong $ 316251 $ tứ giác của tập $ S $” nên số phần tử của không gian mẫu là \[ |\Omega|=\mathrm{C}^1_{316251}=316251. \] Gọi $ A $ là biến cố “chọn được một hình chữ nhật”. Vì đa giác đều nên có tâm đường tròn ngoại tiếp, giả sử là tâm $ O $, nó có $ 54 $ đỉnh thì có $ 27 $ đường chéo đi qua $ O $. Cứ $ 2 $ trong số $ 27 $ đường chéo này thì sẽ tạo thành một hình chữ nhật, đo đó số phần tử thuận lợi là \[ |A|=\mathrm{C}^2_{27}=351 \] Xác suất cần tìm là $ \mathrm{P}(A)=\frac{351}{316251}=\frac{1}{901}. $
Câu 24. [Chuyên Hùng Vương — Gia Lai L1 2019] Cho một hình vuông, mỗi cạnh của hình vuông đó được chia thành $ n $ đoạn bằng nhau bởi $ (n-1) $ điểm chia, không tính hai đầu mút mỗi cạnh. Xét các tứ giác có $ 4 $ đỉnh là $ 4 $ điểm chia trên $ 4 $ cạnh của hình vuông đã cho. Gọi $ a $ là số các tứ giác tạo thành và $ b $ là số các hình bình hành trong số đó. Giá trị $ n $ thỏa mãn $ a=9b $ là bao nhiêu?
Hướng dẫn. Mỗi tứ giác được tạo thành bằng cách chọn 4 đỉnh trên 4 cạnh. Số cách chọn một đỉnh trên một cạnh là $ (n-1) $ nên có tất cả $ a=(n-1)^4 $ tứ giác.
Dễ thấy rằng nếu tứ giác $ MNPQ $ là hình bình hành thì $ M $ và $ P,N $ và $ Q $ đối xứng nhau qua tâm của hình vuông. Nên ta chỉ cần chọn đỉnh $ M $ rồi lấy đối xứng qua tâm hình vuông thì được đỉnh $ P $, chọn đỉnh $ N $ rồi lấy đối xứng qua tâm hình vuông được đỉnh $ Q $. Suy ra một hình bình hành được hoàn toàn xác định bằng cách chọn 2 đỉnh liên tiếp trên hai cạnh liên tiếp của hình vuông. Nên có tất cả $ b=(n-1)^2 $ hình bình hành.
Do đó, yêu cầu bài toán tương đương với tìm số tự nhiên $ n $ thỏa mãn $$(n-1)^{4}=9(n-1)^{2}$$ Giải phương trình này tìm được đáp số $ n=4. $
Câu 25. [Nguyễn Thị Minh Khai — Hà Tĩnh L1 2019] Cho một đa giác đều $ 10 $ cạnh nội tiếp đường tròn $(O)$. Hỏi có bao nhiêu hình thang cân có bốn đỉnh là đỉnh của đa giác đều đó?
Hướng dẫn. Đa giác đều có $ 10 $ cạnh nên có $ 5 $ đường chéo đi qua tâm $ O $. Mỗi hình thang cân có bốn đỉnh là đỉnh của đa giác đều đó thì đều có trục đối xứng. Ta xét hai trường hợp:
- Trục đối xứng của hình thang cân là một trong 5 đường chéo đi qua tâm nói trên. Xét một đường kính bất kì, chẳng hạn $ A_1A_6 $, thì số hình thang nhận $ A_1A_6 $ làm trục đối xứng là \[\mathrm{C}^2_4=6 \]Vậy trường hợp này có tất cả $ 5\cdot6=30 $ hình thang cân.
- Trục đối xứng của hình thang cân là đường thẳng vuông góc với hai cạnh đối nhau của đa giác đều. Số hình thang cân là\[ 5\cdot \mathrm{C}^2_5=50 \]
Tuy nhiên, trong số các hình thang cân này thì các hình chữ nhật đã được đếm hai lần, do đó số hình thang cân cần tìm là \[ 30+50-\mathrm{C}^2_5=70 \]
Câu 26. Gọi $A$ là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự nhiên thuộc vào tập $A$. Tính xác suất để chọn được một số thuộc $A$ và số đó chia hết cho $3$.
Hướng dẫn. Trước tiên, ta tính số phần tử của tập hợp $A$. Với số tự nhiên có chín chữ số đôi một khác nhau thì chữ số đầu tiên có $9$ cách chọn và có $\mathrm{A}_9^8$ cách sắp xếp cho tám vị trí còn lại. Do đó, số phần tử của tập hợp $ A $ là
$$|A| = 9\cdot\mathrm{A}_9^8=3265920.$$ Phép thử là “chọn một số tự nhiên từ $ 3265920 $ số tự nhiên của tập $ A $” nên không gian mẫu có số phần tử là \[ |\Omega|=\mathrm{C}^1_{3265920}=3265920. \] Giả sử $B = \{0;1;2; \ldots ;9\}$. Ta thấy tổng các phần tử của $B$ bằng $45 \mathrel{\vdots} 3$ nên số có chín chữ số đôi một khác nhau và chia hết cho $3$ sẽ được tạo thành từ chín chữ số của các tập $B \setminus \{0\}$, $B \setminus \{3\}$, $B \setminus \{6\}$, $B \setminus \{9\}$. Do đó, số phần tử thuận lợi là $$9! + 3\cdot 8 \mathrm{A}_8^8.$$ Xác suất cần tìm là $\mathrm{P} = \frac{9! + 3 \cdot 8 \mathrm{A}_8^8}{9\mathrm{A}_9^8} = \frac{11}{27}$.
Câu 27. [Hải Hậu A — Nam Định L1 2019] Có bao nhiêu cách chia hết $ 4 $ chiếc bánh khác nhau cho 3 em nhỏ, biết rằng mỗi em nhận được ít nhất $ 1 $ chiếc.
Hướng dẫn. Giả sử ba em nhỏ là Xuân, Hạ, Thu. Vì mỗi em nhận được ít nhất $ 1 $ chiếc nên sẽ chỉ có thể xảy ra khả năng, một em nhận được 2 chiếc, hai em còn lại mỗi em nhận được 1 chiếc. Ta xét ba trường hợp:
- Xuân nhận được 2 chiếc bánh, Hạ được 1 chiếc, Thu được 1 chiếc. Số cách chia là \[ \mathrm{C}^2_4\cdot \mathrm{C}^1_2\cdot \mathrm{C}^1_1=12 \]
- Hai trường hợp còn lại, làm tương tự, mỗi trường hợp cũng có $ 12 $ cách chia bánh.
Theo quy tắc cộng, có tất cả $ 36 $ cách chia bánh thỏa mãn yêu cầu.
Câu 28. [Cù Huy Cận — Hà Tĩnh L1 2019] Một lớp có 36 ghế đơn được xếp thành hình vuông $ 6\times 6 $. Giáo viên muốn xếp 36 học sinh, trong đó có hai anh em là Kỷ và Hợi. Tính xác suất để hai anh em Kỷ và Hợi luôn được ngồi cạnh nhau theo chiều dọc hoặc ngang.
Hướng dẫn. Mỗi một cách sắp xếp chỗ ngồi cho $ 36 $ học sinh là một hoán vị của tập gồm $ 36 $ phần tử, nên không gian mẫu có $ 36! $ phần tử.
Để hai anh em Kỷ và Hợi ngồi cạnh nhau theo chiều ngang, ta thấy có 6 trường hợp:
- Kỷ và Hợi ngồi cạnh nhau ở hàng thứ nhất, có $ 2!\cdot 5\cdot 34! $ cách.
- Tương tự cho các trường hợp ngồi ở hàng thứ hai, thứ ba… cho đến hàng thứ sáu.
Vậy nếu ngồi cạnh nhau theo chiều ngang thì có tất cả \[ 2!\cdot 5\cdot 34!\cdot 6\text{ cách.} \] Tương tự, nếu ngồi cạnh nhau theo chiều dọc thì cũng có $ 2!\cdot 5\cdot 34!\cdot 6 $ cách. Do đó, xác suất cần tìm là \[ \mathrm{P}= \frac{2!\cdot 5\cdot 34!\cdot 6\cdot 2}{36!}=\frac{2}{21}.\]
Câu 29. [HSG Thanh Hóa lớp 12 năm học 2015 – 2016] Trong kỳ thi học sinh giỏi cấp trường , một trường THPT đã dùng 7 cuốn sách tham khảo môn Toán, 6 cuốn sách tham khảo môn Vật lí, 5 cuốn sách tham khảo môn Hóa học để làm phần thưởng cho 9 học sinh có kết quả cao nhất. Các cuốn sách cùng thể loại: Toán, Vật lí, Hóa học đều giống nhau. Mỗi học sinh nhận thưởng sẽ được 2 cuốn sách khác thể loại. Trong số 9 học sinh trên có hai học sinh tên là An và Bình. Tìm xác suất để hai học sinh An và Bình có phần thưởng giống nhau.
Hướng dẫn. Gọi $ x,y,z $ lần lượt là số học sinh nhận được phần thưởng là hai cuốn sách Toán và Lý, Toán và Hoá, Lý và Hoá thì ta có hệ phương trình \[ \begin{cases} x+y=7\\ y+z=6\\ z+x=5 \end{cases}
\Leftrightarrow
\begin{cases} x=4\\ y=3 \\ z=2 \end{cases} \] Phép thử là “Trao phần thưởng cho 9 học sinh”. Nghĩa là, chọn ra 5 trong 9 học sinh để trao sách Toán và Lý; sau đó chọn tiếp 3 trong 5 học sinh còn lại để trao sách Toán và Hoá; cuối cùng chọn 2 học sinh còn lại để trao sách Lý và Hoá. Do đó, không gian mẫu có $ |\Omega|=\mathrm{C}^4_9\cdot \mathrm{C}^3_5\cdot \mathrm{C}^2_2=1260 $ phần tử.
Xét biến cố $ A $ là “An và Bình có phần thưởng giống nhau.” Biến cố $ A $ xảy ra khi và chỉ khi
- An và Bình cùng nhận được sách Toán và Lý, có $ \mathrm{C}^2_7\cdot \mathrm{C}^3_5\cdot \mathrm{C}^2_2 $ cách.
- An và Bình cùng nhận được sách Toán và Hoá, có $ \mathrm{C}^1_7\cdot \mathrm{C}^4_6\cdot \mathrm{C}^2_2 $ cách.
- An và Bình cùng nhận được sách Lý và Hoá, có $ \mathrm{C}^0_7\cdot \mathrm{C}^4_7\cdot \mathrm{C}^3_3 $ cách.
Như vậy, số phần tử thuận lợi cho $ A $ là $$ |A|= \mathrm{C}^2_7\cdot \mathrm{C}^3_5\cdot \mathrm{C}^2_2 + \mathrm{C}^1_7\cdot \mathrm{C}^4_6\cdot \mathrm{C}^2_2 + \mathrm{C}^0_7\cdot \mathrm{C}^4_7\cdot \mathrm{C}^3_3 =350$$
Suy ra, xác suất cần tìm là $ \mathrm{P}(A)=\frac{350}{1260}=\frac{5}{18}. $
Câu 30. [Liên trường TP Vinh — L1 2019] Có 3 quyển sách toán, 4 quyển sách lí và 5 quyển sách hóa khác nhau được sắp xếp ngẫu nhiên lên một giá sách gồm có 3 ngăn, các quyển sách được sắp dựng đứng thành một hàng dọc vào một trong ba ngăn (mỗi ngăn đủ rộng để chứa tất cả quyển sách). Tính xác suất để không có bất kì hai quyển sách toán nào đứng cạnh nhau.
Hướng dẫn. Mỗi cách sắp xếp các cuốn sách lên giá sách có ba ngăn là một hoán vị của tập 14 phần tử gồm 12 cuốn sách và hai vách ngăn giữa ba ngăn của giá sách. Do đó, không gian mẫu có $ 14! $ phần tử.
Để sắp xếp thỏa mãn yêu cầu các cuốn sách toán không xếp cạnh nhau, ta thực hiện hai bước:
- Bước 1. Sắp xếp 11 phần tử gồm 4 cuốn sách lí, 5 cuốn sách hóa và 2 vách ngăn, thì có $ 11! $ cách.
- Bước 2. Chọn 3 trong 12 vị trí, gồm có 10 vị trí là các khoảng trống giữa 11 phần tử ở bước 1 cộng thêm 2 vị trí đầu tiên và cuối cùng, rồi sắp xếp các cuốn sách toán vào. Có tất cả $ \mathrm{C}^3_{12}\cdot 3! $ cách.
Theo quy tắc nhân, có tất cả $ 11!\cdot \mathrm{C}^3_{12}\cdot 3! $ cách. Xác suất cần tìm là \[ \mathrm{P}=\frac{11!\cdot \mathrm{C}^3_{12}\cdot 3!}{14!}=\frac{55}{91}. \]
Câu 31. [Chuyên KHTN HN năm 2020] Giải bóng chuyền VTV Cup có 12 đội tham gia trong đó có 9 đội nước ngoài và 3 đội của Việt Nam. Ban tổ chức cho bốc thăm ngẫu nhiên để chia thành 3 bảng đấu A ,B ,C mỗi bảng 4 đội. Tính xác suất để 3 đội Việt Nam nằm ở 3 bảng khác nhau.
Hướng dẫn. Việc chia bảng được thực hiện như sau:
Chọn $ 4$ đội vào bảng A, có $ \mathrm{C}^4_{12}$ cách. Còn lại $ 8$ đội, chọn tiếp $ 4$ đội vào bảng B, có $\mathrm{C}^4_8 $ cách. Cuối cùng, chọn $ 4$ đội vào bảng $ C$, có $ \mathrm{C}^4_4$ cách. Suy ra, số phần tử của không gian mẫu là $$ |\Omega|= \mathrm{C}^4_{12}\cdot \mathrm{C}^4_{8}\cdot \mathrm{C}^4_{4} = 34650.$$
Để 3 đội của Việt Nam nằm ở 3 bảng khác nhau thì mỗi bảng gồm 1 đội Việt Nam và 2 đội nước ngoài. Số phần tử thuận lợi là $$ \mathrm{C}^1_3\cdot\mathrm{C}^3_{9}\cdot \mathrm{C}^1_2\cdot \mathrm{C}^3_{6}\cdot\mathrm{C}^1_1 \cdot\mathrm{C}^3_{3}=10080 $$ Xác suất cần tìm là $$ \mathrm{P}=\frac{10080}{34650}=\frac{16}{55} $$
Câu 32. [Chuyên KHTN — HN 2020] Từ một hộp chứa $ 19$ tấm thẻ đánh số từ $ 1$ đến $ 19$, chọn ngẫu nhiên hai thẻ. Tính xác suất để chọn được hai thẻ mà tích của hai số ghi trên hai thẻ là một số chẵn.
Hướng dẫn. Phép thử là “chọn ngẫu nhiên hai thẻ từ $ 19$ thẻ” nên số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^2_{19} =171$$ Trong $ 19$ thẻ này có $ 10$ thẻ ghi số lẻ và $ 9$ thẻ ghi số chẵn. Để tích hai thẻ là một số chẵn thì ta xét hai trường hợp:
- Chọn được hai thẻ chẵn từ $ 10$ thẻ ghi số chẵn, số cách chọn là $$ \mathrm{C}^2_{10}=45 $$
- Chọn được một thẻ chẵn từ $ 10$ thẻ ghi số chẵn và một thẻ lẻ từ $ 9$ thẻ ghi số lẻ. Số cách chọn là $$ \mathrm{C}^1_{10}\cdot \mathrm{C}^1_{9}=90 $$
Suy ra, số phần tử thuận lợi là $$ 45+90=135 $$ Xác suất cần tìm là $ \mathrm{P}=\frac{135}{171}=\frac{15}{19}.$
Câu 33. [Lương Thế Vinh — HN 2020] Một em bé có một bộ 6 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 3 thẻ chữ T, một thẻ chữ N, một thẻ chữ H và một thẻ chữ P. Em bé đó xếp ngẫu nhiên 6 thẻ đó thành một hàng ngang. Tính xác suất em bé xếp được thành dãy TNTHPT
Hướng dẫn. Không gian mẫu có $ 6!=720$ phần tử.
Để xếp được chữ TNTHPT thì em bé có tất cả $3!=6$ cách. Xác suất cần tìm là $$ \mathrm{P}=\frac{6}{720}=\frac{1}{120}$$
Câu 34. [Trần Phú — Hà Tĩnh 2020] Một nhóm có 12 học sinh, trong đó có 10 học sinh nam và 2 học sinh nữ. Giáo viên chủ nhiệm xếp ngẫu nhiên 12 học sinh đó thành một hàng dọc. Tính xác suất để hai học sinh nữ không đứng cạnh nhau.
Hướng dẫn. Số phần tử của không gian mẫu là $$ |\Omega|=12! $$ Số cách sắp xếp để hai học sinh nữ đứng cạnh nhau là $$ 2!\cdot 11! $$ Suy ra, xác suất cần tính là $$ \mathrm{P}=1-\frac{2!\cdot 11!}{12!}=\frac{1}{6} $$
Câu 35. Cho $ S=\{1,2,3,4,5,6\}$. Lấy ngẫu nhiên một số tự nhiên có 5 chữ số được lập từ các chữ số thuộc $ S$. Tính xác suất để lấy được số mà chỉ có đúng 3 chữ số khác nhau.
Hướng dẫn. Có tất cả $ 6^5=7776$ số tự nhiên có 5 chữ số được lập từ tập $ S$. Lấy ngẫu nhiên một số trong $ 7776$ số này, nên số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^1_{7776}=7776$$ Số được lấy có đúng ba chữ số khác nhau, chúng ta có hai trường hợp:
- Số được tạo thành từ năm chữ số có dạng $ a,a,a,b,c$. Chọn $ 3$ trong $ 6$ chữ số, có $ \mathrm{C}^3_6$ cách. Chọn chữ số $ a$ trong 3 chữ số vừa lấy, có $ \mathrm{C}^1_3$ cách. Sắp xếp 5 số vào 5 vị trí có $ 5!$ cách. Tuy nhiên, chữ số $ a$ đã được hoán vị $ 3!$ lần, nên thực tế chỉ có $ \frac{5!}{3!}$ cách. Do đó, số phần tử của trường hợp này là $$ \mathrm{C}^3_6\cdot \mathrm{C}^1_3\cdot\frac{5!}{3!}=1200$$
- Số được tạo thành từ năm chữ số có dạng $ a,a,b,b,c$. Chọn $ 3$ trong $ 6$ chữ số, có $ \mathrm{C}^3_6$ cách. Chọn chữ số $a$ và $ b$ trong 3 chữ số vừa lấy, có $ \mathrm{C}^2_3$ cách. Sắp xếp 5 số vào 5 vị trí có $ 5!$ cách. Tuy nhiên, chữ số $ a$ đã được hoán vị $ 2!$ lần, chữ số $ b$ cũng được hoán vị $ 2!$ lần nên thực tế chỉ có $ \frac{5!}{2!2!}$ cách. Do đó, số phần tử của trường hợp này là $$ \mathrm{C}^3_6\cdot \mathrm{C}^2_3\cdot\frac{5!}{2!2!}=1800$$
Tóm lại, số phần tử thuận lợi là $ 1200+1800=3000$. Xác suất cần tính là $$ \mathrm{P}=\frac{3000}{7776}=\frac{125}{324}.$$
Câu 36. [AMS HK2 2020] Một nhóm nhảy có 3 học sinh lớp 12A, 4 học sinh lớp 12B và 5 học sinh lớp 12C. Chọn ngẫu nhiên 4 học sinh từ nhóm trên để biễu diễn vào ngày bế giảng. Xác suất để trong 4 học sinh được chọn, mỗi lớp A,B, C có ít nhất một học sinh là bao nhiêu?
Hướng dẫn. Tổng số học sinh của nhóm nhảy là $$ 3+4+5=12$$ Số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^4_{12}=495 $$ Để mỗi lớp được họn có ít nhất một học sinh, chúng ta có ba trường hợp:
- Nhóm gồm 2 học sinh lớp A, 1 học sinh lớp B và 1 học sinh lớp C. Số cách chọn là $$ \mathrm{C}^2_3\cdot \mathrm{C}^1_4\cdot \mathrm{C}^1_5= 60$$
- Nhóm gồm 1 học sinh lớp A, 2 học sinh lớp B và 1 học sinh lớp C. Số cách chọn là $$ \mathrm{C}^1_3\cdot \mathrm{C}^2_4\cdot \mathrm{C}^1_5= 90$$
- Nhóm gồm 1 học sinh lớp A, một học sinh lớp B và 2 học sinh lớp C. Số cách chọn là $$ \mathrm{C}^1_3\cdot \mathrm{C}^1_4\cdot \mathrm{C}^2_5= 120$$
Suy ra, có tất cả $ 60+90+120=270$ cách chọn thỏa mãn yêu cầu. Xác suất cần tính là $$ \mathrm{P}=\frac{270}{495}=\frac{6}{11}. $$
Câu 37. [SGD Vĩnh Phúc — 2020] Gọi $ S$ là tập các số tự nhiên có sáu chữ số trong đó có đúng ba chữ số $ 1$, ba chữ số còn lại khác nhau và khác $ 0$. Lấy ngẫu nhiên một số từ tập $ S$. Xác suất để lấy được số mà trong đó không có hai chữ số 1 nào đứng cạnh nhau là bao nhiêu?
Hướng dẫn. Để lập được các số tự nhiên của tập $ S$, ta thực hiện các bước sau:
- Chọn 3 trong 6 vị trí để viết chữ số $ 1$.
- Chọn 3 trong 8 chữ số từ 2 đến 9 và sắp xếp vào 3 vị trí còn lại.
Suy ra, số phần tử của tập $ S$ là $ \mathrm{C}^3_6\cdot \mathrm{A}^3_8=6720$. Do đó, số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^1_{6720}=6720 $$ Để lấy được số mà không có hai chữ số 1 nào đứng cạnh nhau thì số được chọn phải có dạng $ \overline{1*1*1*}$ hoặc $ \overline{1*1**1}$ hoặc $ \overline{1**1*1}$ hoặc $ \overline{*1*1*1}$. Số cách chọn trong mỗi trường hợp là $$ \mathrm{A}^3_8=336 $$
Do đó, số phần tử thuận lợi là $ 4\cdot 336=1344$. Xác suất cần tìm là $$ \mathrm{P}=\frac{1344}{6720}=\frac{1}{5} $$
Câu 38. [SGD Bắc Ninh — 2020] Gọi $ A$ là tập tất cả các số tự nhiên có $ 8$ chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc $ A$. Tính xác suất để số được chọn chia hết cho $ 25$.
Hướng dẫn. Vì số tự nhiên có $ 8$ chữ số nên chữ số đứng ở vị trí đầu tiên phải khác $ 0$. Số phần tử của tập $ A$ là $$ \mathrm{A}^8_{10}-\mathrm{A}^7_{9}=1632960 $$ Để một số tự nhiên chia hết cho $ 25$ thì hai chữ số tận cùng phải chia hết cho $ 25$, tức là tận cùng chỉ có thể là $$ 00, 25, 50, 75 $$ Nhưng vì các chữ số của số tự nhiên trong tập $ A$ phải khác nhau nên loại trường hợp tận cùng là $ 00$. Do đó, chúng ta chỉ còn ba trường hợp sau:
- Số tự nhiên lấy được tận cùng là $ 50$. Khi đó, mỗi cách chọn và sắp xếp $ 6$ chữ số còn lại tương ứng với một chỉnh hợp chập $ 6$ của $ 8$ phần tử. Trường hợp này lập được tất cả $$ \mathrm{A}^6_8=20160$$ số tự nhiên thỏa mãn yêu cầu.
- Số tự nhiên lấy được tận cùng là $ 25$. Chọn chữ số đầu tiên có $ 7$ cách, vì phải khác $ 0,2,5$. Chọn và sắp xếp $5 $ chữ số còn lại, có $ \mathrm{A}^5_7$ cách. Suy ra, trường hợp này có tất cả $$ 7\cdot \mathrm{A}^5_7=17640 $$ số thỏa mãn yêu cầu.
- Số tự nhiên lấy được tận cùng là $ 75$. Làm tương tự như trường hợp tận cùng là $ 25$, cũng tìm được $17640 $ số thỏa mãn yêu cầu.
Tóm lại, có tất cả $ 20160+2\cdot 17640=55440$ số tự nhiên chia hết cho $ 25$. Xác suất cần tìm là $$ P= \frac{55440}{1632960}=\frac{11}{324}$$
Câu 39. [SGD Hưng Yên 2020]\index{chia hết} Có 40 tấm thẻ đánh số từ 1 đến 40. Rút ngẫu nhiên 3 thẻ. Xác suất để tổng các số ghi trên thẻ chia hết cho 3 bằng bao nhiêu?
Hướng dẫn. Số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^3_{40}=9880 $$
Các 40 thẻ từ 1 đến 40 được chia thành ba loại:
- Các thẻ chia hết cho $ 3$, có $ 13$ thẻ là các thẻ $$ A=\{3,6,9,…,39\} $$
- Các thẻ chia cho $ 3$ dư $ 1$, có $ 14$ thẻ là các thẻ $$ B=\{1,4,7,…,38,40\} $$
- Các thẻ chia cho $ 3$ dư $ 2$, có $ 13$ thẻ là các thẻ $$ C=\{2,5,8,…,37\} $$
Để rút được 3 thẻ chia hết cho $ 3$ thì có các trường hợp sau:
- Rút được 3 thẻ từ tập $ A$, số cách là $$ \mathrm{C}^3_{13}=286 $$
- Rút được 3 thẻ từ tập $ B$, số cách là $$ \mathrm{C}^3_{14}=364 $$
- Rút được 3 thẻ từ tập $ C$, số cách là $$ \mathrm{C}^3_{13}=286 $$
- Rút được 1 thẻ từ tập $ A$, 1 thẻ từ tập $ B$ và 1 thẻ từ tập $ C$, số cách là $$ \mathrm{C}^1_{13}\cdot \mathrm{C}^1_{14}\mathrm{C}^1_{13}=2366 $$
Tóm lại, có tất cả $ 286+364+286+2366=3302$ cách lấy ra 3 thẻ thỏa mãn yêu cầu. Xác suất cần tính là $$ \mathrm{P}=\frac{3302}{9880}=\frac{127}{380}. $$
Câu 40. [Chuyên Thái Bình — Lần 4 năm 2020] Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa (các quyển sách cùng môn đôi một khác nhau). Hỏi có bao nhiêu cách lấy ra 3 quyển sách sao cho có ít nhất một quyển sách toán?
Hướng dẫn. Số cách lấy ngẫu nhiên 3 quyển sách từ 9 quyển sách trên giá là $$ \mathrm{C}^3_9=84 $$ Để lấy được ít nhất một quyển sách toán thì ta sẽ đếm số cách lấy mà không có quyển sách toán nào. Để làm được như vậy thì ta phải lấy được 3 quyển sách chỉ gồm lý và hóa, có tất cả $ \mathrm{C}^3_5=10 $ cách.
Suy ra, số cách lấy được ít nhất một quyển sách toán là $$ 84-10=74. $$
Câu 41. [SGD Thái Nguyên 2020] Có hai dãy ghế đối diện nhau, mỗi dãy có 5 ghế. Xếp ngẫu nhiên 10 học sinh gồm 5 học sinh nam và 5 học sinh nữ ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Tính xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ.
Hướng dẫn. Sắp xếp ngẫu nhiên 10 học sinh vào 10 ghế nên không gian mẫu có số phần tử là $$ |\Omega|=10! $$ Để sắp xếp mỗi học sinh nam đều ngồi đối diện với một học sinh nữ, ta thực hiện như sau:
- Chọn 1 trong 10 chỗ cho học sinh nam thứ nhất, có 10 cách.
- Chọn 1 trong 5 học sinh nữ để ngồi đối diện với học sinh nam thứ nhất, có 5 cách.
- Chọn 1 trong 8 ghế còn lại cho học sinh nam thứ hai, có 8 cách.
- Chọn 1 trong 4 học sinh nữ còn lại để ngồi đối diện với học sinh nam thứ hai, có 4 cách.
Tương tự như thế, ta được số cách sắp xếp chỗ ngồi là $$ 10\cdot 5\cdot 8 \cdot 4\cdot 6 \cdot 3\cdot 4\cdot 2\cdot 2\cdot 1 =460800 $$ Xác suất cần tìm là $$ \mathrm{P}=\frac{460800}{10!}=\frac{8}{63}. $$
Câu 42. [Chuyên Lê Hồng Phong — Nam Định 2020] Gọi $ S$ là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Lấy ngẫu nhiên hai số từ tập $ S$. Tính xác suất lấy được ít nhất một số chia hết cho $ 3$.
Hướng dẫn. Số phần tử của tập $ S$ là $$ 9\cdot \mathrm{A}^8_9=3265920. $$ Trong $ 3265920$ số này, chúng ta xem có bao nhiêu số tự nhiên chia hết cho $ 3$.
Nhận xét rằng tổng của $ 10$ chữ số từ $ 0$ đến $ 9$ là $$ 0+1+2+\cdots+9=45 $$ là một số chia hết cho $ 3$. Nên để có được số tự nhiên chia hết cho $ 3$ mà có $ 9$ chữ số thì chúng ta lập từ các chữ số thuộc tập sau \begin{align*}
\{1,2,3,4,5,6,7,8,9\},\,& \{0,1,2,4,5,6,7,8,9\}\\
\{0,1,2,3,4,5,7,8,9\},\, & \{0,1,2,3,4,5,6,7,8\}
\end{align*}
Đối với trường hợp đầu tiên, có $ 9!$ số. Ba trường hợp còn lại, mỗi trường hợp có $8\cdot 8! $ cách. Tóm lại, số lượng các số trong tập $ A$ mà chia hết cho $ 3$ là $$ 9!+3\cdot 8\cdot 8!=1330560. $$ Và hiển nhiên, tập $ A$ có $ 3265920-1330560=1935360$ số không chia hết cho $ 3$.
Phép thử là “lấy ngẫu nhiên hai số từ tập $ S$” nên số phần tử của không gian mẫu là $$ \Omega|=\mathrm{C}^2_{3265920} $$ Để lấy được ít nhất một số chia hết cho $ 3$ thì có hai trường hợp:
- Lấy được cả hai số chia hết cho $ 3$. Có $ \mathrm{C}^2_{1330560}$ cách.
- Lấy được một số chia hết cho $ 3$ và một số không chia hết cho $ 3$, có $ 1330560\cdot 1935360$ cách.
Xác suất cần tìm là $$ \mathrm{P}=\frac{\mathrm{C}^2_{1330560}+1330560\cdot 1935360}{\mathrm{C}^2_{3265920}}\approx 0{,}65. $$
Câu 43. [Đề thi ĐH Khối A năm 2014] Từ một hộp chứa 16 thẻ được đánh số từ 1 đến 16, chọn ngẫu nhiên 4 thẻ. Tính xác suất để 4 thẻ được chọn đều được đánh số chẵn.
Hướng dẫn.
- Phép thử là chọn ngẫu nhiên 4 thẻ trong 16 thẻ nên ta có $|\Omega|=C_{16}^4=1820$.
- Gọi $A$ là biến cố “4 thẻ được chọn đều được đánh số chẵn”, ta có $$|\Omega_A|=C_{8}^4=70$$
- Vậy xác suất để 4 thẻ được chọn đều được đánh số chẵn là $$\mathrm{P}(A)=\dfrac{|\Omega_A|}{|\Omega|}=\dfrac{1}{26}$$
Câu 44. Một nhóm học tập gồm 7 nam và 5 nữ, trong đó có bạn nam $A$ và bạn nữ $B$. Chọn ngẫu nhiên 6 bạn để lập một đội tuyển thi học sinh giỏi. Tính xác suất để đội tuyển có 3 nam và 3 nữ, trong đó phải có hoặc bạn nam $A$, hoặc bạn nữ $B$ nhưng không có cả hai.
Hướng dẫn.
- Phép thử là chọn 6 học sinh trong tổng số 12 học sinh nên số phần tử của không gian mẫu là $$|\Omega|=C_{12}^6=924$$
- Gọi $A$ là biến cố “đội tuyển có 3 nam và 3 nữ, trong đó phải có hoặc bạn nam $A$, hoặc bạn nữ $B$ nhưng không có cả hai”. Số phần tử thuận lợi là $$C_6^2.C_4^3+C_6^3.C_4^2 = 180$$
- Xác suất cần tìm là $$\mathrm{P}(A) = \frac{{180}}{{924}} = \frac{{15}}{{77}}$$
Câu 45. Ba xạ thủ cùng bắn độc lập vào bia, mỗi người bắn một viên đạn. Xác suất bắn trúng của từng xạ thủ lần ượt là 0,6; 0,7 và 0,8. Tính xác suất để có ít nhất một xạ thủ bắn trúng bia.
Hướng dẫn.
- Gọi $A_i\ (i=\overline{1,3})$ là biến cố “người thứ $i$ bắn trúng bia”.
- Ta có $P(A_1)=0,6;P(A_2)=0,7;P(A_3)=0,8$. Suy ra $$P(\overline{A_1})=0,4;P(\overline{A_2})=0,3;P(\overline{A_3})=0,2$$
- Gọi $A$ là biến cố “ít nhất một xạ thủ bắn trúng bia”, ta có $\overline{A}$ “cả ba xạ thủ không bắn trúng bia”.
- Khi đó $\overline{A}=\overline{A_1}.\overline{A_2}.\overline{A_3}$ nên suy ra $$\mathrm{P}(\overline{A})=0,4\times 0,3\times 0,2=0,024$$
- Xác suất cần tìm là $\mathrm{P}(A)=1-\mathrm{P}(\overline{A})=1-0,024=0,976$.
Câu 46. [Đề ĐH Khối B năm 2013] Có hai chiếc hộp đựng bi. Hộp thứ nhất chứa 4 viên bi đỏ và 3 viên bi trắng, hộp thứ hai chứa 2 viên bi đỏ và 4 viên bi trắng. Lấy ngẫu nhiên từ mỗi hộp ra một viên bi, tính xác suất để hai viên bi được lấy ra có cùng màu.
Hướng dẫn.
- Phép thử là lấy mỗi hộp một viên bi nên ta có $|\Omega|=C_7^1\times C_6^1=42$.
- Gọi $A$ là biến cố “hai viên bi lấy ra có cùng màu”. Số phần tử thuận lợi là $$C_4^1.C_2^1+C_3^1.C_4^1=20$$
- Xác suất cần tìm là $$\mathrm{P}(A)=\dfrac{20}{42}=\dfrac{10}{21}$$
Câu 47. [Đề thi ĐH Khối B năm 2012] Trong một lớp học gồm có 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học sinh lên bảng giải bài tập. Tính xác suất để 4 học sinh được gọi có cả nam và nữ.
Hướng dẫn.
- Phép thử là chọn 4 học sinh bất kỳ lên bảng nên ta có $|\Omega|=C_{25}^4=12650$.
- Gọi $A$ là biến cố “chọn 4 học sinh có cả nam và nữ”. Số phần tử thuận lợi là $$C_{15}^3.C_{10}^1+C_{15}^2.C_{10}^2+C_{15}^1.C_{10}^3=11075$$
- Xác suất để 4 học sinh được gọi có cả nam và nữ là $$\mathrm{P}(A) = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}} = \frac{{11075}}{{12650}} = \frac{{443}}{{506}}$$
Câu 48. [Chuyên Hùng Vương — Gia Lai 2020] Cho một đa giác đều có $ 18$ đỉnh nội tiếp trong một đường tròn tâm $ O$. Gọi $ X$ là tập hợp các tam giác có các đỉnh là các đỉnh của đa giác đều trên. Tính xác suất để chọn được một tam giác từ tập $ X$ là tam giác cân nhưng không phải tam giác đều.
Hướng dẫn.
- Số phần tử của không gian mẫu là $$ |\Omega|=\mathrm{C}^3_{18}=816. $$
- Xét một đỉnh bất kỳ của đa giác, gọi là $ A$ chẳng hạn, thì qua đường thẳng $ AO$ sẽ có $ 8$ cặp đỉnh đa giác đối xứng với nhau.
Do đó, ứng với mỗi đỉnh của đa giác thì có tất cả $ 8$ tam giác cân tại đỉnh đó. Trong $ 8$ tam giác cân này thì lại có một tam giác là tam giác đều, nên suy ra số tam giác cân mà không phải tam giác đều là $ 7$.
- Như vậy có tất cả $ 18\cdot 7 =126 $ tam giác cân nhưng không phải tam giác đều và xác suất cần tìm là $$ P=\frac{126}{816} =\frac{21}{136}$$
Câu 49. [Liên trường Nghệ An 2020] Gọi $ S$ là tập hợp tất cả các số tự nhiên có $ 4$ chữ số đôi một khác nhau lập thành từ các chữ số $ 0, 1, 2, 3, 4, 5, 6, 7$. Chọn ngẫu nhiên một số từ tập $ S$. Tính xác suất để số được chọn có đúng hai chữ số chẵn.
Hướng dẫn. Số lượng các số tự nhiên có bốn chữ số đôi một khác nhau lập từ các chữ số $ 0, 1, 2, 3, 4, 5, 6, 7$ là $$ \mathrm{A}^4_8-\mathrm{A}^3_7= 1470$$ Phép thử là “chọn ngẫu nhiên một số từ 1470 số của tập $ S$” nên số phần tử không gian mẫu là $$ |\Omega|=\mathrm{C}^1_{1470}=1470. $$ Để số được chọn có đúng hai chữ số chẵn, ta xét hai trường hợp:
- TH1. Hai chữ số chẵn đều khác $ 0$.
- Chọn hai chữ số chẵn từ các chữ số $ 2,4,6$, có $ \mathrm{C}^2_3=3$ cách.
- Chọn hai chữ số lẻ từ các chữ số $ 1,3,5,7$, có $ \mathrm{C}^2_4=6$ cách.
- Sắp xếp bốn chữ số này vào bốn vị trí, có $ 4!$ cách.
Suy ra, số lượng các số tự nhiên của trường hợp này là $ 3\cdot 6\cdot 4!=432$ số.
- TH2. Hai chữ số chẵn có bao gồm chữ số $ 0$.
- Chọn vị trí cho chữ số 0, có $ 3$ vị trí vì chữ số 0 không thể đứng đầu.
- Chọn một chữ số chẵn từ $ 2,4,6$, có $ \mathrm{C}^1_3=3$ cách.
- Chọn hai chữ số lẻ từ các chữ số $ 1,3,5,7$, có $ \mathrm{C}^2_4=6$ cách.
- Sắp xếp ba chữ số này vào ba vị trí còn lại, có $ 3!$ cách.
Suy ra, trường hợp này có tất cả $ 3\cdot 3\cdot 6\cdot 3!=324 $ số.
Tóm lại, số phần tử thuận lợi là $ 432+324=756$. Xác suất cần tìm là $$ \mathrm{P}=\frac{756}{1470}=\frac{18}{35}. $$
Câu 50. Cho tập \(X = \left\{ {0;1;2;4;6;7} \right\}\). Chọn ngẫu nhiên một số tự nhiên có 4 chữ số được lập X. Tính xác suất để số được chọn có một chữ số xuất hiện đúng hai lần và các chữ số còn lại xuất hiện không quá một lần.
Hướng dẫn. Chọn ngẫu nhiên một số tự nhiên có bốn chữ số được lập từ \(X = \left\{ {0;1;2;4;6;7} \right\}\). Số phần tử không gian mẫu: \(\left| \Omega \right| = {5.6^3} = 1080.\)
Gọi \(A\)là biến cố cần tìm xác suất. Ta có các trường hợp sau:
- Trường hợp 1: Chữ số \(0\)xuất hiện 2 lần.
- Có \(C_3^2\)cách chọn 2 vị trí cho chữ số $0$.
- Có \(A_5^2\)cách xếp 2 chữ số trong 5 chữ số vào 2 vị trí còn lại.
- Suy ra trường hợp này có: \(C_3^2.A_5^2 = 60\)số thỏa mãn.
- Trường hợp 2: Chữ số \(x\) (khác 0) xuất hiện 2 lần và \(x\) ở vị trí hàng nghìn.
- Có 5 cách chọn \(x\)từ tập \(X\).
- Có 3 cách chọn thêm một vị trí nữa cho \(x\).
- Có \(A_5^2\)cách xếp 2 chữ số trong 5 chữ số vào 2 vị trí còn lại.
- Suy ra trường hợp này có \(5.3.A_5^2 = 300\)số thỏa mãn.
- Trường hợp 3: Chữ số \(x\) (khác 0) xuất hiện 2 lần và \(x\)không nằm ở vị trí hàng nghìn.
- Có 5 cách chọn \(x\).
- Có \(C_3^2\)cách chọn vị trí cho chữ số\(x\).
- Có 4 cách chọn một chữ số (khác \(0\)và khác \(x\))vào vị trí hàng nghìn.
- Có 4 cách chọn một chữ số vào vị trí còn lại.
- Suy ra: trường hợp này có \(5.4.4.C_3^2 = 240\)số thỏa mãn.
Do đó, theo quy tắc cộng có \(\left| {{\Omega _A}} \right| = 60 + 300 + 240 = 600.\)
Vậy xác suất của biến cố \(A\): \(P\left( A \right) = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}} = \frac{{600}}{{1080}} = \frac{5}{9}.\)
Câu 51. Từ một hộp có 4 bút bi màu xanh, 5 bút bi màu đen và 6 bút bi màu đỏ, chọn ngẫu nhiên 5 bút. Xác suất để 5 bút được chọn chỉ có đúng hai màu là bao nhiêu?
Hướng dẫn. Gọi$A$ là biến cố: “ 5 bút được chọn có đúng hai màu”.
Ta có $n\left( \Omega \right) = C_{15}^5$.
Vì 5 bút được chọn có đúng hai màu nên có 3 trường hợp:
TH1: Có đúng hai màu xanh và đen:
- Chọn 5 bút trong hai màu xanh, đen (có 9 bút), có $C_9^5$ cách chọn.
- Trong $C_9^5$ cách chọn 5 bút trên, có $C_5^5$ cách chọn cả 5 bút đều màu đen và không có cách chọn nào để cả 5 bút đều màu xanh.
Số cách chọn 5 bút có đúng hai màu xanh và đen bằng $C_9^5 – C_5^5$.
TH2: Có đúng hai màu đen và đỏ:
- Chọn 5 bút trong hai màu đen, đỏ (có 11 bút), có $C_{11}^5$ cách chọn.
- Trong $C_{11}^5$ cách chọn 5 bút trên, có $C_5^5$ cách chọn cả 5 bút đều màu đen và $C_6^5$ cách chọn cả 5 bút đều màu đỏ.
Số cách chọn 5 bút có đúng hai màu đỏ và đen bằng $C_{11}^5 – C_5^5 – C_6^5$.
TH3: Có đúng hai màu đỏ và xanh:
- Chọn 5 bút trong hai màu đỏ, xanh (có 10 bút), có $C_{10}^5$ cách chọn.
- Trong $C_{10}^5$ cách chọn 5 bút trên, có $C_6^5$ cách chọn cả 5 bút đều màu đỏ và không có cách chọn cả 5 bút đều màu xanh.
Số cách chọn 5 bút có đúng hai màu đỏ và xanh bằng $C_{10}^5 – C_6^5$.
Vậy $P\left( A \right) = \frac{{\left( {C_9^5 – C_5^5} \right) + \left( {C_{11}^5 – C_5^5 – C_6^5} \right) + \left( {C_{10}^5 – C_6^5} \right)}}{{C_{15}^5}} = \frac{{118}}{{429}}$.
Câu 52. Một hộp đựng thẻ được đánh số từ 1, 2, 3,…, 8. Rút ngẫu nhiên hai lần, mỗi lần một thẻ và nhân số ghi trên hai thẻ với nhau, xác suất để tích nhận được là số chẵn là
A.$\frac{3}{{14}}$. B. $\frac{{25}}{{36}}$. C. $\frac{1}{2}.$ D.$\frac{{11}}{{14}}$.
Hướng dẫn. Chọn D
Số phần tử không gian mẫu: $n\left( \Omega \right) = 8 \times 7 = 56$.
Gọi $\bar A$ là biến cố: “tích nhận được là số lẻ”.
\(n\left( {\bar A} \right) = 4 \times 3 = 12\).
$ \Rightarrow n(A) = 56 – 12 = 44$.
Suy ra xác suất biến cố $A$: $P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{44}}{{56}} = \frac{{11}}{{14}}.$
Câu 53. Đội thanh niên tình nguyện của một trường THPT gồm 15 HS, trong đó có 4 HS khối 12, 5 HS khối 11 và 6 HS khối 10. Chọn ngẫu nhiên 6 HS đi thực hiện nhiệm vụ. Tính xác suất để 6 HS được chọn có đủ 3 khối.
A. $\frac{{4248}}{{5005}}.$ B. $\frac{{757}}{{5005}}.$ C. $\frac{{151}}{{1001}}.$ D. \(\frac{{850}}{{1001}}.\)
Hướng dẫn. Chọn D
Số phần tử của không gian mẫu $n\left( \Omega \right) = C_{15}^6 = 5005$.
Gọi A là biến cố: “6 HS được chọn có đủ 3 khối”.
Xét các trường hợp của biến cố \(\overline A \)
- Số cách chọn được 6 HS bao gồm cả khối 10 và 11: $C_{11}^6 – C_6^6$
- Số cách chọn được 6 HS bao gồm cả khối 10 và 12: $C_{10}^6 – C_6^6$
- Số cách chọn được 6 HS bao gồm cả khối 11 và 12: $C_9^6$
- Số cách chọn được 6 HS khối 10: $C_6^6$
Vậy $n\left( {\overline A } \right) = C_{11}^6 + C_{10}^6 + C_9^6 – C_6^6 = 755 \Rightarrow n\left( A \right) = 5005 – 755 = 4250$
Vậy xác suất cần tìm là: $P\left( A \right) = \frac{{4250}}{{5005}} = \frac{{850}}{{1001}}.$
Câu 54. Chọn ngẫu nhiên một số tự nhiên có hai chữ số. Tính xác suất để số được chọn có hai chữ số giống nhau.
Hướng dẫn. Số phần tử trong không gian mẫu là $n(\Omega ) = 90$.
Gọi A là biến cố “số được chọn có 2 chữ số giống nhau” A= $\left\{ {11;22;33;44;55;66;77;88;99} \right\}$ ; $n(A) = 9$
Do đó xác suất để số được chọn có hai chữ số giống nhau là $P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{9}{{90}} = 0,1$.
Câu 55. Một hộp đựng thẻ được đánh số từ $1, 2, 3,…, 9$. Rút ngẫu nhiên hai lần, mỗi lần một thẻ và nhân số ghi trên hai thẻ với nhau, xác suất để tích nhận được là số chẵn là bao nhiêu?
Hướng dẫn. Số phần tử không gian mẫu: $n\left( \Omega \right) = 9 \times 8 = 72$.
Gọi $\bar A$ là biến cố: “tích nhận được là số lẻ” thì \(n\left( {\bar A} \right) = 5 \times 4 = 20\).
Suy ra $ n(A) = 72 – 20 = 52$. Xác suất của biến cố $A$ là $$P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{52}}{{72}} = \frac{{13}}{{18}}.$$
Câu 56. Một hộp kín có 5 bút bi màu xanh khác nhau và 10 bút bi màu đỏ khác nhau. Lấy ngẫu nhiên 3 bút bi. Xác suất để lấy được 1 bút bi xanh và 2 bút bi đỏ là…
Hướng dẫn. Số phần tử của không gian mẫu $n\left( \Omega \right) = C_{15}^3$.
Gọi A là biến cố lấy được 1 bút bi xanh và 2 bút bi đỏ $ \Rightarrow n\left( A \right) = C_5^1.C_{10}^2$.
Xác suất của biến cố A là $P\left( A \right) = \frac{{C_5^1.C_{10}^2}}{{C_{15}^3}} = \frac{{45}}{{91}}$
Câu 57. Chọn ngẫu nhiên một số từ tập các số tự nhiên có năm chữ số khác nhau đôi một. Xác suất để số được chọn có ba chữ số chẵn và hai chữ số lẻ còn lại đứng kề nhau?
Hướng dẫn. Số phần tử của không gian mẫu là $n\left( \Omega \right) = 9.A_9^4$.
Gọi A là biến cố: “Số được chọn có ba chữ số chẵn và hai chữ số lẻ còn lại đứng kề nhau”.
Có $C_5^3$cách chọn 3 chữ số chẵn, có $A_5^2$ cách chọn 2 chữ số lẻ và xếp chúng kề nhau, có 4! Cách xếp sao cho 2 chữ số lẻ đứng kề nhau. Suy ra có $C_5^3.A_5^2.4!$ cách xếp thoả mãn (kể cả chữ số 0 đứng đầu).
Ta tính số các số thoả mãn đề mà có số chữ số 0 đứng đầu, ta xét 4 chữ số cuối: Có $C_4^2$ cách chọn 2 chữ số trong 4 chữ số chẵn, có $C_5^2$ cách chọn 2 chữ số lẻ, coi 2 chữ số lẻ là một nhóm ta có số các số là $C_4^2.C_5^2.2!.3!$.
Suy ra số các số thoả mãn đề bài là: $n\left( A \right) = C_5^3.A_5^2.4! – C_4^2.C_5^2.2!.3! = 4080$.
$P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{4080}}{{9.A_9^4}} = \frac{{85}}{{567}}$.
Câu 58. Từ một hộp có 4 bút bi màu xanh, 5 bút bi màu đen và 6 bút bi màu đỏ, chọn ngẫu nhiên 5 bút. Xác suất để 5 bút được chọn chỉ có đúng hai màu là bao nhiêu?
Hướng dẫn. Gọi$A$ là biến cố: “ 5 bút được chọn có đúng hai màu”.
Ta có $n\left( \Omega \right) = C_{15}^5$.
Vì 5 bút được chọn có đúng hai màu nên có 3 trường hợp:
TH1: Có đúng hai màu xanh và đen:
- Chọn 5 bút trong hai màu xanh, đen (có 9 bút), có $C_9^5$ cách chọn.
- Trong $C_9^5$ cách chọn 5 bút trên, có $C_5^5$ cách chọn cả 5 bút đều màu đen và không có cách chọn nào để cả 5 bút đều màu xanh.
Số cách chọn 5 bút có đúng hai màu xanh và đen bằng $C_9^5 – C_5^5$.
TH2: Có đúng hai màu đen và đỏ:
- Chọn 5 bút trong hai màu đen, đỏ (có 11 bút), có $C_{11}^5$ cách chọn.
- Trong $C_{11}^5$ cách chọn 5 bút trên, có $C_5^5$ cách chọn cả 5 bút đều màu đen và $C_6^5$ cách chọn cả 5 bút đều màu đỏ.
Số cách chọn 5 bút có đúng hai màu đỏ và đen bằng $C_{11}^5 – C_5^5 – C_6^5$.
TH3: Có đúng hai màu đỏ và xanh:
- Chọn 5 bút trong hai màu đỏ, xanh (có 10 bút), có $C_{10}^5$ cách chọn.
- Trong $C_{10}^5$ cách chọn 5 bút trên, có $C_6^5$ cách chọn cả 5 bút đều màu đỏ và không có cách chọn cả 5 bút đều màu xanh.
Số cách chọn 5 bút có đúng hai màu đỏ và xanh bằng $C_{10}^5 – C_6^5$.
Vậy $P\left( A \right) = \frac{{\left( {C_9^5 – C_5^5} \right) + \left( {C_{11}^5 – C_5^5 – C_6^5} \right) + \left( {C_{10}^5 – C_6^5} \right)}}{{C_{15}^5}} = \frac{{118}}{{429}}$.
Câu 59. Chọn ngẫu nhiên hai số khác nhau từ 27 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng
A.\(\frac{{13}}{{27}}\) B. \(\frac{{14}}{{27}}\) C. \(\frac{1}{2}\) D. \(\frac{{365}}{{729}}\)
Hướng dẫn. Chọn A
Gọi A là tập tất cả các số nguyên dương đầu tiên, \(A = \left\{ {1;\,\,2;\,\,3;\,……;\,\,26;\,\,27} \right\}\)
Chọn hai số khác nhau từ A có: \(n\left( \Omega \right) = C_{27}^2 = 351\). Tổng hai số là số chẵn khi cả hai số đó đều chẵn hoặc đều lẻ. Do đó:
Chọn hai số chẵn khác nhau từ tập A có: \(C_{13}^2 = 78\)
Chọn hai số lẻ khác nhau từ tập A có: \(C_{14}^2 = 91\)
Số cách chọn là: \(78 + 91 = 169\)
Xác suất cần tìm là: \(P = \frac{{169}}{{351}} = \frac{{13}}{{27}}\)
Câu 60. Cho tập hợp $A = \left\{ {1;2;…;100} \right\}$. Chọn ngẫu nhiên 3 phần tử của $A$. Xác suất để 3 phần tử được chọn lập thành một cấp số cộng bằng bao nhiêu?
Hướng dẫn. Chọn ngẫu nhiên 3 phần tử từ tập $A \Rightarrow $ Không gian mẫu là $\left| \Omega \right| = C_{100}^3$.
Gọi biến cố A:“Ba phần tử được chọn lập thành một cấp số cộng”.
Cách 1. Giả sử 3 phần tử đó là $x;x + d;x + 2d$.
- Với $x = 1$ thì ta có $x + 2d \le 100 \Leftrightarrow d \le \frac{{99}}{2} \Rightarrow d \in \left\{ {1;2;…;49} \right\} \Rightarrow $ có 49 bộ ba số thỏa mãn.
- Với $x = 2$ thì ta có $x + 2d \le 100 \Leftrightarrow d \le \frac{{98}}{2} \Rightarrow d \in \left\{ {1;2;…;49} \right\} \Rightarrow $ có 49 bộ ba số thỏa mãn.
- Với $x = 3$ thì ta có $x + 2d \le 100 \Leftrightarrow d \le \frac{{97}}{2} \Rightarrow d \in \left\{ {1;2;…;48} \right\} \Rightarrow $ có 48 bộ ba số thỏa mãn.
- …
- Với $x = 97$ thì ta có $x + 2d \le 100 \Leftrightarrow d \le \frac{3}{2} \Rightarrow d \in \left\{ 1 \right\} \Rightarrow $ có 1 bộ ba số thỏa mãn.
- Với $x = 98$ thì ta có $x + 2d \le 100 \Leftrightarrow d \le 1 \Rightarrow d \in \left\{ 1 \right\} \Rightarrow $ có 1 bộ ba số thỏa mãn.
- Với $x = 99$ thì ta có $x + 2d \le 100 \Leftrightarrow d \le \frac{1}{2} \Rightarrow d \in \emptyset \Rightarrow $ không có bộ ba số thỏa mãn.
Do đó ta thấy có tất cả $2\left( {49 + 48 + 47 + … + 2 + 1} \right) = 2.\frac{{49\left( {49 + 1} \right)}}{2} = 2450$ bộ ba số thỏa mãn.
Cách 2. Giả sử 3 phần tử đó là $a;b;c$ với $a,b,c \in A$.
- Trong tập $A$ có 50 số lẻ, 50 số chẵn.
- Do $a,b,c$ lập thành một CSC nên $a + c = 2b$ là một số chẵn.
- Do đó hai số $a,c$ cùng chẵn hoặc cùng lẻ.
- Đồng thời ứng với 1 cách chọn hai số $a,c$ thì xác định được duy nhất 1 số $b$.
- Tổng số bộ ba số $a,b,c$ là $C_{50}^2 + C_{50}^2 = 2450$ (bộ ba).
Vậy xác suất của biến cố A là $P = \frac{{2450}}{{C_{100}^3}} = \frac{1}{{66}}$.
Câu 61. Cho tập \(A = \left\{ {1;2;3;4;5;6} \right\}\). Tính xác suất biến cố chọn được số tự nhiên có \(3\) chữ số khác nhau lập từ tập A, sao cho tổng \(3\) chữ số bằng \(9\).
Hướng dẫn. Gọi \(A\) là biến cố “số tự nhiên 3 chữ số khác nhau, có tổng \(3\) chữ số bằng\(9\)”.
- Số số tự nhiên có \(3\) chữ số khác nhau có thể lập được là: $A_6^3 = 120$. Suy ra không gian mẫu có số phần tử là:$$\left| \Omega \right| = 120$$
- Ta có $1 + 2 + 6 = 9;1 + 3 + 5 = 9;2 + 3 + 4 = 9$.
- Số số tự nhiên có \(3\) chữ số khác nhau có tổng bằng \(9\) là:$3! + 3! + 3! = 18.$
- $n\left( A \right) = 18.$
Vậy $P\left( A \right) = \frac{{n\left( A \right)}}{{\left| \Omega \right|}} = \frac{{18}}{{120}} = \frac{3}{{20}}$.
Câu 62. Có $60$ tấm thẻ đánh số từ $1$ đến $50$. Rút ngẫu nhiên $3$ thẻ. Tính xác suất để tổng các số ghi trên thẻ chia hết cho $3$.
Hướng dẫn. Số phần tử không gian mẫu: $\left| \Omega \right| = C_{50}^3 = 19600$.
Gọi $A$ là tập các thẻ đánh số $a$ sao cho $1 \le a \le 50$ và $a$ chia hết cho $3$. $A = \left\{ {3;6;…;48} \right\} \Rightarrow \left| A \right| = 16$.
Gọi $B$ là tập các thẻ đánh số $b$ sao cho $1 \le b \le 50$ và $b$ chia $3$ dư $1$. $B = \left\{ {1;4;…;49} \right\} \Rightarrow \left| B \right| = 17$.
Gọi $C$ là tập các thẻ đánh số $c$ sao cho $1 \le c \le 50$ và $c$ chia $3$ dư $2$. $C = \left\{ {2;5;…;59} \right\} \Rightarrow \left| C \right| = 17$.
Với $D$ là biến cố: “Rút ngẫu nhiên $3$ thẻ được đánh số từ $1$ đến $50$ sao cho tổng các số ghi trên thẻ chia hết cho $3$”. Ta có $4$ trường hợp xảy ra:
- Trường hợp 1: Rút $3$ thẻ từ $A$: Có $C_{16}^3$ (cách).
- Trường hợp 2: Rút $3$ thẻ từ $B$: Có $C_{17}^3$ (cách).
- Trường hợp 3: Rút $3$ thẻ từ $C$: Có $C_{17}^3$ (cách).
- Trường hợp 4: Rút mỗi tập $1$ thẻ: Có $16.17.17 = 4624$ (cách).
Suy ra $\left| D \right| = 2.C_{17}^3 + C_{16}^3 + 4624 = 6544$.
Vậy xác suất cần tìm $P = \frac{{\left| D \right|}}{{\left| \Omega \right|}} = \frac{{6544}}{{19600}} = \frac{{409}}{{1225}}$.
Câu 63. Gọi A là tập hợp các số tự nhiên chẵn có 3 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số trong tập hợp \(A.\) Tính xác suất để số đó chia hết cho 5.
Hướng dẫn. Gọi số tự nhiên có 3 chữ số có dạng \(\overline {abc} \)
Vì \(\overline {abc} \) là số tự nhiên chẵn nên \(c \in \left\{ {0,2,4,6,8} \right\}\)
TH1: \(c = 0\). Ta có \(A_9^2 = 72\) số tự nhiên chẵn
TH2: \(c = 2,4,6,8\). Ta có \(4\left( {A_9^2 – A_8^1} \right) = 256\) số tự nhiên chẵn.
Vậy, số phần tử trong tập hợp A là: 328 số tự nhiên chẵn, suy ra \(\left| \Omega \right| = 328\)
Gọi X là biến cố số lấy ngẫu nhiên ra từ A chia hết cho 5, suy ra \(\left| {{\Omega _A}} \right| = 72\)
Vậy, xác suất xảy ra biến cố A là \({P_A} = \frac{{\left| {{\Omega _A}} \right|}}{{\left| \Omega \right|}} = \frac{{72}}{{328}} = \frac{9}{{41}}\)
Câu 64. Một người đang đứng tại gốc $O$ của trục tọa độ $Oxy$. Do say rượu nên người này bước ngẫu nhiên sang trái hoặc sang phải trên trục tọa độ với độ dài mỗi bước bằng 1 đơn vị. Xác suất để sau $10$ bước người này quay lại đúng gốc tọa độ $O$ bằng bao nhiêu?
Hướng dẫn. Mỗi bước người này có $2$ lựa chọn sang trái hoặc phải nên số phần tử không gian mẫu là ${2^{10}}$.
Để sau đúng $10$ bước người này quay lại đúng gốc tọa độ $O$ thì người này phải sang trái $5$ lần và sang phải $5$ lần, do đó số cách bước trong $10$ bước này là $C_{10}^5$.
Xác suất cần tính bằng $\frac{{C_{10}^5}}{{{2^{10}}}} = \frac{{63}}{{256}}$.
Câu 65. Chọn ngẫu nhiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để số được chọn có tổng các chữ số là lẻ bằng?
Hướng dẫn. Số phần tử không gian mẫu: $n(\Omega ) = 9 \times 9 \times 8 = 648.$
Gọi A là biến cố: “tổng các chữ số là số lẻ ”. Gọi số cần tìm là $\overline{abc}$:
Th1: ba chữ số $a,b,c$ đều lẻ có $5 \times 4 \times 3 = 60$ số.
Th 2: hai chữ số chẵn một chữ số lẻ có:
- $a$ chẵn,$b$chẵn, $c$lẻ có $4 \times 4 \times 5 = 80$ số.
- $a$ chẵn,$b$lẻ, $c$chẵn có $4 \times 5 \times 4 = 80$ số.
- $a$ lẻ,$b$chẵn, $c$chẵn có $5 \times 5 \times 4 = 100$ số.
Suy ra $ n(A) = 60 + 80 + 80 + 100 = 320$.
Suy ra xác suất biến cố $A$: $P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{320}}{{648}} = \frac{{40}}{{81}}.$
Câu 66. Cho tập hợp \(S = \left\{ {1;\,2;\,3;\,4;\,…..;\,17} \right\}\) gồm 17 số. Chọn ngẫu nhiên một tập con có ba phần tử của tập \(S\). Tính xác suất để tập hợp được chọn có tổng các phần tử chia hết cho 3.
A.\(\frac{{27}}{{34}}\). B.\(\frac{{23}}{{68}}\). C.\(\frac{9}{{34}}\). D.\(\frac{9}{{12}}\).
Hướng dẫn. Chọn B
Tập hợp các số từ tập \(S\)chia hết cho \(3\)là \(\left\{ {3;6;9;12;15} \right\}\).
Tập hợp các số từ tập \(S\)chia cho \(3\) dư 1 là \(\left\{ {1;4;7;10;13;16} \right\}\).
Tập hợp các số từ tập \(S\)chia cho \(3\) dư 2 là \(\left\{ {2;5;8;11;14;17} \right\}\).
- TH1: Ba số lấy từ tập \(S\)đều chia hết cho \(3\): Có \(C_5^3\) cách chọn.
- TH2: Ba số lấy từ tập \(S\)đều chia \(3\) dư 1: Có \(C_6^3\) cách chọn.
- TH3: Ba số lấy từ tập \(S\)đều chia 3 dư 2: Có \(C_6^3\) cách chọn.
- TH4: Một số chia hết cho 3, một số chia 3 dư 1, một số chia 3 dư 2: Có \(C_5^1.C_6^1.C_6^1\)cách chọn.
Vậy số phần tử của biến cố \(A\): “ Chọn được ba số có tổng chia hết cho 3” là:
\(n\left( A \right) = C_5^3 + C_6^3 + C_6^3 + C_5^1.C_6^1.C_6^1 = 230\).
Số phần tử không gian mẫu là \(n\left( \Omega \right) = C_{17}^3\).
Xác suất của biến cố \(A\)là \(P\left( A \right) = \frac{{230}}{{C_{17}^3}} = \frac{{23}}{{68}}\).
Câu 67. Gọi M là tập tất cả các số tự nhiên có sáu chữ số đôi một khác nhau và có dạng $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} $. Chọn ngẫu nhiên một số từ tập M. Tính xác suất để số được chọn là một số chẵn, đồng thời thỏa mãn ${a_1} > {a_2} > {a_3} > {a_4} > {a_5} > {a_6}.$
A.\(\frac{{35}}{{34020}}\) B.\(\frac{{37}}{{34020}}\). C.\(\frac{{37}}{{3402}}\). D.\(\frac{{74}}{{34020}}\).
Hướng dẫn. Chọn B
Gọi A là biến cố “chọn ra được một số tự nhiên chẵn từ tập M đồng thời thỏa mãn ${a_1} > {a_2} > {a_3} > {a_4} > {a_5} > {a_6}$”. Khi đó: \(n\left( M \right) = 9.A_9^5\) (số có sáu chữ số đôi một khác nhau thì \({a_1}\) có chín cách chọn, $\overline {{a_2}{a_3}{a_4}{a_5}{a_6}} $ là chỉnh hợp chập 5 của 9 phần tử nên có \(A_9^5\)).
- TH1: ${a_6} = 0$thì $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}} $ có $C_9^5$ cách chọn.
- TH2: ${a_6} = 2$thì $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}} $ có $C_7^5$ cách chọn.
- TH3: ${a_6} = 4$thì $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}} $ có $C_5^5$ cách chọn.
Suy ra $n\left( A \right) = C_9^5 + C_7^5 + C_5^5 = 148$
Do đó \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{148}}{{9.A_9^5}} = \frac{{37}}{{34020}}\).
Câu 68. Cho tập hợp A ={1; 2; 3; 4; 5}. Gọi S là tập hợp tất cả các số tự nhiên có ít nhất 3 chữ số đôi một khác nhau được lập thành từ các chữ số thuộc tập#A. Chọn ngẫu nhiên một số từ S, tính xác xuất để số được chọn có tổng các chữ số bằng 10.
Hướng dẫn. Số phần tử của tập $n\left( S \right) = A_5^3 + A_5^4 + {P_5} = 300$
Các bộ số có tổng 10: $\left\{ {\left( {2,3,5} \right);\left( {1,4,5} \right);(1,2,3,4)} \right\}$
$n\left( B \right) = 2{P_3} + {P_4} = 36 \Rightarrow P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( S \right)}} = \frac{{36}}{{300}} = \frac{3}{{25}}$
Câu 69. Có $60$ tấm thẻ đánh số từ $1$ đến $50$. Rút ngẫu nhiên $3$ thẻ. Tính xác suất để tổng các số ghi trên thẻ chia hết cho $3$.
Hướng dẫn. Số phần tử không gian mẫu: $\left| \Omega \right| = C_{50}^3 = 19600$.
Gọi $A$ là tập các thẻ đánh số $a$ sao cho $1 \le a \le 50$ và $a$ chia hết cho $3$.
$A = \left\{ {3;6;…;48} \right\} \Rightarrow \left| A \right| = 16$.
Gọi $B$ là tập các thẻ đánh số $b$ sao cho $1 \le b \le 50$ và $b$ chia $3$ dư $1$. $B = \left\{ {1;4;…;49} \right\} \Rightarrow \left| B \right| = 17$.
Gọi $C$ là tập các thẻ đánh số $c$ sao cho $1 \le c \le 50$ và $c$ chia $3$ dư $2$. $C = \left\{ {2;5;…;59} \right\} \Rightarrow \left| C \right| = 17$.
Với $D$ là biến cố: “Rút ngẫu nhiên $3$ thẻ được đánh số từ $1$ đến $50$ sao cho tổng các số ghi trên thẻ chia hết cho $3$”. Ta có $4$ trường hợp xảy ra:
- Trường hợp 1: Rút $3$ thẻ từ $A$: Có $C_{16}^3$ (cách).
- Trường hợp 2: Rút $3$ thẻ từ $B$: Có $C_{17}^3$ (cách).
- Trường hợp 3: Rút $3$ thẻ từ $C$: Có $C_{17}^3$ (cách).
- Trường hợp 4: Rút mỗi tập $1$ thẻ: Có $16.17.17 = 4624$ (cách).
Suy ra $\left| D \right| = 2.C_{17}^3 + C_{16}^3 + 4624 = 6544$.
Vậy xác suất cần tìm $P = \frac{{\left| D \right|}}{{\left| \Omega \right|}} = \frac{{6544}}{{19600}} = \frac{{409}}{{1225}}$.
Câu 70. Trên mặt phẳng $Oxy,$ta xét một hình chữ nhật $ABCD$với các điểm $A\left( { – 2;0} \right),$$B\left( { – 2;2} \right),$$C\left( {4;2} \right),$$D\left( {4;0} \right)$ (hình vẽ). Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm $M\left( {x;y} \right)$ mà $x + y < 2.$
Hướng dẫn. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là $7.3 = 21$ điểm vì $$\left\{ \begin{array}{l} x \in \left\{ { – 2; – 1;0;1;2;3;4} \right\}\\ y \in \left\{ {0;1;2} \right\} \end{array} \right.$$ Để con châu chấu đáp xuống các điểm $M\left( {x,y} \right)$ có $x + y < 2$ thì con châu chấu sẽ nhảy trong khu vực hình thang $BEIA.$ Để $M\left( {x,y} \right)$có tọa độ nguyên thì $$\left\{ \begin{array}{l} x \in \left\{ { – 2; – 1;0;1;2} \right\}\\ y \in \left\{ {0;1;2} \right\} \end{array} \right.$
- Nếu $x \in \left\{ { – 2; – 1} \right\}$thì $y \in \left\{ {0;1;2} \right\} \Rightarrow $có $2.3 = 6$ điểm.
- Nếu $x = 0$ thì $y \in \left\{ {0;1} \right\} \Rightarrow $ có 2 điểm.
- Nếu $x = 1 \Rightarrow y = 0 \Rightarrow $có 1 điểm.
Suy ra, có tất cả $6 + 2 + 1 = 9$ điểm thỏa mãn.
Vậy xác suất cần tính $P = \frac{9}{{21}} = \frac{3}{7}.$
Câu 71. Chọn ngẫu nhiên một số từ tập các số tự nhiên có ba chữ số đôi một khác nhau. Xác suất để số được chọn có tổng các chữ số là số lẻ bằng bao nhiêu?
Hướng dẫn. Số phần tử của không gian mẫu \(n(\Omega ) = 9.9.8 = 648\)
A: “Số được chọn có tổng các chữ số là số lẻ”
- Trường hợp 1: Số được chọn có 3 chữ số lẻ. Số cách chọn ra và sắp xếp ba chữ số lẻ là \(A_5^3\).
- Trường hợp 2: Số được chọn gồm có 2 chữ số chẵn và 1 chữ số lẻ.
- Số cách chọn ra và sắp xếp 2 chữ số là số chẵn và 1 chữ số là số lẻ là \(C_5^2.C_5^1.3!\)
- Số cách chọn ra và sắp xếp 2 chữ số là số chẵn và 1 chữ số lẻ có số 0 đứng đầu là \(C_4^1.C_5^1.2!\)
Vậy nên số số thỏa biến cố A là: \(C_5^2.C_5^1.3! – C_4^1.C_5^1.2! = 260\).
Số kết quả thuận lợi cho biến cố A là \(n(A) = 60 + 260 = 320\)
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{320}}{{648}} = \frac{{40}}{{81}}\).
Câu 72. Gọi X là tập hợp tất cả các số tự nhiên có 8 chữ số được lập từ các chữ số 1, 2, 3, 4, 5, 6, 7, 8, 9. Lấy ngẫu nhiên một số trong tập hợp X. Gọi A là biến cố lấy được số có đúng hai chữ số 1, có đúng hai chữ số 2, bốn chữ số còn lại đôi một khác nhau, đồng thời các chữ số giống nhau không đứng liền kề nhau. Xác suất của biến cố A bằng bao nhiêu?
Hướng dẫn. Ta có: $n(\Omega ) = {9^8}.$
TH1: Xếp bất kỳ
- Xếp hai chữ số 1, hai chữ số 2 bất kỳ và 4 chữ số còn lại: Có \(C_8^2.C_6^2.A_7^4 = 352.800\) (cách).
TH2: Số các cách xếp sao cho không thỏa mãn yêu cầu bài toán
- Xếp hai chữ số 1 đứng liền nhau: $7.C_6^2.A_7^4$ cách.
- Xếp hai chữ số 2 đứng liền nhau: $7.C_6^2.A_7^4$ cách.
- Số các cách xếp thuộc cả hai trường hợp trên:
- Coi hai chữ số 1 đứng liền nhau là nhóm X, hai chữ số 2 đứng liền nhau là nhóm Y
- Xếp X, Y và 4 số còn lại có: $C_7^4.6!$ (cách)
Vậy số cách xếp không thỏa mãn yêu cầu là: \(2.7.C_6^2.A_7^4 – C_7^4.6! = 151200\)(cách)
Vậy $n(A) = 352.800 – 151.200 = 201.600 \Rightarrow p(A) = \frac{{201600}}{{{9^8}}}$, chọn D.
Câu 73. Có \(3\) quyển sách Văn học khác nhau, \(4\) quyển sách Toán học khác nhau và \(7\) quyển sách Tiếng Anh khác nhau được xếp lên một kệ ngang. Tính xác suất để hai cuốn sách cùng môn không ở cạnh nhau.
Hướng dẫn.
| |
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
T.A |
|
| 1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
Gọi $\Omega $ là biến cố “xếp \(14\) quyển sách lên kệ sách một cách tùy ý” $ \Rightarrow n\left( \Omega \right) = 14!$.
Gọi $A$ là biến cố “xếp \(14\) cuốn sách lên kệ sách sao cho hai cuốn sách cùng môn không ở cạnh nhau”.
– Xếp \(7\) quyển sách Tiếng Anh vào kệ có $7!$ cách.
– \(7\) quyển sách Tiếng Anh tạo ra \(8\) chỗ trống (gồm \(6\) chỗ trống ở giữa và \(2\) chỗ trống trước sau).
Đánh số từ \(1\) đến \(8\), từ trái sang phải cho các chỗ trống. Khi đó ta xét các trường hợp:
TH1: Xếp sách Văn hoặc Toán vào vị trí từ \(1\) đến \(7\) có $7!$ cách.
TH2: Xếp sách Văn hoặc Toán vào vị trí từ \(2\) đến \(8\) có $7!$ cách.
TH3: Xếp \(1\) cặp sách Văn – Toán chung vào ngăn \(2\), các ngăn \(3,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}7\) xếp tùy ý số sách còn lại. Ta có:
+ Số cách chọn \(1\) cặp sách Văn – Toán: $3.4$ cách.
+ Vị trí \(2\) cuốn sách trong cặp sách: $2!$ cách.
+ Xếp các sách còn lại vào các ngăn \(3,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}7\) có $5!$ cách.
Vậy ta có số cách xếp \(1\) cặp sách Văn – Toán chung vào ngăn \(2\), các ngăn \(3,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}7\) xếp tùy ý số sách còn lại là $3.4.2!.5!$ cách.
Tương tự cho xếp cặp sách Văn – Toán lần lượt vào các ngăn \(3,{\rm{ }}4,{\rm{ }}5,{\rm{ }}6,{\rm{ }}7\).
Số trường hợp thuận lợi của biến cố là $n\left( A \right) = 7!\left( {2.7! + 3.4.2.6.5!} \right)$
Vậy $P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{19}}{{12012}}$.
Câu 74. Xếp ngẫu nhiên bốn bạn nam và năm bạn nữ ngồi vào chín ghế kê theo hàng ngang. Xác suất để có được năm bạn nữ ngồi cạnh nhau bằng?
Hướng dẫn. Ta có: \(n\left( \Omega \right) = 9! = 362880\)
Gọi biến cố \(A:\) “Xếp năm bạn nữ ngồi cạnh nhau” \( \Rightarrow n\left( A \right) = C_5^1 \times 5! \times 4! = 14400\)
Khi đó: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{14400}}{{362880}} = \frac{5}{{126}} \).






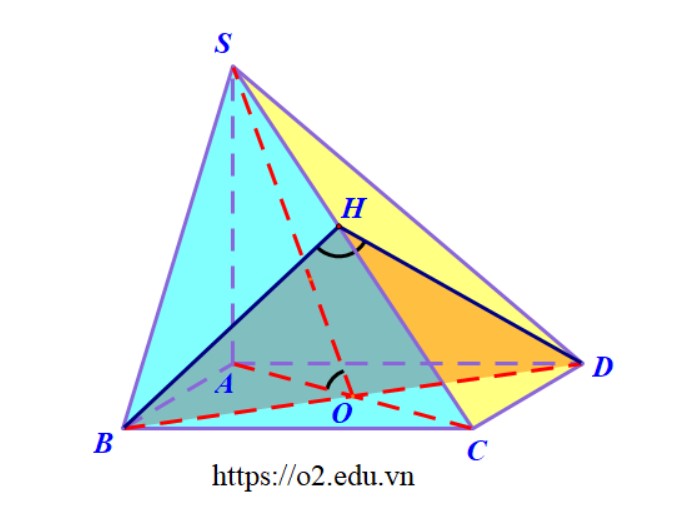

 Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).
Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).