Category Toán 11
Một số bài tập giới hạn khó
Tính các giới hạn sau: \( \lim \left(\sqrt{16^n+3^n}-\sqrt{16^n+4^n}\right) \) \( \lim\limits_{x\to 2}\frac{x^6-64}{x-2} \) \( \lim\limits_{x\to 1}\frac{x^5-1}{x^2-1} \) \( \lim\limits_{x\to 1}\frac{x^25-1}{x-1} \) \( \lim\limits_{x\to 0}\frac{\sqrt{x+9}+\sqrt{x+16}-7}{x} \) \( \lim\limits_{x\to 3}\frac{3\sqrt{x+1}-x-1}{x^2-9} \) \( \lim\limits_{x\to 2}\frac{\sqrt{1+4x}\sqrt{4+6x}-12}{x-2} \) \( \lim\limits_{x\to 0}\frac{(x^3+4)\sqrt{x+1}-4}{x} \) \( \lim\limits_{x\to 0}\frac{\sqrt{1+2x}\sqrt[3]{1+4x}-1}{x}…
Các quy tắc biểu diễn hình trong không gian
Các quy tắc biểu diễn hình trong không gian Để vẽ hình biểu diễn của các hình không gian, chúng ta sử dụng các quy tắc biểu diễn hình trong không gian sau: Hình biểu diễn của đường thẳng là…
Chứng minh ba đường thẳng đồng quy trong không gian
Chứng minh ba đường thẳng đồng quy trong không gian Nhờ việc sử dụng định lí về giao tuyến của ba mặt phẳng phân biệt trong không gian hoặc đồng quy, hoặc đôi một so sánh nên trong không gian…
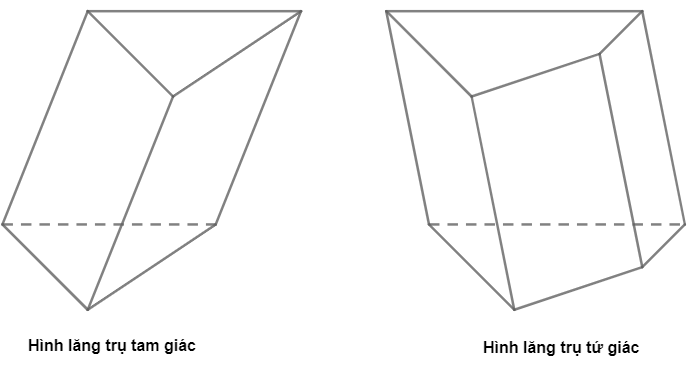
Hình chóp, hình lăng trụ, hình hộp là gì?
Hình chóp, hình lăng trụ, hình hộp là gì? Hình chóp, hình lăng trụ, hình hộp là những hình cơ bản trong hình học không gian. Đa số các bài toán ở cấp THPT đều làm việc trên các hình…
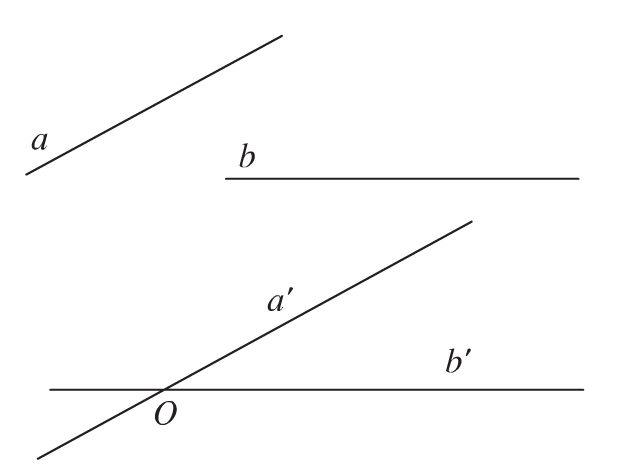
Góc giữa hai đường thẳng trong không gian
Góc giữa hai đường thẳng trong không gian 1. Góc giữa hai đường thẳng trong không gian là gì? Trong không gian cho 2 đường thẳng a, b bất kỳ. Từ một điểm O nào đó ta vẽ 2 đường…
Giới hạn của dãy số
Giới hạn của dãy số Nếu nhìn các đại lượng vô hạn dưới con mắt hữu hạn, chúng ta sẽ gặp vô vàn nghịch lí, như nghịch lí Zeno: Achilles và con rùa. Trong một cuộc chạy đua, người chạy…
Limit of a Sequence
Limit of a sequence 1. Basic keywords Some basic limits: $ \lim c=c$ $ \lim \frac{1}{n}=0 $ $ \lim \frac{c}{n^k}=0 $ for some positive integers $ k $ $ \lim \frac{1}{\sqrt{n}}=0 $ $ \lim \frac{1}{\sqrt[k]{n}}=0 $ for some positive integers…
Dãy Fibonacci là gì?
Dãy Fibonacci là gì? Dãy Fibonacci là dãy vô hạn các số tự nhiên bắt đầu bằng hai phần tử 0 và 1 hoặc 1 và 1, các phần tử sau đó được thiết lập theo quy tắc mỗi phần…
Phương trình đối xứng đối với sin x và cos x
Phương trình đối xứng đối với sin x và cos x Phương trình đối xứng đối với sin x và cos x là một dạng phương trình quan trọng bên cạnh các phương trình lượng giác thường gặp (phương trình…