O₂ Education

Tag: suy luận

  • Phương pháp suy luận đơn giản

    Phương pháp suy luận đơn giản

    Phương pháp suy luận đơn giản cho học sinh tiểu học

    Phương pháp suy luận đơn giản là một trong CÁC PHƯƠNG PHÁP BỒI DƯỠNG HỌC SINH GIỎI TOÁN TIỂU HỌC. Dưới đây, chúng tôi xin giới thiệu một số bài toán tiêu biểu để các em tự luyện tập.

    1. Phương pháp suy luận logic là gì?

    Suy luận là một hình thức cơ bản của tư duy, trong đó từ một hay nhiều phán đoán đã có ta tìm ra được phán đoán mới theo quy tắc lôgic xác định.

    Loại toán này đa dạng về đề tài và đòi hỏi học sinh phải biết suy luận đúng đắn, phải biết vận dụng những kiến thức đã học kết hợp kinh nghiệm sống phong phú của mình. Nó đòi hỏi học sinh phải biết cách lập luận, xem xét các khả năng có thể xảy ra của một sự kiện. Cũng có khi để giải được bài toán loại này, chỉ cần những kiến thức toán học đơn giản nhưng lại đòi hỏi khả năng chọn lọc trường hợp, suy luận chặt chẽ, rõ ràng.

    Đối với học sinh tiểu học, nhất lại là học sinh tiểu học thì việc giải toán suy luận là không hề dễ dàng bởi kiến thức, kinh nghiệm sống cũng như khả năng tư duy của các em còn có hạn.

    2. Một số bài toán suy luận đơn giản cho học sinh lớp 2-3

    Bài 1. Hùng đi câu cá về. Nam hỏi Hùng câu được bao nhiêu con cá. Hùng nói:

    – Số cá tớ câu được gồm 6 con không có đầu, 9 con không có đuôi và 8 con bị chặt đôi. Đố cậu biết tớ câu được bao nhiêu con cá?

    Nam nghĩ mãi không ra, bạn có thể giúp Nam được không?

    Phân tích. Các con số : 6,9 và 8 khi bị bỏ đi một phần đều giống nhau, nên đây là một bài toán mẹo.

    Lời giải.

    Ta thấy số 6 nếu bỏ đầu sẽ được số 0, số 9 nếu bỏ đuôi cũng được số 0 và số 8 nếu cắt đôi cũng được số 0.

    Như vậy Hùng không câu được con cá nào cả.

    Bài 2. Biết 2 gói kẹo nặng bằng 3 cái bánh. Hỏi:

    • 3 gói kẹo nặng hơn hay nhẹ hơn 5 cái bánh?
    • 5 gói kẹo năng hơn hay nhẹ hơn 8 cái bánh?

    Phân tích. Cho biết 2 gói kẹo bằng 3 cái bánh thì ta sẽ suy luận bắt đầu từ 1 gói kẹo.

    Lời giải.

    • Vì 2 gói kẹo nặng bằng 3 cái bánh nên 1 gói kẹo sẽ nhẹ hơn 2 cái bánh.
      Do đó: 2 gói kẹo + 1 gói kẹo sẽ nhẹ hơn 3 cái bánh + 2 cái bánh.
      Hay 3 gói kẹo nhẹ hơn 5 cái bánh.
    • Ta có 2 gói kẹo bằng 3 cái bánh nên 4 gói kẹo sẽ nặng bằng 6 cái bánh.
      Vì 2 gói kẹo nặng bằng 3 cái bánh nên 1 gói kẹo sẽ nhẹ hơn 2 cái bánh.
      Do đó 4 gói kẹo + 1 gói kẹo sẽ nhẹ hơn 6 cái bánh + 2 cái bánh.
      Hay 5 gói kẹo nhẹ hơn 8 cái bánh.

    Bài 3. Một con ốc  bò từ mặt đất lên đầu một chiếc cọc cao 20dm. Biết rằng cứ ban ngày nó bò lên được 5dm thì tối đến nó lại bị tụt xuống 2dm. Hỏi nếu con ốc bắt đầu bò từ sáng hôm nay thì sau bao lâu nó mới bò lên đến đỉnh cọc?

    Phân tích. Bài toán này học sinh rất dễ nhầm nếu phân tích thiếu chặt chẽ. Bởi vì cứ ban ngày con ốc bò được 5dm thì đêm lại bị tụt xuống 2dm. Tức là nếu tính 1 ngày 1 đêm thì con ốc chỉ bò được 5 – 2 = 3 dm. Nhưng nếu tính chắc ban ngày thì con ốc bò được 5dm. Vì vậy cần xác định rõ cho học sinh khi ốc bò được 20dm (lên đến đỉnh) là thời điểm nào.

    Lời giải.

    Sau 1 ngày và 1 đêm thì con ốc bò được một đoạn dài là:

    5 – 2 = 3 (dm)

    Sau 5 ngày và 5 đêm thì con ốc bò được một đoạn dài là :

    3 × 5 = 15 (dm)

    Đến tối ngày thứ 6 thì con ốc bò được một đoạn dài là :

    15 + 5 = 20 (dm)

    Như vậy đến tối ngày thứ 6 thì con ốc bò lên đến đỉnh cọc.

    Bài 4. Có 10kg gạo và một chiếc cân thăng bằng với 1 quả cân 1kg.

    a. Làm thế nào để lấy được 3kg gạo chỉ với 2 lần cân.

    b. Làm thế nào để lấy được 4kg gạo chỉ với 2 lần cân.

    Phân tích. 10kg gạo nên chia đều vào hai đĩa cân cho thăng bằng.

    Lời giải.

    a. Chia đều 10kg gạo vào 2 đĩa cân cho thăng bằng.

    Mỗi đĩa cân có số gạo là:

    10 : 2 = 5 (kg)

    Đặt quả cân lên một đĩa cân rồi chia đều 5kg gạo vào 2 đĩa cân sao cho thăng bằng. Như vậy tổng số gạo và quả cân ở 2 đĩa cân là:

    1 + 5  = 6(kg)

    Đĩa cân không có cân sẽ có số gạo là:

    6 : 2 = 3 (kg)

    b. Chia đều 10 kg gạo vào 2 đĩa cân cho thăng bằng.

    Mỗi đĩa cân chứa số gạo là:

    10 : 2 = 5 (kg)

    Cân tiếp 1 kg gạo ở 1 trong 2 đĩa cân, số gạo còn lại ở đĩa cân đó là:

    5 – 1 = 4 (kg)

    Bài 5. Đội tuyển học sinh giỏi của khối 2 có bốn bạn Hưng, Hà, Thái và Bình, trong đó có một bạn học lớp 2A, 2 bạn học lớp 2B và có một bạn học lớp 2C. Mỗi bạn chỉ tham gia thi một trong ba môn: Toán, Tiếng Việt hoặc Tiếng Anh. Biết rằng Hà và bạn ở lớp 2C thi Tiếng Việt, Thái và bạn ở lớp 2A thi Tiếng Anh, Hà không học lớp 2A, Thái và Bình không cùng học lớp 2C. Hỏi mỗi bạn học lớp nào?

    Phân tích. Bài toán này học sinh cần dùng phương pháp suy luận loại trừ.

    Lời giải.

    Lớp 2C có một bạn đi thi, Hà và bạn ở lớp 2C thi môn Tiếng Việt vì vậy Hà không học lớp 2C nữa.

    Thái và bạn ở lớp 2A thi Tiếng Anh, mà lớp 2A chỉ có một bạn đi thi vì vậy Hà cũng không học lớp 2A. Do đó Hà học lớp 2B.

    Lớp 2B có hai bạn đi thi,Thái và Bình cùng không học lớp 2C. Hà cũng không học lớp 2C. Vậy Hưng học ở lớp 2C.

    Lớp 2B có hai bạn đi thi, Thái và bạn ở lớp 2A thi Tiếng Anh vì vậy Thái không học ở lớp 2A, Thái cũng không học ở lớp 2C. Do đó Thái học ở lớp 2B.

    Vậy Bình học lớp 2A.

    Bài 6. Huy có 1 tờ giấy bạc loại 10 nghìn đồng, 1 tờ giấy bạc loại 5 nghìn đồng, 1 tờ giấy bạc loại 2 nghìn đồng và 1 tờ giấy bạc loại 1 nghìn đồng. Hỏi Huy sẽ đưa cho người bán hàng những tờ giấy bạc loại nào và người bán hàng trả lại cho Huy những tờ giấy bạc loại nào nếu:

    a. Huy mua 2 quyển vở hết 6 nghìn đồng.

    b. Huy mua 2 cái bút hết 4 nghìn đồng.

    Phân tích. Huy có tất cả 18 nghìn đồng. Tờ giấy bạc lớn nhất là 10 nghìn đồng. Tờ giấy bạc nhỏ nhất là 1 nghìn đồng. Tất cả có 4 tờ giấy bạc. Học sinh phải xác định được Huy có thể đưa cho người bán hàng những tờ giấy bạc loại nào mà người bán hàng phải trả lại cho Huy nữa.

    Lời giải.

    Huy có nhiều cách đưa cho người bán hàng số tiền như sau:

    • 1 tờ 10 nghìn (10 nghìn)
    • 1 tờ 10 nghìn và 1 tờ 1 nghìn (11 nghìn)
    • 1 tờ 10 nghìn và 1 tờ 2 nghìn (12 nghìn)
    • 1 tờ 10 nghìn, 1 tờ 2 nghìn và 1 tờ 1 nghìn (13 nghìn)

    Tức là Huy có thể đưa cho người bán hàng và nhận của người bán hàng các tờ giấy bạc như sau:

    a. Khi Huy mua 2 quyển vở hết 6 nghìn đồng:

    • Huy có thể đưa 10 nghìn – cô bán hàng trả lại 4 nghìn (cô đem 1 tờ 1 nghìn hoặc 2 tờ 2 nghìn).
    • Huy có thể đưa 11 nghìn – cô bán hàng trả lại 5 nghìn (cô đem 1 tờ 5 nghìn hoặc 5 tờ 1 nghìn hoặc 2 tờ 2 nghìn và 1 tờ 1 nghìn).
    • Huy có thể đưa 12 nghìn – cô bán hàng trả lại 6 nghìn(cô đem 1 tờ 5 nghìn và 1 tờ 1 nghìn; hoặc 3 tờ 2 nghìn hoặc 6 tờ 1 nghìn).

    b. Khi Huy mua 2 cái bút hết 4 nghìn đồng:

    • Huy có thể đưa 5 nghìn đồng – cô bán hàng trả lại 1 nghìn đồng.
    • Huy có thể đưa 10 nghìn đồng –  cô bán hàng trả lại 6 nghìn đồng.(cô đem 1 tờ 5 nghìn và 1 tờ 1 nghìn; hoặc 3 tờ 2 nghìn hoặc 6 tờ 1 nghìn).
    • Huy có thể đưa 11 nghìn đồng – cô bán hàng trả lại 7 nghìn đồng.(cô đem 1 tờ 5 nghìn và 2 tờ 2 nghìn ; hoặc 7 tờ 1 nghìn; hoặc 3 tờ 2 nghìn và 1 tờ 1 nghìn).

    Bài 7. Em có 7 quả bóng, vừa bóng xanh vừa bóng đỏ vừa bóng vàng. Hỏi em có mấy quả bóng xanh, mấy quả bóng vàng, mấy quả bóng đỏ? Biết số bóng xanh nhiều hơn bóng vàng nhưng lại ít hơn bóng đỏ?

    Phân tích. Có 7 quả bóng gồm ba màu xanh, đỏ, vàng. Số bóng xanh nhiều hơn bóng vàng nhưng lại ít hơn bóng đỏ nên số quả bóng sẽ là ba số khác nhau.

    Lời giải.

    Phân tích 7 thành tổng của 3 số khác nhau:

    7 = 1 + 2 + 4

    Vì số bóng vàng < số bóng xanh < số bóng đỏ. Vậy có 1 quả bóng màu vàng, 2 quả bóng màu xanh, 4 quả bóng màu đỏ.

    Bài 8. Trong hộp có 4 bút màu đỏ, 6 bút màu xanh và 3 bút màu vàng. Bạn An lấy từ trong hộp ra 10 cái bút. Có thể nói chắc chắn rằng trong 10 cái bút An lấy ra:

    a. Có ít nhất 1 cái bút màu vàng không?

    b. Có ít nhất 1 cái bút màu đỏ không?

    Phân tích. Số bút lấy ra là 10 cái, ta phải lọc hết tất cả khả năng xảy ra phù hợp với yêu cầu.

    Lời giải.

    a. Khi lấy ra 10 bút trong hộp, vẫn có thể xảy ra trường hợp An lấy đúng 4 cái bút màu đỏ và 6 cái bút màu xanh, không có cái bút màu vàng nào. Vì vậy không thể nói chắc chắn trong 10 cái bút An lấy ra có ít nhất 1 cái bút màu vàng được.

    b. Trong hộp bút có cả ba màu đỏ, vàng, xanh. Mọi khả năng An lấy ra 1,2,3 hay cái bút màu đỏ đều có thể xảy ra. Vì vậy khả năng trong 10 cái bút lấy ra sẽ có 1 cái màu đỏ. Nên có thể nói chắc chắn “ trong 10 cái bút An lấy ra có ít nhất 1 cái bút màu đỏ”.

    3. Một số bài toán suy luận đơn giản cho học sinh lớp 5

    Bài 1. Trong 1 ngôi đền có 3 vị thần ngồi cạnh nhau. Thần thật thà (luôn luôn nói thật); Thần dối trá (luôn nói dối) ; Thần khôn ngoan (lúc nói thật, lúc nói dối). Một nhà toán học hỏi 1 vị thần bên trái: Ai ngồi cạnh ngài?

    • Thần thật thà.

    Nhà toán học hỏi người ở giữa:

    • Ngài là ai?
    • Là thần khôn ngoan.

    Nhà toán học hỏi người bên phải:

    • Ai ngồi cạnh ngài?
    • Thần dối trá.

    Hãy xác định tên của các vị thần.

    Lời giải. Cả 3 câu hỏi của nhà toán học đều nhằm xác định 1 thông tin: Thần ngồi giữa là thần gì? Kết quả có 3 câu trả lời khác nhau.

    Ta thấy thần ngồi bên trái không phải là thần thật thà vì ngài nói người ngồi giữa là thần thật thà.

    Thần ngồi giữa cũng không phải là thần thật thà vì ngài nói: Tôi là thần khôn ngoan.

    Thần ngồi bên phải là thần thật thà ở giữa là thần dối trá ở bên trái là thần khôn ngoan.

    Bài 2. Một hôm anh Quang mang quyển Album ra giới thiệu với mọi người. Cường chỉ vào đàn ông trong ảnh và hỏi anh Quang: Người đàn ông này có quan hệ thế nào với anh? Anh Quang bèn trả lời: Bà nội của chị gái vợ anh ấy là chị gái của bà nội vợ tôi.
    Bạn cho biết anh Quang và người đàn ông ấy quan hẹ với nhau như thế nào?

    Hướng dẫn. Bà nội của chị gái vợ anh ấy cũng chính là bà nội của vợ anh ấy. Bà nội của vợ anh ấy là chị gái của bà nội vợ anh Quang.

    Vợ anh ấy và vợ anh Quang là chị em con dì con già. Do vậy anh Quang và người đàn ông ấy là 2 anh em rể họ.

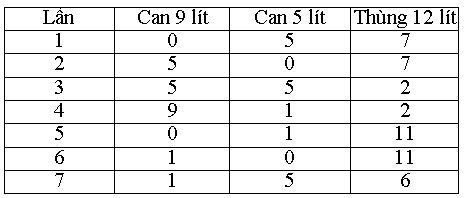
    Bài 3. Có 1 thùng đựng 12 lít dầu hoả. Bằng một can 9 lít và một can 5 lít làm thế nào để lấy ra được 6 lít dầu từ thùng đó?

    phương pháp suy luận đơn giản

    Hướng dẫn.

    phương pháp suy luận đơn giản

    Bài 4. Ở 1 xã X có 2 làng: Dân làng A chuyên nói thật, còn dân làng B chuyên nói dối. Dân 2 làng thường qua lại thăm nhau. Một chàng thanh niên nọ về thăm bạn ở làng A. Vừa bước vào xã X, dang ngơ ngác chưa biết đây là làng nào, chàng thanh niên gặp ngay một cô gái và anh ta hỏi người này một câu. Sau khi nghe trả lời chàng thanh niên bèn quay ra (vì biết chắc mình đang ở làng B) và sang tìm bạn ở làng bên cạnh.
    Bạn hãy cho biết câu hỏi đó thế nào và ccâu trả lời đó ra sao mà chàng thanh niên lại khẳng định chắc chắn như vậy

    Phân tích. Để nghe xong câu trả lời người thanh niên đó có thể khẳng định mình đang đứng trong làng A hay làng B thì anh ta phải nghĩ ra 1 câu hỏi sao cho câu trả lời của cô gái chỉ phụ thuộc vào họ đang đứng trong làng nào.

    Cụ thể hơn: cần đặt câu hỏi để cô gái trả lời là “phải”, nếu họ đang đứng trong làng A và “không phải”, nếu họ đang đứng trong làng B.

    Lời giải.  Câu hỏi của người thanh niên đó là: “Có phải chị người làng này không?”.

    • Trường hợp 1: Họ đang đứng trong làng A: Nếu cô gái là người làng A thì câu trả lời là “phải” (vì dân làng A chuyên nói thật); Nếu cô gái là người làng B thì câu trả lời cũng là “phải” (vì dân làng đó nói dối).
    • Trường hợp 2: Họ đang đứng trong làng B: Nếu cô gái là người làng A thì câu trả lời là: “không phải”; Nếu cô gái là người làng B thì câu trả lời cũng là: “không phải”.

    Như vậy, Nếu họ đang đứng trong làng A thì câu trả lời chỉ có thể là “phải”, còn nếu họ đang đứng trong làng B thì câu trả lời chỉ có thể là “không phải”. Người thanh niên quyết định quay ra, vì anh đã nghe câu trả lời là “không phải”.

    Bài 5. [Câu đố của Einstein] Vào cuối thế kỉ 19, Einstein ra câu đố này và nói rằng chỉ có nhiều nhất là 2% dân số trên thế giới giải được. Bạn có muốn vào con số ít ỏi thế không? Nếu giải được thì chỉ số IQ của bạn không dưới 140 đâu nhé.

    câu đố của einstein

    Có 5 ngôi nhà, mỗi nhà có một màu khác nhau. Trong mỗi nhà ở một người có quốc tịch khác nhau. Mỗi người chỉ thích một loại nước uống, hút thuốc một hãng và nuôi một con vật trong nhà. Cả 5 người không cùng thích một loại nước uống, hút thuốc cùng một hãng hay nuôi cùng một con vật trong nhà như người hàng xóm của mình. Câu hỏi: Ai nuôi cá?, biết rằng:

    • Người Anh ở trong nhà màu đỏ.
    • Người Thuỵ Điển nuôi chó.
    • Người Đan Mạch thích uống trà.
    • Ngôi nhà màu xanh lá cây nằm bên trái ngôi nhà màu trắng.
    • Người ở nhà màu xanh lá cây thích uống cà phê.
    • Người hút thuốc hiệu Pall Mall nuôi chim.
    • Người ở nhà màu vàng hút thuốc hiệu Dunhill.
    • Người ở nhà nằm giữa thích uống sữa.
    • Người Na-uy ở nhà đầu tiên.
    • Người hút thuốc hiệu Blends ở cạnh nhà người có nuôi mèo.
    • Người có nuôi ngựa ở cạnh nhà người hút thuốc hiệu Dunhill.
    • Người hút thuốc hiệu Blue Master thích uống bia.
    • Người Đức hút thuốc hiệu Prince.
    • Người Na-uy ở cạnh nhà màu xanh lơ.
    • Người hút thuốc hiệu Blends có người hàng xóm thích uống nước khoáng.

    Hướng dẫn. Mời các em xem lời giải tại đây Ai là người nuôi cá? Câu đố của Einstein 98% dân số thế giới không giải được!

    Bài 6. [SASMO 2015] Albert, Bernard vừa kết bạn với Cheryl và họ muốn biết ngày sinh nhật của cô. Cheryl đã đưa cho họ một danh sách với 10 ngày là: 15/5, 16/5, 19/5, 17/6, 18/6, 14/7,16/7, 14/8, 15/8 và 17/8.

    Bài toán ngày sinh nhật SASMO 2015

    Cheryl sau đó đã nói riêng với Albert về tháng và Bernard về ngày sinh của mình.

    Albert: Bài Tôi không biết sinh nhật của Cheryl là ngày nào nhưng tôi biết Bernard cũng không biết nhiều hơn.

    Bernard: Bài Lúc đầu tôi không biết sinh nhật Cheryl nhưng bây giờ thì tôi đã biết.

    Albert: Bài Bây giờ tôi cũng biết sinh nhật Cheryl là ngày nào.

    Vậy, Cheryl sinh nhật vào ngày nào?

    Hướng dẫn. Mời bạn xem lời giải tại đây Bài toán ngày sinh nhật SASMO 2015

    Bài 7. Một người nông dân phải đưa một con sói, một con dê và một bắp cải qua sông bằng một chiếc thuyền. Tuy nhiên thuyền của anh ta quá nhỏ, do đó, mỗi lần qua sông anh chỉ mang được mỗi một trong ba đồ vật trên đi cùng với anh ta. Hỏi làm thế nào anh nông dân có thể mang tất cả ba đồ vật trên qua sông, biết rằng con sói không thể để lại ở một mình với con dê, còn con dê thì không thể để ở lại một mình với bắp cải.

    Bài 8. Trong bốn đồng tiền có ba đồng tiền thật khối lượng như nhau và một đồng tiền giả có khối lượng khác. Làm thế nào để tìm được đồng tiền giả bằng hai lần cân, sử dụng cân có hai đĩa và không có quả cân.

    Hướng dẫn. Lần cân thứ nhất, đặt nên mỗi quả cân một đồng tiền…

    Bài 9. Có 16 chai rượu trong đó có một chai rượu giả, nhẹ hơn tất cả các chai còn lại. Làm thế nào chỉ ba lần cân xác định được chai nào giả?

    Hướng dẫn. Chia 16 chai rượu thành 3 nhóm: 2 nhóm 6 và 1 nhóm 4.

    Bài 10. Làm thế nào để lấy được 6 lít nước từ sông về, nếu trong tay chỉ có hai cái thùng, một thùng dung tích 4 lít, một thùng dung tích 9 lít và không thùng nào có vạch chia dung tích?

    Hướng dẫn. Kí hiệu (a,b) là trạng thái thùng 4 lít đang chứa a lít (0⩽a⩽4) và thùng 9 lít đang chứa b lít (0⩽b⩽9). Khi đó việc lấy 6 lít nước từ sông về được diễn tả qua các trạng thái sau:

    (0,0) ➡️ (0,9)➡️(4,5) ➡️ (0,5) ➡️ (4,1) ➡️ (0,1) ➡️ (1,9) ➡️(4,6)

    Bài 11. Trong một can có 16 lít xăng. Làm thế nào để chia số xăng đó thành hai phần bằng nhau, mỗi phần 8 lít, nếu chỉ dùng thêm một can 11 lít và một can 6 lít?

    Hướng dẫn. Kí hiệu (a,b,c) là trạng thái can 16 lít chứa a lít xăng, can 11 lít chứa b lít xăng và can 6 lít chứa c lít xăng.
    Việc chia 16 lít xăng thành 2 phần bằng nhau được diễn tả qua các trạng thái sau:

    (16,0,0) ➡️ (10,0,6) ➡️(10,6,0) ➡️ (4,6,6) ➡️ (4,11,1)➡️ (15,0,1)➡️ (15,1,0) ➡️
    (9,1,6) ➡️(9,7,0) ➡️(3,7,6)➡️(3,11,2) ➡️(14,0,2) ➡️(14,2,0)➡️(8,2,6)➡️(8,8,0).

    Bài 12. Mời các em xem trong bài Đề thi tốt nghiệp Tiểu học Singapore 2021

  • PHƯƠNG PHÁP LỰA CHỌN TÌNH HUỐNG

    PHƯƠNG PHÁP LỰA CHỌN TÌNH HUỐNG

    PHƯƠNG PHÁP LỰA CHỌN TÌNH HUỐNG là một trong những PHƯƠNG PHÁP BỒI DƯỠNG HỌC SINH GIỎI TOÁN TIỂU HỌC. Để giải các bài toán này, các em học sinh cần lựa chọn một trong các tình huống đề bài đưa ra và giả sử nó đúng, từ đó suy luận, xem xét các tình huống khác có hợp lí hay không.

    Thường đối với các bài toán giải bằng PHƯƠNG PHÁP LỰA CHỌN TÌNH HUỐNG, chúng ta có thể kết hợp với việc lập bảng để dễ nhìn và loại bỏ các phương án không hợp lí.

    1. Ví dụ phương pháp lựa chọn tình huống

    Ví dụ 1. Trong kì thi học sinh giỏi tỉnh có 4 bạn Phương, Dương, Hiếu, Hằng tham gia. Được hỏi quê mỗi người ở đâu ta nhận được các câu trả lời sau:
    • Phương: Dương ở Thăng Long còn tôi ở Quang Trung.
    • Dương : Tôi cũng ở Quang Trung còn Hiếu ở Thăng Long.
    • Hiếu : Không, tôi ở Phúc Thành còn Hằng ở Hiệp Hoà.
    • Hằng : Trong các câu trả lời trên đều có 1 phần đúng 1 phần sai.

    Em hãy xác định quê của mỗi bạn.

    Hướng dẫn.

    Vì trong mỗi câu trả lời đều có 1 phần đúng và 1 phần sai nên chúng ta xét câu trả lời của Phương thì có các trường hợp:

    TH1. Dương ở Thăng Long là đúng thì Phương ở Quang Trung là sai.

    • Suy ra Dương ở Quang Trung là sai. Vậy Hiếu ở Thăng Long là đúng.
    • Điều này vô lý vì Dương và Hiếu cùng ở Thăng Long.

    TH2. Dương ở Thăng Long là sai, suy ra Phương ở Quang Trung và do đó Dương ở Quang Trung là sai.

    • Suy ra Hiếu ở Thăng Long. Vậy Hiếu ở Phúc Thành là sai. Suy ra Hằng ở Hiệp Hòa.
    • Còn lại Dương ở Phúc Thành.

    Ví dụ 2. Năm bạn Anh, Bình, Cúc, Doan, An quê ở 5 tỉnh: Bắc Ninh, Hà Tây, Cần Thơ, Nghệ An, Tiền Giang. Khi được hỏi quê ở tỉnh nào, các bạn trả lời như sau:

    • Anh: Tôi quê ở Bắc Ninh còn Doan ở Nghệ An
    • Bình: Tôi cũng quê ở Bắc Ninh còn Cúc ở Tiền Giang
    • Cúc: Tôi cũng quê ở Bắc Ninh còn Doan ở Hà Tây
    • Doan: Tôi quê ở Nghệ An còn An ở Cần Thơ
    • An: Tôi quê ở Cần Thơ còn Anh ở Hà Tây

    Nếu mỗi câu trả lời đều có 1 phần đúng và 1 phhàn sai thì quê mỗi bạn ở đâu?

    Hướng dẫn.

    Vì mỗi bạn có câu trả lời có một phần đúng và một phần sai nên có các trường hợp:

    TH1. Nếu Anh ở Bắc Ninh là đúng Þ Doan không ở Nghệ An.

    • Suy ra Bình và Cúc ở Bắc Ninh là sai. Do đó Cúc ở Tiền Giang và Doan ở Hà Tây.
    • Doan ở Nghệ An là sai suy ra An ở Cần Thơ và Anh ở Hà Tây là sai.
    • Còn bạn Bình ở Nghệ An (Vì 4 bạn quê ở 4 tỉnh rồi)

    TH2. Nếu Anh ở Bắc Ninh là sai và Doan ở Nghệ An là đúng.

    • Suy ra Doan ở Hà Tây là sai, do đó Cúc ở Bắc Ninh.
    • Từ đó Bình ở Bắc Ninh phải sai. Suy ra Cúc ở Tiền Giang. Điều này vô lí vì cúc vừa ở Bắc Ninh vừa ở Tiền Giang (loại)

    Vậy Anh ở Bắc Ninh; Cúc ở Tiền Giang; Doan ở Hà Tây; An ở Cần Thơ và Bình ở Nghệ An.

    Ví dụ 3. Cúp Tiger 98 có 4 đội lọt vào vòng bán kết: Việt Nam, Singapor, Thái Lan và Inđônêxia. Trước khi vào đấu vòng bán kết ba bạn Dũng, Quang, Tuấn dự đoán như sau:

    • Dũng: Singapor nhì, còn Thái Lan ba.
    • Quang: Việt Nam nhì, còn Thái Lan tư.
    • Tuấn: Singapor nhất và Inđônêxia nhì.

    Kết quả mỗi bạm dự đoán đúng một đội và sai một đội. Hỏi mỗi đội đã đạt giải mấy?

    Hướng dẫn.

    • Nếu Singapo đạt giải nhì thì Singapo không đạt giải nhất. Vậy theo Tuấn thì Inđônêxia đạt giải nhì. Điều này vô lý, vì hai đội đều đạt giải nhì.
    • Nếu Singapo không đạt giải nhì thì theo Dũng, Thái Lan đạt giải ba. Như vậy Thái Lan không đạt giải tư. Theo Quang, Việt Nam đạt giải nhì.Thế thì Inđônêxia không đạt giải nhì. Vậy theo Tuấn, Singapor đạt giải nhất, cuối cùng còn đội Inđônê xia đạt giải tư.
    • Kết luận: Thứ tự giải của các đội trong cúp Tiger 98 là:
      • Nhất: Singapo.
      • Nhì: Việt Nam.
      • Ba: Thái Lan.
      • Tư: Inđônêxia

    Ví dụ 4. Gia đình Lan có 5 người: ông nội, bố, mẹ, Lan và em Hoàng. Sáng chủ nhật cả nhà thích đi xem xiếc nhưng chỉ mua được 2 vé. Mọi người trong gia đình đề xuất 5 ý kiến:

    1. Hoàng và Lan đi
    2. Bố và mẹ đi
    3. Ông và bố đi
    4. Mẹ và Hoàng đi
    5. Hoàng và bố đi.

    Cuối cùng mọi người đồng ý với đề nghị của Lan vì theo đề nghị đó thì mỗi đề nghị của 4 người còn lại trong gia đình đều được thoả mãn 1 phần. Bạn hãy cho biết ai đi xem xiếc hôm đó.

    Hướng dẫn. Ta có nhận xét :

    • Nếu chọn đề nghị thứ nhất thì đề nghị thứ hai bị bác bỏ hoàn toàn.  Vậy không thể chọn đề nghị thứ nhất.
    • Nếu chọn đề nghị thứ hai thì đề nghị thứ nhất bị bác bỏ hoàn toàn. Vậy không thể chọn đề nghị thứ hai.
    • Nếu chọn đề nghị thứ ba thì đề nghị thứ tư bị bác bỏ hoàn toàn. Vậy không thể chọn đề nghị thứ ba.
    • Nếu chọn đề nghị thứ tư thì đề nghị thứ ba bị bác bỏ hoàn toàn. Vậy không thể chọn đề nghị thứ tư.
    • Nếu chọn đề nghị thứ năm thì cả 4 đề nghị trên đều thoả mãn một phần và bác bỏ một phần. Vậy sáng hôm đó Hoàng và bố đi xem xiếc.

    Ví dụ 5. Lớp 5A có năm bạn đạt học sinh giỏi nhung chỉ được cử hai bạn đi dự Đại hội cháu ngoan Bác Hồ. Khi cô giáo hỏi ý kiến thì các bạn đều nhường nhau. Cô đề nghị mỗi em giới thiệu hai trong số 5 bạn đạt học sinh giỏi để đi dự Đại hội. Kết quả, các bạn giới thiệu như sau:

    1. Bạn Hùng và bạn Dũng
    2. Bạn Cường và bạn Mạnh
    3. Bạn Cường và bạn Thịnh
    4. Bạn Hùng và bạn Thịnh
    5. Bạn Hùng và bạn Cường

    Cô quyết định chọn đề nghị của bạn Thịnh vì theo đề nghị đó thì mỗi đề nghị của bốn người còn lại đều thoả mãn một phần và bác bỏ một phần.

    Em hãy cho biết bạn nào đã đi dự Đại hội Cháu ngoan Bác Hồ?

    2. Bài tập phương pháp lựa chọn tình huống

    Bài 1: Trong 1 cuộc chạy thi 4 bạn An, Bình, Cường, Dũng đạt 4 giải: nhất, nhì, ba, tư. Khi được hỏi: Bạn Dũng đạt giải mấy thì 4 bạn trả lời:

    • An: Tôi nhì, Bình nhất.
    • Bình: Tôi cũng nhì, Dũng ba.
    • Cường: Tôi mới nhì, Dũng tư.
    • Dũng: 3 bạn nói có 1 ý đúng 1 ý sai.

    Em cho biết mỗi bạn đạt mấy?

    Bài 2: Tổ toán của 1 trường phổ thông trung họccó 5 người: Thầy Hùng, thầy Quân, cô Vân, cô Hạnh và cô Cúc. Kỳ nghỉ hè cả tổ được 2 phiếu đi nghỉ mát. Mọi người đều nhường nhau, thày hiệu trưởng đề nghị mỗi người đề xuất 1 ý kiến. Kết quả như sau:

    1. Thày Hùng và thày Quân đi.
    2. Thày Hùng và cô Vân đi
    3. Thày Quân và cô Hạnh đi.
    4. Cô Cúc và cô Hạnh đi.
    5. Thày Hùng và cô Hạnh đi.

    Cuối cùng thày hiệu trưởng quyết định chọn đề nghị của cô Cúc, vì theo đề nghị đó thì mỗi đề nghị đều thoả mãn 1 phần và bác bỏ 1 phần. Bạn hãy cho biết ai đã đi nghỉ mát trong kỳ nghỉ hè đó?

    Bài 3: Ba bạn Quân, Hùng và Mạnh vừa đạt giải nhất, nhì và ba trong kỳ thi toán quốc tế. Biết rằng:

    1. Không có học sinh trường chuyên nào đạt giải cao hơn Quân.
    2. Nếu Quân đạt giải thấp hơn một bạn nào đó thì Quân không phải là học sinh trường chuyên.
    3. Chỉ có đúng 1 bạn không phải là học sinh trường chuyên
    4. Nếu Hùng và Mạnh đạt giải nhì thì mạnh đạt giải cao hơn bạn quê ở Hải Phòng.

    Bạn hãy cho biết mỗi bạn đã đạt giải nào? bạn nào không học trường chuyên và bạn nào quê ở Hải Phòng.

    Bài 4: Thày Nghiêm được nhà trường cử đưa 4 học sinh Lê, Huy, Hoàng, Tiến đi thi đấu điền kinh. Kết quả có 3 em đạt giải nhất, nhì, ba và 1 em không đạt giải. Khi về trường mọi người hỏi kết quả các em trả lời như sau:

    • Lê: Mình đạt giải nhì hoăc ba.
    • Huy: Mình đạt giải nhất.
    • Hoàng: Mình đạt giải nhất.
    • Tiến: Mình không đạt giải.

    Nghe xong thày Nghiêm mỉm cười và nói: “Chỉ có 3 bạn nói thật, còn 1 bạn đã nói đùa”. Bạn hãy cho biết học sinh nào đã nói đùa, ai đạt giải nhất và ai không đạt giải.

    Bài 5: Cúp Euro 96 có 4 đội lọt vào vòng bán kết: Đức, Cộng hoà Séc, Anh và Pháp. Trước khi thi đấu 3 bạn Hùng, Trung vàĐức dự đoán như sau:

    • Hùng: Đức nhất và Pháp nhì
    • Trung: Đức nhì và Anh ba
    • Đức: Cộng hoà Séc nhì và Anh tư.

    Kết quả mỗi bạn dự đoán một đội đúng, một đội sai. Hỏi mỗi đội đã đạt giải mấy?

    Bài 6. Trong Hội khoẻ Phù Đổng, đội tuyển của bốn trường tiểu học: Hoà Bình, Nguyễn Du, Hoàng Diệu và Điện Biên lọt vào vòng bán kết thi đấu cầu. Trước khi vào đấu vòng bán kết, ba bạn Nam, Bình và Quân dự đoán như sau:

    • Nam: Hoà Bình giải nhì còn Nguyễn Du giải ba
    • Bình: Hoàng Diệu giải nhì còn Nguễn Du giải tư
    • Quân: Hoà Bình giải Nhất còn Điện Biên giải nhì

    Kết quả mỗi bạn đoán đúng một đội và sai một đội. Hỏi mỗi trường đã đạt giải mấy?

    Bài 7. Năm cô giáo Nga, Dung, Cúc, Hồng và Anh dạy năm khối 1, 2, 3, 4 và 5. Khi được hỏi các cô dạy lớp mấy thì các cô trả lời như sau:

    • Cô Nga: Tôi dạy khối 1 còn cô Hòng dạy khối 4
    • Cô Dung: Tôi cũng dạy khối 1 còn cô Cúc dạy khối 5
    • Cô Cúc: Tôi cũng dạy khối 1 còn cô Hòng dạy khối 2
    • Cô Hồng: Tôi dạy khối 4 còn cô Anh dạy khối 3
    • Cô Anh: Tôi dạy khối 3 còn cô Nga dạy khối 2

    Nếu không ai trả lời sai hoàn toàn thì mỗi cô dạy lớp mấy?

    Bài 8. Các bạn Cháu ngoan Bác Hồ của trường tiểu học Kim Liên đi tham quan danh lam thắng cảnh của thủ đô Hà Nội. Buổi trưa cả đoàn rẽ vào quán ăn trưa. Thực đơn của quán có tám món; Thịt lợn kho, lạc rang, trứng rán, đậu sốt, rau luộc, cá rán, dưa chua và canh măng. Toàn đoàn thống nhất sẽ gọi 3 món trong thực đơn của bữa ăn. Nguyện vọng của các bạn chia thành 5 nhóm như sau:

    • Nhóm 1: Thịt kho, lạc rang và trứng rán
    • Nhóm 2: Đậu sốt, rau luộc và cá rán
    • Nhóm 3: Rau luộc, cá rán và dưa chua
    • Nhóm 4: Lạc rang, dưa chua và canh măng
    • Nhóm 5. Thịt lợn kho, rau luộc và canh măng

    Cuối cùng các bạn nhất trí với thực đơn của liên đội trưởng, và theo thực đơn đó, mỗi nhóm đều có ít nhất một món mà mình ưa thích.
    Hỏi toàn đoàn hôm đó đã chọn những món ăn nào?

    Bài 9. Trong đại hội cháu ngoan Bác Hồ, bốn bạn Tâm, Đào, Nghĩa và Thảo là học sinh của bốn quận trong thủ đô Hà Nội. Khi hỏi các bạn là học sinh của quận nào thì bạn Cúc nhận được câu trả lời như sau:

    • Tâm: Đào ở quận Hoàn Kiếm, còn mình ở Đống Đa
    • Đào: Mình ở Đống Đa, còn Nghĩa ở Hoàn Kiếm
    • Nghĩa: Mình ở Hai Bà, còn Thảo ở Ba Đình
    • Thảo xưa nay vốn là người thật thà khong thích nói đùa nên nói với Cúc: “Trong câu trả lời của mỗi bạn đều có một phần đúng và một phần sai”

    Hỏi mỗi bạn ở Quận nào?

    Bài 10. Gia đình Hoa có 6 người: ông, bà, bố, m, Hoa và em Đào. Ngày chủ nhật gia đình dự định đi xem xiếc nhưng chỉ mua được ba vé. Mọi người trong gia đình đề xuất 5 ý kiến:

    1. Ông, bố và em Đào đi
    2. Bố, mẹ và Hoa đi
    3. Bà, mẹ và Hoa đi
    4. Ông, bà và em Đào đi
    5. Bà, mẹ vè em Đào đi

    Cuối cùng mọi người đồng ý với đề nghị của ông vì theo đề nghị đó thì mỗi đề nghị còn lại không có đề nghị nào bị bác bỏ hoàn toàn.
    Hỏi gia đình Hoa hôm đó có những ai đi xem xiếc?

    Bài 11. Thầy Minh được trường cử đưa bốn học sinh Lê, Huy, Hoàng và Tiến đi thi đấu điền kinh. Kết quả có ba em đạt giải nhất, nhì, ba và một bạn không đạt giải. Khi về trường mọi người hỏi kết quả, các em trả lời như sau:

    • Lê: Mình đạt giả nhì hoặc ba
    • Huy: Mình đã đạt giải
    • Hoàng: Mình đạt giải nhất
    • Tiến: Mình không đạt giải
    • Nghe xong thầy Minh mỉm cười:”Chí có ba bạn nói thật, còn một bạn nói đùa”.

    Bạn hãy cho biết ai nói đùa, ai đạt giải nhất và ai không đạt giải?

    Bài 12. Bốn bạn Lan, Hà, Đức và Vân được nhà trường của di thi bốn môn: bóng bàn, cờ vua, đá cầu và nhảy cao tại Hội khoẻ Phù Đổng. Khi được hỏi mỗi bạn thi đấu môn gì, các bạn trả lời như sau:

    • Lan: Mình thi đấu đá cầu hoặc đấu cờ vua
    • Hà: Mình không thi nhảy cao
    • Đức: Mình thi đấu bóng bàn
    • Văn: Mình thi nhảy cao

    Nếu chỉ có ba bạn trả lời đúng, còn một bạn trả lời sai thì hai bạn Hà và Văn đã tham gia thi đấu môn gì?

  • Giải toán Tiểu học bằng phương pháp thử chọn

    Giải toán Tiểu học bằng phương pháp thử chọn

    Phương pháp thử chọn là gì?

    Phương pháp thử chọn chính là thử và chọn. Có những bài toán chúng ta không thể tìm ra được một phương án duy nhất, mà từ một giả thiết nào đó ta chỉ suy luận ra được nhiều khả năng có thể đúng. Lúc đó chúng ta sẽ lần lượt thay các phương án này vào những giả thiết còn lại để kiểm tra và chọn ra đáp án phù hợp.

    Phương pháp thử chọn có thể dùng để giải các bài toán về cấu tạo số tự nhiên, cấu tạo số thập phân, cấu tạo phân số và cả các bài toán có văn về hình học, toán về chuyển động đều, toán tính tuổi…

    Ví dụ 1. Biết rằng hiệu giữa chữ số hàng chục và hàng đơn vị của một số lẻ có hai chữ số bằng 3. Nếu thêm vào số đó 3 đơn vị ta được số có hai chữ số giống nhau. Tìm số đó.

    Hướng dẫn. Gọi số cần tìm là \(\overline{ab}\)

    Những số lẻ mà hiệu giữa hai chữ số của nó bằng 3 là: 25; 41; 47; 63; 69; 85.

    Ta lập bảng như sau:
    \(\overline{ab}\) \(\overline{ab}+3\) Kết luận
    25 28 loại
    41 44 chọn
    47 50 loại
    63 66 chọn
    69 72 loại
    85 88 chọn

    Vậy số cần tìm là 41; 63 và 85.

    Ví dụ 2. Chữ số hàng chục của một số tự nhiên có ba chữ số khác nhau gấp 2 lần chữ số hàng đơn vi. Nếu lấy tích của chữ số hàng chục và hàng đơn vị chia cho chữ số hàng trăm được thương bằng 8. Tìm số đó.

    Hướng dẫn.

    Gọi số cần tìm là \(\overline{abc}\). Theo đề bài, số \(\overline{abc}\) chỉ có thể ở những dạng \(\overline{a21}\), \(\overline{a42}\), \(\overline{a63}\) hoặc \(\overline{a84}\).

    Ta lập bảng sau để kiểm tra:

    \(\overline{abc}\) \((b\times c) : 8\) Kết luận
    a21 2*1 : 8 Loại
    a42 4*2 : 8 = 1 Chọn
    a63 6*3 : 8 Loại
    a84 8*4 : 8 = 4 Loại

    Vậy số cần tìm là 142.

    Ví dụ 3: Tìm một số tự nhiên có bốn chữ số, biết rằng tổng các chữ số của số đó bằng 18, tích các chữ số của nó bằng 64 và nếu viết các chữ số của số đó theo thứ tự ngược lại thì số đó không thay đổi.

    Hướng dẫn.

    Theo đề bài thì số cần tìm có dạng \(\overline{abba}\).

    Tổng của hai chữ số \(a\) và \(b\) là: $$18 : 2 = 9$$ Số 9 có thể phân tích thành tổng của những cặp số sau:

    • 0 và 9;
    • 1 và 8;
    • 2 và 7;
    • 3 và 6;
    • 4 và 5.

    Số cần tìm có thể là: 9009; 1881; 8118; 7227; 2772; 6336; 3663; 4554; 5445.

    Ta lập bảng sau để kiểm tra:

    abba a*b*b*a Kết Luận
    9009 9*0*0*9 = 0 Loại
    1881 1*8*8*1 = 64 Chọn
    8118 8*1*1*8 = 64 Chọn
    7227 7*2*2*7 = 196 Loại
    2772 2*7*7*2 = 196 Loại
    6336 6*3*3*6 = 324 Loại
    3663 3*6*6*3 = 324 Loại
    4554 4*5*5*4 = 400 Loại
    5445 5*4*4*5 = 400 Loại

    Vậy số cần tìm là 1881 hoặc 8118.

    BÀI TẬP PHƯƠNG PHÁP THỬ CHỌN

    Bài 1: Biết rằng hiệu giữa chữ số hàng chục và hàng đơn vị của một số lẻ có 2 chữ số bằng 3. Nếu thêm vào số đó 3 đơn vị ta được số có 2 chữ số giống nhau. Tìm số đó.

    Bài 2: Chữ số hàng chục của một số tự nhiên có 3 chữ số khác nhau gấp 2 lần chữ số hàng đơn vị. Nếu lấy tích của chữ số hàng chục và hàng đơn vị chia cho chữ số hàng trăm ta được thương bằng 8. Tìm số đó.

    Bài 3: Tìm số tự nhiên có 4 chữ số, biết rằng tổng các chữ số của số đó bằng 18, tích các chữ số của nó bằng 64 và nếu viết các chữ số của số đó theo thứ tự ngược lại thì số đó không thay đổi.

    Bài 4: Tìm số có 4 chữ số, biết rằng số đó cộng với số có hai chữ số tạo bởi chữ số hàng nghìn, hàng trăm và số có 2 chữ số tạo bởi chữ số hàng chục và hàng đơn vị của số đó ta được tổng là 7968.

    Bài 5: Các chữ số hàng nghìn hàng trăm , hàng chục và hàng đơn vị của một số tự nhiên có 4 chữ số theo thứ tự là 4 số tự nhiên liên tiếp. Số này sẽ thay đổi như thế nào nếu ta viết các chữ số của nó theo thứ tự ngược lại?

    Bài 6: Các chữ số hàng nghìn hàng trăm, hàng chục và hàng đơn vị của một số tự nhiên có 4 chữ số theo thứ tự là 4 số lẻ liên tiếp. Số này sẽ thay đổi như thế nào nếu ta viết các chữ số của nó theo thứ tự ngược lại?

    Bài 7: Tìm số tự nhiên có 2 chữ số, biết rằng tích các chữ số của số đó là số tròn chục có hai chữ số, nếu bớt số đó đi 3 đơn vị ta được số có 2 chữ số giống nhau.

    Bài 8: Các chữ số hàng trăm, hàng chục và hàng đơn vị của một số tự nhiên có 3 chữ số theo thứ tự là 3 số lẻ liên tiếp. Khi bớt số đó đi 24 đơn vị ta được số có 3 chữ số giống nhau và chia hết cho 5. Tìm số đó.

    Bài 9: Các chữ số hàng trăm, hàng chục và hàng đơn vị của một số chẵn có 3 chữ số theo thứ tự là 3 số tự nhiên liên tiếp. Tổng các chữ số của nó bằng 9. Tìm số đó.

    Bài 10: Tổng các chữ số của một số chẵn có 4 chữ số bằng 22, tích các chữ số của nó là số tròn chục. Khi đổi chỗ chữ số hàng trăm và chữ số hàng đơn vị hoặc chữ số hàng nghìn và chữ số hàng chục thì số đó không thay đổi. Tìm số đó.