Tag: toán 11

Chuyên đề thiết diện trong hình học không gian
Chuyên đề thiết diện trong hình học không gian

Thầy cô tải file PDF chuyên đề thiết diện ở cuối bài viết.

Xem thêm: Thiết diện là gì và các phương pháp tìm thiết diện

Bài toán xác định thiết diện của một hình chóp, một hình lăng trụ khi cắt bởi một mặt phẳng gắn liền với các cách xác định một mặt phẳng trong không gian.

Ở bài này, chúng tôi xin giới thiệu 3 loại toán xác định thiết diện của một hình không gian cắt bởi mặt phẳng $\left( \alpha \right)$ trong các trường hợp sau:

1. Mặt phẳng $\left( \alpha \right)$ xác định bởi ba điểm phân biệt không thẳng hàng.

Đối với loại toán này, chúng tôi giới thiệu 2 phương pháp để xác định thiết diện là phương pháp giao tuyến gốc và phương pháp phép chiếu xuyên tâm.

1.1. Phương pháp giao tuyến gốc (Trace method)
- Xác định giao tuyến $d$ của mặt phẳng $\left( \alpha \right)$ với một mặt ${\cal H}$ của hình chóp, hình lăng trụ (thường là với mặt đáy).
- Tìm các giao điểm của giao tuyến $d$ với các cạnh, đường chéo của mặt ${\cal H}$.
- Các giao điểm này thuộc mặt đáy nhưng cũng thuộc vào các mặt bên của hình ${\cal H}$. Từ các giao điểm này, chúng ta sẽ xác định được giao tuyến của $\left( \alpha \right)$ và các mặt còn lại của hình chóp. Từ đó dựng được thiết diện.
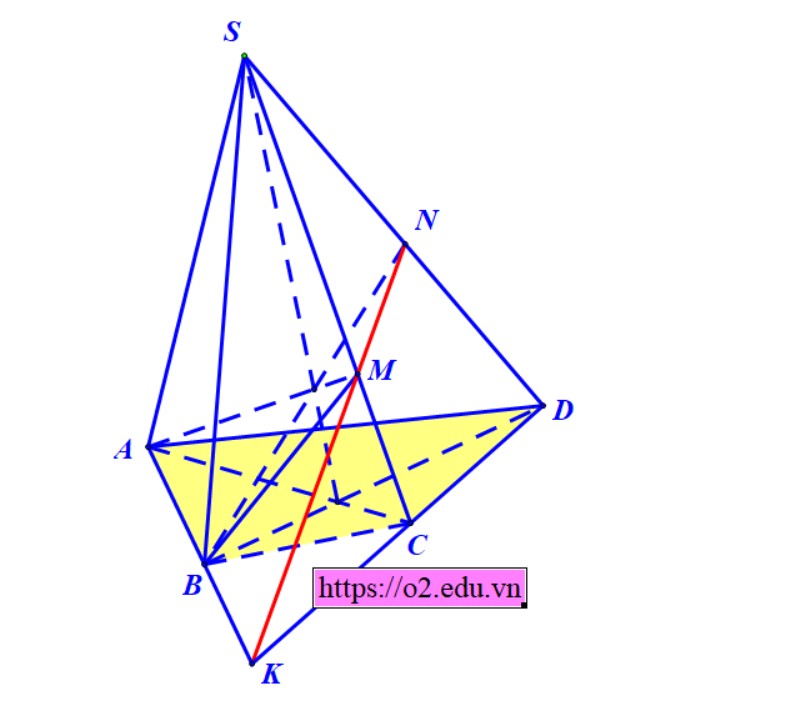
Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy không là hình thang. Giả sử $M$ là một điểm trên $SD$, xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {ABM} \right)$.

Hướng dẫn.
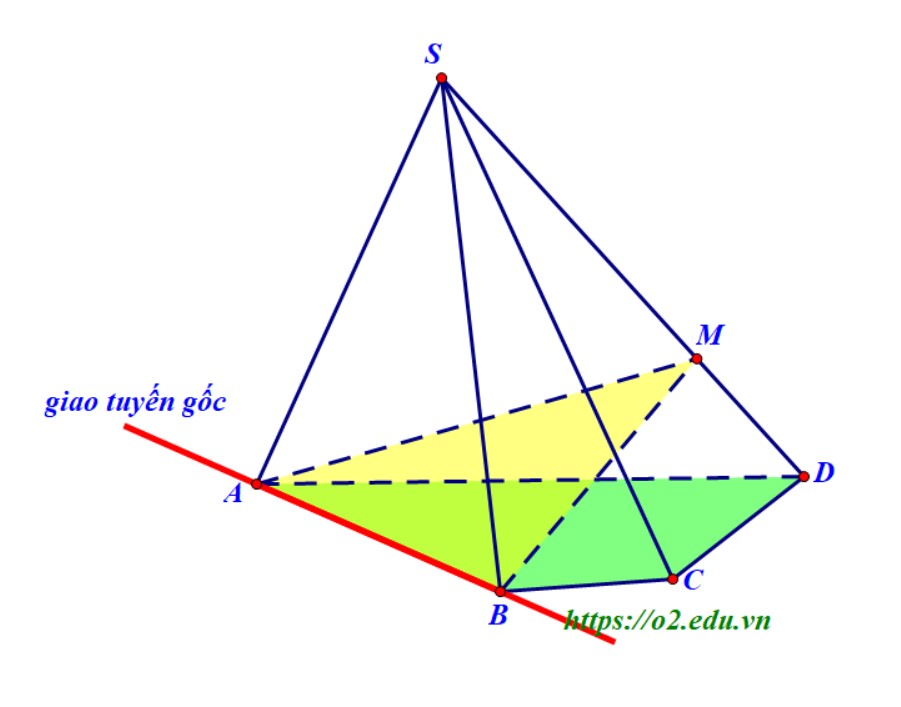
- Rõ ràng rằng giao tuyến của mặt phẳng $\left( {ABM} \right)$ với mặt đáy $\left( {ABCD} \right)$ là đường thẳng $AB$, nên chúng ta lựa chọn đường thẳng $AB$ làm giao tuyến gốc.
- Tiếp theo, ta xác định các giao điểm của đường thẳng $AB$ với các cạnh của đáy, nếu không được thì sẽ sử dụng đến giao điểm với đường chéo. Vì tứ giác $ABCD$ không là hình thang nên kéo dài hai đường thẳng $AB$ và $CD$ thì chúng sẽ cắt nhau, giả sử là điểm $I$.
- Lúc này, đường thẳng $IM$ nằm trong mặt phẳng $\left( {SCD} \right)$ nên nó sẽ cắt được đường thẳng $SC$, giả sử cắt tại điểm $N$.
- Thấy ngay, mặt phẳng $\left( {ABM} \right)$ lần lượt cắt các mặt của hình chóp $S.ABCD$ theo các giao tuyến tạo thành một tứ giác là $AMNB$ nên thiết diện chính là tứ giác $AMNB$.
Ví dụ 2. Cho tứ diện $ABCD$ có $M,N$ là trung điểm của $AB,CD$. Giả sử $P$ là một điểm nằm trên cạnh $AD$ nhưng không là trung điểm. Xác định thiết diện của mặt phẳng $\left( {MNP} \right)$ và tứ diện?

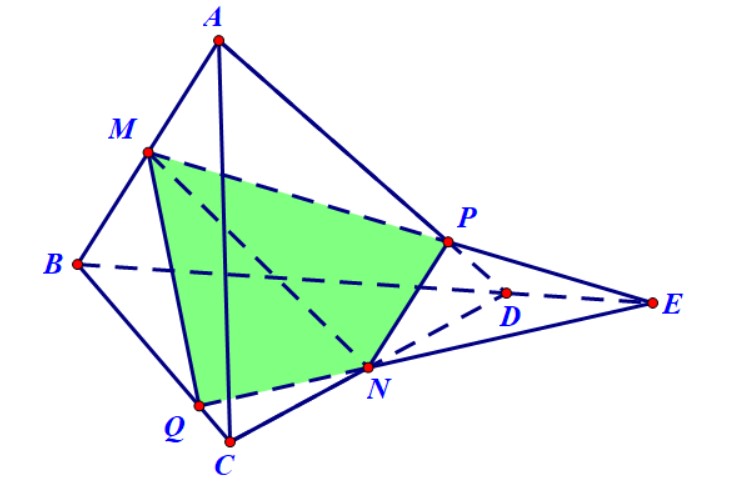
Hướng dẫn. Chúng ta lựa chọn $MP$ là giao tuyến gốc. Trong mặt phẳng $\left( {ABD} \right),\;$kéo dài $MP$ cắt $BD$ tại $E$. Trong mặt phẳng $\left( {BCD} \right)$, nối $EN$ cắt $BC$ tại $Q$. Thiết diện là tứ giác $MPNQ$.

Ví dụ 3. Cho hình chóp $S.ABCD$ có điểm $M$ là trung điểm $SC,N$ là một điểm trên cạnh $SD$ sao cho $SN < DN$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {AMN} \right)$.

Hướng dẫn. Chúng ta lựa chọn $MN$ làm giao tuyến gốc. Trong mặt phẳng $\left( {SCD} \right)$, kéo dài $MN$ cắt $CD$ tại $P$. Trong mặt phẳng $\left( {ABCD} \right)$, nối $AP$ cắt $BC$ tại $Q$, tùy thuộc vào vị trí điểm $Q$ nằm trong hay ngoài đoạn $BC$ mà ta được thiết diện là như trong 2 hình vẽ sau đây.

Ví dụ 4. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M,N,P$ lần lượt là trung điểm của $BC,CD$ và $SA$. Xác định thiết diện của hình chóp và mặt phẳng $\left( {MNP} \right)$.

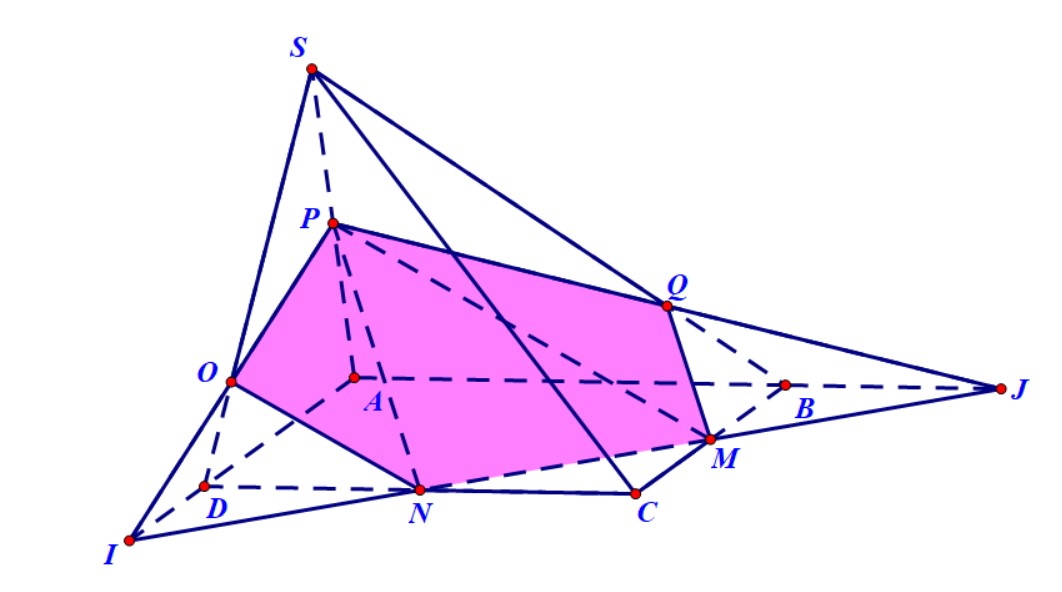
Hướng dẫn. Chúng ta chọn $MN$ làm giao tuyến gốc. Trong mặt phẳng $\left( {ABCD} \right)$, kéo dài $MN$ cắt $AB,AD$ lần lượt tại $J,I$. Trong mặt phẳng $\left( {SAD} \right)$, gọi giao điểm của $PI$ và $SD$ là $O.$ Trong mặt phẳng $\left( {SAB} \right)$, gọi $Q$ là giao điểm của $PJ$ và $SB$. Thiết diện là ngũ giác $MNOPQ$.

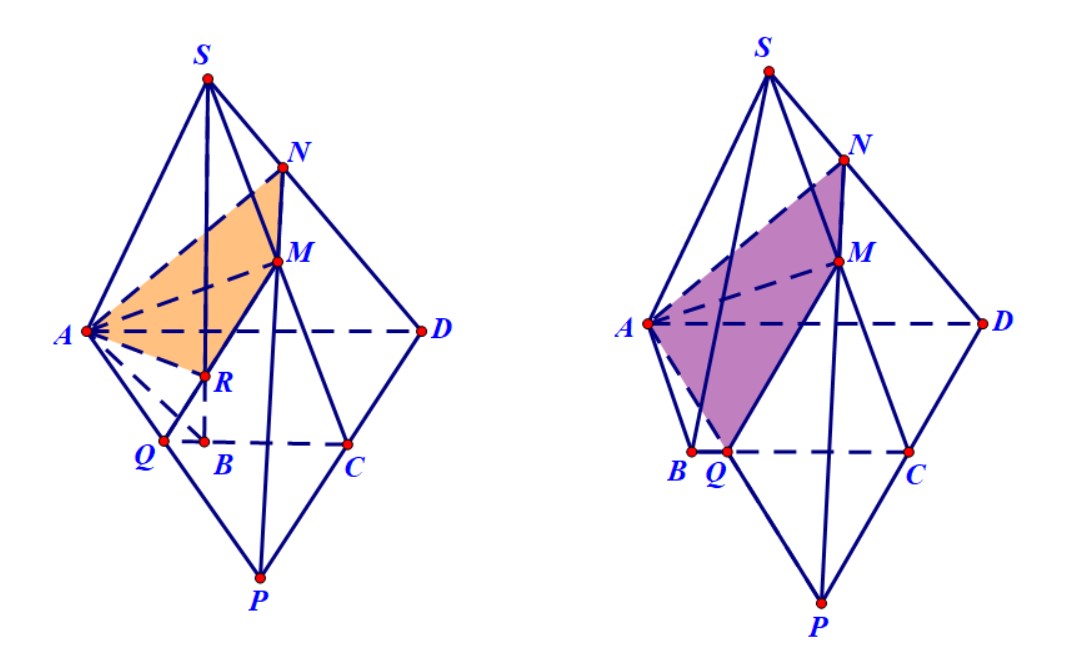
Ví dụ 5. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $M,N,P$ lần lượt là trung điểm của $CD,BC$ và $SB$. Xác định thiết diện của hình chóp và mặt phẳng $\left( {MNP} \right)$.

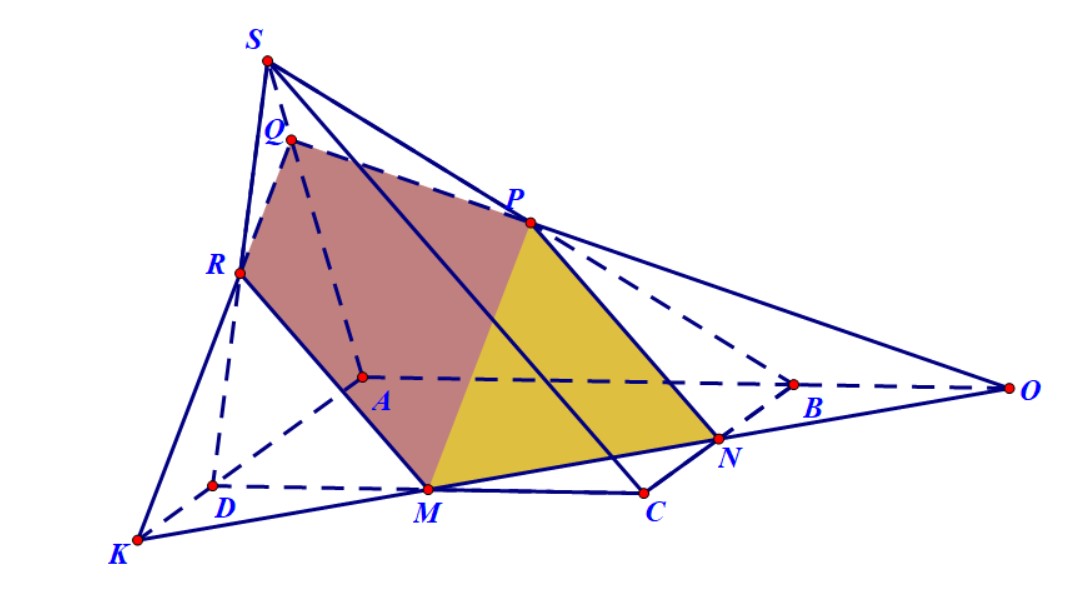
Hướng dẫn. Trong mặt phẳng $\left( {ABCD} \right)$ gọi $O,K$ lần lượt là giao điểm của $MN$ với $AB$ và $AD$. Trong mặt phẳng $\left( {SAB} \right)$ gọi $Q$ là giao điểm của $SA$ và $PO$. Trong mặt phẳng $\left( {SAD} \right)$ gọi $R$ là giao điểm của $QK$ và $SD$. Thiết diện là ngũ giác $MNPQR$.

Ví dụ 6. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$. Gọi $M,N$ lần lượt là trung điểm của $BC,CD$. Trên đoạn $SO$ lấy điểm $P$ sao cho $SP > OP$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {MNP} \right)$.

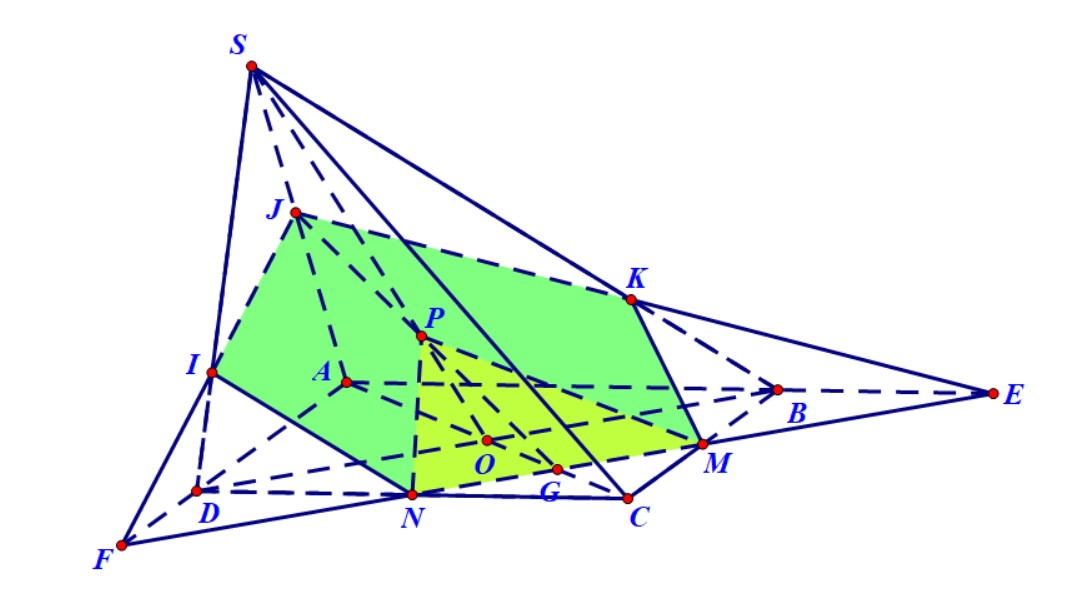
Hướng dẫn. Trong mặt phẳng $\left( {ABCD} \right)$ gọi $E,F,G$ lần lượt là giao điểm của $MN$ với $AB,AD,AC$. Trong mặt phẳng $\left( {SAC} \right)$ gọi $J = \;GP \cap SA$, trong $\left( {SAB} \right)$ gọi $K = JE \cap SB$, trong $\left( {SAD} \right)$ gọi$\;I = JF \cap SD$. Thiết diện là ngũ giác $MNIJK$.

Ví dụ 7. Cho tứ diện $ABCD$ có $M$ là trung điểm của $AB$ và $G$ là trọng tâm tam giác $ACD.\;N$ là một điểm bất kì thuộc đoạn $BC$. Xác định thiết diện của tứ diện khi cắt bởi mặt phẳng $\left( {MNG} \right).$

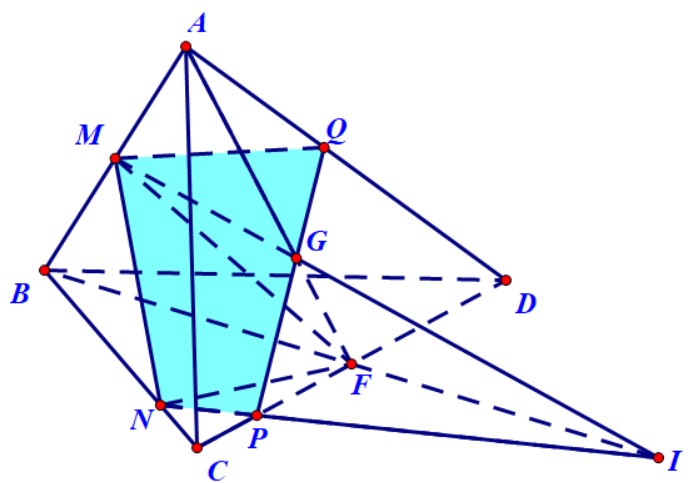
Hướng dẫn. Tình huống này học sinh dễ ngộ nhận $MN$ cắt $AC,\;$điều này chưa chắc xảy ra vì nếu $N$ ở vị trí trung điểm $BC$ thì khi đó $MN$ và $AC$ song song với nhau.

Chúng ta có thể sử dụng phương pháp phép chiếu xuyên tâm hoặc chọn giao tuyến gốc như sau:
- Trong mặt phẳng $(ACD$), kéo dài $AG$ cắt $CD$ tại $F$.
- Trong mặt phẳng $\left( {ABF} \right)$ gọi $I$ là giao điểm của $MG$ và $BF$, hai đường thẳng này chắc chắn cắt nhau vì $\frac{{AM}}{{AB}} = \frac{1}{2} \ne \frac{{AG}}{{AF}} = \frac{1}{3}$. Giao tuyến gốc ở đây chính là đường thẳng $NI$.
- Trong mặt phẳng $\left( {BCD} \right)$ gọi $P$ là giao điểm của $CD$ và $NI$.
- Thiết diện là tứ giác $MNPQ$.
1.2. Phương pháp phép chiếu xuyên tâm (Inner Projection Method).

Phép chiếu xuyên tâm (còn được gọi là phép phối cảnh, tiếng Anh: inner projection) được giới thiệu ngay từ lớp 8, trong chương trình công nghệ – vẽ kỹ thuật.

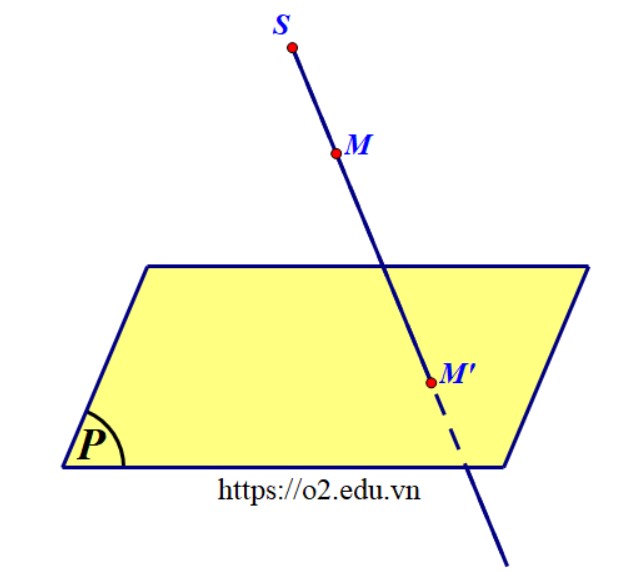
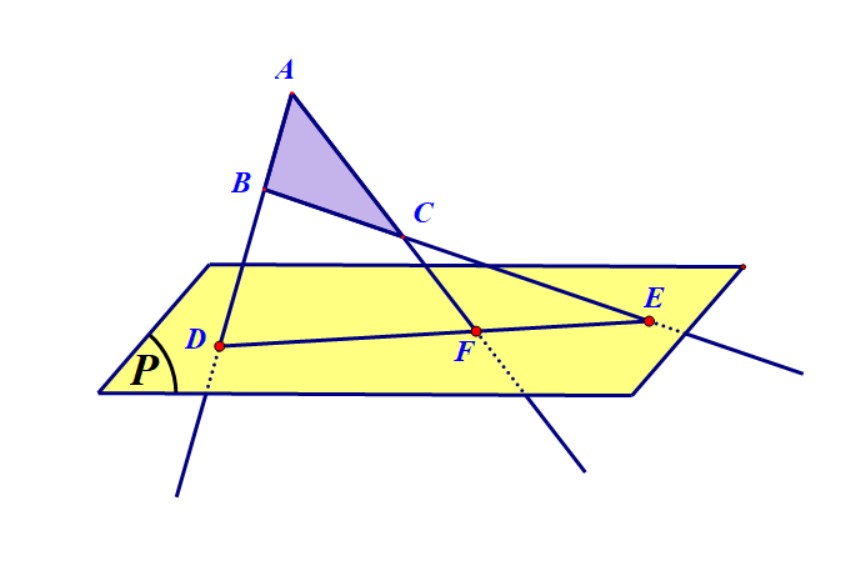
Trong không gian, cho một điểm $S$ và một mặt phẳng $\left( P \right)$ không đi qua $S$. Quy tắc biến mỗi điểm $M$ trong không gian thành điểm là giao điểm của mặt phẳng $\left( P \right)$ và đường thẳng $SM$ được gọi là phép chiếu xuyên tâm (tâm $S$) xuống mặt phẳng $\left( P \right)$.

Phương pháp phép chiếu xuyên tâm còn được gọi là phương pháp đường gióng.
- Chọn một tam giác trên mặt phẳng $\left( \alpha \right)$ làm tam giác cơ sở và xác định hình chiếu của nó lên mặt đáy qua phép chiếu xuyên tâm với tâm là đỉnh của hình chóp.
- Xác định các giao điểm của tam giác hình chiếu với các cạnh, đường chéo của đáy.
- Dựa vào quan hệ liên thuộc, tìm các điểm trên mặt phẳng $\left( \alpha \right)$ tương ứng với các điểm ở dưới mặt đáy.
Ví dụ 1. Cho hình chóp $S.ABCD$ có $C’$ là một điểm trên cạnh $SC$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {ABC’} \right)$ trong trường hợp:
1. $AB$ không song song với $CD$;
2. $AB$ song song với $CD$.
Hướng dẫn. Rõ ràng phần 1 học sinh có thể làm bằng phương pháp giao tuyến gốc. Tuy nhiên sang phần 2 học sinh sẽ không thể giải được theo phương pháp đó mà phải sử dụng phương pháp phép chiếu xuyên tâm.
- Chọn tam giác $ABC’$ làm tam giác cơ sở. Qua phép chiếu xuyên tâm $S$ lên mặt phẳng $(ABCD$) thì tam giác cơ sở biến thành tam giác $ABC$. Chúng ta sẽ lần lượt đi tìm giao điểm của các cạnh tam giác này với các cạnh và đường chéo của đáy.
- Trong mặt phẳng $\left( {ABCD} \right)$ gọi $O$ là giao điểm của $AC$ và $BD$. Nhận thấy rằng điểm $O$ thuộc tam giác $ABC$ thì sẽ có một điểm $O’$ tương ứng thuộc tam giác cơ sở $ABC’$ mà qua phép chiếu sinh ra điểm $O$ này. Nhiệm vụ của chúng ta là tìm ra điểm $O’$ đó.
- Trong mặt phẳng $\left( {SAC} \right)$ thấy ngay $O’$ là giao điểm của $SO$ và $AC’$.
- Cuối cùng, trong mặt phẳng $\left( {SBD} \right)$ gọi $D’$ là giao điểm của $BO’$ và $SD$. Thiết diện là tứ giác $ABC’D’.$
Ví dụ 2. Cho hình chóp $S.ABCD$ có ba điểm $M,N,P$ lần lượt thuộc $SA,SB,SC$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {MNP} \right)$.

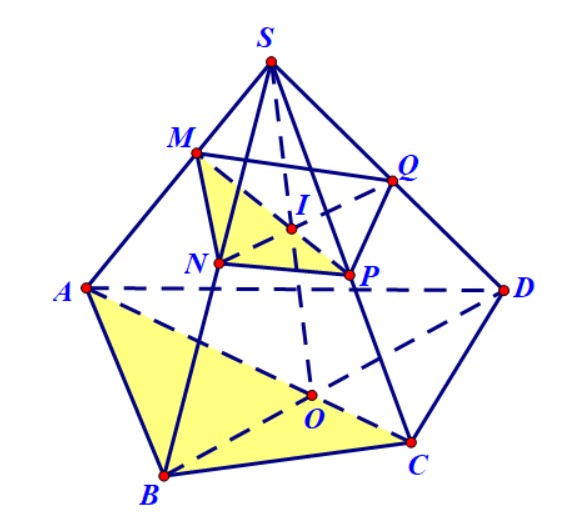
Hướng dẫn. Chọn tam giác $MNP$ làm tam giác cơ sở. Chiếu lên đáy được tam giác $ABC$. Cạnh $AC$ của tam giác hình chiếu này cắt đường chéo $BD$ của đáy tại $O$. Trong mặt phẳng $\left( {SAC} \right)$ gọi $I$ là giao điểm của $SO$ và $MN$. Trong mặt phẳng $\left( {SBD} \right)$ gọi $Q$ là giao điểm của $NI$ và $SD$. Thiết diện là tứ giác $MNPQ.$

Ví dụ 3. [Ví dụ 7 ở phần 1.1.] Cho tứ diện $ABCD$ có $M$ là trung điểm của $AB$ và $G$ là trọng tâm tam giác $ACD.\;N$ là một điểm bất kì thuộc đoạn $BC$. Xác định thiết diện của tứ diện khi cắt bởi mặt phẳng $\left( {MNG} \right).$

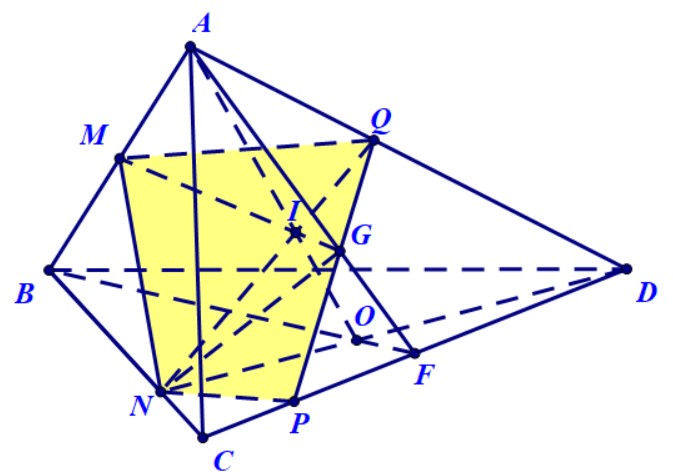
Hướng dẫn.
- Chọn tam giác $MNG$ làm tam giác cơ sở, chiếu lên đáy được tam giác $BNF$. Cạnh $BF$ của tam giác hình chiếu này cắt $ND$ tại $O$.
- Trong mặt phẳng $\left( {ABF} \right)$, gọi giao điểm của $MG$ và $SO$ là $I$.
- Trong mặt phẳng $\left( {AND} \right)$, đường thẳng $NI$ cắt $AD$ tại $Q.$
- Trong mặt phẳng $\left( {ACD} \right)$, đường thẳng $QG$ cắt $CD$ tại $P$.
- Thiết diện là tứ giác $MNPQ.$
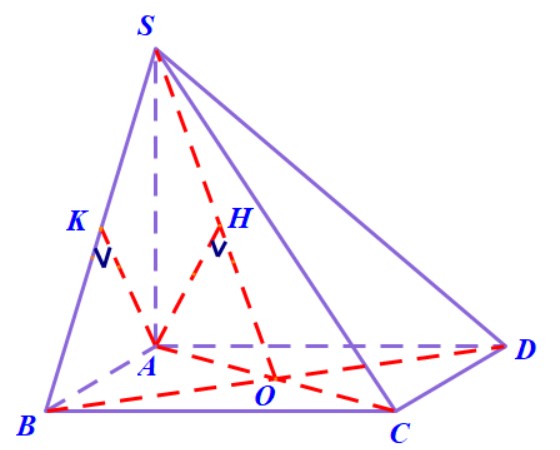
Ví dụ 4. Cho hình chóp $S.ABCD$ có $M$ là một điểm thuộc miền trong tam giác $SCD$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( {ABM} \right)$.

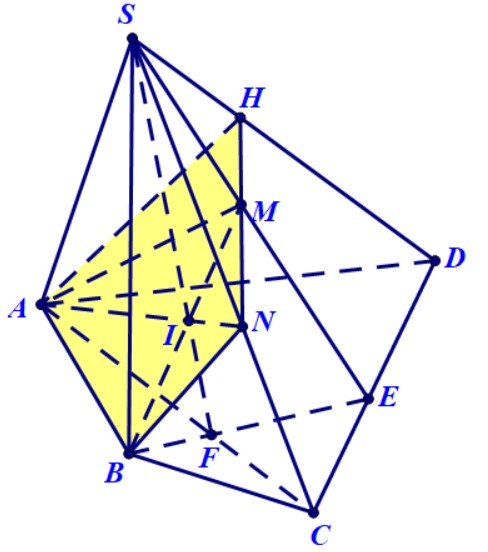
Hướng dẫn. Trong mặt phẳng $\left( {SCD} \right)$ gọi $E = SM \cap CD$, trong mặt phẳng $\left( {ABCD} \right)$ gọi $F = AC \cap BE$, trong mặt phẳng $\left( {SBE} \right)$ gọi$\;I = BM \cap SF$, trong mặt phẳng $\left( {SAC} \right)$ gọi $N = AI \cap SC$, trong mặt phẳng $\left( {SCD} \right)$ gọi $H = MN \cap SD$. Thiết diện là tứ giác $ABNH$.

Ví dụ 5. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O.$ Gọi $M,N$ lần lượt là trung điểm $SA,SD$. Xác định thiết diện của hình chóp và mặt phẳng $\left( {OMN} \right).$

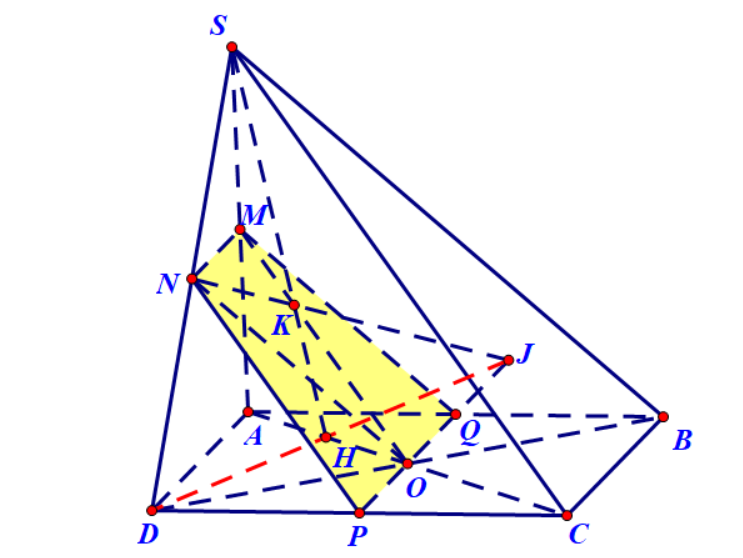
Hướng dẫn. Nếu ta chọn tam giác cơ sở là $OMN$ thì chiếu xuống mặt đáy được tam giác $OAD$. Tam giác hình chiếu này không cắt được cạnh nào của hình bình hành $ABCD$. Do đó ta pahir chọn một tam giác cơ sở khác.

Lấy điểm $K$ bất kì thuộc $MO$ và chọn $MNK$ làm tam giác cơ sở. Chiếu tam giác này lên mặt đáy được tam giác $ADH$. Kéo dài $DH$ cắt $NK$ tại $J$. Đường thẳng $OJ$ cắt $AB,CD$ tại $Q,P$. Thiết diện là tứ giác $MNPQ.$

Cách giải khác cho ví dụ này xin mời xem Ví dụ 1 ở phần 2 sau đây.

2. Mặt phẳng $\left( \alpha \right)$ đi qua một điểm và song song với hai đường thẳng

Chúng ta thường sử dụng 2 kết quả sau để dựng thiết diện.
- Nếu mặt phẳng $\left( \alpha \right){\rm{\;}}$chứa đường thẳng $d$ mà $d\parallel \left( \beta \right)$ thì giao tuyến của hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ cũng song song với đường thẳng $d$.
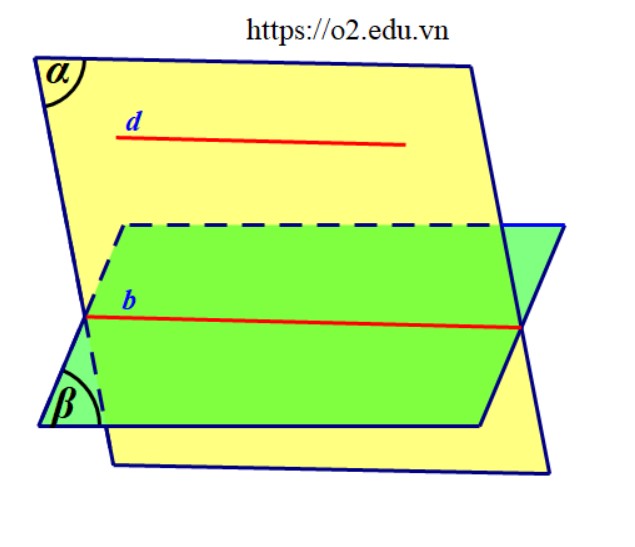
- Hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng cũng song song với đường thẳng đó.
Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $O$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( \alpha \right)$ đi qua $O$ và song song với $SB,SC.$ Thiết diện là hình gì?

Hướng dẫn.
- Qua $O$ kẻ đường thẳng song song với $SB$, nó cắt $SD$ tại $N$. $N$ là trung điểm $SD$ vì $ON$ là đường trung bình của tam giác $SBD.$
- Tương tự, qua $O$ kẻ đường thẳng song song với $SC$, nó cắt $SA$ tại trung điểm $M$.
- Mặt phẳng $\left( \alpha \right)$ chính là mặt phẳng $\left( {OMN} \right)$.
- Đường thẳng $MN$ nằm trong mặt phẳng $\left( {OMN} \right)$ và song song với $\left( {ABCD} \right)$, nên giao tuyến $d$ của hai mặt phẳng $\left( {OMN} \right)$ và $\left( {ABCD} \right)$ phải song song với đường thẳng $MN$.
- Mà giao tuyến $d$ chắc chắn phải chứa điểm $O$. Do đó, $d$ là đường thẳng đi qua $O$ và song song $MN$, tức là cũng song song với $AD$.
- Đường thẳng $d$ cắt $AB,CD\;$tại $Q,P$ thì thiết diện là hình thang $MNPQ$.
Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $\left( P \right)$ là mặt phẳng đi qua điểm $M$ thuộc đoạn $AC$ và song song với hai đường thẳng $BD,SA$. Hãy dựng thiết diện của hình chóp với mặt phẳng $\left( P \right).$

Hướng dẫn. Chúng ta phải xét hai trường hợp, điểm $M$ nằm trong đoạn $AO$ và nằm trong đoạn $OC$, với $O$ là tâm hình bình hành.

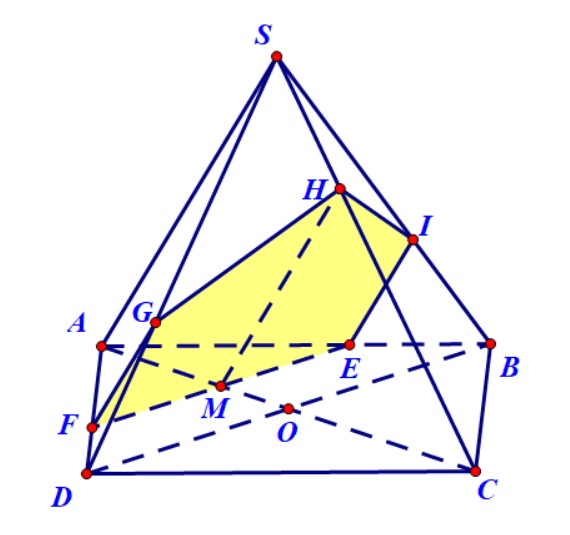
Trường hợp 1. Nếu $M$ nằm trong đoạn $AO.$
- Qua $M$ dựng đường thẳng song song với $BD$, nó cắt $AB$ ở $E$, cắt $AD$ ở $F.$
- Qua $E,M,F$ lần lượt dựng các đường thẳng song song với $SA.$ Chúng cắt $SB,SC,SD$ lần lượt tại $I,H,G$.
- Thiết diện là ngũ giác $EFGHI$.
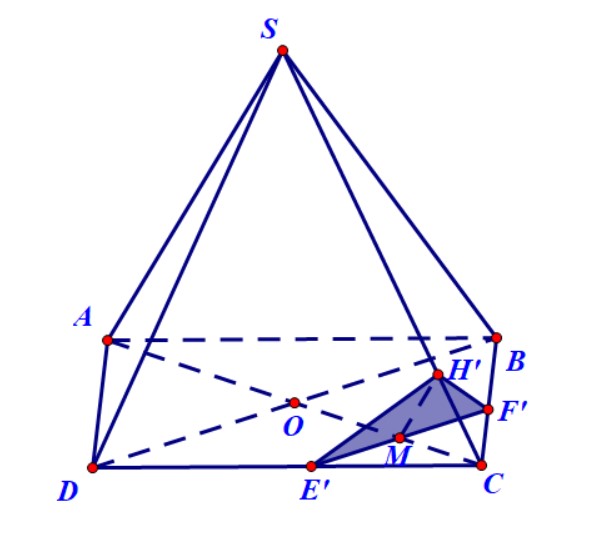
Trường hợp 2. Nếu $M$ nằm trong đoạn $OC.$
- Qua $M$ dựng đường thẳng song song với $BD$, nó cắt $DC$ ở $E’$, cắt $BC$ ở $F’.$
- Qua $M$ dựng đường thẳng song song với $SA$, nó cắt $SC$ tại $H’$.
- Thiết diện là tam giác $E’F’H’.$
Ví dụ 3. Cho tứ diện $ABCD$ có $I,J$ lần lượt là trung điểm của $AB,CD$. Gọi $M$ là một điểm trên đoạn $IJ$ và $\left( \alpha \right)$ là mặt phẳng qua $M$ đồng thời song song với $AB,CD$. Xác định thiết diện của tứ diện khi cắt bởi mặt phẳng $\left( \alpha \right)$, thiết diện là hình gì?

Hướng dẫn.
- Trong mặt phẳng $\left( {ABJ} \right),$ qua $M$ kẻ đường thẳng $d$ song song với $AB.$ Đường thẳng $d$ cắt $BJ,AJ$ lần lượt tại $E$ và $F.$
- Qua $E$ kẻ đường thẳng song song với $CD$, nó cắt $BC,BD$ tại $H$ và $K$.
- Qua $F$ kẻ đường thẳng song song với $CD$, nó cắt $AC,AD$ tại $P$ và $Q$.
- Thiết diện là hình bình hành $HKQP$.
Ví dụ 4. Cho hình chóp $S.ABCD$ có $M,\;N$ là hai điểm trên $AB,\;CD$. Gọi $\left( \alpha \right)\;$là mặt phẳng chứa $MN$ và song song với $SA$. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $\left( \alpha \right)$.

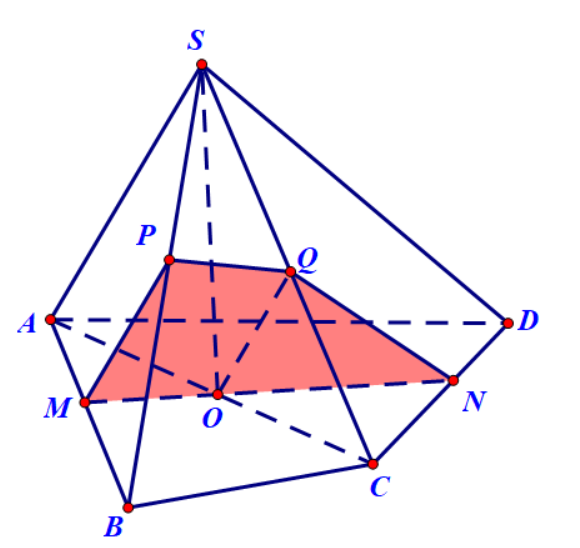
Hướng dẫn. Gọi $MN \cap AC = O$. Qua $M,O$ các kẻ đường thẳng song song với $SA,$ chúng cắt $SB,SC$ lần lượt tại $P,Q$. Thiết diện là tứ giác $MNQP$.

3. Mặt phẳng $\left( \alpha \right)$ đi qua một điểm và vuông góc với một đường thẳng

Chúng ta chuyển quan hệ vuông góc sang quan hệ song song nhờ định lý:

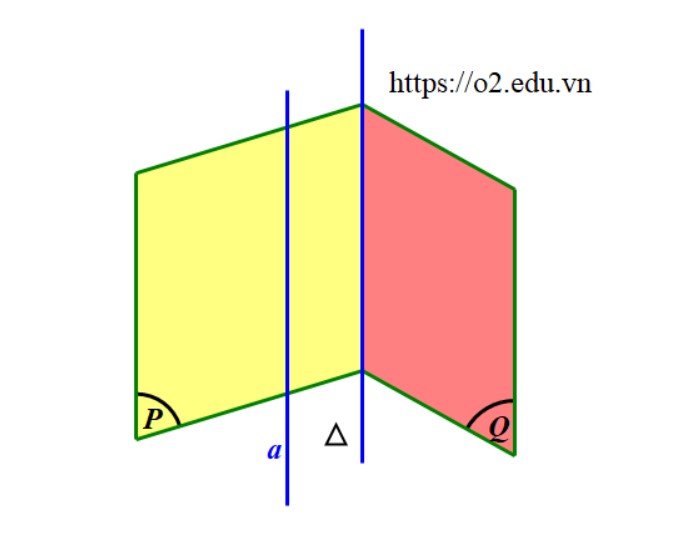
Cho đường thẳng $d$ vuông góc với mặt phẳng $\left( P \right)$ thì mọi đường thẳng $\Delta $ vuông góc với $d$ đều song song hoặc nằm trong mặt phẳng $\left( P \right).$

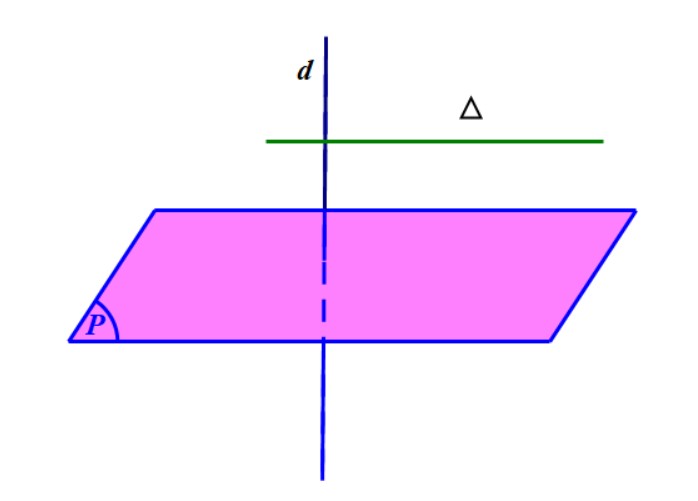
Trường hợp mặt phẳng $\left( \alpha \right)$ chứa đường thẳng $a$ và vuông góc với mặt phẳng $\left( P \right)$ thì chúng ta tìm một đường thẳng $b$ vuông góc với mặt phẳng $\left( P \right).\;$Khi đó, mặt phẳng $\left( \alpha \right)$ sẽ song song hoặc chứa đường thẳng $b$.

Ví dụ 1. Cho lăng trụ đứng $ABC.A’B’C’$ có đáy là tam giác nhọn$.$ Mặt phẳng $\left( P \right)$ đi qua $A$ và vuông góc với $A’C$. Biết rằng $CC’ > AC,$ hãy dựng thiết diện của lăng trụ khi cắt bởi mặt phẳng $\left( P \right)$.

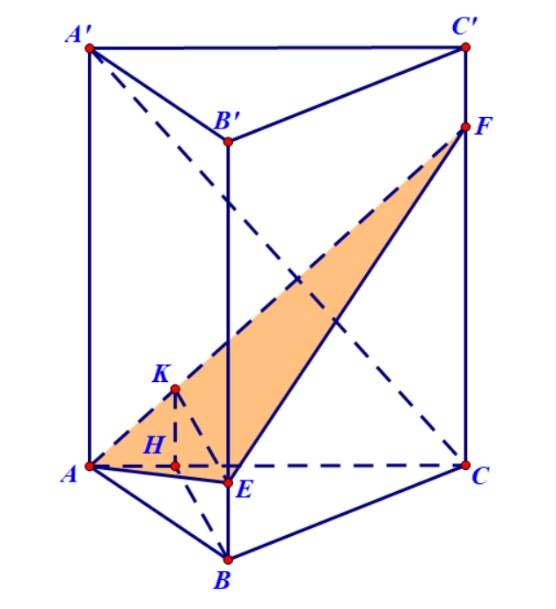
Hướng dẫn.
- Kẻ đường cao $BH$ của tam giác $ABC$ thì dễ thấy $BH$ vuông góc với $\left( {ACC’A’} \right).$ Do đó $BH$ vuông góc với $CA’$. Mà $\left( P \right)$ cũng vuông góc với $CA’$ nên suy ra $BH$ song song hoặc nằm trong $\left( P \right)$. Dễ thấy khả năng $BH$ nằm trong mặt phẳng $\left( P \right)$ không xảy ra, vì khi đó $AH$ vuông góc với $A’C$, đây là điều vô lý.
- Trong mặt phẳng $\left( {ACC’A’} \right)$ kẻ đường thẳng vuông góc với $A’C$, đường thẳng này cắt $CC’$ tại $F$. Điểm $F$ nằm trong đoạn $CC’$, vì $CC’ > AC.$
- Qua $H$ kẻ đường thẳng song song với $AA’,$ nó cắt $AF$ tại $K$. Từ $K$ kẻ đường thẳng song song với $BH,$ đường thẳng này cắt $BB’$ tại $E.$
- Thiết diện cần tìm là tam giác $AEF.$
Ví dụ 2. Cho lăng trụ đứng $ABC.A’B’C’$ có đáy là tam giác nhọn$.$ Mặt phẳng $\left( P \right)$ đi qua $B$ và vuông góc với $A’C$. Biết rằng $CC’ > AC,$ hãy dựng thiết diện của lăng trụ khi cắt bởi mặt phẳng $\left( P \right)$.

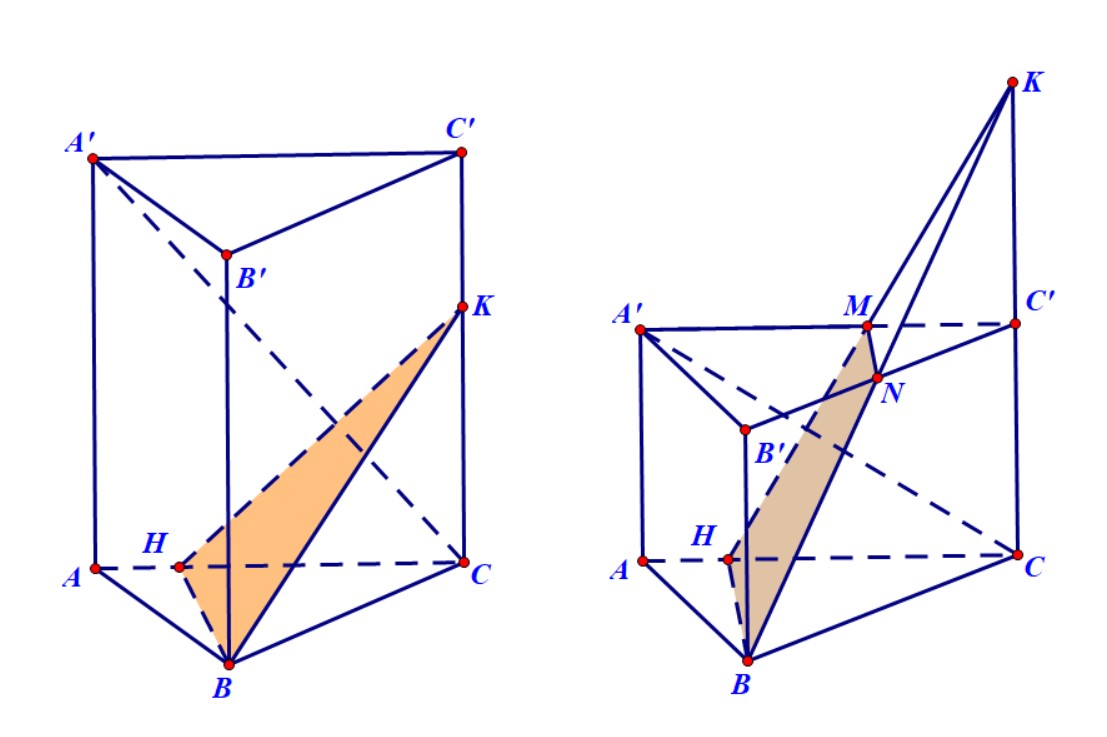
Hướng dẫn. Kẻ đường cao $BH$ của tam giác $ABC$ thì dễ thấy $BH$ vuông góc với $\left( {ACC’A’} \right).$ Do đó $BH$ vuông góc với $CA’$. Mà $\left( P \right)$ chứa $B$ và vuông góc với $CA’$ nên suy ra $BH$ nằm trong mặt phẳng $\left( P \right)$.

Qua $H$, kẻ đường thẳng $d$ vuông góc với $A’C$. Lúc này có 2 trường hợp có thể xảy ra:
- Đường thẳng $d$ cắt $CC’$ tại $K$ nằm trong đoạn $CC’$ thì thiết diện là tam giác $BHK$.
- Đường thẳng $d$ cắt $CC’$ tại $K$ nằm ngoài đoạn $CC’$ và cắt cạnh $A’C’$ tại $M$. Nối $BK$ cắt $B’C’$ tại $N$. Thiết diện là hình thang $BHMN.$
Ví dụ 3. Hình chóp $S.ABCD$ có đáy là hình vuông, cạnh $SA$ vuông góc với đáy $\left( {ABCD} \right).$ Gọi $\left( P \right)$ là mặt phẳng đi qua $A$ và vuông góc với $SC$. Xác định thiết diện của hình chóp và mặt phẳng $\left( P \right).$

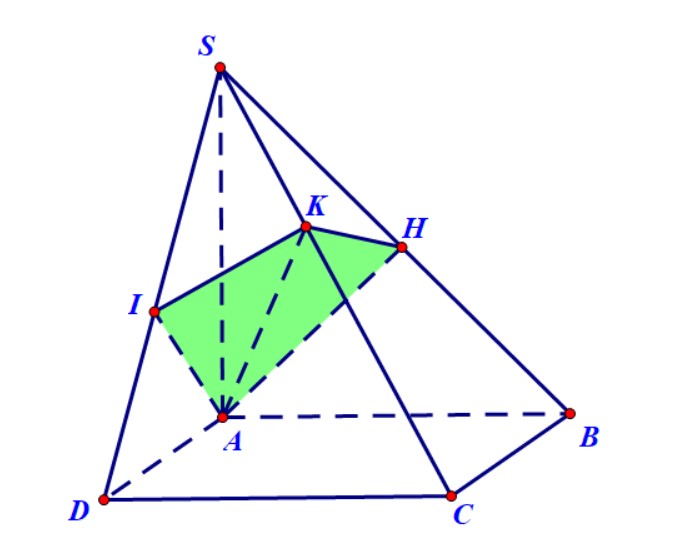
Hướng dẫn.
- Gọi $H,K,I$ lần lượt là hình chiếu vuông góc của $A$ lên các cạnh $SB,SC,SD$.
- Ta có $AK$ vuông góc với $SC$ mà mặt phẳng $\left( P \right)$ chứa $A$ và vuông góc với $SC$ nên suy ra $AK$ nằm trong mặt phẳng $\left( P \right)$.
- Chứng minh được $AH$ vuông góc với $\left( {SBC} \right)$ nên suy ra $AH \bot SC$. Mà $\left( P \right) \bot SC$, nên suy ra $AH$ cũng nằm trong mặt phẳng $\left( P \right)$.
- Chứng minh tương tự có $AI$ cũng nằm trong mặt phẳng $\left( P \right)$.
- Thiết diện là tứ giác $AHKI.$
Ví dụ 4. Hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, cạnh $SA = a\sqrt 2 $ và vuông góc với đáy. Dựng đường cao $AH$ của tam giác $SAB$. Chứng minh tỉ số $\frac{{SH}}{{SB}} = \frac{2}{3}$. Gọi $\left( P \right)$ là mặt phẳng qua $A$ và vuông góc với $SB$. Mặt phẳng $\left( P \right)$ cắt hình chóp theo thiết diện là hình gì? Tính diện tích thiết diện.

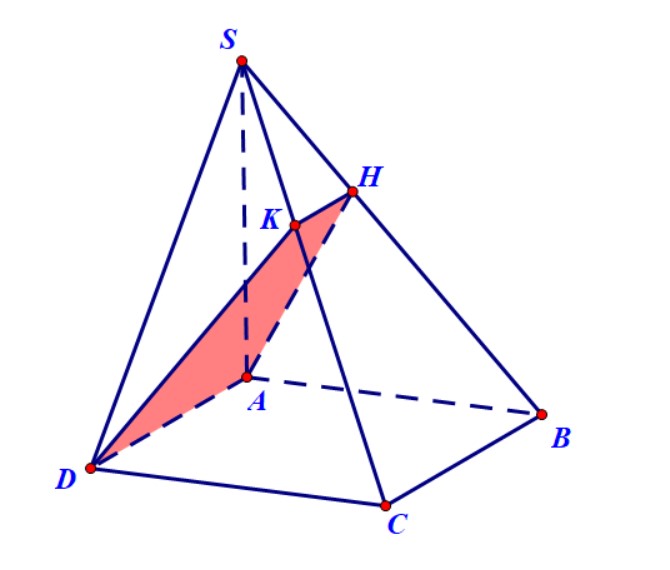
Hướng dẫn.
- Chứng minh được $CB$ vuông góc với $\left( {SAB} \right)$ nên suy ra $CB$ vuông góc với $SB$.
- Mà $\left( P \right)$ vuông góc với $SB$ nên suy ra $CB$ song song với $\left( P \right),CB$ không thể nằm trong mặt phẳng $\left( P \right)$ vì khi đó $A,B,C,D$ đồng phẳng.
- Qua $H$ kẻ đường thẳng song song với $CB$, nó cắt $SC$ tại $K.$
- Thiết diện là hình thang $AHKD,$ diện tích bằng $\frac{{5{a^2}\sqrt 6 }}{{18}}$.
Ví dụ 5. Hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $B$ với $AB = BC = a,\;AD = 2a$. Cạnh $SA = 2a$ và vuông góc với đáy $\left( {ABCD} \right).$ Gọi $M$ là một điểm trên cạnh $AB$ sao cho $AM = x$ với$\;0\; < \;x\; < \;a$. Giả sử mặt phẳng $\left( P \right)$ là mặt phẳng qua $M$ đồng thời vuông góc với $AB$. Xác định thiết diện của hình chóp với mặt phẳng $\left( P \right)$, thiết diện là hình gì? Tính diện tích thiết diện theo $a$ và $x$.

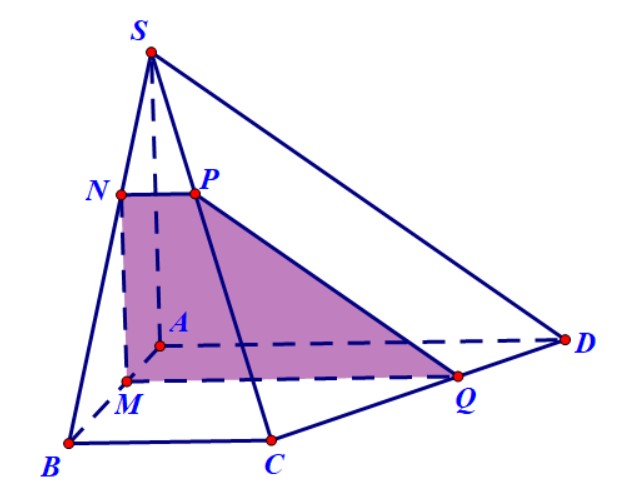
Hướng dẫn. Vì $\left( P \right)$ và $SA$ cùng vuông góc với $AB$ nên suy ra $SA$ song song với $\left( P \right).$ Qua $M$ kẻ các đường thẳng song song với $SA,AD$, chúng cắt $SB,CD$ lần lượt tại $M$ và $Q$. Qua $N$ kẻ đường thẳng song song với $AD,$ nó cắt $SC$ tại $P$.

Thiết diện là hình thang vuông $MNPQ$ có diện tích bằng $2a\left( {a – x} \right)$.

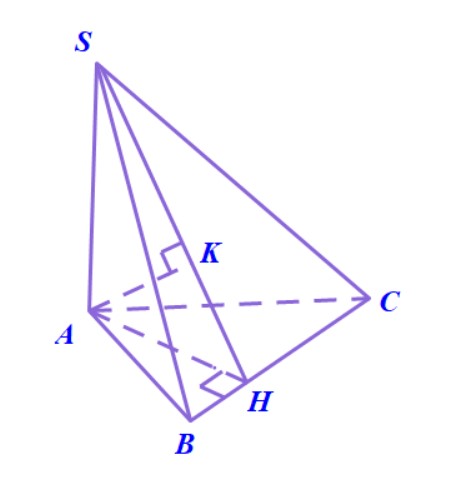
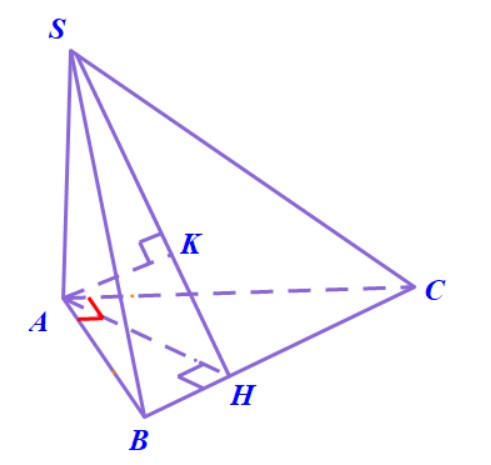
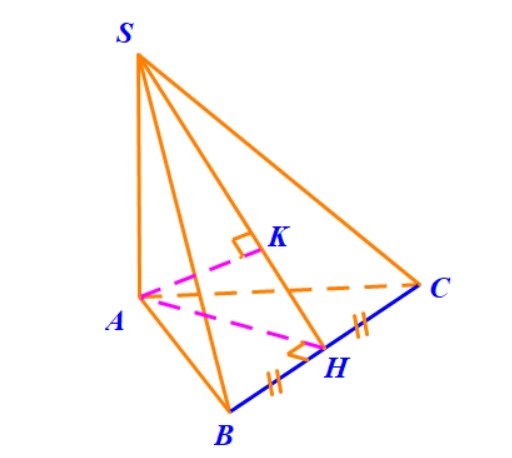
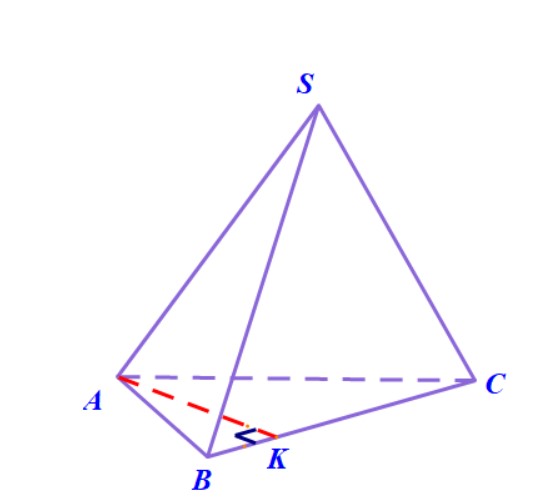
Ví dụ 6. Hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a$. Cạnh $SA = 2a$ và vuông góc với đáy. Mặt phẳng $\left( P \right)$ qua $B$ và vuông góc với $SC$. Tìm thiết diện của hình chóp với mặt phẳng $\left( P \right)$ và tính diện tích của thiết diện này.

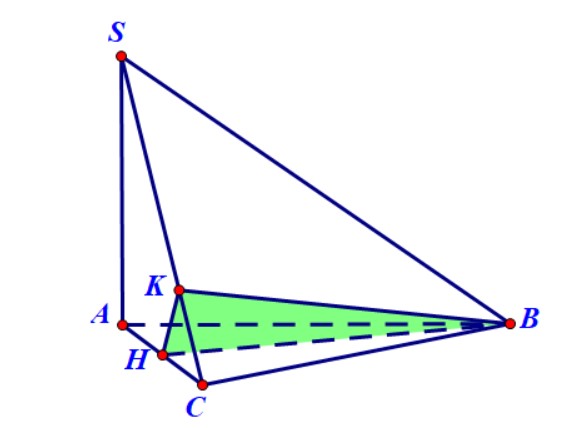
Hướng dẫn.
- Gọi $H$ là trung điểm $AC$ thì vì tam giác $ABC$ đều nên có $BH \bot AC$. Mà $BH \bot SA$ nên suy ra $BH \bot \left( {SAC} \right).$
- Suy ra $BH \bot SC$, tức là $BH$ nằm trong mặt phẳng $\left( P \right).$
- Qua $H$ kẻ đường thẳng vuông góc với $SC,$ nó cắt $SC$ tại $K$.
- Thiết diện cần tìm là tam giác $BHK$ vuông tại $H$. Dễ dàng có $BH = \frac{{a\sqrt 3 }}{2}$. Từ tam giác đồng dạng $SAC$ và $HKC$ tính được $HK$ và suy ra diện tích tam giác $BHK$ bằng $\frac{{{a^2}\sqrt {15} }}{{20}}$.
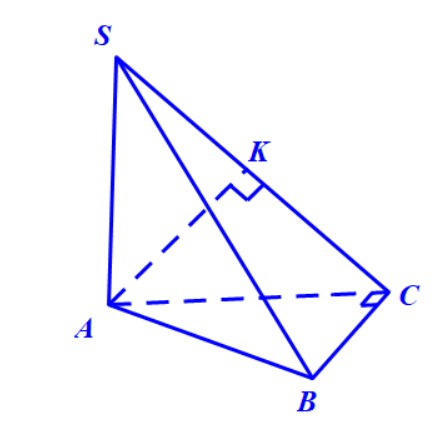
Ví dụ 7. Hình chóp $S.ABC$ có đáy là tam giác vuông cân tại $B$, cạnh $AB = a$. Cạnh $SA = a\sqrt 3 $ và vuông góc với đáy. Lấy $M$ là một điểm tuỳ ý trên cạnh $AB$, đặt $AM\; = \;x$ với $0\; < \;x\; < \;a.$ Gọi $\left( P \right)$ là mặt phẳng qua $M$ và vuông góc với $AB$. Xác định thiết diện của hình chóp và mặt phẳng$\;\left( P \right)$. Tính diện tích của thiết diện đó theo $a$ và $x$, tìm $x$ để diện tích thiết diện có giá trị lớn nhất.

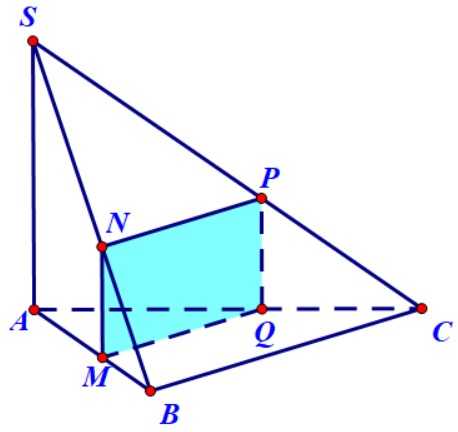
Hướng dẫn.
- Mặt phẳng $\left( P \right)$ chính là mặt phẳng đi qua $M$ và song song với $SA,BC$.
- Qua $M$ kẻ các đường thẳng song song với $SA,BC$, chúng cắt $SB,AC$ lần lượt tại $N,Q$.
- Qua $N$ kẻ đường thẳng song song với $BC$, nó cắt $SC$ tại $P$.
- Thiết diện là hình chữ nhật $MNPQ$ nên diện tích được tính bởi công thức $$s = MN \times MP$$
- Vì $MN\parallel SA$ nên có $\frac{{MN}}{{SA}} = \frac{{MB}}{{AB}}$ từ đó tính được $MN = \sqrt 3 \left( {a – x} \right)$. Làm tương tự, cũng tính được $MP = x$ và suy ra diện tích thiết diện là $s = \sqrt 3 x\left( {a – x} \right)$. Sử dụng bất đẳng thức Cauchy, chúng ta có $$\sqrt {x\left( {a – x} \right)} \le \frac{{x + a – x}}{2} = \frac{a}{2}\;$$
- Từ đó suy ra diện tích lớn nhất là $\frac{{{a^2}\sqrt 3 }}{4}$ đạt được khi $x = \frac{a}{2}$.
Link tải Chuyên đề thiết diện

Quý thầy cô tải tại đây chuyen_de_thiet_dien
28/12/2020
Phương pháp tìm thiết diện bằng phép chiếu xuyên tâm
Phương pháp tìm thiết diện bằng phép chiếu xuyên tâm

Khi mà học sinh chưa được học về quan hệ song song trong không gian thì bài toán xác định thiết diện của hình chóp khi cắt bởi một mặt phẳng khá hạn chế. Lúc đó, để giải quyết các bài toán mà đáy là hình bình hành, hình thoi, hình chữ nhật… chúng ta phải sử dụng đến phương pháp phép chiếu xuyên tâm (còn được gọi là Phương pháp đường gióng – đường dóng).

Xem thêm:
- Thiết diện là gì và các phương pháp tìm thiết diện
- Xác định thiết diện sử dụng quan hệ vuông góc trong không gian
1. Phép chiếu xuyên tâm là gì?

Phép chiếu xuyên tâm (còn được gọi là phép phối cảnh, tiếng Anh: inner projection) được giới thiệu ngay từ lớp 8, trong chương trình công nghệ – vẽ kỹ thuật.

Trong không gian, cho một điểm S và một mặt phẳng (P) không đi qua S. Quy tắc biến mỗi điểm M trong không gian thành điểm M’ là giao điểm của mặt phẳng (P) và đường thẳng SM được gọi là phép chiếu xuyên tâm (tâm S) xuống mặt phẳng (P).
- Trong phép chiếu này, các điểm M nằm trong mặt phẳng (Q) đi qua S và song song với (P) thì không có ảnh. Trong chương trình vẽ kỹ thuật, để cho mọi điểm trong không gian đều có ảnh, người ta bổ sung cho (P) một đường thẳng ở vô tận, coi như giao của (P) và (Q).
- Nếu ta hạn chế chỉ xét phép chiếu trên một mặt (R) nào đó trong không gian thì phép chiếu xuyên tâm nói trên gọi là phép chiếu xuyên tâm (tâm S) từ mặt (R) xuống mặt phẳng (P).
- Phép chiếu xuyên tâm bảo toàn tỉ số kép.
2. Các ví dụ xác định thiết diện bằng phép chiếu xuyên tâm

Bài toán. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $(\alpha)$.

Phương pháp phép chiếu xuyên tâm (Inner Projection Method)
- Chọn một tam giác trên mặt phẳng $(\alpha)$, gọi là tam giác cơ sở và xác định hình chiếu của tam giác cơ sở đó lên mặt đáy qua phép chiếu xuyên tâm với tâm là đỉnh của hình chóp.
- Xác định các giao điểm của tam giác hình chiếu với các cạnh, đường chéo của đáy.
- Dựa vào quan hệ liên thuộc, tìm các điểm trên mặt phẳng $(\alpha)$ tương ứng với các điểm ở dưới mặt đáy.
Ví dụ 1. Cho hình chóp $S.ABCD$ có $ C’ $ là một điểm trên cạnh $ SC. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABC’). $

Hướng dẫn.
- Rõ ràng vì đáy là một tứ giác bất kỳ, nên có nhiều khả năng kéo dài các cạnh đáy chúng sẽ không thể cắt nhau. Do đó ta không thể sử dụng phương pháp giao tuyến gốc.
- Trong mặt phẳng $(ABC’)$, ta chọn một tam giác làm tam giác cơ sở, chính là tam giác $ABC’$ luôn. Ta tìm ảnh của nó qua phép chiếu xuyên tâm $S$ lên mặt phẳng đáy, chính là tam giác $ABC$.
- Tiếp theo, ta xác định giao điểm của tam giác $ABC$ này với các cạnh và đường chéo của đáy. Ta tìm thấy $ O$ là giao điểm của $AC$ và $BD $.
  Lưu ý rằng, điểm $O$ trên mặt phẳng đáy, mà $ O$ thuộc vào cạnh $ AC$, cạnh $ AC$ lại là ảnh của cạnh $ AC’$ qua phép chiếu. Điều này chứng tỏ phải có một điểm nào đó (tạm đặt tên là $ I$), mà qua phép chiếu thì tạo thành điểm $ O$. Mục đích của ta là đi tìm điểm $ I$ này.
- Trong mặt phẳng $ (SAC) $ giao điểm của $SO$ và $AC’ $ chính là điểm $I$ nói trên. Lúc này, mặt phẳng $ (ABC,)$ xuất hiện một đường thẳng mới là đường thẳng $ BI$, mà đường thẳng này có thể cắt được $ SD.$
- Trong mặt phẳng $ (SBD) $ gọi $ D’$ là giao điểm của $BI$ và $ SD. $
- Dễ dàng chỉ ra thiết diện cần tìm là tứ giác $ ABC’D’. $
Ví dụ 2. Cho hình chóp $S.ABCD$ có ba điểm $ M,N,P $ lần lượt thuộc $ SA,SB,SC. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (MNP). $

Ví dụ 3. Cho hình chóp $S.ABCD$ có $ M $ là một điểm thuộc miền trong tam giác $ SCD. $ Tìm thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM). $

Ví dụ 4. Cho hình chóp $ S.ABCD $ có đáy là hình bình hành và $ M $ là trung điểm $ SB. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (AMD). $

Ví dụ 5. Cho hình chóp $S.ABCD$ có $ M $ là một điểm thuộc miền trong tam giác $ SCD. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM). $
Hướng dẫn.
Trong mặt phẳng $ (SCD) $ gọi $ E=SM\cap CD, $ trong mặt phẳng $ (ABCD) $ gọi $ F=AC\cap BE, $ trong mặt phẳng $ (SBE) $ gọi $ I=BM\cap SF, $ trong mặt phẳng $ (SAC) $ gọi $ N=AI\cap SC, $ trong mặt phẳng $ (SCD) $ gọi $ H=MN\cap SD. $ Thiết diện là tứ giác $ ABNH. $

3. Bài tập tìm thiết diện sử dụng phép chiếu xuyên tâm
06/11/2020
Xác định thiết diện bằng phương pháp giao tuyến gốc
Xác định thiết diện bằng phương pháp giao tuyến gốc

Để xác định thiết diện của một hình chóp khi cắt bởi một mặt phẳng, chúng ta có hai phương pháp là phương pháp xác định thiết diện bằng giao tuyến gốc và xác định thiết diện bằng phép chiếu xuyên tâm. Bài viết này xin trình bày chi tiết phương pháp giao tuyến gốc và các ví dụ vận dụng.

1. Phương pháp giao tuyến gốc là gì?

Bài toán. Xác định thiết diện của một hình chóp khi cắt bởi mặt phẳng $(\alpha)$.

Phương pháp giao tuyến gốc (Trace method).
- Xác định giao tuyến $ d $ của mặt phẳng $(\alpha)$ với một mặt $ \mathcal{H} $ của hình chóp (thường là với mặt đáy).
- Tìm các giao điểm của giao tuyến $ d $ với các cạnh, đường chéo của mặt $ \mathcal{H} $.
- Dựa vào các giao điểm này và giao tuyến $ d, $ tìm tiếp các giao tuyến của mặt phẳng $(\alpha)$ với những mặt còn lại của hình chóp.
2. Ví dụ tìm thiết diện bằng phương pháp giao tuyến gốc

Ví dụ 1. Cho hình chóp $S.ABCD$ có đáy không là hình thang. Giả sử $ M $ là một điểm trên $ SD $, xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (ABM).$

Hướng dẫn.
- Rõ ràng rằng giao tuyến của mặt phẳng $ (ABM)$ với mặt đáy $ (ABCD)$ là đường thẳng $AB$, nên chúng ta lựa chọn đường thẳng $AB$ làm giao tuyến gốc.
- Tiếp theo, ta xác định các giao điểm của đường thẳng $AB$ với các cạnh của đáy, nếu không được thì sẽ sử dụng đến giao điểm với đường chéo. Vì tứ giác $ ABCD$ không là hình thang nên kéo dài hai đường thẳng $ AB$ và $ CD$ thì chúng sẽ cắt nhau, giả sử là điểm $ I$.
- Lúc này, đường thẳng $ IM$ nằm trong mặt phẳng $ (SCD)$ nên nó sẽ cắt được đường thẳng $ SC$, giả sử cắt tại điểm $ N$.
- Rõ ràng, mặt phẳng $ (ABM)$ lần lượt cắt các mặt của hình chóp $S.ABCD$ theo các giao tuyến tạo thành một tứ giác là $ AMNB$ nên thiết diện chính là tứ giác $ AMNB.$
Ví dụ 2. Cho tứ diện $ ABCD $ có $ M,N $ là trung điểm của $ AB,CD. $ Giả sử $ P $ là một điểm nằm trên cạnh $ AD $ nhưng không là trung điểm. Xác định thiết diện của mặt phẳng $ (MNP) $ và tứ diện.

Ví dụ 3. Cho tứ diện $ ABCD $ có $ I,J $ lần lượt là trọng tâm các tam giác $ ABC $ và $ ACD. $ Trên cạnh $ AB $ lấy điểm $ K $ sao cho $ AK>BK. $ Xác định thiết diện của tứ diện khi cắt bởi mặt phẳng $ (IJK). $

Ví dụ 4. Cho hình chóp $ S.ABCD $ có điểm $ M $ là trung điểm $ SC,N $ là một điểm trên cạnh $ SD $ sao cho $ SN<DN. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ AMN $.

Ví dụ 5. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ BC,CD $ và $ SA. $ Xác định thiết diện của hình chóp và mặt phẳng $ (MNP) $.

Ví dụ 6. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ CD,BC $ và $ SB. $ Xác định thiết diện của hình chóp và mặt phẳng $ (MNP) $.

Hướng dẫn. Trong mặt phẳng $ (ABCD) $ gọi $ E,F $ lần lượt là giao điểm của $ MN $ với $ AB $ và $ AD. $ Trong mặt phẳng $ (SAB) $ gọi $ Q=PE\cap SA, $ trong mặt phẳng $ (SAD) $ gọi $ R=QF\cap SD. $ Thiết diện là ngũ giác $ MNPQR. $

Ví dụ 7. Cho hình chóp $S.ABCD$ có đáy là hình bình hành tâm $ O. $ Gọi $ M,N $ lần lượt là trung điểm của $ BC,CD. $ Trên đoạn $ SO $ lấy điểm $ P $ sao cho $ SP>OP. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (MNP)$.

Hướng dẫn. Trong mặt phẳng $ (ABCD) $ gọi $ E,F,G $ lần lượt là giao điểm của $ MN $ với $ AB,AD,AC. $ Trong mặt phẳng $ (SAC) $ gọi $ J= GP\cap SA, $ trong $ (SAB) $ gọi $ K=JE\cap SB, $ trong $ (SAD) $ gọi $ I=JF\cap SD. $ Thiết diện là ngũ giác $ MNIJK. $

Ví dụ 8. Cho hình chóp $ S.ABCD $ có $ G $ là trọng tâm tam giác $ SCD $ và $ M $ là trung điểm cạnh $ SD. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (AGM)$.

Ví dụ 9. Cho hình chóp $S.ABCD$ có $ G $ là trọng tâm tam giác $ SCD, H$ là một điểm thuộc cạnh $ SA $ sao cho $ SH>AH. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (CGH). $

Hướng dẫn. Gọi $ M $ là trung điểm $ SD,E=HM\cap AD,K=CE\cap AB. $ Thiết diện là tứ giác $ CMHK. $

Ví dụ 10. Cho hình chóp $S.ABCD$ có $ G $ là trọng tâm tam giác $ SCD, H$ là một điểm thuộc cạnh $ SA $ sao cho $ SH<AH. $ Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng $ (CGH). $

Hướng dẫn. Gọi $ M $ là trung điểm $ SD,E=HM\cap AD,F=CE\cap AB,K=HF\cap SB. $ Thiết diện là tứ giác $ CMHK. $
06/11/2020
3 cách chứng minh hai mặt phẳng song song
3 cách chứng minh hai mặt phẳng song song trong không gian

Để biết cách chứng minh hai mặt phẳng song song, chúng ta cần phải xem thế nào là hai mặt phẳng song song, và từ đó sẽ có các phương pháp chứng minh 2 mặt phẳng song song trong không gian.

1. Thế nào là hai mặt phẳng song song?

1.1. Vị trí tương đối của hai mặt phẳng.

Trong không gian, cho hai mặt phẳng $(\alpha)$ và $ (\beta) $ thì có ba khả năng về vị trí của chúng:
- Mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $ trùng nhau. Khi đó, hai mặt phẳng có vô số điểm chung.
- Mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $ cắt nhau theo giao tuyến là một đường thẳng. Khi đó, hai mặt phẳng có vô số điểm chung.
- Mặt phẳng $(\alpha)$ và mặt phẳng $ (\beta) $ song song. Khi đó, hai mặt phẳng không có điểm chung.
Từ đó, người ta định nghĩa hai mặt phẳng song song như sau:

Hai mặt phẳng gọi là song song với nhau nếu chúng không có điểm chung

1.2. Định lý về hai mặt phẳng song song
- Nếu một mặt phẳng chứa hai đường thẳng cắt nhau mà cả hai đường thẳng này song song với mặt phẳng còn lại thì hai mặt phẳng đó song song với nhau.
Xem thêm: Cách chứng minh đường thẳng song song với mặt phẳng.
- Nếu một mặt phẳng chứa hai đường thẳng cắt nhau mà hai đường thẳng này lần lượt song song với hai đường thẳng của mặt phẳng còn lại thì hai mặt phẳng đó song song với nhau.
1.3. Tính chất hai mặt phẳng song song
- Cho hai mặt phẳng song song, mọi đường thẳng nằm trên mặt phẳng thứ nhất đều song song với mặt phẳng thứ hai.
- Hai mặt phẳng cùng song song với mặt phẳng thứ ba thì song song với nhau.
- Hai mặt phẳng song song bị cắt bởi mặt phẳng thứ ba thì hai giao tuyến song song với nhau.
- Định lý Thales trong không gian: Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
1.4. Hình lăng trụ, hình chóp cụt
- Hình lăng trụ là hình gồm có hai đáy là hai đa giác bằng nhau đồng thời nằm trên hai mặt phẳng song song và các mặt bên là các hình bình hành.
- Hình lăng trụ có đáy là hình bình hành thì gọi là hình hộp. Như vậy, hình hộp là hình có tất cả các mặt đều là hình bình hành.
- Cắt hình chóp bởi một mặt phẳng song song với đáy thu được một hình chóp mới và một hình chóp cụt.
2. Cách chứng minh hai mặt phẳng song song

Phương pháp chứng minh hai mặt phẳng song song: Để chứng minh hai mặt phẳng song song chúng ta có thể sử dụng một trong ba cách:
- Chỉ ra trong mặt phẳng thứ nhất chứa hai đường thẳng cắt nhau, mà hai đường thẳng này lần lượt song song với mặt phẳng thứ hai.
- Chỉ ra trong mặt phẳng thứ nhất chứa hai đường thẳng cắt nhau, mà hai đường thẳng này lần lượt song song với hai đường thẳng của mặt phẳng thứ hai.
- Chứng minh chúng cùng song song với một mặt phẳng thứ ba.
3. Ví dụ về cách chứng minh hai mặt phẳng song song

Ví dụ 1. Cho hai hình bình hành $ ABCD $ và $ ABEF $ nằm trong hai mặt phẳng khác nhau.
1. Chứng minh rằng $ (ADF)\parallel(BCE) $;
2. Gọi $ I,J,K $ là trung điểm của các cạnh $ AB,CD,EF $. Chứng minh rằng $ (DIK)\parallel(JBE) $.
Ví dụ 2. Cho tứ diện $ ABCD $ có $ M,N,P $ lần lượt là trọng tâm của các tam giác $ ABC, ABD, ACD $. Chứng minh rằng $ (MNP)\parallel(BCD) $.

Ví dụ 3. Cho hình bình hành $ ABCD.$ Từ $ A $ và $ C $ kẻ hai tia $ Ax $ và $ Cy $ song song, cùng chiều và không nằm trong mặt phẳng $ (ABCD). $ Chứng minh mặt phẳng $ (BAx)\parallel (DCy). $

Ví dụ 4. Cho hình chóp $ S.ABCD $ với $ ABCD $ là hình bình hành. Gọi $ I $ là trung điểm của $ SD. $
1. Xác định giao điểm $K$ của $BI $ và $(SAC)$.
2. Trên $ IC $ lấy điểm $ H $ sao cho $ HC=2HI $. Chứng minh $ KH\parallel(SAD)$.
3. Gọi $ N $ là điểm trên $ SI $ sao cho $ SN=2NI $. Chứng minh $ (KHN)\parallel(SBC) $.
4. Dựng thiết diện của hình chóp với mặt phẳng $ (KHN). $
Hướng dẫn. Chỉ ra $ K $ là trọng tâm tam giác $ SBD. $

Ví dụ 5. Cho lăng trụ tam giác $ ABC.A’B’C’ $ có $ I ,K ,G $ lần lượt là trọng tâm của các tam giác $ ABC, A’B’C’ $ và $ ACC’ $. Chứng minh rằng: $ (IKG) \parallel (BB’C’C), (A’KG)\parallel(AIB’) $.

Hướng dẫn. Gọi $ M,N $ lần lượt là trung điểm của $ BC $ và $ B’C’ $ thì mặt phẳng $ (A’KG) $ chính là mặt phẳng $ (A’CN) $, còn mặt phẳng $ (AIB’) $ chính là mặt phẳng $ (AMB’). $ Hai mặt phẳng này song song vì có $ AM\parallel A’N $ và $ B’M\parallel CN. $

4. Bài tập chứng minh 2 mặt phẳng song song

Bài 1. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O$. Gọi $M, N, P, Q$ là trung điểm $SA, SD, AB, ON.$ Chứng minh: $(OMN) \parallel (SBC)$. Chứng minh: $PQ \parallel (SBC)$.

Bài 2. Cho hình chóp $S.ABCD$ đáy là hình bình hành tâm $O$. Gọi $M, N, P$ là trung điểm $SA, CD, AD.$ Chứng minh $(OMN) \parallel (SBC)$. Gọi $I$ là điểm trên $MP$. Chứng minh: $OI \parallel (SCD)$.

Bài 3. Cho hình chóp $S.ABCD$, đáy là hình bình hành. Gọi $M, N, P, Q$ là trung điểm $BC, AB, SB, AD.$ Chứng minh $(MNP) \parallel (SAC)$, $PQ \parallel (SCD)$. Gọi $I$ là giao điểm $AM$ và $BD, JSA$ sao cho $AJ = 2JS$, chứng minh $IJ \parallel (SBC)$. Gọi $K$ là một điểm trên $AC$, tìm giao tuyến $(SKM)$ và $(MNC)$.

Bài 4. Cho hình chóp $S.ABCD$ đáy là hình bình hành. Gọi $I, J, G, P, Q$ là trung điểm $DC, AB, SB, BG, BI.$ Chứng minh $(IJG) \parallel (SAD)$, $PQ \parallel (SAD)$. Tìm giao tuyến của $(SAC)$ và $(IJG)$; $(ACG)$ và $(SAD)$.

Bài 5. Cho hai hình bình hành $ABCD$ và $ABEF$ không đồng phẳng. Gọi $I, J, K$ là trung điểm $AB, CD, EF.$ Chứng minh $(ADF) \parallel (BCE)$; $(DIK) \parallel (JBE)$.
31/10/2020
Cách chứng minh thẳng hàng trong hình học không gian
Chứng minh thẳng hàng trong hình học không gian

1. Chứng minh ba điểm thẳng hàng trong không gian

Phương pháp. Để chứng minh ba điểm thẳng hàng ta chứng minh chúng cùng thuộc hai mặt phẳng, tức là cùng thuộc giao tuyến của hai mặt phẳng đó.

Xem lại Cách tìm giao tuyến của hai mặt phẳng trong không gian

Như vậy, để chứng minh 3 điểm $ A,B,C$ thẳng hàng. Ta chỉ ra ba điểm $ A,B,C$ cùng thuộc hai mặt phẳng $(P)$ và mặt phẳng $(Q)$ nào đó. Tức là ta chỉ ra đường thẳng $ AB$ là giao tuyến của hai mặt phẳng $(P)$ và $(Q)$. Sau đó chỉ ra điểm $ C$ cũng thuộc vào giao tuyến này, hay nói cách khác chỉ ra $ C$ cũng là một điểm chung của cả hai mặt phẳng $(P)$ và $(Q)$.

2. Ví dụ chứng minh thẳng hàng trong hình học không gian

Ví dụ 1. Cho tam giác $ABC$ nằm ngoài mặt phẳng $ (\alpha). $ Giả sử các cạnh $ AB,BC,CA $ kéo dài lần lượt cắt mặt phẳng $(\alpha)$ tại $ D,E,F. $ Chứng minh ba điểm $ D,E,F $ thẳng hàng.

Hướng dẫn. Rõ ràng, ba điểm $ D,E,F $ cùng thuộc hai mặt phẳng $(ABC)$ và mặt phẳng $(\alpha)$. Nên chúng cùng nằm trên giao tuyến của hai mặt phẳng đó, nói cách khác ba điểm $D,E,F$ thẳng hàng.

Ví dụ 2. Cho hình chóp $ S.ABC $. Trên các đoạn $ SA, SB, SC $ lần lượt lấy các điểm $ A’,B’,C’ $ sao cho $ A’B’ $ cắt $AB$ tại $ I,A’C’$ cắt $AC$ tại $J,B’C’$ cắt $BC $ tại $ K. $ Chứng minh ba điểm $ I, J, K $ thẳng hàng.

Hướng dẫn.
- Ta có $ I$ là giao điểm của hai đường thẳng $ A’B’$ và $ AB$. Mà $ AB$ nằm trong mặt phẳng $ (ABC)$, $ A’B’$ nằm trong mặt phẳng $(A’B’C’)$, nên suy ra $ I$ là một điểm chung của hai mặt phẳng $ (ABC)$ và $ (A’B’C’)$.
- Chứng minh tương tự có $ J,K$ cũng là điểm chung của hai mặt phẳng $ (ABC)$ và $ (A’B’C’)$.
- Suy ra, $ J,J,K$ cùng thuộc giao tuyến của hai mặt phẳng $ (ABC)$ và $ (A’B’C’)$. Mà giao tuyến của hai mặt phẳng là một đường thẳng, suy ra $ I,J,K$ cùng thuộc một đường thẳng. Nói cách khác, ba điểm $ I,J,K$ thẳng hàng.
Ví dụ 3. Cho hình chóp tứ giác $ S.ABCD $ có $ M $ là điểm trên đoạn $ SC $. Tìm giao điểm $ N $ của $ SD $ với mặt phẳng $ (ABM) $. Giả sử $ AB $ cắt $ CD $ tại $ K, $ chứng minh ba điểm $ M, N, K $ thẳng hàng.

Hướng dẫn.
- Trong mặt phẳng $ (ABCD)$, gọi $ O$ là giao điểm của $ AC$ và $ BD$. Trong mặt phẳng $ (SAC)$, gọi $ I$ là giao điểm của $ SO$ và $ AM$. Chỉ ra được $ N$ chính là giao điểm của $ BI$ và $ SD$.
- Chúng ta có $ MN$ là giao tuyến của hai mặt phẳng $ (ABM)$ và $ (SCD)$. Mặt khác, $ K$ cũng là điểm chung của hai mặt phẳng này nên suy ra $ K$ phải nằm trên giao tuyến $ MN$. Nói cách khác, ba điểm $ M,N,K$ thẳng hàng.
Ví dụ 4. Cho hình chóp $S.ABCD$ có đáy là hình bình hành. Gọi $ M,N $ lần lượt là trung điểm của $ AB $ và $ SC $. Xác định giao điểm $ I,J $ của $ AN,MN $ với mặt phẳng $ (SBD). $ Chứng minh ba điểm $ I , J , B $ thẳng hàng.

Hướng dẫn. Chỉ ra $ I,J,B $ cùng thuộc giao tuyến của hai mặt phẳng $ (ANB) $ và $ (SBD) $.

Ví dụ 5. Cho tứ giác hình chóp $ S.ABCD $ có $ I, J $ là hai điểm trên $ AD,SB $. Giả sử $ AD $ cắt $ BC $ tại $ O, OJ$ cắt $ SC $ tại $ M $. Tìm các giao điểm $ K,L $ của $ IJ,DJ $ và $ (SAC). $ Chứng minh bốn điểm $ A ,K ,L ,M $ thẳng hàng.

Hướng dẫn. Chỉ ra bốn điểm cùng thuộc giao tuyến của hai mặt phẳng $ (SAC) $ và $ (AJO) $.
17/09/2020
Đề thi Học kì II Toán 11
ĐỀ THI HỌC KÌ II TOÁN 11 NĂM 2018–2019

Xem thêm Đề thi GK2 Toán 11 Xuân Trường B Năm 2017

1. Đề thi HK2 Toán 11 – Trắc nghiệm

Câu 1: Tính giới hạn $\lim \frac{2n-1}{n+3}$.

A. $2$
B. $\frac{2}{3}$
C. $\frac{1}{2}$
D. $-\frac{1}{3}$

Câu 2: Dãy số nào sau đây có giới hạn bằng 0?

A. $\left(-\frac{2}{3}\right)^n$
B. $\left(\frac{3}{2}\right)^n$
C. $n^2-3n$
D. $\pi ^n$

Câu 3: Tính tổng S của cấp số nhân lùi vô hạn có số hạng đầu $u_1=1$ và công bội $q=-\frac{1}{2}.$

A. $S=2$
B. $S=\frac{3}{2}$
C. $S=1$
D. $S=\frac{2}{3}$

Câu 4: Tính giới hạn $\lim \frac{\sqrt{4{{n}^{2}}+1}-\sqrt{n+2}}{2n-3}.$

A. $\frac{3}{2}$
B. 2
C. 1
D. $+\infty$

Câu 5: Tính giới hạn $\lim \left( \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\cdots +\frac{1}{n(n+1)} \right).$

A. 0
B. 2
C. 1
D. $\frac{100}{101}$

Câu 6: Tính giới hạn $\underset{x\to -2}{\mathop{\lim }}\,\frac{{{x}^{2}}-\sqrt{6-5x}}{x+2}.$

A. $-2$
B. $-\frac{27}{8}$
C. $-3,37499$
D. $-3$

Câu 7: Hàm số nào sau đây liên tục trên tập R?

A. $y=\tan x$
B. $y=\frac{1}{x}$
C. $y=\sqrt{2x+1}$
D. $y=\sqrt{x^2+1}$

Câu 8: Viết phương trình tiếp tuyến của đồ thị hàm số $f(x)=x^{3}-2 x^{2}+3 x+1$ tại điểm có hoành độ $x=2.$

A. $y=-x-7$
B. $y=7 x-14$
C. $y=7 x-7$
D. $y=-x+9$

Câu 9: Tính đạo hàm của hàm số $y=-{{x}^{7}}+2{{x}^{5}}+3{{x}^{3}}.$

A. ${y}’=-{{x}^{6}}+2{{x}^{4}}+3{{x}^{2}}$
B. ${y}’=-7{{x}^{6}}-10{{x}^{4}}-6{{x}^{2}}$
C. ${y}’=7{{x}^{6}}-10{{x}^{4}}-6{{x}^{2}}$
D. ${y}’=-7{{x}^{6}}+10{{x}^{4}}+9{{x}^{2}}$

Câu 10: Tính đạo hàm của hàm số $y=\frac{{{x}^{2}}+x}{{{x}^{2}}+2}.$

A. $y’=\frac{2x+1}{2x}$
B. $y’=\frac{2x+1}{(x^2+2)^2}$
C. $y’=\frac{-x^{2}+4x+2}{\left( x^{2}+2\right) ^{2}}$
D. $y’=\frac{4x^3+3x^{2}+4x+2}{\left( x^{2}+2\right) ^{2}}$

Câu 11: Tính đạo hàm của hàm số $y=\sin x+\cos x$.

A. $y{\prime}=2 \cos x$
B. $y{\prime}=2 \sin x$
C. $y{\prime}=\sin x-\cos x$
D. $y{\prime}=\cos x-\sin x$

Câu 12: Tính đạo hàm của hàm số $y=\sin ^{2} 3 x$.

A. $y\prime =\sin 6x$
B. $y\prime =2\sin 3x$
C. $y{\prime}=3 \sin 6 x$
D. $y\prime =6\sin 3x$

Câu 13: Cho $f(x)=x^{3}-\frac{1}{2} x^{2}-4 x,$ tìm tất cả giá trị thực của $x$ sao cho $f\prime (x)<0.$

A. $x>\frac{4}{3}$ hoặc $x<-1 .$
B. $-1<x<\frac{4}{3}$
C. $x \geq \frac{4}{3}$ hoặc $x \leq-1 .$
D. $-1 \leq x \leq \frac{4}{3}$

Câu 14: Tính vi phân của hàm số $y=\sqrt{x}.$

A. $\mathrm{d}y =\sqrt{x} \mathrm{d}x$
B. $\mathrm{d}y = \frac{1}{2\sqrt{x}}\mathrm{d}x$
C. $\mathrm{d}y = \frac{1}{2\sqrt{x}\mathrm{d}x}$
D. $\mathrm{d}y = \frac{1}{\sqrt{x}}\mathrm{d}x$

Câu 15: Cho hàm số $f(x)=x^{3}+2 x$, giá trị của ${f}”(1)$ bằng

A. 6
B. 8
C. 3
D. 2

Câu 16: Cho hàm số $y=\sin 2x.$ Khẳng định nào sau đây là đúng?

A. ${{y}^{2}}+{{\left( y\prime \right)}^{2}}=1$
B. $4 y-y{\prime \prime}=0$
C. $4 y+y{\prime \prime}=0$
D. $y=y{\prime} \tan 2 x$

Câu 17: Cho hình hộp $ABCD.{A}'{B}'{C}'{D}’$, khẳng định nào sau đây là đúng?

A. $\overrightarrow{AC’}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA’}$
B. $\overrightarrow{AB}.\overrightarrow{AD}=0$
C. $\overrightarrow{AC’}=\overrightarrow{AC}+\overrightarrow{A’A}$
D. $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{CB}$

Câu 18: Cho lăng trụ tam giác đều $ABC.{A}'{B}'{C}’$ có tất cả các cạnh cùng bằng 4. Khẳng định nào sau đây là sai?

A. $\overrightarrow{AB’}.\overrightarrow{CB}=\overrightarrow{AB}.\overrightarrow{CB}$
B. $\overrightarrow{AB’}.\overrightarrow{CB}=8$
C. $\overrightarrow{AB’}.\overrightarrow{CB}=\overrightarrow{AB’}.\overrightarrow{B’C’}$
D. $\overrightarrow{AB’}.\overrightarrow{CB}=\overrightarrow{BA’}.\overrightarrow{CA}$

Câu 19: Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.
B. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
C. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.
D. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau.

Câu 20: Cho hình hộp $ABCD.{A}'{B}'{C}'{D}’$ có tất cả các cạnh bằng nhau. Trong các mệnh đề sau, mệnh đề nào sai?

A. $BB’\perp BD$
B. $A’C’\perp BD$
C. $A’B \perp DC’$
D. $BC’ \perp A’ D$

Câu 21: Cho hình chóp S.ABCD có đáy là hình vuông cạnh $a,SA=a\sqrt{2}$ và SA vuông góc với mặt đáy. Tính góc giữa đường thẳng SC và mặt phẳng $(ABCD)$.

A. $60^\circ$
B. $30^\circ$
C. $45^\circ$
D. $90^\circ$

Câu 22: Cho G là trọng tâm tứ diện ABCD, O là một điểm tùy ý. Trong các khẳng định sau, khẳng định nào sai?

A. $\overrightarrow{A G}=\frac{1}{4}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})$
B. $\overrightarrow{AG}=\frac{2}{3}(\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{AD})$
C. $\overrightarrow{G A}+\overrightarrow{G B}+\overrightarrow{G C}+\overrightarrow{G D}=\overrightarrow{0}$
D. $\overrightarrow{OG}=\frac{1}{4}(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD})$

Câu 23: Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}’.$ Khẳng định nào sau đây là khẳng định sai?

A. Góc giữa hai đường thẳng ${B}'{D}’$ và $A{A}’$ bằng ${{60}^{\circ }}$
B. Góc giữa hai đường thẳng ${B}'{D}’$ và AC bằng ${{90}^{\circ }}$
C. Góc giữa hai đường thẳng AD và ${B}’C$ bằng ${{45}^{\circ }}$
D. Góc giữa hai đường thẳng BD và ${A}'{C}’$ bằng ${{90}^{\circ }}$

Câu 24: Gọi $\alpha$ là số đo góc giữa mặt bên và mặt đáy của một tứ diện đều. Khẳng định nào đúng?

A. tan $\alpha=\sqrt{8}$
B. $\tan \alpha=3 \sqrt{2}$
C. tan $\alpha=2 \sqrt{3}$
D. $\tan \alpha=4 \sqrt{2}$

Câu 25: Cho hình chóp S.ABCD có đáy là hình vuông. Hai mặt phẳng $\left( SAB \right)$ và $\left( SAD \right)$ cùng vuông góc với đáy và $SA=a\sqrt{3}$. Biết diện tích tam giác $SAB$ bằng $\frac{a^{2} \sqrt{3}}{2}$, tính khoảng cách từ $B$đến mặt phẳng $(SAC)$.

A. $\frac{a \sqrt{10}}{3}$
B. $\frac{a \sqrt{10}}{5}$
C. $\frac{a \sqrt{2}}{3}$
D. $\frac{a \sqrt{2}}{2}$

2. Đề thi học kì II Toán 11 – Tự luận

Câu 1. (1,0 điểm) Tính đạo hàm của các hàm số sau:
1. $y=\sin x-\cos 3x+1$
2. $y={{x}^{4}}+\sqrt{x}$
Câu 2. (1,0 điểm) Tính các giới hạn sau:
1. $\underset{x\to 2}{\mathop{\lim }}\,\frac{(3-x)(2-x)}{x-2}$
2. $\underset{x\to +\infty }{\mathop{\lim }}\,\left( \sqrt{{{x}^{2}}+x+1}-x \right)$
Câu 3. (0,5 điểm) Chứng minh rằng phương trình ${{x}^{3}}-3{{x}^{2}}+5x+7=0$ có nghiệm thuộc khoảng $\left( -1;0 \right).$

Câu 4. (0,5 điểm) Cho hàm số $y={{x}^{3}}-3x+1$ có đồ thị $(C)$. Một điểm $M$ có hoành độ bằng $a\ne 0$ và thuộc đồ thị $(C).$ Tiếp tuyến của $(C)$ tại điểm $M$ cắt $(C)$ tại một điểm $N$ khác $M.$ Tìm hoành độ điểm $N$ theo $a.$

Câu 5. (2,0 điểm) Hình chóp $S.ABCD$ có đáy là hình thang vuông tại $A$ và $D,AB=2a,AD=CD=a.$ Cạnh bên $SA=a\sqrt{3}$ và vuông góc với mặt đáy hình chóp.
1. Chứng minh rằng đường thẳng $AD$ vuông góc với mặt phẳng $(SAB)$.
2. Tính góc giữa hai mặt phẳng $(SCD)$ và $(ABCD)$.
3. Tính khoảng cách giữa hai đường thẳng $AC$ và $SB$ theo $a$.
—– HẾT—–
19/06/2020
Bài tập cấp số cộng – cấp số nhân
Bài tập cấp số cộng – cấp số nhân

Xem thêm Báo cáo kinh nghiệm dạy Toán bằng tiếng Anh chương Cấp số cộng

1. Tóm tắt lý thuyết cấp số cộng và cấp số nhân

1.1. Cấp số cộng
- Định nghĩa. Dãy số $ (u_n) $ được xác định bởi $\begin{cases} u_1=u\\u_{n}=u_{n-1}+d \end{cases}$ được gọi là cấp số cộng với số hạng đầu bằng $ u $ và công sai $ d. $
- Tính chất 3 số hạng liên tiếp của cấp số cộng $$ u_k=\frac{u_{k-1}+u_{k+1}}{2} $$
- Công thức số hạng tổng quát của cấp số cộng $$ u_n=u_1+(n-1)d $$
- Tổng $ n $ số hạng đầu tiên của cấp số cộng $$ S_n=u_1+u_2+…+u_n=\frac{n(u_1+u_n)}{2} $$
https://www.youtube.com/watch?v=ZbBZiMQnkbQ

1.2. Cấp số nhân
- Định nghĩa. Dãy số $ (u_n) $ được xác định bởi $\begin{cases} u_1=u\\u_{n}=u_{n-1}\cdot q \end{cases}$ được gọi là cấp số nhân với số hạng đầu bằng $ u$ và công bội $ q. $
- Công thức số hạng tổng quát của cấp số nhân $$ u_n=u_1\cdot q^{n-1} $$
- Tính chất 3 số hạng liên tiếp của cấp số nhân $$ u_k^2=u_{k-1}.u_{k+1} $$
- Tổng $ n $ số hạng đầu tiên của cấp số nhân $$ S_n=u_1+u_2+…+u_n=u_1\frac{1-q^n}{1-q} \,\,\, (q\ne 1)$$
2. Bài tập cấp số cộng

Ví dụ 1. Cho cấp số cộng có $ u_1=10,d=-4. $ Tìm $ u_{10} $ và $ S_{10} $.

Hướng dẫn. Sử dụng công thức số hạng tổng quát, ta có số hạng thứ $10$ của cấp số cộng là $$ u_{10}=u_1 + (10-1)d = 10+9(-4)=-26 $$ Tổng \( 10 \) số hạng đầu tiên của cấp số cộng đã cho là $$ S_{10} = \frac{10\left(u_1+u_{10}\right)}{2}=-80 $$

Ví dụ 2. Cho ba số dương $ a, b, c $ lập thành cấp số cộng. Chứng minh rằng:
- ${{a}^{2}}+2bc={{c}^{2}}+2ab$
- ${{a}^{2}}+8bc={{(2b+c)}^{2}}$
- $({{a}^{2}}+ab+{{b}^{2}}),({{a}^{2}}+ac+{{c}^{2}}),({{b}^{2}}+bc+{{c}^{2}})$ lập thành cấp số cộng
Hướng dẫn. Ta có ba số dương $ a, b, c $ lập thành cấp số cộng khi và chỉ khi $ 2b=a+c $.
- ${{a}^{2}}+2bc={{c}^{2}}+2ab$ tương đương với $$ a^2+(a+c)c=c^2+(a+c)a $$ Khai triển hai vế đẳng thức này được điều hiển nhiên đúng.
- ${{a}^{2}}+8bc={{(2b+c)}^{2}}$ tương đương với $$ a^2+4c(a+c)=(a+c+c)^2 $$ Khai triển hai vế đẳng thức này được điều hiển nhiên đúng.
- $({{a}^{2}}+ab+{{b}^{2}}),({{a}^{2}}+ac+{{c}^{2}}),({{b}^{2}}+bc+{{c}^{2}})$ lập thành cấp số cộng khi và chỉ khi
  $$ ({{a}^{2}}+ab+{{b}^{2}}) + ({{b}^{2}}+bc+{{c}^{2}}) = 2 ({{a}^{2}}+ac+{{c}^{2}})$$ Khai triển và rút gọn ta được \begin{align*}
  &ab+bc+2b^2=a^2+2ac+c^2\\
  \Leftrightarrow & (a+c)b+2b^2=(a+c)^2
  \end{align*} Thay \( a+c=2b \) vào hai vế đẳng thức trên ta được \( 4b^2=4b^2 \), đây là điều hiển nhiên đúng.
Ví dụ 3. Tìm số hạng đầu và công sai của cấp số cộng $ (u_n) $ biết
- $ \begin{cases} u_1-u_3+u_5=10\\ u_1+u_6=17 \end{cases} $
- $ \begin{cases} u_7-u_3=8\\u_2.u_{15}=75 \end{cases} $
- $ \begin{cases} u_1+u_4+u_5=25\\u2-u_8=-24 \end{cases} $
Ví dụ 4. Xác định $ x $ để ba số $ 10 – 3x, 2x^2 + 3, 7 – 4x $ lập thành một cấp số cộng.

Hướng dẫn. Ba số $ 10 – 3x, 2x^2 + 3, 7 – 4x $ lập thành một cấp số cộng khi và chỉ khi $$ 10-3x+7-4x=2(2x^2+3) $$ Giải phương trình này, tìm được \( x=1, x=-\frac{11}{4} \).

Ví dụ 5. Xác định một cấp số cộng có 3 số hạng, biết tổng của chúng bằng 9 và tổng bình phương là 125.

Giải: Gọi $d$ là công sai của cấp số cộng và ba số phải tìm là $(x – d),x, (x + d)$ thì ta có hệ phương trình:

$$ \begin{cases}
x-d+x+x+d=9\\ (x-d)^2+x^2+(x+d)^2=125
\end{cases} $$

Giải hệ trên, ta tìm được với $d = 7$ cấp số cộng đó là $-4, 3, 10$ và với $d = -7$ cấp số là $10;,3,-4$.

Ví dụ 6. Xác định 4 góc của một tứ giác lồi, biết rằng số đo 4 góc lập thành một cấp số cộng và góc lớn nhất bằng 5 lần góc nhỏ nhất.

Hướng dẫn. Gọi $d=2a$ là công sai thì bốn số phải tìm là $$x – 3a,x – a,x + a,x + 3a$$ Ta có hệ phương trình: $$ \begin{cases}
\left( x-3\text{a} \right)+\left( x-a \right)+\left( x+a \right)+\left( x+3a \right)=360^\circ\\
\left( x+3a \right)=5\left( x-3a \right)
\end{cases} $$ Giải hệ này, tìm được \( x=90^\circ \) và \( a=20^\circ \). Suy ra, bốn góc phải tìm là:A = 30⁰; B = 70⁰ ; C = 110⁰ ; D = 150⁰.

Ví dụ 7. Tìm tổng các số hạng liên tiếp từ thứ 6 đến thứ 14 của cấp số cộng có số hạng thứ ba là 16 và công sai bằng 4.

Ví dụ 8. Cho hàm số $ y=x^3-3x^2-9x+m $ có đồ thị là $ (C). $ Tìm $m$ để đồ thị $(C)$ cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành một cấp số cộng?

Hướng dẫn. Giả sử ba hoành độ là $ x_1,x_2,x_3 $. Từ $ x_1+x_3=2x_2 $ và Viét suy ra $ x_2=1. $ Từ đó tìm được $ m $ và thử lại. Đáp số $ m=11. $

Ví dụ 9. Tìm $m$ để đồ thị hàm số $ y=x^4-2(m-1)x^2+2m+1 $ cắt trục hoành tại bốn điểm phân biệt lập thành một cấp số cộng.
Đáp số. $ m=4 $ và $ m=-\frac{4}{9}. $

Ví dụ 10. Cho phương trình : ${{x}^{4}}+3{{x}^{2}}-\left( 24+m \right)x-26-n=0$. Tìm hệ thức liên hệ giữa $m$ và $n$ để phương trình có 3 nghiệm phân biệt ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ lập thành một cấp số cộng?

Hướng dẫn. Vì 3 nghiệm phân biệt : ${{x}_{1}},{{x}_{2}},{{x}_{3}}$ lập thành cấp số cộng , nên ta có thể đặt: $${{x}_{1}}={{x}_{0}}-d,{{x}_{2}}={{x}_{0}},{{x}_{3}}={{x}_{0}}+d\left( d\ne 0 \right)$$ Theo giả thiết ta có: $${x^3} + 3{x^2} – \left( {24 + m} \right)x – 26 – n = \left( {x – {x_1}} \right)\left( {x – {x_2}} \right)\left( {x – {x_3}} \right)$$

Nhân ra và đồng nhất hệ số ở hai vế của phương trình ta có hệ: $$\begin{array}{l}
\,\,\,\,\,\,\,\left\{ \begin{array}{l}
– 3{x_0} = 3\\
3x_0^2 – {d^2} = – \left( {24 + m} \right)\\
– x_0^3 + {x_0}{d^2} = – 26 – n
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
{x_0} = – 1\\
3 – {d^2} = – 24 – m\\
1 – {d^2} = – 26 – n
\end{array} \right.\\
\Leftrightarrow \left\{ \begin{array}{l}
{x_0} = – 1\\
m = n
\end{array} \right.
\end{array}$$ Vậy với $m=n$ thì ba nghiệm phân biệt của phương trình lập thành cấp số cộng.

Ví dụ 11. Tính tổng tất cả các nghiệm của phương trình $ \sin^23x-5\sin3x+4=0 $ trên khoảng $ (0;50\pi) $.

Đáp số. $ \frac{3725\pi}{2} $.

3. Bài tập cấp số nhân

Ví dụ 1. Cho dãy số $({u_n})$ xác định bởi ${u_n} = \frac{5}{2}$ và ${u_{n + 1}} = 3{u_n} – 1$ với mọi $n \geqslant 1$. Chứng minh rằng dãy số $({v_n})$ xác định bởi ${v_n} = {u_n} = \frac{{ – 1}}{2}$ với mọi $n \geqslant 1$ là một cấp số nhân. Hãy cho biết số hạng đầu và công bội của cấp số nhân đó.

Hướng dẫn. Từ công thức xác định dãy số $ (u_n) $ và $ (v_n) $ ta có
$${v_{n + 1}} = {u_{n + 1}} – \frac{1}{2} = 3{u_n} – 1 – \frac{1}{2} = 3\left( {{u_n} – \frac{1}{2}} \right) = 3{v_n} \text{ với mọi }n\geqslant 1. $$ Ta thấy ngay, $ (v_n) $ là một cấp số nhân với số hạng đầu $ v_1=2 $ và công bội $ q=3. $

Ví dụ 2. Một cấp số nhân có 5 số hạng , công bội bằng một phần bốn số hạng thứ nhất , tổng của hai số hạng đầu bằng 24. Tìm cấp số nhân đó.

Hướng dẫn. Theo giả thiết ta có $$\begin{array}{l}
\,\,\,\,\,\,{u_1} + {u_2} = {u_1} + \frac{1}{4}\left( {{u_1}} \right) = 24\\
\Rightarrow {u_1} + \frac{1}{4}u_1^2 – 24 = 0\\
\Leftrightarrow {u_1} = – 12 \vee {u_1} = 8
\end{array}$$ Vậy có hai cấp số nhân tương ứng là $8,16,32,128$ hoặc $-12,36,-108,-972$.

Ví dụ 3. Tìm số hạng đầu và công bội của cấp số nhân $ (u_n) $ biết
- $ \begin{cases} u_4-u_2=72\\u_5-u_3=144 \end{cases} $
- $ \begin{cases} u_1-u_3+u_5=65\\u_1+u_7=325 \end{cases} $
Ví dụ 4. Tìm bốn góc của một tứ giác, biết rằng các góc đó lập thành cấp số nhân và góc cuối gấp 9 lần góc thứ hai.

Ví dụ 5. Tìm các số dương $ a,b $ sao cho $ a,a+2b,2a+b $ lập thành một cấp số cộng còn $ (b+1)^2,ab+5,(a+1)^2 $ lập thành một cấp số nhân.

Ví dụ 6. Tìm $m$ để phương trình $ x^3+2x^2+(m+1)x+2(m+1)=0 $ có ba nghiệm lập thành một cấp số nhân.

Hướng dẫn. Phương trình đã cho tương đương với $$ (x+2)(x^{2}+m+1)=0 \Leftrightarrow \left[\begin{array}{l}
x=-2 \\ x^{2}=-m-1\end{array}\right.$$
Phương trình đã cho có ba nghiệm khi và chỉ khi $$ \begin{cases}m<-1\\m\neq{-5}\end{cases} $$ Khi đó, ba nghiệm của phương trình là $$ x=-2;x=\sqrt{-m-1};x=-\sqrt{-m-1} $$ Chúng ta xét hai trường hợp:
- TH1. \( -5<m<-1 \) thì 3 nghiệm theo thứ tự là $$ -2;-\sqrt{-m-1};\sqrt{-m-1} $$ Để chúng lập thành cấp số nhân thì $$ -2\sqrt{-m-1}=-m-1 $$ Chú ý điều kiện \( -5<m<-1 \) nên phương trình ẩn \( m \) này vô nghiệm.
- TH2. \( m<-5 \) thì 3 nghiệm theo thứ tự là $$ -\sqrt{-m-1};-2;\sqrt{-m-1} $$ Để chúng lập thành cấp số nhân thì $$ 4=-(-m-1)\Leftrightarrow m=3 $$ So sánh với điều kiện, thấy giá trị này không thỏa mãn.
Tóm lại, không có giá trị nào của \( m \) thỏa mãn yêu cầu.

Ví dụ 7. Tính tổng $$ S=1+\frac{1}{3}+\frac{1}{3^2}+\cdots+\frac{1}{3^{2015}} $$

Ví dụ 8. Tìm các số hạng đầu của cấp số nhân $(u_n)$ biết rằng $$ \begin{cases}
u_1+u_2+u_3+u_4=15\\
u_1^2+u_2^2+u_3^2+u_4^2=85
\end{cases} $$
Hướng dẫn. Giả sử cấp số nhân cần tìm có số hạng đầu bằng \( x \) và công bội \( q \ne 1\). Sử dụng công thức tổng $n$ số hạng đầu của một cấp số nhân, chúng ta có
$$ u_1+u_2+u_3+u_4=\frac{x\left(q^4-1\right)}{q-1}=15 $$ Bình phương hai vế ta được $$ x^2(q^4-1)^2/(q-1)^2 = 225 $$ Đối với tổng $ u_1^2+u_2^2+u_3^2+u_4^2$ ta có thể coi đây chính là tổng bốn số hạng đầu của một cấp số nhân với số hạng đầu là \( x^2 \) và công bội \( q^2 \) nên tổng của chúng là $$u_1^2+u_2^2+u_3^2+u_4^2=\frac{x^2\left(q^8-1\right)}{q^2-1}=85 $$

Chia từng vế hai phương trình trên ta được $$ \frac{\left(q^4-1\right)\left(q^2-1\right)}{\left(q-1\right)^2\left(q^8-1\right)} =\frac{225}{85}$$
Rút gọn rồi nhân chéo ta được phương trình $$ 14q^4 – 17q^3 – 17q^2 – 17q + 14 = 0 $$ Đến đây có thể sử dụng máy tính để giải, tìm được nghiệm \( q=2,q=\frac{1}{2} \). Hoặc đặt \( t=q+\frac{1}{q} \) và đưa về phương trình bậc hai ẩn \( t \).

Lời giải chi tiết cho ví dụ này, mời thầy cô và các em học sinh xem trong video sau:

https://www.youtube.com/watch?v=KnwhxAgPL04
05/06/2020
Đề thi GK2 Toán 11 Xuân Trường B Năm 2017

Đề thi GK2 Toán 11 Xuân Trường B Năm 2017

Đề thi GK2 Toán 11 Xuân Trường B – Nam Định năm 2017 gồm 25 câu trắc nghiệm và 3 câu tự luận về cấp số cộng, giới hạn dãy số, giới hạn hàm số, đường thẳng vuông góc với mặt phẳng, góc giữa đường thẳng và mặt phẳng.

1. Phần trắc nghiệm

Câu 1: Cho hai đường thẳng phân biệt $a, b$ và mặt phẳng $(P)$, trong đó \(a\perp \left( P \right) \). Mệnh đề nào sau đây là sai?
A. Nếu \(b\perp a \) thì \(b\parallel \left( P \right). \)
B. Nếu \(b\perp \left( P \right) \) thì \(b\parallel a. \)
C. Nếu \(b\parallel \left( P \right) \) thì \(b\perp a. \)
D. Nếu \(b\parallel a \) thì \(b\perp \left( P \right). \)

Câu 2: Cho dãy số $\left( {{u}_{n}} \right)$, biết ${{u}_{n}}={{2}^{n}}$. Ta có số hạng ${{u}_{n+1}}$ bằng
A. ${{2}^{n}}+1.$
B. ${{2}^{n}}+2.$
C. ${{2.2}^{n}}.$
D. $2\left( n+2 \right)$.

Câu 3: Giá trị của $\lim \frac{2{{n}^{2}}-1}{n-{{n}^{2}}}$ bằng
A. $2.$
B. $-2.$
C. $+\infty .$
D. $0.$

Câu 4: Cho dãy số 1, 6, 11, … là cấp số cộng. Tìm x, biết: $$\left( x+1 \right)+\left( x+6 \right)+\left( x+11 \right)+…+\left( x+96 \right)=980$$
A. $x=-\frac{1}{2}.$
B. $x=\frac{1}{2}.$
C. $x=-1.$
D. $x=1.$

Câu 5: Cho hai đường thẳng $a, b$ chéo nhau và vuông góc với nhau. Qua đường thẳng $b$ có mấy mặt phẳng vuông góc với đường thẳng $a$?
A. 1.
B. 0.
C. 2.
D. Vô số.

Câu 6: Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông cân tại $B$, $AB=a,SA=\sqrt{2}a$ và $SA\perp \left( ABC \right)$. Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng:
A. ${{45}^\circ}.$
B. ${{30}^\circ}.$
C. ${{60}^\circ}.$
D. ${{90}^\circ}.$

Câu 7: Cho hình chóp \( S.ABC \) có tam giác \( ABC \) vuông tại \( B \), $SA\perp \left( ABC \right)$. Gọi \( M \) là trung điểm của \( AB \). Mặt phẳng $\left( \alpha \right)$ qua \( M \) và vuông góc với \( SB \) cắt hình chóp đã cho theo thiết diện là hình gì?
A. Hình thang vuông.
B. Tam giác.
C. Hình bình hành.
D. Hình chữ nhật.

Câu 8: Giá trị của $\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{x-2}{x-1}$ bằng
A. $\frac{1}{2}.$
B. $-\infty .$
C. $-\frac{3}{2}.$
D. $+\infty .$

Câu 9: Giá trị của $\lim \left( \sqrt{{{n}^{2}}+n}-n \right)$ bằng
A. $-\infty .$
B. 1.
C. $\frac{1}{2}.$
D. $+\infty .$

Câu 10: Cho cấp số cộng $\left( {{u}_{n}} \right)$, biết ${{u}_{n}}=3n-1$. Tìm công sai d của cấp số cộng đó.
A. $d=4.$
B. $d=5.$
C. $d=3.$
D. $d=2.$

Câu 11: Cho hình chóp \( S.ABCD \) có đáy \( ABCD \) là hình vuông, $SA\perp \left( ABCD \right)$. Khi đó đường thẳng \(
B. \) vuông góc với mặt phẳng nào trong các mặt phẳng sau:
A. $\left( SAD \right).$
B. $\left( SBC \right).$
C. $\left( SAC \right).$
D. $\left( SAB \right).$

Câu 12: Giá trị của $\underset{x\to -\infty }{\mathop{\lim }}\,\left( \sqrt{{{x}^{2}}-1}-x \right)$ bằng
A. $-\infty .$
B. 0.
C. $+\infty .$
D. 1.

Câu 13: Tế bào E. Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Nếu có 1000 tế bào thì sau đúng 3 giờ sẽ phân chia thành bao nhiêu tế bào?
A. $256000$ (tế bào).
B. $512000$ (tế bào).
C. $1024000$ (tế bào).
D. $2048000$ (tế bào).

Câu 14: Giá trị của $\underset{x\to -2}{\mathop{\lim }}\,\left( {{x}^{2}}-x+2 \right)$ bằng
A. $+\infty .$
B. 0.
C. 4.
D. 8.

Câu 15: Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a.$ Ta có $\overrightarrow{AB}.\overrightarrow{AC’}$ bằng
A. $\sqrt{3}{{a}^{2}}.$
B. 0.
C. ${{a}^{2}}.$
D. $\sqrt{2}{{a}^{2}}.$

Câu 16: Dãy số nào sau đây là dãy số giảm ?
A. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}=\frac{{{\left( -1 \right)}^{n}}}{n}.$
B. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}=\sqrt{n+1}-\sqrt{n}.$
C. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}={{2}^{n}}.$
D. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}=2+n.$

Câu 17: Cho cấp số cộng $\left( {{u}_{n}} \right)$ với ${{u}_{2}}=1$, công bội $d=2$. Tính tổng ${{S}_{20}}$ của 20 số hạng đầu.
A. ${{S}_{20}}=370.$
B. ${{S}_{20}}=390.$
C. ${{S}_{20}}=400.$
D. ${{S}_{20}}=360.$

Câu 18: Cho cấp số nhân $\left( {{u}_{n}} \right)$, biết ${{u}_{1}}=2,{{u}_{2}}=-6$. Khẳng định nào sau đây là đúng ?
A. ${{u}_{3}}=-14.$
B. ${{u}_{3}}=14.$
C. ${{u}_{3}}=-18.$
D. ${{u}_{3}}=18.$

Câu 19: Dãy số nào sau đây là cấp số nhân ?
A. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}={{\left( -2 \right)}^{n}}.$
B. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}=2n+1.$
C. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}=\frac{n}{n+1}.$
D. $\left( {{u}_{n}} \right)$ với ${{u}_{n}}={{\left( -1 \right)}^{n}}n.$

Câu 20: Trong các mệnh đề sau, mệnh đề nào đúng ?
A. $\lim \left| {{u}_{n}} \right|=+\infty $ thì $\lim {{u}_{n}}=-\infty .$
B. $\lim {{u}_{n}}=-a$ thì $\lim \left| {{u}_{n}} \right|=a.$
C. $\lim \left| {{u}_{n}} \right|=+\infty $ thì $\lim {{u}_{n}}=+\infty .$
D. $\lim {{u}_{n}}=0$ thì $\lim \left| {{u}_{n}} \right|=0.$

Câu 21: Cho hình lập phương $ABCD.A’B’C’D’$. Ta có góc giữa hai đường thẳng $AB’$ và $DB$ bằng
A. ${{45}^\circ}.$
B. ${{60}^\circ}.$
C. ${{90}^\circ}.$
D. ${{120}^\circ}.$

Câu 22: Cho tứ diện $ABCD$ có $AB, BC, CD$ đôi một vuông góc. Khẳng định nào sau đây là đúng?
A. $BC\perp AD.$
B. $AC\perp CD.$
C. $CD\perp AD.$
D. $AC\perp BD.$

Câu 23: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là nửa lục giác đều nội tiếp đường tròn đường kính $AD$, $SA\perp \left( ABCD \right)$. Gọi $I$ là điểm cách đều các đỉnh của hình chóp đã cho. Khi đó điểm $I$ là trung điểm của
A. $SD.$
B. $SC.$
C. $SB.$
D. $AD.$

Câu 24: Tìm tất cả giá trị của tham số $a$ để $\underset{x\to -1}{\mathop{\lim }}\,\frac{{{x}^{2}}+\left( 1-a \right)x-a}{{{x}^{2}}+3x+2}=2$.
A. 2.
B. $-2.$
C. $3.$
D. $-3.$

Câu 25: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $O$. Đẳng thức nào sau đây là sai?
A. $\overrightarrow{SA}+\overrightarrow{SB}=\overrightarrow{SC}+\overrightarrow{SD}.$
B. $\overrightarrow{SA}+\overrightarrow{SB}+\overrightarrow{SC}+\overrightarrow{SD}=4.\overrightarrow{SO}.$
C. $\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}.$
D. $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}.$

2. Phần tự luận

Câu 1 (1,5 điểm).
a) Cho cấp số cộng $\left( {{u}_{n}} \right)$ với ${{u}_{10}}=25,\text{ }{{u}_{20}}=55$. Tìm công thức của số hạng tổng quát ${{u}_{n}}$.
b) Tính tổng của cấp số nhân lùi vô hạn $\left( {{u}_{n}} \right)$, biết số hạng đầu ${{u}_{1}}=2$, công bội $q=-\frac{1}{2}$.

Câu 2 (2,0 điểm). Tính các giới hạn sau:
a) $\lim \frac{{{2}^{n}}+{{3}^{n+2}}}{{{4}^{n}}-1}$; b) $\lim \left( n+\sqrt[3]{{{n}^{2}}-{{n}^{3}}} \right)$;
c) $\underset{x\to -\infty }{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}-x}}{x}$; d) $\underset{x\to 1}{\mathop{\lim }}\,\frac{\sqrt{3-2x}+{{x}^{3}}-2{{x}^{2}}+2x-2}{{{x}^{3}}-3x+2}$ .

Câu 3 (1,5 điểm). Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB=a,\text{ }AD=\sqrt{2}a$, $SA=a$ và \(SA\bot \left( ABCD \right) \).
a) Chứng minh: $BC\bot \left( SAB \right)$.
b) Kẻ đường cao $AH$ của tam giác SAD. Chứng minh:$AH\bot SC$.
c) Gọi $\left( \alpha \right)$ là mặt phẳng qua $A$ và vuông góc với $SC$. Tính góc giữa đường thẳng $BC$ và mặt phẳng $\left( \alpha \right)$.

———– Hết ———–

Mời thầy cô và các em tải đề thi Giữa học kì 2 năm 2017 môn Toán 11 tại đây 2017 GK2 Toan11

04/06/2020
Cách tính khoảng cách từ một điểm đến một mặt phẳng
BỘ SÁCH HHKG GIÁ TỐT TRÊN SHOPEE

Bài toán khoảng cách trong hình học không gian là một vấn đề quan trọng, thường xuất hiện ở các câu hỏi có mức độ vận dụng và vận dụng cao. Các bài toán tính khoảng cách trong không gian bao gồm:
1. Khoảng cách từ một điểm tới một mặt phẳng;
2. Khoảng cách giữa hai mặt phẳng song song: Chính bằng khoảng cách từ một điểm bất kì trên một mặt phẳng tới mặt phẳng còn lại;
3. Khoảng cách giữa đường thẳng và mặt phẳng song song: Chính bằng khoảng cách từ một điểm bất kì trên đường thẳng tới mặt phẳng đã cho;
4. Khoảng cách giữa hai đường thẳng chéo nhau trong không gian.
Như vậy, 3 dạng toán đầu tiên đều quy về Cách tính khoảng cách từ một điểm đến một mặt phẳng, chính là nội dung của bài viết này.

BỘ SÁCH HHKG GIÁ TỐT TRÊN SHOPEE

Ngoài ra, các em cũng cần thành thạo 2 dạng toán liên quan đến góc trong không gian:
- Cách tính góc giữa đường thẳng và mặt phẳng
- Cách tính góc giữa hai mặt phẳng trong không gian
1. Phương pháp tìm khoảng cách từ điểm đến mặt phẳng

Để tính khoảng cách từ một điểm đến một mặt phẳng, bài toán quan trọng nhất là phải dựng được hình chiếu vuông góc của điểm đó lên mặt phẳng.

Nếu như ở bài toán chứng minh đường thẳng vuông góc với mặt phẳng thì ta đã biết trước mục tiêu cần hướng đến, thì ở bài toán dựng đường thẳng vuông góc với mặt phẳng chúng ta phải tự tìm ra đường thẳng (tự dựng hình) và chứng minh đường thẳng đó vuông góc với mặt phẳng đã cho, tức là mức độ sẽ khó hơn bài toán chứng minh rất nhiều.

Tuy nhiên, phương pháp xác định hình chiếu vuông góc của một điểm lên mặt phẳng sẽ trở nên dễ dàng hơn nếu chúng ta nắm chắc hai kết quả [bài toán] sau đây.

Bài toán 1. Dựng hình chiếu vuông góc từ chân đường cao tới một mặt phẳng.

Cho hình chóp $ S.ABC $ cho có $ SA $ vuông góc với mặt đáy $ (ABC) $. Hãy xác định hình chiếu vuông góc của điểm $A$ lên mặt phẳng $(SBC)$.

Phương pháp. Để dựng hình chiếu của điểm $ A $ lên mặt phẳng $ (SBC) $, ta chỉ việc kẻ vuông góc hai lần như sau:
- Trong mặt phẳng đáy $ (ABC) $, kẻ $ AH $ vuông góc với $ BC, H $ thuộc $ BC. $
- Trong mặt phẳng $ (SAH) $, kẻ $ AK $ vuông góc với $ SH, K $ thuộc $ SH. $
Dễ dàng chứng minh được $ K $ chính là hình chiếu vuông góc của điểm $ A $ lên mặt phẳng $(P)$. Thật vậy, chúng ta có $$ \begin{cases}
BC\perp SA\\
BC \perp AH\\
\end{cases} $$ Mà $SA$ và $AH$ là hai đường thẳng cắt nhau nằm trong mặt phẳng $ (SAH)$, nên suy ra \( BC \) vuông góc với \( (SAH) \), nên \( BC\perp AK \). Như vậy lại có
$$ \begin{cases}
AK\perp BC\\ AK\perp SH
\end{cases} $$ Mà $BC, AH $ là hai đường thẳng cắt nhau nằm trong mặt phẳng $(SBC)$, nên suy ra \( AK \) vuông góc với \( (SBC) \), hay \( K \) là hình chiếu vuông góc của \( A \) lên mặt phẳng \( (SBC) \).

Nếu bài viết hữu ích, bạn có thể tặng tôi 1 cốc cafe vào số tài khoản Agribank 3205215033513. Xin cảm ơn!

Dưới đây là hình minh họa trong các trường hợp đáy $ABC$ là tam giác vuông tại $ A,$ vuông tại $B,$ vuông tại $C $, tam giác cân, tam giác đều…
- Đáy $ABC$ là tam giác vuông tại $A$, lúc đó $H$ chính là chân đường cao kẻ từ đỉnh $A$ của tam giác \(ABC\), và dễ dàng tìm được công thức tính độ dài đoạn $AK$ như sau: $$ \frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AB^2}+\frac{1}{AC^2} $$
- Đáy $ABC$ là tam giác vuông tại $B$ (lúc đó $H$ trùng với điểm $B$).
- Đáy $ABC$ là tam giác vuông tại $C$ (lúc đó $H$ trùng với điểm $C$).
- Đáy $ABC$ là tam giác cân tại $A$ hoặc là tam giác đều (lúc đó $H$ chính là trung điểm của $BC$).
Bài toán 2. Dựng hình chiếu vuông góc sử dụng giao tuyến hai mặt phẳng vuông góc.

Cho hình chóp $ S.ABC $ cho có hai mặt phẳng $ (SBC) $ và $ (ABC) $ vuông góc với nhau. Hãy xác định hình chiếu vuông góc của điểm $A$ lên mặt phẳng $(SBC)$.

Phương pháp. Rõ ràng ở đây hai mặt phẳng vuông góc $ (SBC) $ và $ (ABC) $ cắt nhau theo giao tuyến là đường thẳng $BC$. Nên để dựng hình chiếu vuông góc của \( A \) lên mặt phẳng \( (SBC) \) ta chỉ việc hạ \( AK \) vuông góc với giao tuyến \( BC \) là xong. $$ \begin{cases}
(SBC)\perp (ABC)\\ (SBC)\cap (ABC) = BC\\ AK\subset (ABC)\\ AK\perp BC \end{cases} $$ Suy ra đường thẳng $AK$ vuông góc với mặt phẳng $(SBC)$, và $K$ chính là hình chiếu vuông góc của $A$ lên mặt phẳng $(SBC)$.

Ở đây chúng ta sử dụng định lý, hai mặt phẳng vuông góc với nhau và cắt nhau theo một giao tuyến. Đường thẳng nào nằm trong mặt phẳng thứ nhất và vuông góc với giao tuyến thì cũng vuông góc với mặt phẳng thứ hai.

2. Các ví dụ tính khoảng cách từ một điểm đến một mặt phẳng

Ví dụ 1. Cho hình chóp $ S.ABC,$ có $ SA $ vuông góc với đáy, $ SA=3a,$ $AB=a,$ $BC=2a,$ $\widehat{ABC}=60^\circ. $ Chứng minh tam giác $ ABC $ vuông và tính khoảng cách từ điểm $ B$ tới mặt phẳng $(SAC), $ khoảng cách từ điểm $ A $ đến mặt phẳng $ (SBC). $

Hướng dẫn. Áp dụng định lí cosin trong tam giác \(ABC\), ta có $$ AC^2=AB^2+BC^2-2AB\cdot BC\cdot \cos\widehat{B}=3a^2 $$ Rõ ràng \( BC^2=AB^2+AC^2 \) nên tam giác \(ABC\) vuông tại $A$. Lúc này, dễ dàng nhận thấy \( A \) chính là hình chiếu vuông góc của \( B \) lên mặt phẳng \( (SAC) \), và khoảng cách cần tìm $$ d(B,(SAC))=BA=a. $$

Em nào chưa biết cách chứng minh đường thẳng vuông góc với mặt phẳng thì có thể xem lại bài viết Cách chứng minh đường thẳng vuông góc với mặt phẳng

Để tính khoảng cách từ điểm $ A $ đến mặt phẳng $ (SBC) $, ta trình bày như bài toán 1 trường hợp đáy là tam giác vuông (ở đây thầy không viết lại nữa), đáp số$$ d(A,(SBC))=AK=\frac{3a}{\sqrt{13}}$$

Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $ a.$ Hai mặt phẳng $ (SAB),$ $(SAD) $ cùng vuông góc với đáy và cạnh $ SD $ tạo với đáy một góc $ 45^\circ. $ Tính khoảng cách từ điểm $ A $ đến mặt phẳng $ (SBC),$ khoảng cách từ điểm $ A $ đến mặt phẳng $(SBD) $.

Hướng dẫn. Hai mặt phẳng $ (SAB),(SAD) $ cùng vuông góc với đáy nên giao tuyến của chúng, là đường thẳng \( SA \) cũng vuông góc với mặt phẳng đáy \( (ABCD) \).

Nhặc lại định lý quan trọng, hai mặt phẳng vuông góc cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng (nếu có) cũng vuông góc với mặt phẳng thứ ba đó.

Lúc này, góc giữa đường thẳng \( SD \) và đáy chính là góc \( \widehat{SDA} \) và góc này bằng \( 45^\circ \). Suy ra, tam giác \( SAD \) vuông cân tại \( A \) và \( SA=AD=a \).

Tam giác \( SAB \) vuông cân có \( AK \) là đường cao và cũng là trung tuyến ứng với cạnh huyền, nên \( AK=\frac{1}{2}SB=\frac{a\sqrt{2}}{2} \).

Để tính khoảng cách từ điểm $ A $ đến mặt phẳng $ (SBC),$ chúng ta cố gắng nhìn ra mô hình giống như trong bài toán 1. Bằng việc kẻ vuông góc hai lần, lần thứ nhất, trong mặt phẳng \( (ABCD) \) ta hạ đường vuông góc từ \( A \) tới \( BC \), chính là điểm \( B \) có sẵn luôn. Kẻ vuông góc lần thứ hai, trong mặt phẳng \( (SAB) \) ta hạ đường vuông góc từ \( A \) xuống \( SB \), gọi là \( AK \) thì độ dài đoạn \( AK \) chính là khoảng cách cần tìm.

Để tính khoảng cách từ điểm $ A $ đến mặt phẳng $(SBD) $ ta vẫn tiếp tục làm như kỹ thuật trong bài toán 1. Chúng ta kẻ vuông góc hai lần, lần thứ nhất từ \( A \) kẻ vuông góc xuống \( BC \), chính là tâm \( O \) của hình vuông luôn (vì hình vuông thì hai đường chéo vuông góc với nhau). Nối \( S \) với \( O \) và từ \( A \) tiếp tục hạ đường vuông góc xuống \( SO \), gọi là \(AH \) thì chứng minh được \( H \) là hình chiếu vuông góc của \( A \) lên mặt phẳng \( (SBD) \). Chúng ta có ngay

$$ \frac{1}{AH^2}=\frac{1}{AS^2}+\frac{1}{AB^2}+\frac{1}{AD^2}=\frac{3}{a^2} $$

Từ đó tìm được $AH=\frac{a\sqrt{3}}{3}$ và khoảng cách cần tìm là $ d(A,(SBD)=AH=\frac{a\sqrt{3}}{3}$.

Ví dụ 3. Cho hình tứ diện $ ABCD $ có cạnh $ AD $ vuông góc với mặt phẳng $ (ABC) $, ngoài ra $ AD = AC = 4 $ cm; $ AB = 3 $ cm; $ BC = 5 $ cm. Tìm khoảng cách từ $ A $ đến mặt phẳng $ (BCD). $

Ví dụ 4. [Đề thi ĐH khối D năm 2003] Cho hai mặt phẳng $ (P),(Q) $vuông góc với nhau và cắt nhau theo giao tuyến $ \Delta. $ Lấy $ A , B $ thuộc $ \Delta $ và đặt $ AB=a $. Lấy $ C , D $ lần lượt thuộc hai mặt phẳng $ (P),(Q) $ sao cho $ AC , BD $ vuông góc với $ \Delta $ và $ AC=BD=a. $ Tính khoảng cách từ $ A $ đến mặt phẳng $ (BCD).$

Hướng dẫn. Hạ $ AH\perp BC $ thì $ d(A,(BCD))=AH=\frac{a}{\sqrt{2}} $.

Ví dụ 5. [Đề thi ĐH Khối D năm 2012] Cho hình hộp đứng $ $ABCD$.A’B’C’D’ $ có đáy là hình vuông, tam giác $ A’AC $ vuông cân, $ A’C=a $. Tính khoảng cách từ điểm $ A $ đến mặt phẳng $ (BCD’) $ theo $ a. $

Hướng dẫn. Chú ý rằng mặt phẳng $ (BCD’) $ chính là mặt phẳng $ (BCD’A’) $. Đáp số, khoảng cách từ $ A$ đến mặt phẳng $(BCD’) $ bằng $\frac{a\sqrt{6}}{3}$.

Khi việc tính trực tiếp gặp khó khăn, ta thường sử dụng kĩ thuật dời điểm, để đưa về tính khoảng cách của những điểm dễ tìm được hình chiếu vuông góc hơn.

Ví dụ 6. Cho hình lăng trụ đứng tam giác $ ABC.A’B’C’ $ có đáy $ ABC $ là tam giác vuông tại $ A,AB=3a,AC=4a. $ Biết cạnh bên $ AA’=4a$ và $ M $ là trung điểm $ AA’ $. Hãy tính khoảng cách $ {d}(M,(A’B’C)) $ và $ {d}(M,(A’B’C)) $.

Ví dụ 7. Cho hình chóp $ S.ABC $ có đáy là tam giác vuông tại $ B,$ $AB=3a,$ $ BC=4a.$ Mặt phẳng $ (SBC) $ vuông góc với mặt đáy và $ SB=2a\sqrt{3},$ $\widehat{SBC}=30^\circ. $ Tính khoảng cách từ điểm $B$ tới mặt phẳng $(SAC). $

Hướng dẫn. Gọi $ SH $ là đường cao của tam giác $ SBC $ thì $ SH\perp (ABC). $ Ta có $$ \frac{{d}(B,(SAC))}{{d}(H,(SAC))}=\frac{BC}{HC}=4 $$ Từ đó tính được $ {d}(B,(ABC)) =\frac{6a}{\sqrt{7}}.$

3. Bài tập về khoảng cách từ điểm đến mặt phẳng

Mời thầy cô và các em học sinh tải các tài liệu về bài toán khoảng cách trong hình học không gian tại đây:
Tổng hợp tài liệu HHKG lớp 11 và ôn thi ĐH, THPT QG đầy đủ nhất, mời thầy cô và các em xem trong bài viết 38+ tài liệu hình học không gian 11 hay nhất
02/06/2020