MỘT SỐ BÀI TOÁN QUY HOẠCH ĐỘNG ĐIỂN HÌNH
Quy hoạch động là gì?
Theo wiki, quy hoạch động (tiếng Anh: dynamic programming) là một phương pháp giảm thời gian chạy của các thuật toán thể hiện các tính chất của các bài toán con gối nhau (overlapping subproblem) và cấu trúc con tối ưu (optimal substructure).
Cấu trúc con tối ưu có nghĩa là các lời giải tối ưu cho các bài toán con có thể được sử dụng để tìm các lời giải tối ưu cho bài toán toàn cục. Ví dụ, đường đi ngắn nhất tới một đỉnh trong một đồ thị có thể được tìm thấy bằng cách: trước hết tính đường đi ngắn nhất tới đích từ tất cả các đỉnh kề nó, rồi dùng kết quả này để chọn đường đi toàn cục tốt nhất, như trong hình sau.
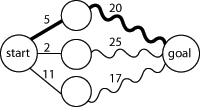
Nói chung, ta có thể giải một bài toán với cấu trúc con tối ưu bằng một quy trình ba bước:
- Chia bài toán thành các bài toán con nhỏ hơn.
- Giải các bài toán này một cách tối ưu bằng cách sử dụng đệ quy quy trình ba bước này.
- Sử dụng các kết quả tối ưu đó để xây dựng một lời giải tối ưu cho bài toán ban đầu.
Các bài toán con được giải bằng cách chia chúng thành các bài toán nhỏ hơn, và cứ tiếp tục như thế, cho đến khi ta đến được trường hợp đơn giản dễ tìm lời giải.
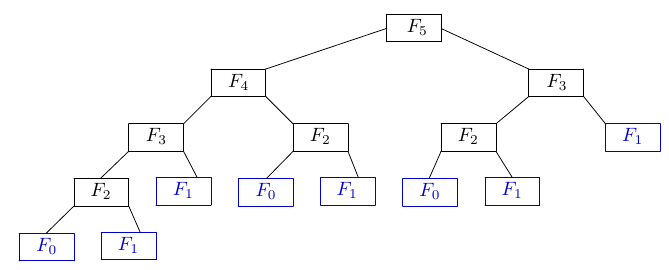
Nói rằng một bài toán có các bài toán con trùng nhau có nghĩa là mỗi bài toán con đó được sử dụng để giải nhiều bài toán lớn hơn khác nhau. Ví dụ, trong dãy Fibonacci, F3 = F1 + F2 và F4 = F2 + F3 — khi tính mỗi số đều phải tính F2. Vì tính F5 cần đến cả F3 và F4, một cách tính F5 một cách ngây thơ có thể sẽ phải tính F2 hai lần hoặc nhiều hơn. Điều này áp dụng mỗi khi có mặt các bài toán con gối nhau: một cách tiếp cận ngây thơ có thể tốn thời gian tính toán lại lời giải tối ưu cho các bài toán con mà nó đã giải.
Xem thêm: Giải thuật Đệ quy là gì?
Dãy con đơn điệu dài nhất
1. Mô hình
Cho dãy a_1, a_2,… a_n. Hãy tìm một dãy con tăng có nhiều phần tử nhất của nó.
Đặc trưng:
- Các phần tử trong dãy kết quả chỉ xuất hiện một lần. Vì vậy phương pháp làm là ta sẽ dùng vòng lặp
for duyệt qua các phần tử a_i trong dãy, khác với các bài toán của mô hình 4 (đặc trưng là bài toán đổi tiền), các phần tử trong dãy có thể được chọn nhiều lần nên ta thực hiện bằng phương pháp cho giá trị cần quy đổi tăng dần từng đơn vị.
- Thứ tự của các phần tử được chọn phải được giữ nguyên so với dãy ban đầu.
Đặc trưng này có thể mất đi trong một số bài toán khác tùy vào yêu cầu cụ thể, chẳng hạn bài Tam giác bao nhau.
2. Công thức quy hoạch động
Hàm mục tiêu: f = độ dài dãy con.
Vì độ dài dãy con chỉ phụ thuộc vào một yếu tố là dãy ban đầu nên bảng phương án là bảng một chiều. Gọi L(i) là độ dài dãy con tăng dài nhất, các phần tử lấy trong miền từ a_1đến a_i và phần tử cuối cùng là a_i.
Nhận xét với cách làm này ta đã chia bài toán lớn (dãy con của n số) thành các bài toán con cùng kiểu có kích thước nhỏ hơn (dãy con của dãy i số). Vấn đề là công thức truy hồi để phối hợp kết quả của các bài toán con.
Ta có công thức QHĐ để tính L(i) như sau:
L(1) = 1. (Hiển nhiên)L(i) = max(1, L(j)+1) với mọi phần tử j thỏa mãn 0<j<i và a_j <= a_i.
Tính L(i): Phần tử đang được xét là a_i. Ta tìm đến phần tử a_j < a_i có L(j) lớn nhất. Khi đó nếu bổ sung a_i vào sau dãy con ...a_j ta sẽ được dãy con tăng dần dài nhất xét từ a_1đến a_i.
3. Cài đặt
Bảng phương án là một mảng một chiều L để lưu trữ các giá trị của hàm QHĐ L(i). Đoạn chương trình tính các giá trị của mảng L như sau:
for i: = 1 to n do begin
L[i]: = 1;
for j:=1 to i–1 do
if (a[j]<=a[i]) and (L[i]<L[j]+1) then
L[i]:=L[j]+1;
end;
Như vậy chi phí không gian của bài toán là O(n), chi phí thời gian là O(n2). Có một phương pháp cài đặt tốt hơn so với phương pháp trên, cho chi phí thời gian là O(n log(n)).
4. Một số bài toán khác
Bài toán dãy con đơn điệu tăng dài nhất có biến thể đơn giản nhất là bài toán dãy con đơn điệu giảm dài nhất, tuy nhiên chúng ta có thể coi chúng như là một. Sau đây là một số bài toán khác.
a) Bố trí phòng họp (mất tính thứ tự so với dãy ban đầu)
Có n cuộc họp, cuộc họp thứ i bắt đầu vào thời điểm a_i và kết thúc ở thời điểm b_i. Do chỉ có một phòng hội thảo nên hai cuộc họp bất kì sẽ được cùng bố trí phục vụ nếu khoảng thời gian làm việc của chúng chỉ giao nhau tại đầu mút. Hãy bố trí phòng họp để phục vụ được nhiều cuộc họp nhất.
Hướng dẫn: Sắp xếp các cuộc họp tăng dần theo thời điểm kết thúc b_i. Thế thì cuộc họp i sẽ bố trí được sau cuộc họp j nếu và chỉ nếu j<i và b_j <= a_i. Yêu cầu bố trí được nhiều cuộc họp nhất có thể đưa về việc tìm dãy các cuộc họp dài nhất thoả mãn điều kiện trên.
b) Cho thuê máy
Trung tâm tính toán hiệu năng cao nhận được đơn đặt hàng của n khách hàng. Khách hàng i muốn sử dụng máy trong khoảng thời gian từ a_i đến b_i và trả tiền thuê là c_i. Hãy bố trí lịch thuê máy để tổng số tiền thu được là lớn nhất mà thời gian sử dụng máy của hai khách hàng bất kì được phục vụ đều không giao nhau (cả trung tâm chỉ có một máy cho thuê).
Hướng dẫn: Tương tự như bài toán a), nếu sắp xếp các đơn đặt hàng theo thời điểm kết thúc, ta sẽ đưa được bài toán b) về bài toán tìm dãy con có tổng lớn nhất. Bài toán này là biến thể của bài toán tìm dãy con tăng dài nhất, ta có thể cài đặt bằng đoạn chương trình như sau:
for i:=1 to n do begin
L[i]:=c[i];
for j:=1 to i–1 do
if (b[j]<=a[i]) and (L[i]<L[j]+c[i]) then
L[i]:=L[j]+c[i];
end;
c) Dãy tam giác bao nhau
Cho n tam giác trên mặt phẳng. Tam giác i bao tam giác j nếu ba đỉnh của tam giác j đều nằm trong tam giác i (có thể nằm trên cạnh). Hãy tìm dãy tam giác bao nhau có nhiều tam giác nhất.
Hướng dẫn: Sắp xếp các tam giác tăng dần về diện tích. Khi đó tam giác i sẽ bao tam giác j nếu j<i và ba đỉnh của j nằm trong i. Từ đó có thể đưa về bài toán tìm dãy “tăng” dài nhất.
Việc kiểm tra điểm M có nằm trong tam giác ABC không có thể dựa trên phương pháp tính diện tích: Điểm M nằm trong nếu S(ABC) = S(ABM) + S(ACM) + S(BCM).
Bài toán có một số biến thể khác như tìm dãy hình tam giác, hình chữ nhật… bao nhau có tổng diện tích lớn nhất.
d) Dãy số WAVIO
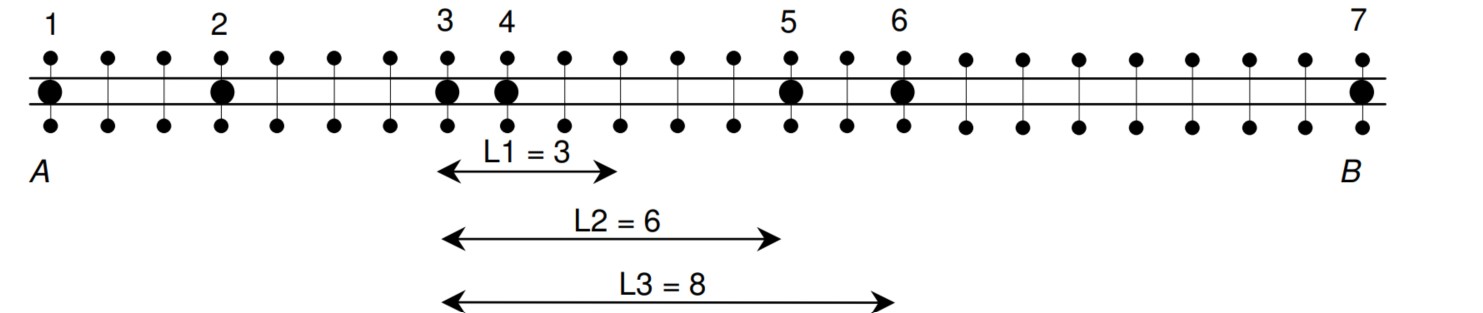
Dãy số Wavio là dãy số nguyên thỏa mãn các tính chất, các phần tử đầu sắp xếp thành một dãy tăng dần đến một phần tử đỉnh sau đó giảm dần. Ví dụ dãy số 1 2 3 4 5 2 1 là dãy Wavio độ dài 7.
Cho một dãy gồm N số nguyên, hãy chỉ ra một dãy con WAVIO có độ dài lớn nhất trích ra từ dãy đó.
Hướng dẫn: L1[i] là mảng ghi độ dài lớn nhất của 1 dãy con tăng dần trích ra từ dãy N phần tử kể từ phần tử 1 đến phần tử ai. L2[i]: mảng ghi độ dài lớn nhất của dãy con giảm dần trích ra từ dãy N phần tử kể từ phần tử aN đến ai. Ta tìm phần tử j trong 2 mảng L1, L2 thỏa mãn L1[j]+L2[j] lớn nhất.
e) Xếp các khối đá
Cho N khối đá (N≤5000). Các khối đá đều có dạng hình hộp chữ nhật và được đặc trưng bới 3 kích thước: dài, rộng, cao. Một cách xây dựng tháp là một cách đặt một số các khối đá trong các khối đá đã cho chồng lên nhau theo quy tắc:
- Chiều cao mỗi khối đá là kích thước nhỏ nhất trong 3 kích thước.
- Các mép của khối đá được đặt song song với nhau sao cho không có phần nào của khối trên nằm chìa ra ngoài khối dưới.
a) Hãy chỉ ra cách để xây dựng được một cái tháp sao cho số khối đá được dùng là nhiều nhất.
b) Hãy chỉ ra cách để xây dựng được một cái tháp sao cho chiều cao của cái tháp là cao nhất.
Dữ liệu vào TOWER.INP có cấu trúc như sau:
- Dòng đầu là số N.
- N dòng sau dòng i ghi 3 số nguyên ≤ 255 là 3 kích thước của khối đá i.
Dữ liệu ra: TOWER1.OUT, TOWER2.OUT ghi theo quy cách:
- Dòng đầu ghi số các khối đá được chọn theo thứ tự dùng để xây tháp từ chân lên đỉnh.
- Các dòng sau ghi các khối được chọn, mỗi khối đá ghi 4 số T, D, R, C trong đó T là số thứ tự của mỗi khối đá. D, R, C là kích thước của khối đá tương ứng.
II. Vali (B)
1. Mô hình
Có n đồ vật, vật thứ i có trọng lượng a[i] và giá trị b[i]. Hãy chọn ra một số các đồ vật, mỗi vật một cái để xếp vào 1 vali có trọng lượng tối đa W sao cho tổng giá trị của vali là lớn nhất.
2. Công thức
Hàm mục tiêu: f: tổng giá trị của vali.
Nhận xét: giá trị của vali phụ thuộc vào 2 yếu tố: có bao nhiêu vật đang được xét và trọng lượng của các vật. Do đó bảng phương án sẽ là bảng 2 chiều.
L[i,j]: tổng giá trị lớn nhất của vali khi xét từ vật 1..vật i và trọng lượng của vali chưa vượt quá j. Chú ý rằng khi xét đến L[i,j] thì các giá trị trên bảng phương án đều đã được tối ưu.
Tính L[i,j]: vật đang xét là ai với trọng lượng của vali không được quá j. Có 2 khả năng xảy ra:
- Nếu chọn aiđưa vào vali, trọng lượng vali trước đó phải ≤ j-a[i]. Vì mỗi vật chỉ được chọn 1 lần nên giá trị lớn nhất của vali lúc đó là L[i-1,j-a[i]) + b[i]
- Nếu không chọn ai , trọng lượng của vali là như cũ (như lúc trước khi chọn ai ): L[i-1,j].
Tóm lại ta có L[i,j]=max(L(i-1,j-a[i]) + b[i], L[i-1,j]).
3. Cài đặt
For i:=1 to n do
For j:=1 to W do
If b[i]<=j then
L[i,j]:=max(L(i-1,j-a[i]) + b[i], L[i-1,j])
else L[i,j]:=L[i-1,j];
4. Một số bài toán khác
a) Dãy con có tổng bằng S
Cho dãy a1,a2,..an. Tìm một dãy con của dãy đó có tổng bằng S.
Hướng dẫn
Đặt L[i,t)=1 nếu có thể tạo ra tổng t từ một dãy con của dãy gồm các phần tử a1,a2,..ai. Ngược lại thì L[i,t)=0. Nếu L[n,S)=1 thì đáp án của bài toán trên là “có”.
Ta có thể tính L[i,t] theo công thức: L[i,t]=1 nếu L[i–1,t]=1 hoặc L[i–1,t–a[i]]=1.
Cài đặt
Nếu áp dụng luôn công thức trên thì ta cần dùng bảng phương án hai chiều. Ta có thể nhận xét rằng để tính dòng thứ i, ta chỉ cần dòng i–1. Bảng phương án khi đó chỉ cần 1 mảng 1 chiều L[0..S] và được tính như sau:
L[t]:=0; L[0]:=1;
for i: = 1 to n do
for t: = S downto a[i] do
if (L[t]=0) and (L[t–a[i]]=1) then L[t]:=1;
Dễ thấy chi phí không gian của cách cài đặt trên là O(m), chi phí thời gian là O(nm), với m là tổng của n số. Hãy tự kiểm tra xem tại sao vòng for thứ 2 lại là for downto chứ không phải là for to.
b) Chia kẹo
Cho n gói kẹo, gói thứ i có ai viên. Hãy chia các gói thành 2 phần sao cho chênh lệch giữa 2 phần là ít nhất.
Hướng dẫn: Gọi T là tổng số kẹo của n gói. Chúng ta cần tìm số S lớn nhất thoả mãn:
- S≤T/2.
- Có một dãy con của dãy a có tổng bằng S.
Khi đó sẽ có cách chia với chênh lệch 2 phần là T–2S là nhỏ nhất và dãy con có tổng bằng S ở trên gồm các phần tử là các gói kẹo thuộc phần thứ nhất. Phần thứ hai là các gói kẹo còn lại.
c) Market (Olympic Balkan 2000)
Người đánh cá Clement bắt được n con cá, khối lượng mỗi con là ai, đem bán ngoài chợ. Ở chợ cá, người ta không mua cá theo từng con mà mua theo một lượng nào đó. Chẳng hạn 3kg, 5kg…
Ví dụ: có 3 con cá, khối lượng lần lượt là: 3, 2, 4. Mua lượng 6 kg sẽ phải lấy con cá thứ 2 và và thứ 3. Mua lượng 3 kg thì lấy con thứ nhất. Không thể mua lượng 8 kg.
Nếu bạn là người đầu tiên mua cá, có bao nhiêu lượng bạn có thể chọn?
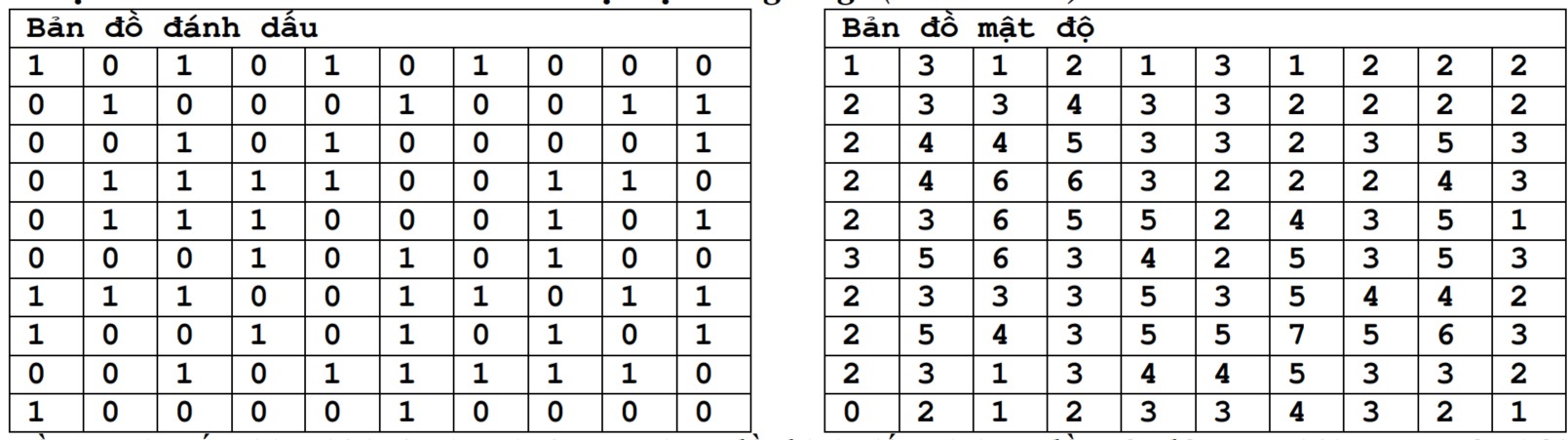
Hướng dẫn: Thực chất bài toán là tìm các số S mà có một dãy con của dãy a có tổng bằng S. Ta có thể dùng phương pháp đánh dấu của bài chia kẹo ở trên rồi đếm các giá trị t mà L[t]=1.
d) Điền dấu
Cho n số tự nhiên a1,a2,. ..,an. Ban đầu các số được đặt liên tiếp theo đúng thứ tự cách nhau bởi dấu “?”: a1?a2?…?an. Cho trước số nguyên S, có cách nào thay các dấu “?” bằng dấu + hay dấu – để được một biểu thức số học cho giá trị là S không?
Hướng dẫn: Đặt L(i,t)=1 nếu có thể điền dấu vào i số đầu tiên và cho kết quả bằng t. Ta có công thức sau để tính L:
- L(1,a[1]) =1.
- L(i,t)=1 nếu L(i–1,t+a[i])=1 hoặc L(i–1,t–a[i])=1.
Nếu L(n,S)=1 thì câu trả lời của bài toán là có. Khi cài đặt, có thể dùng một mảng 2 chiều (lưu toàn bộ bảng phương án) hoặc 2 mảng một chiều (để lưu dòng i và dòng i–1). Chú ý là chỉ số theo t của các mảng phải có cả phần âm (tức là từ –T đến T, với T là tổng của n số), vì trong bài này chúng ta dùng cả dấu – nên có thể tạo ra các tổng âm.
Bài này có một biến thể là đặt dấu sao cho kết quả là một số chia hết cho k. Ta có thuật giải tương tự bài toán trên bằng cách thay các phép cộng, trừ bằng các phép cộng và trừ theo môđun k và dùng mảng đánh dấu với các giá trị từ 0 đến k–1 (là các số dư có thể có khi chia
cho k). Đáp số của bài toán là L(n,0).
e) Expression (ACM 10690)
Cho n số nguyên. Hãy chia chúng thành 2 nhóm sao cho tích của tổng 2 nhóm là lớn nhất.
Hướng dẫn: Gọi T là tổng n số nguyên đó. Giả sử ta chia dãy thành 2 nhóm, gọi S là tổng của một nhóm, tổng nhóm còn lại là T–S và tích của tổng 2 nhóm là S*(T–S). Bằng phương pháp đánh dấu ta xác định được mọi số S là tổng của một nhóm (như bài Market) và tìm số S sao
cho S*(T–S) đạt max.
III. Biến đổi xâu
1. Mô hình
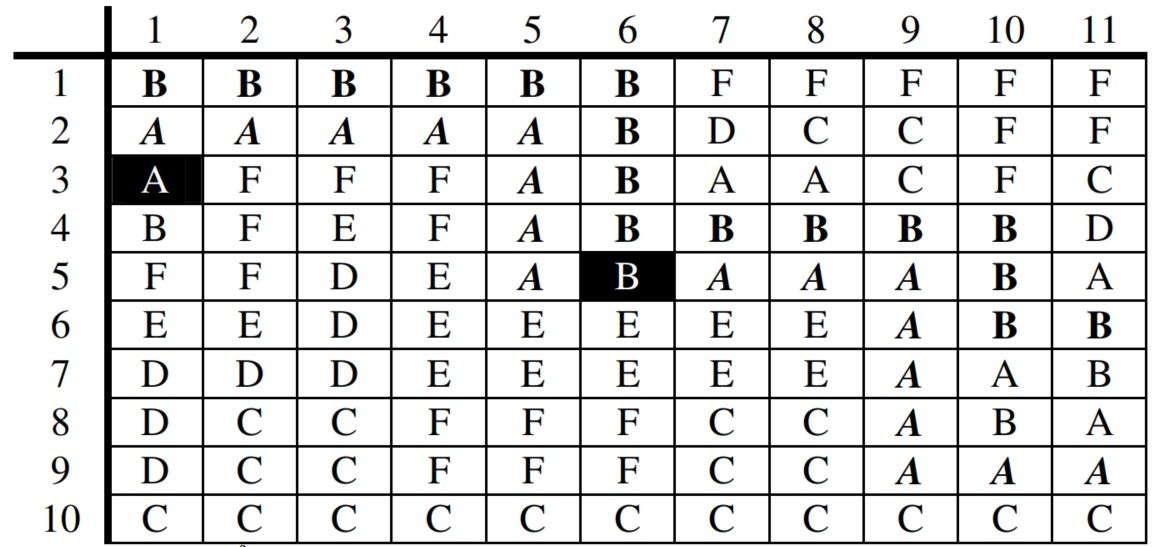
Cho 2 xâu X,F. Xâu nguồn có n kí tự X1X2…Xn , xâu đích có m kí tự F1F2…Fm. Có 3 phép biến đổi:
- Chèn một kí tự vào sau kí tự thứ i: I i C
- Thay thế kí tự ở vị trí thứ i bằng kí tự C: R i C.
- Xoá kí tự ở vị trí thứ i. D i
Hãy tìm số ít nhất các phép biến đổi để biến xâu X thành xâu F.
Hướng dẫn:
Hàm mục tiêu: f: số phép biến đổi.
Dễ thấy số phép biến đổi phụ thuộc vào vị trí i đang xét của xâu X và vị trí j đang xét cuả xâu F. Do vậy để cài đặt cho bang phương án ta sẽ dùng mảng 2 chiều Gọi L(i,j) là số phép biến đổi ít nhất để biến xâu X(i) gồm i kí tự phần đầu của X (X(i)=X[1..i]) thành xâu F(j) gồm j kí tự phần đầu của F(F(j) =F[1..j]). Dễ thấy F(0,j)=j và F(i,0)=i.
Có 2 trường hợp xảy ra:
Nếu X[i]=F[j]:
X1X2…Xi-1 Xi
F1F2…Fj-1 Xi
thì ta chỉ phải biến đổi xâu X(i-1) thành xâu Y(j-1). Do đó F(i,j)=F(i-1,j-1).
Ngược lại, ta có 3 cách biến đổi:
Xoá kí tự X[i]: X1X2…Xi-1 Xi
F1F2…Fj-1 Fj
Xâu X(i-1) thành F(j). Khi đó F(i,j)=F(i-1,j)+1.(Cộng 1 là do ta đã dùng 1 phép xóa)
Thay thế X[i] bởi F[j]: X1X2…Xi-1 Fj
| F1F2…Fj-1 |
Fj |
| Xâu X(i-1) thành F(j-1). Khi đó F(i,j)=F(i-1,j-1)+1. |
| Chèn F[j] vào X(i): |
X1X2…Xi-1XiFj |
F1F2…Fj-1 Fj
Xâu X(i) thành Y(j-1). Khi đó F(i,j)=F(i,j-1)+1.
Tổng kết lại, ta có công thức QHĐ:
- F(0,j)=j
- F(i,0)=i
- F(i,j) =F(i-1,j-1) nếu X[i] = Y[j].
- F(i,j) = min(F(i-1,j),F(i,j-1),F(i-1,j-1))+1 nếu X[i]≠Y[j].
Bài này ta có thể tiết kiệm biến hơn bằng cách dùng 2 mảng 1 chiều tính lẫn nhau và một mảng đánh dấu 2 chiều để truy vết.
4. Một số bài toán khác
a) Xâu con chung dài nhất
Cho 2 xâu X,Y. Hãy tìm xâu con của X và của Y có độ dài lớn nhất.
Công thức QHĐ
Gọi L(i,j) là độ dài xâu con chung dài nhất của xâu X(i) gồm i kí tự phần đầu của X (X(i)=
X[1..i]) và xâu Y(j) gồm j kí tự phần đầu của Y (Y(j) =Y[1..j]).
Ta có công thức quy hoạch động như sau:
• L(0,j)=L(i,0)=0.
• L(i,j) = L(i-1,j-1)+1 nếu X[i] = Y[j].
• L(i,j) = max(L(i-1,j), L(i,j-1)) nếu X[i]≠Y[j].
Cài đặt
Bảng phương án là một mảng 2 chiều L[0..m,0..n] để lưu các giá trị của hàm QHĐ L(i,j).
Đoạn chương trình cài đặt công thức QHĐ trên như sau:
for i:=0 to m do L[i,0]:=0;
for j:=0 to n do L[0,j]:=0;
for i:=1 to m do
for j:=1 to n do
if X[i]=Y[j] then
L[i,j]:=L[i–1,j–1]+1
else
L[i,j]:=max(L[i–1,j],L[i,j–1]]);
Như vậy chi phí không gian của bài toán là O(n2), chi phí thời gian là O(n2). Có một phương
pháp cài đặt tốt hơn, chỉ với chi phí không gian O(n) dựa trên nhận xét sau: để tính ô L[i,j]
của bảng phương án, ta chỉ cần 3 ô L[i–1,j–1],L[i–1,j] và L[i,j–1]. Tức là để tính dòng L[i]
thì chỉ cần dòng L[i–1]. Do đó ta chỉ cần 2 mảng 1 chiều để lưu dòng vừa tính (P) và dòng
đang tính (L) mà thôi. Cách cài đặt mới như sau:
for j:=0 to n do P[j]:=0;
for i:=1 to m do begin
L[0]: = 0;
for j:=1 to n do
if X[i]=Y[j] then
L[i,j]:=P[j–1]+1
else L[i,j]:=max(P[j], L[j–1]);
P: = L;
end;
c) Bắc cầu
Hai nước Anpha và Beta nằm ở hai bên bờ sông Omega, Anpha nằm ở bờ bắc và có M thành phố được đánh số từ 1 đến m, Beta nằm ở bờ nam và có N thành phố được đánh số từ 1 đến n (theo vị trí từ đông sang tây). Mỗi thành phố của nước này thường có quan hệ kết nghĩa với một số thành phố của nước kia. Để tăng cường tình hữu nghị, hai nước muốn xây các cây cầu bắc qua sông, mỗi cây cầu sẽ là nhịp cầu nối 2 thành phố kết nghĩa. Với yêu cầu là các cây cầu không được cắt nhau và mỗi thành phố chỉ là đầu cầu cho nhiều nhất là một cây cầu, hãy chỉ ra cách bắc cầu được nhiều cầu nhất.
Hướng dẫn: Gọi các thành phố của Anpha lần lượt là a1,a2,…am; các thành phố của Beta là
b1,b2,…bn. Nếu thành phố ai và bj kết nghĩa với nhau thì coi ai “bằng” bj. Để các cây cầu
không cắt nhau, nếu ta đã chọn cặp thành phố (ai,bj) để xây cầu thì cặp tiếp theo phải là cặp
(au,bv) sao cho u>i và v>j. Như vậy các cặp thành phố được chọn xây cầu có thể coi là một
dãy con chung của hai dãy a và b.
Bài toán của chúng ta trở thành bài toán tìm dãy con chung dài nhất, ở đây hai phần tử “bằng” nhau nếu chúng có quan hệ kết nghĩa.
d) Palindrom (IOI 2000)
Một xâu gọi là xâu đối xứng (palindrom) nếu xâu đó đọc từ trái sang phải hay từ phải sang
trái đều như nhau. Cho một xâu S, hãy tìm số kí tự ít nhất cần thêm vào S để S trở thành xâu
đối xứng.
Hướng dẫn: Bài toán này có một công thức QHĐ như sau:
Gọi L(i,j) là số kí tự ít nhất cần thêm vào xâu con S[i..j] của S để xâu đó trở thành đối xứng.
Đáp số của bài toán sẽ là L(1,n) với n là số kí tự của S. Ta có công thức sau để tính L(i,j):
• L(i,i)=0.
• L(i,j)=L(i+1,j–1) nếu S[i]=S[j]
• L(i,j)=max(L(i+1,j), L(i,j–1)) nếu S[i]≠S[j]
Bạn đọc dễ dàng có thể kiểm chứng công thức đó. Ta có thể cài đặt trực tiếp công thức đó
bằng phương pháp đệ quy có nhớ. Tuy nhiên khi đó chi phí không gian là O(n2). Có một
phương pháp cài đặt tiết kiệm hơn (bạn đọc có thể tham khảo ở bài báo trên của thầy Trần Đỗ
Hùng), tuy nhiên phương pháp đó khá phức tạp.
Ta có thuật toán đơn giản hơn như sau:
Gọi P là xâu đảo của S và T là xâu con chung dài nhất của S và P. Khi đó các kí tự của S
không thuộc T cũng là các kí tự cần thêm vào để S trở thành đối xứng. Đáp số của bài toán sẽ
là n–k, với k là độ dài của T.
Ví dụ: S=edbabcd, xâu đảo của S là P=dcbabde. Xâu con chung dài nhất của S và P là
T=dbabd. Như vậy cần thêm 2 kí tự là e và c vào để S trở thành xâu đối xứng.
IV. Vali (A)
1. Mô hình
Cho n vật, vật i nặng ai và có giá trị bi. Hãy chọn ra một số vật để cho vào balô sao cho tổng
khối lượng không vượt quá W và tổng giá trị là lớn nhất. Chú ý rằng mỗi vật có thể được chọn
nhiều lần.
2. Công thức
Gọi L(i,j) là tổng giá trị lớn nhất khi được chọn i vật từ 1 đến i cho vào balô với tổng khối
lượng không vượt quá j. L(n,W) sẽ là đáp số của bài toán (là giá trị lớn nhất có được nếu chọn
n vật và tổng khối lượng không vượt quá W).
Công thức tính L(i,t) như sau:
• L(i,0)=0; L(0,j)=0.
• L(i,j)=L(i,j) nếu t<ai.
• L(i,t)=max(L(i-1,j), L(i,j–ai)+bi) nếu t ≥ai.
Trong đó: L(i–1,j) là giá trị có được nếu không đưa vật i vào balô, L(i,j–ai)+bi là giá trị có
được nếu chọn vật i.
3. Cài đặt
Ta có thể dùng một mảng 2 chiều để lưu bảng phương án, tuy nhiên dựa trên nhận xét rằng để
tính dòng i của bảng phương án chỉ cần dòng i–1, ta chỉ cần dùng 2 mảng một chiều P và L có
chỉ số từ 0 đến m để lưu 2 dòng đó. Đoạn chương trình con tính bảng phương án như sau.
L[t]: = 0; {với mọi t}
for i: = 1 to n do begin
P:=L;
for t: = 0 to m do
if t<a[i] then L[t]:=P[t]
else L[t]: = max(P[t],P[t–a[i]]);
end;
Nếu để ý kĩ bạn sẽ thấy rằng đoạn trình trên chỉ viết giống công thức QHĐ chứ chưa tối ưu.
Chẳng hạn đã có lệnh gán P:=L, sau đó lại có gán L[t]:=P[t] với các giá trị t<a[i] là không cần
thiết. Bạn đọc có thể tự cải tiến để chương trình tối ưu hơn.
Chi phí không gian của cách cài đặt trên là O(m) và chi phí thời gian là O(n.m).
4. Một số bài toán khác
a) Farmer (IOI 2004)
Một người có N mảnh đất và M dải đất. Các mảnh đất có thể coi là một tứ giác và các dải đất
thì coi như một đường thẳng. Dọc theo các dải đất ông ta trồng các cây bách, dải đất thứ i có
ai cây bách. Ông ta cũng trồng các cây bách trên viền của các mảnh đất, mảnh đất thứ j có bj
cây bách. Cả ở trên các mảnh đất và dải đất, xen giữa 2 cây bách ông ta trồng một cây ôliu.
Ông ta cho con trai được chọn các mảnh đất và dải đất tuỳ ý với điều kiện tổng số cây bách
không vượt quá Q. Người con trai phải chọn thế nào để có nhiều cây ôliu (loài cây mà anh ta
thích) nhất.
Hướng dẫn: Dễ thấy mảnh đất thứ i có ai cây ôliu và dải đất thứ j có bj–1 cây ôliu. Coi các
mảnh đất và dải đất là các “đồ vật”, đồ vật thứ k có khối lượng wk và giá trị vk (nếu k là mảnh
đất i thì wk=vk=ai, nếu k là dải đất j thì wk=bj, vk=bj–1). Ta cần chọn các “đồ vật”, sao cho
tổng “khối lượng” của chúng không vượt Q và tổng “giá trị” là lớn nhất. Đây chính là bài toán
xếp balô đã trình bày ở trên.
b) Đổi tiền
Ở đất nước Omega người ta chỉ tiêu tiền xu. Có N loại tiền xu, loại thứ i có mệnh giá là ai
đồng. Một người khách du lịch đến Omega du lịch với số tiền M đồng. Ông ta muốn đổi số
tiền đó ra tiền xu Omega để tiện tiêu dùng. Ông ta cũng muốn số đồng tiền đổi được là ít nhất
(cho túi tiền đỡ nặng khi đi đây đi đó). Bạn hãy giúp ông ta tìm cách đổi tiền.
Hướng dẫn: Bài toán này khá giống bài toán xếp balô (“khối lượng” là mệnh giá, “giá trị” là
1), chỉ có một số thay đổi nhỏ: số đồng xu mỗi loại được chọn tuỳ ý (trong bài toán xếp balô
mỗi đồ vật chỉ được chọn 1 lần) và tổng giá trị yêu cầu là nhỏ nhất.
Do đó ta cũng xây dựng hàm QHĐ một cách tương tự: Gọi L(i,t) là số đồng xu ít nhất nếu đổi
t đồng ra i loại tiền xu (từ 1 đến i). Công thức tính L(i,t) như sau:
• L(i,0)=0;
• L(0,t)= ∞ với t>0.
• L(i,t)=L(i–1,t) nếu t<ai.
• L(i,t)=min(L(i–1,t), L(i,t–ai)+1) nếu t ≥ai.
Công thức này khác công thức của bài xếp balô ở chỗ: dùng hàm min chứ không phải hàm
max (vì cần tìm cách chọn ít hơn) và nếu chọn đồng xu thứ i thì L(i,t)=L(i,t–ai)+1 (vì ta vẫn
còn được chọn đồng xu thứ i đó nữa), khác với khi xếp balô là: nếu chọn đồ vật thứ i thì
L(i,t)=L(i–1,t–ai)+bi vì đồ vật i chỉ được chọn một lần.
V. Nhân ma trận
1. Mô hình
Nhân một ma trận kích thước m×n với một ma trận n×p, số phép nhân phải thực hiện là m.n.p. Mặt khác phép nhân các ma trận có tính kết hợp, tức là: (A.B).C = A.(B.C)
Do đó khi tính tích nhiều ma trận, ta có thể thực hiện theo các trình tự khác nhau, mỗi trình tự tính sẽ quyết định số phép nhân cần thực hiện.
Cho N ma trận A1,A2…An, ma trận Ai có kích thước là di–1×di. Hãy xác định trình tự nhân ma trận A1.A2…An sao cho số phép nhân cần thực hiện là ít nhất.
2. Công thức
Gọi F(i,j) là số phép nhân để tính tích các ma trận từ Aiđến Aj (Ai.Ai+1….Aj).
• F(i,i)=0.
• F(i,i+1)=di–1.di.di+1
• F(i,j) = min(F(i,k)+F(k+1,j)+di–1.dk.dj với k=i+1,i+2,…j–1)
Công thức hơi phức tạp nên tôi xin giải thích như sau:
• F(i,i)=0 là hiển nhiên.
• F(i,i+1) là số phép nhân khi nhân Ai và Ai+1. Ai có kích thước di–1×di, Ai+1 có kích thước
di×di+1, do đó F(i,i+1)=di–1.di.di+1.
• Với j>i+1 thì ta thấy có thể tính Ai.Ai+1….Aj bằng cách chọn một vị trí k nào đó để đặt
ngoặc theo trình tự:
Ai.Ai+1….Aj = (Ai..Ak).(Ak+1..Aj)
Ma trận kết quả của phép nhân (Ai..Ak) có kích thước di–1×dk, ma trận kết quả của phép nhân
(Ak+1..Aj) có kích thước dk×dj. Với cách đặt đó ta sẽ mất F(i,k) phép nhân để có kết quả trong
dấu ngoặc thứ nhất, mất thêm F(k+1,j) phép nhân để có kết quả trong dấu ngoặc thứ hai, và
cuối cùng mất di–1.dk.dj để nhân 2 ma trận kết quả đó. Từ đó tổng số phép nhân của cách đặt
đó là: F(i,k)+F(k+1,j)+di–1.dk.dj.
Ta chọn vị trí k cho số phép nhân ít nhất.
3. Cài đặt
Bảng phương án là một mảng 2 chiều F để lưu F(i,j). Chú ý khi cài đặt là để tính được F(i,j),
ta phải tính F(i,k) và F(k+1,j) trước. Phương pháp đơn giản để làm điều đó là phương pháp đệ
quy có nhớ.
Tuy nhiên dựa vào nhận xét là trong công thức QHĐ: j–i lớn hơn k–i và j–k, ta có thể tính
theo trình tự khác: tính các phần tử F(i,j) với j–i từ nhỏ đến lớn (không phải là tính các giá
trị F(i,j) với i,j từ nhỏ đến lớn như vẫn làm). Với cách đó, khi tính đến F(i,j) thì ta đã có F(i,k)
và F(k+1,j).
Đoạn chương trình tính bảng phương án như sau:
for i:=1 to n do F[i,i]:=0;
for i:=1 to n–1 do
F[i,i+1]: = d[i–1]*d[i]*d[i+1];
for m:=2 to n–1 do begin
for i:=1 to n–m do begin
j:=i+m; F[i,j]:=oo;
for k:=i+1 to j–1 do
F[i,j]:=min(F[i,j],
F[i,k]+F[k+1,j]+d[i–1]*d[k]*d[j]);
end;
end;
Với cách cài đặt trên,chi phí không gian là O(n2), chi phí thời gian là O(n3) (đây là bài toán có
chi phí lớn nhất trong tất cả các bài toán QHĐ thường gặp).
4. Một số bài toán khác
a) Chia đa giác
Cho một đa giác lồi N đỉnh. Bằng các đường chéo không cắt nhau, ta có thể chia đa giác thành
N–2 tam giác. Hãy xác định cách chia có tổng các đường chéo ngắn nhất.
Hướng dẫn: Để đơn giản ta coi mọi đoạn thẳng nối 2 đỉnh đều là “đường chéo” (nếu nối 2
đỉnh trùng nhau hoặc 2 đỉnh liên tiếp thì có độ dài bằng 0).
Gọi F(i,j) là tổng độ dài các đường chéo khi chia đa giác gồm các đỉnh từ i đến j thành các
tam giác. Nếu j<i+3 thì đa giác đó có ít hơn 4 đỉnh, không cần phải chia nên F(i,j)=0. Ngược
lại ta xét cách chia đa giác đó bằng cách chọn một đỉnh k nằm giữa i,j và nối i,j với k. Khi đó
F(i,j)=F(i,k)+F(k,j)+d(i,k)+d(k,j); d(i,k) là độ dài đường chéo (i,k).
Tóm lại công thức QHĐ như sau:
• F(i,j)=0 với j<i+3.
• F(i,j)=min(F(i,k)+F(k,j)+d(i,k)+d(k,j) với k=i+1,…j–1).
F(1,n) là tổng đường chéo của cách chia tối ưu.
b) Biểu thức số học (IOI 1999)
Cho biểu thức a1•a2•…•an, trong đó ai là các số thực không âm và • là một phép toán + hoặc
× cho trước. Hãy đặt các dấu ngoặc để biểu thức thu được có kết quả lớn nhất.
Hướng dẫn: Gọi F(i,j) là giá trị lớn nhất có thể có của biểu thức ai•ai+1•…•aj. Dễ thấy nếu i=j
thì F(i,j)=ai, nếu j=i+1 thì F(i,j)=ai•aj. Nếu j>i+1 thì có thể tính biểu thức ai•ai+1•…•aj bằng
cách chia thành 2 nhóm: (ai•ai+1•…•ak)•(ak+1•…•aj), Khi đó F(i,j)=F(i,k)•F(k+1,j).
Tóm lại, công thức QHĐ là:
Trang11
• F(i,i)=ai
• F(i,i+1)=ai•ai+1
• F(i,j)=max(F(i,k)•F(k+1,j) với k=i+1,i+2,..j–1).
(Chú là là các hạng tử của dãy đều không âm và các phép toán là + hoặc × nên F(i,k) và
F(k+1,j) đạt max thì F(i,k)•F(k+1,j) cũng đạt max).
VI. Ghép cặp
1.Mô hình
Có n lọ hoa sắp thẳng hàng và k bó hoa được đánh số thứ tự từ nhỏ đến lớn. Cần cằm k bó hoa trên
vào n lọ sao cho hoa có số thứ tự nhỏ phải đứng trước hoa có số thứ tự lớn. Giá trị thẩm mỹ tương ứng
khi cắm hoa i vào lọ thứ j là v(i,j) Hãy tìm 1 cách cắm sao cho tổng giá trị thẫm mỹ là lớn nhất. Chú ý
rằng mỗi bó hoa chỉ được cắm vào 1 lọ và mỗi lọ cũng chỉ cắm được 1 bó hoa. (IOI –1999)
2. Công thức
Nhận xét rằng bài toán nêu trên là một bài toán ghép cặp có yêu cầu về thứ tự nên ta có thể
giải quyết bằng phương pháp QHĐ.
Hàm mục tiêu: f: tổng giá trị thẩm mỹ của cách cắm.
Giá trị thẩm mỹ phụ thuộc vào các hoa và các lọ đang được xét nên ta sẽ dùng mảng 2 chiều
để lưu bảng phương án.
L(i,j): tổng giá trị thẩm mỹ lớn nhất khi xét đến hoa i và lọ j. Khi tính L(i,j) hoa đang xét sẽ là
hoa i và lọ j.
• Nếu i = j. Chỉ có một cách cắm L(i,i):= v[1,1]+v[2,2]+…v[i,i]
• Nếu i>j. Không có cách cắm hợp lý
• Nếu i<j: Có 2 trường hợp xảy ra:
Cắm hoa i vào lọ j. Tổng giá trị thẩm mỹ là L(i-1,j-1)+v(i,j). (Bằng tổng giá trị trước khi
cắm cộng với giá trị thẩm mỹ khi cắm hoa i vào lọ j)
Không cắm hoa i vào lọ j (có thể cắm vào lọ trước j), giá trị thẫm mỹ của cách cắm là như
cũ: L(i,j-1)
3. Cài đặt
L[i,j]:= -maxint;
For i:=1 to k do
For j:=i to n do
If i = j then L[i,j]:=sum(i)
else
if i<j then L[i,j]:=max(L[i-1,j-1]+v[i,j],L[i,j-1]);
4. Một số bài toán khác
a) Câu lạc bộ:( Đề thi chọn HSG Tin Hà Nội năm 2000)
Có n phòng học chuyên đề và k nhóm học được đánh số thứ tự từ nhỏ đến lớn. Cần xếp k nhóm trên vào n phòng học sao cho nhóm có số hiệu nhỏ được xếp vào phòng có số hiệu nhỏ, nhóm có số hiệu lớn phải được xếp vào phòng có số hiệu lớn.Với mỗi phòng có chứ học sinh,
các ghế thừa phải được chuyển ra hết, nếu thiếu ghế thì lấy vào cho đủ ghế. Biết phòng i có
a(i) ghế, nhóm j có b(j) học sinh. Hãy chọn 1 phương án bố trí sao cho tổng số lần chuyển ghế
ra và vào là ít nhất.
Hướng dẫn : Khi xếp nhóm i vào phòng j thì số lần chuyển ghế chính là độ chênh lệch giữa
số ghế trong phòng i và số học sinh trong nhóm. Đặt v[i,j]:=|a(i)-b(j)|
b) Mua giày (Đề QG bảng B năm 2003)
Trong hiệu có n đôi giày, đôi giày i có kích thước hi. Có k người cần mua giày, người i cần
mua đôi giày kích thước si . Khi người i chọn mua đôi giày j thì độ lệch sẽ là |h(i)-s(j)|. Hãy
tìm cách chọn mua giày cho k người trên sao cho tổng độ lệch là ít nhất. Biết rằng mỗi người
chỉ mua 1 đôi giày và 1 đôi giày cũng chỉ có một người mua.
Hướng dẫn : Lập công thức giải như bài Câu lạc bộ. Chú ý chứng minh tính đúng đắn của bổ
đề heuristic sau: Cho 2 dãy tăng dần các số dương a1a2…an , b1b2…bn. Gọi c1c2…cn là một
hoán vị của dãy {bn}. Khi đó: |a(1)-b(1)|+ |a(2)-b(2)|+…+ |a(n)-b(n)|< |a(1)-c(1)|+ |a(2)-
c(2)|+…+ |a(n)-c(n)|
VII. Di chuyển
1. Mô hình
Cho bảng A gồm MxN ô. Từ ô (i,j) có thể di chuyển sang 3 ô (i+1,j), (i+1,j–1) và (i+1,j+1). Hãy xác định một lộ trình đi từ hàng 1 đến hàng M sao cho tổng các ô đi qua là lớn nhất.
2. Công thức
Gọi F(i,j) là giá trị lớn nhất có được khi di chuyển đến ô (i,j). Có 3 ô có thể đi đến ô (i,j) là (i–1,j), (i–1,j–1) và (i–1,j+1). Do đó ta có công thức QHĐ như sau:
- F(1,j)=A[1,j]
- F(i,j)=max(F(i–1,j),F(i–1,j–1),F(i–1,j+1))+A[i,j] với i>1
3. Cài đặt
Bảng phương án là bảng 2 chiều F[0..m,0..n]. (Tất cả các ô trên biên đều cho giá trị bằng 0).
Quá trình tính như sau:
for i:=1 to m do
for j: = 1 to n do
F[i,j]=max[F[i–1,j],F[i–1,j–1],F[i–1,j+1]]+A[i,j];
Cách cài đặt này cho chi phí không gian và thời gian đều là O(n2). Ta có thể tiết kiệm không gian nhớ bằng cách tính trực tiếp trên mảng A.
4. Một số bài toán khác
a) Tam giác (IOI 1994)
Cho một tam giác gồm các số nguyên không âm. Hãy tính tổng lớn nhất các số trên đường đi từ đỉnh tam giác xuống một điểm nào đó ở đáy tam giác nào đó. Tại mỗi ô ta chỉ có đi thẳng xuống, sang ô bên trái hoặc bên phải.
Hướng dẫn: Mô tả các phần tử của tam giác số như một ma trận, A[i,j] là phần tử thứ j trên dòng i (với 1≤i≤N và 1≤j≤i). Có 2 ô có thể di chưyển đến ô (i,j) là ô (i–1,j–1) và ô (i–1,j). Gọi F(i,j) là tổng lớn nhất có thể có khi đi đến ô (i,j) ta có:
- F(1,1)=A[1,1]
- F(i,1)=F(i–1,1)+A[i,1]
- F(i,j)=max(F(i–1,j–1),F(i–1,j))+A[i,j]
b) Con kiến
Có một ống hình trụ, khi trải phẳng ra có thể là một bảng MxN ô. Giá trị A[i,j] là lượng thức ăn có ở ô ở dòng i cột j. Một con kiến xuất phát từ một ô ở mép bên trái của hình trụ và bò sang mép bên phải. Từ ô (i,j) kiến có thể bò sang 1 trong 3 ô (i–1,j+1), (i,j+1) hoặc (i+1,j+1). (Chú ý: vì ống hình trụ nên kiến đang ở dòng 1 có thể bò xuống dòng M và ngược lại). Bò qua ô nào thì kiến mang theo toàn bộ lượng thức ăn ở ô đó. Hãy tìm đường đi mà kiến kiếm được nhiều thức ăn nhất.
Hướng dẫn: Để xử lí tình huống hình trụ, ta lưu dòng 0 là dòng M và dòng M+1 là dòng 1. Khi đó tương tự như bài toán ban đầu, gọi F(i,j) là lượng thức ăn kiến có được khi bò đến ô (i,j), ta thiết lập được công thức QHĐ sau:
- F(i,1)=A[i,1]
- F(i,j)=max(F(i–1,j–1),F(i,j–1),F(i+1,j+1))+A[i,j] với j>1