Category: TOÁN HỌC

Đề thi HSG Toán tiếng Anh lớp 10 Nam Định 2021
Đề thi HSG Toán tiếng Anh lớp 10 Nam Định 2021

Xem thêm:
- Đề thi HSG Toán tiếng Anh Lớp 11 SGD Nam Định năm 2018
- Đề thi HSG Toán tiếng Anh Lớp 11 năm 2019 SGD Nam Định
PART 1. MULTIPLE CHOICE QUESTIONS (7,0 points)

Question 1. Given three distinct points $A$, $B$ and $C$. Which of the following statements is true?
A. \( \overrightarrow{CA}-\overrightarrow{AB}=\overrightarrow{CB} \).
B. \( \overrightarrow{AB}=\overrightarrow{CA}=-\overrightarrow{BC} \).
C. \( \overrightarrow{BA}=\overrightarrow{AC}=\overrightarrow{CB} \).
D. \( \overrightarrow{BA}-\overrightarrow{BC}=\overrightarrow{AC} \).

Question 2. In the \( Oxy \) coordinate plane, given \( \triangle ABC \) with \( A(-1;-4) ,B(6;7)\) and \( C(-2;9) \). Let \( G \) be the centroid of \( \triangle ABC \). The coordinates of \( G \) are
A. \( G(1;4) \).
B. \( G(-1;4) \).
C. \( G(1;-4) \).
D. \( G(3;12) \).

Question 3. Given a right triangle \( ABC \) at A. Which of the following statements is false?
A. \( \overrightarrow{AB}\cdot \overrightarrow{AC} < \overrightarrow{BA}\cdot \overrightarrow{BC} \).
B. \( \overrightarrow{AC}\cdot \overrightarrow{BC} < \overrightarrow{BC}\cdot \overrightarrow{AB} \).
C. \( \overrightarrow{AB}\cdot \overrightarrow{BC} < \overrightarrow{CA}\cdot \overrightarrow{CB} \).
D. \( \overrightarrow{AC}\cdot \overrightarrow{CB} < \overrightarrow{AC}\cdot \overrightarrow{BC} \).

Question 4. Given \( A=\{1;2;3;4\}\). How many subsets does the set \( A \) have?
A. $18$.
B. $16$.
C. $15$.
D. $14$.

Question 5. Given equation \( (x^2-x+1)(x-1)(x+1)=0 \). Which of the following equations is equivalent to the given equation?
A. \( x+1=0 \).
B. \( x-1=0 \).
C. \( x^2-x+1=0 \).
D. \( (x-1)(x+1)=0 \).

Question 6. Find all values of \( m \) such that function \( y=(m-1)x+2-21 \) is decreasing on its domain.
A. \(m>1\).
B. \( m \geqslant 1 \).
C. \( m \leqslant 1 \).
D. \( m<1 \).

Question 7. Let $a, b, c$ be three positive real numbers satisfying $a+b+c=3$. Determine the maximum value of $T=\sqrt{a b}+\sqrt{b c}+\sqrt{c a}$.
A. $3$.
B. $4$.
C. $2$.
D. $6$.

Question 8. Given the fact that the system of equations $\left\{\begin{array}{l}x^{3}(2+3 y)=8 \\ \left(y^{3}-2\right) x=6\end{array}\right.$ has exactly two distinct solutions $\left(x_{1}, y_{1}\right) ;\left(x_{2}, y_{2}\right)$. The value of $S=x_{1}^{4}+y_{1}^{4}+x_{2}^{4}+y_{2}^{4}$ is
A. $34$.
B. $40$.
C. $28$.
D. $36$.

Question 9. Find all parameters $m$ such that equation $x^{2}+(m-1) x+m^{2}-1=0$ has two distinct roots and these roots have the same sign.
A. $m<-1$ or $m>1$.
B. $1<m<\frac{5}{3}$.
C. $-1<m<1$.
D. $\frac{-5}{3}<m<-1$.

Question 10. Given two equations $m x^{2}-2(m-1) x+m-2=0$ and $(m-2) x^{2}-3 x+m^{2}-15=0$. How many values of $m$ which make these above equations equivalent?
A. $2$.
B. $3$.
C. $0$.
D. $1$.

Question 11. Given $\triangle A B C$ with $A B=13, B C=2 \sqrt{33}, C A=17$. Compute the length of the median $A M$ of $\triangle A B C$.
A. $A M=2 \sqrt{35}$.
B. $A M=15$.
C. $A M=\sqrt{194}$.
D. $A M=14$.

Question 12. A ball is thrown straight up from 60 meters above the ground with a velocity of 20 meters per second $(20 \mathrm{~m} / \mathrm{s})$. The height of the ball at second $t$ after throwing can be computed by the quadratic function $s(t)=-5 t^{2}+20 t+60$, where $s(t)$ is in meters. After how many seconds does the ball hit the ground?
A. $t=2$.
B. $t=1$.
C. $t=4$.
D. $t=6$.

Question 13. Given $\triangle A B C$ with the sides $A C=3 \sqrt{3}$, side $B C=3 \sqrt{2}, A=45^{\circ}$ and $B>A+C$. Compute the degree measure of $\widehat{A B C}$.
A. $\widehat{A B C}=60^{\circ}$.
B. $\widehat{A B C}=150^{\circ}$.
C. $\widehat{A B C}=30^{\circ}$.
D. $\widehat{A B C}=120^{\circ}$.

Question 14. In the $O x y$ coordinate plane, given Parabol $(P): y=x^{2}-5 x+2 m$. Let $S$ be the set of all values of $m$ such that the Parabol $(P)$ cuts $O x$ at two distinct points $A, B$ satisfying $O A=4 O B$. Determine the sum of all elements of $S$.
A. $\frac{2}{9}$.
B. $\frac{-32}{9}$.
C. $2$.
D. $\frac{-16}{9}$.

Question 15. Which of the following two inequations are not equivalent?
A. $2 x-1>0$ and $2 x-1+\frac{1}{2 x^{2}+1}>\frac{1}{2 x^{2}+1}$.
B. $-2 x+1>0$ and $2 x-1<0$.
C. $3 x^{2}+1 \leq 2 x-1$ and $3 x^{2}-2 x+2 \leq 0$.
D. $5 x-1+\frac{1}{x-2}>\frac{1}{x-2}$ and $5 x-1>0$.

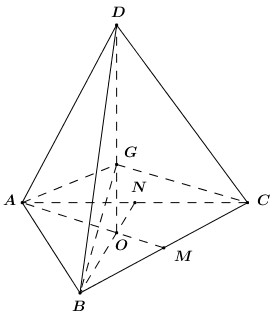
Question 16. Given an isosceles right triangle $A B C$ with sides $A B=A C=42 \mathrm{~cm} .$ Two medians $B E$ and $C F$ intersect at point $G$. The area of the triangle $G E C$ is
A. $7 \sqrt{21} \mathrm{~cm}^{2}$.
B. $21 \sqrt{7} \mathrm{~cm}^{2}$.
C. $147 \mathrm{~cm}^{2}$.
D. $174 \mathrm{~cm}^{2}$.

Question 17. In the $O x y$ coordinate plane, given two vectors $\vec{a}=(6 ;-4)$ and $\vec{b}=(-10,-2) .$ Compute the angle between two vectors $\vec{a}$ and $\vec{b}$.
A. $45^{\circ}$.
B. $60^{\circ}$.
C. $135^{\circ}$.
D. $120^{\circ}$.

Question 18. Given rectangle $A B C D$ with $A D=2$. Suppose that $E$ is the point which lies on the side $A B$ such that $A E=2 B E$ and $\sin \widehat{B D E}=\frac{1}{5}$. Compute the length of the segment $A B$.
A. $A B=2 \sqrt{2}$.
B. $A B=3 \sqrt{3}$.
C. $A B=\sqrt{3}$.
D. $A B=\sqrt{6}$.

Question 19. In the $O x y$ coordinate plane, given $A(2 ;-6)$. Let $B$ be the point which is symmetric to point $A$ with respect to the origin $O$. Find the coordinates of point $C$ satisfying that its horizontal coordinate equals $-4$ and $\triangle A B C$ has the right angle at $C$.
A. $C(2 \sqrt{6} ;-4)$ or $C(-2 \sqrt{6} ;-4)$.
B. $C(-4 ; 24)$ or $C(-4 ;-24)$.
C. $C(-4 ;-2 \sqrt{6})$ or $C(-4 ; 2 \sqrt{6})$.
D. $C(24 ;-4)$ or $C(-24 ;-4)$.

Question 20. In the $O x y$ coordinate plane, let $M$ be the vertex of Parabol $y=a x^{2}+b x+c(a \neq 0)$. The coordinates of $M$ are
A. $\left(\frac{b}{2 a} ; \frac{4 a c-b^{2}}{4 a}\right)$.
B. $\left(\frac{-b}{4 a} ; \frac{4 a c-b^{2}}{4 a}\right)$.
C. $\left(\frac{-b}{2 a} ; \frac{b^{2}-4 a c}{4 a}\right)$.
D. $\left(\frac{-b}{2 a} ; \frac{4 a c-b^{2}}{4 a}\right)$.

Question 21. In the $O x y$ coordinate plane, given $A(1 ;-3)$ and $B(-5 ; 4)$. The coordinates of vector $\overrightarrow{B A}$ are
A. $\overrightarrow{B A}=(6 ; 7)$.
B. $\overrightarrow{B A}=(6 ;-7)$.
C. $\overrightarrow{B A}=(-4 ; 1)$.
D. $\overrightarrow{B A}=(-6 ; 7)$.

Question 22. Among the following propostions, whose inverse proposition is true?
A. If a triangle is not regular then it has at least one interior angle less than 60 degrees.
B. If two triangles are congruent then their corresponding angles are equal.
C. If $n$ is a natural number then $n$ is a real number.
D. If a quadrilateral is an isosceles trapezoid then its two diagonals have the same length.

Question 23. Given $\triangle A B C$. Let $M$ and $N$ be the mid-points of sides $A B$ and $A C$, respectively. Find the scalars $m$ and $n$ such that $\overrightarrow{N M}=m \overrightarrow{A B}-n \overrightarrow{A C}$.

A. $m=-\frac{1}{2}, n=\frac{1}{2}$.
B. $m=-\frac{1}{2}, n=-\frac{1}{2}$.
C. $m=\frac{1}{2}, n=\frac{1}{2}$.
D. $m=\frac{1}{2}, n=-\frac{1}{2}$.

Question 24. Given two non-zero vectors $\vec{a}$ and $\vec{b}$. Which of the following statements is false?
A. Two vectors $\vec{a}$ and $\vec{b}$ with opposite direction to another nonzero vector are parallel.
B. Two vectors $\vec{a}$ and $k \vec{a}$ are parallel.
C. Two vectors $\vec{a}$ and $-3 \vec{a}$ have the same direction.
D. Two vectors $\vec{a}$ and $\vec{b}$ with the same direction are parallel.

Question 25. The domain of the function $y=\frac{2}{\sqrt{6-2 x}}$ is
A. $D=(-\infty ; 3]$.
B. $D=(-\infty ; 3)$.
C. $D=(3 ;+\infty)$.
D. $D=\mathbb{R} \backslash\{3\}$.

Question 26. In the $O x y$ coordinate plane, given $\triangle A B C$. Points $M(-2 ; 3), N(4 ;-1), P(1 ; 1)$ are the mid-points of sides $B C, C A$ and $A B$, respectively. The coordinates of vertex $A$ are
A. $A(-10 ; 0)$.
B. $A(7 ;-3)$.
C. $A(-7 ; 3)$.
D. $A(10 ; 0)$.

Question 27. Which of the following sentences is not a proposition?
A. Five divides twenty.
B. If “$3+x=4$” then “$x=1$”.
C. If “$1+2=7$” then “$7$ is an odd number.
D. What a nice day!

Question 28. In the $O x y$ coordinate plane, let $A(-3 ;-5) ; B(2 ; 5)$. Determine the slope of line $A B$.
A. $-5$.
B. $5$.
C. $2$.
D. $-3$.

Question 29. Given a right triangle $A B C$ at $B$ with $A B=2 a, A C=5 a$. Compute the dot product $\overrightarrow{A B} \cdot \overrightarrow{C A}$.
A. $-5 a^{2}$
B. $4 a^{2}$.
C. $-4 a^{2}$
D. $5 a^{2}$

Question 30. Given an isosceles triangle $A B C$ with the right angle $A$, inscribed in a circle with center $O$ and radius $R$. Let $r$ be the radius of the incircle of triangle $A B C$. The ratio of $R$ to $r$ is
A. $\frac{R}{r}=\frac{1+\sqrt{2}}{2}$.
B. $\frac{R}{r}=1+\sqrt{2}$.
C. $\frac{R}{r}=\frac{2+\sqrt{2}}{2}$
D. $\frac{R}{r}=\frac{\sqrt{2}-1}{2}$.

Question 31. A man travels from city $X$ to city $Y$ by train, then returns to city $Y$ by his car. Given that the distance between these two cities is $200 \mathrm{~km}$ and the average speed of his car is $10 \mathrm{~km} / \mathrm{h}$ faster than the train’s average speed. His journey takes 9 hours, find the sum of average speeds of the train and his car.
A. $90$.
B. $80$.
C. $60$.
D. $100$.

Question 32. Let $a, b, c$ be real numbers and $a+2021 c>b+2021 c$. Which of the following statements is true?
A. $a^{2}>b^{2}$.
B. $-2020 a>-2020 b$.
C. $2021 a>2021 b$
D. $\frac{1}{a}>\frac{1}{b}$.

Question 33. Given two sets $X=\{A ; 1 ; 2 ; 4 ; 6\}, Y=\{3 ; 7 ; 4 ; \varnothing\}$, the union of $X$ and $Y$ is
A. $\{1 ; 2 ; 3 ; 4 ; 6 ; 7\}$.
B. $\{A ; 1 ; 2 ; 3 ; 4 ; 6 ; 7 ; \varnothing\}$.
C. $\{1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7\}$.
D. $\{A ; 1 ; 2 ; 3 ; 4 ; 6 ; 7\}$.

Question 34. In the $O x y$ coordinate plane, let Parabol $(P): y=a x^{2}+b x+3$ and a point $M(-1 ; 9)$ belongs to the graph of $(P)$. The symmetric axis of $(P)$ has equation $x=-2$. Find the value of $S=a+b$.
A. $-6$.
B. $16$.
C. $6$.
D. $-10$.

Question 35. The negation of the proposition “Fourteen is a composite number” is
A. Fourteen has four positive factors.
B. Fourteen has only two factors 1 and 14 .
C. Fourteen is a prime number.
D. Fourteen is not a composite number.

PART 2. PROBLEMS SOLVING (3,0 points)

Write the solutions to the following problems in the provided space on your answer sheet.

Problem 1. (1,0 point)

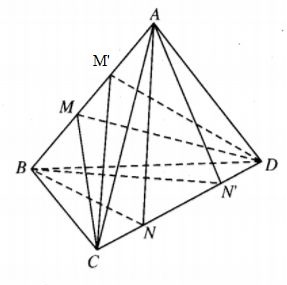
To measure the height of the Cham temple tower Po Klong Garai in Ninh Thuan province (Figure 1), two points $A$ and $B$ which are chosen on the ground with the length $A B=16 \mathrm{~m}$ and the bottom $C$ of the tower are collinear (Figure 2). Two total stations whose tripods have a height $h=1,6 m$ are put at point $A$ and point $B$. Let $D$ be the top of the tower and two points $A_{1}, B_{1}$ be collinear to $C_{1}$ on height $C D$ of the tower. The measurements are $\widehat{D A_{1} C_{1}}=54^{0}$ and $\widehat{D B_{1} C_{1}}=32^{\circ} .$ Caculate the height $C D$ of the tower then round the result to 3 decimal places.

Problem 2 (1,0 point).

Let $f(x)=a x^{3}+b x^{2}+c x+d$ be a cubic function with $f(0)=k, f(1)=2 k, f(-1)=3 k$, where $k$ is a given constant. What is the value of $f(2)+f(-2)$?

Problem 3 (1,0 point).

The sum of 2025 consecutive positive integers is a perfect square. Find the minimum value of the largest of these integers?
29/09/2021
SỬ DỤNG AM-GM ĐỂ CHỨNG MINH BẤT ĐẲNG THỨC DẤU BẰNG KHÔNG TẠI TÂM
SỬ DỤNG AM-GM ĐỂ CHỨNG MINH BẤT ĐẲNG THỨC DẤU BẰNG KHÔNG TẠI TÂM

Bài viết của tác giả Lê Khánh Sỹ. O2 Education đã xin phép tác giả để đăng lại trên website.

Bất đẳng thức AM-GM là một trong những bất đẳng thức thường sử dụng. Ở Việt Nam, chúng ta hay gọi bất đẳng thức này là bất đẳng thức Cauchy, dù không phải do ông lần đầu tiên đưa ra bất đẳng thức này.

1. Sử dụng AM-GM để chứng minh bất đẳng thức dấu bằng không tại tâm

Bài tập 1. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}\ge 2\sqrt{1+\dfrac{abc}{(a+b)(b+c)(c+a)}}.$$

Hướng dẫn. Nhân hai vế bầt đẳng thức cho $\sqrt{(a+b)(b+c)(c+a)}$ bất đẳng thức viết lại như sau $$\sqrt{a(a+b)(a+c)}+\sqrt{b(b+c)(b+a)}+\sqrt{c(c+a)(c+b)}\ge 2\sqrt{(a+b+c)(ab+bc+ca)}.$$
Áp dụng Mincopxki, ta có $$\sqrt{a^2(a+b+c)+abc}+\sqrt{b^2(a+b+c)+abc}+\sqrt{c^2(a+b+c)+abc}\ge \sqrt{(a+b+c)^3+9abc}$$ Áp dụng Schur có $$\sqrt{(a+b+c)^3+9abc}\ge\sqrt{4(a+b+c)(ab+bc+ca)}.$$
Hoàn tất chứng minh. Đẳng thức xảy ra khi $a=b=c>0$, hoặc $a=0$ và $b=c>0$, hoặc các hoán vị.

Nếu chọn $ab+bc+ca=1$ thì chúng ta thu được đó là bất đẳng thức Iran 2008: $$\sqrt{a^3+a}+\sqrt{b^3+b}+\sqrt{c^3+c}\ge 2\sqrt{a+b+c}.$$ Nếu chọn $a+b+c=1$ thì cũng là bài toán quen thuộc thường thấy trên diễn đàn toán học: $$\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}\ge 2\sqrt{ab+bc+ca}.$$

Bài toán trên cũng liên quan mật thiết đến bài Jack garfunkel $$\dfrac{a^2+b^2+c^2}{ab+bc+ca}+\dfrac{8abc}{(a+b)(b+c)(c+a)}\ge 2.$$

Bài tập 2. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}+\dfrac{16(ab+bc+ca)}{(a+b+c)^2}\ge 6.$$

Hướng dẫn. Nhân hai vế của bất đẳng thức cho $(ab+bc+ca)$, ta được
$$a^2+b^2+c^2+abc\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)+\dfrac{16(ab+bc+ca)^2}{(a+b+c)^2}\ge 6(ab+bc+ca),$$
hay
$$(a+b+c)^2+abc\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)+\dfrac{16(ab+bc+ca)^2}{(a+b+c)^2}\ge 8(ab+bc+ca),$$
Bất đẳng thức trên luôn đúng do AM-GM với hai số dương $$(a+b+c)^2+\dfrac{16(ab+bc+ca)^2}{(a+b+c)^2}\ge 8(ab+bc+ca),$$
và $$abc\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge 0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra khi hoán vị $(a,b,c)\sim (0,t,t)$ với $t>0.$

Tiếp cận cách khác: Bất đẳng thức viết lại như sau $$(a+b+c)\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)+\dfrac{16(ab+bc+ca)}{(a+b+c)^2}\ge 9.$$ Vì $abc\ge 0$ do đó theo tính chất bắc cần chúng ta đi chứng minh $$(a+b+c)\left[\dfrac{a^2+b^2+c^2+3(ab+bc+ca)}{(a+b+c)(ab+bc+ca)}\right]+\dfrac{16(ab+bc+ca)}{(a+b+c)^2}\ge 9.$$ Vì $abc\ge 0$ do đó theo tính chất bắc cần chúng ta đi chứng minh $$(a+b+c)\left[\dfrac{a^2+b^2+c^2+3(ab+bc+ca)}{(a+b+c)(ab+bc+ca)}\right]+\dfrac{16(ab+bc+ca)}{(a+b+c)^2}\ge 9,$$
hay
$$\dfrac{a^2+b^2+c^2}{ab+bc+ca}+\dfrac{16(ab+bc+ca)}{(a+b+c)^2}\ge 6,$$
hay
$$\left[a^2+b^2+c^2-2(ab+bc+ca)\right]^2\ge 0.$$ Hiển nhiên đúng.

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 16$ thì $$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}+\dfrac{k(ab+bc+ca)}{(a+b+c)^2}\ge 2\left(\sqrt{k}-1 \right).$$

Bài tập 3. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng
$$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}+\dfrac{16(ab+bc+ca)}{a^2+b^2+c^2}\ge 8.$$

Hướng dẫn. Nhân hai vế của bất đẳng thức cho $(ab+bc+ca)$, ta được $$a^2+b^2+c^2+abc\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)+\dfrac{16(ab+bc+ca)^2}{a^2+b^2+c^2}\ge 8(ab+bc+ca).$$ Bất đẳng thức trên luôn đúng do AM-GM với hai số dương
$$a^2+b^2+c^2+\dfrac{16(ab+bc+ca)^2}{a^2+b^2+c^2}\ge 8(ab+bc+ca),$$ và
$$abc\left(\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}\right)\ge 0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=4.$

Tiếp cận cách khác. Áp dụng Bài tập 2 chúng ta cần chứng minh $$\dfrac{a^2+b^2+c^2+3(ab+bc+ca)}{ab+bc+ca} +\frac{16(ab+bc+ca)}{a^2+b^2+c^2}\ge 11,$$ hay $$\dfrac{a^2+b^2+c^2}{ab+bc+ca} +\frac{16(ab+bc+ca)}{a^2+b^2+c^2}\ge 8,$$
Đây chính là AM-GM bài toán chứng minh xong.

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 4$ thì $$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}+\dfrac{k(ab+bc+ca)}{a^2+b^2+c^2}\ge 2\sqrt{k}.$$

Bài tập 4. Cho các số thực không âm $a,b,c$. Chứng minh rằng $$\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}+\dfrac{27(a+b+c)^2}{a^2+b^2+c^2}\ge 52.$$

Hướng dẫn. Ta có $$ \dfrac{a^2(ab+bc+ca)^2}{b^2+c^2}= \dfrac{a^2\left[a^2(b^2+c^2)+2abc(b+c+a)+b^2c^2 \right]}{b^2+c^2}\ge a^4.$$ Do đó nhân hai vế cho $(ab+bc+ca)$ và để bất đẳng thức đúng chúng cần chứng minh $$a^4+b^4+c^4+ \dfrac{27(a+b+c)^2(ab+bc+ca)^2}{a^2+b^2+c^2}\ge 52(ab+bc+ca)^2.$$ Mà $$a^4+b^4+c^4=(a^2+b^2+c^2)^2-2(ab+bc+ca)^2+4abc(a+b+c)\ge (a^2+b^2+c^2)^2-2(ab+bc+ca)^2.$$ Do đó theo tính chất bắc cầu ta đi chứng minh
$$(a^2+b^2+c^2)^2+\dfrac{27(a+b+c)^2(ab+bc+ca)^2}{a^2+b^2+c^2}\ge 54(ab+bc+ca)^2,$$ hay
$$(a^2+b^2+c^2)^3+54(ab+bc+ca)^3\ge 27(a^2+b^2+c^2)(ab+bc+ca)^2.$$

Bất đẳng thức trên luôn đúng theo AM-GM do $$(a^2+b^2+c^2)^3+ 27(ab+bc+ca)^2+27(ab+bc+ca)^2\ge 3\sqrt[3]{27^2(a^2+b^2+c^2)^3(ab+bc+ca)^6}$$$$= 27(a^2+b^2+c^2)(ab+bc+ca)^2.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=3.$

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 8$ thì $$\dfrac{a^2}{b^2+c^2}+\dfrac{b^2}{c^2+a^2}+\dfrac{c^2}{a^2+b^2}+\dfrac{k(a+b+c)^2}{a^2+b^2+c^2}\ge k+3\sqrt[3]{k^2}-2+\dfrac{4abc(a+b+c)}{(ab+bc+ca)^2}.$$

Bài tập 5. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}+\dfrac{9\sqrt{ab+bc+ca}}{a+b+c} \ge 6 .$$

Hướng dẫn. Ta có $$\sqrt{\dfrac{a(ab+bc+ca)}{b+c}}=\sqrt{a^2+\dfrac{abc}{b+c}}\ge a.$$ Do đó nhân hai vế cho $\sqrt{ab+bc+ca}$ và để bất đẳng thức đúng chúng cần chứng minh $$a+b+c+\dfrac{9(ab+bc+ca)}{a+b+c}\ge 6\sqrt{ab+bc+ca},$$ hay $$\left(a+b+c-3\sqrt{ab+bc+ca} \right)^2\ge 0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=7.$

Tổng quát:
- Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 4$ thì $$\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}+\dfrac{k\sqrt{ab+bc+ca}}{a+b+c} \ge 2\sqrt{k}.$$
- Với các số thực không âm $x,y,z,a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 4\min\{xy,yz,zx\}$ thì $$x\sqrt{\dfrac{a}{b+c}}+y\sqrt{\dfrac{b}{c+a}}+z\sqrt{\dfrac{c}{a+b}}+\dfrac{k\sqrt{ab+bc+ca}}{xa+yb+zc} \ge 2\sqrt{k}.$$
Bài tập 6. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}+\sqrt{\dfrac{27(ab+bc+ca)}{a^2+b^2+c^2}}\ge \dfrac{7\sqrt{2}}{2} .$$

Hướng dẫn. Ta có $$\sqrt{\dfrac{a(ab+bc+ca)}{b+c}}=\sqrt{a^2+\dfrac{abc}{b+c}}\ge a.$$ Do đó nhân hai vế cho $\sqrt{ab+bc+ca}$ và để bất đẳng thức đúng chúng cần chứng minh $$a+b+c+\dfrac{3\sqrt{3}(ab+bc+ca)}{\sqrt{a^2+b^2+c^2}}\ge \dfrac{7\sqrt{2}}{2}\sqrt{ab+bc+ca},$$ hay
$$\sqrt{a^2+b^2+c^2+2(ab+bc+ca)}+\dfrac{3\sqrt{3}(ab+bc+ca)}{\sqrt{a^2+b^2+c^2}}\ge \dfrac{7\sqrt{2}}{2}\sqrt{ab+bc+ca}.$$ Đặt $t=\sqrt{\dfrac{a^2+b^2+c^2}{ab+bc+ca}+2}\ge \sqrt{3}$ chúng ta cần chứng minh $$f(x):=x+\dfrac{3\sqrt{3}}{\sqrt{x^2-2}}-\dfrac{7\sqrt{2}}{2}\ge 0$$ Dễ thấy rằng $f'(x)=0$ khi $x=2\sqrt{2}$, khi đó $$f(x)\ge f(2\sqrt{2})=0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=6.$

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge \sqrt{2}$ thì $$\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}+k\sqrt{\dfrac{ab+bc+ca}{a^2+b^2+c^2}} \ge x+\dfrac{k}{\sqrt{x^2-2}}.$$
Với
$$x=\sqrt{ \dfrac{k^2}{\sqrt[3]{27k^2+3\sqrt{81k^4-3k^6}}} +\dfrac{\sqrt[3]{27k^2+3\sqrt{81k^4-3k^6}}}{3}+2 }.$$

Bài tập 7. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}+\dfrac{8}{a+b+c}\ge \dfrac{6}{\sqrt{ab+bc+ca}}.$$

Hướng dẫn. Viết lại bất đẳng thức như sau $$\dfrac{a^2+b^2+c^2+3(ab+bc+ca)}{(a+b+c)(ab+bc+ca)-abc}+\dfrac{8}{a+b+c}\ge \dfrac{6}{\sqrt{ab+bc+ca}}.$$ Bất đẳng thức đúng thì chúng ta chỉ cần chứng minh $$\dfrac{a^2+b^2+c^2+3(ab+bc+ca)}{(a+b+c)(ab+bc+ca)}+\dfrac{8}{a+b+c}\ge \dfrac{6}{\sqrt{ab+bc+ca}},$$ hay $$\left(a+b+c-3\sqrt{ab+bc+ca} \right)^2\ge 0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=7.$

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 3$ thì $$\dfrac{1}{b+c}+\dfrac{1}{c+a}+\dfrac{1}{a+b}+\dfrac{k}{a+b+c}\ge \dfrac{2\sqrt{k+1}}{\sqrt{ab+bc+ca}}.$$

Bài tập 8. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\dfrac{1}{(a+b)^2}+\dfrac{1}{(b+c)^2}+\dfrac{1}{(c+a)^2}+\dfrac{24}{(a+b+c)^2}\ge \dfrac{8}{ab+bc+ca} .$$

Hướng dẫn. Nhân hai vế của bất đẳng thức cho $(a+b+c)^2$, ta được $$2\left(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\right)+\left(\dfrac{a}{b+c}\right)^2+\left(\dfrac{b}{c+a}\right)^2+\left(\dfrac{c}{a+b}\right)^2+27\ge \dfrac{8(a+b+c)^2}{ab+bc+ca}.$$ Như trên thì ta có $$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge \dfrac{a^2+b^2+c^2}{ab+bc+ca},$$
và \begin{align}\left(\dfrac{a}{b+c}\right)^2+\left(\dfrac{b}{c+a}\right)^2+\left(\dfrac{c}{a+b}\right)^2\ge \dfrac{a^4+b^4+c^4}{(ab+bc+ca)^2}\\
\ge \dfrac{(a^2+b^2+c^2)^2-2(ab+bc+ca)^2}{(ab+bc+ca)^2}\\
=\left(\dfrac{a^2+b^2+c^2}{ab+bc+ca}\right)^2-2.\end{align} Đặt $y=\dfrac{a^2+b^2+c^2}{ab+bc+ca}\ge 1$ bài toán cần chứng minh theo tính chất bắc cầu qua ngôn ngữ $y$ như sau $$2y+y^2+25\ge 8(y+2),$$ hay $$(y-3)^2\ge 0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=3.$

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $k\ge 15$ thì $$\dfrac{1}{(a+b)^2}+\dfrac{1}{(b+c)^2}+\dfrac{1}{(c+a)^2}+\dfrac{k}{(a+b+c)^2}\ge \dfrac{2\left(\sqrt{k+1}-1 \right)}{ab+bc+ca}.$$

Bài tập 9. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\ge \dfrac{5}{2(ab+bc+ca)} .$$

Hướng dẫn. Giả sử rằng $c=\min\{a,b,c\}$ khi đó ta có $$\dfrac{1}{a^2+b^2}+\dfrac{1}{b^2+c^2}+\dfrac{1}{c^2+a^2}\ge \dfrac{1}{\left(a+\dfrac{c}{2} \right)^2+\left(b+\dfrac{c}{2} \right)^2}+\dfrac{1}{\left(b+\dfrac{c}{2} \right)^2}+\dfrac{1}{\left(a+\dfrac{c}{2} \right)^2},$$ và $$\left(a+\dfrac{c}{2}\right)\left(b+\dfrac{c}{2}\right)-(ab+bc+ca)=\dfrac{c(c-2a-2b)}{4}\le 0. $$Do đó chúng ta cần chứng minh bài toán qua ngôn ngữ $x,y$ như sau $$\dfrac{1}{x^2+y^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge \dfrac{5}{2xy},$$
hay $$\dfrac{(x-y)^2(2x^2+2y^2-xy)}{2x^2y^2(x^2+y^2)}\ge 0. $$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $a=b>0$.

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không thì $$\dfrac{1}{a^2-kab+b^2}+\dfrac{1}{b^2-kbc+c^2}+\dfrac{1}{c^2-kca+a^2}\ge \dfrac{E_k}{(ab+bc+ca)},$$ khi đó $$E_k=\begin{cases} \dfrac{5-2k}{2-k},\ \ \ \ 0\le k\le 1\\
2+k,\ \ \ \ 1\le k\le 2\end{cases}.$$ Thật vậy, dễ thấy rằng ba phân thức vế trái là dương. Giả sử $a\ge b\ge c$. Ta có $$a^2-kab+b^2- \left[\left( a+\dfrac{c}{2}\right)^2-k\left( a+\dfrac{c}{2}\right)\left( b+\dfrac{c}{2} \right)+\left( b+\dfrac{c}{2} \right)^2 \right]=\dfrac{(k-2)(2a+2b+c)c}{4}\le 0,$$ $$a^2-kac+c^2 \le\left( a+\dfrac{c}{2}\right)^2,$$ và $$b^2-kbc+c^2 \le\left( b+\dfrac{c}{2}\right)^2,$$ $$\left(a+\dfrac{c}{2}\right)\left(b+\dfrac{c}{2}\right)\le ab+bc+ca.$$ Do đó chúng ta cần chứng minh bất đẳng thức theo ngôn ngữ $x,y$ dương như sau $$\dfrac{1}{x^2-kxy+y^2}+\frac{1}{x^2}+\dfrac{1}{y^2}\ge \dfrac{E_k}{xy}.$$ Nếu $1\le k\le 2$ bất đẳng thức viết lại $$\dfrac{xy}{x^2-kxy+y^2}+\dfrac{x^2-kxy+y^2}{xy}+k\ge E_k.$$ Áp dụng AM-GM, ta có $$\dfrac{xy}{x^2-kxy+y^2}+\dfrac{x^2-kxy+y^2}{xy}+k\ge 2+k=E_k.$$ Nếu $0\le k\le 1$ bất đẳng thức viết lại $$\dfrac{xy}{x^2-kxy+y^2}+\dfrac{x^2-kxy+y^2}{xy}+k\ge E_k.$$ Chú ý rằng trong trường hợp này đẳng thức xảy ra khi $x=y$, do đó trọng số của $\dfrac{xy}{x^2-kxy+y^2}= \dfrac{1}{2-k}$ vậy nên chúng ta phải phân tích như sau. Bất đẳng thức viết lại \begin{align}\dfrac{xy}{x^2-kxy+y^2}+\dfrac{x^2-kxy+y^2}{(2-k)^2xy}
+\left[1-\dfrac{1}{(2-k)^2}\right]\left(\dfrac{x}{y}+\dfrac{y}{x}\right)+\dfrac{k}{(2-k)^2}\\
\ge \dfrac{2}{2-k}+2\left[1-\dfrac{1}{(2-k)^2}\right]+\dfrac{k}{(2-k)^2}\\
=E_k.\end{align} Hoàn tất chứng minh.

Bài tập 10. Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng $$4\left(\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}\right)+9\ge\dfrac{27(a^2+b^2+c^2)}{(a+b+c)^2}.$$

Hướng dẫn. Dễ thấy rằng $$\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}\ge \dfrac{a+b+c}{\sqrt{ab+bc+ca}}.$$ Vì thế chúng ta chỉ cần chứng minh với ngôn ngữ $x\ge 1$ như sau $$4\sqrt{x+2}+9\ge \dfrac{27x}{x+2},$$ hay $$\dfrac{54}{x+2}+2\sqrt{x+2} +2\sqrt{x+2}\ge 18.$$ Đây chính là bất đẳng thức AM-GM cơ bản.

Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=7.$

Tổng quát: Với các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không và $0<k\le \dfrac{3}{2}$ thì $$4k^3\left(\sqrt{\dfrac{a}{b+c}}+\sqrt{\dfrac{b}{c+a}}+\sqrt{\dfrac{c}{a+b}}\right)+9(3-2k^2)\ge \dfrac{27(a^2+b^2+c^2)}{(a+b+c)^2}.$$

Bài tập 11. Cho các số thực không âm $a,b,c$. Chứng minh rằng $$\left|(a-b)(b-c)(c-a)\right|\le \dfrac{(a+b+c)^3}{6\sqrt{3}}.$$

Hướng dẫn. Bình phương hai vế, ta được $$(a-b)^2(b-c)^2(c-a)^2\le \dfrac{(a+b+c)^6}{108}.$$
Giả sử rằng $c=\min\{a,b,c\}$ khi đó ta có \begin{align} (a-b)^2(b-c)^2(c-a)^2\le (a^2-2ab+b^2).ab.ab \\
\text{(Áp dụng AM-GM)}\ \ \le\dfrac{1}{4}\cdot \dfrac{(a^2-2ab+b^2+2ab+2ab)^3}{27}\\
\le \dfrac{(a+b)^6}{108}\\
\le \dfrac{(a+b+c)^6}{108}.
\end{align} Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=4.$

Tổng quát: Với các số thực không âm $a,b,c$ và $\dfrac{2}{3}\le k\le 2$. Khi đó ta có $$(a^2-kab+b^2)(b^2-kbc+c^2)(c^2-kca+a^2)\le \dfrac{4(a+b+c)^6}{27(2+k)^2}.$$ Thật vậy không mất tính tổng quát giả sử rằng $c=\min\{a,b,c\}$. Khi đó ta có
$$0\le b^2-kbc+c^2\le b(b-kc+c),$$ và $$0\le c^2-kca+a^2 \le a(c-kc+a).$$ Do đó chúng ta cần chứng minh $$(a^2-kab+b^2)(ab-kca+ca)(bc-kbc+ab)\le \dfrac{4(a+b+c)^6}{27(2+k)^2},$$ hay $$(a^2-kab+b^2).x(ab-kca+ca).x(bc-kbc+ab)\le \dfrac{(a+b+c)^6}{27} \left(x=1+\dfrac{k}{2}\right).$$ Áp dụng AM-GM thì ta cần chứng minh $$\left[(a+b)^2+\left(1+\dfrac{k}{2}\right)(1-k)(a+b)c \right]^3\le (a+b+c)^6,$$ hay $$c\left[(k^2+k+2)(a+b)+2c\right]\ge 0.$$ Hoàn tất chứng minh. Đẳng thức xảy ra hoán vị cặp nghiệm $c=0$ và $\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{2+3k}{2}.$

2. Bài tập tự luyện

Cho các số thực không âm $a,b,c$ không có hai số nào đồng thời bằng không. Chứng minh rằng với $k\ge 1$ ta luôn có 2 bài toán sau:
$$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}+k\cdot\dfrac{(a+b)(b+c)(c+a)}{a^3+b^3+c^3}\ge 2\sqrt{k}+1.$$
$$\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}+k\cdot\dfrac{(a+b+c)(ab+bc+ca)}{a^3+b^3+c^3}\ge 2\sqrt{k}+1.$$
25/09/2021
Các bất đẳng thức thường sử dụng
Các bất đẳng thức thường sử dụng

1. Các bất đẳng thức thường sử dụng

Bất đẳng thức AM-GM

Với $a_1,a_2,\ldots,a_n$ là các số thực không âm, khi đó $$a_1+a_2+\cdots +a_{n}\ge n\sqrt[n]{a_1a_2\ldots a_n}.$$ Dấu bằng xảy ra khi và chỉ khi $a_1=a_2=\cdots =a_n$.

Chứng minh bất đẳng thức AM-GM cho hai số không âm bằng hình học

Bất đẳng thức AM-GM suy rộng

Cho $p_1,p_2\ldots p_n$ là các số thực dương thỏa $$p_1+p_2+\cdots +p_n=1.$$ Với $a_1,a_2\ldots a_n$ là các số thực không âm thì ta có $$p_1a_1+p_2a_2+\cdots +p_na_n\ge a_1^{p_1}a_2^{p_2}\ldots a_n^{p_n}.$$ Dấu bằng xảy ra khi và chỉ khi $a_1=a_2=\cdots =a_n.$

Bất đẳng thức AM-HM

Với $a_1,a_2,\ldots,a_n$ là các số thực không âm, khi đó $$\left(a_1+a_2+\cdots +a_n \right)\left(\dfrac{1}{a_1}+\dfrac{1}{a_2}\cdots +\dfrac{1}{a_n} \right)\ge n^2$$ Dấu bằng xảy ra khi và chỉ khi $a_1=a_2=\cdots =a_n.$

Bất đẳng thức Bernoulli

Với số thực $x\ge -1$, ta có:
- $(1+x)^r\ge 1+rx $ khi $r\ge 1$ hoặc $r\le 0$
- $(1+x)^r\le 1+rx $ khi $0\le r\le 1$
Bất đẳng thức Cauchy-Schwarz

Cho các số thực $a_1,a_2,\ldots ,a_n$ và $b_1,b_2,\ldots ,b_n$, ta có $$\left(a_1^2+a_2^2+\cdots +a_n^2\right)\left(b_1^2+b_2^2+\cdots +b_n^2\right)\ge \left(a_1b_1+a_2b_2+\cdots +a_nb_n\right)^2.$$ Dấu bằng xảy ra khi và chỉ khi $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots =\dfrac{a_n}{b_n}.$

Bất đẳng thức Hölder

Cho $x_{ij}$ là các số thực không âm (với $i=\overline{1;m}, \ \ j=\overline{1;n}$ ), khi đó ta có $$\prod_{i=1}^{m}\left(\sum_{j=1}^n x_{ij}\right)\ge \left(\sum_{j=1}^{n}\sqrt[m]{\prod_{i=1}^{m}x_{ij}} \right)^m.$$

Bất đẳng thức Chebyshev

Cho $a_1\ge a_2\ge\cdots\ge a_n$ là các số thực.
1. Nếu $b_1\ge b_2\ge\cdots\ge b_n$ thì $$n\sum_{i=1}^na_ib_i\ge\left(\sum_{i=1}^n a_i\right)\left(\sum_{i=1}^n b_i\right).$$
2. Nếu $b_1\le b_2\le\cdots\le b_n$ thì $$n\sum_{i=1}^na_ib_i\le\left(\sum_{i=1}^n a_i\right)\left(\sum_{i=1}^n b_i\right).$$
Bất đẳng thức hoán vị

Cho $a_1\ge a_2\ge\ldots\ge a_n$ là hai dãy số thực và $(z_1,z_2,\ldots ,z_n)$ là hoán vị nào đó của $(x_1,x_2,\ldots ,x_n)$. Khi đó ta có:
1. Nếu $b_1\ge b_2\ge\cdots\ge b_n$ thì $$a_1b_1+a_2b_2+\cdots a_nb_n\ge z_1b_2+z_2b_2+\cdots +z_nb_n.$$
2. Nếu $b_1\le b_2\le\cdots\le b_n$ thì $$a_1b_1+a_2b_2+\cdots a_nb_n\le z_1b_2+z_2b_2+\cdots +z_nb_n.$$
Bất đẳng thức Maclaurin và bất đẳng thức Newton

Với $a_1,a_2,\ldots,a_n$ là các số thực không âm, khi đó:
1. (Maclaurin) $S_1\ge S_2\ge \cdots\ge S_n$
2. (Newton) $S_k^2\ge S_{k-1}S_{k+1}$
với $$S_{k}=\sqrt[k]{\dfrac{\displaystyle\sum_{1\le i_1< i_2<\cdots <i_n}^n a_{i_1}a_{i_2}\ldots a_{i_n} }{ C_{n}^k}}.$$

Bất đẳng thức Karamata

Cho hai bộ số $(x_1,x_2\ldots ,x_n)$ và $(y_1,y_2\ldots ,y_n)$ với $(x_1,x_2\ldots ,x_n)\succ\succ(y_1,y_2\ldots ,y_n)$ sao cho $x_i,y_i\in \mathbb{I}\subseteq \mathbb{R}$. Nếu hàm số $f$ xác định lồi trên khoảng $\mathbb{I}\subseteq \mathbb{R}$ thì
$$f(x_1)+f(x_2)+\cdots +f(x_n)\ge f(y_1)+f(y_2)+\cdots +f(y_n).$$

Ghi chú: $$(x_1,x_2\ldots ,x_n)\succ\succ(y_1,y_2\ldots ,y_n)\Leftrightarrow\begin{cases}x_1\ge y_1\\
x_2+x_2\ge y_1+y_2\\
\cdots \cdots \cdots\cdots \cdots \cdots\cdots \cdots\\
x_1+x_2+\cdots +x_{n-1}\ge y_1+y_2+\cdots +y_{n-1}\\
x_1+x_2+\cdots +x_{n}= y_1+y_2+\cdots +y_{n}\end{cases}$$

Bất đẳng thức Popoviciu

Cho hàm số $f$ xác định lồi trên khoảng $\mathbb{I}\subseteq \mathbb{R}$. Khi đó với $a_1,a_2,\ldots ,a_n\in\mathbb{I}$ thì
$$f(a_1)+f(a_2)+\cdots +f(a_n)+n(n-2)f\left(\dfrac{a_1+a_2+\cdots +a_n}{n}\right)\ge (n-1)\left[f(b_1)+f(b_2)+\cdots +f(b_2)\right],$$ với $$b_i=\dfrac{1}{n-1}\sum_{j\neq i}a_j \ \ ,\ \ i=\overline{1;n}.$$

Bất đẳng thức Schur
- Cho các số thực không âm $a,b,c$ và số thực dương k, khi đó ta có $$a^k(a-b)(a-c)+b^k(b-c)(b-a)+c^k(c-a)(c-b)\ge 0,$$ Đẳng thức xảy ra khi $a=b=c$ hoặc $a=0$ và $b=c$ hoặc một vài hoán vị.
- Với $k=1$ chúng ta thu được một vài phát biểu quen thuộc sau: $$a^3+b^3+c^3+3abc\ge ab(a+b)+bc(b+c)+ca(c+a)$$
  $$(a+b+c)^3+9abc\ge 4(a+b+c)(ab+bc+ca)$$ $$a^2+b^2+c^2+\dfrac{9abc}{a+b+c}\ge 2(ab+bc+ca)$$ $$\sum_{cyc}\dfrac{a}{b+c} +\dfrac{4abc}{(a+b)(b+c)(c+a)}\ge 2.$$
Bất đẳng thức Vornicu-Schur

Cho các số thực không âm $a,b,c,x,y,z$ sao cho $(a,b,c)$ và $(x,y,z)$ đều là các bộ đơn điệu. Khi đó ta có $$x(a-b)(a-c)+y(b-a)(b-c)+z(c-a)(c-b)\ge 0$$

Bất đẳng thức Vasc

Với mọi số thực $a,b,c$, ta có $$(a^2+b^2+c^2)^2\ge 3(a^3b+b^3c+c^3a). $$ Đẳng thức xảy ra khi $a=b=c$ hoặc $\dfrac{a}{sin^2\dfrac{4\pi}{7}}=\dfrac{b}{sin^2\dfrac{2\pi}{7}}=\dfrac{c}{sin^2\dfrac{\pi}{7}}$, (hoặc một vài hoán vị).

Bất đẳng thức Vasc

Cho $f_{n}(a,b,c)$ là một đa thức đối xứng bậc $n=3$, $n=4$, $n=5.$
1. Với $a,b,c$ các số thực thì $f_{4}(a,b,c)\ge 0$ khi và chỉ khi $f_{4}(a,1,1)\ge 0$
2. Với $a,b,c$ các số thực không âm thì $f_{n}(a,b,c)\ge 0$ khi và chỉ khi $f_{n}(a,1,1)\ge 0$ và $f_{n}(0,b,c)\ge 0$.
Bất đẳng thức $(a-b)^2(b-c)^2(c-a)^2\ge 0$

Với các số thực $a,b,c$, ta có $$27(a-b)^2(b-c)^2(c-a)^2= 4(p^2-3q)^3-(2p^3-9pq+27r)^2\ge 0,$$ từ đây ta có
$$ \dfrac{-2p^3+9pq-2(p^2-3q)\sqrt{p^2-3q}}{27} \le r\le \dfrac{-2p^3+9pq+2(p^2-3q)\sqrt{p^2-3q}}{27} $$

2. Một số tiêu chuẩn khi chứng minh bất đẳng thức

SOS

Cho các số thực không âm thỏa $a\ge b\ge c $ và cần chứng minh $$f(a,b,c)=(a-b)^2S_c+(b-c)^2S_a+(c-a)^2S_b\ge 0.$$
Sau đấy chúng ta sẽ tạo ra một vài tiêu chuẩn thường sử dụng:
1. Tiêu chuẩn 1. Nếu $S_a,S_b,S_c\ge 0$ thì $f(a,b,c)\ge 0$ là hiển nhiên.
2. Tiêu chuẩn 2. Nếu $S_b\ge 0$ và $S_b+S_c\ge 0$ và $S_a+S_b\ge 0$ thì $f(a,b,c)\ge 0$.
  Thật vậy $$(a-c)^2=(a-b)^2+(b-c)^2+2(a-b)(b-c)\ge (a-b)^2+(b-c)^2,$$
  do đó ta có $$f(a,b,c)\ge (a-b)^2(S_b+S_c)+(b-c)^2(S_a+S_b)\ge 0,$$ do đó để bất đẳng thức đúng ta cần chứng minh $S_b+S_c\ge 0$ và $S_a+S_b\ge 0$.
3. Tiêu chuẩn 3. Nếu $S_b\le 0$ và $S_a+2S_b\ge 0$ và $S_c+2S_b\ge 0$ thì $f(a,b,c)\ge 0$.
  Thật vậy $$(a-c)^2=(a-b)^2+(b-c)^2+2(a-b)(b-c)\le 2\left[(a-b)^2+(b-c)^2 \right]$$ do đó ta có
  $$f(a,b,c)\ge (a-b)^2(S_c+2S_b)+(b-c)^2(S_a+2S_b),$$ vậy nên để bất đẳng thức đúng ta cần chứng minh $S_c+2S_b\ge 0$ và $S_a+2S_b\ge 0$.
4. Tiêu chuẩn 4. Nếu $S_b,S_c\ge 0$ và $b^2S_a+a^2S_b\ge 0$ thì $f(a,b,c)\ge 0$.
  Thật vậy theo bất đẳng thức tỉ lệ thì $$\dfrac{a-c}{b-c}\ge \dfrac{a}{b},$$ do đó ta có $$f(a,b,c)\ge (b-c)^2S_a+\dfrac{(b-c)^2a^2}{b^2}S_b,$$ vậy nên để bất đẳng thức đúng ta cần chứng minh $b^2S_a+a^2S_b\ge 0.$
5. Tiêu chuẩn 5. Nếu $S_b,S_c\ge 0$ và $b(b-c)S_a+a(a-c)S_b\ge 0$ thì $f(a,b,c)\ge 0$.
  Thật vậy theo bất đẳng thức tỉ lệ thì $$\dfrac{a-c}{b-c}\ge \dfrac{a}{b},$$ do đó ta có $$f(a,b,c)\ge (b-c)^2S_a+\dfrac{(b-c)^2a(a-c)}{b(b-c)}S_b,$$ vậy nên để bất đẳng thức đúng ta cần chứng minh $b(b-c)S_a+a(a-c)S_b\ge 0.$
Tiêu chuẩn Vornicu-Schur

\begin{aligned}x(a-b)(a-c)&+y(b-c)(b-a)+z(c-a)(c-b)=\left[a\sqrt{x}-(\sqrt{x}+\sqrt{z})b+c\sqrt{z} \right]^2+\\
&+(\sqrt{x}-\sqrt{y}+\sqrt{z})^2(a-b)(b-c)+2\sqrt{y}(a-b)(b-c)(\sqrt{x}-\sqrt{y}+\sqrt{z})\end{aligned}
25/09/2021
Good Questions in Limits
Good Questions in Limits

Credit: www.math.cornell.edu

1. Good Questions in Limits

Question 1. Let $f$ be the function defined by $f(x)=\sin x+\cos x$ and let $g$ be the function defined by $g(u)=\sin u+\cos u$, for all real numbers $x$ and $u$. Then,
- (a) $f$ and $g$ are exactly the same functions
- (b) if $x$ and $u$ are different numbers, $f$ and $g$ are different functions
- (c) not enough information is given to determine if $f$ and $g$ are the same.
Question 2. TRUE or FALSE. If
- $f(x)=\displaystyle{\frac{x^2-4}{x-2}}$ and
- $g(x)=x+2$, then we can say the functions $f$ and $g$ are equal.
Question 3. Imagine that there is a rope around the equator of the earth. Add a 20 meter segment of rope to it. The new rope is held in a circular shape centered about the earth. Then the following can walk beneath the rope without touching it:
- (a) an amoeba
- (b) an ant
- (c) I (the student)
- (d) all of the above
Question 4. Given two infinite decimals $a=0. 3939393939…$ and $b=0.67766777666…$, their sum $a+b$
- (a) is not defined because the sum of a rational and irrational number is not defined.
- (b) is not a number because not all infinite decimals are real numbers.
- (c) can be defined precisely by using successively better approximations
- (d) is not a real number because the pattern may not be predictable indefinitely.
Question 5. TRUE or FALSE. As $x$ increases to $100$, $f(x)=1/x$ gets closer and closer to $0$, so the limit as $x$ goes to $100$ of $f(x)$ is $0$. Be prepared to justify your answer.

Question 6. TRUE or FALSE. $\displaystyle{\lim_{x\rightarrow a}f(x)=L}$ means that if $x_1$ is closer to $a$ than $x_2$ is, then $f(x_1)$ will be closer to $L$ than $f(x_2)$ is. Be prepared to justify your answer with an argument or counterexample.

Question 7. You’re trying to guess $\displaystyle{\lim_{x \rightarrow 0}f(x)}$. You plug in $x=0.1, 0.01, 0.001, \dots$ and get $f(x)=0$ for all these values. In fact, you’re told that for all $n=1, 2, \dots, f\left(\frac{1}{10^n}\right)=0$.

TRUE or FALSE: Since the sequence $0.1, 0.01, 0.001, \dots$ goes to $0$, we know $\displaystyle{\lim_{x \rightarrow 0} f(x)}=0$.

Question 8. Suppose you have an infinite sequence of closed intervals, each one contains the next, and suppose too that the width of the $n$th interval is less than $\frac{1}{n}$. If $a$ and $b$ are in each of these intervals,
- (a) $a$ and $b$ are very close but they don’t have to be equal
- (b) either $a$ or $b$ must be an endpoint of one of the intervals
- (c) $a=b$
Question 9. Consider the function $$f(x)=\left\{\begin{array}{ll} x^2 & \mbox{$x$ is rational, $x\neq 0$} \\ -x^2 & \mbox{$x$ is irrational} \\ \mbox{undefined} & x=0 \end{array}\right.$$ Then
- (a) there is no $a$ for which $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists
- (b) there may be some $a$ for which $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists, but it is impossible to say without more information
- (c) $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists only when $a=0$
- (d) $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists for infinitely many $a$
Question 10. The statement “Whether or not $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists, depends on how $f(a)$ is defined,” is true
- (a) sometimes
- (b) always
- (c) never
See more: Function Exercise

Question 11. If a function $f$ is not defined at $x=a$,
- (a) $\displaystyle{\lim_{x\rightarrow a} f(x)}$ cannot exist
- (b) $\displaystyle{\lim_{x\rightarrow a} f(x)}$ could be $0$
- (c) $\displaystyle{\lim_{x\rightarrow a} f(x)}$ must approach $\infty$
- (d) none of the above.
Question 12. If $\displaystyle{\lim_{x\rightarrow a} f(x)=0}$ and $\displaystyle{\lim_{x\rightarrow a} g(x)=0}$, then $\displaystyle{\lim_{x\rightarrow a} \frac{f(x)}{g(x)}}$
- (a) does not exist
- (b) must exist
- (c) not enough information
The following two problems to be used in a sequence:

Question 13. The reason that $\displaystyle{\lim_{x\rightarrow 0}\sin (1/x)}$ does not exist is:
- (a) because no matter how close $x$ gets to $0$, there are $x$’s near $0$ for which $\sin(1/x) =1$, and some for which $\sin (1/x)=-1$
- (b) because the function values oscillate around $0$
- (c) because $1/0$ is undefined
- (d) all of the above
Question 14. $\displaystyle{\lim_{x\rightarrow 0}x^2\sin (1/x)}$
- (a) does not exist because no matter how close $x$ gets to $0$, there are $x$’s near $0$ for which $\sin(1/x) =1$, and some for which $\sin (1/x)=-1$
- (b) does not exist because the function values oscillate around $0$
- (c) does not exist because $1/0$ is undefined
- (d) equals $0$
- (e) equals $1$
Question 15. Suppose you have two linear functions $f$ and $g$ shown below.

Then $\displaystyle{\lim_{x\rightarrow a}\frac{f(x)}{g(x)}}$ is
- (a) 2
- (b) does not exist
- (c) not enough information
- (d) 3
Question 16. TRUE or FALSE. Consider a function $f(x)$ with the property that $\displaystyle{\lim_{x\rightarrow a} f(x) =0}$. Now consider another function $g(x)$ also defined near $a$. Then $\displaystyle{\lim_{x\rightarrow a} [f(x)g(x)] = 0}$.

Question 17. TRUE or FALSE.

If $\displaystyle{\lim_{x\rightarrow a} f(x) =\infty}$ and $\displaystyle{\lim_{x\rightarrow a} g(x) =\infty}$, then $\displaystyle{\lim_{x\rightarrow a} [f(x)-g(x)] =0}$.

Question 18. Suppose you have two linear function $f$ and $g$ shown below.

Then $\displaystyle{\lim_{x\rightarrow \infty}\frac{f(x)}{g(x)}}$ is
- (a) 2
- (b) does not exist
- (c) not enough information
- (d) 3
Question 19. What is the maximum number of horizontal asymptotes that a function can have?
- (a) one
- (b) two
- (c) three
- (d) as many as we want
Question 20. TRUE or FALSE. A function can cross its horizontal asymptote.

2. Answer

Question 1. Let $f$ be the function defined by $f(x)=\sin x+\cos x$ and let $g$ be the function defined by $g(u)=\sin u+\cos u$, for all real numbers $x$ and $u$. Then,
- (a) $f$ and $g$ are exactly the same functions
- (b) if $x$ and $u$ are different numbers, $f$ and $g$ are different functions
- (c) not enough information is given to determine if $f$ and $g$ are the same.
Answer: (a). Both $f$ and $g$ are given by the same rule, and are defined on the same domain, hence they are the same function.

Question 2. TRUE or FALSE. If
- $f(x)=\displaystyle{\frac{x^2-4}{x-2}}$ and
- $g(x)=x+2$, then we can say the functions $f$ and $g$ are equal.
Answer: FALSE. Note that even if the two functions have the same rule, they are defined on different domains, i.e., $f$ is not defined at 2.

Question 3. Imagine that there is a rope around the equator of the earth. Add a 20 meter segment of rope to it. The new rope is held in a circular shape centered about the earth. Then the following can walk beneath the rope without touching it:
- (a) an amoeba
- (b) an ant
- (c) I (the student)
- (d) all of the above
Answer: (d). This question is quite difficult for students because it is very counter-intuitive. A little algebra needs to be done to see that as long as the student is not over $\frac{20}{2\pi}$ meters tall, she should be able to walk under the rope.

Students should know or be provided with the perimeter of a circle. There is no need to know the radius of the Earth at equator. The problem encourages using a mathematical model to check one’s intuition. Instructors should validate students’ intuition: the change in radius is very small relative to the radius, and this may lead to the erroneous conclusion that a human would not be able to walk underneath the rope; however, a human’s height is also very small relative to the radius.

Question 4. Given two infinite decimals $a=0. 3939393939…$ and $b= 0. 67766777666…$, their sum $a+b$
- (a) is not defined because the sum of a rational and irrational number is not defined.
- (b) is not a number because not all infinite decimals are real numbers.
- (c) can be defined precisely by using successively better approximations
- (d) is not a real number because the pattern may not be predictable indefinitely.
Answer: (c). Students may be unsure about real numbers as infinite decimals. Students know that all rational numbers have terminating or repeating decimal representations. They also know that there are irrational numbers, hence there are some numbers that are represented as infinite decimals. However, they may not know that every infinite decimal represents a number (although not uniquely in the case of repeating 9’s and repeating 0’s) -The phrase “can be defined precisely” may cause some to reject this as a solution. In discussing this question, instructors can introduce the idea that every infinite decimal is a number and the Archimedian Axiom can help us see how we can tell whether two numbers are the same.

Question 5. TRUE or FALSE. As $x$ increases to $100$, $f(x)=1/x$ gets closer and closer to $0$, so the limit as $x$ goes to $100$ of $f(x)$ is $0$. Be prepared to justify your answer.

Answer: FALSE. As $x$ increases to $100$, $f(x)=1/x$ gets closer and closer to $0$, gets closer and closer to $1/1000$, but not as close as to $1/100$.
The question points out the weakness of the statement “$f(x)$ gets closer to $L$ as $x\to a$, and therefore $\displaystyle{\lim_{x\rightarrow a}f(x)=L}$”.

Question 6. TRUE or FALSE. $\displaystyle{\lim_{x\rightarrow a}f(x)=L}$ means that if $x_1$ is closer to $a$ than $x_2$ is, then $f(x_1)$ will be closer to $L$ than $f(x_2)$ is. Be prepared to justify your answer with an argument or counterexample.

Answer: FALSE. Going to the limit is not monotonic! As a counterexample you can consider $$ f(x)=\left\{ \begin{array}{cl}
2x & x\ge 0 \\ -x & x<0 \end{array}\right. $$ Then $\displaystyle{\lim_{x\rightarrow 0}f(x)=0}$, and take $x_1=0.25$, $x_2=-0.35$.

Question 7. You’re trying to guess $\displaystyle{\lim_{x \rightarrow 0}f(x)}$. You plug in $x=0.1, 0.01, 0.001, \dots$ and get $f(x)=0$ for all these values. In fact, you’re told that for all $n=1, 2, \dots,f\left(\frac{1}{10^n}\right)=0$.

TRUE or FALSE: Since the sequence $0.1, 0.01, 0.001, \dots$ goes to $0$, we know $\displaystyle{\lim_{x \rightarrow 0} f(x)}=0$.

Answer: FALSE. The goal is to see whether the students understand that it’s not enough to check the limit for one particular sequence of numbers that goes to 0. The instructor may want to recall the function $\displaystyle{\sin (\frac{\pi}{x})}$ from Stewart, as $x$ goes to 0, in order to discuss the problem. Make sure to point out this problem as an example of the danger of using calculators to “find” limits.

Question 8. Suppose you have an infinite sequence of closed intervals, each one contains the next, and suppose too that the width of the $n$th interval is less than $\frac{1}{n}$. If $a$ and $b$ are in each of these intervals,
- (a) $a$ and $b$ are very close but they don’t have to be equal
- (b) either $a$ or $b$ must be an endpoint of one of the intervals
- (c) $a=b$
Answer: (c). If using this problem, the instructor should briefly talk about the Archimedian Axiom, and how intersection of nested closed intervals $I_n$ of respective lengths $\frac{1}{n}$, is a single point. Since both $a$ and $b$ are in each of these $I_n$, this single point of intersection is $a=b$. Students have a hard time understanding the Squeeze Theorem, so this might be a good place to start in attacking that problem.

Question 9. Consider the function $$f(x)=\left\{\begin{array}{ll} x^2 & \mbox{$x$ is rational, $x\neq 0$} \\ -x^2 & \mbox{$x$ is irrational} \\ \mbox{undefined} & x=0 \end{array}\right.$$ Then
- (a) there is no $a$ for which $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists
- (b) there may be some $a$ for which $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists, but it is impossible to say without more information
- (c) $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists only when $a=0$
- (d) $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists for infinitely many $a$
Answer: (c). Students should be encouraged to draw the graph and discuss.

Question 10. The statement “Whether or not $\displaystyle{\lim_{x\rightarrow a}f(x)}$ exists, depends on how $f(a)$ is defined,” is true
- (a) sometimes
- (b) always
- (c) never
Answer: (c). Use this problem to stress that $f(a)$ need not be defined in order for $\displaystyle{\lim_{x\rightarrow a}f(x)}$ to exist. Students have a difficult time asserting “never”. The problem provides an opportunity to discuss what a limit is.

Question 11. If a function $f$ is not defined at $x=a$,
- (a) $\displaystyle{\lim_{x\rightarrow a} f(x)}$ cannot exist
- (b) $\displaystyle{\lim_{x\rightarrow a} f(x)}$ could be $0$
- (c) $\displaystyle{\lim_{x\rightarrow a} f(x)}$ must approach $\infty$
- (d) none of the above.
Answer: (b). Answers $(a)$ and $(c)$ are very popular. $f(a)$ need not be defined in order for $\displaystyle{\lim_{x\rightarrow a}f(x)}$ to exist, and it does not have to approach $\infty$. However, the limit could be 0, for example consider $f(x)= 0$ for all $x \neq a$, and $f(a)$ not defined. The student has to note the difference between “cannot”, “could” and “must”.

Question 12. If $\displaystyle{\lim_{x\rightarrow a} f(x)=0}$ and $\displaystyle{\lim_{x\rightarrow a} g(x)=0}$, then $\displaystyle{\lim_{x\rightarrow a} \frac{f(x)}{g(x)}}$
- (a) does not exist
- (b) must exist
- (c) not enough information
Answer: (c). Point out that $\frac{0}{0}$ is not always equal to $1$. If this question is used after any of the previous two problems, more students will be able to answer correctly.

The following two problems to be used in a sequence:

Question 13. The reason that $\displaystyle{\lim_{x\rightarrow 0}\sin (1/x)}$ does not exist is:
- (a) because no matter how close $x$ gets to $0$, there are $x$’s near $0$ for which $\sin(1/x) =1$, and some for which $\sin (1/x)=-1$
- (b) because the function values oscillate around $0$
- (c) because $1/0$ is undefined
- (d) all of the above
Answer: (a). Illustrate why (b) and (c) are not the reason why the limit does not exist, by introducing the next problem.

Question 14. $\displaystyle{\lim_{x\rightarrow 0}x^2\sin (1/x)}$
- (a) does not exist because no matter how close $x$ gets to $0$, there are $x$’s near $0$ for which $\sin(1/x) =1$, and some for which $\sin (1/x)=-1$
- (b) does not exist because the function values oscillate around $0$
- (c) does not exist because $1/0$ is undefined
- (d) equals $0$
- (e) equals $1$
Answer: (d). As in the previous problem, the function oscillates and $1/0$ is undefined, however, this limit exists. This is also a nice application of The Squeeze Theorem: $$\displaystyle{\lim_{x\rightarrow 0} (-x^2)}\le \displaystyle{\lim_{x\rightarrow 0}x^2\sin (1/x)} \le \displaystyle{\lim_{x\rightarrow 0} x^2}$$ Therefore, the limit equals $0$.

Question 15. Suppose you have two linear functions $f$ and $g$ shown below.

Then $\displaystyle{\lim_{x\rightarrow a}\frac{f(x)}{g(x)}}$ is
- (a) 2
- (b) does not exist
- (c) not enough information
- (d) 3
Answer: (a). This problem requires a geometrical argument:

Solution 1: By similar triangles, $\frac{f(x)}{6}=\frac{ x-a}{0-a}=\frac{ g(x)}{3}$, and therefore $\frac {f(x)}{g(x)}=\frac {6}{3}=2$.

Solution 2: $$\displaystyle{\lim_{x\rightarrow a} \frac {f(x)}{g(x)}}=\displaystyle{\lim_{x\rightarrow a} \frac {\frac{f(x)}{-a}}{\frac{g(x)}{-a}}}=\displaystyle{\lim_{x\rightarrow a} \frac {\mbox{slope of } f}{\mbox{slope of } g}}=\frac{6}{3}=2$$ This problem is a nice preview of L’Hospital’s Rule.

Question 16. TRUE or FALSE. Consider a function $f(x)$ with the property that $\displaystyle{\lim_{x\rightarrow a} f(x) =0}$. Now consider another function $g(x)$ also defined near $a$. Then $\displaystyle{\lim_{x\rightarrow a} [f(x)g(x)] = 0}$.

Answer: FALSE. Students might justify a True answer by “zero times any number equals zero”. Point out that it is possible that $\displaystyle{\lim_{x\rightarrow a} g(x) =\infty}$. A quick counterexample can be $a=0$, $f(x)=x$ and $g(x)=1/x$.

Question 17. TRUE or FALSE.

If $\displaystyle{\lim_{x\rightarrow a} f(x) =\infty}$ and $\displaystyle{\lim_{x\rightarrow a} g(x) =\infty}$, then $\displaystyle{\lim_{x\rightarrow a} [f(x)-g(x)] =0}$.

Answer: FALSE. Students might be thinking that $\infty$ is a number, and therefore $\infty -\infty=0$. As a quick counterexample, consider $f(x)=x^2$ and $g(x)=x$.

Question 18. Suppose you have two linear function $f$ and $g$ shown below.

Then $\displaystyle{\lim_{x\rightarrow \infty}\frac{f(x)}{g(x)}}$ is
- (a) 2
- (b) does not exist
- (c) not enough information
- (d) 3
Answer: (a). Recall problem $6.$ in Section $2.3$. $\frac{f(x)}{6}=\frac{ x-a}{0-a}=\frac{ g(x)}{3}$, and therefore $\frac {f(x)}{g(x)}=\frac {6}{3}=2$.

Question 19. What is the maximum number of horizontal asymptotes that a function can have?
- (a) one
- (b) two
- (c) three
- (d) as many as we want
Answer: (b). Students must pay attention to the way horizontal asymptotes are defined. Point out that asymptotes are defined as we go to $\infty$ and to $-\infty$, even though a function may have asymptotic behavior at other points.

Question 20. TRUE or FALSE. A function can cross its horizontal asymptote.

Answer: TRUE. It is easy to sketch a function that crosses its horizontal asymptote. For example, consider $\frac{\sin x}{x}$.
24/09/2021
Phương pháp so sánh thể tích
Phương pháp so sánh thể tích

Để tính thể tích của một khối chóp, khối lăng trụ chúng ta có thể tính trực tiếp bằng cách xác định diện tích đáy và chiều cao như trong bài Tính thể tích khối chóp. Tuy nhiên, có một cách rất hiệu quả để tính thể tích của khối chóp, khối lăng trụ, khối đa diện mà đề bài yêu cầu là so sánh chúng với các khối có thể tích dễ dàng tính được.

1. Lý thuyết Phương pháp so sánh thể tích

Từ công thức tính thể tích khối chóp, ta thấy thể tích của khối chóp không đổi khi:
- Đáy cố định, đỉnh của hình chóp di chuyển trên một mặt phẳng hoặc một đường thẳng song song với đáy.
- Đỉnh của hình chóp cố định, đáy của hình chóp biến đổi trên một mặt phẳng cố định thành những đa giác tương đương (tức là những đa giác có cùng diện tích).
Do đó, khi tính thể tích khối chóp, chúng ta thường sử dụng các kết quả:
- Hai khối chóp có chung đáy thì ta đi so sánh vị trí của hai đỉnh.
- Hai khối chóp có chung đỉnh thì ta đi so sánh diện tích của hai đáy.
- Sử dụng công thức tỉ số thể tích.
2. Ví dụ Phương pháp so sánh thể tích

Ví dụ 1. Chia khối lăng trụ $ABC.A’B’C’$ thành ba khối tứ diện bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$. Hãy kể tên ba khối tứ diện đó và chứng tỏ rằng chúng có cùng thể tích.

Lời giải
- Chia khối lăng trụ $ABC.A’B’C’$ bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$ thành ba khối tứ diện: $CC’A’B’$, $CBA’B’$, $CABA’$.
- Xét hai hình chóp $C.ABA’$ và $C.BA’B’$ có cùng độ dài đường cao là khoảng cách từ $C$ tới mặt phẳng $(ABB’A’)$ và đáy là các tam giác $ABA’$, $BB’A’$ là hai tam giác cùng diện tích (cùng bằng một nửa diện tích của hình bình hành $ABB’A’$). Vậy \[{{V}_{C.{ABA}}}={{V}_{C.{BA}B’}}\] hay \[{{V}_{{CABA}}}={{V}_{{CBA}B’}}\]
- Ta có: $BB’//(ACC’A’)$ nên suy ra $d(B; (ACC’A’))=d(B’; (ACC’A’))$ hay $$d(B; (ACA’))=d(B’; (CC’A’)).$$
- Lại có $ACA’$ và $CC’A’$ la hai tam giác có cùng diện tích nên \[V_{B.ACA’}=V_{B’.CC’A}\] hay \[V_{CABA’}=V_{CC’AB’}\]
Từ đó suy ra điều phải chứng minh.

Ví dụ 2. [CĐ2011] Cho hình chóp $ S.ABC $ có đáy là tam giác vuông cân tại $ B, AB=a,SA $ vuông góc với đáy. Góc giữa hai mặt phẳng $ (SBC) $ và $ (ABC) $ bằng $ 30^\circ. $ Gọi $ M,N $ lần lượt là trung điểm $ SC,AB $. Tính thể tích các khối chóp $ S.ABM, S.BMN. $

Hướng dẫn. Chỉ ra $ \widehat{SBA}=30^\circ $ và $ V_{S.ABM}=\frac{1}{2}V_{S.ABC} =\frac{a^3\sqrt{3}}{36}. $

Ví dụ 3. Cho hình chóp $ S.ABC $ có đáy là $ \Delta ABC $ vuông cân ở $ B$, $AC=a\sqrt{2},SA\perp\left( ABC \right), SA=a $. Gọi $ G $ là trọng tâm của $ \Delta SBC $, mặt phẳng $ \left( \alpha \right) $ đi qua $ AG $ và song song với $ BC $ cắt $ SC,SB $ lần lượt tại $ M,N $. Tính thể tích khối chóp $ S.AMN $?

Hướng dẫn. Tính được $ V_{S.ABC}=\frac{{{a}^{3}}}{6}. $ Ta có \[ \frac{{{V}_{S.AMN}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=\frac{4}{9} \] Suy ra $ {{V}_{S.AMN}}=\frac{4}{9}.{{V}_{S.ABC}}=\frac{4}{9}.\frac{{{a}^{3}}}{6}=\frac{2{{a}^{3}}}{27}. $

Ví dụ 4. [D2006] Cho hình chóp $ S.ABC $ có đáy là $ \Delta ABC $ đều cạnh $ a $ và $ SA\perp \left( ABC \right), SA=2a $. Gọi $ H,K $ lần lượt là hình chiếu vuông góc của điểm $ A $ lần lượt lên cạnh $ SB,SC $. Tính thể tích khối $ A.BCKH $ theo $ a $.

Hướng dẫn. Tính ngay được \[{{V}_{S.ABC}}=\frac{1}{3}.{{S}_{\Delta ABC}}.SA=\frac{1}{3}.\frac{{{a}^{2}}\sqrt{3}}{4}.2a=\frac{{{a}^{3}}\sqrt{3}}{6}\] Mặt khác lại có \[\frac{{{V}_{S.AHK}}}{{{V}_{S.ABC}}}=\frac{SA}{SA}.\frac{SH}{SB}.\frac{SK}{SC}=\frac{SH.SB}{S{{B}^{2}}}.\frac{SK.SC}{S{{C}^{2}}}=\frac{16}{25}\] Suy ra \[ {{V}_{A.BCKH}}={{V}_{S.ABC}}-{{V}_{S.AHK}}=\frac{9}{25}.{{V}_{S.ABC}}=\frac{3{{a}^{3}}\sqrt{3}}{50} \]

Ví dụ 5. Cho hình chóp tứ giác đều $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh bên tạo với đáy một góc $ 60^\circ $. Gọi $ M $ là trung điểm $ SC $. Mặt phẳng đi qua $ AM $ và song song với $ BD $, cắt $ SB $ tại $ E $ và cắt $ SD $ tại $ F $. Tính thể tích khối chóp $ S.AEMF $.

Hướng dẫn. $ {{V}_{SAMF}}=\frac{1}{3}{{V}_{SACD}}=\frac{1}{6}{{V}_{S.ABCD}}=\frac{{{a}^{3}}\sqrt{6}}{36}\Rightarrow {{V}_{S.AEMF}}=2.\frac{{{a}^{3}}\sqrt{6}}{36}=\frac{{{a}^{3}}\sqrt{6}}{18} $

Ví dụ 6. Cho hình chóp $S.ABC$ có các góc $ \widehat{ASB}=\widehat{BSC}=\widehat{CSA}=60^\circ $. Độ dài các cạnh $ SA,SB,SC $ lần lượt là $ a,b,c $. Tính thể tích khối chóp $ S.ABC. $

Hướng dẫn.
Trên các cạnh $ SB,SC $ lần lượt lấy $ B’,C’ $ sao cho $ SB’=SC’=SA=a $. Như vậy, hình chóp $S.AB’C’$ là một tứ diện đều cạnh bằng $ a $ nên có thể tích \[ V_{SAB’C’}=\frac{a^3\sqrt{2}}{12}. \] Mặt khác, theo tỉ số thể tích thì
\[ \frac{V_{S.ABC}}{V_{S.AB’C’}}=\frac{SA}{SA}\cdot\frac{SB}{SB’}\cdot\frac{SC}{SC’}=\frac{bc}{a^2}\]
Do đó, thể tích khối chóp cần tìm là \[ V_{S.ABC}=\frac{abc\sqrt{2}}{12}. \]

Ví dụ 7. [CĐ2008] Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy $AB=a$, cạnh bên $SA=a\sqrt{2}$. Gọi $M,N,P$ lần lượt là trung điểm của $SA,SB,CD$. Tính thể tích tứ diện $AMNP$?

Hướng dẫn. Vì $MS=MA$ nên $ d\left(A,(MNP) \right)=d\left(S,(MNP) \right)$. Do đó $ V_{A.MNP}=V_{S.MNP} $. Mặt khác \[\frac{{{V}_{S.MNP}}}{{{V}_{S.ABP}}}=\frac{SM}{SA}.\frac{SN}{SB}.\frac{SP}{SP}=\frac{1}{4}\]
Từ đó tìm được $ {{V}_{A.MNP}}=\frac{{{a}^{3}}\sqrt{6}}{48}. $

3. Bài tập sử dụng Phương pháp so sánh thể tích

Bài 1. [CĐ2009] Cho hình chóp tứ giác đều $ S.ABCD $ có $ AB=a,SA=a\sqrt{2} $. Gọi $ M,N,P $ lần lượt là trung điểm của các cạnh $ SA,SB,CD $. Chứng minh rằng đường thẳng $ MN $ vuông góc với đường thẳng $ SP $. Tính theo $ a $ thể tích khối tứ diện $ AMNP $.

Hướng dẫn. Vì $ MN\parallel CD $ mà $ CD\perp SP $ nên $ MN\perp SP. $ Ta có $ V_{AMNP}=\frac{1}{4}V_{ABSP}= \frac{1}{8}V_{S.ABCD}$. Đáp số. $ V=\frac{a^3\sqrt{6}}{48} $

Bài 2. Cho tứ diện đều $ ABCD $ có cạnh $ a $. Lấy các điểm $ B’,C’ $ trên $ AB $ và $ AC $ sao cho $ AB’=\frac{a}{2},AC’=\frac{2a}{3} $. Tính thể tích khối tứ diện $ AB’C’D $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{2}}{36} $.

Bài 3. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a, SC\perp(ABCD) $ cho $ SA=a\sqrt{3} $. Gọi $ H $ là hình chiếu của $ C $ lên $ SB,K $ là trung điểm của $ SD. $ Tính thể tích khối chóp $ S.ABCD $ và khối chóp $ C.BDKH? $

Hướng dẫn. Xét tam giác vuông $ SCB $ có $ SH.SB=SC^2 $ nên $ \frac{SH}{SB}=\frac{SC^2}{SB^2}=\frac{2}{3}. $ Suy ra \[ \frac{V_{S.CKH}}{V_{S.CDB}}=\frac{SC}{SC}.\frac{SK}{SD}.\frac{SH}{SB}=\frac{1}{3} \] Do đó, $ V_{C.BDKH}=\frac{2}{3}V_{S.CBD}=\frac{1}{3}V_{S.ABCD} $

Đáp số. $ V_{S.ABCD}=\frac{a^3\sqrt{2}}{3}$, $V_{C.BDKH}=\frac{a^3\sqrt{2}}{9}. $

Bài 4. Cho hình chóp $ S.ABCD $ có đáy là hình chữ nhật với $ AB=a,\,AD=2a, $ cạnh $ SA $ vuông góc với đáy, cạnh $ SB $ tạo với mặt đáy một góc $ {{60}^{\circ }} $. Trên cạnh $ SA $ lấy điểm $ M $ sao cho $ AM=\frac{a\sqrt{3}}{3} $. Mặt phẳng $ (BCM) $ cắt cạnh $ SD $ tại $ N $. Tính thể tích khối chóp $ S.BCMN? $

Hướng dẫn. $ {{V}_{S.BCMN}}={{V}_{SMBC}}+{{V}_{SMNC}}=\frac{5}{9}{{V}_{S.ABCD}}=\frac{5}{9}.\frac{1}{3}.SA.{{S}_{ABCD}}=\frac{10\sqrt{3}}{27}{{a}^{3}} $

Bài 5. Cho hình chóp $ S.ABCD $ có đáy là hình vuông cạnh $ a $, cạnh bên $ SA $ vuông góc với đáy và $ SA = a $. Gọi $ M $ là một điểm trên cạnh $ SA $ sao cho $ AM = x $. Mặt phẳng $ (MBC) $ cắt $ SD $ tại $ N $. Tính thể tích khối đa diện $ ABCDMN $ theo $ a $ và $ x $.

Đáp số. $ V=\frac{ax.(3a-x)}{6} $

Bài 6. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác đều cạnh $ a\sqrt{3} $, đường cao $ SA=a $. Mặt phẳng qua điểm $ A $ và vuông góc với $ SB $ tại $ H $ và cắt $ SC $ tại $ K $. Tính thể tích hình chóp $ S.AHK $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{3}}{40} $.

Bài 7. Cho hình chóp $ S.ABCD $ có $ ABCD $ là hình bình hành, $ M $ thuộc cạnh $ SA $ và $ \frac{SM}{SA}=x $. Tìm $ x $ để mặt phẳng $ (MBC) $ chia hình chóp thành hai phần có thể tích bằng nhau?

Hướng dẫn. Mặt phẳng $ (MBC) $ cắt $ (SAD) $ theo giao tuyến $ MN\parallel AD. $ Phân chia $ V_{S.MNBC} =V_{S.MBC}+V_{S.MNC} $ để so sánh.

Đáp số. $ x=\frac{-1+\sqrt{5}}{2} $

Bài 8. [DB B2006] Cho hình chóp $ S.ABCD $ có đáy $ ABCD $ là hình thoi cạnh $ a $ và góc $ \widehat{BAD}={{60}^\circ} $. Biết rằng $ SA\perp \left( ABCD \right),SA=a $. Gọi $ C’ $ là trung điểm của cạnh $ SC $. Mặt phẳng $ \left( P \right) $ đi qua $ AC’ $ và song song với $ BD $, cắt các cạnh $ SB,SD $ lần lượt tại $ B’ $ và $ D’ $. Tính thể tích khối chóp $ S.ABC’D’ $.

Đáp số. $ V=\frac{{{a}^{3}}\sqrt{3}}{18} $.

Bài 9. Cho hình chóp $ S.ABCD $ có thể tích là $ V.$ Tứ giác $ ABCD $ là hình bình hành, $ M $ là trung điểm của $ BC $ và $ G $ là trọng tâm tam giác $ SCD $. Tính thể tích tứ diện $ SAMG? $

Hướng dẫn. So sánh thể tích hình chóp $ S.AMG $ với thể tích hình chóp $ S.AMN $ bằng cách coi $ \Delta SAM $ làm đáy chung.

Đáp số. $ V_{SAMG}=\frac{1}{4}V $

Bài 10. Cho hình chóp $ S.ABCD $ có thể tích là $ V.$ Tứ giác $ ABCD $ là hình bình hành. Gọi $ M,N,P $ lần lượt là trung điểm của $ BC,CD,SD $. Tính thể tích tứ diện $ AMNP? $

Bài 11. Cho hình chóp $ S.ABC $ có điểm $ M\in SA,N\in SB $ sao cho $ \frac{SM}{MA}=\frac{1}{2},\frac{SN}{NB}=2. $ Gọi $ (\alpha) $ là mặt phẳng qua $ MN $ và song song với $ SC $. Mặt phẳng này cắt $ AC $ tại $ E,BC $ tại $ F. $
1. Chứng minh rằng $ AB,MN,EF $ đồng quy, gọi điểm này là $ I, $ tính tỉ số $ \frac{BI}{BA}? $
2. Mặt phẳng $ (\alpha) $ chia hình chóp thành hai phần. Tính tỉ số thể tích của hai phần này?
Hướng dẫn. Gọi $ L $ là trung điểm của $ SN. $

Đáp số. $ \frac{BI}{BA}=\frac{1}{3},\frac{V_1}{V_2}=\frac{4}{5}. $
24/09/2021
Câu đố hình học của thủ tướng Nga

Câu đố hình học của thủ tướng Nga

Đầu năm 2020 Tổng cục trưởng Cục thuế Nga Mikhail Mishustin “đánh đùng một cái” được Putin chỉ định lên thay Thủ tướng Medvedev.

1/9/2021 nhân khai giảng Thủ tướng Nga Mikhail Mishustin đi thăm trường học – đây là trường chuyên lý mang tên viện sỹ Kapitsa, ở ngoại ô Moscow, dạy từ lớp 5 đến 12. Mỗi năm trường này cũng đem về vài chục huân chương từ các cuộc thi trong nước và quốc tế.

Vào thăm một lớp 11, ông thấy thày giáo và học sinh đang bàn về một đề án kinh doanh, Thủ tướng xin phát biểu, đại ý rằng kinh doanh thì rất tốt, nhưng theo tôi ở tuổi này các em nên học kiến thức khoa học cơ bản (toán, lý, hóa) cho giỏi, còn sau này ứng dụng tốt thì làm gì cũng được, kể cả kinh doanh.

Thủ tướng Nga Mikhail Mishustin viết trên bảng đen khi thăm Lyceum Vật lý và Công nghệ Kapitsa (Ảnh: Dmitry Astakhov/TASS)

Thế rồi Mishustin ra một đề toán, bảo các học sinh giải đi, ông đi thăm trường tiếp rồi chốc nữa quay lại xem thế nào. Khi quay lại các học sinh (không biết vô tình hay cố ý) vẫn chưa giải được bài toán ấy, các bạn thử sức xem, cũng đơn giản mà rất hay:

“Có một đường thẳng chạy qua tâm hình tròn, trên đường tròn có một điểm. Chỉ dùng thước kẻ hãy kẻ đường vuông góc từ điểm đó xuống đường thẳng kia”.

Điểm thú vị của bài toán này là việc chỉ sử dụng một chiếc thước kẻ không có chia độ, cũng không được phép được đánh dấu để đo khoảng cách, chỉ được sử dụng để vẽ các đường thẳng.

Lời giải Câu đố hình học của thủ tướng Nga

Đầu tiên, chúng ta hãy tìm cách dựng một đường thẳng vuông góc với đường kính trước. Giả sử đường kính là $AB$, điểm cần dựng đường vuông góc xuống là $C$.

Lấy một điểm $D$ bất kì thuộc nửa đường tròn chứa điểm $C$, không trùng với $C$. Kéo dài $AD$ và $BC$ cắt nhau tại $E$. Tam giác $ABE$ có hai đường cao là $AC$ và $BD$. Gao điểm của hai đường cao này chính là trực tâm $H$ của tam giác $ABE$ và ta có ngay $EH$ vuông góc với đường kính $AB$.

Tiếp theo, chúng ta đi dựng một đường thẳng đi quá $C$ và song song với $EH$ thì đó chính là đường thẳng mà đề bài yêu cầu.

Giả sử $EH$ cắt đường tròn tại hai điểm $I,J$ như hình vẽ. Nối $CI$ cắt đường kính $AB$ tại $K$. Nối $JK$ cắt đường tròn tại $M$ thì $CM$ chính là đường thẳng cần tìm. (Bạn đọc tự chỉ ra $CMIJ$ là hình thang để từ đó có $CM$ song song với $IJ$).

23/09/2021
Phương pháp phân chia khối đa diện
Phương pháp phân chia khối đa diện

Để tính thể tích của một khối đa diện, nếu đó là các khối cơ bản như khối chóp, khối lăng trụ thì chúng ta có thể tính trực tiếp (xem trong bài Tính thể tích khối chóp) hoặc so sánh thể tích của chúng với các khối dễ tính thể tích hơn.

Tuy nhiên, đối với các khối đa diện phức tạp, hoặc việc tính thể tích của chúng một cách trực tiếp gặp khó khăn, chúng ta có thể nghĩ tới việc phân chia khối đa diện thành các khối đơn giản, dễ tính thể tích hơn.

Để làm quen với việc phân chia và lắp ghép khối đa diện, chúng ta sẽ làm một số ví dụ trước khi đi vào các bài tập tính thể tích.

Ví dụ phương pháp phân chia khối đa diện

Ví dụ 1. Chia khối lăng trụ $ABC.A’B’C’$ thành ba khối tứ diện bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$. Hãy kể tên ba khối tứ diện đó.

Hướng dẫn

Chia khối lăng trụ $ABC.A’B’C’$ bởi các mặt phẳng $(A’BC’)$ và $(A’BC)$ ta được ba khối tứ diện: $CC’A’B’$, $CBA’B’$, $CABA’$.

Ví dụ 2. Có thể chia một khối lập phương thành bao nhiêu khối tứ diện bằng nhau?

Hướng dẫn

Dùng mặt phẳng $(BDD’B’)$ ta chia thành hai khối lập phương thành hai khối lăng trụ $ABD.A’B’D’$ và $BCD.B’C’D’$. Tương tự như ví dụ 1, chúng ta có:
- Khối lăng trụ tam giác $ABD.A’B’D’$ ta lần lượt dùng các mặt phẳng $(ABD’)$ và $(A’BD’)$ chia thành ba khối tứ diện bằng nhau.
- Tương tự với khối lăng trụ tam giác $BCD.B’C’D’$, ta cũng chia được thành ba khối tứ diện đều bằng nhau.
Vậy có tất cả 6 khối tứ diện bằng nhau.

Ví dụ 3. Mặt phẳng $( AB’C’)$ chia khối lăng trụ $ABC.A’B’C’$ thành các khối đa diện nào?

Hướng dẫn

Dựa vào hình vẽ, ta thấy mặt phẳng $(AB’C’)$ chia khối lăng trụ $ABC.A’B’C’$ thành một khối chóp tam giác $A.A’B’C’$ và một khối chóp tứ giác $A.BCC’B’$.

Ví dụ 4. Cho khối chóp $S. ABCD$, hỏi hai mặt phẳng $(SAC)$ và $(SBD)$ chia khối chóp $S.ABCD$ thành bao nhiêu khối chóp?

Hướng dẫn

Gọi $O$ là giao điểm của $AC$ và $BD$. Mặt phẳng $(SAC)$ và $(SBD)$ chia khối chóp $S.ABCD$ thành 4 khối chóp: $S.ABO$, $S.ADO$, $S.CDO$ và $S.BCO$.

Ví dụ 5. Cho tứ diện $ABCD$. Lấy một điểm $M$ nằm trong đoạn $AB$, điểm $N$ nằm trong đoạn $CD$. Chia tứ diện đã cho bằng hai mặt phẳng $(MCD)$ và $(NAB)$ ta được 4 khối tứ diện nào?

Hướng dẫn
- Mặt phẳng $(MCD)$ chia tứ diện đã cho thành hai khối $(MACD)$ và $(MBCD)$.
- Mặt phẳng $(ABN)$ chia khối $(MACD)$ thành hai khối $(MANC)$ và $(MAND)$.
- Mặt phẳng $(ABN)$ chia khối $(MBCD)$ thành hai khối $(MBCN)$ và $(MBND)$.
Ví dụ 6. Chia một khối tứ diện đều thành bốn tứ diện bằng nhau.

Hướng dẫn.
- Xét tứ diện đều $ $A B C D$ . Gọi $ $G$ là giao điểm của các đường thẳng nối đỉnh với trọng tâm của mặt đối diện.
- Dễ thấy các tứ diện $ $G A B C, G B C D, G C D A, G D A B$ bằng nhau.
- Thật vậy, các tứ diện trên đều có đáy là các tam giác đều có cạnh bằng nhau, các cạnh bên $ $G A = G B = G C = G D$ . Vậy ta đã chia được tứ diện đều thành $4$ tứ diện bằng nhau.
Ví dụ 7. Hãy dùng 4 mặt phẳng để chia một khối tứ diện đã cho thành 9 khối tứ diện.

Hướng dẫn.
- Giả sử $ABCD$ là khối tứ diện đã cho.
- Chia cạnh $AB$ thành ba đoạn thẳng bởi các điểm chia $M$ và $M’$. Chia cạnh $CD$ thành ba đoạn thẳng bởi các điểm $N$ và $N’$.
- Khi đó 4 mặt phẳng $(ABN)$, $(ABN’)$, $(CDM)$, $(CDM’)$ sẽ phân chia khối tứ diện $ABCD$ thành 9 khối tứ diện.
Sử dụng Phương pháp phân chia khối đa diện để tính thể tích

Ví dụ 1. Cho khối hộp ABCD.A’B’C’D’. Tính thể tích của khối hộp này biết tứ diện ACB’D’ có thể tích bằng V.

Ví dụ 2. Cho hình hộp chữ nhật ABCD.A’B’C’D’ có đáy là hình vuông cạnh a , chiều cao AA’ = b . Gọi M là trung điểm cạnh CC’ . Tính thể tích khối tứ diện BDA’M .

(đang tiếp tục bổ sung)
23/09/2021
Toán 10 Hàm số bậc nhất y=ax+b
Toán 10 Hàm số bậc nhất y=ax+b

1. Hàm số bậc nhất là gì?

Hàm số bậc nhất đối với biến số $x$ là hàm số có dạng $y = ax + b$ trong đó $a\ne 0$.

Tập xác định: $\mathcal{D}=\mathbb{R}$.

Xem thêm: Cách tìm tập xác định của hàm số

Sự biến thiên:
- Khi $a > 0$, hàm số đồng biến trên $\mathbb{R}$.
- Khi $a < 0$, hàm số nghịch biến trên $\mathbb{R}$.
Đồ thị hàm số bậc nhất là đường thẳng có hệ số góc bằng $a$, cắt trục tung tại điểm có toạ độ $(0; b)$, cắt trục hoành tại điểm có toạ độ $(-\frac{b}{a};0)$.

2. Vị trí tương đối của hai đồ thị hàm số bậc nhất

Cho hai đường thẳng $d: y = ax + b$ và $d’: y = a’x + b’$:
- $d$ song song $d’$ khi và chỉ khi $a = a’$ và $b\ne b’$.
- $d$ trùng $d’$ khi và chỉ khi $a = a’$ và $b=b’$.
- $d$ cắt $d’$ khi và chỉ khi $a \ne a’$.
- $d$ vuông góc $d’$ khi và chỉ khi $a\cdot a’=-1$.
3. Hàm số y = b

Trong trường hợp đặc biệt, khi $a=0$ thì hàm số bậc nhất trở thành hàm số hằng (hàm hằng) có đồ thị là một đường thẳng song song hoặc trùng với trục hoành, cắt trục tung tại điểm $(0;b)$ như hình dưới đây:

4. Hàm số $y=\left| ax+b \right|$

Sử dụng định nghĩa giá trị tuyệt đối chúng ta viết lại hàm số $y=\left| ax+b \right|$ dưới dạng $$y=\begin{cases} ax+b& \text{khi } x\ge -\frac{b}{a} \\ -(ax+b)&\text{khi } x<-\frac{b}{a} \end{cases} $$

Để vẽ đồ thị của hàm số $y=\left| ax+b \right|$ ta có thể vẽ hai đường thẳng $y = ax + b$ và $y = –ax – b$, rồi xoá đi hai phần đường thẳng nằm ở phía dưới trục hoành.

Đồ thị hàm số $y=\left| ax+b \right|$ có dạng như hình vẽ sau:

5. Bài tập Toán 10 Hàm số bậc nhất $y=ax+b$

Bài 1. Vẽ đồ thị của các hàm số sau:

a) $y=2x-7$
b) $y=-3x+5$
c) $y=\frac{x-3}{2}$
d) $y=\frac{5-x}{3}$

Bài 2. Tìm toạ độ giao điểm của các cặp đường thẳng sau:

a) $y=3x-2;y=2x+3$
b) $y=-3x+2;y=4(x-3)$
c) $y=2x;y=-x-3$
d) $y=\frac{x-3}{2};y=\frac{5-x}{3}$

Bài 3. Trong mỗi trường hợp sau, tìm giá trị $k$ để đồ thị của hàm số $y=-2x+k(x+1)$:
1. Đi qua gốc tọa độ $O$
2. Đi qua điểm $M(–2 ; 3)$
3. Song song với đường thẳng $y=\sqrt{2} x$
Bài 4. Xác định $a$ và $b$ để đồ thị của hàm số $y=ax+b$:
1. Đi qua hai điểm $A(–1; –20), B(3; 8)$.
2. Đi qua điểm $M(4; –3)$ và song song với đường thẳng $d: y=-\frac{2}{3}x+1$.
3. Cắt đường thẳng $d_1: y=2x+5$ tại điểm có hoành độ bằng $–2$ và cắt đường thẳng $d_2:y=3x+4$ tại điểm có tung độ bằng $–2$.
4. Song song với đường thẳng $y=\frac{1}{2}x$ đồng thời đi qua giao điểm của hai đường thẳng $y=-\frac{1}{2}x+1$ và $y=3x+5$.
Bài 5. Trong mỗi trường hợp sau, tìm các giá trị của $m$ sao cho ba đường thẳng sau phân biệt và đồng qui:
1. $y=2x;y=-x-3;y=mx+5$
2. $y=5(x+1);y=mx+3;y=3x+m$
3. $y=2x-1;y=8-x;y=(3-2m)x+2$
4. $y=(5-3m)x+m-2;y=-x+11;y=x+3$
5. $y=-x+5;y=2x-7;y=(m-2)x+{{m}^{2}}+4$
Bài 6. Tìm điểm sao cho đường thẳng sau luôn đi qua dù $m$ lấy bất cứ giá trị nào:
1. $y=2mx+1-m$
2. $y=mx-3-x$
3. $y=(2m+5)x+m+3$
4. $y=m(x+2)$
5. $y=(2m-3)x+2$
6. $y=(m-1)x-2m$
Bài 7. Với giá trị nào của $m$ thì hàm số sau đồng biến? nghịch biến?
1. $y=(2m+3)x-m+1$
2. $y=(2m+5)x+m+3$
3. $y=mx-3-x$
4. $y=m(x+2)$
Bài 8. Tìm các cặp đường thẳng song song trong các đường thẳng cho sau đây:
1. $3y-6x+1=0$
2. $y=-0,5x-4$
3. $y=3+\frac{x}{2}$
4. $2y+x=6$
5. $2x-y=1$
6. $y=0,5x+1$
Bài 9. Với giá trị nào của $m$ thì đồ thị của các cặp hàm số sau song song với nhau:
1. $y=(3m-1)x+m+3;y=2x-1$
2. $y=\frac{m}{1-m}x+\frac{2(m+2)}{m-1};y=\frac{3m}{3m+1}x-\frac{5m+4}{3m+1}$
3. $y=m(x+2);y=(2m+3)x-m+1$
Bài 10. Vẽ đồ thị của các hàm số sau:
1. $y= \begin{cases} -x&\text{khi }x\le -1 \\ 1&\text{khi }-1<x<2 \\ x-1&\text{khi }x\ge 2 \\
  \end{cases} $
2. $y= \begin{cases} -2x-2&\text{khi }x<-1 \\ 0&\text{khi }-1\le x\le 2 \\ x-2&\text{khi }x\ge 2 \\ \end{cases} $
3. $y=\left| 3x+5 \right|$
4. $y=-2\left| x-1 \right|$
5. $y=-\frac{1}{2}\left| 2x+3 \right|+\frac{5}{2}$
6. $y=\left| x-2 \right|+\left| 1-x \right|$
7. $y=\left| x \right|-\left| x-1 \right|$
8. $y=x+\left| x-1 \right|+\left| x+1 \right|$
22/09/2021
Bài tập trắc nghiệm Tổng của hai véc-tơ

Bài tập trắc nghiệm Tổng của hai véc-tơ

Các em truy cập link sau để làm https://forms.office.com/r/5YjEdbDtxp hoặc làm trực tiếp ở phần dưới đây

22/09/2021