Giải phương trình chứa căn bằng cách phân tích thành tích
Giải phương trình chứa căn thức, bất PT chứa căn (PT, BPT vô tỷ) ngoài cách nâng lên lũy thừa thì chúng ta còn có thể phân tích thành tích các nhân tử, mỗi nhân tử là một PT, BPT đơn giản hơn.
Xem thêm:
- Cách giải phương trình chứa căn, bất phương trình chứa căn
- Phương pháp biến đổi tương đương giải phương trình, bất phương trình chứa căn
- Tìm điều kiện để tam thức bậc hai luôn dương, luôn âm
- Giải phương trình bằng phương pháp nhân liên hợp
Một số hằng đẳng thức hay sử dụng:
- $u+v=1+uv\Leftrightarrow \left( u-1 \right)\left( v-1 \right)=0$
- $au+bv=ab+vu\Leftrightarrow \left( u-b \right)\left( v-a \right)=0$
Sau đây, chúng ta cùng xem xét một số ví dụ.
1. Ví dụ giải phương trình, bất phương trình chứa căn bằng phân tích thành tích
Ví dụ 1. Giải phương trình $$\sqrt{x+3}+2x\sqrt{x+1}=2x+\sqrt{{{x}^{2}}+4x+3}$$ Hướng dẫn. Phương trình đã cho tương đương với
\begin{align*}
& \sqrt {x + 3} – \sqrt {\left( {x + 1} \right)\left( {x + 3} \right)} – \left( {2x – 2x\sqrt {x + 1} } \right) = 0\\
\Leftrightarrow\;& \sqrt {x + 3} \left( {1 – \sqrt {x + 1} } \right) – 2x\left( {1 – \sqrt {x + 1} } \right) = 0 \\
\Leftrightarrow\;& \left( {1 – \sqrt {x + 1} } \right)\left( {\sqrt {x + 3} – 2x} \right) = 0\\
\Leftrightarrow\;& \left[ \begin{array}{l}
1 – \sqrt {x + 1} = 0\\
\sqrt {x + 3} – 2x = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = 1
\end{array} \right.
\end{align*} Đối chiếu điều kiện được nghiệm của phương trình là $ x=0,x=1. $
Ví dụ 2. Giải phương trình $$\sqrt[3]{x+1}+\sqrt[3]{x+2}=1+\sqrt[3]{{{x}^{2}}+3x+2}$$ Hướng dẫn. Biến PT đổi thành $$\left( {\sqrt[3]{{x + 1}} – 1} \right)\left( {\sqrt[3]{{x + 2}} – 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = – 1
\end{array} \right.$$ Đáp số $ x=0,x=-1. $
Ví dụ 3. Giải phương trình $$\sqrt{{{x}^{2}}-3x+2}-\sqrt{2{{x}^{2}}-3x+1}\ge x-1$$ Hướng dẫn. Điều kiện $x\in ( -\infty ;\frac{1}{2} ]\cup \left\{ 1 \right\}\cup \left[ 2;+\infty \right)$ nên ta xét ba khả năng:
- $ x = 1 $ là nghiệm.
- $ x\ge 2 $: Bất phương trình tương đương với $\sqrt{x-2}\ge \sqrt{x-1}+\sqrt{2x-1}$ vô nghiệm.
- $x\le \frac{1}{2}$: Bất phương trình $\Leftrightarrow \sqrt{2-x}+\sqrt{1-x}\ge \sqrt{1-2x}$ có nghiệm $x\le \frac{1}{2}$.
Vậy bất phương trình có tập nghiệm $S=( -\infty ;\frac{1}{2} ]\cup \left\{ 1 \right\}$
Ví dụ 4. Giải bất phương trình $$ 14\sqrt{x+5}\ge 3x+23+7\sqrt{x-3} $$ Hướng dẫn. Điều kiện $ x\ge 3. $ Bất phương trình đã cho tương đương với
\begin{align*}
&x-3-7\sqrt{x-3}-4(x+5)+14\sqrt{x+5}\ge 0\\
\Leftrightarrow\;&\left(\sqrt{x-3}-2\sqrt{x+5}\right)\left(\sqrt{x-3}+2\sqrt{x+5}-7\right)\ge0
\end{align*} Đến đây chia ba trường hợp hoặc nhân liên hợp, được tập nghiệm là $ S=[3;4]. $
Ví dụ 5. Giải phương trình $${{x}^{2}}-2x-3=\sqrt{x+3}$$ Hướng dẫn. Biến đổi phương trình đã cho thành \[\begin{array}{l}
\,\,\,\,\,\,{x^2} – x + \frac{1}{4} = x + 3 + \sqrt {x + 3} + \frac{1}{4}\\
\Leftrightarrow {\left( {x – \frac{1}{2}} \right)^2} = {\left( {\sqrt {x + 3} + \frac{1}{2}} \right)^2}
\end{array}\] Đến đây tách thành hai phương trình đơn giản hơn. Đáp số. $x = \frac{{3 + \sqrt {17} }}{2} \vee x = 1 – \sqrt {13}$.
Ví dụ 6. Giải phương trình $$x-2\sqrt{x-1}-\sqrt{x}\left( x-1 \right)+\sqrt{{{x}^{2}}-x}=0$$ Hướng dẫn. Bình phương, biến đổi thành \[\begin{array}{l}
\,\,\,\,\,\,\,2x\sqrt {{x^2} – x} – 4\sqrt {{x^2} – x} + {x^3} – 4{x^2} + 6x – 4 = 0\\
\Leftrightarrow (x – 2)(2\sqrt {{x^2} – x} + {x^2} – 2x + 2) = 0
\end{array}\] Đáp số. $x=2$.
Ví dụ 7. Chứng minh rằng với mọi giá trị dương của tham số $ m, $ phương trình sau có hai nghiệm thực phân biệt: \[{{x}^{2}}+2x-8=\sqrt{m\left( x-2 \right)}\] Hướng dẫn. Điều kiện $x\ge 2$, do $ m > 0. $ PT tương đương với \[\left( {x – 2} \right)\left( {x + 4} \right) = \sqrt {m\left( {x – 2} \right)} .\]Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi PT \[{x^3} + 6{x^2} – 32 = 0\,\,\,\,\,\,\,(*)\] có một nghiệm khác 2.
Thật vậy, đặt $ f\left( x \right)={{x}^{3}}+6{{x}^{2}}-32,x\ge 2 $ thì ta có \[f(2) = 0,\mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} f\left( x \right) = + \infty ,f’\left( x \right) = 3{x^2} + 12x > 0,\forall x \ge 2\] Suy ra $ f(x) $ là hàm liên tục trên $ \left[ 2;+\infty \right) $ và đồng biến trên khoảng đó. Do đó, với mọi $m>0$ phương trình (*) luôn có nghiệm $ x_0 $ mà $2 < x_0 <+\infty $.
2. Bài tập phân tích thành tích giải phương trình, bất phương trình
Giải các phương trình, bất phương trình sau:
Bài 1. Giải phương trình $ (x+3)\sqrt{10-x^2}=x^2-x-12 $
Đáp số. $ x=-3 $
Bài 2. Giải phương trình $\left( {{x}^{2}}-3x \right)\sqrt{2{{x}^{2}}-3x-2}\ge 0$
Đáp số. $\left( -\infty ;-\frac{1}{2} \right]\cup \left\{ 2 \right\}\cup \left[ 3;+\infty \right)$
Bài 3. Giải bất phương trình $\left( x-3 \right)\sqrt{{{x}^{2}}+4}\le {{x}^{2}}-9$
Hướng dẫn. Xét ba trường hợp $ x=3, x>3 và x<3. $ Đáp số. $x<-\frac{5}{6}\vee x\ge 3$
Bài 4. Giải BPT $ \frac{\sqrt{ 12+x-x^2}}{x-11}\ge \frac{\sqrt{ 12+x-x^2}}{2x-9} $
Đáp số. $ -3;\left[-2,4\right] $
Bài 5. Giải bất phương trình chứa căn $\frac{\sqrt{51-2x-{{x}^{2}}}}{1-x}<1$
Hướng dẫn. Xét hai trường hợp của $ x-1. $ Đáp số. $1-\sqrt{52}\le x<-5\vee x>1$
Bài 6. Giải BPT $\frac{{{x}^{2}}}{{{\left( 1+\sqrt{1+x} \right)}^{2}}}>x-4$
Đáp số. $-1\le x<8$
Bài 7. Giải PT $ \sqrt[3]{x+1}+\sqrt[3]{x+2}=1+\sqrt[3]{x^2+3x+2} $
Hướng dẫn. Nhóm thành $ \left(\sqrt[3]{x+1}-1\right) +\left(\sqrt[3]{x+2}-\sqrt[3]{x^2+3x+2}\right)=0$ rồi phân tích thành tích.
Đáp số. $ x=0,x=-1 $
Bài 8. Giải phương trình $\sqrt[3]{x+1}+\sqrt[3]{{{x}^{2}}}=\sqrt[3]{x}+\sqrt[3]{{{x}^{2}}+x}$
Hướng dẫn. Nhận xét $ x=0 $ không là nghiệm, chia hai vế cho $ x $ được: $$\sqrt[3]{\frac{x+1}{x}}+\sqrt[3]{x}=1+\sqrt[3]{x+1}$$ $$\Leftrightarrow \left( \sqrt[3]{\frac{x+1}{x}}-1 \right)\left( \sqrt[3]{x}-1 \right)=0$$ Đáp số. $x=1$
Bài 9. Giải phương trình $\sqrt{x+3}+\frac{4x}{\sqrt{x+3}}=4\sqrt{x}$
Hướng dẫn. Chia cả hai vế cho $\sqrt{x+3}$ và biến đổi \[\begin{array}{l}
\,\,\,\,\,\,\,1 + \frac{{4x}}{{x + 3}} = 2\sqrt {\frac{{4x}}{{x + 3}}} \\
\Leftrightarrow {\left( {1 – \sqrt {\frac{{4x}}{{x + 3}}} } \right)^2} = 0\\
\Leftrightarrow x = 1.
\end{array}\]
Bài 10. Giải phương trình $ x+2\sqrt{7-x}=2\sqrt{x-1}+\sqrt{-x^2+8x-7}+1 $
Hướng dẫn. Biến đổi thành $ \left(x-1-2\sqrt{x-1}\right) +\left(2\sqrt{7-x}-\sqrt{(7-x)(x-1)}\right)=0$…
Đáp số. $ x=5,x=4 $
Bài 11. Giải phương trình $ \sqrt{x^2+10x+21}=3\sqrt{x+3}+2\sqrt{x+7}-6 $
Hướng dẫn. $ \sqrt{x+3}\left(\sqrt{x+7}-3\right)-2\left(\sqrt{x+7}-3\right)=0 $
Đáp số. $ x=1,x=2 $
Bài 12. Giải phương trình $ \sqrt{ x^2+3x}+2 \sqrt{ x+2}=2x+\sqrt{x+\frac{6}{x}+5} $
Hướng dẫn. \[\begin{array}{l}
x\sqrt {\frac{{x + 3}}{x}} – \sqrt {\frac{{(x + 2)(x + 3)}}{x}} + 2\sqrt {x + 2} – 2x = 0\\
\Leftrightarrow \left( {x – \sqrt {x – 2} } \right)\left( {\sqrt {\frac{{x + 3}}{x}} – 2} \right) = 0
\end{array}\] Đáp số. $ x=1,x=2 $
Bài 13. Giải phương trình $\sqrt{x+3}+2x\sqrt{x+1}=2x+\sqrt{x^2+4x+3}$
Hướng dẫn. Phân tích thành tích $ \left( \sqrt{x+3}-2x \right)\left( \sqrt{x+1}-1 \right)=0 $
Đáp số. $x=0,x=1$
Bài 14. Giải phương trình $ \sqrt{2x-1}+x^2-3x+1=0 $
Đáp số. $x= 1;x=2-\sqrt{2} $
Bài 15. Giải phương trình $\sqrt{x+3}+\frac{4x}{\sqrt{x+3}}=4\sqrt{x}$
Hướng dẫn. Chia cả hai vế cho $\sqrt{x+3}$ được $ \left( 1-\sqrt{\frac{4x}{x+3}} \right)^2=0 $
Đáp số. $x=1$
Bài 16. Giải phương trình $ 2 x^2-6x+10-5(x-2)\sqrt{x+1}=0 $
Hướng dẫn. Biến đổi thành \[\begin{array}{l}
2{(x – 2)^2} + 2(x + 1) – 5(x – 2)\sqrt {x + 1} = 0\\
\Leftrightarrow \left( {2(x – 2) – \sqrt {x + 1} } \right)\left( {(x – 2) – 2\sqrt {x + 1} } \right) = 0
\end{array}\] Đáp số. $ x=3,x=8 $
Bài 17. Giải phương trình $ 4x^2+\sqrt{ 2x+3}=8x+1 $
Hướng dẫn. $ 4x^2-6x+\frac{9}{4}=\left(\sqrt{2x+3}\right)^2-2\sqrt{2x+3}+\frac{1}{4}$
Đáp số. $x= \frac{5-\sqrt{21}}{4},x=\frac{3+\sqrt{17}}{4} $
Bài 18. Giải phương trình $ \sqrt{ x^2+x+2}=\frac{x^2+5x+2}{2x+2} $
Hướng dẫn. Nhân chéo, nhóm thành $$ \left(\sqrt{x^2+x+2}\right)^2-2x\sqrt{x^2+x+2}-2\sqrt{x^2+x+2}+4x=0 $$
Đáp số. $ x=1,x=-2 $
Bài 19. Giải phương trình $ 2\sqrt{2x+3}-\frac{3}{x}=x+2 $
Hướng dẫn. Biến đổi thành $ \frac{1}{x}\left(x-\sqrt{2x+3}\right)^2=0 $
Đáp số. $x=3$
Bài 20. $ \sqrt[3]{x-1}+\sqrt{x}=1+\sqrt[6]{x^5-2x^4+x^3} $
Hướng dẫn. Phân tích thành tích $ \left(1-\sqrt[3]{x-1}\right)(1-\sqrt{x})=0 $
Đáp số. $x=1,x=2$
Bài 21. Giải phương trình $ 2\sqrt{x+1}+\sqrt{2x^2+6x}=2\sqrt{2x}+\sqrt{x^2+4x+3} $
Hướng dẫn. Biến đổi thành $ \left(\sqrt{ x+1}-\sqrt{ 2x}\right)\left(2-\sqrt{x+3}\right)=0 $
Đáp số. $x=1$
Bài 22. Giải phương trình $ 4x\sqrt{x+7}+3x\sqrt{7x-3}=6x^2+2\sqrt{ 7x^2 +46x-21} $
Hướng dẫn. Phân tích thành tích $$ \left(2x-\sqrt{7x-3}\right)\left(2\sqrt{x+7}-3x\right)=0 $$Đáp số. $x=1,x=2,x=\frac{3}{4}$
Bài 23. Giải phương trình $\sqrt{\sqrt{3}-x}=x\sqrt{\sqrt{3}+x}$
Hướng dẫn. Biến đổi thành \[\begin{array}{l}
\,\,\,\,\,\,\,{x^3} + \sqrt 3 {x^2} + x – \sqrt 3 = 0\\
\Leftrightarrow {\left( {x + \frac{1}{{\sqrt 3 }}} \right)^3} = \frac{{10}}{{3\sqrt 3 }}
\end{array}\] Đáp số. $x=\frac{\sqrt[3]{10}-1}{\sqrt{3}}$
Bài 24. Giải phương trình $2\sqrt{x+3}=9{{x}^{2}}-x-4$
Hướng dẫn. Biến đổi thành ${{\left( 1+\sqrt{3+x} \right)}^{2}}=9{{x}^{2}}$
Đáp số. $x=1,x=\frac{-5-\sqrt{97}}{18}$
Bài 25. Giải phương trình $2+3\sqrt[3]{9{{x}^{2}}\left( x+2 \right)}=2x+3\sqrt[3]{3x{{\left( x+2 \right)}^{2}}}$
Hướng dẫn. Biến đổi thành $ \left( \sqrt[3]{x+2}-\sqrt[3]{3x} \right)^3=0 $
Đáp số. $x=1$
Bài 26. Giải phương trình $\sqrt[4]{x+1}+\sqrt{x}=1+\sqrt[4]{{{x}^{3}}+{{x}^{2}}}$
Đáp số. $x=0, x=1$
Bài 27. Giải phương trình $\sqrt{x+3}+2x\sqrt{x+1}=2x+\sqrt{{{x}^{2}}+4x+3}$
Hướng dẫn. Phân tích thành tích bằng biến đổi $$ au+bv=ab+uv \Leftrightarrow (u-b)(v-a)=0 $$Đáp số. $x=0, x=1$
Bài 28. Giải phương trình $2+3\sqrt[3]{9{{x}^{2}}\left( x+2 \right)}=2x+3\sqrt[3]{3x{{\left( x+2 \right)}^{2}}}$
Hướng dẫn. Sử dụng biến đổi $ a^3-b^3=0 \Leftrightarrow a=b$
Đáp số. $x=1$
Bài 29. Giải phương trình $4{{x}^{2}}+3x+3=4x\sqrt{x+3}+2\sqrt{2x-1}$
Hướng dẫn. Phân tích thành tích $$\left( 4{{x}^{2}}-4x\sqrt{x+3}+x+3 \right)\left( 1-2\sqrt{2x-1}+2x-1 \right)=0$$Đáp số. $x=1$
Bài 30. Giải phương trình $\frac{x^2}{\sqrt{3x-2}}-\sqrt{3x-2}=1-x$
Đáp số. $ x=1 $
Bài 31. Giải phương trình $\sqrt{{{x}^{3}}+{{x}^{2}}+3x+3}+\sqrt{2x}=\sqrt{{{x}^{2}}+3}+\sqrt{2{{x}^{2}}+2x}$
Hướng dẫn. Phân tích thành tích bằng biến đổi $$ au+bv=ab+uv \Leftrightarrow (u-b)(v-a)=0 $$ Đáp số. $x=0$




















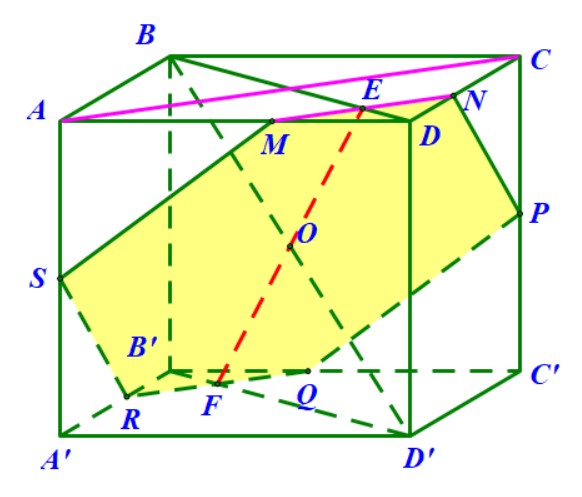

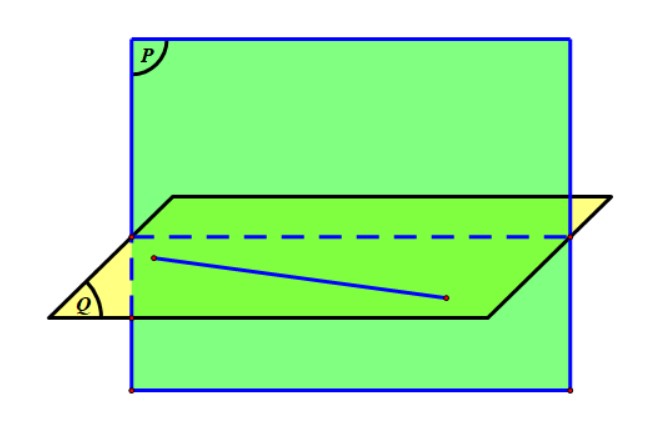
 Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).
Hướng dẫn. Gọi \( M \) là trung điểm \( BC \) thì có \( BC \) vuông góc với \( AM \) và \( DM \) nên suy ra \( AMD \) chính là mặt phẳng \((P)\) trung trực của \( BC \). Thiết diện cần tìm là tam giác \( AMD \).