3000+ Hebrew Children’s Stories Download
You can download more than 3000+ Hebrew Children’s Stories from http://sefer-li.net/
See more 500 Hebrew Words
Category: TỔNG HỢP
-
Các phần mềm của Adobe và công dụng để làm gì?
Danh sách các phần mềm của Adobe là rất nhiều. List phần mềm Adobe bao trùm tất cả các lĩnh vực thiết kế từ chỉnh sửa ảnh, xử lý hậu kì, biên tập video, chỉnh sửa video, thiết kế logo, làm banner quảng cáo, làm phim hoạt hình, phát triển web…
Hầu hết các phần mềm Adobe đều yêu cầu đăng ký. Bạn có thể chọn đăng ký chỉ một ứng dụng hoặc cả bộ Creative Cloud. Bài viết này, chúng tôi xin giới thiệu, giải thích ý nghĩa, công dụng của từng phần mềm Adobe.
Nhưng hầu hết các phần mềm Adobe đều yêu cầu đăng ký. Mặc dù có tổng cộng hơn 50, có 50 ứng dụng, nhưng có 12 ứng dụng chính mà bạn chắc chắn cần biết.
- ✅ Hướng dẫn sử dụng Canva chi tiết nhất.
- ✅ KHÓA HỌC CANVA CƠ BẢN
- ✅ KHÓA HỌC CANVA NÂNG CAO
1. Adobe Photoshop là gì?
Phần mềm Adobe Photoshop sử dụng để chỉnh sửa ảnh, biên tập ảnh và hơn thế nữa.
Được sử dụng cho: Chỉnh sửa và thao tác hình ảnh, chỉnh sửa ảnh, thiết kế đồ họa, tạo mẫu web và ứng dụng, tạo mô hình 3D
Nền tảng: Mac, Windows, iPad
Nếu bạn muốn chỉnh sửa hình ảnh, Photoshop là tiêu chuẩn công nghiệp; nhiều đến nỗi từ ‘Photoshop’ thậm chí đã trở thành một động từ. Nhưng chỉnh sửa ảnh không phải là tất cả những gì Photoshop làm: nó cũng là một trình chỉnh sửa đồ họa chính thức.
Photoshop có thể được sử dụng, ví dụ, để chỉnh sửa và soạn hình ảnh raster (dù nó cũng có thể tạo và chỉnh sửa đồ họa vector nhưng đó không phải là chức năng chính), đồ họa và văn bản trong nhiều lớp (layer) và tạo và chỉnh sửa đồ họa 3D và video. Khả năng đa dạng này có nghĩa là Photoshop không chỉ được sử dụng bởi các nhiếp ảnh gia và người chỉnh sửa ảnh mà còn được sử dụng bởi các nghệ sĩ kỹ thuật số, nhà thiết kế đồ họa và giám đốc nghệ thuật, thậm chí ngày càng được sử dụng bởi các nhà thiết kế 3D và nghệ sĩ VFX.
Điều quan trọng cần lưu ý là Photoshop hoạt động với đồ họa raster, trái ngược với Illustrator (bên dưới), hoạt động với đồ họa vector.
2. Adobe Illustrator để làm gì?
Phần mềm Adobe Illustrator sử dụng tạo đồ họa vector và hình minh họa tuyệt đẹp
Dùng để: Minh họa, thiết kế đồ họa vector
Nền tảng: Mac, Windows, iPad
Trong khi Photoshop có khả năng mở rộng và không ngừng mở rộng, Illustrator tập trung nhiều hơn vào một nhiệm vụ cụ thể. Về cơ bản nó là một chương trình vẽ dựa trên đồ họa vector (chứa ít chi tiết hơn đồ họa raster và có khả năng zoom vô hạn).
Như cái tên có thể gợi ý, Illustrator được các nghệ sĩ, họa sĩ minh họa và nhà thiết kế đồ họa sử dụng phổ biến nhất, để tạo ra mọi thứ từ đồ họa đơn giản, chẳng hạn như logo, biểu tượng và infographic đến các hình minh họa phức tạp. Illustrator cho iPad gần đây cũng đã được phát hành.
3. Adobe After Effects
Được sử dụng cho: VFX (kĩ xảo điện ảnh) đồ họa chuyển động, biên tập và chỉnh sửa video.
Nền tảng: Mac, Windows
After Effects là một công cụ phổ biến cho hiệu ứng phim ảnh, đồ họa chuyển động. Mặc dù bạn sẽ không sử dụng nó để tạo toàn bộ một bộ phim, nhưng nó có thể được một studio sáng tạo sử dụng để tạo ra các loại hoạt ảnh đơn giản mà bạn sẽ giới thiệu trên một trang web, trong video giải thích hoặc trên một chuỗi tín dụng chẳng hạn.
After Effects cũng được sử dụng trong quá trình hậu kỳ phim và truyền hình, cho các nhiệm vụ như tách nền phông xanh, tracking và tạo hiệu ứng hình ảnh như cháy nổ và sét đánh. Ngoài việc được tích hợp hoàn hảo với các ứng dụng Adobe khác, nó cũng hoạt động tương thích với ứng dụng 3D Cinema 4D của Maxon.
4. Adobe XD
Được sử dụng cho: Tạo mẫu web và ứng dụng (thiết kế UI, UX)
Nền tảng: MacWindows, với ứng dụng iOS và Android để thử nghiệm
Được ra mắt cách đây vài năm với tư cách là đối thủ của Sketch và Figma, Adobe XD là một công cụ UX dựa trên vector để tạo mẫu ứng dụng web và thiết bị di động. Nói cách khác, bạn không tạo toàn bộ ứng dụng trong XD, nhưng sử dụng nó để hình dung giao diện và xác định cách tất cả các phần khác nhau hoạt động và liên quan với nhau như thế nào. Điều này giúp mọi thứ hoạt động chính xác dễ dàng hơn trước khi các lập trình viên bắt tay vào code ứng dụng.
Lưu ý rằng gói thuê bao khởi đầu của XD là miễn phí và bạn không cần đăng ký Creative Cloud để sử dụng.
5. Adobe InDesign CC
Được sử dụng cho: Dàn trang tạp chí, sách báo trong in ấn, xuất bản
Nền tảng: Mac, Windows
InDesign là một công cụ bố cục trang được sử dụng chủ yếu để in, nhưng cũng có khả năng xuất bản kỹ thuật số. Công cụ tiêu chuẩn công nghiệp cho ngành xuất bản, nó thường được các nhà thiết kế đồ họa và nghệ sĩ sản xuất sử dụng để tạo áp phích, tờ rơi, tài liệu quảng cáo, tạp chí, báo, bản trình bày, sách và sách điện tử.
6. Adobe Lightroom
Được sử dụng để: Quản lý và chỉnh sửa hình ảnh (các bức ảnh chụp)
Nền tảng: Windows, Mac, iOS, Android
Lightroom là một nhóm các công cụ để quản lý hình ảnh và chỉnh sửa hình ảnh. Sức mạnh của nó chủ yếu nằm ở chỗ xử lý ảnh RAW, và là một công cụ tốt cho một studio ảnh hoặc nhiếp ảnh gia cần xử lý số lượng lớn hình ảnh.
Nó không có tất cả các tính năng chỉnh sửa hình ảnh như Photoshop hoặc Illustrator, nhưng nhờ đó nó có một giao diện đơn giản hơn, dễ sử dụng hơn cho các tác vụ tiêu chuẩn như chỉnh ánh sáng, độ tương phản, độ bão hòa…
Cũng lưu ý rằng các chỉnh sửa của Lightroom không phá hủy ảnh gốc, nghĩa là cả ảnh gốc và các chỉnh sửa bạn đã áp dụng cho nó đều được lưu riêng biệt. Nhờ vậy, bạn có thể dễ dàng để hoàn tác các thay đổi nếu mọi thứ không diễn ra như bạn muốn.
7. Adobe Premiere Pro
Được sử dụng cho: Biên tập video | Nền tảng: Windows, Mac
Premiere Pro là một công cụ chỉnh sửa video toàn diện, dựa trên dòng thời gian trực quan, được sử dụng rộng rãi trong ngành công nghiệp phim và truyền hình, các YouTuber và các studio phim ảnh cưới, sự kiện, truyền thông và tiếp thị, để chỉnh sửa mọi thứ từ quảng cáo, video ca nhạc đến phim truyền hình và phim truyền hình- phim dài.
Các tính năng mới gần đây bao gồm Auto Reframe, áp dụng điều chỉnh thông minh cho cảnh quay của bạn (giữ hành động bên trong khung cho các tỷ lệ khung hình khác nhau) và khả năng gắn các yếu tố đồ họa vào hướng dẫn, với nhau hoặc vào các mục được theo dõi.
Premiere Pro thường được sử dụng cùng với các ứng dụng Creative Cloud khác bao gồm After Effects, Audition và Photoshop. Đây là một công cụ khá phức tạp để tìm hiểu và vì lý do này, Adobe gần đây đã phát hành một ứng dụng chỉnh sửa video gọn nhẹ hơn là Adobe Rush.
Adobe Premiere Rush, dành cho người mới bắt đầu và người dùng bình thường hơn. Xem thêm So sánh phần mềm chỉnh sửa video Adobe Premiere Pro vs Premiere Rush vs Premiere Elements
8. Adobe Spark
Được sử dụng để: Tạo đồ họa, trang web và video ngắn | Nền tảng: Mac, Windows, iOS, Android
Adobe Spark là một bộ ứng dụng để tạo đồ họa, trang web và video ngắn cho mạng xã hội một cách dễ dàng và nhanh chóng. Nó nhắm đến các chuyên gia tiếp thị và truyền thông xã hội, cũng như những người nghiệp dư và người mới bắt đầu muốn tạo nội dung thú vị cho Facebook, Twitter hoặc Instagram, nhưng không có thời gian để tìm hiểu các phần mềm phức tạp hơn như Photoshop và Illustrator.
9. Adobe Fresco
Được sử dụng cho: Nghệ thuật kỹ thuật số | Nền tảng: iOS phiên bản 12.4 trở lên
Adobe Fresco là một ứng dụng nghệ thuật kỹ thuật số, bắt chước một số yếu tố tốt nhất của các chương trình mỹ thuật khác dành cho iPad. Nó kết hợp sự biểu đạt và sức mạnh của bút vẽ Photoshop, với độ chính xác của bút vẽ vector. Chức năng Live Brush cho phép bạn vẽ bằng màu nước và dầu mà hoa, pha trộn, bôi và nhòe giống như trong cuộc sống thực. Fresco có một giao diện đơn giản và trực quan, tuyệt vời cho người mới bắt đầu và cả những người chuyên nghiệp.
10. Adobe Rush
Được sử dụng cho: Chỉnh sửa video dễ dàng và trực quan | Nền tảng: Mac, Windows, iOS và Android
Adobe Premiere Rush là phần mềm chỉnh sửa video đa nền tảng, tất cả trong một, xử lý và tải lên các video clip một cách nhanh chóng, lý tưởng cho những người sáng tạo nội dung trên mạng xã hội.
Ứng dụng hỗ trợ cắt video, thay đổi kích thước, xoay và chỉnh sửa màu sắc, cùng với một loạt các tính năng chỉnh sửa âm thanh và trình tự. Tất cả nội dung được lưu trên đám mây, lý tưởng để chỉnh sửa trên nhiều thiết bị và có tùy chọn tự động đồng bộ hóa, giúp việc này thậm chí còn dễ dàng hơn.
Rush được thiết kế để giúp việc chỉnh sửa và tải nội dung trực tiếp lên các nền tảng truyền thông xã hội trở nên cực kỳ đơn giản, vì vậy nó không quá nặng nề – nhưng việc tích hợp đầy đủ với Premiere Pro có nghĩa là nó không cần thiết.
11. Adobe Dimension
Được sử dụng để: Tạo, tổng hợp và kết xuất hình ảnh 3D chân thực | Nền tảng: Mac, Windows
Adobe Dimension là một công cụ để mô phỏng, tổng hợp và hiển thị hình ảnh 3D chân thực dựa trên các mô hình 2D và 3D, ảnh và kết cấu bạn đã nhập từ nơi khác, bao gồm cả Adobe Stock. Ví dụ, nó được các nhà thiết kế đồ họa sử dụng để tạo các mô hình sản phẩm, hình ảnh hóa thương hiệu và thiết kế bao bì. Ưu điểm chính là có thể tạo ra những cảnh giống như ảnh chụp mà không cần phải tổ chức một buổi chụp ảnh.
12. Adobe Dreamweaver
Phần mềm kỳ cựu để xây dựng trang web trực quan.
Được sử dụng để: Tạo trang web | Nền tảng: Mac, Windows
Được tạo ra lần đầu tiên vào năm 1997, Dreamweaver là công cụ của Adobe dành cho những người muốn xây dựng trang web mà không cần học cách viết mã. Vào thời điểm đó, công cụ này rất tiên tiến, nhưng ngày nay có rất nhiều công cụ thay thế cung cấp các khả năng tương tự, đặc biệt là Muse CC của riêng Adobe. Vì vậy, lý do chính để sử dụng Dreamweaver vào năm 2019 là bạn đã sử dụng nó trước đó, nhưng đối với những người không quen với nó, không có lý do thực sự thuyết phục. Chắc chắn hãy kiểm tra danh sách các nhà xây dựng trang web tốt nhất của chúng tôi trước để xem liệu có nền tảng nào phù hợp với bạn hơn không.
-
Tìm hai số khi biết hai hiệu số
Tìm hai số khi biết hai hiệu số
Bài toán Tìm hai số khi biết hai hiệu số là một trong những dạng toán thường gặp trong kì thi HSG. Để tìm được hai số, chúng ta sử dụng phương pháp khử.
Xem thêm các dạng toán tìm 2 số ở tiểu học:
- Tìm hai số khi biết tổng và hiệu của hai số đó lớp 4
- Tìm hai số khi biết tổng và tỉ số của hai số
- Tìm hai số khi biết hiệu và tỉ số của hai số
1. Phương pháp tìm hai số khi biết hai hiệu số
Chúng ta tiến hành các bước sau:
- Bước 1. Tìm được hai hiệu số (Hai hiệu số này thuộc hai đại lượng khác nhau.)
- Bước 2. Tìm mối liên hệ giữa hai hiệu số vừa tìm được. Từ đó, đặt phép chia thích hợp để tìm giá trị của một đơn vị thuộc đại lượng thứ
2. Ví dụ tìm 2 số khi biết hiệu 2 số
Ví dụ 1. Để chuẩn bị cho năm học mới, hai bạn An và Bình rủ nhau đi mua sắm sách vở. An mua 15 quyển vở, Bình mua nhiều hơn hơn An 5 quyển vở cùng loại và phải trả nhiều hơn An 20.000 đồng. Hỏi mỗi bạn phải trả bao nhiêu tiền mua vở?
Phân tích.
- Bình mua nhiều hơn An 5 quyển vở là hiệu số thứ nhất.
- Bình phải trả nhiều 20.000 đồng là hiệu số thứ hai.
- 20.000 đồng này chính là giá tiền của 5 quyển vở, từ đó chúng ta tìm được giá tiền của 1 quyển vở.
- Từ giá tiền của 1 quyển vở, chúng ta tìm được số tiền mỗi bạn phải trả.
Lời giải.
Giá tiền một quyển vở là:
20.000 : 5 = 4.000 (đồng)
Số tiền bạn An mua hết là:
4.000 x 15 = 60.000 (đồng)
Số tiền bạn Bình mua hết là:
60.000 + 20.000 = 80.000 (đồng)
Đáp số: Bình: 60.000 đồng, An: 80.000 đồng.
Ví dụ 2. Một hiệu sách, lần thứ nhất bán được 27 quyển vở. Lần thứ hai bán được 40 quyển vở cùng loại và thu được nhiều tiền hơn lần trước 52.000 đồng. Hỏi mỗi lần bán hiệu sách nhận bao nhiêu tiền?
Lời giải
Số quyển vở lần sau bán nhiều hơn làn trước là:
40 – 27 = 13 (quyển)
Giá tiền một quyển vở là:
52.000 : 13 = 4.000 (đồng)
Số tiền hiệu sách nhận được khi bán lần thứ hai là:
4.000 x 40 = 160.000 (đồng)
Số tiền hiệu sách nhận được khi bán lần thứ nhất là:
160.000 – 52.000 = 108.000 (đồng)
Đáp số: Lần thứ nhất: 108.000 đồng; Lần thứ hai: 160.000 đồng
Ví dụ 3. Một vườn ươm bán cây, lần thứ nhất bán 10 cây phượng và 8 cây xà cừ được tất cả 64.000 đồng. Lần thứ hai bán 7 cây phượng và 8 cây xà cừ được tất cả 52.000 đồng. Tính giá tiền một cây phượng, một cây xà cừ?
Lời giải
Ta có: 10 cây phượng + 8 cây xà cừ = 64.000 đồng
7 cây phượng + 8 cây xà cừ = 52.000 đồng
Ta thấy, trong hai lần bán, số cây xà là như nhau nên 3 cây phượng con có giá là:
64.000 – 52.000 = 12.000 (đồng)
Suy ra, giá tiền một cây phượng là:
12.000 : 3 = 4.000 (đồng).
Mua 10 cây phượng hết số tiền là:
4.000 x 10 = 40.000 (đồng)
Mua 8 cây xà cừ hết số tiền là:
64.000 – 40.000 = 24.000 (đồng)
Giá tiền một cây xà cừ là:
24.000 : 8 = 3.000 (đồng)
Đáp số: Phượng: 4.000 đồng; Xà cừ: 3.000 đồng
Ví dụ 4. Bà chia kẹo cho các cháu. Nếu bà chia cho mỗi cháu 5 cái kẹo thì bà còn thừa 3 cái kẹo. Nếu bà chia cho mỗi cháu 7 cái kẹo thì bà thiếu mất 9 cái kẹo. Hỏi bà chia kẹo cho mấy cháu và bà có bao nhiêu cái kẹo?
Lời giải.
Mỗi cháu chia 7 kẹo nhiều hơn mỗi cháu 2 kẹo là:
7-5 = 2 (cái kẹo)
Số kẹo chia đủ cho mỗi cháu 7 các nhiều hơn số kẹo chia cho mỗi cháu 5 cái là
3+9 =12 (cái kẹo)
Số cháu được bà chia kẹo là:
12: 2= 6 (cháu)
Số kẹo bà có là
5×6 + 3= 33 (cái)
Đáp số: 6 cháu và 33 cái kẹo
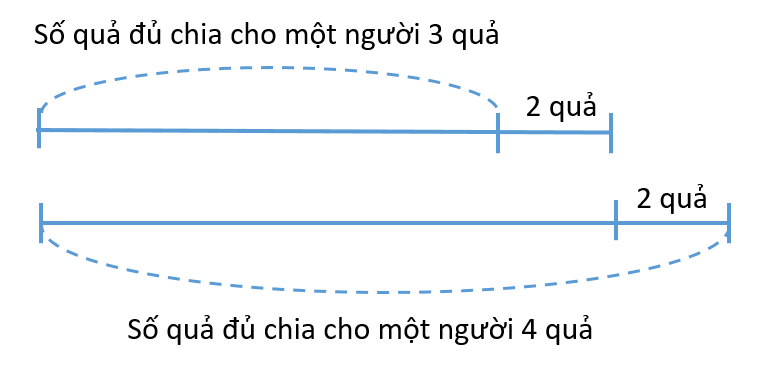
Ví dụ 5. Chị chia đào cho các em, nếu cho mỗi em 3 quả, thì thừa 2 quả. Nếu chia mỗi em 4 quả thì thiếu 2 quả. Hỏi có bao nhiêu quả đào và bao nhiêu em được chia tào ?
Lời giải:
Vì nếu mỗi người được 3 quả thì thừa 2 quả, mỗi người 4 quả thì thiếu 2 quả, nên ta có sơ đồ:
Nhìn vào sơ đồ, ta thấy số quả đào đủ để chia cho mỗi em 4 quả nhiều hơn số đào đủ chia cho mỗi em 3 quả là:
2 + 2 = 4 (quả)
Khi chia cho mỗi em 4 quả thì nhiều hơn khi chia cho mỗi em 3 quả là
4 – 3 = 1 (quả)
Do đó, số em được chia đào là:
4 : 1 = 4 (em)
Số đào là:
3 x 4 + 2 = 14 (quả)
-
Tóm tắt lý thuyết phương trình đường thẳng lớp 10
Tóm tắt lý thuyết Phương trình đường thẳng lớp 10
Lập phương trình đường thẳng là một bài toán quan trọng của chương phương pháp tọa độ trong mặt phẳng thuộc chương trình hình học lớp 10. Có hai bài toán cơ bản cần ghi nhớ là lập phương trình tổng quát của đường thẳng, lập phương trình tham số của đường thẳng.
Ngoài ra còn có phương trình chính tắc của đường thẳng, cách lập phương trình đường thẳng đi qua hai điểm, lập phương trình đường thẳng biết hệ số góc…
Xem thêm 100 Bài tập phương pháp tọa độ trong mặt phẳng
1. Phương trình tham số của đường thẳng
Một véc-tơ $\overrightarrow{u}\ne \vec{0}$ được gọi là véc-tơ chỉ phương của đường thẳng nếu nó có giá song song hoặc trùng với đường thẳng đó.
- Phương trình tham số của đường thẳng $\Delta$ đi qua $M(x_{0},y_{0})$ và có một véc-tơ chỉ phương $\vec{u}(a,b)$ là:\[
\begin{cases} x =x_{0}+at\\ y =y_{0}+bt \end{cases}, (t\in \mathbb{R})\]
Ví dụ 1. Lập phương trình tham số của đường thẳng $d$ có véc-tơ chỉ phương là $ \vec{u}(3;4) $ và đi qua điểm $ M(7;2) $.
Hướng dẫn.
Phương trình tham số của đường thẳng $d$ có véc-tơ chỉ phương là $ \vec{u}(3;4) $ và đi qua điểm $ M(7;2) $ là $$ \begin{cases}
x=3t+7\\
y=4t+2
\end{cases} (t\in \mathbb{R}) $$Nhận xét
- Một đường thẳng có vô số vectơ chỉ phương và tất cả chúng đều cùng phương với nhau.
- Nếu \(\overrightarrow{u}\) là một vectơ chỉ phương của đường thẳng \(d\) thì \(k.\overrightarrow{u}\) cũng là vectơ chỉ phương của \(d.\)
2. Phương trình tổng quát của đường thẳng
Một véc-tơ $\overrightarrow{n}\ne \vec{0}$ được gọi là véc-tơ pháp tuyến của đường thẳng nếu nó có giá vuông góc với đường thẳng đó.
2.1. Phương trình tổng quát của đường thẳng
- Trong mặt phẳng tọa độ $Oxy$, phương trình tổng quát của đường thẳng có dạng $$ax+by+c=0$$ với $a,b$ không đồng thời bằng $0$ (có thể viết tắt là $a^2+b^2 \ne 0$).
- Khi đó, một véc-tơ pháp tuyến của đường thẳng là $\vec{n}(a;b)$.
- Lấy một điểm bất kì thuộc đường thẳng ta có thể cho $x$ nhận một giá trị tùy ý rồi tìm giá trị của $y$ tương ứng, hoặc cho $y$ một giá trị tùy ý rồi tìm $x$ tương ứng.
Ví dụ 2. Cho đường thẳng $\Delta$ có phương trình $2x+3y-5=0$ thì chúng ta có:
- Một véc-tơ pháp tuyến là $\vec{n}=(2;3)$.
- Lấy một điểm thuộc $\Delta$. Cho $x=2$ thì có $2\cdot 2+3y-5=0$, do đó tìm được $y=\frac{1}{3}$. Vậy tọa độ một điểm thuộc đường thẳng $\Delta$ là $\left (2;\frac{1}{3}\right)$.
2.2. Cách lập phương trình tổng quát của đường thẳng
Ta cần tìm một véc-tơ pháp tuyến $\vec{n}$ và tìm tọa độ của một điểm $M$ thuộc đường thẳng. Sau đó sử dụng kết quả:
Phương trình tổng quát của đường thẳng $\Delta$ có một véc-tơ pháp tuyến $\vec{n}(a,b)$ và đi qua điểm $M(x_{0},y_{0})$ là: \[ ax+by-(ax_{0}+by_{0})=0\]
Ví dụ 3. Lập phương trình tổng quát của đường thẳng $\Delta$ biết nó có véc-tơ pháp tuyến $ \vec{n}(3;4) $ và đi qua điểm $ M(0;7) $.
Hướng dẫn. Đường thẳng $\Delta$ có véc-tơ pháp tuyến $ \vec{n}(3;4) $ và đi qua điểm $ M(0;7) $ nên có phương trình tổng quát:
$$ 3x+4y-(3\cdot 0+4\cdot 7)=0 $$ hay chính là $ 3x+4y-28=0 $.Ví dụ 4. Lập phương trình đường trung trực của đoạn thẳng $EF$ với $ E(1;9) $ và $ F(3;-3) $
Hướng dẫn.
- Gọi đường trung trực của $ EF $ là $ d $ thì đường thẳng $d$ vuông góc với $ EF $ và đi qua trung điểm của $ EF. $
- Vì $d$ vuông góc với $ EF $ nên đường thẳng $d$ có véc-tơ pháp tuyến chính là $ \overrightarrow{EF}(2;-12) $.
- Gọi trung điểm của $ EF $ là $ M $ thì tìm được $ M(2;3) $.
- Đường thẳng $ d $ có véc-tơ pháp tuyến chính là $ \overrightarrow{EF}(2;-12) $ và đi qua điểm $ M(2;3) $ nên có phương trình tổng quát: $$ 2x-12y+32=0. $$
2.3. Mối quan hệ giữa véc-tơ chỉ phương và véc-tơ pháp tuyến của đường thẳng
- Véctơ chỉ phương và véc-tơ pháp tuyến của một đường thẳng thì vuông góc với nhau, do đó nếu véc-tơ pháp tuyến là $\vec{n}=(a,b)$ thì có thể chọn véc-tơ chỉ phương $\vec{u}=(-b,a)$ hoặc $\vec{u}=(b,-a);$ và ngược lại, nếu \(\overrightarrow{u}=(p,q)\) là một vectơ chỉ phương của một đường thẳng thì đường thẳng đó có một vectơ pháp tuyến là \(\overrightarrow{n}=(q,-p)\) hoặc \(\overrightarrow{n’}=(-q,p).\)
- Hai đường thẳng song song thì có cùng các véc-tơ chỉ phương, cùng các véc-tơ pháp tuyến.
- Hai đường thẳng vuông góc thì véc-tơ chỉ phương của đường thẳng này là véc-tơ pháp tuyến của đường thẳng kia và ngược lại.
Nếu đường thẳng $\Delta$ có phương trình: $ax+by+c=0$ thì đường thẳng $\Delta’$
- vuông góc với $\Delta$ là $\Delta’:-bx+ay+c’=0$ hoặc $\Delta’:bx-ay+c’=0$.
- song song với $\Delta$ là $\Delta’:ax+by+c’=0$ với $ c\ne c’. $
Ví dụ 5. Lập phương trình tổng quát của đường thẳng $ AB $ với $ A(1;2) $ và $ B(-3;5) $.
Hướng dẫn.
- Đường thẳng $ AB $ chứa $ \overrightarrow{AB}(-4;3) $ nên $ \overrightarrow{AB}(-4;3) $ chính là véc-tơ chỉ phương của đường thẳng $AB$.
- Suy ra, đường thẳng $AB$ có véc-tơ pháp tuyến là $ \vec{n}(3;4) $.
- Như vậy, đường thẳng $AB$ có véc-tơ pháp tuyến là $ \vec{n}(3;4) $ và đi qua điểm $ A(1;2) $ nên có phương trình tổng quát: $$ 3x+4y-11=0. $$
3. Góc và khoảng cách lớp 10
- Khoảng cách từ điểm $ M(x_0,y_0) $ đến đường thẳng $ \Delta:ax+by+c=0 $ là $$ d(M,\Delta)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
- Góc giữa hai véc-tơ $ \vec{a},\vec{b} $ có $$\cos(\vec{a},\vec{b})=\frac{\vec{a}.\vec{b}}{|\vec{a}|.|\vec{b}|}=\frac{\text{tích vô hướng}}{\text{tích độ dài}} $$
- Góc giữa hai đường thẳng $ \Delta $ và $ \Delta’ $ có $$\cos(\Delta,\Delta’)=\left|\cos(\vec{n},\vec{n’})\right|=\frac{|\vec{n}.\vec{n’}|}{|\vec{n}|.|\vec{n’}|}$$
Góc giữa hai đường thẳng có cosin bằng trị tuyệt đối của tích vô hướng chia tích độ dài các véc-tơ pháp tuyến của hai đường thẳng.
Ví dụ 6. Tính khoảng cách từ điểm $ A(1 , 3) $ đến đường thẳng $ \Delta: 3x – 4y + 4 = 0 $
Hướng dẫn. Khoảng cách từ điểm $ A $ đến đường thẳng $\Delta$ là $$ d(A,\Delta) = \frac{\left|3\cdot 1-4\cdot 3 +4\right|}{\sqrt{3^2+(-4)^2}}=1 $$
Ví dụ 7. Tính khoảng cách từ điểm $ P(3 , 12) $ đến đường thẳng $ \Delta:\begin{cases} x=2+t\\y=5-3t \end{cases} $
Hướng dẫn. Trước tiên, chúng ta cần chuyển phương trình đường thẳng $\Delta$ từ dạng tham số về dạng tổng quát. Từ phương trình thứ nhất của hệ, chúng ta có $ t=x-2 $. Thế vào phương trình thứ hai của hệ ta được $ y=5-3(x-2) $ hay chính là $$ 3x+y-11=0 $$
Đây chính là phương trình tổng quát của đường thẳng $\Delta$. Từ đó, khoảng cách cần tìm là $$ d(P,\Delta)=\frac{|3\cdot 3+ 12 -11|}{\sqrt{3^2+1^2}} = \sqrt{10} . $$Ví dụ 8. Tính khoảng cách giữa hai đường thẳng song song $ d : 5x + 3y – 5 = 0 $ và $ d’ : 5x + 3y + 8 = 0 $.
Hướng dẫn. Vì hai đường thẳng đã cho song song với nhau, nên khoảng cách giữa chúng chính bằng khoảng cách từ một điểm bất kì thuộc đường thẳng này tới đường thẳng còn lại.
Lấy một điểm bất kì thuộc đường thẳng $ d $, chẳng hạn $ M(1;0) $ thì khoảng cách cần tìm là \begin{align}
d(d,d’) &= d(M,d’) \\
&=\frac{|5\cdot 1+3\cdot 0+8|}{\sqrt{5^2+3^2}}\\
& = \frac{13\sqrt{34}}{34}.
\end{align}Ví dụ 9. Tính góc giữa hai đường thẳng $ \Delta: x-3y+5=0 $ và $ \Delta’:2x-3y+7=0 $.
Hướng dẫn.
- Đường thẳng $\Delta$ có véc-tơ pháp tuyến là $ \vec{n}(1;-3) $, đường thẳng $\Delta’$ có véc-tơ pháp tuyến là $ \vec{n}'(2;-3) $ nên góc giữa hai đường thẳng có \begin{align}
\cos(\Delta,\Delta’)&=\frac{|\vec{n}\cdot \vec{n}’|}{\big|\vec{n}|\cdot|\vec{n}’\big|}\\
&=\frac{\big|1\cdot 2+(-3)\cdot (-3)\big|}{\sqrt{1^2+(-3)^2}\cdot\sqrt{2^2+(-3)^2}}\\
&= \frac{11}{\sqrt{130}}.
\end{align} - Suy ra, góc giữa hai đường thẳng là $ (\Delta,\Delta’)\approx 15.26^\circ. $
4. Các dạng phương trình đường thẳng lớp 10 khác
4.1. Phương trình chính tắc của đường thẳng
- Phương trình chính tắc của đường thẳng đi qua $ M(x_0,y_0) $ và có véc-tơ chỉ phương $ \vec{u}(a,b) $ mà $ ab\ne0 $ là $$\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}$$
4.2. Phương trình đường thẳng biết hệ số góc
- Đường thẳng đi qua điểm $M(x_{0},y_{0})$ và có hệ số góc $k$ có phương trình: $$y-y_{0}=k(x-x_{0})$$
4.3. Phương trình đường thẳng đi qua 2 điểm
- Nếu hai điểm $ A(x_A;y_A) $ và $ B(x_B;y_B) $ mà có $ x_B-x_A\ne 0 $ và $ y_B-y_A\ne 0 $ thì có phương trình
$$ \frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-yA} $$
4.4. PT đường thẳng cắt hai trục tọa độ
- Đường thẳng cắt hai trục tọa độ tại $A(a,0)$ và $B(0,b)$ có phương trình: $$\frac{x}{a}+\frac{y}{b}=1$$
- Phương trình này được gọi là phương trình đoạn chắn.
5. Bài tập phương trình đường thẳng lớp 10
Quý thầy cô và các em học sinh tham khảo trong bài Bài tập phương pháp tọa độ trong mặt phẳng
- Phương trình tham số của đường thẳng $\Delta$ đi qua $M(x_{0},y_{0})$ và có một véc-tơ chỉ phương $\vec{u}(a,b)$ là:\[
-
CÁC BẢNG ĐƠN VỊ ĐO LỚP 5
CÁC BẢNG ĐƠN VỊ ĐO LỚP 5
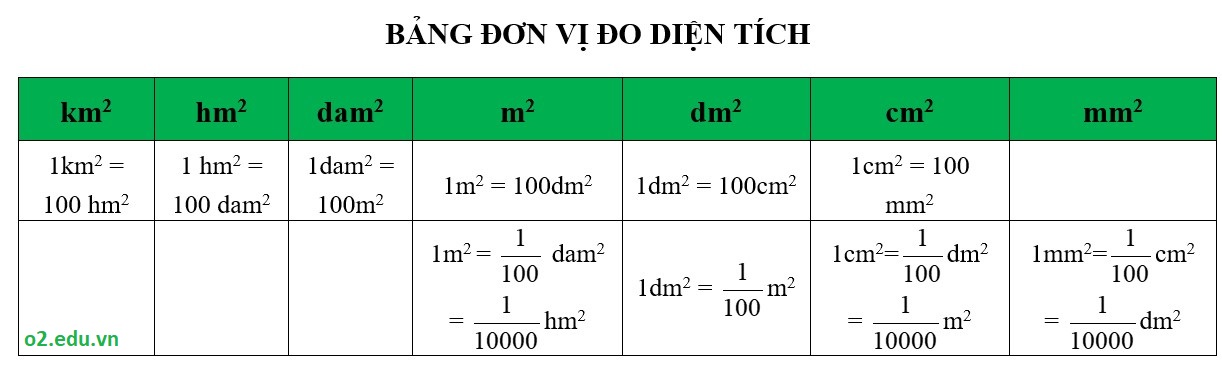
Các bảng đơn vị đo lớp 5 gồm có bảng đơn vị đo thời gian, bảng đơn vị đo khối lượng, bảng đơn vị đo độ dài và bảng đơn vị đo diện tích.
Xem thêm: 120 BÀI TOÁN THI VIOLYMPIC LỚP 5
1. Bảng đơn vị đo thời gian
- 1 giờ = 60 phút; 1 phút = 60 giây; 1 ngày = 24 giờ; 1 tuần = 7 ngày;
- 1 năm thường có 365 ngày, 1 năm nhuận có 366 ngày ( cứ 4 năm có một năm nhuận)
- Tháng một, tháng ba, tháng năm, tháng bảy, tháng tám, tháng mười, tháng mười hai có 31 ngày.
- Tháng tư, tháng sáu, tháng chín, tháng mười một có 30 ngày.
- Tháng hai có 28 ngày (vào năm nhuận có 29 ngày)
- 1 quý có 3 tháng; 1 năm có 4 quý.
- 1 thập kỉ = 10 năm; 1 thế kỉ = 100 năm; 1 thiên niên kỉ = 1000 năm.
2. Bảng đơn vị đo khối lượng lớp 5
a) Các đơn vị đo khối lượng từ bé đến lớn: g, dag, hg, kg, yến, tạ, tấn
b) Hai đơn vị đo khối lượng liền nhau :
- Đơn vị lớn gấp 10 lần đơn vị bé
- Đơn vị bé bằng 1/10 đơn vị lớn
3. Bảng đơn vị đo độ dài lớp 5
a) Các đơn vị đo độ dài từ lớn đến bé: km, hm, dam, m, dm, cm, mm
b) Hai đơn vị đo độ dài liền nhau :
- Đơn vị lớn gấp 10 lần đơn vị bé.
- Đơn vị bé bằng 1/10 đơn vị lớn.
4. Bảng đơn vị đo diện tích lớp 5
a) Trong bảng đơn vị đo diện tích, hai đơn vị đo liền nhau hơn (kém) nhau 100 lần, tức là:
- Đơn vị lớn gấp 100 lần đơn vị bé.
- Đơn vị bé bằng 1/100 đơn vị lớn.
b) mét vuông là diện tích của hình vuông có cạnh dài 1m.
c) Đề-ca-mét vuông là diện tích của hình vuông có cạnh dài 1dam.
d) Héc-tô-mét vuông là diện tích của hình vuông có cạnh dài 1hm.
e) Mi-li-mét vuông là diện tích của hình vuông có cạnh dài 1mm.
5. BÀI TẬP BẢNG ĐƠN VỊ ĐO ĐỘ DÀI, KHỐI LƯỢNG, DIỆN TÍCH
Bài 1: Viết số hoặc phân số thích hợp vào chỗ chấm:
a) 1mm = … m
b) 1cm = … dm
c) 1dam = … km
Bài 2: Viết số hoặc phân số thích hợp vào chỗ chấm:
a) 1kg = … tạ
b) 1g = … kg
c) 1 tạ = … tấn
Bài 3: Viết số hoặc phân số thích hợp vào chỗ chấm:
a) 450hm\(^2\) = … km\(^2\) … hm\(^2\)
b) 6240m\(^2\) = … dam\(^2\) … m\(^2\)
c) 3750mm\(^2\) = … cm\(^2\) … mm\(^2\)
Bài 4: Viết các số đo dưới dạng số đo có đơn vị là ki-lô-mét vuông:
a) 3km\(^2\) 3hm\(^2\) = …
b) 16km\(^2\) 267m\(^2\) = …
Bài 5: Một đội công nhân trong ba ngày sửa được 2km đường. Ngày thứ nhất đội sửa được 620m đường, ngày thứ hai sửa được số mét đường gấp đôi ngày thứ nhất. Hỏi ngày thứ ba đội công nhân đó sửa được bao nhiêu mét đường?
Bài 6: Viết tiếp vào chỗ chấm:
a) Hai đơn vị đo độ dài liền nhau:
– Đơn vị lớn gấp … đơn vị bé.
– Đơn vị bé bằng … đơn vị lớn.
b) Hai đơn vị đo khối lượng liền nhau:
– Đơn vị lớn gấp … đơn vị bé.
– Đơn vị bé bằng … đơn vị lớn.
c) Hai đơn vị đo diện tích liền nhau:
– Đơn vị lớn gấp … đơn vị bé.
– Đơn vị bé bằng … đơn vị lớn.
Bài 7: Trong một ku cư dân mới, người ta dùng một nửa diện tích đất để làm đường đi và các công trình công cộng, nửa diện tích đất còn lại được chia đều thành 2000 mảnh hình chữ nhật, mỗi mảnh có chiều rộng 10m, chiều dài 25m để xây nhà ở. Hỏi diện tích khu dân cư đó là bao nhiêu ki-lô-mét vuông?
Bài 8: Một xe chở 12 tạ gạo tẻ và 80 yến gạo nếp. Tính khối lượng gạo xe đó chở được.
Bài 9: Một người đi xe máy từ A qua C đến B. Đoạn đường AC ngắn hơn đoạn đường CB là 13km 500m. Tính quãng đường AB, biết đoạn đường AC bằng \(\dfrac{2}{5}\) đoạn đường CB.
Bài 10: Cửa hàng có số gạo tẻ nhiều hơn số gạo nếp là 1 tạ 50kg. Sau khi bán đi 25kg gạo mỗi loại thì còn lại lượng gạo nếp bằng \(\dfrac{2}{5}\) lượng gạo tẻ. Hỏi lúc đầu cửa hàng có bao nhiêu ki-lô-gam gạo mỗi loại?
-
Tìm hai số khi biết tổng và tỉ số của hai số
Tìm hai số khi biết tổng và tỉ số của hai số
Dạng toán Tìm hai số khi biết tổng và tỉ số của hai sốđó thường xuất hiện trong các đề thi, đề kiểm tra của chương trình toán lớp 5, toán lớp 4. Dưới đây, chúng tôi xin giới thiệu phương pháp giải dạng toán tìm 2 số biết tổng tỉ của chúng và các ví dụ mẫu.
Xem thêm: Tìm hai số khi biết hiệu và tỉ số của hai số
1. Cách giải bài toán tìm hai số khi biết tổng và tỉ số của hai số
1.1. Phương pháp giải dạng toán tìm 2 số khi biết tổng và tỉ
- Bước 1. Vẽ sơ đồ theo dữ kiện bài ra.
- Bước 2. Tìm tổng số phần bằng nhau
- Bước 3. Tìm số bé và số lớn (có thể tìm số lớn trước hoặc tìm số bé trước) bằng công thức
Số bé = (Tổng : số phần bằng nhau) x số phần của số bé (hoặc tổng – số lớn)
Số lớn = (Tổng: số phần bằng nhau) x số phần của số lớn (hoặc tổng – số bé)- Bước 4. Kết luận đáp số(Học sinh có thể tiến hành thêm bước thử lại để kiểm chứng kết quả)
1.2. Các trường hợp đặc biệt tìm hai số khi biết tổng và tỉ số
Đề bài nhiều bài toán lại không cho dữ kiện đầy đủ về tổng và tỉ số mà có thể cho dữ kiện như sau:
- Thiếu (ẩn) tổng (Cho biết tỉ số, không cho biết tổng số)
- Thiếu (ẩn) tỉ (Cho biết tổng số, không cho biết tỉ số)
- Cho dữ kiện thêm, bớt số, tạo tổng (tỉ) mới tìm số ban đầu.
Với những bài toán cho dữ kiện như vậy, cần tiến hành thêm một bước chuyển về bài toán cơ bản.
2. Ví dụ mẫu và bài tập tìm 2 số biết tổng và tỉ
2.1. Tìm hai số biết tổng và tỉ cơ bản
Đối với dạng bài này, chúng ta so sánh giá trị của số lớn với giá trị của số bé.
Ví dụ 1. Hai bạn Minh và Khôi có 25 quyển vở. Số vở của Minh bằng số vở của Khôi. Hỏi mỗi bạn có bao nhiêu quyển vở?
Bước 1: Học sinh đọc đề toán.
Bước 2: Phân tích – tóm tắt bài toán.
- Bài toán cho biết gì? (Minh và Khôi có 25 quyển vở, số vở của Minh bằng số vở của Khôi).
- Bài toán hỏi gì? (Bài toán yêu cầu tìm số vở của Minh và số vở của Khôi)
- Bài toán thuộc dạng toán gì đã được học? (Bài toán thuộc dạng “Tìm hai số khi biết tổng và tỉ số của hai số đó”)
Bước 3: Tìm cách giải bài toán:
Tóm tắt bài toán bằng sơ đồ đoạn thẳng:
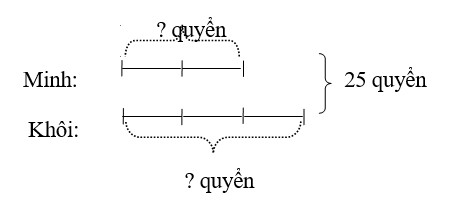
Theo sơ đồ tổng số phần bằng nhau là:
2 + 3 = 5 (phần)
Giá trị của một phần là:
25 : 5 = 5 (quyển)
Số vở của bạn Minh là:
5 x 2 = 10 (quyển)
Số vở của bạn Khôi là:
5 x 3 = 15 (quyển)
hoặc: 25 – 10 = 15 (quyển)
Đáp số: Minh: 10 quyển vở;
Khôi: 15 quyển vở.
Ví dụ 2. Tuổi Mẹ và An 36 tuổi. tuổi mẹ bằng 7/2 tuổi An. Hỏi mỗi người bao nhiêu tuổi?
Hướng dẫn.
- Tóm tắt bài toán bằng sơ đồ đoạn thẳng như sau:
- Tổng số phần bằng nhau:
7 + 2 = 9 (phần)
- Giá trị một phần:
36: 9 = 4 (tuổi)
- Số tuổi của mẹ:
4 x 7 = 28(tuổi)
- Số tuổi của An:
4 x 2 = 8(tuổi)
Đáp số: mẹ 28 tuổi; An 8 tuổi.
Ví dụ 3. Đặt đề toán và giải bài toán theo sơ đồ sau.
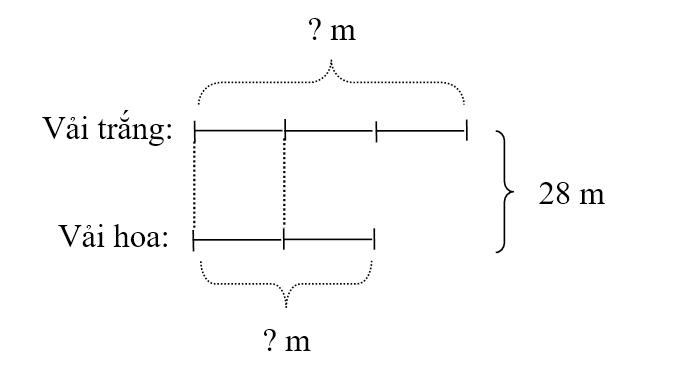
Hướng dẫn học sinh dựa vào sơ đồ để xác định được dạng toán và đặt đề toán.
- Bài toán yêu cầu chúng ta làm gì? (Bài toán yêu cầu nêu đề bài toán rồi giải theo sơ đồ).
- Quan sát sơ đồ và cho biết bài toán thuộc dạng toán gì? (Bài toán thuộc dạng tìm hai số khi biết tổng và tỉ số của hai số đó).
- Tổng của hai số là bao nhiêu? (Tổng của hai số là 28m)
- Tỉ số của hai số là bao nhiêu? (Tỉ số của hai số là )
- Giáo viên yêu cầu học sinh dựa vào sơ đồ đặt đề toán.
Đặt đề toán. Một cửa hàng đã bán 28m vải, trong đó số vải hoa bằng số vải trắng. Hỏi cửa hàng đó đã bán được bao nhiêu mét vải mỗi loại?
Giải bài toán.
- Xác định được tổng và tỉ số đã cho.
- Xác định được hai số phải tìm là số nào?
2.2. Dạng toán tổng (ẩn) – tỉ:
Ví dụ 4. Hình chữ nhật có chu vi là 200m. Chiều dài bằng 3/2 chiều rộng. tính diện tích của hình chữ nhật?
Sơ đồ số phần bằng nhau:
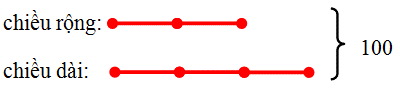
Tổng chiều dài và chiều rộng:
200: 2 = 100 (m)
Tổng số phần bằng nhau:
3 + 2 = 5 (phần)
Giá trị một phần:
100: 5 = 20 (m)
Chiều dài của hình chữ nhật:
20 x 3 = 60 (m)
Chiều rộng của hình chữ nhật:
20 x 3 = 40 (m)
Diện tích của hình chữ nhật:
60 x 40 = 2 400 (m2)
Đáp số: 2 400 (m2).
2.3. Dạng toán tổng – tỉ (ẩn):
Ví dụ 5. Có hai thùng đựng 96 lít dầu. 5 lần thùng thứ nhất bằng 3 lần thùng thứ hai. Hỏi mỗi thùng đựng bao nhiêu lít dầu?
Lời giải.
Ta có: “5 lần thùng thứ nhất bằng 3 lần thùng thứ hai” nghĩa là “Thùng thứ nhất bằng 3/5 thùng thứ hai”. Do đó, nếu thùng thứ nhất biểu diễn bởi 3 đoạn thẳng bằng nhau thì thùng thứ 2 biểu diễn bởi 5 đoạn thẳng bằng nhau. Sơ đồ số phần bằng nhau:
Tổng số phần bằng nhau:
3 + 5 = 8 (phần)
Giá trị một phần:
96: 8 = 12 (lít)
Số lít dầu thùng thứ nhất đựng:
12 x 3 = 36 (lít)
Số lít dầu thùng thứ hai đựng:
12 x 5 = 60 (lít)
Đáp số: 36 (lít); 60 (lít).
2.4. Dạng toán tổng (ẩn) – tỉ (ẩn):
Ví dụ 6. Tìm hai số tự nhiên, biết trung bình cộng của chúng là 120 và 1/3 số thứ nhất bằng 1/7 số thứ hai.
Hướng dẫn. Để giải được bài toán này, các em học sinh cần xem lại CÁC BÀI TOÁN VỀ TRUNG BÌNH CỘNG LỚP 4
Lời giải.
Trung bình cộng của hai số là 120 nên suy ra tổng của hai số là:
120 x 2 = 240
“1/3 số thứ nhất bằng 1/7 số thứ hai” nghĩa là “số thứ nhất bằng 3/7 số thứ hai”. Từ đó, chúng ta có sơ đồ sau:
Tổng số phần bằng nhau là:
3 + 7 = 10 (phần)
Như vậy, 10 phần này có tổng giá trị là 240 nên suy ra giá trị của một phần là:
240: 10 = 24
Số thứ nhất là:
24 x 3 = 72
Số thứ hai là:
24 x 7 = 168
Đáp số: 72 và 168.
3. Bài tập tìm hai số khi biết tổng và tỉ
Bài 1: Tổng của hai số bằng số lớn nhất của số có hai chữ số. Tỉ số của hai số đó là 4/5. Tìm hai số đó.
Bài 2: Một hình chữ nhật có chu vi là 350m, chiều rộng bằng 3/4 chiều dài. Tìm chiều dài, chiều rộng của hình chữ nhật đó?
Bài 3. Một sợi dây dài 28m được cắt thành hai đoạn, đoạn thứ nhất dài gấp 3 lần đoạn dây thứ hai. Hỏi mỗi đoạn dài bao nhiêu mét?
Bài 4. Tổng của hai số là 72. Tìm hai số đó, biết rằng nếu số lớn giảm 5 lần thì được số bé.
Bài 5: Tổng của hai số là 96. Tỉ số của hai số đó là 3/5. Tìm hai số đó?
Bài 6: Minh và Khôi có 25 quyển vở. Số vở của Minh bằng 2/3 số vở của Khôi. Hỏi mỗi bạn có bao nhiêu quyển vở
Bài 7: Tổng của hai số là 333. Tỉ của hai số là 2/7. Tìm hai số đó.
Bài 8: Hai kho chứa 125 tấn thóc. Số thóc ở kho thứ nhất bằng 3/2 số thóc ở kho thứ 2. Hỏi mỗi kho chứa bao nhiêu tấn thóc?
Bài 9: Một miếng vườn hình chữ nhật, có chu vi 200 m, chiều dài gấp 3 lần chiều rộng. Tính diện tích miếng vườn?
Bài 10: Miếng đất hình chữ nhật có chu vi 240m, chiều rộng bằng 2/3 chiều dài. Tính diện tích hình chữ nhật đó.
Bài 11: Tìm 2 số. Biết tổng của chúng bằng 48, nếu lấy số lớn chia cho số bé thì được thương là 3.
Bài 12: Tìm 2 số, biết tổng của chúng bằng số bé nhất có 3 chữ số. Nếu lấy số này chia cho số kia ta được thương là 4.
Bài 13: Tổng 2 số bằng số lớn nhất có 4 chữ số. Nếu lấy số lớn chia cho số bé ta được thương là 10. Tìm 2 số đó.
Bài 14: Một trường tiểu học có tất cả 567 học sinh. Biết rằng với 5 học sinh nam thì có 2 học sinh nữ. Hỏi trường tiểu học đó có bao nhiêu học sinh nam? Bao nhiêu học sinh nữ?
Bài 15: Tìm số tự nhiên. Biết rằng khi ta thêm vào bên phải số đó 1 chữ số 0 thì ta được số mới và tổng của số mới và số cũ là 297.
Bài 16: Trung bình cộng của 2 số là 440. Nếu ta thêm 1 chữ số 0 vào bên phải số bé thì ta được số lớn. Tìm 2 số đó.
Bài 17: Tìm số tự nhiên. Biết rằng nếu ta thêm vào bên phải của số đó một chữ số 2 thì ta được số mới. Tổng của số mới và số cũ là 519.
Bài 18: Tìm hai số có tổng là 107. Biết rằng nếu xoá đi chữ số 8 ở hàng đơn vị của số lớn ta được số bé.
Bài 19: Tìm số tự nhiên. Biết rằng khi viết thêm vào bên phải số đó số 52 ta được số mới. Tổng của số mới và số đó bằng 5304.
Bài 20: Trung bình cộng của 3 số là 85. Nếu thêm 1 chữ số 0 vào bên phải số thứ hai thì được số thứ nhất, nếu gấp 4 lần số thứ hai thì được số thứ ba. Tìm 3 số đó.
Bài 21: Tổng 2 số bằng 385. Một trong hai số có số tận cùng bằng chữ số 0, nếu xóa chữ số 0 đó thì ta được 2 số bằng nhau. Tìm hai số đó.
Bài 22: Hai số có tổng là 1/4 và thương cũng là 1/4. Tìm 2 số đó.
Bài 23: Bính và Đinh có hai thửa ruộng, tổng diện tích của hai thửa ruộng đó là 780 m2. Nếu chuyển 1/6 diện tích ruộng của Bính sang cho Đinh thì diện tích của hai thửa sẽ bằng nhau. Tính diện tích của mỗi thửa ruộng bằng mét vuông.
Bài 24: Lớp 5A và lớp 5B nhận chăm sóc hai thửa ruộng có tổng diện tích là 1560 m2. Nếu lấy 1/4 diện tích thửa ruộng của lớp 5A chuyển sang cho lớp 5B chăm sóc thì diện tích chăm sóc của hai lớp bằng nhau. Tính diện tích của mỗi thửa ruộng.
Bài 25: Hai hầm đông lạnh chưa 180 tấn tôm. Nếu người ta chuyển 2/7 khối lượng tôm ở hầm thứ nhất sang hầm thứ hai, thì khối lượng tôm ở hai hầm bằng nhau. Hỏi mỗi hầm chứa bao nhiêu tấn tôm?
Bài 26: Đội tuyển bóng đá mi ni của huyện A tham dự hội khỏe Phù Đổng cấp tỉnh gồm các bạn học sinh lớp 4 và lớp 5. Dự định số bạn tham gia đội tuyển bóng đá đang học lớp 4 chiếm 1/5 của cả đội. Nhưng do một bạn đang học lớp 4 không tham gia được mà thay bởi một bạn đang học lớp 5, khi đó số bạn đang học lớp 4 tham gia chỉ bằng 1/10 số thành viên của cả đội. Tính tổng số thành viên của cả đôi bóng đá mi ni?
Bài 27: Đội tuyển của trường A tham gia Hội khoẻ Phù Đổng cấp huyện gồm các bạn học sinh nam và học sinh nữ. Dự định số bạn nữ tham gia đội tuyển chiếm 1/4 số nam nhưng do điều kiện thay bởi một bạn nữ bằng một bạn nam. Khi đó số bạn nữ chiếm 1/5 số nam. Tính xem đội tuyển của trường A đi dự hội thao bao nhiêu học sinh?
Bài 28: Đội tuyển trường em tham gia Hội khỏe Phù Đổng cấp huyện, ban đầu số nữ bằng 2/3 số nam. Sau khi xét theo yêu cầu thay thế một bạn nữ bằng một bạn nam vì thế số nữ lúc này bằng 3/4 số nam. Hỏi đội tuyển trường em có bao nhiêu bạn?
Bài 29: Một tủ sách có hai ngăn. Số sách ở ngăn dưới gấp 3 lần số sách ngăn trên. Nếu chuyển 10 quyển sách ở ngăn trên xuống ngăn dưới thì số sách ngăn dưới gấp 7 lần ngăn trên. Tính số sách mỗi ngăn.
Bài 30: Lúc đầu số vịt dưới ao nhiều gấp 5 lần số vịt trên bờ. Nhưng sau khi có 3 con vịt từ trên bờ nhảy xuống ao bơi lội thì số vịt dưới ao nhiều gấp 8 lần số vịt trên bờ. Hỏi cả đàn có bao nhiêu con?
Bài 31: Một hình chữ nhật có chiều rộng bằng 2/5 chiều dài. Nếu thêm vào chiều rộng 4 m và đồng thời bớt chiều dài 4 m thì lúc đó chiều rộng bằng 2/3 chiều dài. Tính diện tích của hình chữ nhật đó.
Bài 32: Cuối học kì I lớp 5A có số học sinh giỏi bằng 3/7 số học sinh còn lại của lớp. Cuối năm học sinh lớp 5A có thêm 4 học sinh giỏi nên tổng số học sinh giỏi bằng 2/3 số học sinh còn lại của lớp. Hỏi lớp 5 A có bao nhiêu học sinh?
Bài 33: Một giá sách gồm hai ngăn: Số sách ngăn dưới bằng 6/5 số sách ngăn trên. Nếu xếp 15 quyển sách mới mua vào ngăn trên thì lúc đó số sách ở ngăn dưới bằng 12/11 số sách ngăn trên. Hỏi lúc đầu ở mỗi ngăn có bao nhiêu quyển sách?
Bài 34: Số gà mái nhiều gấp 6 lần số gà trống. Sau đó mua thêm 5 con gà trống nữa nên bây giờ số gà trống bằng 1/4 số gà mái. Hỏi lúc đầu có bao nhiêu con gà mái, gà trống?
Bài 35: Một cửa hàng nhập về một số xe máy. Người bán hàng lấy ra trưng bày để bán 1/8 số xe nhập về, số xe còn lại bỏ trong kho. Sau khi bán 3 chiếc xe ở quầy trưng bày thì người chủ quầy nhận thấy số xe ở trong kho nhiều gấp 10 lần số xe còn lại ở quầy trưng bày xe. Hỏi cửa hàng lúc đầu nhập về bao nhiêu chiếc xe máy?
Bài 36: Để chuẩn bị tham gia Hội khỏe Phù Đổng cấp tỉnh, huyện em đã thành lập đội tuyển tham dự trong đó số nữ bằng 2/3 số nam. Sau khi đội được bổ sung 20 nữ và 15 nam nên lúc này số nữ bằng 4/5 số nam. Tính xem đội tuyển của huyện tham gia Hội khỏe Phù đổng cấp tỉnh có tất cả bao nhiêu bận động viên tham gia?
Bài 37: Trong đợt thi tuyển chọn học sinh đi tham dự giao lưu Toán Tuổi thơ lần thứ Tư của tỉnh A, trong đó số học sinh nữ bằng 2/3 số học sinh nam. Nếu có thêm 10 học sinh nam tham gia dự thi thì số nữ lúc này bằng 3/5 số học sinh nam. Hỏi có bao nhiêu học sinh tham gia thi tuyển?
Bài 38: Tủ sách thư viện trường em có hai ngăn: Ngăn thứ nhất có số sách bằng 2/3 số sách thứ hai. Nếu xếp thêm vào ngăn thứ nhất 80 cuốn và ngăn thứ hai 40 cuốn thì số sách ngăn thứ nhất bằng 3/4 số sách ngăn thứ hai. Hỏi ban đầu mỗi ngăn tủ có bao nhiêu cuốn sách?
Bài 39:: Tí có một số bi không quá 80 viên, trong đó số bi đỏ gấp 5 lần số bi xanh. Nếu Tí có thêm 3 viên bi xanh nữa thì số bi đỏ gấp 4 lần số bi xanh. Hỏi lúc đầu Tí có mấy viên bi đỏ, mấy viên bi xanh?
Bài 40: Tuổi của con hiện nay bằng 1/2 hiệu tuổi của bố và tuổi con. Bốn năm trước, tuổi con bằng 1/3 hiệu tuổi của bố và tuổi con. Hỏi khi tuổi con bằng 1/4 hiệu tuổi của bố và tuổi của con thì tuổi của mỗi người là bao nhiêu?
Bài 41: Tìm hai số biết rằng tổng của chúng gấp 5 lần hiệu của chúng và tích của chúng là 4008. Tìm hiệu của chúng.
Bài 42: Một hình bình hành có diện tích 216 cm2 và chiều cao là 12cm. Nếu tăng chiều cao gấp 2 lần và giảm chiều dài đi 6cm thì diện tích hình mới sẽ thay đổi như thế nào so với diện tích hình bình hành ban đầu?
Bài 43: Người bán hàng có một bao gạo, lần đầu bán 3kg, lần sau bán 1/3 số gạo còn lại thì còn 18kg. Hỏi lúc đầu bao gạo nặng bao nhiêu kg?
Bài 44: Tổng số tuổi hiện nay của hai cha con là 50 tuổi. Năm năm sau tuổi cha sẽ gấp 3 lần tuổi con. Tính tuổi mỗi người hiện nay?
Bài 45: Chú Tuân đến chơi nhà chú Hùng. Chú Hùng và cô Lan cùng ngồi tiếp chuyện. Chú Hùng nói với chú Tuân: “Ngày hai chúng mình đi bộ đội thì tuổi cô Lan bằng 1/3 tuổi tôi thế mà đến bây giờ tổng số tuổi của hai anh em tôi đã là 48 tuổi và tuổi cô Lan đúng bằng tuổi tôi ngày tôi đi bộ đội.” Bạn tính xem cô Lan năm nay bao nhiêu tuổi?
Bài 46: Nhân dịp tết cửa hàng có nhận về một số hộp mứt. Vì quầy chật nên người bán hàng chỉ để 1/10 số hộp mứt ở quầy, số còn lại đem cất vào trong. Sau khi bán 4 hộp ở quầy thì số hộp cất đi gấp 15 lần số hộp còn lại ở ngoài quầy. Hỏi lúc đầu cửa hàng nhận về bao nhiêu hộp mứt?
Bài 47: Một con mèo đuổi bắt một con chuột cách nó 3m. Mỗi bước con mèo nhảy được 8dm, con chuột nhảy được 3dm. Hỏi sau bao nhiêu bước thì mèo bắt được chuột?
Bài 48: Hiện nay tuổi bố gấp 7 lần tuổi con. Sau 10 năm nữa tuổi bố gấp 3 lần tuổi con. Tính tuổi mỗi người hiện nay.
Bài 49: Một chiều mùa hè hai cha con dạo chơi trên bãi biển. Trong cuộc dạo chơi đó có 997 lần bước chân hai cha con ngang hàng nhau. Hỏi quãng đường hai cha con đã đi dài bao nhiêu mét? (Biết trung bình một bước của con là 4dm, của cha là 5dm)
Bài 50: Bố hơn con 30 tuổi, biết 1/2 tuổi con bằng 1/8 tuổi bố và bằng 1/14 tuổi ông. Tính tuổi mỗi người hiện nay.
Bài 51: Trước đây 4 năm tuổi mẹ gấp 6 lần tuổi con, sau 10 năm nữa thì tỉ số tuổi giữa hai mẹ con là 8/3. Tính tuổi mỗi người hiện nay.
Bài 52: Hiện nay tuổi anh gấp 3 lần tuổi em. Sau 14 năm nữa tỉ số tuổi giữa hai anh em là 5/4. Tính tuổi mỗi người hiện nay.
Bài 53: Tết trồng cây, ba bạn Hạ, Thu, Đông cùng đi trồng cây. Số cây của bạn Đông trồng được ít hơn số cây của bạn Hạ và bạn Thu là 8 cây, số cây của bạn Hạ trồng được bằng 3/5 số cây của bạn Thu. Biết số cây của ba bạn, Hạ, Thu, Đông trồng được là 40 cây. Tính số cây của mỗi bạn đã trồng.
Bài 54: Tháng 9, số học sinh trường tiểu học Kim Đồng được điểm 10 bằng 1/6 số học sinh còn lại của trường. Tháng 10 số học sinh đạt điểm 10 bằng 1/3 số học sinh còn lại của trường. Biết rằng tháng 10 số học sinh đạt điểm 10 nhiều hơn số học sinh tháng 9 đạt điểm 10 là 60 bạn. Hỏi toàn trường có bao hiêu học sinh?
Bài 55: Có hai tấm bia hình vuông, Tấm bìa nhỏ có số đo cạnh bằng nửa số đo cạnh của tấm bia hình vuông lớn. Người ta cắt tấm bia có số đo cạnh lớn hơn thành các hình vuông nhỏ. Rồi người ta ghép tất cả các hình lại với nhau thành một hình vuông, thì hình vuông mới có diện tích là 180 cm2. Tính số đo cạnh của mỗi hình ban đầu.
Bài 56: Cho phân số có tổng của tử số và mẫu số là 3345. Biết 2 lần mẫu số bằng 3 lần tử số. Tìm phân số đó?
Bài 57: Một cửa hàng đã bán được 49kg gạo, trong đó số gạo nếp bằng 2/5 số gạo tẻ. Hỏi cửa hàng đó đã bắn bao nhiêu ki-lô-gam gạo?
Bài 58: Tỉ của hai số là 3/4. Tổng của hai số đó là 658. Tìm hai số đó
Bài 59: Chu vi hình chữ nhật là 630 cm, chiều dài gấp rưỡi chiều rộng. Tìm chiều dài, chiều rộng của hình đó.
Bài 60: Buổi sáng và buồi chiều cửa hàng bán được 24 xe đạp. Số xe bán buổi sáng gấp đôi số xe bán buổi chiều. Hỏi buổi mỗi cửa hàng bán được bao nhiêu xe đạp?
Bài 61: Hai túi gạo cân nặng 54kg. Túi thứ nhất cân nặng bằng 4/5 túi thứ hai. Hỏi mỗi túi cân nặng bao nhiêu ki-lô-gam?
Bài 62: Hình vuông có cạnh 3m. Hình chữ nhật có chiều rộng 3m, chiều dài 5m. Tìm tỉ số của diện tích hình vuông và diện tích hình chữ nhật.
Bài 63: Tổng của hai số là 40. Tỉ của hai số là 3/5. Tìm hai số đó
Bài 64: Có tất cả 35 con gà. Trong đó số gà trống bằng 2/3 số gà mái. Hỏi số gà trống và số gà mái là bao nhiêu?
Bài 65: Tổng hai số là 888. Tỉ hai số đó là 5/3. Tìm hai số đó
Bài 66: Hai kho gạo chứa 121 tấn gạo, trong đó số gạo ở kho thứ nhất bằng 3/8 số gạo ở kho thứ hai. Hỏi mỗi kho gạo chứa bao nhiêu tấn gạo?
Bài 67: Lớp 4A có 30 học sinh. Lớp 4B có 35 học sinh. Nhà trường phát cho cả hai lớp 260 cuốn vở. Hỏi mỗi lớp được bao nhiêu cuốn vở? (Mỗi học sinh được số vở như nhau)
Bài 68: Cả đàn trâu, bò có 24 con. Số trâu nhiều gấp 3 lần số bò. Tính số trâu, số bò.
Bài 69: Có tất cả 18kg gạo. Trong đó số gạo tẻ bằng một nửa số gạo nếp. Hỏi số gạo mỗi loại?
Bài 70: Thời gian từ đầu tháng đến ngày sinh của mẹ gấp ba lần khoảng thời gian từ sau ngày sinh của mẹ đến cuối tháng. Hỏi mẹ sinh ngày nào, tháng nào?
Bài 71: Chu vi hình bình hành ABCD bằng 20cm. Biết rằng cạnh AB dài gấp rưỡi cạnh BC. Hãy tính độ dài các cạnh của hình bình hành.
Bài 72: Thời gian từ đầu ngày đến bây giờ bằng một nửa thời gian bây giờ đến cuối ngày. Hỏi bây giờ là mấy giờ?
Bài 73: Tổng của hai số là 36. Tỉ số của hai số đó là 5/4 Tìm số lớn.
Bài 74: Một lớp có 35 học sinh, trong đó số học sinh nữ bằng 3/4 số học sinh nam. Tính số học sinh nữ của lớp đó.
Bài 75: Chu vi một mảnh vườn hình chữ nhật là 144m, chiều rộng bằng 2/7 chiều dài. Tính chiều rộng mảnh đất đó.
Bài 76: Tổng của hai số là 135. Nếu số lớn thêm 5 đơn vị và giữ nguyên số bé thì số bé bằng 2/3 số lớn. Tìm số lớn ban đầu.
Bài 77: Tổng của hai số là 84. Nếu số bé giảm 7 đơn vị và giữ nguyên số lớn thì được số bé mới bằng 3/4 số lớn. Tìm số bé ban đầu.
Bài 78: Tổng của hai số là số lớn nhất có ba chữ số. Tỉ của hai số là 5/4. Tìm số lớn, số bé.
Bài 79: Hai thùng đựng tất cả 112 lít nước mắm. Nếu đổ từ thùng thứ nhất sang thùng thứ hai 7 lít thì số mắm ở thùng thứ hai bằng 5/3 số mắm ở thùng thứ nhất. Hỏi lúc đầu thùng thứ nhất có bao nhiêu lít nước mắm.
Bài 80: Bác An và bác Bình làm được tất cả 108 sản phầm. Trong đó bác An làm việc trong 5 giờ, bác Bình làm việc trong 7 giờ và mức làm việc của mỗi người như nhau. Hỏi mỗi bác làm được bao nhiêu sản phẩm?
Bài 81: Hiện nay tổng tuổi của 2 mẹ con là 35 tuổi. Tuổi con bằng 2/5 tuổi mẹ. Tính tuổi con cách đây 2 năm.
Bài 82: Hiện nay tổng tuổi của 2 bố con là 50 tuổi. Tuổi bố gấp 4 lần tuổi con. Tính tuổi bố sau 5 năm.
Bài 83: Hiện nay tổng tuổi của 2 mẹ con là 36 tuổi. Sau 3 năm nữa tuổi con bằng 1/5 tuổi mẹ. Tính tuổi mẹ hiện nay.
Bài 84: Hiện nay tổng tuổi của hai chị em là 16 tuổi. Trước đây 2 năm tuổi chị gấp 3 lần tuổi em. Tính tuổi em trước đây 2 năm.
Bài 85: Chu vi của cái chiếu hoa hình chữ nhật là 7m 2dm. Tính diện tích của cái chiều đó. (Biết chiều rộng bằng 4/5 chiều dài)
Bài 86: Trung bình cộng của hai số là 35. Số thứ nhất bằng 2/3 số thứ hai. Tìm hai số đó
Bài 87: Cho một số tự nhiên có hàng đơn vị là 9. Nếu xóa đi chữ số 9 đó thì được số mới mà tổng số mới và số ban đầu là 34 362. Tìm số tự nhiên đã cho.
Bài 88: Trong phong trào kế hoạch nhỏ, lớp 4A và lớp 4B góp được 50kg giấy vụn. Tìm số giấy vụn của mỗi lớp, biết rằng 4/7 số giấy vụn của lớp 4A bằng 8/11 số giấy vụn của lớp 4B.
Bài 89: Tìm số tự nhiên, biết rằng nếu viết thêm chữ số 6 vào bên phải số đó thì ta được số mới mà tổng số mới và số phải tìm là 13 591.
Bài 90: Hình chữ nhật có chu vi 64cm. Nếu giảm chiều rộng 2cm, thêm chiều dài 2cm thì được hình chữ nhật mới có chiều dài gấp 3 lần chiều rộng. Tính chiều dài và chiều rộng hình chữ nhật ban đầu.
Bài 91: Một chiếc đồng hồ cứ 30 phút chạy nhanh 2 phú. Lúc 6 giờ sáng người ta lấy lại giờ nhưng không chỉnh lại đồng hồ nên nó vẫn chạy nhanh. Hỏi khi đồng hồ chỉ 16giờ 40phút thì khi đó là mấy giờ đúng?
Bài 92: Chu vi của một hình chữ nhật là 84 m. Chiều rộng bằng 3/4 chiều dài. Tìm diện tích của hình chữ nhật đó.
Bài 93: Một người có 1 tạ rưỡi gạo gồm gạo nếp và gạo tẻ. Sau khi bán 15kg gạo nếp và 35kg gạo tẻ thì còn lại số gạo nếp bằng 2/3 số gạo tẻ. Hỏi lúc đầu người đó có bao nhiêu ki-lô-gam gạo mỗi loại?
Bài 94: Trung bình cộng của 3 số là 75. Nếu thêm 1 chữ số 0 vào bên phải số thứ hai thì được số thứ nhất. Tính số thứ 2 biết rằng số đó kém số thứ ba 4 lần.
Bài 95: Cho phân số 9/11. Tìm một số tự nhiên để khi cộng số đó vào cả tử số và mẫu số thì được phân số có giá trị là 5/6.
-
Tìm hai số khi biết hiệu và tỉ số của hai số
Tìm hai số khi biết hiệu và tỉ số của hai số
Cùng với bài toán Tìm hai số khi biết tổng và tỉ số của hai số thì bài toán Tìm hai số khi biết hiệu và tỉ số của hai số là những dạng toán quan trọng của chương trình toán tiểu học.
1. Phương pháp giải dạng toán tìm hai số khi biết hiệu và tỉ
Để giải bài toán tìm hai số khi biết hiệu và tỉ số của hai số, chúng ta thực hiện các bước sau:
- Vẽ sơ đồ đoạn thẳng biểu diễn cho hai số
- Tìm hiệu số phần bằng nhau
- Tìm số bé bằng công thức
- Tìm số lớn bằng công thức
Có thể tóm tắt các bước giải bài toán tìm 2 số khi biết hiệu và tỉ số của chúng như sau:
Tuy nhiên, trong nhiều bài toán, đề bài không cho dữ kiện đầy đủ về hiệu và tỉ số mà có thể cho dữ kiện như sau:
- Chỉ cho biết tỉ số, không có biết hiệu số
- Cho biết hiệu số, không cho biết tỉ số
- Cho dữ kiện thêm, bớt số, tạo hiệu (tỉ) mới tìm số ban đầu
Với những bài toán này, chúng ta cần tiến hành tìm hiệu, tìm tỉ để chuyển về bài toán cơ bản ở trên.
Xem thêm TOÁN 4: DẠNG TOÁN TÌM PHÂN SỐ CỦA MỘT SỐ
2. Các dạng toán tìm hai số biết hiệu và tỉ số của hai số
2.1. Dạng toán hiệu – tỉ cơ bản:
Ví dụ 1. Hiệu của hai số là 24. Tỉ số của hai số đó
-
17 KĨ THUẬT DẠY HỌC TÍCH CỰC DÀNH CHO GIÁO VIÊN
17 KĨ THUẬT DẠY HỌC TÍCH CỰC DÀNH CHO GIÁO VIÊN
Có rất nhiều kĩ thuật dạy học tích cực mà những nhà nghiên cứu giáo dục đã đưa ra nhằm dạy học sinh không chỉ tiếp thu kiến thức tốt mà còn phát triển năng lực. Điều quan trọng là giáo viên linh hoạt tuỳ theo bài học để chọn kĩ thuật phù hợp.
Kĩ thuật dạy học là những biện pháp, cách thức hành động của của giáo viên và học sinh trong các tình huống hành động nhỏ nhằm thực hiện và điều khiển quá trình dạy học. Các kĩ thuật dạy học là những đơn vị nhỏ nhất của phương pháp dạy học.
Xem thêm: Mẫu giáo án phát triển năng lực (kế hoạch dạy học PTNL)
1. Kĩ thuật dạy học tích cực “Các mảnh ghép”
1.1. Thế nào là kĩ thuật “Các mảnh ghép”?
Là hình thức học tập hợp tác kết hợp giữa cá nhân, nhóm và liên kết giữa các nhóm nhằm:
- Giải quyết một nhiệm vụ phức hợp (có nhiều chủ đề)
- Kích thích sự tham gia tích cực của HS:
- Nâng cao vai trò của cá nhân trong quá trình hợp tác (Không chỉ hoàn thành nhiệm vụ ở Vòng 1 mà còn phải truyền đạt lại kết quả vòng 1 và hoàn thành nhiệm vụ ở Vòng 2).
1.2. Cách tiến hành kĩ thuật “Các mảnh ghép”
Vòng 1: Nhóm chuyên gia:
- Hoạt động theo nhóm 3 đến 8 người [số nhóm được chia = số chủ đềx n (n = 1,2,…)]
- Mỗi nhóm được giao một nhiệm vụ [Ví dụ: nhóm 1: nhiệm vụ A; nhóm 2: nhiệm vụ B, nhóm 3: nhiệm vụ C, … (có thể có nhóm cùng nhiệm vụ)]
- Mỗi cá nhân làm việc độc lập trong khoảng vài phút, suy nghĩ về câu hỏi, chủ đề và ghi lại những ý kiến của mình
- Khi thảo luận nhóm phải đảm bảo mỗi thành viên trong từng nhóm đều trả lời được tất cả các câu hỏi trong nhiệm vụ được giao và trở thành “chuyên gia” của lĩnh vực đã tìm hiểu và có khả năng trình bày lại câu trả lời của nhóm ở vòng 2.
Vòng 2: Nhóm các mảnh ghép
- Hình thành nhóm 3 đến 6 người mới (1 – 2 người từ nhóm 1, 1 – 2 người từ nhóm 2, 1 – 2 người từ nhóm 3…)
- Các câu trả lời và thông tin của vòng 1 được các thành viên trong nhóm mới chia sẻ đầy đủ với nhau
- Khi mọi thành viên trong nhóm mới đều hiểu được tất cả nội dung ở vòng 1 thì nhiệm vụ mới sẽ được giao cho các nhóm để giải quyết
- Các nhóm mới thực hiện nhiệm vụ, trình bày và chia sẻ kết quả
Một vài ý kiến cá nhân với kĩ thuật “Các mảnh ghép”:
- Kĩ thuật này áp dụng cho hoạt động nhóm với nhiều chủ đề nhỏ trong tiết học, học sinh được chia nhóm ở vòng 1 (chuyên gia) cùng nghiên cứu một chủ đề.
- Phiếu học tập mỗi chủ đề nên sử dụng trên giấy cùng màu có đánh số 1,2,…,n (nếu không có giấy màu có thể đánh thêm kí tự A, B, C,… Ví dụ A1, A2,… An, B1, B2,…, Bn, C1, C2,…, Cn).
- Sau khi các nhóm ở vòng 1 hoàn tất công việc giáo viên hình thành nhóm mới (mảnh ghép) theo số đã đánh, có thể có nhiều số trong 1 nhóm mới. Bước này phải tiến hành một cách cẩn thận tránh làm cho học sinh ghép nhầm nhóm.
- Trong điều kiện phòng học hiện nay việc ghép nhóm vòng 2 sẽ gây mất trật tự.
Ví dụ kĩ thuật dạy học mảnh ghép: Bài học tiếng Việt
– Vòng 1:
- Chủ đề A: Thế nào là câu đơn? Nêu ví dụ minh họa và phân tích. (màu đỏ)
- Chủ đề B: Thế nào là câu ghép? Nêu ví dụ minh họa và phân tích. (màu xanh)
- Chủ đề C: Thế nào là câu phức? Nêu ví dụ minh họa và phân tích. (màu vàng)
Lớp có 45 học sinh, có 12 bàn học. Giáo viên có thể chia thành 6 nhóm: mỗi nhóm gồm học sinh 2 bàn ghép lại (mỗi nhóm có 7 hoặc 8 học sinh). Giao nhiệm vụ: nhóm 1,2 nhận chủ đề A, nhóm 3,4 nhận chủ đề B, nhóm 5,6 nhận chủ đề C. Phát phiếu học tập cho học sinh. Trên phiếu học tập theo màu có đánh số từ 1 đến 15. Thông báo cho học sinh thời gian làm việc cá nhân và theo nhóm
– Vòng 2:
- Giáo viên thông báo chia thành 12 nhóm mới: mỗi nhóm 1 bàn (mỗi nhóm có từ 3 đến 6 học sinh): nhóm 1 gồm các học sinh có phiếu học tập mang số 1,2; nhóm 2 gồm các học sinh có phiếu học tập mang số 3,4; nhóm 3 gồm các học sinh có phiếu học tập mang số 5; nhóm 4 gồm các học sinh có phiếu học tập mang số 6; … nhóm 12 gồm các học sinh có phiếu học tập mang số 14,15.
- Giáo viên thông báo thời gian làm việc nhóm mới Các chuyên gia sẽ trình bày ý kiến của của nhóm mình ở vòng 1.
- Giao nhiệm vụ mới: Câu đơn, câu phức và câu ghép khác nhau ở điểm nào? Phân tích ví dụ minh hoạ.
2. Kĩ thuật “Khăn trải bàn”
2.1. Thế nào là kĩ thuật “Khăn trải bàn”?
Là hình thức tổ chức hoạt động mang tính hợp tác kết hợp giữa hoạt động cá nhân và hoạt động nhóm nhằm:
- Kích thích, thúc đẩy sự tham gia tích cực
- Tăng cường tính độc lập, trách nhiệm của cá nhân HS
- Phát triển mô hình có sự tương tác giữa HS với HS
2.2. Cách tiến hành kĩ thuật “Khăn trải bàn”
- Hoạt động theo nhóm (4 người / nhóm) (có thể nhiều người hơn)
- Mỗi người ngồi vào vị trí như hình vẽ minh họa
- Tập trung vào câu hỏi (hoặc chủ đề,…)
- Viết vào ô mang số của bạn câu trả lời hoặc ý kiến của bạn (về chủ đề…). Mỗi cá nhân làm việc độc lập trong khoảng vài phút
- Kết thúc thời gian làm việc cá nhân, các thành viên chia sẻ, thảo luận và thống nhất các câu trả lời
- Viết những ý kiến chung của cả nhóm vào ô giữa tấm khăn trải bàn (giấy A0)
2.3. Một vài ý kiến cá nhân với kĩ thuật “Khăn trải bàn”
- Kĩ thuật này giúp cho hoạt động nhóm có hiệu quả hơn, mỗi học sinh đều phải đưa ra ý kiến của mình về chủ đề đang thảo luận, không ỷ lại vào các bạn học khá, giỏi.
- Kĩ thuật này áp dụng cho hoạt động nhóm với một chủ đề nhỏ trong tiết học, toàn thể học sinh cùng nghiên cứu một chủ đề.
- Sau khi các nhóm hoàn tất công việc giáo viên có thể gắn các mẫu giấy “khăn trải bàn” lên bảng để cả lớp cùng nhận xét. Có thể dùng giấy nhỏ hơn, dùng máy chiếu phóng lớn
- Có thể thay số bằng tên của học sinh để sau đó giáo viên có thể đánh giá được khả năng nhận thức của từng học sinh về chủ đề được nêu.
3. Kĩ thuật “Động não”
3.1. Thế nào là kĩ thuật “Động não”?
Động não (công não) là một kỹ thuật nhằm huy động những tư tưởng mới mẻ, độc đáo về một chủ đề của các thành viên trong thảo luận. Các thành viên được cổ vũ tham gia một cách tích cực, không hạn chế các ý tưởng (nhằm tạo ra “cơn lốc” các ý tưởng). Kỹ thuật động não do Alex Osborn (Mỹ) phát triển, dựa trên một kỹ thuật truyền thống từ Ấn độ.
Quy tắc của động não
- Không đánh giá và phê phán trong quá trình thu thập ý tưởng của các thành viên;
- Liên hệ với những ý tưởng đã được trình bày;
- Khuyến khích số lượng các ý tưởng;
- Cho phép sự tưởng tượng và liên tưởng.
3.2. Các bước tiến hành
- Người điều phối dẫn nhập vào chủ đề và xác định rõ một vấn đề;
- Các thành viên đưa ra những ý kiến của mình: trong khi thu thập ý kiến, không đánh giá, nhận xét. Mục đích là huy động nhiều ý kiến tiếp nối nhau;
- Kết thúc việc đưa ra ý kiến;
- Đánh giá: Lựa chọn sơ bộ các suy nghĩ, chẳng hạn theo khả năng ứng dụng
- Có thể ứng dụng trực tiếp;
- Có thể ứng dụng nhưng cần nghiên cứu thêm;
- Không có khả năng ứng dụng.
- Đánh giá những ý kiến đó lựa chọn
- Rút ra kết luận hành động.
3.3. Ứng dụng khi nào?
- Dùng trong giai đoạn nhập đề vào một chủ đề;
- Tìm các phương án giải quyết vấn đề;
- Thu thập các khả năng lựa chọn và ý nghĩ khác nhau.
3.4. Ưu điểm và nhược điểm của kĩ thuật dạy học động não
Ưu điểm:
- Dễ thực hiện;
- Không tốn kém;
- Sử dụng được hiệu ứng cộng hưởng, huy động tối đa trí tuệ của tập thể;
- Huy động được nhiều ý kiến;
- Tạo cơ hội cho tất cả thành viên tham gia.
Nhược điểm
- Có thể đi lạc đề, tản mạn;
- Có thể mất thời gian nhiều trong việc chọn các ý kiến thích hợp;
- Có thể có một số HS “quá tích cực”, số khác thụ động. Kỹ thuật động não được áp dụng phổ biến và nguời ta xây dựng nhiều kỹ thuật khác dựa trên kỹ thuật này, có thể coi là các dạng khác nhau của kỹ thuật động não.
3.5. Lưu ý khi thực hiện kĩ thuật dạy học “động não”
- Kĩ thuật trên có thể biến đổi để trở thành kĩ thuật “Động não viết”: những ý tưởng không được trình bày miệng mà được từng thành viên tham gia trình bày ý kiến bằng cách viết trên giấy về một chủ đề.Trong động não viết, các đối tác sẽ giao tiếp với nhau bằng chữ viết. Các em đặt trước mình một vài tờ giấy chung, trên đó ghi chủ đề ở dạng dòng tiêu đề hoặc ở giữa tờ giấy. Các em thay nhau ghi ra giấy những gì mình nghĩ về chủ đề đó, trong im lặng tuyệt đối. Trong khi đó, các em xem các dòng ghi của nhau và cùng lập ra một bài viết chung. Bằng cách đó có thể hình thành những câu chuyện trọn vẹn hoặc chỉ là bản thu thập các từ khóa.
- Các HS luyện tập có thể thực hiện các cuộc nói chuyện bằng giấy bút cả khi làm bài trong nhóm. Sản phẩm có thể có dạng một bản đồ trí tuệ.
- Ưu điểm của phương pháp này là có thể huy động sự tham gia của tất cả HS trong nhóm; tạo sự yên tĩnh trong lớp học; động não viết tạo ra mức độ tập trung cao. Vì những HS tham gia sẽ trình bày những suy nghĩ của mình bằng chữ viết nên có sự chú ý cao hơn so với các cuộc nói chuyện bình thường bằng miệng; các HS đối tác cùng hoạt động với nhau mà không sử dụng lời nói. Bằng cách đó, thảo luận viết tạo ra một dạng tương tác xã hội đặc biệt; những ý kiến đóng góp trong cuộc nói chuyện bằng giấy bút thường được suy nghĩ đặc biệt kỹ.
- Tuy nhiên, nhược điểm là có thể HS sa vào những ý kiến tản mạn, xa đề; do được tham khảo ý kiến của nhau, có thể một số HS ít có sự độc lập.
4. Kĩ thuật “Ổ bi”
Thế nào là kĩ thuật “Ổ bi”?
Kĩ thuật “Ổ bi” là một kỹ thuật dùng trong thảo luận nhóm, trong đó HS chia thành hai nhóm ngồi theo hai vòng tròn đồng tâm như hai vòng của một ổ bi và đối diện nhau để tạo điều kiện cho mỗi HS có thể nói chuyện với lần lượt các HS ở nhóm khác.
Cách thực hiện
- Khi thảo luận, mỗi HS ở vòng trong sẽ trao đổi với HS đối diện ở vòng ngoài, đây là dạng đặc biệt của phương pháp luyện tập đối tác;
- Sau một ít phút thì HS vòng ngoài ngồi yên, HS vòng trong chuyển chỗ theo chiều kim đồng hồ, tương tự như vòng bi quay, để luôn hình thành các nhóm đối tác mới.
5. Kĩ thuật “Bể cá”
Thế nào là kĩ thuật “Bể cá”?
Kĩ thuật “Bể cá” là một kĩ thuật dùng cho thảo luận nhóm, trong đó một nhóm HS ngồi giữa lớp và thảo luận với nhau, còn những HS khác trong lớp ngồi xung quanh ở vòng ngoài theo dõi cuộc thảo luận đó và sau khi kết thúc cuộc thảo luận thì đưa ra những nhận xét về cách ứng xử của những HS thảo luận.
Trong nhóm thảo luận có thể có một vị trí không có người ngồi. HS tham gia nhóm quan sát có thể ngồi vào chỗ đó và đóng góp ý kiến vào cuộc thảo luận, ví dụ đưa ra một câu hỏi đối với nhóm thảo luận hoặc phát biểu ý kiến khi cuộc thảo luận bị chững lại trong nhóm. Cách luyện tập này được gọi là phương pháp thảo luận “bể cá”, vì những người ngồi vòng ngoài có thể quan sát những người thảo luận, tương tự như xem những con cá trong một bể cá cảnh. Trong quá trình thảo luận, những người quan sát và những người thảo luận sẽ thay đổi vai trò với nhau.
Bảng câu hỏi dành cho những người quan sát:
- Người nói có nhìn vào những người đang nói với mình không?
- Họ có nói một cách dễ hiểu không?
- Họ có để những người khác nói hay không?
- Họ có đưa ra được những luận điểm đáng thuyết phục hay không?
- Họ có đề cập đến luận điểm của người nói trước mình không?
- Họ có lệch hướng khỏi đề tài hay không?
- Họ có tôn trọng những quan điểm khác hay không?
6. Kĩ thuật “Tia chớp”
Thế nào là kĩ thuật “Tia chớp”?
Kỹ thuật tia chớp là một kỹ thuật huy động sự tham gia của các thành viên đối với một câu hỏi nào đó, hoặc nhằm thu thông tin phản hồi nhằm cải thiện tình trạng giao tiếp và không khí học tập trong lớp học, thông qua việc các thành viên lần lượt nêu ngắn gọn và nhanh chóng (nhanh như chớp!) ý kiến của mình về câu hỏi hoặc tình trạng vấn đề.
Quy tắc thực hiện
- Có thể áp dụng bất cứ thời điểm nào khi các thành viên thấy cần thiết và đề nghị;
- Lần lượt từng người nói suy nghĩ của mình về một câu hỏi đã thoả thuận, ví dụ: Hiện tại tôi có hứng thú với chủ đề thảo luận không?
- Mỗi người chỉ nói ngắn gọn 1-2 câu ý kiến của mình;
- Chỉ thảo luận khi tất cả đã nói xong ý kiến.
7. Kĩ thuật “XYZ”
Thế nào là kĩ thuật “XYZ”?
Kĩ thuật “XYZ” là một kỹ thuật nhằm phát huy tính tích cực trong thảo luận nhóm. X là số người trong nhóm, Y là số ý kiến mỗi người cần đưa ra, Z là phút dành cho mỗi người.
Ví dụ kỹ thuật 635 thực hiện như sau:
- Mỗi nhóm 6 người, mỗi người viết 3 ý kiến trên một tờ giấy trong vòng 5 phút về cách giải quyết 1 vấn đề và tiếp tục chuyển cho người bên cạnh;
- Tiếp tục như vậy cho đến khi tất cả mọi người đều viết ý kiến của mình, có thể lặp lại vòng khác;
- Con số X-Y-Z có thể thay đổi;
- Sau khi thu thập ý kiến thì tiến hành thảo luận, đánh giá các ý kiến.
8. Kĩ thuật “Lược đồ tư duy” Thế nào là kĩ thuật “Lược đồ tư duy”?
Lược đồ tư duy (còn được gọi là bản đồ khái niệm) là một sơ đồ nhằm trình bày một cách rõ ràng những ý tưởng mang tính kế hoạch hay kết quả làm việc của cá nhân hay nhóm về một chủ đề. Lược đồ tư duy có thể được viết trên giấy, trên bản trong, trên bảng hay thực hiện trên máy tính.
Cách làm
- Viết tên chủ đề ở trung tâm, hay vẽ một hình ảnh phản ánh chủ đề.
- Từ chủ đề trung tâm, vẽ các nhánh chính. Trên mỗi nhánh chính viết một khái niệm, phản ánh một nội dung lớn của chủ đề, viết bằng CHỮ IN HOA. Nhánh và chữ viết trên đó được vẽ và viết cùng một màu. Nhánh chính đó được nối với chủ đề trung tâm. Chỉ sử dụng các thuật ngữ quan trọng để viết trên các nhánh.
- Từ mỗi nhánh chính vẽ tiếp các nhánh phụ để viết tiếp những nội dung thuộc nhánh chính đó. Các chữ trên nhánh phụ được viết bằng chữ in thường.
- Tiếp tục như vậy ở các tầng phụ tiếp theo.
Ứng dụng
- Lược đồ tư duy có thể ứng dụng trong nhiều tình huống khác nhau như:
- Tóm tắt nội dung, ôn tập một chủ đề;
- Trình bày tổng quan một chủ đề;
- Chuẩn bị ý tưởng cho một báo cáo hay buổi nói chuyện, bài giảng;
- Thu thập, sắp xếp các ý tưởng;
- Ghi chép khi nghe bài giảng.
Ưu điểm
- Các hướng tư duy được để mở ngay từ đầu;
- Các mối quan hệ của các nội dung trong chủ đề trở nên rõ ràng;
- Nội dung luôn có thể bổ sung, phát triển, sắp xếp lại;
- Học sinh được luyện tập phát triển, sắp xếp các ý tưởng.
9. Kĩ thuật “Chia sẻ nhóm đôi”
Thế nào là kĩ thuật “Chia sẻ nhóm đôi”?
Chia sẻ nhóm đôi (Think, Pair, Share) là một kỹ thuật do giáo sư Frank Lyman đại học Maryland giới thiệu năm 1981. Kỹ thuật này giới thiệu hoạt động làm việc nhóm đôi, phát triển năng lực tư duy của từng cá nhân trong giải quyết vấn đề.
Dụng cụ: Hoạt động này phát triển kỹ năng nghe và nói nên không cần thiết sử dụng các dụng cụ hỗ trợ.
Cách thực hiện:
- Giáo viên giới thiệu vấn đề, đặt câu hỏi mở, dành thời gian để học sinh suy nghĩ.
- Sau đó học sinh thành lập nhóm đôi và chia sẻ ý tưởng, thảo luận, phân loại.
- Nhóm đôi này lại chia sẻ tiếp với nhóm đôi khác hoặc với cả lớp.
Lưu ý
- Điều quan trọng là người học chia sẻ được cả ý tưởng mà mình đã nhận được, thay vì chỉ chia sẻ ý kiến cá nhân.
- Giáo viên cần làm mẫu hoặc giải thích.
Ưu điểm: Thời gian suy nghĩ cho phép học sinh phát triển câu trả lời, có thời gian suy nghĩ tốt, học sinh sẽ phát triển được những câu trả lời tốt, biết lắng nghe, tóm tắt ý của bạn cùng nhóm.
Hạn chế: Học sinh dễ dàng trao đổi những nội dung không liên quan đến bài học do giáo viên không thể bao quát hết hoạt động của cả lớp.
10. Kĩ thuật Kipling
Rudyard Kipling (1865 – 1936) là nhà thơ, nhà văn Anh nổi tiếng, tác giả quyển sách “Cậu bé rừng xanh” và rất nhiều bài thơ hay. Ông từng viết 4 câu thơ:
“I have six honest serving men
They taught me all I knew
I call them What and Where and When
And How and Why and Who”
Rudyard Kipling (1865 – 1936)Kĩ thuật này thường được dùng cho các trường hợp khi cần có thêm ý tưởng mới, hoặc xem xét nhiều khía cạnh của vấn đề, chọn lựa ý tưởng để phát triển.
Dụng cụ: Giấy bút cho người tham gia.
Thực hiện: Các câu hỏi được đưa ra theo thứ tự ngẫu nhiên hoặc theo một trật tự định ngầm trước, với các từ khóa: Cái gì, Ở đâu, Khi nào, Thế nào, Tại sao, Ai.
Ví dụ:
- Vấn đề là gì?
- Vấn đề xảy ra ở đâu?
- Vấn đề xảy ra khi nào?
- Tại sao vấn đề lại xảy ra?
- Làm thế nào để giải quyết vấn đề?
- Ai sẽ tham gia giải quyết vấn đề?
- Khi nào thì vấn đề giải quyết xong?
Lưu ý
- Các câu hỏi cần ngắn gọn, đi thẳng vào chủ đề.
- Các câu hỏi cần bám sát vào hệ thống từ khóa 5W1H (What, where, when, who, why, how).
Ưu điểm
- Nhanh chóng, không mất thời gian, mang tính logic cao.
- Có thể áp dụng cho nhiều tình huống khác nhau.
- Có thể áp dụng cho cá nhân.
Hạn chế
- Ít có sự phối hợp của các thành viên.
- Dễ dẫn đến tình trạng “9 người 10 ý”.
- Dễ tạo cảm giác “Bị điều tra”.
11. Kĩ thuật KWL
Thế nào là kĩ thuật KWL?
KWL do Donna Ogle giới thiệu năm 1986, vốn là một hình thức tổ chức dạy học hoạt động đọc hiểu. Học sinh bắt đầu bằng việc động não tất cả những gì các em đã biết về chủ đề bài đọc. Thông tin này sẽ được ghi nhận vào cột K của biểu đồ. Sau đó học sinh nêu lên danh sách các câu hỏi về những điều các em muốn biết thêm trong chủ đề này. Những câu hỏi đó sẽ được ghi nhận vào cột W của biểu đồ. Trong quá trình đọc hoặc sau khi đọc xong, các em sẽ tự trả lời cho các câu hỏi ở cột W. Những thông tin này sẽ được ghi nhận vào cột L. (Trích từ Ogle, D.M. (1986). KW-L: A teaching model that develops active reading of expository text. Reading Teacher, 39, 564-570). Donna Ogle.
Mục đích sử dụng biểu đồ KWL
Biểu đồ KWL phục vụ cho các mục đích sau:
• Tìm hiểu kiến thức có sẵn của học sinh về bài đọc
• Đặt ra mục tiêu cho hoạt động đọc
• Giúp học sinh tự giám sát quá trình đọc hiểu của các em
• Cho phép học sinh đánh giá quá trình đọc hiểu của các em.
• Tạo cơ hội cho học sinh diễn tả ý tưởng của các em vượt ra ngoài khuôn khổ bài đọc.Sử dụng biểu đồ KWL như thế nào?
- Chọn bài đọc. Phương pháp này đặc biệt có hiệu quả với các bài đọc mang ý nghĩa gợi mở, tìm hiểu, giải thích
- Tạo bảng KWL. Giáo viên vẽ một bảng lên bảng, ngoài ra, mỗi học sinh cũng có một mẫu bảng của các em. Có thể sử dụng mẫu sau.
- Dạng bảng KWL: Đề nghị học sinh động não nhanh và nêu ra các từ, cụm từ có liên quan đến chủ đề. Cả giáo viên và học sinh cùng ghi nhận hoạt động này vào cột K. Hoạt động này kết thúc khi học sinh đã nêu ra tất cả các ý tưởng. Tổ chức cho học sinh thảo luận về những gì các em đã ghi nhận.
- Một số lưu ý tại cột K:
- Chuẩn bị những câu hỏi để giúp học sinh động não. Đôi khi để khởi động, học sinh cần nhiều hơn là chỉ đơn giản nói với các em: “Hãy nói những gì các em đã biết về…”
- Khuyến khích học sinh giải thích. Điều này rất quan trọng vì đôi khi những điều các em nêu ra có thể là mơ hồ hoặc không bình thường.
- Hỏi học sinh xem các em muốn biết thêm điều gì về chủ đề. Cả giáo viên và học sinh ghi nhận câu hỏi vào cột W. Hoạt động này kết thúc khi học sinh đã nêu ra tất cả các ý tưởng. Nếu học sinh trả lời bằng một câu phát biểu bình thường, hãy biến nó thành câu hỏi trước khi ghi nhận vào cột W.
- Một số lưu ý tại cột W: Hỏi những câu hỏi tiếp nối và gợi mở. Nếu chỉ hỏi các em: “Các em muốn biết thêm điều gì về chủ đề này?” Đôi khi học sinh trả lời đơn giản “không biết”, vì các em chưa có ý tưởng. Hãy thử sử dụng một số câu hỏi sau: “Em nghĩ mình sẽ biết thêm được điều gì sau khi em đọc chủ đề này?” Chọn một ý tưởng từ cột K và hỏi: “Em có muốn tìm hiểu thêm điều gì có liên quan đến ý tưởng này không?”
- Chuẩn bị sẵn một số câu hỏi của riêng bạn để bổ sung vào cột W. Có thể bạn mong muốn học sinh tập trung vào những ý tưởng nào đó, trong khi các câu hỏi của học sinh lại không mấy liên quan đến ý tưởng chủ đạo của bài đọc. Chú ý là không được thêm quá nhiều câu hỏi của bạn. Thành phần chính trong cột W vẫn là những câu hỏi của học sinh.
- Yêu cầu học sinh đọc và tự điền câu trả lời mà các em tìm được vào cột L. Trong quá trình đọc, học sinh cũng đồng thời tìm ra câu trả lời của các em và ghi nhận vào cột W.
- Học sinh có thể điền vào cột L trong khi đọc hoặc sau khi đã đọc xong.
- Một số lưu ý tại cột L:
- Ngoài việc bổ sung câu trả lời, khuyến khích học sinh ghi vào cột L những điều các em cảm thấy thích. Để phân biệt, có thể đề nghị các em đánh dấu những ý tưởng của các em. Ví dụ các em có thể đánh dấu tích vào những ý tưởng trả lời cho câu hỏi ở cột W, với các ý tưởng các em thích, có thể đánh dấu sao.
- Đề nghị học sinh tìm kiếm từ các tài liệu khác để trả lời cho những câu hỏi ở cột W mà bài đọc không cung cấp câu trả lời. (Không phải tất cả các câu hỏi ở cột W đều được bài đọc trả lời hoàn chỉnh)
- Thảo luận những thông tin được học sinh ghi nhận ở cột L. Khuyến khích học sinh nghiên cứu thêm về những câu hỏi mà các em đã nêu ở cột W nhưng chưa tìm được câu trả lời từ bài đọc.
Phát triển kỹ thuật KWL thành KWLH
Cột H được thêm vào biểu đồ KWL là để khuyến khích học sinh tiếp tục tìm tòi, nghiên cứu. Sau khi học sinh đã hoàn tất nội dung ở cột L, các em có thể muốn tìm hiểu thêm về một thông tin. Các em sẽ nêu biện pháp để tìm thông tin mở rộng. Những biện pháp này sẽ được ghi nhận ở cột H.
Một ví dụ về dùng kỹ thuật KWLH:
Chủ đề bài đọc: Trò chơi – Tên bài đọc: Chú Đất Nung (Tiếng Việt 4 tập Một). GV dùng kỹ thuật này để giao nhiệm vụ cho HS chuản bị bài trước khi học.
K W L H - Những đồ chơi nặn bằng đất: con chó, con cá, cái
nồi, búp bê - Trẻ em ở quê
ngày xưa chơi đồ
chơi nặn bằng đất
có sơn màu xanh,
đỏ, vàng
- Đồ chơi làm bằng đất nặn khi gặp nước có bị hỏng không?
- Làm thế nào để đồ chơi bằng đất chơi được lâu và không giây bẩn?
- Bây giờ người ta còn làm đồ chơi bằng đất nung không? Ở đâu làm những thứ đó?
- Đồ chơi làm bằng đất nặn mà gặp nước thì bị nhão ra và hỏng
- Để đồ chơi bằng đất chơi được lâu, bền thì phải nung nó bằng lửa
- Tham quan làng nghề gốm để biết đồ dùng, đồ chơi bằng đất nặn được nung thế nào.
- Tìm hiểu trên mạng để biết được có những đồ chơi nào làm bằng đất nung? Bây giờ có những người nào dùng thứ đồ chơi
đó? - Xin bố mẹ mua cho một vài đồ chơi bằng đất nung
12. Kỹ thuật đặt câu hỏi
Kỹ thuật này dùng trong hầu hết các môn học.
Việc đặt câu hỏi cần đảm bảo những nguyên tắc sau:
- CH phải liên kết logic với bài học
- Ngôn ngữ trình bày câu hỏi rõ vấn đề hỏi (từ nghi vấn phù hợp )
- Phù hợp với trình độ tư duy của lứa tuổi HS
- Kích thích HS suy nghĩ (hạn chế câu hỏi nhắc lại thuần túy)
- Đặt câu hỏi đúng lúc và đúng chỗ (đúng lúc HS đang suy nghĩ, đúng chỗ có vấn đề trong bài học)
- Mỗi CH chỉ hỏi 1 vấn đề
- Dùng từng CH một, không dùng nhiều CH để hỏi cùng lúc
13. Kỹ thuật chia nhóm
- Kỹ thuật này dùng để dạy HS học tập hợp tác. Nó có thể được dùng trong nhiều đoạn của bài học (chia sẻ những trải nghiệm, khám phá kiến thức / kỹ năng mới, Luyện tập thực hành, Vận dụng)
- Cách chia nhóm:
- Có nhiều cách chia nhóm. Chia theo cách nào là tùy thuộc vào nhiệm vụ
- GV giao cho HS thực hiện. Có những cách chia nhóm sau:
– Theo sở thích
– Theo trình độ
– Hỗn hợp trình độ
– Ngẫu nhiên
Các bước tổ chức hoạt động nhóm:
B1: Làm việc chung cả lớp
– GV chia nhóm
– GV giao nhiệm vụ
– GV hướng dẫn cách làm việc nhóm( rất quan trọng)
B2: HS làm việc theo nhóm:
– HS làm việc cá nhân.
– HS nêu ý kiếm cá nhân
– Nhóm thảo luận chia sẻ, thống nhất
B3: Đại diện nhóm báo cáo.
14. Kỹ thuật Đọc tích cực
Kĩ thuật này nhằm giúp HS tăng cường khả năng tự học và giúp GV tiết kiệm thời gian đối với những bài học / phần đọc có nhiều nội dung nhưng không quá khó đối với HS. Kỹ thuật được áp dụng với những bài học được trình bày thành bài đọc tương đối dài (Ví dụ: Lịch sử, Địa lý, Khoa học)
Cách tiến hành như sau:
- GV nêu câu hỏi/yêu cầu định hướng HS đọc bài/phần đọc.
- HS làm việc cá nhân:
- Đoán trước khi đọc: Để làm việc này, HS cần đọc lướt qua bài đọc/phần đọc để tìm ra những gợi ý từ hình ảnh, tựa đề, từ/cụm từ quan trọng.
- Đọc và đoán nội dung: HS đọc bài/phần đọc và biết liên tưởng tới những gì mình đã biết và đoán nội dung khi đọc những từ hay khái niệm mà các em phải tìm ra.
- Tìm ý chính: HS tìm ra ý chính của bài/phần đọc qua việc tập trung vào các ý quan trọng theo cách hiểu của mình.
- Tóm tắt bài dựa trên ý chính, đề mục.
- HS chia sẻ kết quả đọc của mình theo nhóm 2, hoặc 4 và giải thích cho nhau thắc mắc (nếu có), thống nhất với nhau ý chính của bài/phần đọc đọc.
- HS nêu câu hỏi để GV giải đáp (nếu có).
- Đoán trước khi đọc: Để làm việc này, HS cần đọc lướt qua bài đọc/phần đọc để tìm ra những gợi ý từ hình ảnh, tựa đề, từ/cụm từ quan trọng.
Lưu ý: Một số câu hỏi GV thường dùng để giúp HS tóm tắt ý chính:
- Em có chú ý gì khi đọc nội dung A ?
- Em nghĩ gì về đọc nội dung B ?
- Em so sánh A và B như thế nào?
- A và B giống và khác nhau như thế nào?
15. Kỹ thuật “Viết tích cực”
Kĩ thuật này có thể sử dụng sau tiết học để tóm tắt nội dung đã học, để HS phản hồi cho GV về việc nắm kiến thức của các em và những chỗ các em còn hiểu sai.
Cách thực hiên:
- GV đặt câu hỏi và dành thời gian cho HS tự do viết câu trả lời. GV cũng có thể yêu cầu HS liệt kê ngắn gọn những gì các em biết về chủ đề đang học trong khoảng thời gian nhất định.
- GV yêu cầu một vài HS chia sẻ nội dung mà các em đã viết trước lớp.
16. Kỹ thuật / Phương pháp Đóng vai
Đóng vai là kỹ thuật HS làm thử một một công việc hoặc thực hiện một ứng xử trong tình huống giả định. Kỹ thuật này giúp HS suy nghĩ về một vấn đề bằng cách tập trung vào một sự việc cụ thể mà các em quan sát được hoặc chính mình trải nghiệm. Đóng vai không chỉ bao gồm việc diễn mà quan trọng hơn là cuộc trao đổi sau việc diễn. Kỹ thuật này thường dùng trong những phần học về Kể chuyện, Đạo đức, phần học ứng dụng của các môn học.
Cách thực hiện:
- Bước 1: GV giao nhiệm vụ cho HS: yêu cầu đóng vai cho nhóm, thời gian cho việc chuẩn bị đóng vai
- Bước 2: Các nhóm chuẩn bị đóng vai: phần lời của từng vai cần nhớ, phần diễn của từng vai, phối hợp diễn thử các vai( Gv lắng nghe, quan sát, gợi ý bàng câu hỏi)
- Bước 3: Từng nhóm trình bày đóng vai (diễn)( GV theo dõi, phát hiện cách ứng xử khác)
- Bước 4: Nhận xét / thảo luận về việc đóng vai theo các tiêu chí về lời và hành động diễn có thể hiện đúng nội dung chính của bài và gây cảm xúc tích cực cho người xem không.( Giúp HS thảo luận về ích lợi hoặc tác hại hay hạn chế của từng cách ứng xử. Sau đó tổng hợp ý kiến)
- Bước 5: Kết luận được rút ra từ nhiệm vụ đóng vai tập trung vào hiểu, vận dụng kiến thức kỹ năng mới của bài và thực tiễn.
17. Kỹ thuật “Trình bày một phút”
Kỹ thuật này dùng trong quá trình HS học bài trên lớp vào cuối mỗi bài.
Cách thực hiên:
- GV đặt câu hỏi: Bài này các em đã học được cái gì mới? Có điều quan trọng gì các em muốn giải đáp thêm?
- HS suy nghĩ, viết ra giấy ý kiến của cá nhân
- Mỗi HS được trình bày ý kiến của mình trong 1 phút
Lưu ý: Khuyến khích trình bày có phương tiện hỗ trợ: tranh ảnh, CNTT
18. Kỹ thuật “Chúng em biết 3”
Kỹ thuật này dùng trong thảo luận nhóm nhằm tập hợp những thông tin được chọn lọc từ thảo luận. Kỹ thuật này tạo cơ hội cho những HS có trình độ khá hỗ trợ HS có trình độ thấp hơn.
Cách thực hiện:
- GV nêu chủ đề thảo luận (có thể bằng câu kể hoặc câu hỏi, Ví dụ: Học sinh đi đường an toàn / Học sinh đi đường thế nào để đảm bảo an toàn?)
- Mỗi nhóm 3 (có thể hơn 3) HS sẽ chia sẻ những điều các em biết rồi chọn ra 3 điều quan trọng nhất
- Đại diện mỗi nhóm trình bày 3 điều nhóm đã chọn
-
Integration by Substitution
Integration by Substitution
“Integration by Substitution” (also called “u-Substitution” or “The Reverse Chain Rule”) is a method to find an integral, but only when it can be set up in a special way.
The first and most vital step is to be able to write our integral in this form:
Note that we have $g(x)$ and its derivative $g'(x)$Like in this example:
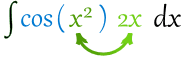
Here $f=cos$, and we have $g=x^2$ and its derivative $2x$.This integral is good to go!
When our integral is set up like that, we can do this substitution:
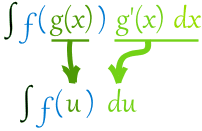
Then we can integrate $f(u)$, and finish by putting $g(x)$ back as $u$.
Substitution Rule
Example Integration by Substitution
Example 1. Find the integral $$\int \cos(x^2) 2x dx$$
We know (from above) that it is in the right form to do the substitution:
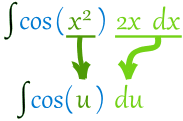
Now integrate: $$\int \cos(u) du = \sin(u) + C$$ And finally put $u=x^2$ back again: $$\sin(x^2) + C$$ So $\displaystyle \int\cos(x^2) 2x dx = \sin(x^2) + C.$$
That worked out really nicely! (Well, I knew it would.)
But this method only works on some integrals of course, and it may need rearranging:
Example 2. Find the integral $$\int \cos(x^2) 6x dx$$Oh no! It is $6x$, not $2x$ like before. Our perfect setup is gone.
Never fear! Just rearrange the integral like this: $$\int\cos(x^2) 6x dx = 3\int\cos(x^2) 2x dx$$
(We can pull constant multipliers outside the integration, see Rules of Integration.)
Then go ahead as before: $$3\int\cos(u) du = 3 \sin(u) + C$$
Now put $u=x^2$ back again: $$3 sin(x^2) + C$$
Done!
Now let’s try a slightly harder example:
Example 3. Find the integral $$\int \frac{x}{x^2+1} dx$$Let me see … the derivative of x^2 +1 is 2x … so how about we rearrange it like this: $$\int \frac{x}{x^2 +1} dx = \frac{1}{2}\int \frac{2x}{x^2 +1} dx$$ Then we have:
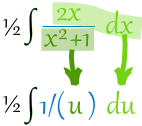
Then integrate:$$\frac{1}{2} \int \frac{1}{u} du = \frac{1}{2} \ln(u) + C$$
Now put $u=x^2 +1$ back again: $$\frac{1}{2}\ln(x^2 +1) + C$$
And how about this one:
Example 4. Find the integral $$\int (x+1)^3 dx$$
Let me see … the derivative of $x+1$ is … well it is simply 1.
So we can have this:$$\int (x+1)^3 dx = \int (x+1)^3 \cdot 1 dx$$ Then we have:
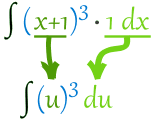
Then integrate:$$\int u^3 du = \frac{1}{4}\cdot u^4 + C$$
Now put $u=x+1$ back again:$$ \frac{(x+1)^4}{4} + C$$
We can take that idea further like this:
Example 5. Find the integral $$\int (5x+2)^7 dx$$
If it was in THIS form we could do it:$$\int (5x+2)^7\cdot 5dx$$
So let’s make it so by doing this: $$\frac{1}{5} \int (5x+2)^7\cdot 5dx$$ The $\frac{1}{5}$ and 5 cancel out so all is fine.
And now we can have $u=5x+2$
And then integrate: $$\frac{1}{5} \int u^7 du = \frac{1}{5} \cdot \frac{1}{8} u^8 +C$$ Now put $u=5x+2$ back again, and simplify: $$\frac{(5x+2)^8}{40} + C$$
Now get some practice, OK?
In Summary
- When we can put an integral in this form:
- Then we can make $u=g(x)$ and integrate $\displaystyle \int f(u) du$
- And finish up by re-inserting $g(x)$ where $u$ is $g(x)$.
(https://www.mathsisfun.com/calculus/integration-by-substitution.html)
Nếu tăng chiều rộng thêm 20 m thì hình chữ nhật trở thành hình vuông, tức là khi đó chiều rộng sẽ dài bằng chiều dài. Hay nói cách khác, hiệu chiều dài và chiều rộng là 20 m.
