| U+002B |
PLUS SIGN |
+ |
| U+003C |
LESS-THAN SIGN |
< |
| U+003D |
EQUALS SIGN |
= |
| U+003E |
GREATER-THAN SIGN |
> |
| U+007C |
VERTICAL LINE |
| |
| U+007E |
TILDE |
~ |
| U+00AC |
NOT SIGN |
¬ |
| U+00B1 |
PLUS-MINUS SIGN |
± |
| U+00D7 |
MULTIPLICATION SIGN |
× |
| U+00F7 |
DIVISION SIGN |
÷ |
| U+03F6 |
GREEK REVERSED LUNATE EPSILON SYMBOL |
϶ |
| U+0606 |
ARABIC-INDIC CUBE ROOT |
؆ |
| U+0607 |
ARABIC-INDIC FOURTH ROOT |
؇ |
| U+0608 |
ARABIC RAY |
؈ |
| U+2044 |
FRACTION SLASH |
⁄ |
| U+2052 |
COMMERCIAL MINUS SIGN |
⁒ |
| U+207A |
SUPERSCRIPT PLUS SIGN |
⁺ |
| U+207B |
SUPERSCRIPT MINUS |
⁻ |
| U+207C |
SUPERSCRIPT EQUALS SIGN |
⁼ |
| U+208A |
SUBSCRIPT PLUS SIGN |
₊ |
| U+208B |
SUBSCRIPT MINUS |
₋ |
| U+208C |
SUBSCRIPT EQUALS SIGN |
₌ |
| U+2118 |
SCRIPT CAPITAL P |
℘ |
| U+2140 |
DOUBLE-STRUCK N-ARY SUMMATION |
⅀ |
| U+2141 |
TURNED SANS-SERIF CAPITAL G |
⅁ |
| U+2142 |
TURNED SANS-SERIF CAPITAL L |
⅂ |
| U+2143 |
REVERSED SANS-SERIF CAPITAL L |
⅃ |
| U+2144 |
TURNED SANS-SERIF CAPITAL Y |
⅄ |
| U+214B |
TURNED AMPERSAND |
⅋ |
| U+2190 |
LEFTWARDS ARROW |
← |
| U+2191 |
UPWARDS ARROW |
↑ |
| U+2192 |
RIGHTWARDS ARROW |
→ |
| U+2193 |
DOWNWARDS ARROW |
↓ |
| U+2194 |
LEFT RIGHT ARROW |
↔ |
| U+219A |
LEFTWARDS ARROW WITH STROKE |
↚ |
| U+219B |
RIGHTWARDS ARROW WITH STROKE |
↛ |
| U+21A0 |
RIGHTWARDS TWO HEADED ARROW |
↠ |
| U+21A3 |
RIGHTWARDS ARROW WITH TAIL |
↣ |
| U+21A6 |
RIGHTWARDS ARROW FROM BAR |
↦ |
| U+21AE |
LEFT RIGHT ARROW WITH STROKE |
↮ |
| U+21CE |
LEFT RIGHT DOUBLE ARROW WITH STROKE |
⇎ |
| U+21CF |
RIGHTWARDS DOUBLE ARROW WITH STROKE |
⇏ |
| U+21D2 |
RIGHTWARDS DOUBLE ARROW |
⇒ |
| U+21D4 |
LEFT RIGHT DOUBLE ARROW |
⇔ |
| U+21F4 |
RIGHT ARROW WITH SMALL CIRCLE |
⇴ |
| U+21F5 |
DOWNWARDS ARROW LEFTWARDS OF UPWARDS ARROW |
⇵ |
| U+21F6 |
THREE RIGHTWARDS ARROWS |
⇶ |
| U+21F7 |
LEFTWARDS ARROW WITH VERTICAL STROKE |
⇷ |
| U+21F8 |
RIGHTWARDS ARROW WITH VERTICAL STROKE |
⇸ |
| U+21F9 |
LEFT RIGHT ARROW WITH VERTICAL STROKE |
⇹ |
| U+21FA |
LEFTWARDS ARROW WITH DOUBLE VERTICAL STROKE |
⇺ |
| U+21FB |
RIGHTWARDS ARROW WITH DOUBLE VERTICAL STROKE |
⇻ |
| U+21FC |
LEFT RIGHT ARROW WITH DOUBLE VERTICAL STROKE |
⇼ |
| U+21FD |
LEFTWARDS OPEN-HEADED ARROW |
⇽ |
| U+21FE |
RIGHTWARDS OPEN-HEADED ARROW |
⇾ |
| U+21FF |
LEFT RIGHT OPEN-HEADED ARROW |
⇿ |
| U+2200 |
FOR ALL |
∀ |
| U+2201 |
COMPLEMENT |
∁ |
| U+2202 |
PARTIAL DIFFERENTIAL |
∂ |
| U+2203 |
THERE EXISTS |
∃ |
| U+2204 |
THERE DOES NOT EXIST |
∄ |
| U+2205 |
EMPTY SET |
∅ |
| U+2206 |
INCREMENT |
∆ |
| U+2207 |
NABLA |
∇ |
| U+2208 |
ELEMENT OF |
∈ |
| U+2209 |
NOT AN ELEMENT OF |
∉ |
| U+220A |
SMALL ELEMENT OF |
∊ |
| U+220B |
CONTAINS AS MEMBER |
∋ |
| U+220C |
DOES NOT CONTAIN AS MEMBER |
∌ |
| U+220D |
SMALL CONTAINS AS MEMBER |
∍ |
| U+220E |
END OF PROOF |
∎ |
| U+220F |
N-ARY PRODUCT |
∏ |
| U+2210 |
N-ARY COPRODUCT |
∐ |
| U+2211 |
N-ARY SUMMATION |
∑ |
| U+2212 |
MINUS SIGN |
− |
| U+2213 |
MINUS-OR-PLUS SIGN |
∓ |
| U+2214 |
DOT PLUS |
∔ |
| U+2215 |
DIVISION SLASH |
∕ |
| U+2216 |
SET MINUS |
∖ |
| U+2217 |
ASTERISK OPERATOR |
∗ |
| U+2218 |
RING OPERATOR |
∘ |
| U+2219 |
BULLET OPERATOR |
∙ |
| U+221A |
SQUARE ROOT |
√ |
| U+221B |
CUBE ROOT |
∛ |
| U+221C |
FOURTH ROOT |
∜ |
| U+221D |
PROPORTIONAL TO |
∝ |
| U+221E |
INFINITY |
∞ |
| U+221F |
RIGHT ANGLE |
∟ |
| U+2220 |
ANGLE |
∠ |
| U+2221 |
MEASURED ANGLE |
∡ |
| U+2222 |
SPHERICAL ANGLE |
∢ |
| U+2223 |
DIVIDES |
∣ |
| U+2224 |
DOES NOT DIVIDE |
∤ |
| U+2225 |
PARALLEL TO |
∥ |
| U+2226 |
NOT PARALLEL TO |
∦ |
| U+2227 |
LOGICAL AND |
∧ |
| U+2228 |
LOGICAL OR |
∨ |
| U+2229 |
INTERSECTION |
∩ |
| U+222A |
UNION |
∪ |
| U+222B |
INTEGRAL |
∫ |
| U+222C |
DOUBLE INTEGRAL |
∬ |
| U+222D |
TRIPLE INTEGRAL |
∭ |
| U+222E |
CONTOUR INTEGRAL |
∮ |
| U+222F |
SURFACE INTEGRAL |
∯ |
| U+2230 |
VOLUME INTEGRAL |
∰ |
| U+2231 |
CLOCKWISE INTEGRAL |
∱ |
| U+2232 |
CLOCKWISE CONTOUR INTEGRAL |
∲ |
| U+2233 |
ANTICLOCKWISE CONTOUR INTEGRAL |
∳ |
| U+2234 |
THEREFORE |
∴ |
| U+2235 |
BECAUSE |
∵ |
| U+2236 |
RATIO |
∶ |
| U+2237 |
PROPORTION |
∷ |
| U+2238 |
DOT MINUS |
∸ |
| U+2239 |
EXCESS |
∹ |
| U+223A |
GEOMETRIC PROPORTION |
∺ |
| U+223B |
HOMOTHETIC |
∻ |
| U+223C |
TILDE OPERATOR |
∼ |
| U+223D |
REVERSED TILDE |
∽ |
| U+223E |
INVERTED LAZY S |
∾ |
| U+223F |
SINE WAVE |
∿ |
| U+2240 |
WREATH PRODUCT |
≀ |
| U+2241 |
NOT TILDE |
≁ |
| U+2242 |
MINUS TILDE |
≂ |
| U+2243 |
ASYMPTOTICALLY EQUAL TO |
≃ |
| U+2244 |
NOT ASYMPTOTICALLY EQUAL TO |
≄ |
| U+2245 |
APPROXIMATELY EQUAL TO |
≅ |
| U+2246 |
APPROXIMATELY BUT NOT ACTUALLY EQUAL TO |
≆ |
| U+2247 |
NEITHER APPROXIMATELY NOR ACTUALLY EQUAL TO |
≇ |
| U+2248 |
ALMOST EQUAL TO |
≈ |
| U+2249 |
NOT ALMOST EQUAL TO |
≉ |
| U+224A |
ALMOST EQUAL OR EQUAL TO |
≊ |
| U+224B |
TRIPLE TILDE |
≋ |
| U+224C |
ALL EQUAL TO |
≌ |
| U+224D |
EQUIVALENT TO |
≍ |
| U+224E |
GEOMETRICALLY EQUIVALENT TO |
≎ |
| U+224F |
DIFFERENCE BETWEEN |
≏ |
| U+2250 |
APPROACHES THE LIMIT |
≐ |
| U+2251 |
GEOMETRICALLY EQUAL TO |
≑ |
| U+2252 |
APPROXIMATELY EQUAL TO OR THE IMAGE OF |
≒ |
| U+2253 |
IMAGE OF OR APPROXIMATELY EQUAL TO |
≓ |
| U+2254 |
COLON EQUALS |
≔ |
| U+2255 |
EQUALS COLON |
≕ |
| U+2256 |
RING IN EQUAL TO |
≖ |
| U+2257 |
RING EQUAL TO |
≗ |
| U+2258 |
CORRESPONDS TO |
≘ |
| U+2259 |
ESTIMATES |
≙ |
| U+225A |
EQUIANGULAR TO |
≚ |
| U+225B |
STAR EQUALS |
≛ |
| U+225C |
DELTA EQUAL TO |
≜ |
| U+225D |
EQUAL TO BY DEFINITION |
≝ |
| U+225E |
MEASURED BY |
≞ |
| U+225F |
QUESTIONED EQUAL TO |
≟ |
| U+2260 |
NOT EQUAL TO |
≠ |
| U+2261 |
IDENTICAL TO |
≡ |
| U+2262 |
NOT IDENTICAL TO |
≢ |
| U+2263 |
STRICTLY EQUIVALENT TO |
≣ |
| U+2264 |
LESS-THAN OR EQUAL TO |
≤ |
| U+2265 |
GREATER-THAN OR EQUAL TO |
≥ |
| U+2266 |
LESS-THAN OVER EQUAL TO |
≦ |
| U+2267 |
GREATER-THAN OVER EQUAL TO |
≧ |
| U+2268 |
LESS-THAN BUT NOT EQUAL TO |
≨ |
| U+2269 |
GREATER-THAN BUT NOT EQUAL TO |
≩ |
| U+226A |
MUCH LESS-THAN |
≪ |
| U+226B |
MUCH GREATER-THAN |
≫ |
| U+226C |
BETWEEN |
≬ |
| U+226D |
NOT EQUIVALENT TO |
≭ |
| U+226E |
NOT LESS-THAN |
≮ |
| U+226F |
NOT GREATER-THAN |
≯ |
| U+2270 |
NEITHER LESS-THAN NOR EQUAL TO |
≰ |
| U+2271 |
NEITHER GREATER-THAN NOR EQUAL TO |
≱ |
| U+2272 |
LESS-THAN OR EQUIVALENT TO |
≲ |
| U+2273 |
GREATER-THAN OR EQUIVALENT TO |
≳ |
| U+2274 |
NEITHER LESS-THAN NOR EQUIVALENT TO |
≴ |
| U+2275 |
NEITHER GREATER-THAN NOR EQUIVALENT TO |
≵ |
| U+2276 |
LESS-THAN OR GREATER-THAN |
≶ |
| U+2277 |
GREATER-THAN OR LESS-THAN |
≷ |
| U+2278 |
NEITHER LESS-THAN NOR GREATER-THAN |
≸ |
| U+2279 |
NEITHER GREATER-THAN NOR LESS-THAN |
≹ |
| U+227A |
PRECEDES |
≺ |
| U+227B |
SUCCEEDS |
≻ |
| U+227C |
PRECEDES OR EQUAL TO |
≼ |
| U+227D |
SUCCEEDS OR EQUAL TO |
≽ |
| U+227E |
PRECEDES OR EQUIVALENT TO |
≾ |
| U+227F |
SUCCEEDS OR EQUIVALENT TO |
≿ |
| U+2280 |
DOES NOT PRECEDE |
⊀ |
| U+2281 |
DOES NOT SUCCEED |
⊁ |
| U+2282 |
SUBSET OF |
⊂ |
| U+2283 |
SUPERSET OF |
⊃ |
| U+2284 |
NOT A SUBSET OF |
⊄ |
| U+2285 |
NOT A SUPERSET OF |
⊅ |
| U+2286 |
SUBSET OF OR EQUAL TO |
⊆ |
| U+2287 |
SUPERSET OF OR EQUAL TO |
⊇ |
| U+2288 |
NEITHER A SUBSET OF NOR EQUAL TO |
⊈ |
| U+2289 |
NEITHER A SUPERSET OF NOR EQUAL TO |
⊉ |
| U+228A |
SUBSET OF WITH NOT EQUAL TO |
⊊ |
| U+228B |
SUPERSET OF WITH NOT EQUAL TO |
⊋ |
| U+228C |
MULTISET |
⊌ |
| U+228D |
MULTISET MULTIPLICATION |
⊍ |
| U+228E |
MULTISET UNION |
⊎ |
| U+228F |
SQUARE IMAGE OF |
⊏ |
| U+2290 |
SQUARE ORIGINAL OF |
⊐ |
| U+2291 |
SQUARE IMAGE OF OR EQUAL TO |
⊑ |
| U+2292 |
SQUARE ORIGINAL OF OR EQUAL TO |
⊒ |
| U+2293 |
SQUARE CAP |
⊓ |
| U+2294 |
SQUARE CUP |
⊔ |
| U+2295 |
CIRCLED PLUS |
⊕ |
| U+2296 |
CIRCLED MINUS |
⊖ |
| U+2297 |
CIRCLED TIMES |
⊗ |
| U+2298 |
CIRCLED DIVISION SLASH |
⊘ |
| U+2299 |
CIRCLED DOT OPERATOR |
⊙ |
| U+229A |
CIRCLED RING OPERATOR |
⊚ |
| U+229B |
CIRCLED ASTERISK OPERATOR |
⊛ |
| U+229C |
CIRCLED EQUALS |
⊜ |
| U+229D |
CIRCLED DASH |
⊝ |
| U+229E |
SQUARED PLUS |
⊞ |
| U+229F |
SQUARED MINUS |
⊟ |
| U+22A0 |
SQUARED TIMES |
⊠ |
| U+22A1 |
SQUARED DOT OPERATOR |
⊡ |
| U+22A2 |
RIGHT TACK |
⊢ |
| U+22A3 |
LEFT TACK |
⊣ |
| U+22A4 |
DOWN TACK |
⊤ |
| U+22A5 |
UP TACK |
⊥ |
| U+22A6 |
ASSERTION |
⊦ |
| U+22A7 |
MODELS |
⊧ |
| U+22A8 |
TRUE |
⊨ |
| U+22A9 |
FORCES |
⊩ |
| U+22AA |
TRIPLE VERTICAL BAR RIGHT TURNSTILE |
⊪ |
| U+22AB |
DOUBLE VERTICAL BAR DOUBLE RIGHT TURNSTILE |
⊫ |
| U+22AC |
DOES NOT PROVE |
⊬ |
| U+22AD |
NOT TRUE |
⊭ |
| U+22AE |
DOES NOT FORCE |
⊮ |
| U+22AF |
NEGATED DOUBLE VERTICAL BAR DOUBLE RIGHT TURNSTILE |
⊯ |
| U+22B0 |
PRECEDES UNDER RELATION |
⊰ |
| U+22B1 |
SUCCEEDS UNDER RELATION |
⊱ |
| U+22B2 |
NORMAL SUBGROUP OF |
⊲ |
| U+22B3 |
CONTAINS AS NORMAL SUBGROUP |
⊳ |
| U+22B4 |
NORMAL SUBGROUP OF OR EQUAL TO |
⊴ |
| U+22B5 |
CONTAINS AS NORMAL SUBGROUP OR EQUAL TO |
⊵ |
| U+22B6 |
ORIGINAL OF |
⊶ |
| U+22B7 |
IMAGE OF |
⊷ |
| U+22B8 |
MULTIMAP |
⊸ |
| U+22B9 |
HERMITIAN CONJUGATE MATRIX |
⊹ |
| U+22BA |
INTERCALATE |
⊺ |
| U+22BB |
XOR |
⊻ |
| U+22BC |
NAND |
⊼ |
| U+22BD |
NOR |
⊽ |
| U+22BE |
RIGHT ANGLE WITH ARC |
⊾ |
| U+22BF |
RIGHT TRIANGLE |
⊿ |
| U+22C0 |
N-ARY LOGICAL AND |
⋀ |
| U+22C1 |
N-ARY LOGICAL OR |
⋁ |
| U+22C2 |
N-ARY INTERSECTION |
⋂ |
| U+22C3 |
N-ARY UNION |
⋃ |
| U+22C4 |
DIAMOND OPERATOR |
⋄ |
| U+22C5 |
DOT OPERATOR |
⋅ |
| U+22C6 |
STAR OPERATOR |
⋆ |
| U+22C7 |
DIVISION TIMES |
⋇ |
| U+22C8 |
BOWTIE |
⋈ |
| U+22C9 |
LEFT NORMAL FACTOR SEMIDIRECT PRODUCT |
⋉ |
| U+22CA |
RIGHT NORMAL FACTOR SEMIDIRECT PRODUCT |
⋊ |
| U+22CB |
LEFT SEMIDIRECT PRODUCT |
⋋ |
| U+22CC |
RIGHT SEMIDIRECT PRODUCT |
⋌ |
| U+22CD |
REVERSED TILDE EQUALS |
⋍ |
| U+22CE |
CURLY LOGICAL OR |
⋎ |
| U+22CF |
CURLY LOGICAL AND |
⋏ |
| U+22D0 |
DOUBLE SUBSET |
⋐ |
| U+22D1 |
DOUBLE SUPERSET |
⋑ |
| U+22D2 |
DOUBLE INTERSECTION |
⋒ |
| U+22D3 |
DOUBLE UNION |
⋓ |
| U+22D4 |
PITCHFORK |
⋔ |
| U+22D5 |
EQUAL AND PARALLEL TO |
⋕ |
| U+22D6 |
LESS-THAN WITH DOT |
⋖ |
| U+22D7 |
GREATER-THAN WITH DOT |
⋗ |
| U+22D8 |
VERY MUCH LESS-THAN |
⋘ |
| U+22D9 |
VERY MUCH GREATER-THAN |
⋙ |
| U+22DA |
LESS-THAN EQUAL TO OR GREATER-THAN |
⋚ |
| U+22DB |
GREATER-THAN EQUAL TO OR LESS-THAN |
⋛ |
| U+22DC |
EQUAL TO OR LESS-THAN |
⋜ |
| U+22DD |
EQUAL TO OR GREATER-THAN |
⋝ |
| U+22DE |
EQUAL TO OR PRECEDES |
⋞ |
| U+22DF |
EQUAL TO OR SUCCEEDS |
⋟ |
| U+22E0 |
DOES NOT PRECEDE OR EQUAL |
⋠ |
| U+22E1 |
DOES NOT SUCCEED OR EQUAL |
⋡ |
| U+22E2 |
NOT SQUARE IMAGE OF OR EQUAL TO |
⋢ |
| U+22E3 |
NOT SQUARE ORIGINAL OF OR EQUAL TO |
⋣ |
| U+22E4 |
SQUARE IMAGE OF OR NOT EQUAL TO |
⋤ |
| U+22E5 |
SQUARE ORIGINAL OF OR NOT EQUAL TO |
⋥ |
| U+22E6 |
LESS-THAN BUT NOT EQUIVALENT TO |
⋦ |
| U+22E7 |
GREATER-THAN BUT NOT EQUIVALENT TO |
⋧ |
| U+22E8 |
PRECEDES BUT NOT EQUIVALENT TO |
⋨ |
| U+22E9 |
SUCCEEDS BUT NOT EQUIVALENT TO |
⋩ |
| U+22EA |
NOT NORMAL SUBGROUP OF |
⋪ |
| U+22EB |
DOES NOT CONTAIN AS NORMAL SUBGROUP |
⋫ |
| U+22EC |
NOT NORMAL SUBGROUP OF OR EQUAL TO |
⋬ |
| U+22ED |
DOES NOT CONTAIN AS NORMAL SUBGROUP OR EQUAL |
⋭ |
| U+22EE |
VERTICAL ELLIPSIS |
⋮ |
| U+22EF |
MIDLINE HORIZONTAL ELLIPSIS |
⋯ |
| U+22F0 |
UP RIGHT DIAGONAL ELLIPSIS |
⋰ |
| U+22F1 |
DOWN RIGHT DIAGONAL ELLIPSIS |
⋱ |
| U+22F2 |
ELEMENT OF WITH LONG HORIZONTAL STROKE |
⋲ |
| U+22F3 |
ELEMENT OF WITH VERTICAL BAR AT END OF HORIZONTAL STROKE |
⋳ |
| U+22F4 |
SMALL ELEMENT OF WITH VERTICAL BAR AT END OF HORIZONTAL STROKE |
⋴ |
| U+22F5 |
ELEMENT OF WITH DOT ABOVE |
⋵ |
| U+22F6 |
ELEMENT OF WITH OVERBAR |
⋶ |
| U+22F7 |
SMALL ELEMENT OF WITH OVERBAR |
⋷ |
| U+22F8 |
ELEMENT OF WITH UNDERBAR |
⋸ |
| U+22F9 |
ELEMENT OF WITH TWO HORIZONTAL STROKES |
⋹ |
| U+22FA |
CONTAINS WITH LONG HORIZONTAL STROKE |
⋺ |
| U+22FB |
CONTAINS WITH VERTICAL BAR AT END OF HORIZONTAL STROKE |
⋻ |
| U+22FC |
SMALL CONTAINS WITH VERTICAL BAR AT END OF HORIZONTAL STROKE |
⋼ |
| U+22FD |
CONTAINS WITH OVERBAR |
⋽ |
| U+22FE |
SMALL CONTAINS WITH OVERBAR |
⋾ |
| U+22FF |
Z NOTATION BAG MEMBERSHIP |
⋿ |
| U+2320 |
TOP HALF INTEGRAL |
⌠ |
| U+2321 |
BOTTOM HALF INTEGRAL |
⌡ |
| U+237C |
RIGHT ANGLE WITH DOWNWARDS ZIGZAG ARROW |
⍼ |
| U+239B |
LEFT PARENTHESIS UPPER HOOK |
⎛ |
| U+239C |
LEFT PARENTHESIS EXTENSION |
⎜ |
| U+239D |
LEFT PARENTHESIS LOWER HOOK |
⎝ |
| U+239E |
RIGHT PARENTHESIS UPPER HOOK |
⎞ |
| U+239F |
RIGHT PARENTHESIS EXTENSION |
⎟ |
| U+23A0 |
RIGHT PARENTHESIS LOWER HOOK |
⎠ |
| U+23A1 |
LEFT SQUARE BRACKET UPPER CORNER |
⎡ |
| U+23A2 |
LEFT SQUARE BRACKET EXTENSION |
⎢ |
| U+23A3 |
LEFT SQUARE BRACKET LOWER CORNER |
⎣ |
| U+23A4 |
RIGHT SQUARE BRACKET UPPER CORNER |
⎤ |
| U+23A5 |
RIGHT SQUARE BRACKET EXTENSION |
⎥ |
| U+23A6 |
RIGHT SQUARE BRACKET LOWER CORNER |
⎦ |
| U+23A7 |
LEFT CURLY BRACKET UPPER HOOK |
⎧ |
| U+23A8 |
LEFT CURLY BRACKET MIDDLE PIECE |
⎨ |
| U+23A9 |
LEFT CURLY BRACKET LOWER HOOK |
⎩ |
| U+23AA |
CURLY BRACKET EXTENSION |
⎪ |
| U+23AB |
RIGHT CURLY BRACKET UPPER HOOK |
⎫ |
| U+23AC |
RIGHT CURLY BRACKET MIDDLE PIECE |
⎬ |
| U+23AD |
RIGHT CURLY BRACKET LOWER HOOK |
⎭ |
| U+23AE |
INTEGRAL EXTENSION |
⎮ |
| U+23AF |
HORIZONTAL LINE EXTENSION |
⎯ |
| U+23B0 |
UPPER LEFT OR LOWER RIGHT CURLY BRACKET SECTION |
⎰ |
| U+23B1 |
UPPER RIGHT OR LOWER LEFT CURLY BRACKET SECTION |
⎱ |
| U+23B2 |
SUMMATION TOP |
⎲ |
| U+23B3 |
SUMMATION BOTTOM |
⎳ |
| U+23DC |
TOP PARENTHESIS |
⏜ |
| U+23DD |
BOTTOM PARENTHESIS |
⏝ |
| U+23DE |
TOP CURLY BRACKET |
⏞ |
| U+23DF |
BOTTOM CURLY BRACKET |
⏟ |
| U+23E0 |
TOP TORTOISE SHELL BRACKET |
⏠ |
| U+23E1 |
BOTTOM TORTOISE SHELL BRACKET |
⏡ |
| U+25B7 |
WHITE RIGHT-POINTING TRIANGLE |
▷ |
| U+25C1 |
WHITE LEFT-POINTING TRIANGLE |
◁ |
| U+25F8 |
UPPER LEFT TRIANGLE |
◸ |
| U+25F9 |
UPPER RIGHT TRIANGLE |
◹ |
| U+25FA |
LOWER LEFT TRIANGLE |
◺ |
| U+25FB |
WHITE MEDIUM SQUARE |
◻ |
| U+25FC |
BLACK MEDIUM SQUARE |
◼ |
| U+25FD |
WHITE MEDIUM SMALL SQUARE |
◽ |
| U+25FE |
BLACK MEDIUM SMALL SQUARE |
◾ |
| U+25FF |
LOWER RIGHT TRIANGLE |
◿ |
| U+266F |
MUSIC SHARP SIGN |
♯ |
| U+27C0 |
THREE DIMENSIONAL ANGLE |
⟀ |
| U+27C1 |
WHITE TRIANGLE CONTAINING SMALL WHITE TRIANGLE |
⟁ |
| U+27C2 |
PERPENDICULAR |
⟂ |
| U+27C3 |
OPEN SUBSET |
⟃ |
| U+27C4 |
OPEN SUPERSET |
⟄ |
| U+27C7 |
OR WITH DOT INSIDE |
⟇ |
| U+27C8 |
REVERSE SOLIDUS PRECEDING SUBSET |
⟈ |
| U+27C9 |
SUPERSET PRECEDING SOLIDUS |
⟉ |
| U+27CA |
VERTICAL BAR WITH HORIZONTAL STROKE |
⟊ |
| U+27CB |
MATHEMATICAL RISING DIAGONAL |
⟋ |
| U+27CC |
LONG DIVISION |
⟌ |
| U+27CD |
MATHEMATICAL FALLING DIAGONAL |
⟍ |
| U+27CE |
SQUARED LOGICAL AND |
⟎ |
| U+27CF |
SQUARED LOGICAL OR |
⟏ |
| U+27D0 |
WHITE DIAMOND WITH CENTRED DOT |
⟐ |
| U+27D1 |
AND WITH DOT |
⟑ |
| U+27D2 |
ELEMENT OF OPENING UPWARDS |
⟒ |
| U+27D3 |
LOWER RIGHT CORNER WITH DOT |
⟓ |
| U+27D4 |
UPPER LEFT CORNER WITH DOT |
⟔ |
| U+27D5 |
LEFT OUTER JOIN |
⟕ |
| U+27D6 |
RIGHT OUTER JOIN |
⟖ |
| U+27D7 |
FULL OUTER JOIN |
⟗ |
| U+27D8 |
LARGE UP TACK |
⟘ |
| U+27D9 |
LARGE DOWN TACK |
⟙ |
| U+27DA |
LEFT AND RIGHT DOUBLE TURNSTILE |
⟚ |
| U+27DB |
LEFT AND RIGHT TACK |
⟛ |
| U+27DC |
LEFT MULTIMAP |
⟜ |
| U+27DD |
LONG RIGHT TACK |
⟝ |
| U+27DE |
LONG LEFT TACK |
⟞ |
| U+27DF |
UP TACK WITH CIRCLE ABOVE |
⟟ |
| U+27E0 |
LOZENGE DIVIDED BY HORIZONTAL RULE |
⟠ |
| U+27E1 |
WHITE CONCAVE-SIDED DIAMOND |
⟡ |
| U+27E2 |
WHITE CONCAVE-SIDED DIAMOND WITH LEFTWARDS TICK |
⟢ |
| U+27E3 |
WHITE CONCAVE-SIDED DIAMOND WITH RIGHTWARDS TICK |
⟣ |
| U+27E4 |
WHITE SQUARE WITH LEFTWARDS TICK |
⟤ |
| U+27E5 |
WHITE SQUARE WITH RIGHTWARDS TICK |
⟥ |
| U+27F0 |
UPWARDS QUADRUPLE ARROW |
⟰ |
| U+27F1 |
DOWNWARDS QUADRUPLE ARROW |
⟱ |
| U+27F2 |
ANTICLOCKWISE GAPPED CIRCLE ARROW |
⟲ |
| U+27F3 |
CLOCKWISE GAPPED CIRCLE ARROW |
⟳ |
| U+27F4 |
RIGHT ARROW WITH CIRCLED PLUS |
⟴ |
| U+27F5 |
LONG LEFTWARDS ARROW |
⟵ |
| U+27F6 |
LONG RIGHTWARDS ARROW |
⟶ |
| U+27F7 |
LONG LEFT RIGHT ARROW |
⟷ |
| U+27F8 |
LONG LEFTWARDS DOUBLE ARROW |
⟸ |
| U+27F9 |
LONG RIGHTWARDS DOUBLE ARROW |
⟹ |
| U+27FA |
LONG LEFT RIGHT DOUBLE ARROW |
⟺ |
| U+27FB |
LONG LEFTWARDS ARROW FROM BAR |
⟻ |
| U+27FC |
LONG RIGHTWARDS ARROW FROM BAR |
⟼ |
| U+27FD |
LONG LEFTWARDS DOUBLE ARROW FROM BAR |
⟽ |
| U+27FE |
LONG RIGHTWARDS DOUBLE ARROW FROM BAR |
⟾ |
| U+27FF |
LONG RIGHTWARDS SQUIGGLE ARROW |
⟿ |
| U+2900 |
RIGHTWARDS TWO-HEADED ARROW WITH VERTICAL STROKE |
⤀ |
| U+2901 |
RIGHTWARDS TWO-HEADED ARROW WITH DOUBLE VERTICAL STROKE |
⤁ |
| U+2902 |
LEFTWARDS DOUBLE ARROW WITH VERTICAL STROKE |
⤂ |
| U+2903 |
RIGHTWARDS DOUBLE ARROW WITH VERTICAL STROKE |
⤃ |
| U+2904 |
LEFT RIGHT DOUBLE ARROW WITH VERTICAL STROKE |
⤄ |
| U+2905 |
RIGHTWARDS TWO-HEADED ARROW FROM BAR |
⤅ |
| U+2906 |
LEFTWARDS DOUBLE ARROW FROM BAR |
⤆ |
| U+2907 |
RIGHTWARDS DOUBLE ARROW FROM BAR |
⤇ |
| U+2908 |
DOWNWARDS ARROW WITH HORIZONTAL STROKE |
⤈ |
| U+2909 |
UPWARDS ARROW WITH HORIZONTAL STROKE |
⤉ |
| U+290A |
UPWARDS TRIPLE ARROW |
⤊ |
| U+290B |
DOWNWARDS TRIPLE ARROW |
⤋ |
| U+290C |
LEFTWARDS DOUBLE DASH ARROW |
⤌ |
| U+290D |
RIGHTWARDS DOUBLE DASH ARROW |
⤍ |
| U+290E |
LEFTWARDS TRIPLE DASH ARROW |
⤎ |
| U+290F |
RIGHTWARDS TRIPLE DASH ARROW |
⤏ |
| U+2910 |
RIGHTWARDS TWO-HEADED TRIPLE DASH ARROW |
⤐ |
| U+2911 |
RIGHTWARDS ARROW WITH DOTTED STEM |
⤑ |
| U+2912 |
UPWARDS ARROW TO BAR |
⤒ |
| U+2913 |
DOWNWARDS ARROW TO BAR |
⤓ |
| U+2914 |
RIGHTWARDS ARROW WITH TAIL WITH VERTICAL STROKE |
⤔ |
| U+2915 |
RIGHTWARDS ARROW WITH TAIL WITH DOUBLE VERTICAL STROKE |
⤕ |
| U+2916 |
RIGHTWARDS TWO-HEADED ARROW WITH TAIL |
⤖ |
| U+2917 |
RIGHTWARDS TWO-HEADED ARROW WITH TAIL WITH VERTICAL STROKE |
⤗ |
| U+2918 |
RIGHTWARDS TWO-HEADED ARROW WITH TAIL WITH DOUBLE VERTICAL STROKE |
⤘ |
| U+2919 |
LEFTWARDS ARROW-TAIL |
⤙ |
| U+291A |
RIGHTWARDS ARROW-TAIL |
⤚ |
| U+291B |
LEFTWARDS DOUBLE ARROW-TAIL |
⤛ |
| U+291C |
RIGHTWARDS DOUBLE ARROW-TAIL |
⤜ |
| U+291D |
LEFTWARDS ARROW TO BLACK DIAMOND |
⤝ |
| U+291E |
RIGHTWARDS ARROW TO BLACK DIAMOND |
⤞ |
| U+291F |
LEFTWARDS ARROW FROM BAR TO BLACK DIAMOND |
⤟ |
| U+2920 |
RIGHTWARDS ARROW FROM BAR TO BLACK DIAMOND |
⤠ |
| U+2921 |
NORTH WEST AND SOUTH EAST ARROW |
⤡ |
| U+2922 |
NORTH EAST AND SOUTH WEST ARROW |
⤢ |
| U+2923 |
NORTH WEST ARROW WITH HOOK |
⤣ |
| U+2924 |
NORTH EAST ARROW WITH HOOK |
⤤ |
| U+2925 |
SOUTH EAST ARROW WITH HOOK |
⤥ |
| U+2926 |
SOUTH WEST ARROW WITH HOOK |
⤦ |
| U+2927 |
NORTH WEST ARROW AND NORTH EAST ARROW |
⤧ |
| U+2928 |
NORTH EAST ARROW AND SOUTH EAST ARROW |
⤨ |
| U+2929 |
SOUTH EAST ARROW AND SOUTH WEST ARROW |
⤩ |
| U+292A |
SOUTH WEST ARROW AND NORTH WEST ARROW |
⤪ |
| U+292B |
RISING DIAGONAL CROSSING FALLING DIAGONAL |
⤫ |
| U+292C |
FALLING DIAGONAL CROSSING RISING DIAGONAL |
⤬ |
| U+292D |
SOUTH EAST ARROW CROSSING NORTH EAST ARROW |
⤭ |
| U+292E |
NORTH EAST ARROW CROSSING SOUTH EAST ARROW |
⤮ |
| U+292F |
FALLING DIAGONAL CROSSING NORTH EAST ARROW |
⤯ |
| U+2930 |
RISING DIAGONAL CROSSING SOUTH EAST ARROW |
⤰ |
| U+2931 |
NORTH EAST ARROW CROSSING NORTH WEST ARROW |
⤱ |
| U+2932 |
NORTH WEST ARROW CROSSING NORTH EAST ARROW |
⤲ |
| U+2933 |
WAVE ARROW POINTING DIRECTLY RIGHT |
⤳ |
| U+2934 |
ARROW POINTING RIGHTWARDS THEN CURVING UPWARDS |
⤴ |
| U+2935 |
ARROW POINTING RIGHTWARDS THEN CURVING DOWNWARDS |
⤵ |
| U+2936 |
ARROW POINTING DOWNWARDS THEN CURVING LEFTWARDS |
⤶ |
| U+2937 |
ARROW POINTING DOWNWARDS THEN CURVING RIGHTWARDS |
⤷ |
| U+2938 |
RIGHT-SIDE ARC CLOCKWISE ARROW |
⤸ |
| U+2939 |
LEFT-SIDE ARC ANTICLOCKWISE ARROW |
⤹ |
| U+293A |
TOP ARC ANTICLOCKWISE ARROW |
⤺ |
| U+293B |
BOTTOM ARC ANTICLOCKWISE ARROW |
⤻ |
| U+293C |
TOP ARC CLOCKWISE ARROW WITH MINUS |
⤼ |
| U+293D |
TOP ARC ANTICLOCKWISE ARROW WITH PLUS |
⤽ |
| U+293E |
LOWER RIGHT SEMICIRCULAR CLOCKWISE ARROW |
⤾ |
| U+293F |
LOWER LEFT SEMICIRCULAR ANTICLOCKWISE ARROW |
⤿ |
| U+2940 |
ANTICLOCKWISE CLOSED CIRCLE ARROW |
⥀ |
| U+2941 |
CLOCKWISE CLOSED CIRCLE ARROW |
⥁ |
| U+2942 |
RIGHTWARDS ARROW ABOVE SHORT LEFTWARDS ARROW |
⥂ |
| U+2943 |
LEFTWARDS ARROW ABOVE SHORT RIGHTWARDS ARROW |
⥃ |
| U+2944 |
SHORT RIGHTWARDS ARROW ABOVE LEFTWARDS ARROW |
⥄ |
| U+2945 |
RIGHTWARDS ARROW WITH PLUS BELOW |
⥅ |
| U+2946 |
LEFTWARDS ARROW WITH PLUS BELOW |
⥆ |
| U+2947 |
RIGHTWARDS ARROW THROUGH X |
⥇ |
| U+2948 |
LEFT RIGHT ARROW THROUGH SMALL CIRCLE |
⥈ |
| U+2949 |
UPWARDS TWO-HEADED ARROW FROM SMALL CIRCLE |
⥉ |
| U+294A |
LEFT BARB UP RIGHT BARB DOWN HARPOON |
⥊ |
| U+294B |
LEFT BARB DOWN RIGHT BARB UP HARPOON |
⥋ |
| U+294C |
UP BARB RIGHT DOWN BARB LEFT HARPOON |
⥌ |
| U+294D |
UP BARB LEFT DOWN BARB RIGHT HARPOON |
⥍ |
| U+294E |
LEFT BARB UP RIGHT BARB UP HARPOON |
⥎ |
| U+294F |
UP BARB RIGHT DOWN BARB RIGHT HARPOON |
⥏ |
| U+2950 |
LEFT BARB DOWN RIGHT BARB DOWN HARPOON |
⥐ |
| U+2951 |
UP BARB LEFT DOWN BARB LEFT HARPOON |
⥑ |
| U+2952 |
LEFTWARDS HARPOON WITH BARB UP TO BAR |
⥒ |
| U+2953 |
RIGHTWARDS HARPOON WITH BARB UP TO BAR |
⥓ |
| U+2954 |
UPWARDS HARPOON WITH BARB RIGHT TO BAR |
⥔ |
| U+2955 |
DOWNWARDS HARPOON WITH BARB RIGHT TO BAR |
⥕ |
| U+2956 |
LEFTWARDS HARPOON WITH BARB DOWN TO BAR |
⥖ |
| U+2957 |
RIGHTWARDS HARPOON WITH BARB DOWN TO BAR |
⥗ |
| U+2958 |
UPWARDS HARPOON WITH BARB LEFT TO BAR |
⥘ |
| U+2959 |
DOWNWARDS HARPOON WITH BARB LEFT TO BAR |
⥙ |
| U+295A |
LEFTWARDS HARPOON WITH BARB UP FROM BAR |
⥚ |
| U+295B |
RIGHTWARDS HARPOON WITH BARB UP FROM BAR |
⥛ |
| U+295C |
UPWARDS HARPOON WITH BARB RIGHT FROM BAR |
⥜ |
| U+295D |
DOWNWARDS HARPOON WITH BARB RIGHT FROM BAR |
⥝ |
| U+295E |
LEFTWARDS HARPOON WITH BARB DOWN FROM BAR |
⥞ |
| U+295F |
RIGHTWARDS HARPOON WITH BARB DOWN FROM BAR |
⥟ |
| U+2960 |
UPWARDS HARPOON WITH BARB LEFT FROM BAR |
⥠ |
| U+2961 |
DOWNWARDS HARPOON WITH BARB LEFT FROM BAR |
⥡ |
| U+2962 |
LEFTWARDS HARPOON WITH BARB UP ABOVE LEFTWARDS HARPOON WITH BARB DOWN |
⥢ |
| U+2963 |
UPWARDS HARPOON WITH BARB LEFT BESIDE UPWARDS HARPOON WITH BARB RIGHT |
⥣ |
| U+2964 |
RIGHTWARDS HARPOON WITH BARB UP ABOVE RIGHTWARDS HARPOON WITH BARB DOWN |
⥤ |
| U+2965 |
DOWNWARDS HARPOON WITH BARB LEFT BESIDE DOWNWARDS HARPOON WITH BARB RIGHT |
⥥ |
| U+2966 |
LEFTWARDS HARPOON WITH BARB UP ABOVE RIGHTWARDS HARPOON WITH BARB UP |
⥦ |
| U+2967 |
LEFTWARDS HARPOON WITH BARB DOWN ABOVE RIGHTWARDS HARPOON WITH BARB DOWN |
⥧ |
| U+2968 |
RIGHTWARDS HARPOON WITH BARB UP ABOVE LEFTWARDS HARPOON WITH BARB UP |
⥨ |
| U+2969 |
RIGHTWARDS HARPOON WITH BARB DOWN ABOVE LEFTWARDS HARPOON WITH BARB DOWN |
⥩ |
| U+296A |
LEFTWARDS HARPOON WITH BARB UP ABOVE LONG DASH |
⥪ |
| U+296B |
LEFTWARDS HARPOON WITH BARB DOWN BELOW LONG DASH |
⥫ |
| U+296C |
RIGHTWARDS HARPOON WITH BARB UP ABOVE LONG DASH |
⥬ |
| U+296D |
RIGHTWARDS HARPOON WITH BARB DOWN BELOW LONG DASH |
⥭ |
| U+296E |
UPWARDS HARPOON WITH BARB LEFT BESIDE DOWNWARDS HARPOON WITH BARB RIGHT |
⥮ |
| U+296F |
DOWNWARDS HARPOON WITH BARB LEFT BESIDE UPWARDS HARPOON WITH BARB RIGHT |
⥯ |
| U+2970 |
RIGHT DOUBLE ARROW WITH ROUNDED HEAD |
⥰ |
| U+2971 |
EQUALS SIGN ABOVE RIGHTWARDS ARROW |
⥱ |
| U+2972 |
TILDE OPERATOR ABOVE RIGHTWARDS ARROW |
⥲ |
| U+2973 |
LEFTWARDS ARROW ABOVE TILDE OPERATOR |
⥳ |
| U+2974 |
RIGHTWARDS ARROW ABOVE TILDE OPERATOR |
⥴ |
| U+2975 |
RIGHTWARDS ARROW ABOVE ALMOST EQUAL TO |
⥵ |
| U+2976 |
LESS-THAN ABOVE LEFTWARDS ARROW |
⥶ |
| U+2977 |
LEFTWARDS ARROW THROUGH LESS-THAN |
⥷ |
| U+2978 |
GREATER-THAN ABOVE RIGHTWARDS ARROW |
⥸ |
| U+2979 |
SUBSET ABOVE RIGHTWARDS ARROW |
⥹ |
| U+297A |
LEFTWARDS ARROW THROUGH SUBSET |
⥺ |
| U+297B |
SUPERSET ABOVE LEFTWARDS ARROW |
⥻ |
| U+297C |
LEFT FISH TAIL |
⥼ |
| U+297D |
RIGHT FISH TAIL |
⥽ |
| U+297E |
UP FISH TAIL |
⥾ |
| U+297F |
DOWN FISH TAIL |
⥿ |
| U+2980 |
TRIPLE VERTICAL BAR DELIMITER |
⦀ |
| U+2981 |
Z NOTATION SPOT |
⦁ |
| U+2982 |
Z NOTATION TYPE COLON |
⦂ |
| U+2999 |
DOTTED FENCE |
⦙ |
| U+299A |
VERTICAL ZIGZAG LINE |
⦚ |
| U+299B |
MEASURED ANGLE OPENING LEFT |
⦛ |
| U+299C |
RIGHT ANGLE VARIANT WITH SQUARE |
⦜ |
| U+299D |
MEASURED RIGHT ANGLE WITH DOT |
⦝ |
| U+299E |
ANGLE WITH S INSIDE |
⦞ |
| U+299F |
ACUTE ANGLE |
⦟ |
| U+29A0 |
SPHERICAL ANGLE OPENING LEFT |
⦠ |
| U+29A1 |
SPHERICAL ANGLE OPENING UP |
⦡ |
| U+29A2 |
TURNED ANGLE |
⦢ |
| U+29A3 |
REVERSED ANGLE |
⦣ |
| U+29A4 |
ANGLE WITH UNDERBAR |
⦤ |
| U+29A5 |
REVERSED ANGLE WITH UNDERBAR |
⦥ |
| U+29A6 |
OBLIQUE ANGLE OPENING UP |
⦦ |
| U+29A7 |
OBLIQUE ANGLE OPENING DOWN |
⦧ |
| U+29A8 |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING UP AND RIGHT |
⦨ |
| U+29A9 |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING UP AND LEFT |
⦩ |
| U+29AA |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING DOWN AND RIGHT |
⦪ |
| U+29AB |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING DOWN AND LEFT |
⦫ |
| U+29AC |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING RIGHT AND UP |
⦬ |
| U+29AD |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING LEFT AND UP |
⦭ |
| U+29AE |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING RIGHT AND DOWN |
⦮ |
| U+29AF |
MEASURED ANGLE WITH OPEN ARM ENDING IN ARROW POINTING LEFT AND DOWN |
⦯ |
| U+29B0 |
REVERSED EMPTY SET |
⦰ |
| U+29B1 |
EMPTY SET WITH OVERBAR |
⦱ |
| U+29B2 |
EMPTY SET WITH SMALL CIRCLE ABOVE |
⦲ |
| U+29B3 |
EMPTY SET WITH RIGHT ARROW ABOVE |
⦳ |
| U+29B4 |
EMPTY SET WITH LEFT ARROW ABOVE |
⦴ |
| U+29B5 |
CIRCLE WITH HORIZONTAL BAR |
⦵ |
| U+29B6 |
CIRCLED VERTICAL BAR |
⦶ |
| U+29B7 |
CIRCLED PARALLEL |
⦷ |
| U+29B8 |
CIRCLED REVERSE SOLIDUS |
⦸ |
| U+29B9 |
CIRCLED PERPENDICULAR |
⦹ |
| U+29BA |
CIRCLE DIVIDED BY HORIZONTAL BAR AND TOP HALF DIVIDED BY VERTICAL BAR |
⦺ |
| U+29BB |
CIRCLE WITH SUPERIMPOSED X |
⦻ |
| U+29BC |
CIRCLED ANTICLOCKWISE-ROTATED DIVISION SIGN |
⦼ |
| U+29BD |
UP ARROW THROUGH CIRCLE |
⦽ |
| U+29BE |
CIRCLED WHITE BULLET |
⦾ |
| U+29BF |
CIRCLED BULLET |
⦿ |
| U+29C0 |
CIRCLED LESS-THAN |
⧀ |
| U+29C1 |
CIRCLED GREATER-THAN |
⧁ |
| U+29C2 |
CIRCLE WITH SMALL CIRCLE TO THE RIGHT |
⧂ |
| U+29C3 |
CIRCLE WITH TWO HORIZONTAL STROKES TO THE RIGHT |
⧃ |
| U+29C4 |
SQUARED RISING DIAGONAL SLASH |
⧄ |
| U+29C5 |
SQUARED FALLING DIAGONAL SLASH |
⧅ |
| U+29C6 |
SQUARED ASTERISK |
⧆ |
| U+29C7 |
SQUARED SMALL CIRCLE |
⧇ |
| U+29C8 |
SQUARED SQUARE |
⧈ |
| U+29C9 |
TWO JOINED SQUARES |
⧉ |
| U+29CA |
TRIANGLE WITH DOT ABOVE |
⧊ |
| U+29CB |
TRIANGLE WITH UNDERBAR |
⧋ |
| U+29CC |
S IN TRIANGLE |
⧌ |
| U+29CD |
TRIANGLE WITH SERIFS AT BOTTOM |
⧍ |
| U+29CE |
RIGHT TRIANGLE ABOVE LEFT TRIANGLE |
⧎ |
| U+29CF |
LEFT TRIANGLE BESIDE VERTICAL BAR |
⧏ |
| U+29D0 |
VERTICAL BAR BESIDE RIGHT TRIANGLE |
⧐ |
| U+29D1 |
BOWTIE WITH LEFT HALF BLACK |
⧑ |
| U+29D2 |
BOWTIE WITH RIGHT HALF BLACK |
⧒ |
| U+29D3 |
BLACK BOWTIE |
⧓ |
| U+29D4 |
TIMES WITH LEFT HALF BLACK |
⧔ |
| U+29D5 |
TIMES WITH RIGHT HALF BLACK |
⧕ |
| U+29D6 |
WHITE HOURGLASS |
⧖ |
| U+29D7 |
BLACK HOURGLASS |
⧗ |
| U+29DC |
INCOMPLETE INFINITY |
⧜ |
| U+29DD |
TIE OVER INFINITY |
⧝ |
| U+29DE |
INFINITY NEGATED WITH VERTICAL BAR |
⧞ |
| U+29DF |
DOUBLE-ENDED MULTIMAP |
⧟ |
| U+29E0 |
SQUARE WITH CONTOURED OUTLINE |
⧠ |
| U+29E1 |
INCREASES AS |
⧡ |
| U+29E2 |
SHUFFLE PRODUCT |
⧢ |
| U+29E3 |
EQUALS SIGN AND SLANTED PARALLEL |
⧣ |
| U+29E4 |
EQUALS SIGN AND SLANTED PARALLEL WITH TILDE ABOVE |
⧤ |
| U+29E5 |
IDENTICAL TO AND SLANTED PARALLEL |
⧥ |
| U+29E6 |
GLEICH STARK |
⧦ |
| U+29E7 |
THERMODYNAMIC |
⧧ |
| U+29E8 |
DOWN-POINTING TRIANGLE WITH LEFT HALF BLACK |
⧨ |
| U+29E9 |
DOWN-POINTING TRIANGLE WITH RIGHT HALF BLACK |
⧩ |
| U+29EA |
BLACK DIAMOND WITH DOWN ARROW |
⧪ |
| U+29EB |
BLACK LOZENGE |
⧫ |
| U+29EC |
WHITE CIRCLE WITH DOWN ARROW |
⧬ |
| U+29ED |
BLACK CIRCLE WITH DOWN ARROW |
⧭ |
| U+29EE |
ERROR-BARRED WHITE SQUARE |
⧮ |
| U+29EF |
ERROR-BARRED BLACK SQUARE |
⧯ |
| U+29F0 |
ERROR-BARRED WHITE DIAMOND |
⧰ |
| U+29F1 |
ERROR-BARRED BLACK DIAMOND |
⧱ |
| U+29F2 |
ERROR-BARRED WHITE CIRCLE |
⧲ |
| U+29F3 |
ERROR-BARRED BLACK CIRCLE |
⧳ |
| U+29F4 |
RULE-DELAYED |
⧴ |
| U+29F5 |
REVERSE SOLIDUS OPERATOR |
⧵ |
| U+29F6 |
SOLIDUS WITH OVERBAR |
⧶ |
| U+29F7 |
REVERSE SOLIDUS WITH HORIZONTAL STROKE |
⧷ |
| U+29F8 |
BIG SOLIDUS |
⧸ |
| U+29F9 |
BIG REVERSE SOLIDUS |
⧹ |
| U+29FA |
DOUBLE PLUS |
⧺ |
| U+29FB |
TRIPLE PLUS |
⧻ |
| U+29FE |
TINY |
⧾ |
| U+29FF |
MINY |
⧿ |
| U+2A00 |
N-ARY CIRCLED DOT OPERATOR |
⨀ |
| U+2A01 |
N-ARY CIRCLED PLUS OPERATOR |
⨁ |
| U+2A02 |
N-ARY CIRCLED TIMES OPERATOR |
⨂ |
| U+2A03 |
N-ARY UNION OPERATOR WITH DOT |
⨃ |
| U+2A04 |
N-ARY UNION OPERATOR WITH PLUS |
⨄ |
| U+2A05 |
N-ARY SQUARE INTERSECTION OPERATOR |
⨅ |
| U+2A06 |
N-ARY SQUARE UNION OPERATOR |
⨆ |
| U+2A07 |
TWO LOGICAL AND OPERATOR |
⨇ |
| U+2A08 |
TWO LOGICAL OR OPERATOR |
⨈ |
| U+2A09 |
N-ARY TIMES OPERATOR |
⨉ |
| U+2A0A |
MODULO TWO SUM |
⨊ |
| U+2A0B |
SUMMATION WITH INTEGRAL |
⨋ |
| U+2A0C |
QUADRUPLE INTEGRAL OPERATOR |
⨌ |
| U+2A0D |
FINITE PART INTEGRAL |
⨍ |
| U+2A0E |
INTEGRAL WITH DOUBLE STROKE |
⨎ |
| U+2A0F |
INTEGRAL AVERAGE WITH SLASH |
⨏ |
| U+2A10 |
CIRCULATION FUNCTION |
⨐ |
| U+2A11 |
ANTICLOCKWISE INTEGRATION |
⨑ |
| U+2A12 |
LINE INTEGRATION WITH RECTANGULAR PATH AROUND POLE |
⨒ |
| U+2A13 |
LINE INTEGRATION WITH SEMICIRCULAR PATH AROUND POLE |
⨓ |
| U+2A14 |
LINE INTEGRATION NOT INCLUDING THE POLE |
⨔ |
| U+2A15 |
INTEGRAL AROUND A POINT OPERATOR |
⨕ |
| U+2A16 |
QUATERNION INTEGRAL OPERATOR |
⨖ |
| U+2A17 |
INTEGRAL WITH LEFTWARDS ARROW WITH HOOK |
⨗ |
| U+2A18 |
INTEGRAL WITH TIMES SIGN |
⨘ |
| U+2A19 |
INTEGRAL WITH INTERSECTION |
⨙ |
| U+2A1A |
INTEGRAL WITH UNION |
⨚ |
| U+2A1B |
INTEGRAL WITH OVERBAR |
⨛ |
| U+2A1C |
INTEGRAL WITH UNDERBAR |
⨜ |
| U+2A1D |
JOIN |
⨝ |
| U+2A1E |
LARGE LEFT TRIANGLE OPERATOR |
⨞ |
| U+2A1F |
Z NOTATION SCHEMA COMPOSITION |
⨟ |
| U+2A20 |
Z NOTATION SCHEMA PIPING |
⨠ |
| U+2A21 |
Z NOTATION SCHEMA PROJECTION |
⨡ |
| U+2A22 |
PLUS SIGN WITH SMALL CIRCLE ABOVE |
⨢ |
| U+2A23 |
PLUS SIGN WITH CIRCUMFLEX ACCENT ABOVE |
⨣ |
| U+2A24 |
PLUS SIGN WITH TILDE ABOVE |
⨤ |
| U+2A25 |
PLUS SIGN WITH DOT BELOW |
⨥ |
| U+2A26 |
PLUS SIGN WITH TILDE BELOW |
⨦ |
| U+2A27 |
PLUS SIGN WITH SUBSCRIPT TWO |
⨧ |
| U+2A28 |
PLUS SIGN WITH BLACK TRIANGLE |
⨨ |
| U+2A29 |
MINUS SIGN WITH COMMA ABOVE |
⨩ |
| U+2A2A |
MINUS SIGN WITH DOT BELOW |
⨪ |
| U+2A2B |
MINUS SIGN WITH FALLING DOTS |
⨫ |
| U+2A2C |
MINUS SIGN WITH RISING DOTS |
⨬ |
| U+2A2D |
PLUS SIGN IN LEFT HALF CIRCLE |
⨭ |
| U+2A2E |
PLUS SIGN IN RIGHT HALF CIRCLE |
⨮ |
| U+2A2F |
VECTOR OR CROSS PRODUCT |
⨯ |
| U+2A30 |
MULTIPLICATION SIGN WITH DOT ABOVE |
⨰ |
| U+2A31 |
MULTIPLICATION SIGN WITH UNDERBAR |
⨱ |
| U+2A32 |
SEMIDIRECT PRODUCT WITH BOTTOM CLOSED |
⨲ |
| U+2A33 |
SMASH PRODUCT |
⨳ |
| U+2A34 |
MULTIPLICATION SIGN IN LEFT HALF CIRCLE |
⨴ |
| U+2A35 |
MULTIPLICATION SIGN IN RIGHT HALF CIRCLE |
⨵ |
| U+2A36 |
CIRCLED MULTIPLICATION SIGN WITH CIRCUMFLEX ACCENT |
⨶ |
| U+2A37 |
MULTIPLICATION SIGN IN DOUBLE CIRCLE |
⨷ |
| U+2A38 |
CIRCLED DIVISION SIGN |
⨸ |
| U+2A39 |
PLUS SIGN IN TRIANGLE |
⨹ |
| U+2A3A |
MINUS SIGN IN TRIANGLE |
⨺ |
| U+2A3B |
MULTIPLICATION SIGN IN TRIANGLE |
⨻ |
| U+2A3C |
INTERIOR PRODUCT |
⨼ |
| U+2A3D |
RIGHTHAND INTERIOR PRODUCT |
⨽ |
| U+2A3E |
Z NOTATION RELATIONAL COMPOSITION |
⨾ |
| U+2A3F |
AMALGAMATION OR COPRODUCT |
⨿ |
| U+2A40 |
INTERSECTION WITH DOT |
⩀ |
| U+2A41 |
UNION WITH MINUS SIGN |
⩁ |
| U+2A42 |
UNION WITH OVERBAR |
⩂ |
| U+2A43 |
INTERSECTION WITH OVERBAR |
⩃ |
| U+2A44 |
INTERSECTION WITH LOGICAL AND |
⩄ |
| U+2A45 |
UNION WITH LOGICAL OR |
⩅ |
| U+2A46 |
UNION ABOVE INTERSECTION |
⩆ |
| U+2A47 |
INTERSECTION ABOVE UNION |
⩇ |
| U+2A48 |
UNION ABOVE BAR ABOVE INTERSECTION |
⩈ |
| U+2A49 |
INTERSECTION ABOVE BAR ABOVE UNION |
⩉ |
| U+2A4A |
UNION BESIDE AND JOINED WITH UNION |
⩊ |
| U+2A4B |
INTERSECTION BESIDE AND JOINED WITH INTERSECTION |
⩋ |
| U+2A4C |
CLOSED UNION WITH SERIFS |
⩌ |
| U+2A4D |
CLOSED INTERSECTION WITH SERIFS |
⩍ |
| U+2A4E |
DOUBLE SQUARE INTERSECTION |
⩎ |
| U+2A4F |
DOUBLE SQUARE UNION |
⩏ |
| U+2A50 |
CLOSED UNION WITH SERIFS AND SMASH PRODUCT |
⩐ |
| U+2A51 |
LOGICAL AND WITH DOT ABOVE |
⩑ |
| U+2A52 |
LOGICAL OR WITH DOT ABOVE |
⩒ |
| U+2A53 |
DOUBLE LOGICAL AND |
⩓ |
| U+2A54 |
DOUBLE LOGICAL OR |
⩔ |
| U+2A55 |
TWO INTERSECTING LOGICAL AND |
⩕ |
| U+2A56 |
TWO INTERSECTING LOGICAL OR |
⩖ |
| U+2A57 |
SLOPING LARGE OR |
⩗ |
| U+2A58 |
SLOPING LARGE AND |
⩘ |
| U+2A59 |
LOGICAL OR OVERLAPPING LOGICAL AND |
⩙ |
| U+2A5A |
LOGICAL AND WITH MIDDLE STEM |
⩚ |
| U+2A5B |
LOGICAL OR WITH MIDDLE STEM |
⩛ |
| U+2A5C |
LOGICAL AND WITH HORIZONTAL DASH |
⩜ |
| U+2A5D |
LOGICAL OR WITH HORIZONTAL DASH |
⩝ |
| U+2A5E |
LOGICAL AND WITH DOUBLE OVERBAR |
⩞ |
| U+2A5F |
LOGICAL AND WITH UNDERBAR |
⩟ |
| U+2A60 |
LOGICAL AND WITH DOUBLE UNDERBAR |
⩠ |
| U+2A61 |
SMALL VEE WITH UNDERBAR |
⩡ |
| U+2A62 |
LOGICAL OR WITH DOUBLE OVERBAR |
⩢ |
| U+2A63 |
LOGICAL OR WITH DOUBLE UNDERBAR |
⩣ |
| U+2A64 |
Z NOTATION DOMAIN ANTIRESTRICTION |
⩤ |
| U+2A65 |
Z NOTATION RANGE ANTIRESTRICTION |
⩥ |
| U+2A66 |
EQUALS SIGN WITH DOT BELOW |
⩦ |
| U+2A67 |
IDENTICAL WITH DOT ABOVE |
⩧ |
| U+2A68 |
TRIPLE HORIZONTAL BAR WITH DOUBLE VERTICAL STROKE |
⩨ |
| U+2A69 |
TRIPLE HORIZONTAL BAR WITH TRIPLE VERTICAL STROKE |
⩩ |
| U+2A6A |
TILDE OPERATOR WITH DOT ABOVE |
⩪ |
| U+2A6B |
TILDE OPERATOR WITH RISING DOTS |
⩫ |
| U+2A6C |
SIMILAR MINUS SIMILAR |
⩬ |
| U+2A6D |
CONGRUENT WITH DOT ABOVE |
⩭ |
| U+2A6E |
EQUALS WITH ASTERISK |
⩮ |
| U+2A6F |
ALMOST EQUAL TO WITH CIRCUMFLEX ACCENT |
⩯ |
| U+2A70 |
APPROXIMATELY EQUAL OR EQUAL TO |
⩰ |
| U+2A71 |
EQUALS SIGN ABOVE PLUS SIGN |
⩱ |
| U+2A72 |
PLUS SIGN ABOVE EQUALS SIGN |
⩲ |
| U+2A73 |
EQUALS SIGN ABOVE TILDE OPERATOR |
⩳ |
| U+2A74 |
DOUBLE COLON EQUAL |
⩴ |
| U+2A75 |
TWO CONSECUTIVE EQUALS SIGNS |
⩵ |
| U+2A76 |
THREE CONSECUTIVE EQUALS SIGNS |
⩶ |
| U+2A77 |
EQUALS SIGN WITH TWO DOTS ABOVE AND TWO DOTS BELOW |
⩷ |
| U+2A78 |
EQUIVALENT WITH FOUR DOTS ABOVE |
⩸ |
| U+2A79 |
LESS-THAN WITH CIRCLE INSIDE |
⩹ |
| U+2A7A |
GREATER-THAN WITH CIRCLE INSIDE |
⩺ |
| U+2A7B |
LESS-THAN WITH QUESTION MARK ABOVE |
⩻ |
| U+2A7C |
GREATER-THAN WITH QUESTION MARK ABOVE |
⩼ |
| U+2A7D |
LESS-THAN OR SLANTED EQUAL TO |
⩽ |
| U+2A7E |
GREATER-THAN OR SLANTED EQUAL TO |
⩾ |
| U+2A7F |
LESS-THAN OR SLANTED EQUAL TO WITH DOT INSIDE |
⩿ |
| U+2A80 |
GREATER-THAN OR SLANTED EQUAL TO WITH DOT INSIDE |
⪀ |
| U+2A81 |
LESS-THAN OR SLANTED EQUAL TO WITH DOT ABOVE |
⪁ |
| U+2A82 |
GREATER-THAN OR SLANTED EQUAL TO WITH DOT ABOVE |
⪂ |
| U+2A83 |
LESS-THAN OR SLANTED EQUAL TO WITH DOT ABOVE RIGHT |
⪃ |
| U+2A84 |
GREATER-THAN OR SLANTED EQUAL TO WITH DOT ABOVE LEFT |
⪄ |
| U+2A85 |
LESS-THAN OR APPROXIMATE |
⪅ |
| U+2A86 |
GREATER-THAN OR APPROXIMATE |
⪆ |
| U+2A87 |
LESS-THAN AND SINGLE-LINE NOT EQUAL TO |
⪇ |
| U+2A88 |
GREATER-THAN AND SINGLE-LINE NOT EQUAL TO |
⪈ |
| U+2A89 |
LESS-THAN AND NOT APPROXIMATE |
⪉ |
| U+2A8A |
GREATER-THAN AND NOT APPROXIMATE |
⪊ |
| U+2A8B |
LESS-THAN ABOVE DOUBLE-LINE EQUAL ABOVE GREATER-THAN |
⪋ |
| U+2A8C |
GREATER-THAN ABOVE DOUBLE-LINE EQUAL ABOVE LESS-THAN |
⪌ |
| U+2A8D |
LESS-THAN ABOVE SIMILAR OR EQUAL |
⪍ |
| U+2A8E |
GREATER-THAN ABOVE SIMILAR OR EQUAL |
⪎ |
| U+2A8F |
LESS-THAN ABOVE SIMILAR ABOVE GREATER-THAN |
⪏ |
| U+2A90 |
GREATER-THAN ABOVE SIMILAR ABOVE LESS-THAN |
⪐ |
| U+2A91 |
LESS-THAN ABOVE GREATER-THAN ABOVE DOUBLE-LINE EQUAL |
⪑ |
| U+2A92 |
GREATER-THAN ABOVE LESS-THAN ABOVE DOUBLE-LINE EQUAL |
⪒ |
| U+2A93 |
LESS-THAN ABOVE SLANTED EQUAL ABOVE GREATER-THAN ABOVE SLANTED EQUAL |
⪓ |
| U+2A94 |
GREATER-THAN ABOVE SLANTED EQUAL ABOVE LESS-THAN ABOVE SLANTED EQUAL |
⪔ |
| U+2A95 |
SLANTED EQUAL TO OR LESS-THAN |
⪕ |
| U+2A96 |
SLANTED EQUAL TO OR GREATER-THAN |
⪖ |
| U+2A97 |
SLANTED EQUAL TO OR LESS-THAN WITH DOT INSIDE |
⪗ |
| U+2A98 |
SLANTED EQUAL TO OR GREATER-THAN WITH DOT INSIDE |
⪘ |
| U+2A99 |
DOUBLE-LINE EQUAL TO OR LESS-THAN |
⪙ |
| U+2A9A |
DOUBLE-LINE EQUAL TO OR GREATER-THAN |
⪚ |
| U+2A9B |
DOUBLE-LINE SLANTED EQUAL TO OR LESS-THAN |
⪛ |
| U+2A9C |
DOUBLE-LINE SLANTED EQUAL TO OR GREATER-THAN |
⪜ |
| U+2A9D |
SIMILAR OR LESS-THAN |
⪝ |
| U+2A9E |
SIMILAR OR GREATER-THAN |
⪞ |
| U+2A9F |
SIMILAR ABOVE LESS-THAN ABOVE EQUALS SIGN |
⪟ |
| U+2AA0 |
SIMILAR ABOVE GREATER-THAN ABOVE EQUALS SIGN |
⪠ |
| U+2AA1 |
DOUBLE NESTED LESS-THAN |
⪡ |
| U+2AA2 |
DOUBLE NESTED GREATER-THAN |
⪢ |
| U+2AA3 |
DOUBLE NESTED LESS-THAN WITH UNDERBAR |
⪣ |
| U+2AA4 |
GREATER-THAN OVERLAPPING LESS-THAN |
⪤ |
| U+2AA5 |
GREATER-THAN BESIDE LESS-THAN |
⪥ |
| U+2AA6 |
LESS-THAN CLOSED BY CURVE |
⪦ |
| U+2AA7 |
GREATER-THAN CLOSED BY CURVE |
⪧ |
| U+2AA8 |
LESS-THAN CLOSED BY CURVE ABOVE SLANTED EQUAL |
⪨ |
| U+2AA9 |
GREATER-THAN CLOSED BY CURVE ABOVE SLANTED EQUAL |
⪩ |
| U+2AAA |
SMALLER THAN |
⪪ |
| U+2AAB |
LARGER THAN |
⪫ |
| U+2AAC |
SMALLER THAN OR EQUAL TO |
⪬ |
| U+2AAD |
LARGER THAN OR EQUAL TO |
⪭ |
| U+2AAE |
EQUALS SIGN WITH BUMPY ABOVE |
⪮ |
| U+2AAF |
PRECEDES ABOVE SINGLE-LINE EQUALS SIGN |
⪯ |
| U+2AB0 |
SUCCEEDS ABOVE SINGLE-LINE EQUALS SIGN |
⪰ |
| U+2AB1 |
PRECEDES ABOVE SINGLE-LINE NOT EQUAL TO |
⪱ |
| U+2AB2 |
SUCCEEDS ABOVE SINGLE-LINE NOT EQUAL TO |
⪲ |
| U+2AB3 |
PRECEDES ABOVE EQUALS SIGN |
⪳ |
| U+2AB4 |
SUCCEEDS ABOVE EQUALS SIGN |
⪴ |
| U+2AB5 |
PRECEDES ABOVE NOT EQUAL TO |
⪵ |
| U+2AB6 |
SUCCEEDS ABOVE NOT EQUAL TO |
⪶ |
| U+2AB7 |
PRECEDES ABOVE ALMOST EQUAL TO |
⪷ |
| U+2AB8 |
SUCCEEDS ABOVE ALMOST EQUAL TO |
⪸ |
| U+2AB9 |
PRECEDES ABOVE NOT ALMOST EQUAL TO |
⪹ |
| U+2ABA |
SUCCEEDS ABOVE NOT ALMOST EQUAL TO |
⪺ |
| U+2ABB |
DOUBLE PRECEDES |
⪻ |
| U+2ABC |
DOUBLE SUCCEEDS |
⪼ |
| U+2ABD |
SUBSET WITH DOT |
⪽ |
| U+2ABE |
SUPERSET WITH DOT |
⪾ |
| U+2ABF |
SUBSET WITH PLUS SIGN BELOW |
⪿ |
| U+2AC0 |
SUPERSET WITH PLUS SIGN BELOW |
⫀ |
| U+2AC1 |
SUBSET WITH MULTIPLICATION SIGN BELOW |
⫁ |
| U+2AC2 |
SUPERSET WITH MULTIPLICATION SIGN BELOW |
⫂ |
| U+2AC3 |
SUBSET OF OR EQUAL TO WITH DOT ABOVE |
⫃ |
| U+2AC4 |
SUPERSET OF OR EQUAL TO WITH DOT ABOVE |
⫄ |
| U+2AC5 |
SUBSET OF ABOVE EQUALS SIGN |
⫅ |
| U+2AC6 |
SUPERSET OF ABOVE EQUALS SIGN |
⫆ |
| U+2AC7 |
SUBSET OF ABOVE TILDE OPERATOR |
⫇ |
| U+2AC8 |
SUPERSET OF ABOVE TILDE OPERATOR |
⫈ |
| U+2AC9 |
SUBSET OF ABOVE ALMOST EQUAL TO |
⫉ |
| U+2ACA |
SUPERSET OF ABOVE ALMOST EQUAL TO |
⫊ |
| U+2ACB |
SUBSET OF ABOVE NOT EQUAL TO |
⫋ |
| U+2ACC |
SUPERSET OF ABOVE NOT EQUAL TO |
⫌ |
| U+2ACD |
SQUARE LEFT OPEN BOX OPERATOR |
⫍ |
| U+2ACE |
SQUARE RIGHT OPEN BOX OPERATOR |
⫎ |
| U+2ACF |
CLOSED SUBSET |
⫏ |
| U+2AD0 |
CLOSED SUPERSET |
⫐ |
| U+2AD1 |
CLOSED SUBSET OR EQUAL TO |
⫑ |
| U+2AD2 |
CLOSED SUPERSET OR EQUAL TO |
⫒ |
| U+2AD3 |
SUBSET ABOVE SUPERSET |
⫓ |
| U+2AD4 |
SUPERSET ABOVE SUBSET |
⫔ |
| U+2AD5 |
SUBSET ABOVE SUBSET |
⫕ |
| U+2AD6 |
SUPERSET ABOVE SUPERSET |
⫖ |
| U+2AD7 |
SUPERSET BESIDE SUBSET |
⫗ |
| U+2AD8 |
SUPERSET BESIDE AND JOINED BY DASH WITH SUBSET |
⫘ |
| U+2AD9 |
ELEMENT OF OPENING DOWNWARDS |
⫙ |
| U+2ADA |
PITCHFORK WITH TEE TOP |
⫚ |
| U+2ADB |
TRANSVERSAL INTERSECTION |
⫛ |
| U+2ADC |
FORKING |
⫝̸ |
| U+2ADD |
NONFORKING |
⫝ |
| U+2ADE |
SHORT LEFT TACK |
⫞ |
| U+2ADF |
SHORT DOWN TACK |
⫟ |
| U+2AE0 |
SHORT UP TACK |
⫠ |
| U+2AE1 |
PERPENDICULAR WITH S |
⫡ |
| U+2AE2 |
VERTICAL BAR TRIPLE RIGHT TURNSTILE |
⫢ |
| U+2AE3 |
DOUBLE VERTICAL BAR LEFT TURNSTILE |
⫣ |
| U+2AE4 |
VERTICAL BAR DOUBLE LEFT TURNSTILE |
⫤ |
| U+2AE5 |
DOUBLE VERTICAL BAR DOUBLE LEFT TURNSTILE |
⫥ |
| U+2AE6 |
LONG DASH FROM LEFT MEMBER OF DOUBLE VERTICAL |
⫦ |
| U+2AE7 |
SHORT DOWN TACK WITH OVERBAR |
⫧ |
| U+2AE8 |
SHORT UP TACK WITH UNDERBAR |
⫨ |
| U+2AE9 |
SHORT UP TACK ABOVE SHORT DOWN TACK |
⫩ |
| U+2AEA |
DOUBLE DOWN TACK |
⫪ |
| U+2AEB |
DOUBLE UP TACK |
⫫ |
| U+2AEC |
DOUBLE STROKE NOT SIGN |
⫬ |
| U+2AED |
REVERSED DOUBLE STROKE NOT SIGN |
⫭ |
| U+2AEE |
DOES NOT DIVIDE WITH REVERSED NEGATION SLASH |
⫮ |
| U+2AEF |
VERTICAL LINE WITH CIRCLE ABOVE |
⫯ |
| U+2AF0 |
VERTICAL LINE WITH CIRCLE BELOW |
⫰ |
| U+2AF1 |
DOWN TACK WITH CIRCLE BELOW |
⫱ |
| U+2AF2 |
PARALLEL WITH HORIZONTAL STROKE |
⫲ |
| U+2AF3 |
PARALLEL WITH TILDE OPERATOR |
⫳ |
| U+2AF4 |
TRIPLE VERTICAL BAR BINARY RELATION |
⫴ |
| U+2AF5 |
TRIPLE VERTICAL BAR WITH HORIZONTAL STROKE |
⫵ |
| U+2AF6 |
TRIPLE COLON OPERATOR |
⫶ |
| U+2AF7 |
TRIPLE NESTED LESS-THAN |
⫷ |
| U+2AF8 |
TRIPLE NESTED GREATER-THAN |
⫸ |
| U+2AF9 |
DOUBLE-LINE SLANTED LESS-THAN OR EQUAL TO |
⫹ |
| U+2AFA |
DOUBLE-LINE SLANTED GREATER-THAN OR EQUAL TO |
⫺ |
| U+2AFB |
TRIPLE SOLIDUS BINARY RELATION |
⫻ |
| U+2AFC |
LARGE TRIPLE VERTICAL BAR OPERATOR |
⫼ |
| U+2AFD |
DOUBLE SOLIDUS OPERATOR |
⫽ |
| U+2AFE |
WHITE VERTICAL BAR |
⫾ |
| U+2AFF |
N-ARY WHITE VERTICAL BAR |
⫿ |
| U+2B30 |
LEFT ARROW WITH SMALL CIRCLE |
⬰ |
| U+2B31 |
THREE LEFTWARDS ARROWS |
⬱ |
| U+2B32 |
LEFT ARROW WITH CIRCLED PLUS |
⬲ |
| U+2B33 |
LONG LEFTWARDS SQUIGGLE ARROW |
⬳ |
| U+2B34 |
LEFTWARDS TWO-HEADED ARROW WITH VERTICAL STROKE |
⬴ |
| U+2B35 |
LEFTWARDS TWO-HEADED ARROW WITH DOUBLE VERTICAL STROKE |
⬵ |
| U+2B36 |
LEFTWARDS TWO-HEADED ARROW FROM BAR |
⬶ |
| U+2B37 |
LEFTWARDS TWO-HEADED TRIPLE DASH ARROW |
⬷ |
| U+2B38 |
LEFTWARDS ARROW WITH DOTTED STEM |
⬸ |
| U+2B39 |
LEFTWARDS ARROW WITH TAIL WITH VERTICAL STROKE |
⬹ |
| U+2B3A |
LEFTWARDS ARROW WITH TAIL WITH DOUBLE VERTICAL STROKE |
⬺ |
| U+2B3B |
LEFTWARDS TWO-HEADED ARROW WITH TAIL |
⬻ |
| U+2B3C |
LEFTWARDS TWO-HEADED ARROW WITH TAIL WITH VERTICAL STROKE |
⬼ |
| U+2B3D |
LEFTWARDS TWO-HEADED ARROW WITH TAIL WITH DOUBLE VERTICAL STROKE |
⬽ |
| U+2B3E |
LEFTWARDS ARROW THROUGH X |
⬾ |
| U+2B3F |
WAVE ARROW POINTING DIRECTLY LEFT |
⬿ |
| U+2B40 |
EQUALS SIGN ABOVE LEFTWARDS ARROW |
⭀ |
| U+2B41 |
REVERSE TILDE OPERATOR ABOVE LEFTWARDS ARROW |
⭁ |
| U+2B42 |
LEFTWARDS ARROW ABOVE REVERSE ALMOST EQUAL TO |
⭂ |
| U+2B43 |
RIGHTWARDS ARROW THROUGH GREATER-THAN |
⭃ |
| U+2B44 |
RIGHTWARDS ARROW THROUGH SUPERSET |
⭄ |
| U+2B47 |
REVERSE TILDE OPERATOR ABOVE RIGHTWARDS ARROW |
⭇ |
| U+2B48 |
RIGHTWARDS ARROW ABOVE REVERSE ALMOST EQUAL TO |
⭈ |
| U+2B49 |
TILDE OPERATOR ABOVE LEFTWARDS ARROW |
⭉ |
| U+2B4A |
LEFTWARDS ARROW ABOVE ALMOST EQUAL TO |
⭊ |
| U+2B4B |
LEFTWARDS ARROW ABOVE REVERSE TILDE OPERATOR |
⭋ |
| U+2B4C |
RIGHTWARDS ARROW ABOVE REVERSE TILDE OPERATOR |
⭌ |
| U+FB29 |
HEBREW LETTER ALTERNATIVE PLUS SIGN |
﬩ |
| U+FE62 |
SMALL PLUS SIGN |
﹢ |
| U+FE64 |
SMALL LESS-THAN SIGN |
﹤ |
| U+FE65 |
SMALL GREATER-THAN SIGN |
﹥ |
| U+FE66 |
SMALL EQUALS SIGN |
﹦ |
| U+FF0B |
FULLWIDTH PLUS SIGN |
+ |
| U+FF1C |
FULLWIDTH LESS-THAN SIGN |
< |
| U+FF1D |
FULLWIDTH EQUALS SIGN |
= |
| U+FF1E |
FULLWIDTH GREATER-THAN SIGN |
> |
| U+FF5C |
FULLWIDTH VERTICAL LINE |
| |
| U+FF5E |
FULLWIDTH TILDE |
~ |
| U+FFE2 |
FULLWIDTH NOT SIGN |
¬ |
| U+FFE9 |
HALFWIDTH LEFTWARDS ARROW |
← |
| U+FFEA |
HALFWIDTH UPWARDS ARROW |
↑ |
| U+FFEB |
HALFWIDTH RIGHTWARDS ARROW |
→ |
| U+FFEC |
HALFWIDTH DOWNWARDS ARROW |
↓ |
| U+1D6C1 |
MATHEMATICAL BOLD NABLA |
𝛁 |
| U+1D6DB |
MATHEMATICAL BOLD PARTIAL DIFFERENTIAL |
𝛛 |
| U+1D6FB |
MATHEMATICAL ITALIC NABLA |
𝛻 |
| U+1D715 |
MATHEMATICAL ITALIC PARTIAL DIFFERENTIAL |
𝜕 |
| U+1D735 |
MATHEMATICAL BOLD ITALIC NABLA |
𝜵 |
| U+1D74F |
MATHEMATICAL BOLD ITALIC PARTIAL DIFFERENTIAL |
𝝏 |
| U+1D76F |
MATHEMATICAL SANS-SERIF BOLD NABLA |
𝝯 |
| U+1D789 |
MATHEMATICAL SANS-SERIF BOLD PARTIAL DIFFERENTIAL |
𝞉 |
| U+1D7A9 |
MATHEMATICAL SANS-SERIF BOLD ITALIC NABLA |
𝞩 |
| U+1D7C3 |
MATHEMATICAL SANS-SERIF BOLD ITALIC PARTIAL DIFFERENTIAL |
𝟃 |




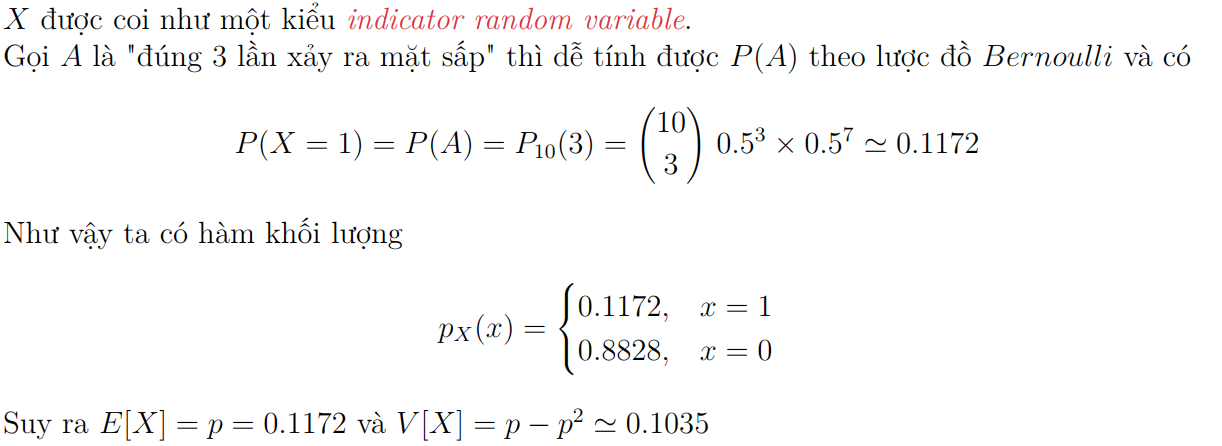




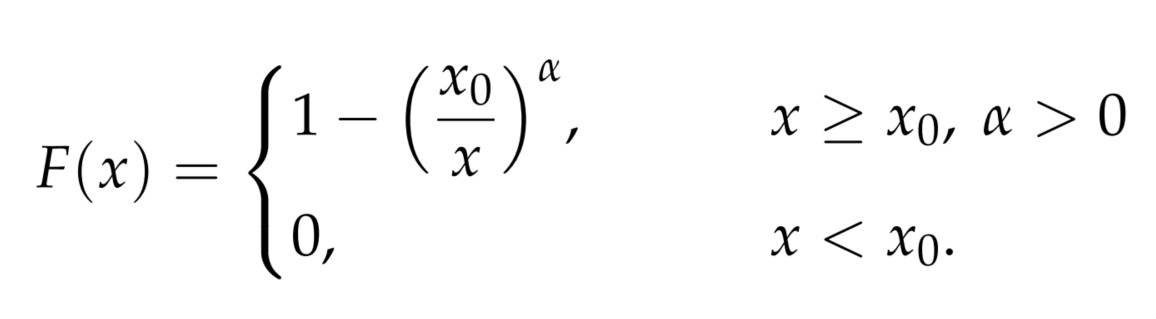
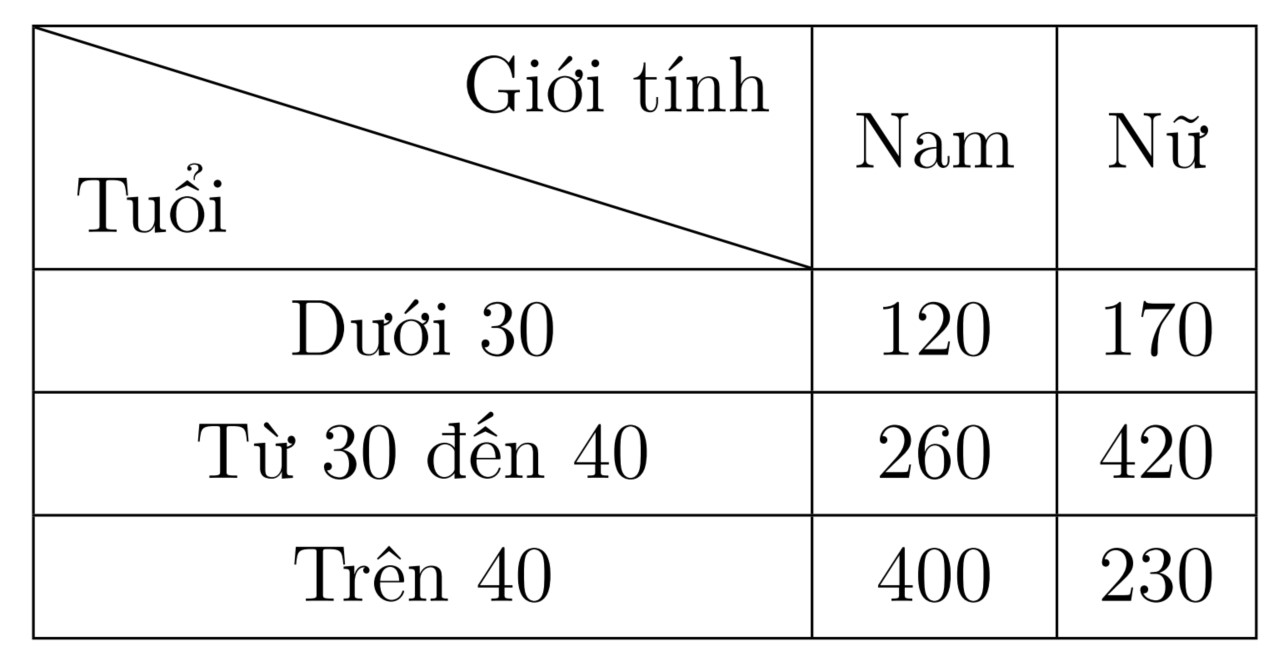















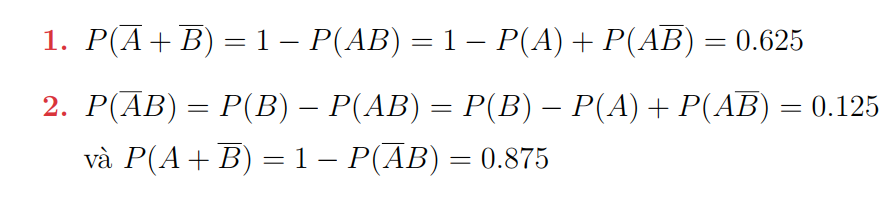


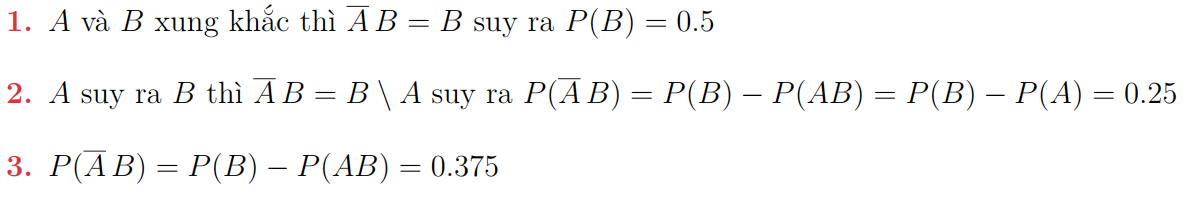
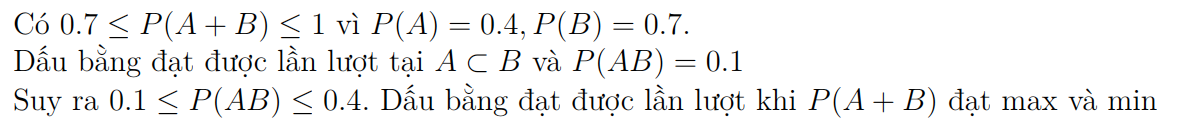
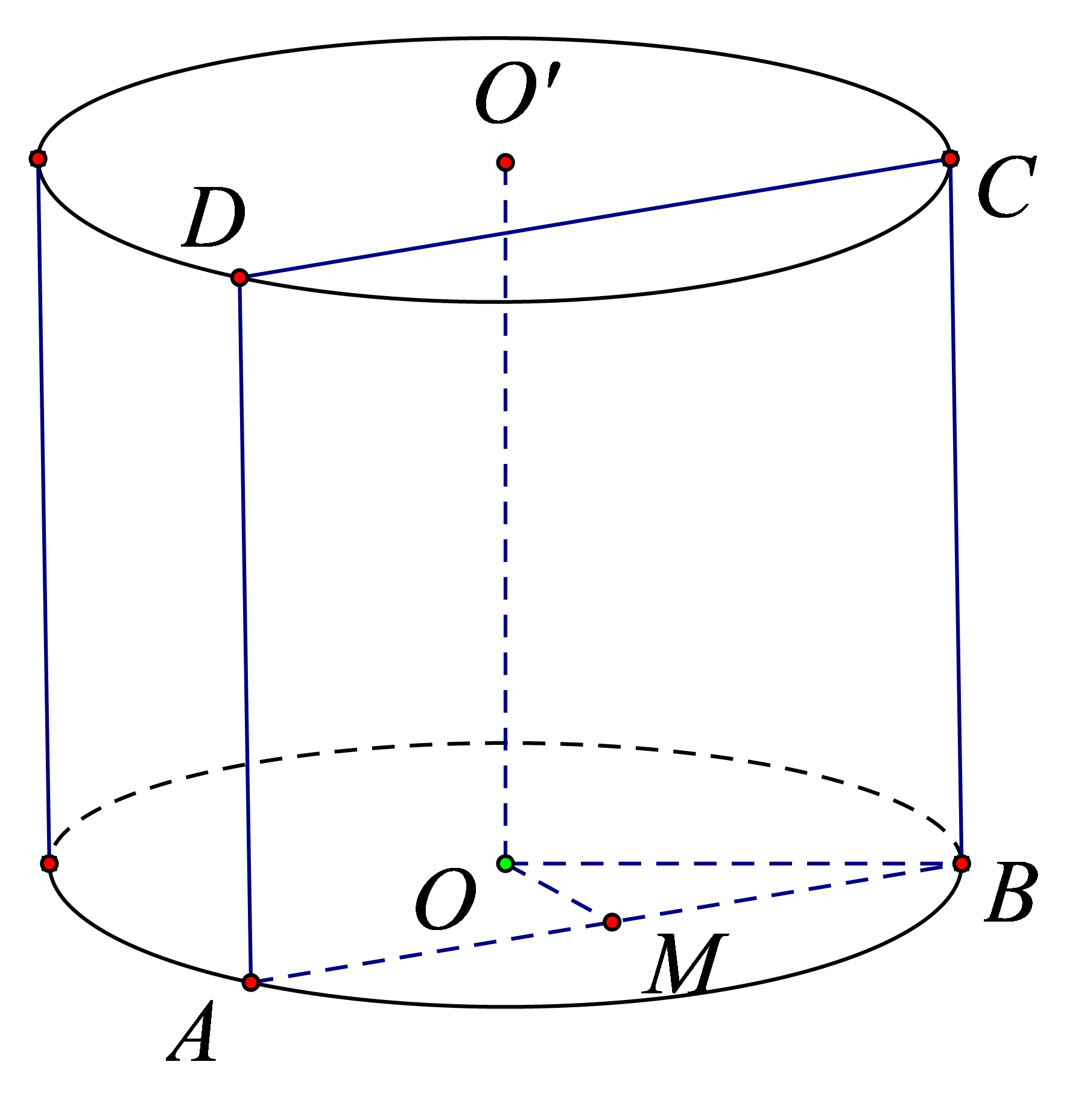


 Chọn B
Chọn B Lời giải. Chọn A
Lời giải. Chọn A