Category: Toán 10
-
Đề cương giữa kì 2 Toán 10 Cánh Diều file Word
Mời Quý thầy cô tham khảo Đề cương giữa kì 2 Toán 10 Cánh Diều năm 2022-2023 của trường THPT Trần Phú HN. File Word mời thầy cô tải ở cuối bài viết.
BÀI TẬP TRẮC NGHIỆM
Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây.
Câu 1: Một tổ có 6 học sinh nữ và 8 học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học sinh của tổ đó đi trực nhật?
A. 28
B. 48
C. 14
D. 8
Câu 2: Có 3 cuốn sách Toán khác nhau và 4 cuốn sách Vật lí khác nhau. Hỏi có bao nhiêu cách chọn một cuốn sách trong số các cuốn sách đó?
A. 12
B. 7
C. 3
D. 4
Câu 3: Trường THPT A, khối 12 có 11 lớp, khối 11 có 10 lớp và khối 10 có 12 lớp. Thầy Tổ trưởng tổ Toán muốn chọn một lớp để dự giờ. Hỏi có tất cả bao nhiêu cách chọn?
A. 3
B. 33
C. 11
D. 10
Câu 4: Giả sử từ tỉnh $A$ đến tỉnh $B$ có thể đi bằng các phương tiện: ô tô, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có 10 chuyến ô tô, 5 chuyến tàu hỏa, 3 chuyến tàu thủy và 2 chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh $A$ đến tỉnh $B$?
A. 20
B. 300
C. 18
D. 15
Câu 5: Có 3 kiểu mặt đồng hồ đeo tay và 4 kiểu dây. Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A. 4
B. 7
C. 12
D. 16
Câu 6: Một người có 4 cái quần, 6 cái áo, 3 chiếc cà vạt. Để chọn mỗi thứ một món thì có bao nhiều cách chọn bộ ” quần-áo-cà vạt” khác nhau?
A. 13
B. 72
C. 12
D. 30
Câu 7: Một thùng trong đó có 12 hộp đựng bút màu đỏ, 18 hộp đựng bút màu xanh. Số cách khác nhau để chọn được đồng thời một hộp màu đỏ, một hộp màu xanh là?
A. 13
B. 12
C. 18
D. 216
Câu 8: Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Số cách khác nhau để chọn được đồng thời một cây bút chì, một cây bút bi và một cuốn tập.
A. 24
B. 48
C. 480
D. 60
Câu 9: Một bó hoa có 5 hoa hồng trắng, 6 hoa hồng đỏ và 7 hoa hồng vàng. Hỏi có mấy cách chọn lấy ba bông hoa có đủ cả ba màu.
A. 240
B. 210
C. 18
D. 120
Câu 10: Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn hai học sinh trong đó có một nam và một nữ đi dự trại hè của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 910000
B. 91000
C. 910
D. 625
Câu 11: Một đội học sinh giỏi của trường THPT, gồm 5 học sinh khối 12,4 học sinh khối 11,3 học sinh khối 10 . Số cách chọn ba học sinh trong đó mỗi khối có một em?
A. 12
B. 220
C. 60
D. 3
Câu 12: Có 10 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng?
A. 100
B. 91
C. 10
D. 90
Câu 13: An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà $A n$ đến nhà Bình có 4 con đường đi, từ nhà Bình tới nhà Cường có 6 con đường đi. HSỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?
A. 6
B. 4
C. 10
D. 24
Câu 14: Có bao nhiêu số tự nhiên có hai chữ số mà cả hai chữ số đều lẻ?
A. 25
B. 20
C. 50
D. 10
Câu 15: Số các số tự nhiên chẵn, gồm bốn chữ số khác nhau đôi một và không tận cùng bằng 0 là :
A. 504
B. 1792
C. 953088
D. 2296
Câu 16: Có bao nhiêu số tự nhiên có 3 chữ số đôi một khác nhau?
A. 1000
B. 720
C. 729
D. 648
Câu 17: Có bao nhiêu số tự nhiên có 3 chữ số được lập từ sáu chữ số $1,2,3,4,5,6$?
A. 10
B. 216
C. 256
D. 20
Câu 18: Cho các số $1,5,6,7$ có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số khác nhau:
A. 12
B. 24
C. 64
D. 256
Câu 19: Cần xếp 3 nam, 3 nữ vào 1 hàng có 6 ghế. Hỏi có bao nhiêu cách xếp sao cho nam nữ ngồi xen kẽ.
A. 36
B. 720
C. 78
D. 72
Câu 20: Từ các số $0,1,2,7,8,9$ tạo được bao nhiêu số lẻ có 5 chữ số khác nhau?
A. 288
B. 360
C. 312
D. 600
Câu 21: Một bạn có 4 áo xanh, 3 áo trắng và 5 quần màu đen. Hỏi bạn đó có bao nhiêu cách chọn một bộ quần áo để mặc?
A. 35
B. 66
C. 12
D. 60
Hoán vị. Chỉnh hợp. Tổ hợp
Câu 22: Công thức tính số hoán vị $P_{n}, n \in \mathbb{N}^{*}$. Chọn công thức đúng?
A. $P_{n}=(n-1)$ !
B. $P_{n}=(n+1)$ !
C. $P_{n}=\frac{n !}{(n-1)}$
D. $P_{n}=n$ !
Câu 23: Có bao nhiêu cách xếp 3 học sinh nam và 4 học sinh nữ theo hàng ngang?
A. 7 !
B. 144
C. 2880
D. 480
Câu 24: Từ các số $1,2,3,4,5$ có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau đôi một?
A. 60
B. 120
C. 24
D. 48
Câu 25: Số cách xếp 3 nam sinh và 4 nữ sinh vào một dãy ghê hàng ngang có 7 chỗ ngồi là
A. 4 ! .3
B. 7 !
C. 4 ! .3 !
D. 4 !
Câu 26: Có 4 cặp vợ chồng ngồi trên một dãy ghế dài. Có bao nhiêu cách sắp xếp sao cho vợ và chồng của mỗi gia đình đều ngồi cạnh nhau.
A. 384
B. 8 !
C. 4 ! .4 !
D. 48
Câu 27: Số cách xếp 5 nam và 4 nữ thành một hàng ngang sao cho 4 nữ luôn đứng cạnh nhau là
A. 362880
B. 2880
C. 5760
D. 17280
Câu 28: Có 4 học sinh nam, 3 học sinh nữ và 2 thầy giáo xếp thành một hàng dọc tham gia một cuộc thi. Hỏi có bao nhiêu cách xếp hàng sao cho nhóm 3 học sinh nữ luôn đứng cạnh nhau và nhóm hai thầy giáo cũng đứng cạnh nhau?
A. 362880
B. 14400
C. 8640
D. 288
Câu 29: Cho tập $A={1,2,3,4,5,6,7,8}$. Từ tập $A$ có thể lập được bao nhiêu số tự nhiên có 8 chữ số phân biệt sao cho các số này lẻ và không chia hết cho 5?
A. 15120
B. 20100
C. 40320
D. 12260
Câu 30: Có bao nhiêu cách xếp chô̂ cho 3 học sinh lớp $\mathrm{A}, 2$ học sinh lớp $\mathrm{B}$ và 1 học sinh lớp $\mathrm{C}$ vào 6 ghế xếp quanh một bàn tròn sao cho học sinh lớp $\mathrm{C}$ ngồi giữa hai học sinh lớp $\mathrm{A}$ và $\mathrm{B}$
A. 12
B. 120
C. 72
D. 48
Câu 31: Có bao nhiêu cách xếp 6 cặp vợ chồng ngồi xung quanh một chiếc bàn tròn, sao cho mỗi bà đều ngồi cạnh chồng của mình?
A. 7680
B. 7860
C. 960
D. 690
Câu 32: Công thức tính số chỉnh hợp chập $k$ của $n$ phần tử là:
A. $A_{n}^{k}=\frac{n !}{(n-k) !}$
B. $A_{n}^{k}=\frac{n !}{(n-k) ! k !}$
C. $C_{n}^{k}=\frac{n !}{(n-k) ! k !}$
D. $C_{n}^{k}=\frac{n !}{(n-k) !}$
Câu 33: Tính số chỉnh hợp chập 4 của 7 phần tử?
A. 24
B. 720
C. 840
D. 35
Câu 34: Từ 7 chữ số $1,2,3,4,5,6,7$ có thể lập được bao nhiêu số tự nhiên có 4 chữ số đôi một khác nhau?
A. $7^{4}$
B. $P_{7}$
C. $C_{7}^{4}$
D. $A_{7}^{4}$
Câu 35: Trong một lớp học có 20 học sinh nữ và 15 học sinh nam. Hỏi giáo viên chủ nhiệm có bao nhiêu cách chọn: ba học sinh làm ba nhiệm vụ lớp trưởng, lớp phó và bí thư?
A. $C_{35}^{3}$
B. 35 !
C. $A_{3}^{35}$
D. $A_{35}^{3}$
Câu 36: Số cách xếp 5 học sinh ngồi vào một dãy gồm 8 chiếc ghế bằng
A. $A_{8}^{5}$
B. $C_{8}^{5}$
C. 5 !
D. 8 !
Câu 37: Trong một cuộc đua thuyền có 16 thuyền cùng xuất phát. Hỏi có bao nhiêu khả năng xếp loại 3 thuyền về nhất, nhì, ba?
A. 5
B. 560
C. 48
D. 3360
Câu 38: Công thức tính số tổ hợp chập $k$ của $n$ phần tử là:
A. $A_{n}^{k}=\frac{n !}{(n-k) !}$
B. $A_{n}^{k}=\frac{n !}{(n-k) ! k !}$
C. $C_{n}^{k}=\frac{n !}{(n-k) ! k !}$
D. $C_{n}^{k}=\frac{n !}{(n-k) !}$
Câu 39: Cho tập hợp $M$ có 10 phần tử. Số tập con gồm 2 phần tử của $M$ là
A. $A_{10}^{8}$
B. $A_{10}^{2}$
C. $C_{10}^{2}$
D. $10^{2}$
Câu 40: Cho tập hợp $M={1 ; 2 ; 3 ; 4 ; 5}$. Số tập con gồm hai phần tử của tập hợp $M$ là:
A. 11
B. $A_{5}^{2}$
C. $C_{5}^{2}$
D. $P_{2}$
Câu 41: Có bao nhiêu cách chọn ra 4 học sinh từ một tổ gồm 15 học sinh?
A. 32760
B. 50625
C. 60
D. 1365
Câu 42: Có bao nhiêu tam giác có ba đỉnh là các đỉnh của hình đa giác đều có 10 cạnh.
A. $C_{11}^{3}$
B. $A_{10}^{3}$
C. $C_{10}^{3}$
D. $A_{11}^{3}$
Câu 43: Từ một lớp gồm 16 học sinh nam và 18 học sinh nữ. Có bao nhiêu cách chọn ra 5 học sinh tham gia đội Thanh niên xung kích, trong đó có 2 học sinh nam và 3 học sinh nữ.
A. $C_{16}^{2} \cdot C_{18}^{3}$
B. $A_{16}^{2} \cdot A_{18}^{3}$
C. $C_{16}^{3} \cdot C_{18}^{2}$
D. $A_{16}^{3} \cdot A_{18}^{2}$
Câu 44: Một lớp có 30 học sinh gồm 20 nam và 10 nữ. Hỏi có bao nhiêu cách chọn ra một nhóm 3 học sinh sao cho nhóm đó có ít nhất một học sinh nữ?
A. 1140
B. 2920
C. 1900
D. 900
Câu 45: Có bao nhiêu số có ba chữ số dạng $\overline{a b c}$ với $a, b, c \in\{0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6\}$ sao cho $a<b<c$.
A. 30
B. 20
C. 120
D. 40
Câu 46: Từ tập $X=\{2,3,4,5,6\}$ có thể lập được bao nhiêu số tự nhiên có ba chữ số mà các chữ số đôi một khác nhau?
A. 60
B. 125
C. 10
D. 6
Nhị thức Newton
Câu 47: Trong khai triển nhị thức Niu-tơn của $(a+b)^{4}$ có bao nhiêu số hạng?
A. 6
B. 3
C. 5
D. 4
Câu 48: Trong khai triển nhị thức Niu-tơn của $(2 x-3)^{4}$ có bao nhiêu số hạng?
A. 6
B. 3
C. 5
D. 4
Câu 49: Trong khai triển nhị thức Niu-tơn của $(a+b)^{4}$, số hạng tổng quát của khai triển là
A. $C_{4}^{k-1} a^{k} b^{5-k}$
B. $C_{4}^{k} a^{4-k} b^{k}$
C. $C_{4}^{k+1} a^{5-k} b^{k+1}$
D. $C_{4}^{k} a^{4-k} b^{4-k}$
Câu 50: Trong khai triển nhị thức Niu-tơn của $(2 x-3)^{4}$, số hạng tổng quát của khai triển là
A. $C_{4}^{k} 2^{k} 3^{4-k} \cdot x^{4-k}$
B. $C_{4}^{k} 2^{4-k}(-3)^{k} \cdot x^{4-k}$
C. $C_{4}^{k} 2^{4-k} 3^{k} \cdot x^{4-k}$
D. $C_{4}^{k} 2^{k}(-3)^{4-k} \cdot x^{4-k}$
Câu 51: Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của $(1-2 x)^{4}$.
A. 1
B. $-1$
C. 81
D. $-81$
Câu 52: Trong khai triển nhị thức Niu-tơn của $(1+3 x)^{4}$, số hạng thứ 2 theo số mũ tăng dần của $x$ là
A. $108 x$
B. $54 x^{2}$
C. 1
D. $12 x$
Câu 53: Tìm hệ số của $x^{2} y^{2}$ trong khai triển nhị thức Niu-tơn của $(x+2 y)^{4}$.
A. 32
B. 8
C. 24
D. 16
Câu 54: Tìm số hạng chứa $x^{2}$ trong khai triển nhị thức Niu-tơn của $P(x)=4 x^{2}+x(x-2)^{4}$.
A. $28 x^{2}$
B. $-28 x^{2}$
C. $-24 x^{2}$
D. $24 x^{2}$
Câu 55: Gọi $n$ là số nguyên dương thỏa mãn $A_{n}^{3}+2 A_{n}^{2}=48$. Tìm hệ số của $x^{3}$ trong khai triển nhị thức Niu-tơn của $(1-3 x)^{n}$.
A. $-108$
B. 81
C. 54
D. $-12$
Câu 56: Tìm số hạng không chứa $x$ trong khai triển nhị thức Niu-tơn của $\left(\frac{1}{x}+x^{3}\right)^{4}$.
A. 1
B. 4
C. 6
D. 12
Câu 57: Viết khai triển theo công thức nhị thức newton $(x+1)^{5}$.
A. $x^{5}+5 x^{4}+10 x^{3}+10 x^{2}+5 x+1$
B. $x^{5}-5 x^{4}-10 x^{3}+10 x^{2}-5 x+1$
C. $x^{5}-5 x^{4}+10 x^{3}-10 x^{2}+5 x-1$
D. $5 x^{5}+10 x^{4}+10 x^{3}+5 x^{2}+5 x+1$
Câu 58: Viết khai triển theo công thức nhị thức newton $(x-y)^{5}$.
A. $x^{5}-5 x^{4} y+10 x^{3} y^{2}-10 x^{2} y^{3}+5 x y^{4}-y^{5}$
B. $x^{5}+5 x^{4} y+10 x^{3} y^{2}+10 x^{2} y^{3}+5 x y^{4}+y^{5}$
C. $x^{5}-5 x^{4} y-10 x^{3} y^{2}-10 x^{2} y^{3}-5 x y^{4}+y^{5}$
D. $x^{5}+5 x^{4} y-10 x^{3} y^{2}+10 x^{2} y^{3}-5 x y^{4}+y^{5}$
Câu 59: Khai triển của nhị thức $(x-2)^{5}$.
A. $x^{5}-100 x^{4}+400 x^{3}-800 x^{2}+800 x-32$
B. $5 x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32$
C. $x^{5}-10 x^{4}+40 x^{3}-80 x^{2}+80 x-32$
D. $x^{5}+10 x^{4}+40 x^{3}+80 x^{2}+80 x+32$
Câu 60: Khai triển của nhị thức $(3 x+4)^{5}$ là
A. $x^{5}+1620 x^{4}+4320 x^{3}+5760 x^{2}+3840 x+1024$
B. $243 x^{5}+405 x^{4}+4320 x^{3}+5760 x^{2}+3840 x+1024$
C. $243 x^{5}-1620 x^{4}+4320 x^{3}-5760 x^{2}+3840 x-1024$
D. $243 x^{5}+1620 x^{4}+4320 x^{3}+5760 x^{2}+3840 x+1024$
Câu 61: Khai triển của nhị thức $(1-2 x)^{5}$ là
A. $5-10 x+40 x^{2}-80 x^{3}-80 x^{4}-32 x^{5}$
B. $1+10 x+40 x^{2}-80 x^{3}-80 x^{4}-32 x^{5}$
C. $1-10 x+40 x^{2}-80 x^{3}-80 x^{4}-32 x^{5}$
D. $1+10 x+40 x^{2}+80 x^{3}+80 x^{4}+32 x^{5}$
Câu 62: Trong khai triển $(2 a-b)^{5}$, hệ số của số hạng thứ 3 bằng:
A. $-80$
B. 80
C. $-10$
D. 10
Câu 63: Tìm hệ số của đơn thức $a^{3} b^{2}$ trong khai triển nhị thức $(a+2 b)^{5}$.
A. 160
B. 11
C. 20
D. 40
Câu 64: Số hạng chính giữa trong khai triển $(3 x+2 y)^{4}$ là:
A. $C_{4}^{2} x^{2} y^{2}$
B. $6(3 x)^{2}(2 y)^{2}$
C. $6 C_{4}^{2} x^{2} y^{2}$
D. $36 C_{4}^{2} x^{2} y^{2}$
Câu 65: Cho $a$ là một số thực bất kì. Rút gọn $M=C_{4}^{0} a^{4}+C_{4}^{1} a^{3}(1-a)+C_{4}^{2} a^{2}(1-a)^{2}+C_{4}^{3} a(1-a)^{3}+C_{4}^{4}(1-a)^{4}$.
A. $M=a^{4}$
B. $M=a$
C. $M=1$
D. $M=-1$
Tọa độ của véctơ. Biểu thức tọa độ của các phép toán véctơ.
Câu 66: Trong mặt phẳng tọa độ $O x y$, tọa độ $\vec{i}$ là
A. $\vec{i}=(0 ; 0)$
B. $\vec{i}=(0 ; 1)$
C. $\vec{i}=(1 ; 0)$
D. $\vec{i}=(1 ; 1)$
Câu 67: Trong hệ tọa độ $O x y$, cho $A(5 ; 2), B(10 ; 8)$ Tìm tọa độ của vectơ $\overrightarrow{A B}$?
A. $(15 ; 10)$
B. $(2 ; 4)$
C. $(5 ; 6)$
D. $(50 ; 16)$
Câu 68: Trong hệ tọa độ $O x y$, cho tam giác $A B C$ có $B(9 ; 7), C(11 ;-1)$. Gọi $M, N$ lần lượt là trung điểm của $A B, A C$. Tìm tọa độ vectơ $\overrightarrow{M N}$?
A. $(2 ;-8)$
B. $(1 ;-4)$
C. $(10 ; 6)$
D. $(5 ; 3)$
Câu 69: Trong hệ tọa độ $O x y$, cho hình vuông $A B C D$ có gốc $O$ làm tâm hình vuông và các cạnh của nó song song với các trục tọa độ. Khẳng định nào đúng?
A. $|\overrightarrow{O A}+\overrightarrow{O B}|=A B$
B. $\overrightarrow{O A}-\overrightarrow{O B}, \overrightarrow{D C}$ cùng hướng
C. $x_{A}=-x_{C}, y_{A}=y_{C}$
D. $x_{B}=-x_{C}, y_{B}=-y_{C}$
Câu 70: Trong hệ tọa độ $O x y$, cho $M(3 ;-4)$ Gọi $M_{1}, M_{2}$ lần lượt là hình chiếu vuông góc của $M$ trên $O x, O y$. Khẳng định nào đúng?
A. $\overline{O M_{1}}=-3$
B. $\overrightarrow{O M_{2}}=4$
C. $\overrightarrow{O M_{1}}-\overrightarrow{O M_{2}}=(-3 ;-4)$
D. $\overrightarrow{O M_{1}}+\overrightarrow{O M_{2}}=(3 ;-4)$
Câu 71: Trong hệ tọa độ $O x y$, cho hình bình hành $O A B C, C \in O x$. Khẳng định nào sau đây đúng?
A. $\overrightarrow{A B}$ có tung độ khác 0
B. $A, B$ có tung độ khác nhau
C. $C$ có hoành độ khác 0
D. $x_{A}+x_{C}-x_{B}=0$
Câu 72: Trong hệ trục tọa độ $(O, \vec{i}, \vec{j})$, cho tam giác đều $A B C$ cạnh $a$, biết $O$ là trung điểm $B C, \vec{i}$ cùng hướng với $\overrightarrow{O C}, \vec{j}$ cùng hướng $\overrightarrow{O A}$. Tìm tọa độ của các đỉnh của tam giác $A B C$. Gọi $x_{A}, x_{B}, x_{C}$ lần lượt là hoành độ các điểm $A, B, C$. Giá trị của biểu thức $x_{A}+x_{B}+x_{C}$ bằng:
A. 0
B. $\frac{a}{2}$
C. $\frac{a \sqrt{3}}{2}$
D. $-\frac{a}{2}$
Câu 73: Trong hệ trục tọa độ $(O, \vec{i}, \vec{j})$, cho tam giác đều $A B C$ cạnh $a$, biết $O$ là trung điểm $B C, \vec{i}$ cùng hướng với $\overrightarrow{O C}, \vec{j}$ cùng hướng $\overrightarrow{O A}$. Tìm tọa độ tâm đường tròn ngoại tiếp tam giác $A B C$.
A. $G\left(0 ; \frac{a \sqrt{3}}{6}\right)$
B. $G\left(0 ; \frac{a \sqrt{3}}{4}\right)$
C. $G\left(\frac{a \sqrt{3}}{6} ; 0\right)$
D. $G\left(\frac{a \sqrt{3}}{4} ; 0\right)$
Câu 74: Trong hệ trục tọa độ $(O, \vec{i}, \vec{j})$, cho hình thoi $A B C D$ tâm $\mathrm{O}$ có $A C=8, B D=6$. Biết $\overrightarrow{O C}$ và $\vec{i}$ cùng hướng, $\overrightarrow{O B}$ và $\vec{j}$ cùng hướng. Tính tọa độ trọng tâm tam giác $A B C$
A. $G(0 ; 1)$
B. $G(-1 ; 0)$
C. $\left(\frac{1}{2} ; 0\right)$
D. $\left(0 ; \frac{3}{2}\right)$
Câu 75: Cho $\vec{a}=(-1 ; 2), \vec{b}=(5 ;-7)$ Tìm tọa độ của $\vec{a}-\vec{b}$.
A. $(6 ;-9)$
B. $(4 ;-5)$
C. $(-6 ; 9)$
D. $(-5 ;-14)$
Câu 76: Cho $\vec{a}=(3 ;-4), \vec{b}=(-1 ; 2)$ Tìm tọa độ của $\vec{a}+\vec{b}$.
A. $(-4 ; 6)$
B. $(2 ;-2)$
C. $(4 ;-6)$
D. $(-3 ;-8)$
Câu 77: Trong hệ trục tọa độ $(O ; \vec{i} ; \vec{j})$ tọa độ $\vec{i}+\vec{j}$ là:
A. $(0 ; 1)$
B. $(1 ;-1)$
C. $(-1 ; 1)$
D. $(1 ; 1)$
Câu 78: Trong mặt phẳng $O x y$ cho $\vec{a}=(-1 ; 3), \vec{b}=(5 ;-7)$. Tọa độ vectơ $3 \vec{a}-2 \vec{b}$ là:
A. $(6 ;-19)$
B. $(13 ;-29)$
C. $(-6 ; 10)$
D. $(-13 ; 23)$
Câu 79: Cho $\vec{a}=2 \vec{i}-3 \vec{j}$ và $\vec{b}=-\vec{i}+2 \vec{j}$. Tìm tọa độ của $\vec{c}=\vec{a}-\vec{b}$.
A. $\vec{c}=(1 ;-1)$
B. $\vec{c}=(3 ;-5)$
C. $\vec{c}=(-3 ; 5)$
D. $\vec{c}=(2 ; 7)$ Câu 80: Cho hai vectơ $\vec{a}=(1 ;-4) ; \vec{b}=(-6 ; 15)$. Tìm tọa độ vectơ $\vec{u}$ biết $\vec{u}+\vec{a}=\vec{b}$
A. $(7 ; 19)$
B. $(-7 ; 19)$
C. $(7 ;-19)$
D. $(-7 ;-19)$
Câu 81: Tìm tọa độ vectơ $\vec{u}$ biết $\vec{u}+\vec{b}=\overrightarrow{0}, \vec{b}=(2 ;-3)$.
A. $(2 ;-3)$
B. $(-2 ;-3)$
C. $(-2 ; 3)$
D. $(2 ; 3)$
Câu 82: Trong hệ tọa độ $O x y$, cho $A(2 ; 5), B(1 ; 1), C(3 ; 3)$. Tìm tọa độ điểm $E$ sao cho $\overrightarrow{A E}=3 \overrightarrow{A B}-2 \overrightarrow{A C}$
A. $(3 ;-3)$
B. $(-3 ; 3)$
C. $(-3 ;-3)$
D. $(-2 ;-3)$
Câu 83: Cho 3 điểm $A(-4 ; 0), B(-5 ; 0), C(3 ; 0)$. Tìm điểm $M$ trên trục $O x$ sao cho $\overrightarrow{M A}+\overrightarrow{M B}+\overrightarrow{M C}=\overrightarrow{0}$.
A. $(-2 ; 0)$
B. $(2 ; 0)$
C. $(-4 ; 0)$
D. $(-5 ; 0)$
Câu 84: Trong hệ trục $(O, \vec{i}, \vec{j})$ cho 2 vectơ $\vec{a}=(3 ; 2), \vec{b}=-\vec{i}+5 \vec{j}$. Mệnh đề nào sau đây sai?
A. $\vec{a}=3 \vec{i}+2 \vec{j}$
B. $\vec{b}=(-1 ; 5)$
C. $\vec{a}+\vec{b}=(2 ; 7)$
D. $\vec{a}-\vec{b}=(2 ;-3)$
Câu 85: Cho $\vec{u}=2 \vec{i}-3 \vec{j}, \vec{v}=-5 \vec{i}-\vec{j}$. Gọi $(X ; Y)$ là tọa độ của $\vec{w}=2 \vec{u}-3 \vec{v}$ thì tích $X Y$ bằng:
A. $-57$
B. 57
C. $-63$
D. 63
Câu 86: Trong hệ tọa độ $O x y$, cho tam giác $A B C$ có $A(3 ; 5), B(1 ; 2), C(5 ; 2)$. Tìm tọa độ trọng tâm $G$ của tam giác $A B C$?
A. $(-3 ; 4)$
B. $(4 ; 0)$
C. $(\sqrt{2} ; 3)$
D. $(3 ; 3)$
Câu 87: Trong hệ tọa độ $O x y$, cho $A(2 ;-3), B(4 ; 7)$. Tìm tọa độ trung điểm $I$ của đoạn thẳng $A B$
A. $(6 ; 4)$
B. $(2 ; 10)$
C. $(3 ; 2)$
D. $(8 ;-21)$
Câu 88: Cho tam giác $A B C$ với $A(-3 ; 6) ; B(9 ;-10)$ và $G\left(\frac{1}{3} ; 0\right)$ là trọng tâm. Tọa độ $C$ là:
A. $C(5 ;-4)$
B. $C(5 ; 4)$
C. $C(-5 ; 4)$
D. $C(-5 ;-4)$
Câu 89: Trong mặt phẳng $O x y$ cho $A(4 ; 2), B(1 ;-5)$. Tìm trọng tâm $G$ của tam giác $O A B$.
A. $G\left(\frac{5}{3} ;-1\right)$
B. $G\left(\frac{5}{3} ; 2\right)$
C. $G(1 ; 3)$
D. $G\left(\frac{5}{3} ; \frac{1}{3}\right)$
Câu 90: Trong hệ tọa độ $O x y$, cho tam giác $A B C$ có $A(-2 ; 2), B(3 ; 5)$ và trọng tâm là gốc $O$. Tìm tọa độ đỉnh $C?$
A. $(-1 ;-7)$
B. $(2 ;-2)$
C. $(-3 ;-5)$
D. $(1 ; 7)$
Câu 91: Trong hệ tọa độ $O x y$, cho tam giác $A B C$ có $M(2 ; 3), N(0 ;-4), P(-1 ; 6)$ lần lượt là trung điểm của các cạnh $B C, C A, A B$. Tìm tọa độ đỉnh $A$?
A. $(1 ; 5)$
B. $(-3 ;-1)$
C. $(-2 ;-7)$
D. $(1 ;-10)$
Câu 92: Trong hệ tọa độ $O x y$, cho ba điểm $A(1 ; 1), B(3 ; 2), C(6 ; 5)$. Tìm tọa độ điểm $D$ để $A B C D$ là hình bình hành.
A. $(4 ; 3)$
B. $(3 ; 4)$
C. $(4 ; 4)$
D. $(8 ; 6)$
Câu 93: Cho $\vec{a}=2 \vec{i}-3 \vec{j}, \vec{b}=m \vec{j}+\vec{i}$. Nếu $\vec{a}, \vec{b}$ cùng phương thì:
A. $m=-6$
B. $m=6$
C. $m=-\frac{2}{3}$
D. $m=-\frac{3}{2}$
Câu 94: Hai vectơ nào có toạ độ sau đây là cùng phương?
A. $(1 ; 0)$ và $(0 ; 1)$
B. $(2 ; 1)$ và $(2 ;-1)$
C. $(-1 ; 0)$ và $(1 ; 0)$
D. $(3 ;-2)$ và $(6 ; 4)$
Câu 95: Trong hệ tọa độ $O x y$, cho tam giác $A B C$ có $A(1 ; 1), B(-2 ;-2), C(-7 ;-7)$. Khẳng định nào sau đây đúng?
A. $G(2 ; 2)$ là trọng tâm tam giác $A B C$
B. $B$ ở giữa hai điểm $A$ và $C$
C. $A$ ở giữa hai điểm $B$ và $C$
D. $\overrightarrow{A B}, \overrightarrow{A C}$ cùng hướng
Câu 96: Trong hệ tọa độ $O x y$, cho $A(-1 ; 5), B(5 ; 5), C(-1 ; 11)$. Khẳng định nào sau đây đúng?
A. $A, B, C$ thẳng hàng
B. $\overrightarrow{A B}, \overrightarrow{A C}$ cùng phương
C. $\overrightarrow{A B}, \overrightarrow{A C}$ không cùng phương
D. $\overrightarrow{A B}, \overrightarrow{A C}$ cùng hướng
Câu 97: Trong hệ tọa độ $O x y$, cho bốn điểm $A(3 ;-2), B(7 ; 1), C(0 ; 1), D(-8 ;-5)$. Khẳng định nào sau đây đúng?
A. $\overrightarrow{A B}, \overrightarrow{C D}$ là hai vectơ đối nhau
B. $\overrightarrow{A B}, \overrightarrow{C D}$ ngược hướng
C. $\overrightarrow{A B}, \overrightarrow{C D}$ cùng hướng
D. $A, B, C, D$ thẳng hàng
Câu 98: Cho $\vec{u}=(3 ;-2), \vec{v}=(1 ; 6)$. Chọn khẳng định đúng?
A. $\vec{u}+\vec{v}$ và $\vec{a}=(-4 ; 4)$ ngược hướng
B. $\vec{u}, \vec{v}$ cùng phương
C. $\vec{u}-\vec{v}$ và $\vec{c}=k \cdot \vec{a}+h \cdot \vec{b}$ cùng hướng
D. $2 \vec{u}+\vec{v}, \vec{v}$ cùng phương
Câu 99: Khẳng định nào sau đây là đúng?
A. $\vec{a}=(-5 ; 0), \vec{b}=(-4 ; 0)$ cùng hướng
B. $\vec{c}=(7 ; 3)$ là vectơ đối của $\vec{d}=(-7 ; 3)$
C. $\vec{u}=(4 ; 2), \vec{v}=(8 ; 3)$ cùng phương
D. $\vec{a}=(6 ; 3), \vec{b}=(2 ; 1)$ ngược hướng
Câu 100: Trong mặt phẳng $O x y$, cho ba vectơ $\vec{a}=(1 ; 2), \vec{b}=(-3 ; 1), \vec{c}=(-4 ; 2)$. Biết $\vec{u}=3 \vec{a}+2 \vec{b}+4 \vec{c}$. Chọn khẳng định đúng.
A. $\vec{u}$ cùng phương với $\vec{i}$
B. $\vec{u}$ không cùng phương với $\vec{i}$
C. $\vec{u}$ cùng phương với $\vec{j}$
D. $\vec{u}$ vuông góc với $\vec{i}$ Câu 101: Cho bốn điểm $A(2 ; 5), B(1 ; 7), C(1 ; 5), D(0 ; 9)$. Ba điểm nào sau đây thẳng hàng:
A. $A, B, C$
B. $A, C, D$
C. $B, C, D$
D. $A, B, D$
Câu 102: Trong mặt phẳng $O x y$ cho $A(-2 m ;-m), B(2 m ; m)$. Với giá trị nào của $m$ thì đường thẳng $A B$ đi qua $O?$
A. $m=3$
B. $m=5$
C. $\forall m \in \mathbb{R}$
D. Không có $m$
Câu 103: Cho 2 điểm $A(-2 ;-3), B(4 ; 7)$. Tìm điểm $M \in y^{\prime} O y$ thẳng hàng với $A$ và $B$.
A. $M\left(\frac{4}{3} ; 0\right)$
B. $M\left(\frac{1}{3} ; 0\right)$
C. $M(1 ; 0)$
D. $M\left(-\frac{1}{3} ; 0\right)$
Câu 104: Cho $A(0 ;-2), B(-3 ; 1)$. Tìm tọa độ giao điểm $M$ của $A B$ với trục $x^{\prime} O x$.
A. $M(-2 ; 0)$
B. $M(2 ; 0)$
C. $M\left(-\frac{1}{2} ; 0\right)$
D. $M(0 ;-2)$
Câu 105: Trong mặt phẳng tọa độ $O x y$, cho ba điểm $A(6 ; 3), B(-3 ; 6), C(1 ;-2)$. Xác định điểm $E$ trên cạnh $B C$ sao cho $B E=2 E C$.
A. $E\left(-\frac{1}{3} ; \frac{2}{3}\right)$
B. $E\left(-\frac{1}{3} ;-\frac{2}{3}\right)$
C. $E\left(\frac{2}{3} ;-\frac{1}{3}\right)$
D. $E\left(-\frac{2}{3} ; \frac{1}{3}\right)$
Câu 106: Trong mặt phẳng tọa độ $O x y$, cho ba điểm $A(6 ; 3), B\left(-\frac{1}{3} ; \frac{2}{3}\right), C(1 ;-2), D(15 ; 0)$. Xác định giao điểm $I$ hai đường thẳng $B D$ và $A C$.
A. $I\left(\frac{7}{2} ;-\frac{1}{2}\right)$
B. $I\left(-\frac{7}{2} ; \frac{1}{2}\right)$
C. $I\left(-\frac{7}{2} ;-\frac{1}{2}\right)$
D. $I\left(\frac{7}{2} ; \frac{1}{2}\right)$
Câu 107: Cho tam giác $A B C$ có $A(3 ; 4), B(2 ; 1), C(-1 ;-2)$. Tìm điểm $M$ trên đường thẳng $B C$ sao cho $S_{A B C}=3 S_{A B M}$
A. $M_{1}(0 ; 1), M_{2}(3 ; 2)$
B. $M_{1}(1 ; 0), M_{2}(3 ; 2)$
C. $M_{1}(1 ; 0), M_{2}(2 ; 3)$
D. $M_{1}(0 ; 1), M_{2}(2 ; 3)$
Câu 108: Cho hình bình hành $A B C D$ có $A(-2 ; 3)$ và tâm $I(1 ; 1)$. Biết điểm $K(-1 ; 2)$ nằm trên đường thẳng $\mathrm{AB}$ và điểm $\mathrm{D}$ có hoành độ gấp đôi tung độ. Tìm các đỉnh $B, D$ của hình bình hành.
A. $B(2 ; 1), D(0 ; 1)$
B. $B(0 ; 1) ; D(4 ;-1)$
C. $B(0 ; 1) ; D(2 ; 1)$
D. $B(2 ; 1), D(4 ;-1)$
BÀI TẬP TỰ LUẬN
Câu 1:
a) Có bao nhiêu cách sắp xếp 5 người ngồi vào một bàn dài có 5 chỗ ngồi?
b) Số cách xếp 3 người ngồi vào 5 ghế xếp thành hàng ngang sao cho mỗi người ngồi một ghế?
c) Có 12 học sinh gồm 8 học sinh nam và 4 học sinh nữ. Các học sinh trên được xếp thành một hàng ngang. Có bao cách sắp xếp sao cho hai học sinh nữ không đứng cạnh nhau?
d) Một nhóm học sinh có 3 học sinh nữ và 7 học sinh nam. Hỏi có bao nhiêu cách sắp xếp 10 học sinh này thành một hàng ngang sao cho mỗi học sinh nữ ngồi giữa hai học sinh nam?
Câu 2: a) Ban chấp hành chi đoàn lớp A có 4 bạn là Tình, Toàn, Nhân, Khánh. Hỏi có bao nhiêu cách phân công các bạn này vào các chức vụ Bí thư, phó Bí thư, Ủy viên và Phụ trách mà không bạn nào kiêm nhiệm (một người giữ nhiều chức vụ)?
b) Trong một ban chấp hành đoàn gồm 7 người. Cần chọn ra 3 người vào ban thường vụ để giữ các chức vụ Bí thư, phó Bí thư, U̇y viên thì có bao nhiêu cách chọn?
c) Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh để tham gia vệ sinh công cộng toàn trường, hỏi có bao nhiêu cách chọn?
d) Một nhóm công nhân gồm 15 nam và 5 nữ. Có bao nhiêu cách chọn từ nhóm ra 5 người để lập thành một tổ công tác trong đó phải có 1 tổ trưởng nam, 1 tổ phó nam và có ít nhất 1 nư??
e) Một đội văn nghệ gồm 20 người, trong đó có 10 nam, 10 nữ. Hỏi có bao nhiêu cách chọn ra 5 người, sao cho:
- Có đúng 2 nam trong 5 người đó?
- Có ít nhất 2 nam, ít nhất 1 nữ trong 5 người đó.
Câu 3:
a) Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Có bao nhiêu cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
b) Có 7 bông hoa khác nhau và 3 lọ hoa khác nhau. Có bao nhiêu cách chọn ra 3 bông hoa cắm vào 3 lọ đã cho (mỗi lọ cắm một bông hoa)?
c) Một túi đựng 6 bi trắng, 5 bi xanh. Lấy ra 4 viên bi từ túi đó. Hỏi có bao nhiêu cách lấy mà 4 viên bi lấy ra có đủ hai màu?
d) Một hộp có 12 viên bi khác nhau gồm: 3 viên bi màu đỏ, 4 viên bi màu trắng và 5 viên bi màu vàng. Chọn ngẫu nhiên 4 viên bi từ hộp đó. Số cách chọn ra 4 viên bi không đủ ba màu?
Câu 4:
a) Trong mặt phẳng cho tập hợp gồm 6 điểm phân biệt. Có bao nhiêu vectơ khác $\overrightarrow{0}$ có điểm đầu và điểm cuối thuộc tập hợp này?
b) Trong mặt phẳng cho 10 điểm, trong đó không có 3 điểm nào thẳng hàng. Hỏi có bao nhiêu đường thẳng khác nhau tạo bởi 2 trong 10 điểm nói trên?
c) Trong mặt phẳng cho 6 điểm phân biệt, trong đó không có 3 điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?
d) Cho hai đường thẳng song song $d_{1}$ và $d_{2}$. Trên $d_{1}$ lấy 17 điểm phân biệt, trên $d_{2}$ lấy 20 điểm phân biệt. Số tam giác có các đỉnh được chọn từ 37 điểm này?
e) Cho đa giác đều $(H)$ có 20 cạnh. Xét tam giác có 3 đỉnh được lấy từ các đỉnh của $(H)$. Hỏi có bao nhiêu tam giác có đúng 1 cạnh là cạnh của $(H)$?
f) Đa giác lồi 10 cạnh có bao nhiêu đường chéo?
Câu 5:
a) Từ các chữ số 1;2;3;4;5;6 có thể lập được bao nhiêu số tự nhiên bé hơn 100?
b) Từ các chữ số $0 ; 1 ; 2 ; 3 ; 4 ; 5$ có thể lập được bao nhiêu số chẵn gồm 4 chữ số khác nhau?
c) Từ các chữ số $0 ; 1 ; 2 ; 3 ; 4 ; 5$ có thể lập được bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau và chia hết cho 3?
d) Cho tập $A={1 ; 2 ; . . ;8 ; 9}$ Có bao nhiêu số tự nhiên gồm 5 chữ số khác nhau được lập từ các số thuộc tập $A$?
e) Có bao nhiêu số tự nhiên:
- Có 3 chữ số khác nhau?
- là số lẻ có 4 chữ số khác nhau?
- có 6 chữ số sao cho chữ số đứng sau lớn hơn chữ số đứng trước?
- gồm 5 chữ số phân biệt sao cho luôn có mặt 3 chữ số $1 ; 2 ; 3$ và 3 chữ số này luôn đứng cạnh nhau?
f) Tập hợp $E={1 ; 2 ; 5 ; 7 ; 8}$. Có bao nhiêu cách lập ra một số có 3 chữ số khác nhau lấy từ E sao cho:
- Số tạo thành là số chẵn?
- Số tạo thành là một số có chữ số 5?
Câu 6: Khai triển nhị thức Newtơn:
a) $(x+2)^{4}$
c) $(x-3 y)^{5}$.
b) $\left(x^{2}+\frac{1}{x}\right)^{4}$
d) $\left(x-\frac{1}{x^{2}}\right)^{5}$
Câu 7: Tìm hệ số của số hạng chứa
a) $x^{3}$ trong khai triển $(2 x-1)^{4}$.
b) $x^{3}$ trong khai triển $\left(x^{3}+\frac{1}{x}\right)^{5}$ với $x \neq 0$.
c) không chứa $x$ trong khai triển $\left(\frac{x}{2}+\frac{4}{x}\right)^{4}$ với $x \neq 0$.
Câu 8: Cho $n$ là số nguyên dương thỏa mãn $C_{n}^{1}+C_{n}^{2}=15$. Tìm số hạng không chứa $x$ trong khai triển $\left(x+\frac{2}{x^{4}}\right)^{n}$.
Câu 9: Tìm hệ số của $x^{10}$ trong khải triển thành đa thức của $\left(1+x+x^{2}+x^{3}\right)^{5}$.
Câu 10: Viết tọa độ của các vectơ sau:
a) $\vec{a}=2 \vec{i}+3 \vec{j} ; \vec{b}=\frac{1}{3} \vec{i}-5 \vec{j} ; \vec{c}=3 \vec{i} ; \vec{d}=-2 \vec{j}$
b) $\vec{a}=\vec{i}-3 \vec{j} ; \vec{b}=\frac{1}{2} \vec{i}+\vec{j} ; \vec{c}=-\vec{i}+\frac{3}{2} \vec{j} ; \vec{d}=-4 \vec{j} ; \vec{e}=3 \vec{i}$
Câu 11: Cho $\vec{a}=(2 ; 0), \vec{b}=\left(-1 ; \frac{1}{2}\right), \vec{c}=(4 ;-6)$ :
a) Tìm toạ độ của vectơ $\vec{d}=2 \vec{a}-3 \vec{b}+5 \vec{c}$.
b) Tìm 2 số $m, n$ sao cho: $m \vec{a}+\vec{b}-n \vec{c}=\overrightarrow{0}$.
c) Biểu diễn vectơ $\vec{c}$ theo $\vec{a}, \vec{b}$.
Câu 12: Trong mặt phẳng toạ độ $O x y$, cho các điềm $A(1 ; 3), B(2 ; 4), C(-3 ; 2)$.
a) Hãy chứng minh rằng $A, B, C$ là ba đỉnh của một tam giác.
b) Tìm toạ độ trung điểm $M$ của đoạn thẳng $A B$.
c) Tìm toạ độ trọng tâm $G$ của tam giác $A B C$.
d) Tìm điểm $D(x ; y)$ để $O(0 ; 0)$ là trọng tâm của tam giác $A B D$.
Câu 13: Cho tam giác $A B C$ có $A(1 ; 2), B(-2 ; 6), C(9 ; 8)$
a) Tính $\overrightarrow{A B} \cdot \overrightarrow{A C}$. Chứng minh tam giác $A B C$ vuông tại $A$.
b) Tìm tâm và bán kính đường tròn ngoại tiếp tam giác $A B C$.
c) Tìm toạ độ trực tâm $H$ và trọng tâm $G$ của tam giác $A B C$. d) Tính chu vi, diện tích tam giác $A B C$.
e) Tìm toạ độ điểm $T$ thoả $\overrightarrow{T A}+2 \overrightarrow{T B}-3 \overrightarrow{T C}=\overrightarrow{0}$.
f) Tìm toạ độ điểm $E$ đối xứng với $A$ qua $B$.
g) Tìm tọa độ điểm $D$ để tứ giác $A B C D$ là hình bình hành.
Câu 14: Trong hệ tọa độ $O x y$ cho ba điểm $A(1 ;-4), B(4 ; 5), C(0 ;-9)$. Điểm $M$ di chuyển trên trục $O x$. Đặt $Q=2|\overrightarrow{M A}+2 \overrightarrow{M B}|+3|\overrightarrow{M B}+\overrightarrow{M C}|$. Biết giá trị nhỏ nhất của $Q$ có dạng $a \sqrt{b}$ trong đó $a, b$ là các số nguyên dương và $a, b<20$. Tính $a-b$.
-

Bài tập thực tế hệ bất phương trình lớp 10
Chúng tôi xin giới thiệu một số bài toán thực tế hệ bất phương trình bậc nhất 2 ẩn trong chương trình Toán 10 mới.
Bài 1. [Đề dự bị kỳ thi THPTQG năm 2015] Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng
tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu; pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điển thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để được số điểm thưởng là lớn nhất?Lời giải. Gọi \(x, y\) lần lượt là số lít nước cam và táo của một đội pha chế \((x, y \geq 0)\).
- Số điểm thưởng của đội chơi này là: \(f(x ; y)=60 x+80 y\).
- Số gam đường cần dùng là: \(30 x+10 y\).
- Số lít nước cần dùng là: \(x+y\).
- Số gam hương liệu cần dùng là: \(x+4 y\).
Vì trong cuộc thi pha chế, mỗi đội chơi sử dụng tối đa \(24 \mathrm{~g}\) hương liệu, 9 lít nước và \(210 \mathrm{~g}\) đường nên ta có hệ bất phương trình: \[\left\{\begin{array}{l}30 x+10 y \leq 210 \\ x+y \leq 9 \\ x+4 y \leq 24 \\ x, y \geq 0\end{array} \Leftrightarrow\left\{\begin{array}{l}3 x+y \leq 21 \\ x+y \leq 9 \\ x+4 y \leq 24 \\ x, y \geq 0\end{array}\right.\right. (*)\]Bài toán trở thành tìm giá trị lớn nhất của hàm số \(f(x ; y)\) trên miền nghiệm của hệ bất phương trình (*).
Miền nghiệm của hệ bất phương trình (*) là ngũ giác \(O A B C D\) (kể cả biên), là phần không bị tô xám trong hình sau:

Hàm số \(f(x ; y)=60 x+80 y\) sẽ đạt giá trị lớn nhất trên miền nghiệm của hệ bất phương trình (*) khi \((x ; y)\) là toạ độ của một trong các đỉnh \(O(0 ; 0)\), \(A(7 ; 0), B(6 ; 3), C(4 ; 5), D(0 ; 6)\). Ta tính được có:
\(f(0 ; 0)=60.0+80.0=0\); \(f(7 ; 0)=60.7+80.0=420\); \(f(6 ; 3)=60.6+80.3=600\); \(f(4 ; 5)=60.4+80.5=640\); \(f(0 ; 6)=60.0+80.6=480\).
Suy ra \(f(4 ; 5)\) là giá trị lớn nhất của hàm số \(f(x ; y)\) trên miền nghiệm của hệ (*). Như vậy để được số điểm thưởng là lớn nhất cần pha chế 6 lít nước cam và 5 lít nước táo.
Bài 2. Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Công ty dự định chi tối đa 16.000.000 đồng cho quảng cáo.
- Gọi x và y lần lượt là số phút mà công ty thuê quảng cáo trên hệ thống phát thanh và truyền hình. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho tổng số tiền công ty chi phí cho quảng cáo không quá 16 triệu đồng.
- Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng tọa độ.
Bài 3. Trong một cuộc thi gói bánh vào dịp năm mới, mỗi đội chơi được sử dụng tối đa 20 kg gạo nếp, 2 kg thịt ba chỉ, 5 kg đậu xanh để gói bánh chưng và bánh ống. Để gói một cái bánh chưng cần 0,4 kg gạo nếp, 0,05 kg thịt và 0,1 kg đậu xanh; để gói một cái bánh ống cần 0,6 kg gạo nếp, 0,075 kg thịt và 0,15 kg đậu xanh. Mỗi cái bánh chưng nhận được 5 điểm thưởng, mỗi cái bánh ống nhận được 7 điểm thưởng. Hỏi cần phải gói mấy cái bánh mỗi loại để được nhiều điểm thưởng nhất?
Bài 4. Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kg thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kg thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn, giá tiền mỗi kg thịt bò là 250.000 đồng, giá tiền mỗi kg thịt lợn là 85.000 đồng. Hỏi chi phí ít nhất để mua thịt mỗi ngày của gia đình đó là bao nhiêu?
Bài 5. Một công ty cần thuê xe để chở 140 người và 9 tấn hàng. Nơi thuê xe có hai loại xe A và B, trong đó loại xe A có 10 chiếc và loại xe B có 9 chiếc. Một chiếc xe loại A cho thuê với giá 4 triệu đồng, một chiếc xe loại B cho thuê với giá 3 triệu. Biết rằng mỗi xe loại A có thể chở tối đa 20 người và 0,6 tấn hàng; mỗi xe loại B có thể chở tối đa 10 người và 1,5 tấn hàng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí bỏ ra là ít nhất?
Bài 6. Một hộ nông dân định trồng đậu và cà trên diện tích 8 ha. Nếu trồng đậu thì cần 20 công và thu 3000000 đồng trên diện tích mỗi ha, nếu trồng cà thì cần 30 công và thu 4000000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất biết rằng tổng số công không quá 180?
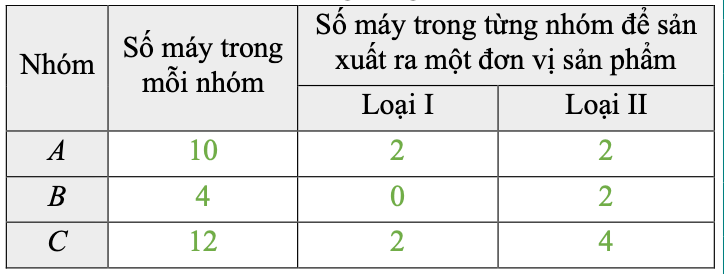
Bài 7. Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một đơn vị sản phẩm mỗi loại phải lần lượt dùng các máy thuộc các nhóm khác nhau. Số máy trong một nhóm và số máy của từng nhóm cần thiết để sản xuất ra một đơn vị sản phẩm thuộc mỗi loại được cho trong bảng sau: Mỗi đơn vị sản phẩm I lãi 3.000 đồng, mỗi đơn vị sản phẩm II lãi 5.000 đồng. Để việc sản xuất hai loại sản phẩm trên có lãi cao nhất thì cần dùng đến mấy máy thuộc nhóm A?
Bài 8. Một phân xưởng có hai máy đặc chủng M1 và M2 sản xuất hai loại sản phẩn ký hiệu là A và B. Một tấn sản phẩm loại A lãi 2 triệu đồng, một tấn sản phẩm loại B lãi 1,6 triệu đồng. Muốn sản xuất một tấn sản phẩm loại A phải dùng máy M1 trong 3 giờ và máy M2 trong 1 giờ. Muốn sản xuất một tấn sản phẩm loại B phải dùng máy M1 trong 1 giờ và máy M2 trong 1 giờ. Một máy không thể dùng để sản xuất đồng thời hai loại sản phẩm. Máy M1 làm việc không quá 6 giờ một ngày, máy M2 làm việc không quá 4 giờ một ngày. Hỏi số tiền lãi lớn nhất mà phân xưởng này có thể thu được trong một ngày là bao nhiêu?
Bài 9. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 140 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 4 triệu đồng, có thể chiết xuất được 20 kg chất A và 0,6 kg chất B. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 10 kg chất A và 1,5 kg chất B. Hỏi phải dùng bao nhiêu tấn nguyên liệu mỗi loại để chi phí mua nguyên liệu là ít nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 10 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II?
Bài 10. Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằng cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồng, trên sóng truyền hình là 4.000.000 đồng. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chương trình dài tối đa là 4 phút. Theo các phân tích cùng thời lượng một phút quảng cáo trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa là 16.000.000 đồng cho quảng cáo. Công ty cần đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất?
Bài 11. Một xưởng sản xuất hai loại sản phẩm, mỗi kg sản phẩm loại một cần 2 kg nguyên liệu và 30 giờ, đem lại mức lợi nhuận 40 000 đồng. Mỗi sản phẩm loại hai cần 4 kg nguyên liệu và 15 giờ đem lại mức lợi nhuận là 30 000 đồng. Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Hỏi cần sản xuất mỗi loại sản phẩm bao nhiêu để có mức lợi nhuận cao nhất?
Bài 12. Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 45 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 80 radio/ngày. Để sản xuất một chiếc radio kiểu một cần 12 linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 250 000 đồng, lãi thu được khi bán một chiếc radio kiểu hai là 180 000 đồng. Hỏi cần sản xuất như thế nào để tiền lãi thu được là nhiều nhất, biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 900?
Bài 13. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo. Để pha chế 1 lít nước cam cần 30 g đường và 1 lít nước; pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu. Mỗi lít nước cam nhận được 20 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để được số tiền thưởng là lớn nhất?
Bài 14. Một xưởng sản xuất hai loại sản phẩm:
- Mỗi kg sản phẩm loại I cần 2 kg nguyên liệu và 30 giờ, đem lại mức lời 40 nghìn;
- Mỗi kg sản phẩm loại II cần 4 kg nguyên liệu và 15 giờ, đem lại mức lời 30 nghìn.
Xưởng có 200 kg nguyên liệu và 1200 giờ làm việc. Nên sản xuất mỗi loại sản phẩm bao nhiêu để có mức lời cao nhất?
Bài 15. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24 g hương liệu, 9 lít nước và 210 g đường để pha chế nước cam và nước táo.
- Để pha chế 1 lít nước cam cần 30 g đường, 1 lít nước và 1 g hương liệu;
- Để pha chế 1 lít nước táo cần 10 g đường, 1 lít nước và 4 g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
Bài 16. Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm I và II . Mỗi sản phẩm I bán lãi 500 nghìn đồng, mỗi sản phẩm II bán lãi 400 nghìn đồng. Để sản xuất được một sản phẩm I thì Chiến phải làm việc trong 3 giờ, Bình phải làm việc trong 1 giờ. Để sản xuất được một sản phẩm II thì Chiến phải làm việc trong 2 giờ, Bình phải làm việc trong 6 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 180 giờ và Bình không thể làm việc quá 220 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là bao nhiêu?
Bài 17. Một nhà khoa học đã nghiên cứu về tác động phối hợp của hai loại Vitamin A và B đã thu được kết quả như sau: Trong một ngày, mỗi người cần từ 400 đến 1000 đơn vị Vitamin cả A lẫn B và có thể tiếp nhận không quá 600 đơn vị vitamin A và không quá 500 đơn vị vitamin B . Do tác động phối hợp của hai loại vitamin trên nên mỗi ngày một người sử dụng số đơn vị vitamin B không ít hơn một nửa số đơn vị vitamin A và không nhiều hơn ba lần số đơn vị vitamin A . Tính số đơn vị vitamin mỗi loại ở trên để một người dùng mỗi ngày sao cho chi phí rẻ nhất, biết rằng mỗi đơn vị vitamin A có giá 9 đồng và mỗi đơn vị vitamin B có giá 7,5 đồng.
Bài 18. Công ty Bao bì Dược cần sản xuất 3 loại hộp giấy: đựng thuốc B1, đựng cao Sao vàng và đựng “Quy sâm đại bổ hoàn”. Để sản xuất các loại hộp này, công ty dùng các tấm bìa có kích thước giống nhau. Mỗi tấm bìa có hai cách cắt khác nhau.
- Cách thứ nhất cắt được 3 hộp B1, một hộp cao Sao vàng và 6 hộp Quy sâm;
- Cách thứ hai cắt được 2 hộp B1, 3 hộp cao Sao vàng và 1 hộp Quy sâm.
Theo kế hoạch, số hộp Quy sâm phải có là 900 hộp, số hộp B1 tối thiểu là 900 hộp, số hộp cao sao vàng tối thiểu là 1000 hộp. Cần phương án sao cho tổng số tấm bìa phải dùng là ít nhất?
Bài 19. Một nhà máy sản xuất, sử dụng ba loại máy đặc chủng để sản xuất sản phẩm A và sản phẩm B trong một chu trình sản xuất. Để sản xuất một tấn sản phẩm A lãi 4 triệu đồng, người ta sử dụng máy I trong 1 giờ, máy II trong 2 giờ và máy III trong 3 giờ. Để sản xuất ra một tấn sản phẩm B lãi được 3 triệu đồng, người ta sử dụng máy I trong 6 giờ,máy II trong 3 giờ và máy III trong 2 giờ. Biết rằng máy I chỉ hoạt động không quá 36 giờ, máy II hoạt động không quá 23 giờ và máy III hoạt động không quá 27 giờ. Hãy lập kế hoạch sản xuất cho nhà máy để tiền lãi được nhiều nhất.
Bài 20. Một máy cán thép có thể sản xuất hai sản phẩm thép tấm và thép cuộn (máy không thể sản xuất hai loại thép cùng lúc và có thể làm việc 40 giờ một tuần). Công suất sản xuất thép tấm là 250 tấn/giờ, công suất sản xuất thép cuộn là 150 tấn/giờ. Mỗi tấn thép tấm có giá 25 USD, mỗi tấn thép cuộn có giá 30 USD. Biết rằng mỗi tuần thị trường chỉ tiêu thụ tối đa 5000 tấn thép tấm và 3500 tấn thép cuộn. Hỏi cần sản xuất bao nhiêu tấn thép mỗi loại trong một tuần để lợi nhuận thu được là cao nhất?
Bài 21. Một hộ nông dân định trồng cà phê và ca cao trên diện tích 10 ha. Nếu trồng cà phê thì cần 20 công và thu về 10000000 đồng trên diện tích mỗi ha, nếu trồng cà thì cần 30 công và thu 12000000 đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện tích là bao nhiêu để thu được nhiều tiền nhất biết rằng số công trồng cà phê không vượt quá 100 công và số công trồng ca cao không vượt quá 180 công.
Bài 22. Một công ty, trong một tháng cần sản xuất ít nhất 12 viên kim cương to và 9 viên kim cương nhỏ. Từ 1 tấn Cacbon loại 1 (giá 100 triệu đồng) có thể chiết xuất được 6 viên kim cương to và 3 viên kim cương nhỏ, từ 1 tấn Cacbon loại 2 (giá 40 triệu đồng) có thể chiết xuất được 2 viên kim cương to và 2 viên kim cương nhỏ. Mỗi viên kim cương to có giá 20 triệu đồng, mỗi viên kim cương nhỏ có giá 10 triệu đồng. Hỏi trong một tháng công ty này thu về được nhiều nhất là bao nhiêu tiền, biết rằng mỗi tháng chỉ có thể sử dụng tối đa 4 tấn Cacbon mỗi loại?
-

Bất đẳng thức Côsi và ứng dụng
Bất đẳng thức CôSi (Cauchy) hay bất đẳng thức AM-GM là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm.
1. Bất đẳng thức Cô-si là gì?
Trong toán học, bất đẳng thức Cauchy là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm được phát biểu như sau.
Với $a_1,a_2,\ldots,a_n$ là các số thực không âm, khi đó $$a_1+a_2+\cdots +a_{n}\ge n\sqrt[n]{a_1a_2\ldots a_n}.$$ Dấu bằng xảy ra khi và chỉ khi $a_1=a_2=\cdots =a_n$.

Chứng minh bất đẳng thức AM-GM cho hai số không âm bằng hình học Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
Các trường hợp đặc biệt của bất đẳng thức Cosi:
- Bất đẳng thức Cô si với 2 số thực không âm $a$ và $b$ thì: \[\frac{a+b}{2} \geqslant \sqrt{ab}\] Dấu “=” xảy ra khi và chỉ khi a = b.
- Bất đẳng thức Cô si với 3 số thực không âm $a,b$ và $c$ thì: \[\frac{a+b+c}{3} \geqslant \sqrt[3]{abc}\] Dấu “=” xảy ra khi và chỉ khi a = b =c.
Tên đúng của bất đẳng thức này là bất đẳng thức AM-GM. Có nhiều cách để chứng minh bđt này nhưng hay nhất là cách chứng minh quy nạp của Cauchy.
2. Các dạng phát biểu của bất đẳng thức Cô-si
a. Dạng tổng quát của bất đẳng thức Cô-si
Cho $x_1, x_2, x_3,…,x_n$ là các số thực dương ta có:
– Dạng 1: \(\dfrac{x_1+x_2+…+x_n}{n} \geqslant \sqrt[n]{x_1 x_2 x_3…x_n}\)
– Dạng 2: \({x_1+x_2+…+x_n} \geqslant n\sqrt[n]{x_1 x_2 x_3…x_n}\)
– Dạng 3: \(\left(\dfrac{x_1+x_2+…+x_n}{n}\right)^n \geqslant x_1 x_2 x_3…x_n\)
– Dạng 4: \(\left(x_1+x_2+…+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+…\frac{1}{x_n} \right) \geqslant n^2\)
Dấu đẳng thức xảy ra khi và chỉ khi $x_1= x_2= x_3=…=x_n$.
b. Dạng đặc biệt của bất đẳng thức Cô-si
Là các trường hợp đặc biệt của dạng tổng quát ở trên khi n=2, n=3.

c. Một số bất đẳng thức được suy ra từ bất đẳng thức Cauchy
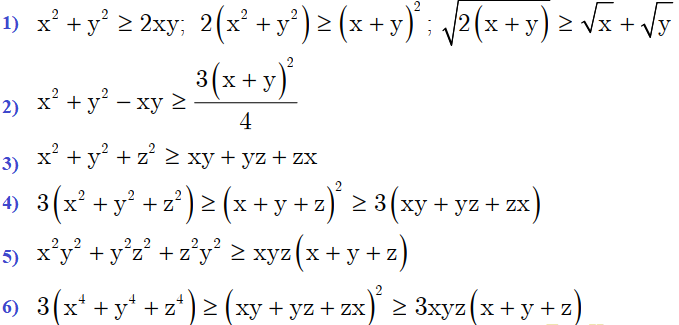
d. Chú ý khi sử dụng bất đẳng thức AM – GM
- Khi áp dụng bất đẳng thức Cô si thì các số phải là những số không âm;
- Bất đẳng thức Côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích;
- Điều kiện xảy ra dấu ‘=’ là các số bằng nhau;
- Bất đẳng thức Côsi còn có hình thức khác thường hay sử dụng.
3. Hệ quả của bất đẳng thức Cô-si
- \(x^{2}+y^{2} \geq 2 x y ; 2\left(x^{2}+y^{2}\right) \geq(x+y)^{2} ; \sqrt{2(x+y)} \geq \sqrt{x}+\sqrt{y}\)
- \(x^{2}+y^{2}-x y \geq \frac{3(x+y)^{2}}{4}\)
- \(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\)
- \(3\left(x^{2}+y^{2}+z^{2}\right) \geq(x+y+z)^{2} \geq 3(x y+y z+z x)\)
- \(x^{2} y^{2}+y^{2} z^{2}+z^{2} y^{2} \geq x y z(x+y+z)+3\left(x^{4}+y^{4}+z^{4}\right) \geq(x y+y z+z x)^{2} \geq 3 x y z(x+y+z)\)
4. Các dạng bài tập bất đẳng thức Cô-si
Bài 1: Tìm giá trị nhỏ nhất của biểu thức $A=x+\frac{7}{x}$ với x > 0.
Lời giải:
Áp dụng bất đẳng thức Cô si cho hai số x > 0 và ta có: \[ x+\frac{7}{x} \geq 2 \sqrt{x \cdot \frac{7}{x}}=2 \sqrt{7} \] Dấu “=” xảy ra khi và chỉ khi \(x=\frac{7}{x} \Leftrightarrow x^{2}=7 \Leftrightarrow x=\sqrt{7}\) (do x>0).
Vậy \(\min A=2 \sqrt{7} \Leftrightarrow x=\sqrt{7}\).
Bài 2: Cho \(x>0, y>0\) thỏa mãn điều kiện \(\frac{1}{x}+\frac{1}{y}=\frac{1}{2}\). Tìm giá trị lớn nhất của biểu thức \(A=\sqrt{x}+\sqrt{y}\).
Lời giải: Áp dụng bdt Cosi ta có \[ \frac{1}{x}+\frac{1}{y} \geq 2 \sqrt{\frac{1}{x} \cdot \frac{1}{y}} \Leftrightarrow \frac{1}{2} \geq \frac{2}{\sqrt{x y}} \Leftrightarrow \sqrt{x y} \geq 4 \]
Lại có, áp dụng bất đẳng thức Cô si cho hai số (x>0, y>0) ta có:
\[\sqrt{x}+\sqrt{y} \geq 2 \sqrt{\sqrt{x y}}=2 \sqrt{4}=4 \] Dấu “=” xảy ra khi và chỉ khi \[ \left\{\begin{array}{l}
x=y \\ \frac{1}{x}+\frac{1}{y}=\frac{1}{2}
\end{array} \right. \Leftrightarrow x=y=4. \]Vậy $\min A = 4$ khi và chỉ khi $x = y = 4$.
Bài 3: Ví dụ: Cho \(a\), \(b\) là số dương thỏa mãn \(a^{2}+b^{2}=2\). Chứng minh rằng \[ (a+b)^{5} \geq 16 a b \sqrt{\left(1+a^{2}\right)\left(1+b^{2}\right)} \]
Lời giải: Ta có \((a+b)^{5}=\left(a^{2}+2 a b+b^{2}\right)\left(a^{3}+3 a b^{2}+3 a^{2} b+b^{3}\right)\)
Áp dụng bdt Côsi ta có \[ \begin{aligned} &a^{2}+2 a b+b^{2} \geq 2 \sqrt{2 a b\left(a^{2}+b^{2}\right)}=4 \sqrt{a b} \text { và } \\ &\left(a^{3}+3 a b^{2}\right)+\left(3 a^{2} b+b^{3}\right) \geq 2 \sqrt{\left(a^{3}+3 a b^{2}\right)\left(3 a^{2} b+b^{3}\right)}=4 \sqrt{a b\left(1+b^{2}\right)\left(a^{2}+1\right)} \end{aligned} \]
Suy ra \(\left(a^{2}+2 a b+b^{2}\right)\left(a^{3}+3 a b^{2}+3 a^{2} b+b^{3}\right) \geq 16 a b \sqrt{\left(a^{2}+1\right)\left(b^{2}+1\right)}\)
Do đó \((a+b)^{5} \geq 16 a b \sqrt{\left(1+a^{2}\right)\left(1+b^{2}\right)}\) (đpcm). Đẳng thức xảy ra khi và chỉ khi \(a=b=1\).
Bài 4: Tìm GTLN của: $y=x^{2}(1-x) \quad, x \in(0,1)$
Lời giải: Do $x, 1-x>0$ nên áp dụng bất đẳng thức Cauchy ta có: $$ 2 y=x^{2}(1-2 x)=x \cdot x \cdot(1-2 x) \leq\left(\frac{x+x+1-2 x}{3}\right)^{3}=\frac{1}{27} \Rightarrow y \leq \frac{1}{54} $$ Dấu ‘=’ xảy ra $\Leftrightarrow x=1-2 x \Leftrightarrow x=\frac{1}{3}$.
Vậy Max $y=\frac{1}{27}$ khi $x=\frac{1}{3}$
Bài 5: Tìm GTNN của: $y=x+\frac{1}{x-1}, x>1$.
Lời giải: Do $x-1>0$ nên áp dụng bất đẳng thức Cauchy ta có: $$ y=(x-1)+\frac{1}{x-1}+1 \geq 2 \sqrt{(x-1) \cdot \frac{1}{x-1}}+1=3 \Rightarrow y \geq 3 $$ Dấu ‘=’ xảy ra $\Leftrightarrow x-1=\frac{1}{x-1} \Leftrightarrow x=2$.
Vậy Min $y=3$ khi $x=2$.
Xem thêm Chọn điểm rơi trong bất đẳng thức Côsi (Cauchy).
Bài 6: Cho 3 số dương \(a, b\), c, hãy chứng minh: \[ \left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right) \geq 8 \]
Hướng dẫn giải: Áp dụng BĐT Cosi, ta có: \[ \begin{aligned} a+\frac{1}{b} \geq 2 \sqrt{\frac{a}{b}};\\ b+\frac{1}{c} \geq 2 \sqrt{\frac{b}{c}};\\ c+\frac{1}{a} \geq 2 \sqrt{\frac{c}{a}} \end{aligned}\]
Nhân theo vế 3 bdt này ta được \[\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right) \geq 8 \sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{c}} \sqrt{\frac{c}{a}}=8 \] Đẳng thức xảy ra khi và chỉ khi \(a=b=c\).
Bài 7: Cho $a, b, c>0$. Chứng minh:
a) $a^2+b^2+4 \geqslant 2a+2b+ab$
b) $a(1+b)+b(1+c)+c(1+a) \geq 3 \sqrt[3]{a b c}(1+\sqrt[3]{a b c})$
c) $a \sqrt{b-1}+b \sqrt{a-1} \leq a b$ với $a, b \geq 1$Lời giải:
a) Áp dụng bât đẳng thức Cauchy ta có: $$ \begin{aligned} &a^{2}+4 \geq 4 a \\ &b^{2}+4 \geq 4 b \\ &a^{2}+b^{2} \geq 2 a b. \end{aligned} $$ Cộng lại ta được: $$ 2 a^{2}+2 b^{2}+8 \geq 4 a+4 b+2 a b $$ Dấu ‘=’ xảy ra $ \Leftrightarrow a=b=2$
b) Ta có : $$ a(1+b)+b(1+c)+c(1+a)=(a+b+c)+(a b+b c+c a) $$ Áp dụng bất đẳng thức Cauchy : $$ \begin{aligned} &a+b+c \geq 3 \sqrt[3]{a b c} \\ &a b+b c+c a \geq 3 \sqrt[3]{a^{2} b^{2} c^{2}} \end{aligned} $$ Cộng lại ta được đpcm.
Dấu ‘=’ xảy ra $\Leftrightarrow a=b=c$.
c) Ta có: $$a \sqrt{b-1}=\sqrt{a} \sqrt{a b-a} \leq \frac{a+a b-a}{2}=\frac{a b}{2}$$Tương tự: $$b \sqrt{a-1} \leq \frac{a b}{2}$$ Cộng lại ta đpcm.
Dấu ‘=’ xảy ra $\Leftrightarrow a=b=2$.
Bài 8: Chứng minh với ba số a, b, c không âm thỏa mãn a + b + c = 3 thì: \[ \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \geq \frac{3}{2} \]
Nhận xét: Bài toán đạt được dấu bằng khi và chi khi $a = b = c = 1$.
Ta sẽ sử dụng phương pháp làm trội làm giảm như sau: \[ \frac{a}{b+c}+\frac{b+c}{4}+\frac{1}{2 a} \geq 3 \sqrt[3]{\frac{a}{b+c} \cdot \frac{b+c}{4} \cdot \frac{1}{2 a}}=3 \sqrt[3]{\frac{1}{8}}=\frac{3}{2} \]
Tương tự ta có \(\frac{b}{c+a}+\frac{c+a}{4}+\frac{1}{2 b} \geq \frac{3}{2}\) và \(\frac{c}{a+b}+\frac{a+b}{4}+\frac{1}{2 c} \geq \frac{3}{2}\).
Cộng vế với vế ta có: \[ \begin{align*}\frac{a}{b+c}+\frac{b+c}{4}+\frac{1}{2 a}+\frac{b}{c+a}+\frac{c+a}{4}+\frac{1}{2 b}+\frac{c}{a+b}+\frac{a+b}{4}+\frac{1}{2 c} & \geq 3 \cdot \frac{3}{2}=\frac{9}{2} \\ \Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{2(a+b+c)}{4}+\frac{a b+b c+c a}{2 a b c} & \geq \frac{9}{2} \\ \Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{a+b+c}{2}+\frac{a+b+c}{2} & \geq \frac{9}{2} \\ \Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} &\geq \frac{9}{2}-3=\frac{3}{2} \end{align*} \]
Dấu “=” xảy ra khi và chỉ khi $a = b = c = 1$.
-

PPCT Toán 10 Cánh Diều
PHÂN PHỐI CHƯƠNG TRÌNH VÀ DỰ KIẾN KẾ HOẠCH DẠY HỌC SÁCH TOÁN 10 (BỘ SÁCH CÁNH DIỀU)
Mời thầy cô tham khảo thêm Giáo án Toán 10 Cánh Diều file Word và Giáo án Toán 10 Kết Nối Tri Thức.
Tên chương, bài học trong sách giáo khoa Toán 10 Số tiết CHƯƠNG I. MỆNH ĐỀ TOÁN HỌC. TẬP HỢP 7 §1. Mệnh đề toán học 3 §2. Tập hợp. Các phép toán trên tập hợp 3 Bài tập cuối chương I 1 CHƯƠNG II. BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN 6 §1. Bất phương trình bậc nhất hai ẩn 2 §2. Hệ bất phương trình bậc nhất hai ẩn 3 Bài tập cuối chương II 1 CHƯƠNG III. HÀM SỐ VÀ ĐỒ THỊ 17 §1. Hàm số và đồ thị 5 §2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng 2 §3. Dấu của tam thức bậc hai 3 §4. Bất phương trình bậc hai một ẩn 3 §5. Hai dạng phương trình quy về phương trình bậc hai 2 Bài tập cuối chương III 2 CHƯƠNG IV. HỆ THỨC LƯỢNG TRONG TAM GIÁC. VECTƠ 16 1. Giá trị lượng giác của một góc từ 0o đến 180o . Định lí côsin và định lí sin trong tam giác 4 §2. Giải tam giác. Tính diện tích tam giác 2 §3. Khái niệm vectơ 2 §4. Tổng và hiệu của hai vectơ 2 §5. Tích của một số với một vectơ 2 §6. Tích vô hướng của hai vectơ 2 Bài tập cuối chương IV 2 HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆMChủ đề 1. Đo góc 3 Chương V. ĐẠI SỐ TỔ HỢP 11 §1. Quy tắc cộng. Quy tắc nhân. Sơ đồ hình cây 4 §2. Hoán vị. Chỉnh hợp 2 §3. Tổ hợp 2 §4. Nhị thức Newton 2 Bài tập cuối chương V 1 Chương VI. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT 17 §1. Số gần đúng. Sai số 3 §2. Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu không ghép nhóm 3 §3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu không ghép nhóm 4 §4. Xác suất của biến cố trong một số trò chơi đơn giản 2 §5. Xác suất của biến cố 3 Bài tập cuối chương VI 2 HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆMChủ đề 2. Xây dựng mô hình hàm số bậc nhất, bậc hai biểu diễn số liệu dạng bảng 4 Chương VII. PHƯƠNG PHÁP TOẠ ĐỘ TRONG MẶT PHẲNG 18 §1. Toạ độ của vectơ 2 §2. Biểu thức toạ độ của các phép toán vectơ 3 §3. Phương trình đường thẳng 3 §4. Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến đường thẳng 2 §5. Phương trình đường tròn 3 §6. Ba đường conic 3 Bài tập cuối chương VII 2 THỰC như sau:Mạch kiến thứcSố tiếtTỉ số %Quy định của CT môn Toán 2018Đại số4343,4%44%Hình học3434,3%35%Thống kê – Xác suất1515,2%14%Hoạt động TH và TN77,1%7% HÀNH PHẦN MỀM GEOGEBRA Tên chuyên đề, bài học trong sách chuyên đề học tập Toán 10 Chuyên đề I. HỆ PHƯƠNG TRÌNH BẬC NHẤT BA ẨN 10 §1. Hệ phương trình bậc nhất ba ẩn 5 §2. Ứng dụng hệ phương trình bậc nhất ba ẩn 5 Chuyên đề II. PHƯƠNG PHÁP QUY NẠP TOÁN HỌC. NHỊ THỨC NEWTON 10 §1. Phương pháp quy nạp toán học 5 §2. Nhị thức Newton 5 Chuyên đề III. BA ĐƯỜNG CONIC VÀ ỨNG DỤNG 15 §1. Elip 4 §2. Hypebol 4 §3. Parabol 3 §4. Ba đường conic 4 Chú ý: Tổng cộng SGK là 99 tiết, còn dư ra 6 tiết phân phối vào các tiết kiểm tra.
-
Giải phương trình \( \sqrt{x} +\sqrt{3x-2}=x^2+1. \)
Giải phương trình \[ \sqrt{x} +\sqrt{3x-2}=x^2+1. \]
Hướng dẫn. Điều kiện \( x \geqslant \frac{2}{3}. \) Dự đoán nghiệm của phương trình là \( 1 \) nên ta nhân hai vế của phương trình với 2 và thêm bớt \( 4x \) ta được
\[2x^2-4x+2 + x-2\sqrt{x}+1 +3x-2 -2\sqrt{3x-2}+1=0 \]
\[ \Leftrightarrow 2(x-1)^2 + \left(\sqrt{x}-1\right)^2+\left(\sqrt{3x-2}-1\right)^2=0 \]
Từ đó suy ra \[ (x-1)^2= \left(\sqrt{x}-1\right)^2=\left(\sqrt{3x-2}-1\right)^2=0 \] và tìm được nghiệm duy nhất \( x=1 \).
\end{proof}
Cách khác, đặt \( u= \sqrt{x}, v=\sqrt{3x-2} \) ta suy ra \( u+v=x^2+1, u^2=x, v^2=3x-2 \) ta đưa về đánh giá các biểu thức đại số không chứa căn.
Cách khác nữa, sử dụng bất đẳng thức Cauchy ta có
\[ \frac{x +1}{2} \geqslant \sqrt{x}; \frac{3x-2+1}{2} \geqslant \sqrt{3x-2} \]
Cộng từng vế hai bất đẳng thức trên ta được \[ 2x \geqslant \sqrt{x} +\sqrt{3x-2}. \] Mà \( \sqrt{x} +\sqrt{3x-2}=x^2+1 \) nên suy ra \[ 2x \geqslant x^2+1 \Leftrightarrow (x-1)^2 \leqslant 0. \] Điều này chỉ xảy ra khi và chỉ khi \( x=1. \) -
HỌC BẤT ĐẲNG THỨC NHƯ THẾ NÀO?
Chúng tôi xin giới thiệu bài viết “HỌC BẤT ĐẲNG THỨC NHƯ THẾ NÀO?” của thầy Phùng Quyết Thắng.
7 kĩ năng quan trọng khi giải các bài toán Bất đẳng thức
Định luật bảo toàn dấu bằng hay còn gọi là điểm rơi của bài toán
Mời bạn xem trong bài Chọn điểm rơi trong bất đẳng thức Côsi (Cauchy)
Bậc của B.Đ.T và kĩ năng đồng bậc hoá
B.Đ.T đồng bậc là tất cả các hạng tử của đa thức đó có bậc bằng nhau.VD: a² +b² ≥ 2ab đều cùng bậc 2 cả vế trái và vế phải.
Đồng bậc hoá B.Đ.T là quá trình sử dụng giả thiết để đưa B.Đ.T không đồng bậc về dạng tương đương với một B.Đ.T đồng bậc. Đây là cơ sở để người ra đề giấu bản chất bài toán, khiến người giải bị lạc lối .
VD: Cho xy= 1. CMR: x² + y² ≥ 2.
B.Đ.T cần chứng minh vế trái và vế phải ko đồng bậc, tìm cách làm vế phải có bậc giống vế trái dựa vào gt và biến đổi tương đương (quy tắc 3), B.Đ.T được giải quyết xong!
x² + y² ≥ 2xy ⇔ (x-y)²≥ 0
Ghép đối xứng
Thành thạo bài toán cosi tổng ta tích với điểm rơi tự nhiên và điều chỉnh hệ số với điểm rơi nhân tạo.
Cosi: mx + n/x ≥ 2√(mn) trong đó điểm rơi tự nhiên: x =√(n/m) > x của TXD
Khi điểm rơi tự nhiên < x của TXD thì hệ số điều chỉnh a = n/x² với x là điểm rơi nhân tạo ≥ x của TXD khi đó biến đổi biểu thức thành dạng n/x + ax + (m-a)x. trong đó n/x + ax đánh giá theo Cosi (m-a)x đánh giá theo TXD
Kĩ thuật biến đổi tương đương
Kĩ thuật biến đổi tương đương: là các phép biến đổi đại số đưa B.Đ.T về dạng tương đương để đánh giá thuận tiện hơn, đa phần B.Đ.T cuối cùng đưa về dạng bậc chẵn hoặc dạng tích mà điều kiện của TXD giúp chúng ta chứng minh được B.Đ.T≥ 0
Sắp xếp các biến
Đây là câu hỏi nhiều bạn ko biết tại sao và khi nào dùng được quy tắc này khi thấy nhiều lời giải hay ghi câu “Không mất tính tổng quát, giả sử a≥b≥c…” mà ko nói tại sao??? họ biết nhưng họ bỏ câu phía trước rồi!
- Tính chất 1: B.Đ.T là hoán vị có thể giả sử một số là lớn nhất (nhỏ nhất) hoặc nằm giữa trong ba số.
- Tính chất 2: B.Đ.T là đối xứng ta có thể giả sử a≥b≥c.
Vậy B.Đ.T có tính hoán vị, đối xứng được định nghĩa ntn?
B.Đ.T f(a,b,c)≥ 0 có tính hoán vị nếu f(a,b,c)=f(b,c,a)=f(c,b,a)
B.Đ.T f(a,b,c) có tính đối xứng là B.Đ.T hoán vị + đổi chỗ b và c vẫn bằng nhau, tức là: f(a,b,c)=f(b,c,a)=f(c,b,a)=f(a,c,b)
Phân biệt và hiểu về độ mạnh yếu (độ chặt) trong B.Đ.T
Hệ quả quan trọng: nếu B.Đ.T (1) suy ra được B.Đ.T (2) nhưng (2) ko suy ngược lại (1) thì B.Đ.T (1) mạnh hơn B.Đ.T (2)
Khái niệm mạnh yếu giúp chúng ta lí giải thật sự logic và rõ ràng tình huống “bị ngược dấu” khi chứng minh B.Đ.T
Một số ý tưởng đơn giản hoá bài toán
- Tìm cách đưa B.Đ.T về bậc càng thấp.
- Giảm số lượng biến bằng hai cách: đổi biến (đặt ẩn phụ) và phương pháp dồn biến.
- B.Đ.T chứa căn thì phải tìm cách phá căn bằng: + Nâng lũy thừa + Đặt ẩn phụ + Áp dụng B.Đ.T cơ bản và bổ đề : cosi tích ra tổng, Bunhiacopsk
-
Chứng minh bất đẳng thức bằng biến đổi tương đương
Chứng minh bất đẳng thức bằng biến đổi tương đương
Chứng minh bất đẳng thức bằng biến đổi tương đương là chúng ta sử dụng định nghĩa và các tính chất cơ bản của bất đẳng thức.
Phương pháp giải. Để chứng minh bất đẳng thức (BĐT) A ≥ B ta có thể sử dụng các cách sau:
- Ta đi chứng minh A-B ≥ 0. Để chứng minh nó ta thường sử dụng các hằng đẳng thức để phân tích A-B thành tổng hoặc tích của những biểu thức không âm.
- Xuất phát từ BĐT đúng, biến đổi tương đương về BĐT cần chứng minh.
Ví dụ minh họa Chứng minh bất đẳng thức bằng biến đổi tương đương
1. Biến đổi tương đương về bất đẳng thức đúng.
Ví dụ 1: Cho hai số thực $a,b,c$. Chứng minh rằng các bất đẳng thức sau:
- $ab\le \frac{{{a}^{2}}+{{b}^{2}}}{2}$
- $ab\le {{\left( \frac{a+b}{2} \right)}^{2}}$
- $3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\ge {{\left( a+b+c \right)}^{2}}$
- ${{\left( a+b+c \right)}^{2}}\ge 3\left( ab+bc+ca \right)$
Lời giải
- Ta có ${{a}^{2}}+{{b}^{2}}-2ab={{(a-b)}^{2}}\ge 0\Rightarrow {{a}^{2}}+{{b}^{2}}\ge 2ab$. Đẳng thức$\Leftrightarrow a=b$.
- Bất đẳng thức tương đương với ${{\left( \frac{a+b}{2} \right)}^{2}}-ab\ge 0$
$\Leftrightarrow {{a}^{2}}+2ab+{{b}^{2}}\ge 4ab\Leftrightarrow {{\left( a-b \right)}^{2}}\ge 0$ (đúng) ĐPCM.
Đẳng thức xảy ra $\Leftrightarrow a=b$ - BĐT tương đương $3\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)\ge {{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca$
$\Leftrightarrow {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}}\ge 0$ (đúng) ĐPCM.
Đẳng thức xảy ra$\Leftrightarrow a=b=c$ - BĐT tương đương ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+2ab+2bc+2ca\ge 3\left( ab+bc+ca \right)$
$\Leftrightarrow 2\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}} \right)-2\left( ab+bc+ca \right)\ge 0$ $\Leftrightarrow {{\left( a-b \right)}^{2}}+{{\left( b-c \right)}^{2}}+{{\left( c-a \right)}^{2}}\ge 0$ (đúng) ĐPCM.
Đẳng thức xảy ra$\Leftrightarrow a=b=c$
Nhận xét: Các BĐT trên được vận dụng nhiều, và được xem như là “bổ đề” trong chứng minh các bất đẳng thức khác.
Ví dụ 2: Cho năm số thực $a,b,c,d,e$. Chứng minh rằng $${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}+{{e}^{2}}\ge a(b+c+d+e)$$.
Lời giải. Ta có: ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}+{{d}^{2}}+{{e}^{2}}-a(b+c+d+e)=$
$=(\frac{{{a}^{2}}}{4}-ab+{{b}^{2}})+(\frac{{{a}^{2}}}{4}-ac+{{c}^{2}})+(\frac{{{a}^{2}}}{4}-ad+{{d}^{2}})+(\frac{{{a}^{2}}}{4}-ae+{{e}^{2}})$
$={{(\frac{a}{2}-b)}^{2}}+{{(\frac{a}{2}-c)}^{2}}+{{(\frac{a}{2}-d)}^{2}}+{{(\frac{a}{2}-e)}^{2}}\ge 0\Rightarrow $ đpcm.
Đẳng thức xảy ra $\Leftrightarrow b=c=d=e=\frac{a}{2}$.Ví dụ 3: Cho $ab\ge 1$. Chứng minh rằng: $$\frac{1}{{{a}^{2}}+1}+\frac{1}{{{b}^{2}}+1}\ge \frac{2}{1+ab}$$
Lời giải. Ta có $\frac{1}{{{a}^{2}}+1}+\frac{1}{{{b}^{2}}+1}-\frac{2}{1+ab}=(\frac{1}{{{a}^{2}}+1}-\frac{1}{1+ab})+(\frac{1}{{{b}^{2}}+1}-\frac{2}{1+ab})$
$=\frac{ab-{{a}^{2}}}{({{a}^{2}}+1)(1+ab)}+\frac{ab-{{b}^{2}}}{({{b}^{2}}+1)(1+ab)}=\frac{a-b}{1+ab}(\frac{b}{1+{{b}^{2}}}-\frac{a}{1+{{a}^{2}}})=\frac{a-b}{1+ab}.\frac{b-a+{{a}^{2}}b-{{b}^{2}}a}{(1+{{b}^{2}})(1+{{a}^{2}})}$$=\frac{a-b}{1+ab}\frac{(a-b)(ab-1)}{(1+{{b}^{2}})(1+{{a}^{2}})}=\frac{{{(a-b)}^{2}}(ab-1)}{(1+ab)(1+{{b}^{2}})(1+{{a}^{2}})}\ge 0$ (Do $ab\ge 1)$.Nhận xét: Nếu $-1<b\,\le 1$ thì BĐT có chiều ngược lại: $\frac{1}{{{a}^{2}}+1}+\frac{1}{{{b}^{2}}+1}\le \frac{2}{1+ab}$.
Ví dụ 4: Cho số thực $x$. Chứng minh rằng
- ${{x}^{4}}+3\ge 4x$
- ${{x}^{4}}+5>{{x}^{2}}+4x$
- ${{x}^{12}}+{{x}^{4}}+1>{{x}^{9}}+x$
Lời giải
- Bất đẳng thức tương đương với ${{x}^{4}}-4x+3\ge 0$
$\Leftrightarrow \left( x-1 \right)\left( {{x}^{3}}+{{x}^{2}}+x-3 \right)\ge 0\Leftrightarrow {{\left( x-1 \right)}^{2}}\left( {{x}^{2}}+2x+3 \right)\ge 0$
$\Leftrightarrow {{\left( x-1 \right)}^{2}}\left[ {{\left( x+1 \right)}^{2}}+1 \right]\ge 0$ (đúng với mọi số thực $x$ )
Đẳng thức xảy ra khi và chỉ khi $x=1$. - Bất đẳng thức tương đương với ${{x}^{4}}-{{x}^{2}}-4x+5>0$
$\Leftrightarrow {{x}^{4}}-2{{x}^{2}}+1+{{x}^{2}}-4x+4>0\Leftrightarrow {{\left( {{x}^{2}}-1 \right)}^{2}}+{{\left( x-2 \right)}^{2}}>0$
Ta có ${{\left( {{x}^{2}}-1 \right)}^{2}}\ge 0,\,{{\left( x-2 \right)}^{2}}\ge 0\Rightarrow {{\left( {{x}^{2}}-1 \right)}^{2}}+{{\left( x-2 \right)}^{2}}\ge 0$
Đẳng thức xảy ra khi và chỉ khi $\left\{ \begin{matrix}
{{x}^{2}}-1=0 \\
x-2=0 \\
\end{matrix} \right.$ (không xảy ra)
Suy ra ${{\left( {{x}^{2}}-1 \right)}^{2}}+{{\left( x-2 \right)}^{2}}>0$ ĐPCM. - Bất đẳng thức tương đương với ${{x}^{12}}-{{x}^{9}}+{{x}^{4}}-x+1>0$
+ Với $x<1$: Ta có ${{x}^{12}}-{{x}^{9}}+{{x}^{4}}-x+1={{x}^{12}}+{{x}^{4}}\left( 1-{{x}^{5}} \right)+\left( 1-x \right)$
Vì $x<1$ nên $1-x>0,\,\,1-{{x}^{5}}>0$ do đó ${{x}^{12}}-{{x}^{9}}+{{x}^{4}}-x+1>0$.
+ Với $x\ge 1$: Ta có ${{x}^{12}}-{{x}^{9}}+{{x}^{4}}-x+1={{x}^{9}}\left( {{x}^{3}}-1 \right)+x\left( {{x}^{3}}-1 \right)+1$
Vì $x\ge 1$ nên ${{x}^{3}}-1\ge 0$ do đó ${{x}^{12}}-{{x}^{9}}+{{x}^{4}}-x+1>0$.
Vậy ta có ${{x}^{12}}+{{x}^{4}}+1>{{x}^{9}}+x$.
Ví dụ 5: Cho $a,b,c$ là các số thực. Chứng minh rằng:
- ${{a}^{4}}+{{b}^{4}}-4ab+2\ge 0$
- $2\left( {{a}^{4}}+1 \right)+{{\left( {{b}^{2}}+1 \right)}^{2}}\ge 2{{\left( ab+1 \right)}^{2}}$
- $3\left( {{a}^{2}}+{{b}^{2}} \right)-ab+4\ge 2\left( a\sqrt{{{b}^{2}}+1}+b\sqrt{{{a}^{2}}+1} \right)$
Lời giải
- BĐT tương đương với $\left( {{a}^{4}}+{{b}^{4}}-2{{a}^{2}}{{b}^{2}} \right)+\left( 2{{a}^{2}}{{b}^{2}}-4ab+2 \right)\ge 0$
$\Leftrightarrow {{\left( {{a}^{2}}-{{b}^{2}} \right)}^{2}}+2{{\left( ab-1 \right)}^{2}}\ge 0$ (đúng)
Đẳng thức xảy ra khi và chỉ khi $a=b=\pm 1$. - BĐT tương đương với $2\left( {{a}^{4}}+1 \right)+\left( {{b}^{4}}+2{{b}^{2}}+1 \right)-2\left( {{a}^{2}}{{b}^{2}}+2ab+1 \right)\ge 0$
$\Leftrightarrow \left( {{a}^{4}}+{{b}^{4}}-2{{a}^{2}}{{b}^{2}} \right)+\left( 2{{a}^{2}}-4ab+2{{b}^{2}} \right)+\left( {{a}^{4}}-4{{a}^{2}}+1 \right)\ge 0$
$\Leftrightarrow {{({{a}^{2}}-{{b}^{2}})}^{2}}+2{{(a-b)}^{2}}+{{({{a}^{2}}-1)}^{2}}\ge 0$(đúng)
Đẳng thức xảy ra khi và chỉ khi $a=b=\pm 1$. - BĐT tương đương với $6\left( {{a}^{2}}+{{b}^{2}} \right)-2ab+8-4\left( a\sqrt{{{b}^{2}}+1}+b\sqrt{{{a}^{2}}+1} \right)\ge 0$
$\Leftrightarrow \left[ {{a}^{2}}-4a\sqrt{{{b}^{2}}+1}+4\left( {{b}^{2}}+1 \right) \right]+\left[ {{b}^{2}}-4b\sqrt{{{a}^{2}}+1}+4\left( {{a}^{2}}+1 \right) \right]+\left( {{a}^{2}}-2ab+{{b}^{2}} \right)\ge 0$
$\Leftrightarrow {{\left( a-2\sqrt{{{b}^{2}}+1} \right)}^{2}}+{{\left( b-2\sqrt{{{a}^{2}}+1} \right)}^{2}}+{{\left( a-b \right)}^{2}}\ge 0$(đúng)
Đẳng thức không xảy ra.
Ví dụ 6: Cho hai số thực $x,\,\,y$ thỏa mãn $x\ge y$. Chứng minh rằng:
- $4\left( {{x}^{3}}-{{y}^{3}} \right)\ge {{\left( x-y \right)}^{3}}$
- ${{x}^{3}}-3x+4\ge {{y}^{3}}-3y$
Lời giải
- Bất đẳng thức tương đương $4\left( x-y \right)\left( {{x}^{2}}+xy+{{y}^{2}} \right)-{{\left( x-y \right)}^{3}}\ge 0$
$\Leftrightarrow \left( x-y \right)\left[ 4\left( {{x}^{2}}+xy+{{y}^{2}} \right)-{{\left( x-y \right)}^{2}} \right]\ge 0\Leftrightarrow \left( x-y \right)\left[ 3{{x}^{2}}+3xy+{{y}^{2}} \right]\ge 0$
$\Leftrightarrow 3\left( x-y \right)\left[ {{\left( x+\frac{y}{2} \right)}^{2}}+\frac{3{{y}^{2}}}{4} \right]\ge 0$ (đúng với $x\ge y$) ĐPCM.
Đẳng thức xảy ra khi và chỉ khi $x=y$. - Bất đẳng thức tương đương ${{x}^{3}}-{{y}^{3}}\ge 3x-3y-4$
Theo câu a) ta có ${{x}^{3}}-{{y}^{3}}\ge \frac{1}{4}{{\left( x-y \right)}^{3}}$, do đó ta chỉ cần chứng minh
$\frac{1}{4}{{\left( x-y \right)}^{3}}\ge 3x-3y-4$ (*), Thật vậy,
BĐT (*) $\Leftrightarrow {{\left( x-y \right)}^{3}}-12\left( x-y \right)+16\ge 0$
$\Leftrightarrow \left( x-y-2 \right)\left[ {{\left( x-y \right)}^{2}}+2\left( x-y \right)-8 \right]\ge 0$
$\Leftrightarrow {{\left( x-y-2 \right)}^{2}}\left( x-y+4 \right)\ge 0$ (đúng với$x\ge y$ )
Đẳng thức xảy không xảy ra.
2. Xuất phát từ một BĐT đúng ta biến đổi đến BĐT cần chứng minh.
Đối với loại này thường cho lời giải không được tự nhiên và ta thường sử dụng khi các biến có những ràng buộc đặc biệt.
Chú ý hai mệnh đề sau thường dùng:
- $a\in \left[ \alpha ;\beta \right]\Rightarrow \left( a-\alpha \right)\left( a-\beta \right)\le 0$ $\left( * \right)$
- $a,b,c\in \left[ \alpha ;\beta \right]\Rightarrow \left( a-\alpha \right)\left( b-\alpha \right)\left( c-\alpha \right)+\left( \beta -a \right)\left( \beta -b \right)\left( \beta -c \right)\ge 0\left( ** \right)$
Ví dụ 7: Cho $a,b,c$ là độ dài ba cạnh tam giác. Chứng minh rằng: $${{a}^{2}}+{{b}^{2}}+{{c}^{2}}<2(ab+bc+ca)$$
Lời giải. Vì a,b,c là độ dài ba cạnh tam giác nên ta có:$$a+b>c\Rightarrow ac+bc>{{c}^{2}}$$ Tương tự $$bc+ba>{{b}^{2}}$$ $$ca+cb>{{c}^{2}}$$ cộng ba BĐT này lại với nhau ta có đpcm.
Nhận xét: Ở trong bài toán trên ta đã xuất phát từ BĐT đúng đó là tính chất về độ dài ba cạnh của tam giác. Sau đó vì cần xuất hiện bình phương nên ta nhân hai vế của BĐT với c.
Ngoài ra nếu xuất phát từ BĐT $|a-b|<c$ rồi bình phương hai vế ta cũng có được kết quả.Ví dụ 8: Cho $a,b,c\in [0;1]$. Chứng minh: $${{a}^{2}}+{{b}^{2}}+{{c}^{2}}\le 1+{{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a$$
Lời giải.Cách 1: Vì $a,b,c\in [0;1]\Rightarrow (1-{{a}^{2}})(1-{{b}^{2}})(1-{{c}^{2}})\ge 0$
$\Leftrightarrow 1+{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}-{{a}^{2}}{{b}^{2}}{{c}^{2}}\ge {{a}^{2}}+{{b}^{2}}+{{c}^{2}}$ (*)
Ta có: ${{a}^{2}}{{b}^{2}}{{c}^{2}}\ge 0;\text{ }{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}\le {{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a$ nên từ (*) ta suy ra
${{a}^{\text{2}}}+{{b}^{2}}+{{c}^{2}}\le 1+{{a}^{2}}{{b}^{2}}+{{b}^{2}}{{c}^{2}}+{{c}^{2}}{{a}^{2}}\le 1+{{a}^{2}}b+{{b}^{2}}c+{{c}^{2}}a$ đpcm.Cách 2: BĐT cần chứng minh tương đương với ${{\text{a}}^{\text{2}}}\left( 1-b \right)+{{b}^{2}}\left( 1-c \right)+{{c}^{2}}\left( 1-a \right)\le 1$
Mà $a,b,c\in \left[ 0;1 \right]$ $\Rightarrow {{a}^{2}}\le a,{{b}^{2}}\le b,{{c}^{2}}\le c$ do đó
${{a}^{2}}\left( 1-b \right)+{{b}^{2}}\left( 1-c \right)+{{c}^{2}}\left( 1-a \right)\le a\left( 1-b \right)+b\left( 1-c \right)+c\left( 1-a \right)$
Ta chỉ cần chứng minh $a\left( 1-b \right)+b\left( 1-c \right)+c\left( 1-a \right)\le 1$
Thật vậy: vì $a,b,c\in \left[ 0;1 \right]$ nên theo nhận xét $\left( ** \right)$ ta có
$abc+\left( 1-a \right)\left( 1-b \right)\left( 1-c \right)\ge 0$
$\Leftrightarrow $$a+b+c-\left( ab+bc+ca \right)\le 1$
$\Leftrightarrow $$a\left( 1-b \right)+b\left( 1-c \right)+c\left( 1-a \right)\le 1$
vậy BĐT ban đầu được chứng minh.Ví dụ 9: Cho các số thực a,b,c thỏa mãn: ${{a}^{\text{2}}}+{{b}^{2}}+{{c}^{2}}=1$. Chứng minh: $$2(1+a+b+c+ab+bc+ca)+abc\ge 0$$
Lời giải. Vì ${{a}^{\text{2}}}+{{b}^{2}}+{{c}^{2}}=1\Rightarrow a,b,c\in [-1;1]$ nên ta có:$$(1+a)(1+b)(1+c)\ge 0\Leftrightarrow 1+a+b+c+ab+bc+ca+abc\ge 0$$ Mặt khác: $$\frac{{{(1+a+b+c)}^{2}}}{2}\ge 0\Leftrightarrow 1+a+b+c+ab+bc+ca\ge 0$$
Cộng hai bất đẳng thức trên ta có đpcm.Ví dụ 10: Chứng minh rằng nếu $a\ge 4,b\ge 5,c\ge 6$ và ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=90$ thì $a+b+c\ge 16$.
Lời giải. Từ giả thiết ta suy ra $a<9,b<8,c\le 7$ do đó áp dụng $\left( * \right)$ ta có
$\left( a-4 \right)\left( a-9 \right)\le 0,\left( b-5 \right)\left( b-8 \right)\le 0,\left( c-6 \right)\left( c-7 \right)\le 0$ nhân ra và cộng các BĐT cùng chiều lại ta được:
${{\text{a}}^{\text{2}}}+{{b}^{2}}+{{c}^{2}}-13(a+b+c)+118\le 0$suy ra
$a+b+c\ge \frac{1}{13}\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}+118 \right)=16$ vì ${{a}^{2}}+{{b}^{2}}+{{c}^{2}}=90$
vậy $a+b+c\ge 16$ dấu “=” xảy ra khi $a=4,b=5,c=7$.Ví dụ 11: Cho ba số $a,\,\,b,\,\,c$ thuộc $\left[ -1;1 \right]$ và không đồng thời bằng không. Chứng minh rằng
$\frac{{{a}^{4}}{{b}^{2}}+{{b}^{4}}{{c}^{2}}+{{c}^{4}}{{a}^{2}}+3}{{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}}\ge 2$Lời giải. Vì ba số $a,\,\,b,\,\,c$ thuộc $\left[ -1;1 \right]$ nên $0\le {{a}^{2}},{{b}^{2}},{{c}^{2}}\le 1$
Suy ra$(1-{{b}^{2}})(1+{{b}^{2}}-{{a}^{4}})\ge 0$$\Leftrightarrow {{a}^{4}}+{{b}^{4}}-{{a}^{4}}{{b}^{2}}\le 1$ (*)
Mặt khác ${{a}^{4}}\ge {{a}^{2012}},\,{{b}^{4}}\ge {{b}^{2012}}$ đúng với mọi $a,\,\,b$ thuộc $\left[ -1;1 \right]$
Suy ra ${{a}^{4}}+{{b}^{4}}-{{a}^{4}}{{b}^{2}}\ge {{a}^{2012}}+{{b}^{2012}}-{{a}^{4}}{{b}^{2}}$ (**)
Từ (*) và (**) ta có ${{a}^{2012}}+{{b}^{2012}}\le {{a}^{4}}{{b}^{2}}+1$ hay $\frac{{{a}^{4}}{{b}^{2}}+{{c}^{2012}}+1}{{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}}\ge 1$
Tương tự ta có $\frac{{{b}^{4}}{{c}^{2}}+{{a}^{2012}}+1}{{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}}\ge 1$ và $\frac{{{c}^{4}}{{a}^{2}}+{{b}^{2012}}+1}{{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}}\ge 1$
Cộng vế với ta được $\frac{{{a}^{4}}{{b}^{2}}+{{b}^{4}}{{c}^{2}}+{{c}^{4}}{{a}^{2}}+{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}+3}{{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}}\ge 3$
Hay $\frac{{{a}^{4}}{{b}^{2}}+{{b}^{4}}{{c}^{2}}+{{c}^{4}}{{a}^{2}}+3}{{{a}^{2012}}+{{b}^{2012}}+{{c}^{2012}}}\ge 2$ ĐPCM. -
Tóm tắt lý thuyết thức bất đẳng thức lớp 10
Tóm tắt lý thuyết thức bất đẳng thức lớp 10
1. Định nghĩa bất đẳng thức
Cho $a,b$ là hai số thực. Các mệnh đề “a>b”, “a<b”, “a≥b”, “a ≤ b” được gọi là những bất đẳng thức.
- Chứng minh bất đẳng thức là chứng minh bất đẳng thức đó đúng (mệnh đề đúng)
- Với $A,B$ là mệnh đề chứa biến thì $A>B$ cũng là mệnh đề chứa biến. Chứng minh bất đẳng thức $A>B$ (với điều kiện nào đó) nghĩa là chứng minh mệnh đề chứa biến $A>B$ đúng với tất cả các giá trị của biến (thỏa mãn điều kiện đó).
- Khi nói ta có bất đẳng thức $A>B$ mà không nêu điều kiện đối với các biến thì ta hiểu rằng bất đẳng thức đó xảy ra với mọi giá trị của biến là số thực.
2. Tính chất của bất đẳng thức lớp 10
- $\begin{cases} a>b\\ b>c \end{cases}\Rightarrow a>c$
- $a>b\Leftrightarrow a+c>b+c$
- $\begin{cases} a>b>0\\ c>d >0\end{cases} \Rightarrow ac>bd$
- $\begin{cases} a>b\\ c>d \end{cases} \Rightarrow a+c>b+d$
- Nếu $c>0$ thì $a>b\Leftrightarrow ac>bc$
- Nếu $c<0$ thì $a>b\Leftrightarrow ac<bc$
- $a>b\ge 0\Rightarrow \sqrt{a}>\sqrt{b}$
- $a\ge b\ge 0\Leftrightarrow {{a}^{2n}}\ge {{b}^{2n}}$, với mọi số tự nhiên dương $n$.
- $a>b \Leftrightarrow {{a}^{2n+1}}>{{b}^{2n+1}}$, với mọi số tự nhiên $n$.
3. Các bất đẳng thức thông dụng
Bất đẳng thức giữa trung bình cộng và trung bình nhân AM-GM (Bất đẳng thức Cauchy)
a) Đối với hai số không âm
Cho \(a\ge 0,b\ge 0\), ta có $$\frac{a+b}{2}\ge \sqrt{ab}$$ Dấu ‘=’ xảy ra khi và chỉ khi $a=b$.
Hệ quả:
- Hai số dương có tổng không đổi thì tích lớn nhất khi hai số đó bằng nhau.
- Hai số dương có tích không đổi thì tổng nhỏ nhất khi hai số đó bằng nhau.
b) Đối với ba số không âm.
Cho $a\ge 0,b\ge 0,c\ge 0$, ta có $$\frac{a+b+c}{3}\ge \sqrt[3]{abc}$$ Dấu ‘=’ xảy ra khi và chỉ khi \(a=b=c\).
Bất đẳng thức Bunhia (Bất đẳng thức Cauchy-Schwarz)
Cho các số thực $a_1,a_2,\ldots ,a_n$ và $b_1,b_2,\ldots ,b_n$, ta có $$\left(a_1^2+a_2^2+\cdots +a_n^2\right)\left(b_1^2+b_2^2+\cdots +b_n^2\right)\ge \left(a_1b_1+a_2b_2+\cdots +a_nb_n\right)^2.$$ Dấu bằng xảy ra khi và chỉ khi $\dfrac{a_1}{b_1}=\dfrac{a_2}{b_2}=\cdots =\dfrac{a_n}{b_n}.$
Bất đẳng thức về giá trị tuyệt đối.
- $-\left| a \right|\le a\le \left| a \right|$ với mọi số thực $a$ .
- $\left| x \right|<a\Leftrightarrow -a<x<a$ ( với $a>0$)
- $\left| x \right|>a\Leftrightarrow \left[ \begin{align} & x>a \\ & x<-a \\ \end{align} \right.$ ( với $a>0$)
Bất đẳng thức tam giác
\[|a|+|b| \geqslant |a\pm b| \geqslant \big| |a|-|b|\big|\]
Ngoài ra còn rất nhiều bất đẳng thức khác, mời các bạn xem trong bài Các bất đẳng thức thường sử dụng