Bất đẳng thức CôSi (Cauchy) hay bất đẳng thức AM-GM là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm.

1. Bất đẳng thức Cô-si là gì?
Trong toán học, bất đẳng thức Cauchy là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân của n số thực không âm được phát biểu như sau.
Với $a_1,a_2,\ldots,a_n$ là các số thực không âm, khi đó $$a_1+a_2+\cdots +a_{n}\ge n\sqrt[n]{a_1a_2\ldots a_n}.$$ Dấu bằng xảy ra khi và chỉ khi $a_1=a_2=\cdots =a_n$.

Trung bình cộng của n số thực không âm luôn lớn hơn hoặc bằng trung bình nhân của chúng, và trung bình cộng chỉ bằng trung bình nhân khi và chỉ khi n số đó bằng nhau.
Các trường hợp đặc biệt của bất đẳng thức Cosi:

- Bất đẳng thức Cô si với 2 số thực không âm $a$ và $b$ thì: \[\frac{a+b}{2} \geqslant \sqrt{ab}\] Dấu “=” xảy ra khi và chỉ khi a = b.
- Bất đẳng thức Cô si với 3 số thực không âm $a,b$ và $c$ thì: \[\frac{a+b+c}{3} \geqslant \sqrt[3]{abc}\] Dấu “=” xảy ra khi và chỉ khi a = b =c.
Tên đúng của bất đẳng thức này là bất đẳng thức AM-GM. Có nhiều cách để chứng minh bđt này nhưng hay nhất là cách chứng minh quy nạp của Cauchy.
2. Các dạng phát biểu của bất đẳng thức Cô-si
a. Dạng tổng quát của bất đẳng thức Cô-si
Cho $x_1, x_2, x_3,…,x_n$ là các số thực dương ta có:
– Dạng 1: \(\dfrac{x_1+x_2+…+x_n}{n} \geqslant \sqrt[n]{x_1 x_2 x_3…x_n}\)
– Dạng 2: \({x_1+x_2+…+x_n} \geqslant n\sqrt[n]{x_1 x_2 x_3…x_n}\)

– Dạng 3: \(\left(\dfrac{x_1+x_2+…+x_n}{n}\right)^n \geqslant x_1 x_2 x_3…x_n\)
– Dạng 4: \(\left(x_1+x_2+…+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+…\frac{1}{x_n} \right) \geqslant n^2\)
Dấu đẳng thức xảy ra khi và chỉ khi $x_1= x_2= x_3=…=x_n$.
b. Dạng đặc biệt của bất đẳng thức Cô-si
Là các trường hợp đặc biệt của dạng tổng quát ở trên khi n=2, n=3.


c. Một số bất đẳng thức được suy ra từ bất đẳng thức Cauchy
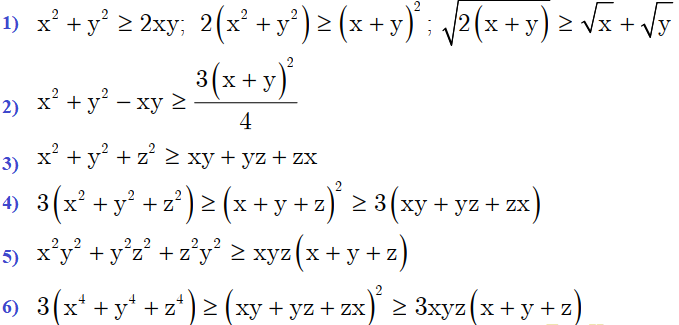
d. Chú ý khi sử dụng bất đẳng thức AM – GM
- Khi áp dụng bất đẳng thức Cô si thì các số phải là những số không âm;
- Bất đẳng thức Côsi thường được áp dụng khi trong BĐT cần chứng minh có tổng và tích;
- Điều kiện xảy ra dấu ‘=’ là các số bằng nhau;
- Bất đẳng thức Côsi còn có hình thức khác thường hay sử dụng.
3. Hệ quả của bất đẳng thức Cô-si
- \(x^{2}+y^{2} \geq 2 x y ; 2\left(x^{2}+y^{2}\right) \geq(x+y)^{2} ; \sqrt{2(x+y)} \geq \sqrt{x}+\sqrt{y}\)
- \(x^{2}+y^{2}-x y \geq \frac{3(x+y)^{2}}{4}\)
- \(x^{2}+y^{2}+z^{2} \geq x y+y z+z x\)
- \(3\left(x^{2}+y^{2}+z^{2}\right) \geq(x+y+z)^{2} \geq 3(x y+y z+z x)\)
- \(x^{2} y^{2}+y^{2} z^{2}+z^{2} y^{2} \geq x y z(x+y+z)+3\left(x^{4}+y^{4}+z^{4}\right) \geq(x y+y z+z x)^{2} \geq 3 x y z(x+y+z)\)
4. Các dạng bài tập bất đẳng thức Cô-si
Bài 1: Tìm giá trị nhỏ nhất của biểu thức $A=x+\frac{7}{x}$ với x > 0.
Lời giải:
Áp dụng bất đẳng thức Cô si cho hai số x > 0 và ta có: \[ x+\frac{7}{x} \geq 2 \sqrt{x \cdot \frac{7}{x}}=2 \sqrt{7} \] Dấu “=” xảy ra khi và chỉ khi \(x=\frac{7}{x} \Leftrightarrow x^{2}=7 \Leftrightarrow x=\sqrt{7}\) (do x>0).
Vậy \(\min A=2 \sqrt{7} \Leftrightarrow x=\sqrt{7}\).

Bài 2: Cho \(x>0, y>0\) thỏa mãn điều kiện \(\frac{1}{x}+\frac{1}{y}=\frac{1}{2}\). Tìm giá trị lớn nhất của biểu thức \(A=\sqrt{x}+\sqrt{y}\).
Lời giải: Áp dụng bdt Cosi ta có \[ \frac{1}{x}+\frac{1}{y} \geq 2 \sqrt{\frac{1}{x} \cdot \frac{1}{y}} \Leftrightarrow \frac{1}{2} \geq \frac{2}{\sqrt{x y}} \Leftrightarrow \sqrt{x y} \geq 4 \]
Lại có, áp dụng bất đẳng thức Cô si cho hai số (x>0, y>0) ta có:
\[\sqrt{x}+\sqrt{y} \geq 2 \sqrt{\sqrt{x y}}=2 \sqrt{4}=4 \] Dấu “=” xảy ra khi và chỉ khi \[ \left\{\begin{array}{l}
x=y \\ \frac{1}{x}+\frac{1}{y}=\frac{1}{2}
\end{array} \right. \Leftrightarrow x=y=4. \]
Vậy $\min A = 4$ khi và chỉ khi $x = y = 4$.
Bài 3: Ví dụ: Cho \(a\), \(b\) là số dương thỏa mãn \(a^{2}+b^{2}=2\). Chứng minh rằng \[ (a+b)^{5} \geq 16 a b \sqrt{\left(1+a^{2}\right)\left(1+b^{2}\right)} \]

Lời giải: Ta có \((a+b)^{5}=\left(a^{2}+2 a b+b^{2}\right)\left(a^{3}+3 a b^{2}+3 a^{2} b+b^{3}\right)\)
Áp dụng bdt Côsi ta có \[ \begin{aligned} &a^{2}+2 a b+b^{2} \geq 2 \sqrt{2 a b\left(a^{2}+b^{2}\right)}=4 \sqrt{a b} \text { và } \\ &\left(a^{3}+3 a b^{2}\right)+\left(3 a^{2} b+b^{3}\right) \geq 2 \sqrt{\left(a^{3}+3 a b^{2}\right)\left(3 a^{2} b+b^{3}\right)}=4 \sqrt{a b\left(1+b^{2}\right)\left(a^{2}+1\right)} \end{aligned} \]
Suy ra \(\left(a^{2}+2 a b+b^{2}\right)\left(a^{3}+3 a b^{2}+3 a^{2} b+b^{3}\right) \geq 16 a b \sqrt{\left(a^{2}+1\right)\left(b^{2}+1\right)}\)
Do đó \((a+b)^{5} \geq 16 a b \sqrt{\left(1+a^{2}\right)\left(1+b^{2}\right)}\) (đpcm). Đẳng thức xảy ra khi và chỉ khi \(a=b=1\).

Bài 4: Tìm GTLN của: $y=x^{2}(1-x) \quad, x \in(0,1)$
Lời giải: Do $x, 1-x>0$ nên áp dụng bất đẳng thức Cauchy ta có: $$ 2 y=x^{2}(1-2 x)=x \cdot x \cdot(1-2 x) \leq\left(\frac{x+x+1-2 x}{3}\right)^{3}=\frac{1}{27} \Rightarrow y \leq \frac{1}{54} $$ Dấu ‘=’ xảy ra $\Leftrightarrow x=1-2 x \Leftrightarrow x=\frac{1}{3}$.
Vậy Max $y=\frac{1}{27}$ khi $x=\frac{1}{3}$
Bài 5: Tìm GTNN của: $y=x+\frac{1}{x-1}, x>1$.

Lời giải: Do $x-1>0$ nên áp dụng bất đẳng thức Cauchy ta có: $$ y=(x-1)+\frac{1}{x-1}+1 \geq 2 \sqrt{(x-1) \cdot \frac{1}{x-1}}+1=3 \Rightarrow y \geq 3 $$ Dấu ‘=’ xảy ra $\Leftrightarrow x-1=\frac{1}{x-1} \Leftrightarrow x=2$.
Vậy Min $y=3$ khi $x=2$.
Xem thêm Chọn điểm rơi trong bất đẳng thức Côsi (Cauchy).
Bài 6: Cho 3 số dương \(a, b\), c, hãy chứng minh: \[ \left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right) \geq 8 \]

Hướng dẫn giải: Áp dụng BĐT Cosi, ta có: \[ \begin{aligned} a+\frac{1}{b} \geq 2 \sqrt{\frac{a}{b}};\\ b+\frac{1}{c} \geq 2 \sqrt{\frac{b}{c}};\\ c+\frac{1}{a} \geq 2 \sqrt{\frac{c}{a}} \end{aligned}\]
Nhân theo vế 3 bdt này ta được \[\left(a+\frac{1}{b}\right)\left(b+\frac{1}{c}\right)\left(c+\frac{1}{a}\right) \geq 8 \sqrt{\frac{a}{b}} \cdot \sqrt{\frac{b}{c}} \sqrt{\frac{c}{a}}=8 \] Đẳng thức xảy ra khi và chỉ khi \(a=b=c\).
Bài 7: Cho $a, b, c>0$. Chứng minh:
a) $a^2+b^2+4 \geqslant 2a+2b+ab$
b) $a(1+b)+b(1+c)+c(1+a) \geq 3 \sqrt[3]{a b c}(1+\sqrt[3]{a b c})$
c) $a \sqrt{b-1}+b \sqrt{a-1} \leq a b$ với $a, b \geq 1$

Lời giải:
a) Áp dụng bât đẳng thức Cauchy ta có: $$ \begin{aligned} &a^{2}+4 \geq 4 a \\ &b^{2}+4 \geq 4 b \\ &a^{2}+b^{2} \geq 2 a b. \end{aligned} $$ Cộng lại ta được: $$ 2 a^{2}+2 b^{2}+8 \geq 4 a+4 b+2 a b $$ Dấu ‘=’ xảy ra $ \Leftrightarrow a=b=2$
b) Ta có : $$ a(1+b)+b(1+c)+c(1+a)=(a+b+c)+(a b+b c+c a) $$ Áp dụng bất đẳng thức Cauchy : $$ \begin{aligned} &a+b+c \geq 3 \sqrt[3]{a b c} \\ &a b+b c+c a \geq 3 \sqrt[3]{a^{2} b^{2} c^{2}} \end{aligned} $$ Cộng lại ta được đpcm.
Dấu ‘=’ xảy ra $\Leftrightarrow a=b=c$.

c) Ta có: $$a \sqrt{b-1}=\sqrt{a} \sqrt{a b-a} \leq \frac{a+a b-a}{2}=\frac{a b}{2}$$Tương tự: $$b \sqrt{a-1} \leq \frac{a b}{2}$$ Cộng lại ta đpcm.
Dấu ‘=’ xảy ra $\Leftrightarrow a=b=2$.
Bài 8: Chứng minh với ba số a, b, c không âm thỏa mãn a + b + c = 3 thì: \[ \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} \geq \frac{3}{2} \]
Nhận xét: Bài toán đạt được dấu bằng khi và chi khi $a = b = c = 1$.

Ta sẽ sử dụng phương pháp làm trội làm giảm như sau: \[ \frac{a}{b+c}+\frac{b+c}{4}+\frac{1}{2 a} \geq 3 \sqrt[3]{\frac{a}{b+c} \cdot \frac{b+c}{4} \cdot \frac{1}{2 a}}=3 \sqrt[3]{\frac{1}{8}}=\frac{3}{2} \]
Tương tự ta có \(\frac{b}{c+a}+\frac{c+a}{4}+\frac{1}{2 b} \geq \frac{3}{2}\) và \(\frac{c}{a+b}+\frac{a+b}{4}+\frac{1}{2 c} \geq \frac{3}{2}\).
Cộng vế với vế ta có: \[ \begin{align*}\frac{a}{b+c}+\frac{b+c}{4}+\frac{1}{2 a}+\frac{b}{c+a}+\frac{c+a}{4}+\frac{1}{2 b}+\frac{c}{a+b}+\frac{a+b}{4}+\frac{1}{2 c} & \geq 3 \cdot \frac{3}{2}=\frac{9}{2} \\ \Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{2(a+b+c)}{4}+\frac{a b+b c+c a}{2 a b c} & \geq \frac{9}{2} \\ \Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}+\frac{a+b+c}{2}+\frac{a+b+c}{2} & \geq \frac{9}{2} \\ \Leftrightarrow \frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b} &\geq \frac{9}{2}-3=\frac{3}{2} \end{align*} \]
Dấu “=” xảy ra khi và chỉ khi $a = b = c = 1$.



Leave a Reply