O₂ Education

Category: Toán 10

  • Bài tập vecto lớp 10 (Khái niệm vector, hai véc-tơ bằng nhau)

    Bài tập vecto lớp 10 (Khái niệm vector, hai véc-tơ bằng nhau)

    Bài tập vecto Lớp 10

    Bài viết này giới thiệu phần bài tập vecto lớp 10 với các dạng bài về Khái niệm vector, các véc-tơ cùng phương, độ dài véc-tơ, hai véc-tơ bằng nhau. Bài tập về các phép toán vecto xin mời các em xem tại đây: Bài tập Các phép toán véc-tơ

    Bài 1. Cho ba điểm $ A, B, C $ không thẳng hàng. Có thể xác định được bao nhiêu véc tơ khác nhau và khác $\overrightarrow{0}$, mà các điểm mút là hai trong ba điểm đó.

    Bài 2. Cho véc tơ $\overrightarrow{AB}$ khác $\overrightarrow{0}$. Hãy vẽ 5 số véc tơ bằng véc tơ $\overrightarrow{AB}$.

    Bài 3. Cho tam giác đều $ ABC $. Các đẳng thức: $\overrightarrow{AB}=\overrightarrow{BC}$, $\overrightarrow{AB}=\overrightarrow{AC}$, $| \overrightarrow{AB} |=| \overrightarrow{AC} |=| \overrightarrow{BC} |$ đúng hay sai? Vì sao?

    Bài 4. Cho ba điểm $ A, B, C $ phân biệt, chứng minh rằng nếu $\overrightarrow{AB}=\overrightarrow{BC}$ thì ba điểm đó thẳng hàng.

    Bài 5. Cho nửa lục giác đều $ ABCD $ nội tiếp trong đường tròn tâm $ O $ đường kính $ AD. $ Chỉ ra các véc-tơ bằng với $ \overrightarrow{BC}. $

    Hướng dẫn. Tứ giác $ ABOA $ là hình thoi nên $ \overrightarrow{AO}=\overrightarrow{BC}=\overrightarrow{OD}. $

    Bài 5. Cho hình vuông $ABCD$ tâm $O$. Liệt kê tất cả các véc-tơ bằng nhau (khác véc-tơ $\overrightarrow{0}$) nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.

    Bài 6. Cho hình bình hành $ ABCD $ và $ E $ là điểm đối xứng của $ C $ qua $ D. $ Chứng tỏ $ \overrightarrow{AE}=\overrightarrow{BD}. $

    Hướng dẫn. Chỉ ra tứ giác $ ABDE $ là hình bình hành.

    Bài 7. Cho tứ giác $ABCD$. Gọi $M,N,P$ và $Q$ lần lượt là trung điểm của các cạnh $AB,BC,CD$ và $DA$. Chứng minh: $\overrightarrow{NP}=\overrightarrow{MQ}$ và $\overrightarrow{PQ}=\overrightarrow{NM}$.

    Bài 8. Cho tam giác $ABC$. Các điểm $M$ và $N$ lần lượt là trung điểm các cạnh $AB$ và $AC$. So sánh độ dài của hai véc-tơ $\overrightarrow{NM}$ và $\overrightarrow{BC}$. Vì sao hai véc-tơ đó cùng phương.

    Bài 9. Cho điểm $ A $ cố định. Tìm tập hợp các điểm $ M $ sao cho:

    • $ |\overrightarrow{AM}|=\SI{4}{cm} $
    • $ \overrightarrow{AM} $ cùng phương với $ \vec{a} $ cho trước.

    Hướng dẫn. Điểm $ A $ cố định và độ dài $ AM = \SI{4}{cm}. $ Vậy tập hợp các điểm $ M $ là đường tròn tâm $ A $ bán kính $ \SI{4}{cm}. $

    $ \overrightarrow{AM} $ cùng phương với $ \vec{a} $ nên $ M $ chạy trên đường thẳng qua $ A $ và song song với giá của véc-tơ $ \vec{a}. $

    Bài 10. Cho 4 điểm phân biệt $A,B,C,D$. Chứng minh rằng nếu $\overrightarrow{AB}=\overrightarrow{DC}$ thì $\overrightarrow{AD}=\overrightarrow{BC}$.

    Bài 11. Xác định vị trí tương đối của 3 điểm phân biệt $A,B$ và $C$ trong các trường hợp sau:

    • $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng,
    • $|\overrightarrow{AB}|>|\overrightarrow{AC}|$.
    • $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng hướng.

    Bài 12. Cho hình bình hành $ABCD$. Dựng $\overrightarrow{AM}=\overrightarrow{BA}$, $\overrightarrow{MN}=\overrightarrow{DA}$,$\overrightarrow{NP}=\overrightarrow{DC}$, $\overrightarrow{PQ}=\overrightarrow{BC}$.

    Chứng minh $\overrightarrow{AQ}=\overrightarrow{0}$.

    Bài 13. Cho tam giác $ABC$ có $D,E,F$ lần lượt là trung điểm của $BC,CA,AB$. Chứng minh: $\overrightarrow{EF}=\overrightarrow{CD}$

    Bài 14. Cho hình bình hành $ABCD$. Hai điểm $M$ và $N$ lần lượt là trung điểm của $BC$ và $AD$. Điểm $I$ là giao điểm của $AM$ và $BN$, $K$ là giao điểm của $DM$ và $CN$. Chứng minh: $$\overrightarrow{AM}=\overrightarrow{NC},\overrightarrow{DK}=\overrightarrow{NI}$$

    Bài 15. Cho tam giác $ABC$ có $H$ là trực tâm và $O$ là tâm đường tròn ngoại tiếp. Gọi $B’$ là điểm đối xứng với $B$ qua $O$, $ K $ là trung điểm của $ AH, I $ là trung điểm của $ BC $. Chứng minh $\overrightarrow{AH}=\overrightarrow{B’C}; \overrightarrow{OK}=\overrightarrow{IH}$

    Bài 16. Cho tam giác $ ABC $ và điểm $ M $ ở trong tam giác. Gọi $A’,B’,C’$ lần lượt là trung điểm của $ BC,CA , AB $ và $ N, P, Q $ lần lượt là điểm đối xứng của $ M $ qua $A’,B’,C’$. Chứng minh:

    • $ \overrightarrow{AQ}=\overrightarrow{CN}$,
    • $\overrightarrow{AM}=\overrightarrow{PC}, $
    • Ba đường thẳng $ AN,BP,CQ $ đồng quy.

    Hướng dẫn. Tứ giác $ AQBM,MBNC $ là hình bình hành vì có hai đường chéo giao nhau tại trung điểm nên ta có $ \overrightarrow{AQ}=\overrightarrow{MB}=\overrightarrow{CN}. $ Và do đó $ ACNQ $ là hình bình hành. Chứng minh tương tự có $ \overrightarrow{QP}=\overrightarrow{PC} $ và $ BCPQ $ cũng là hình bình hành. Suy ra ba đường thẳng $ AN,BP,CQ $ đồng quy.

  • Bài tập Tập hợp Toán 10

    Bài tập Tập hợp Toán 10

    Bài tập Tập hợp Toán 10

    Phần lý thuyết, mời các em xem trong bài Tập hợp và các phép toán tập hợp

    Bài tập Tập hợp Toán 10

    Bài 1. Viết lại các tập hợp sau bằng cách liệt kê các phần tử:

    • $A=\left\{3k-1\mid k\in \mathbb{Z} , -5\leqslant k\leqslant 3\right\}$.
    • $B=\left\{x\in \mathbb{Z} \mid \mid x\mid <10\right\}$.
    • $C=\left\{x\in \mathbb{Z} \mid 3<\mid x\mid \leqslant \frac{19}{2}\right\}.$
    • $D=\left\{x\in\mathbb{Z} \mid 6x^2-5x-1=0\right\} $.
    • $E=\left\{x\in \mathbb{R}\mid x^2-2x+4=0\right\}$.
    • $F=\left\{x=2k \mid k\in \mathbb{Z} \text{ và } -3<x<15\right\}$.
    • $G=\left\{(x;x^2)\mid x\in \left\{-1;0;1\right\}\right\}$.
    • $H=\left\{(x;y)\mid x^2+y^2\leqslant 2\text{ và } x\in \mathbb{Z} \right\}$.
    • $I=\left\{k\in \mathbb{Z} \mid x=3k\text{ với }x\in \mathbb{Z} \text{ và } -12<x\leqslant 6\right\}$.
    • $J=\left\{k\in \mathbb{N}\mid y=2k\text{ với }y\in \mathbb{Z} \text{ và } -4\leqslant y\leqslant 7\right\}$.
    • $K=\left\{k\in \mathbb{Z} \mid z=4k\text{ với }z\in \mathbb{Z} \text{ và } -16\leqslant z< 12 \right\}$.

    Bài 2. Xác định các tập hợp sau bằng cách chỉ ra tính chất đặc trưng:

    • $ A= \left\{1,4,9,16,25,36\right\}. $
    • $ B= \left\{-3,-2,-1,0,1,2,3,4\right\}. $

    Bài 3. Cho $ A= \left\{1,2,3,4,5,6\right\}, B= \left\{2,4,6\right\}, C=\left\{4,6,8\right\}. $ Tìm các tập hợp:

    • $ A\cap B$
    • $B\cap C$
    • $C\cap A$
    • $A\cup B$
    • $B\cup C$
    • $C\cup A$
    • $ A\setminus B$
    • $ B\setminus C$
    • $ A \setminus C$
    • $A\cap B\cap C.$

    Bài 4. Cho $ A=\left\{x\in \mathbb{R}, \mid x-1\mid >2 \right\} $ và $ B=\left\{x\in \mathbb{R}, \mid x+2\mid \leqslant 1 \right\}. $ Tìm $ A\cap B$.

    Bài 5. [Công thức De Morgan]

    Chứng minh $ A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C) $ và $ A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C), $ với $ A,B,C $ là các tập hợp bất kì.

    Bài 6. Cho $ A,B,C $ là các tập hợp bất kì. Chứng minh rằng:

    • $ (A\setminus B)\cap (B\setminus A)=\varnothing \Leftrightarrow A=B$
    • $ A=(A\setminus B)\cup (A\cap B)$
    • $ (A\setminus B)\cup(B\setminus A)=(A\cup B)\setminus (A\cap B) $

    Bài 7. Một số em của nhóm gồm 9 học sinh tham gia ngoại khóa các môn thể thao. Một học sinh tham gia môn cầu lông, sáu học sinh tham gia môn bóng bàn và môn bơi, ba học sinh tham gia môn bơi. Hỏi có bao nhiêu học sinh không tham gia cả ba môn bóng bàn, bơi, cầu lông?

    Hướng dẫn. Sử dụng biểu đồ Venn. Có 2 học sinh.

    Bài 8. Trong một lớp học mọi học sinh nam đều tham gia vào những câu lạc bộ: Bóng đá, bóng chuyền và cầu lông. Qua tìm hiểu thấy rằng: Có 7 em tham gia bóng đá, 6 em bóng chuyền, 5 em cầu lông, 4 em vừa bóng đá vừa bóng chuyền, 3 em vừa bóng đá vừa cầu lông, 2 em vừa bóng chuyền vừa cầu lông, 1 em tham gia cả ba câu lạc bộ. Vậy trong lớp học có bao nhiêu học sinh nam?

    Bài 9. Cho $A,B$ là hai tập hợp, $x\in A$ và $x\notin B$. Xét xem trong các mệnh đề sau, mệnh đề nào đúng?

    • $x\in A\cap B$
    • $x\in A\cup B$
    • $x\in A\setminus B$
    • $x\in B\setminus A$

    Bài 10. Cho $A,B$ là hai tập phân biệt và khác rỗng. Xét xem trong các mệnh đề sau, mệnh đề nào đúng?

    • $A\subset (B\setminus A)$
    • $A\subset A\cup B$
    • $A\cap B\subset A\cup B$
    • $A\setminus B\subset A$

    Bài 11. Tìm các tập hợp $A,B$ biết $A\cap B=\left\{0,1,2,3,4\right\};A\setminus B=\left\{-3,-2\right\}$ và $B\setminus A=\left\{6,9,10\right\}$.

    Bài 12. Cho các tập hợp:

    • $E=\left\{x\in \mathbb{N} \mid 1\leqslant x<7\right\}$
    • $A=\left\{x\in \mathbb{N} \mid (x^2-9)(x^2-5x-6)=0\right\}$
    • $B=\left\{x\in \mathbb{N} \mid x\text{ là số nguyên tố không quá 5}\right\}$

    Chứng minh $A\subset B;B\subset E$. Tìm $C_E A;C_E B;C_E (A\cap B)$.

    Bài 13. Cho các tập hợp:

    $$E=\left\{x\in\mathbb{Z} \mid \mid x\mid \leqslant 5 \right\}$$
    $$A=\left\{x\in\mathbb{N}\mid \mid x\mid \leqslant 5\right\}$$
    $$B=\left\{x\in\mathbb{Z}\mid (x-2)(x+1)(2x^2-x-3)=0\right\}$$

    • Chứng minh $A\subset E$ và $B\subset E$.
    • Tìm $C_{E}(A\cup B)$ và $C_{E}(A\cap B)$.
    • Chứng minh $C_{E}(A\cup B)\subset C_{E}A$.

    Bài 14.  Chứng minh rằng:

    • Nếu $A\subset B$ và $C\subset D$ thì $(A\cup B)\subset (C\cup D)$.
    • $A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)$.
    • $A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)$.

    Bài 15. Cho các tập $$A=\left\{x\in\mathbb{R}\mid 1\leqslant x\leqslant 5\right\}$$ $$B=\left\{x\in \mathbb{R}\mid 4\leqslant x\leqslant 7\right\}$$ $$C=\left\{x\in\mathbb{R}\mid 2\leqslant x<6\right\}$$

    • Tìm các tập sau: $A\cap B;\;A\cap C;\;B\cap C;\;A\cup C;\;A\setminus (B\cup C)$.
    • Gọi $D=\left\{x\in R\mid a\leqslant x\leqslant b\right\}$. Hãy xác định $a,b$ để $D\subset (A\cap B\cap C)$.

    Bài 16. Cho $A=\left\{x\in \mathbb{R}\mid x\leqslant -3\text{ hoặc } x>6\right\}$ và $B=\left\{x\in\mathbb{R}\mid x^2-25\leqslant 0\right\}$.

    Tìm các tập sau:

    • $A\setminus B$,
    • $B\setminus A$,
    • $\mathbb{R} \setminus (A\cup B)$,
    • $ \mathbb{R} \setminus (A\cap B)$,
    • $ \mathbb{R} \setminus (A\setminus B)$.

    Bài 17. Cho $C=\left\{x\in\mathbb{R}\mid x\leqslant a\right\}$ và $D=\left\{x\in\mathbb{R}\mid x\leqslant b\right\}$. Xác định $a,b$ biết rằng $C\cap B$ và $D\cap B$ là các đoạn có độ dài lần lượt bằng 7 và 9.

    Bài 18. Kí hiệu $n(X)$ là số phần tử của tập hợp $X$. Cho hai tập hợp $ A $ và $ B $, biết $n(A)=25;n(B)=29;n(A\cup B)=41$. Tính $n(A\cap B); n(A\setminus B); n(B\setminus A)$.

    Bài tập các tập hợp số

    Bài 1. Xác định tập hợp $A\cap B, A\cup B$ với:

    • $A=[1;5]$ và $B=(-3;2)\cup (3;7)$.
    • $A=(-5;0)\cup (3;5)$ và $B=(-1;2)\cup (4;6]$.

    Bài 2. Dùng kí hiệu khoảng đoạn tìm tập nghiệm của các hệ bất phương trình sau và biểu diễn chúng trên trục số:

    • $ \begin{cases} 2x>12\\4-x>-6 \end{cases} $
    • $ \begin{cases} 2x+3<7x\\x>3 \end{cases} $
    • $ \begin{cases} 3(x-2)<12\\2(x+5)<10 \end{cases} $
    • $ \begin{cases} \mid x\mid >3\\2x-2>0 \end{cases} $
    • $ \begin{cases} \mid x\mid <2\\4-3x>13 \end{cases} $
    • $ \begin{cases} x-2>11x\\-3x>-6 \end{cases} $
    • $ \begin{cases} x>3\\2-x>-6\\3x-1<23 \end{cases} $
    • $ \begin{cases} -2x\geqslant 6\\4+x>6 \end{cases} $
    • $ \begin{cases} x^2>0\\4x\geqslant 0 \end{cases} $

    Bài 3. Biểu diễn trên trục số và thực hiện các phép toán sau:

    • $\left( 1;5 \right)\cap \left( -1;3 \right)$
    • $\left( 2;5 \right)\cap \left[ -1;4 \right]$
    • $\left[ 2;7 \right)\cap \left\{ 2;4;7;8;9 \right\}$
    • $\left[ 2;3 \right]\cap \left( -\infty ;3 \right)$
    • $\left( 3;5 \right)\cap \left[ -4;5 \right]\cap \left\{ 2;3;5 \right\}$
    • $\left( 1;4 \right)\cap \left[ 2;7 \right)$
    • $\left( -1;1 \right)\cap \left[ -5;3 \right]$
    • $\left( -1;1 \right]\cap \left[ 1;5 \right]$
    • $\left( -2;5 \right)\cap \left[ -1;6 \right)\cap \left[ 0;8 \right]$
    • $\left( 2;4 \right)\cap \mathbb{R} \cap \left[ -2;6 \right]$
    • $\left( 1;5 \right)\cup \left( -1;2 \right)$
    • $\left( 2;5 \right)\cup \left[ -1;4 \right]$
    • $\left[ 2;7 \right)\cup \setminus \left\{ 2;4;7;8;9 \right\}$
    • $\left[ -1;4 \right]\cup \left( -\infty ;4 \right)$
    • $\left( 3;5 \right)\cup \left[ -4;5 \right]\cup \setminus\left\{ 2;3;5 \right\}$
    • $\left( 0;4 \right)\cup \left[ 2;7 \right)$
    • $\left( -3;2 \right)\cup \left[ 2;5 \right]$
    • $\left( -1;1 \right]\cup \left[ -1;5 \right]$
    • $\big(\left[ -1;2 \right]\cup \left( -1;2 \right)\big)\cap \left( 2;+\infty \right)$
    • $\big(\left(-\infty;-2 \right]\cup \left(2; +\infty \right)\big)\cap \left[-5;+\infty \right)$
    • $\left( 2;4 \right)\cup \mathbb{R} \cup \varnothing$
    • $\left( 1;5 \right)\setminus\left( -1;2 \right)$
    • $\left( 2;5 \right)\setminus\left[ -1;4 \right]$
    • $\left[ 2;7 \right)\setminus\left\{ 2;4;7;8;9\right\}$
    • $\left[ -1;4 \right]\setminus\left( -\infty ;4 \right)$
    • $\left[ 3;+\infty \right]\setminus\left( 3;+\infty \right)$
    • $\left( -\infty ;1 \right]\setminus\left[ -1;1 \right]$
    • $\mathbb{R}\setminus\left( 2;+\infty \right)$

    Bài 4. Tìm $ m $ sao cho $ (m-7,2)\subset (-4,3). $

    Bài 5. Tùy theo $ m, $ hãy tìm $ (-\infty,m]\cap(5,+\infty). $

    Bài 6. Cho hai tập hợp $A=\left( m;m+5 \right)$ và $B=\left( 3m+2;3m+7 \right)$ trong đó $ m $ là một số thực bất kì. Tìm điều kiện của $ m $ để:

    • Tập hợp $ A $ là một tập hợp con của tập hợp $ B $.
    • Giao của hai tập hợp $ A $ và $ B $ là tập hợp rỗng.
    • Hợp của hai tập hợp $ A $ và $ B $ là tập hợp $ A $.
    • Hiệu của hai tập hợp $ A $ và $ B $ theo thứ tự đó là tập hợp rỗng.

    Hướng dẫn.
    1. $m=-1$, \quad 2. $m\in \left( -\infty ;-\frac{7}{2} \right]\cup \left[ -\frac{3}{2};+\infty \right)$,\quad 3. $m=-1$,\quad 4. $m\in \left( -\infty ;-\frac{7}{2} \right]\cup \left[ -\frac{3}{2};+\infty \right)$.

    Bài 7. Cho $ A=(a;a+1) $ và $ B=(2015;2018).$ Tìm $ a $ để tập $ A\cup B $ là một khoảng.

    Hướng dẫn. $ 2015\leqslant a\le2017 $.

    Bài 8. Cho hai đoạn $ A=[a;a+2] $ và $ B=[b;b+1]. $ Tìm điều kiện của $ a,b $ để tập $ A\cap B\ne \varnothing. $

    Hướng dẫn. $ -2<a-b<1 $.

    Bài 9. Cho $ A=\{x\in \mathbb{R}\mid |x-1|>2\} $ và $ B=\{x\in \mathbb{R}\mid |x+2|<1 \} $. Tìm $ A\cap B. $

    Bài 10. Cho $ A=(a;a+1) $ và $ B=(2010;2012) $. Tìm $ a $ để $ A\cap B $ là một khoảng.

    Bài 11. Cho $a,b,c$ là các số thực và $a<b<c$. Hãy xác định các tập hợp sau:

    • $(a;b)\cap (b;c)$
    • $(a;b)\cup (b;c)$
    • $(a;c)\setminus (b;c)$
    • $(a;b)\setminus (b;c)$

    Bài 12. Hãy xác định các tập hợp sau:

    • $(-\infty;3]\cap (-2;+\infty)$
    • $(-15;7)\cup (-2;14)$
    • $(0;12)\setminus [5;+\infty)$
    • $\mathbb{R} \setminus (-1;1)$

    Bài 13. Hãy xác định các tập hợp sau:

    • $\mathbb{R} \setminus \big((0;1)\cup (2;3)\big)$
    • $\mathbb{R} \setminus \big((3;5)\cap (4;6)\big)$
    • $(-2;7)\setminus [1;3]$
    • $\big((-1;2)\cup (3;5)\big)\setminus (1;4)$

    Bài 14. Hãy xác định các tập hợp sau:

    • $(-3;5]\cap \mathbb{Z} $
    • $(1;2)\cap \mathbb{Z} $
    • $(1;2]\cap \mathbb{Z} $
    • $[-3;5]\cap \mathbb{N} $

    Bài 15. Tìm tập hợp $X$ sao cho $\left\{a,b\right\}\subset X\subset \left\{a,b,c,d,e\right\}$.

    Bài 16.  Viết phần bù trong $\mathbb{R} $ của các tập hợp sau:

    • $A=\left\{x\in \mathbb{R} \mid -2\leqslant x<7\right\}$.
    • $B=\left\{x\in \mathbb{R} \mid \mid x\mid >2\right\}$.
    • $C=\left\{x\in \mathbb{R} \mid -4\leqslant x+3<5\right\}$.

    Bài 17. Cho $A=\left\{1,2\right\}$ và $B=\left\{1,2,3,4,5\right\}$. Xác định các tập hợp $X$ sao cho $A\cup X=B$.

  • Bài tập Mệnh đề toán học

    Bài tập Mệnh đề toán học

    Bài tập Mệnh đề toán học

    Để làm được các Bài tập Mệnh đề toán học này, các em học sinh cần nắm vững lý thuyết ở bài Mệnh đề toán học.

    Bài 1. Trong các câu dưới đây, câu nào là mệnh đề, nếu là mệnh đề thì xét xem nó đúng hay sai?

    • “Số 11 là số nguyên tố.”
    • “Vai trò của Quốc Hội là gì?”
    • “Hà Nội là thủ đô của Việt Nam.”
    • “$\sqrt{3}+\sqrt{2}=\frac{1}{\sqrt{3}-\sqrt{2}}$.”
    • “$ \forall n\in \mathbb{N}, n^2+n $ là số chẵn.”
    • “$ \forall n\in \mathbb{N}, 2n^2+1 $ chia hết cho 3.”
    • “Tam giác nào cũng có ít nhất một góc nhỏ hơn 60$ ^\circ $.”
    • “Tồn tại một hình thang có ba góc tù.”

    Bài 2. Lập mệnh đề phủ định của mỗi mệnh đề sau và xét tính đúng sai của nó:

    • Mọi hình vuông đều là hình thoi.
    • Có một tam giác cân không là tam giác đều.
    • Mọi số tự nhiên đều không chia hết cho 2 và 3.
    • $ \forall x\in \mathbb{R}, f(x)>0 \Rightarrow f(x)\leqslant 0$ vô nghiệm.
    • Phương trình $ x^2+1=0 $ vô nghiệm và phương trình $ x+3=0 $ có nghiệm.

    Bài 3.  Lập mệnh đề phủ định của mỗi mệnh đề sau:

    • $ \forall x\in \mathbb{R}, x^2+1>0 $,
    • $ \forall x\in \mathbb{R}, x^2-3x+2=0$,
    • $ \exists n\in \mathbb{N}, n^2+2 $ chia hết cho 4,
    • $ \exists n\in \mathbb{Q}, 2n+1\ne 0$,
    • $ x\leqslant 0 $ hoặc $ x>1$,
    • $ 1<x<3. $

    Bài 4. Cho đa thức $f(x)=ax^2+bx+c$. Xét mệnh đề: “Nếu $a+b+c=0$ thì phương trình $f(x)=0$ có một nghiệm bằng $ 1 $”. Hãy phát biểu mệnh đề đảo của mệnh đề trên. Nêu một điều kiện cần và đủ để phương trình $f(x)=0$ có một nghiệm bằng $ 1 $.

    Bài 5. Phát biểu định lý sau, sử dụng thuật ngữ “điều kiện đủ”.

    • Nếu hai tam giác bằng nhau thì chúng đồng dạng.
    • Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau.
    • Nếu một số tự nhiên tận cùng là 5 thì số đó chia hết cho 5.

    Bài 6. Phát biểu định lý sau, sử dụng thuật ngữ “điều kiện cần”.

    • Hình chữ nhật có hai đường chéo bằng nhau.
    • Nếu một số tự nhiên chia hết cho 6 thì nó chia hết cho 3.
    • Nếu hai tam giác bằng nhau thì chúng có diện tích bằng nhau.

    Bài 7. Trên bàn là ba cuốn sách giáo khoa: Văn, Toán, Địa lí được bọc ba màu khác nhau: xanh, đỏ, vàng. Biết rằng cuốn bọc bìa màu đỏ đặt giữa cuốn Văn và Địa lí, cuốn Địa lí và cuốn màu xanh mua cùng một ngày. Bạn hãy xác định mỗi cuốn sách đã bọc bìa màu gì.

    Hướng dẫn. Lập bảng dữ kiện. Đáp số: Văn màu xanh, Toán màu đỏ, Địa lí màu vàng.

    Bài 8. Trong một bảng đấu loại bóng đá có bốn đội Mùa Xuân, Mùa Hạ, Mùa Thu và Mùa Đông. Người ta đưa ra 3 dự đoán:

    • Đội Mùa Xuân nhì, đội Mùa Hạ nhất.
    • Đội Mùa Hạ nhì, đội Mùa Đông ba.
    • Đội Mùa Thu nhì, đội Mùa Đông tư.

    Kết quả cả ba dự đoán đều có một ý đúng, một ý sai. Hãy xác định thứ tự của mỗi đội.

    Bài 9. Có ba nhà triết gia Hy-Lạp cổ, sau một cuộc tranh luận căng thẳng và cũng vì trời hè nóng nực nên đã nằm ngủ dưới gốc cây trong vườn của Viện Hàn lâm. Có mấy thợ thông lò đi qua tinh nghịch đã bôi nhọ lên trán cả ba triết gia. Khi ba nhà thông thái tỉnh dậy, họ nhìn nhau và cùng phá lên cười. Ai cũng yên chí rằng chỉ có hai người kia bị nhọ và họ cười nhau, còn mình thì cười họ. Thế nhưng, trong khoảnh khắc, một triết gia không cười nữa vì ông ta suy đoán ra trên trán ông ta cũng bị nhọ. Vậy nhà thông thái đó suy luận như thế nào?

    Bài 10. Đến một ngôi đền cổ có ba vị thần: Thần Thật Thà luôn nói thật, thần Dối Trá luôn nói dối và thần Khôn Ngoan lúc nói thật lúc nói dối. Để biết cách tiêu diệt rồng lửa cứu công chúa, hoàng tử phải hỏi vị thần Thật Thà. Nhưng ba vị thần trông giống hệt nhau. Để xác định vị nào là thần Thật Thà, chàng đã hỏi vị thần bên trái:

    – Bài Ai ngồi cạnh ngài? Đó là thần Thật Thà.

    Hoàng tử hỏi thần ngồi giữa: – Ngài là ai? Ta là thần Khôn Ngoan.

    Sau cùng chàng hỏi thần bên phải: Bài Ai ngồi cạnh ngài? Đó là thần Dối Trá.

    Nghe xong, hoàng tử bối rối không xác định được đâu là thần Thật Thà. Bạn hãy giúp hoàng tử!

    Bài 11. [Câu đố của Einstein] Vào cuối thế kỉ 19, Einstein ra câu đố này và nói rằng chỉ có nhiều nhất là 2% dân số trên thế giới giải được. Bạn có muốn vào con số ít ỏi thế không? Nếu giải được thì chỉ số IQ của bạn không dưới 140 đâu nhé.

    câu đố của einstein

    Có 5 ngôi nhà, mỗi nhà có một màu khác nhau. Trong mỗi nhà ở một người có quốc tịch khác nhau. Mỗi người chỉ thích một loại nước uống, hút thuốc một hãng và nuôi một con vật trong nhà. Cả 5 người không cùng thích một loại nước uống, hút thuốc cùng một hãng hay nuôi cùng một con vật trong nhà như người hàng xóm của mình. Câu hỏi: Ai nuôi cá?, biết rằng:

    • Người Anh ở trong nhà màu đỏ.
    • Người Thuỵ Điển nuôi chó.
    • Người Đan Mạch thích uống trà.
    • Ngôi nhà màu xanh lá cây nằm bên trái ngôi nhà màu trắng.
    • Người ở nhà màu xanh lá cây thích uống cà phê.
    • Người hút thuốc hiệu Pall Mall nuôi chim.
    • Người ở nhà màu vàng hút thuốc hiệu Dunhill.
    • Người ở nhà nằm giữa thích uống sữa.
    • Người Na-uy ở nhà đầu tiên.
    • Người hút thuốc hiệu Blends ở cạnh nhà người có nuôi mèo.
    • Người có nuôi ngựa ở cạnh nhà người hút thuốc hiệu Dunhill.
    • Người hút thuốc hiệu Blue Master thích uống bia.
    • Người Đức hút thuốc hiệu Prince.
    • Người Na-uy ở cạnh nhà màu xanh lơ.
    • Người hút thuốc hiệu Blends có người hàng xóm thích uống nước khoáng.

    Hướng dẫn. Mời các em xem lời giải tại đây Ai là người nuôi cá? Câu đố của Einstein 98% dân số thế giới không giải được!

    Bài 12. [SASMO 2015] Albert, Bernard vừa kết bạn với Cheryl và họ muốn biết ngày sinh nhật của cô. Cheryl đã đưa cho họ một danh sách với 10 ngày là: 15/5, 16/5, 19/5, 17/6, 18/6, 14/7,16/7, 14/8, 15/8 và 17/8.

    Bài toán ngày sinh nhật SASMO 2015

    Cheryl sau đó đã nói riêng với Albert về tháng và Bernard về ngày sinh của mình.

    Albert: Bài Tôi không biết sinh nhật của Cheryl là ngày nào nhưng tôi biết Bernard cũng không biết nhiều hơn.

    Bernard: Bài Lúc đầu tôi không biết sinh nhật Cheryl nhưng bây giờ thì tôi đã biết.

    Albert: Bài Bây giờ tôi cũng biết sinh nhật Cheryl là ngày nào.

    Vậy, Cheryl sinh nhật vào ngày nào?

    Hướng dẫn. Mời bạn xem lời giải tại đây Bài toán ngày sinh nhật SASMO 2015

    Bài 13. Một người nông dân phải đưa một con sói, một con dê và một bắp cải qua sông bằng một chiếc thuyền. Tuy nhiên thuyền của anh ta quá nhỏ, do đó, mỗi lần qua sông anh chỉ mang được mỗi một trong ba đồ vật trên đi cùng với anh ta. Hỏi làm thế nào anh nông dân có thể mang tất cả ba đồ vật trên qua sông, biết rằng con sói không thể để lại ở một mình với con dê, còn con dê thì không thể để ở lại một mình với bắp cải.

    Bài 14. Trong bốn đồng tiền có ba đồng tiền thật khối lượng như nhau và một đồng tiền giả có khối lượng khác. Làm thế nào để tìm được đồng tiền giả bằng hai lần cân, sử dụng cân có hai đĩa và không có quả cân.

    Hướng dẫn. Lần cân thứ nhất, đặt nên mỗi quả cân một đồng tiền…

    Bài 15. Có 16 chai rượu trong đó có một chai rượu giả, nhẹ hơn tất cả các chai còn lại. Làm thế nào chỉ ba lần cân xác định được chai nào giả?

    Hướng dẫn. Chia 16 chai rượu thành 3 nhóm: 2 nhóm 6 và 1 nhóm 4.

    Bài 16. Làm thế nào để lấy được 6 lít nước từ sông về, nếu trong tay chỉ có hai cái thùng, một thùng dung tích 4 lít, một thùng dung tích 9 lít và không thùng nào có vạch chia dung tích?

    Hướng dẫn. Kí hiệu $ (a,b) $ là trạng thái thùng $ 4 $ lít đang chứa $ a $ lít $ (0\leqslant a \leqslant 4) $ và thùng 9 lít đang chứa $ b $ lít $ (0\leqslant b\leqslant 9). $ Khi đó việc lấy 6 lít nước từ sông về được diễn tả qua các trạng thái sau:

    (0,0) ➡️ (0,9)➡️(4,5) ➡️ (0,5) ➡️ (4,1) ➡️ (0,1) ➡️ (1,9) ➡️(4,6)

    Bài 17. Trong một can có 16 lít xăng. Làm thế nào để chia số xăng đó thành hai phần bằng nhau, mỗi phần 8 lít, nếu chỉ dùng thêm một can 11 lít và một can 6 lít?

    Hướng dẫn. Kí hiệu $ (a,b,c) $ là trạng thái can 16 lít chứa $ a $ lít xăng, can 11 lít chứa $ b $ lít xăng và can 6 lít chứa $ c $ lít xăng.
    Việc chia 16 lít xăng thành 2 phần bằng nhau được diễn tả qua các trạng thái sau:

    (16,0,0) ➡️ (10,0,6) ➡️(10,6,0) ➡️ (4,6,6) ➡️ (4,11,1)➡️ (15,0,1)➡️ (15,1,0) ➡️
    (9,1,6) ➡️(9,7,0) ➡️(3,7,6)➡️(3,11,2) ➡️(14,0,2) ➡️(14,2,0)➡️(8,2,6)➡️(8,8,0).

    Bài 18. Chứng minh rằng nếu $n^2 $ là số chẵn thì $ n $ cũng là số chẵn.

    Bài 19. Chứng minh rằng $ \sqrt{2} $ là số vô tỷ.

    Bài 20. Chứng minh rằng có vô hạn số nguyên tố.

    Hướng dẫn. Sử dụng phương pháp phản chứng của Euclide.

    Bài 21. Chứng minh rằng nếu $ x^2+y^2=0 $ thì $ x=0 $ và $ y=0. $

    Bài 22. Chứng minh các định lí sau:

    1. Với mọi số nguyên dương $ n, $ nếu $ n^2 $ là số lẻ thì $ n $ là số lẻ.
    2. Với mọi số nguyên dương $ n, $ nếu $ n^2 $ chia hết cho 3 thì $ n $ chia hết cho 3.
    3. Nếu $ a,b,c $ là ba cạnh tam giác vuông ($ a $ là cạnh huyền) thì $ b $ hay $ c $ chia hết cho 3.

    Hướng dẫn. Ta chứng minh bằng phương pháp phản chứng.

    1. Giả sử ngược lại, $ n $ là số chẵn, thế thì $ n = 2k. $ Suy ra: $ n^2 = 4k^2 $ là số chẵn: vô lí. Vậy điều giả sử là sai, tức là mệnh đề cho là đúng.

    2. Giả sử ngược lại, $ n $ không chia hết cho 3 tức $ n = 3k\pm 1. $ Khi đó: \[ n^2 = 9k^2 \pm 6k + 1 = 3(3k^2 \pm 2k) + 1 \] Tức là $ n^2 $ cũng không chia hết cho 3. Vậy điều giả sử là sai, tức là mệnh đề cho là đúng.

    3. Giả sử ngược lại, $ b $ và $ c $ không chia hết cho 3, thế thì: $ b = 3m\pm 1 , c = 3n\pm 1.$ Suy ra: \[ b^2 + c^2 = 9(m^2 + n^2 ) \pm 6m \pm 6n + 2 \] Số này chia cho 3 thì dư 2, trong khi:

    • Nếu $ a=3k $ thì $ a^2 $ chia hết cho 3.
    • Nếu $ a=3k\pm 1 $ thì $ a^2=3(3k^2\pm 2k)+1 $ chia cho 3 dư 1.

    Do đó $ a^2 $ luôn không có dạng khác $ 3k + 2 $, nên mệnh đề: $ a^2 = b^2 + c^2 $ là sai. Dẫn tới điều giả sử là sai, tức là mệnh đề đã cho là đúng.

    Bài 23. Có 50 đôi tất giống hệt nhau, nhưng bị xếp lộn xộn ở trong tủ. Hỏi phải lấy ít nhất mấy chiếc tất để được một đôi?

    Bài 24. Trên đường tròn có bán kính là 100 m, lấy 630 điểm tùy ý. Chứng minh rằng có ít nhất hai điểm cách nhau không đến 1 m.

    Hướng dẫn. Giả sử không có hai điểm nào cách nhau dưới 1 m , tức mọi cặp điểm đều cách nhau 1 m trở lên. Vì độ dài cung luôn lớn hơn độ dài dây cung, nên chu vi đường tròn sẽ lớn hơn tổng độ dài của 630 dây cung, mỗi dây cung đều dài từ 1 m trở lên. Do đó chu vi đường tròn sẽ lớn hơn 630 m. Nhưng đường tròn có bán kính là 100 m, nên chu vi phải là $ 2\pi R = 200\cdot3,1415.< 630$m: vô lí. Vậy điều giả sử là sai, tức mệnh đề đã cho là đúng.

    Bài 25. Trong hình vuông đơn vị (cạnh bằng 1) có 101 điểm. Chứng minh rằng có năm điểm trong các điểm đã chọn được phủ bởi một đường tròn bán kính $ 1/7. $

    Hướng dẫn. Chia hình vuông ra làm 25 hình vuông bằng nhau, mỗi cạnh của hình vuông là 0,2. Vì có 101 điểm, mà chỉ có 25 hình vuông, nên theo nguyên lí Dirichlet tồn tại hình vuông nhỏ chứa ít nhất năm điểm (trong 101 điểm đã cho). Vì hình vuông này nội tiếp trong đường tròn bán kính $ R<1/7 $

  • Tóm tắt lý thuyết phương trình đường thẳng lớp 10

    Tóm tắt lý thuyết phương trình đường thẳng lớp 10

    Tóm tắt lý thuyết Phương trình đường thẳng lớp 10

    Lập phương trình đường thẳng là một bài toán quan trọng của chương phương pháp tọa độ trong mặt phẳng thuộc chương trình hình học lớp 10. Có hai bài toán cơ bản cần ghi nhớ là lập phương trình tổng quát của đường thẳng, lập phương trình tham số của đường thẳng.

    Ngoài ra còn có phương trình chính tắc của đường thẳng, cách lập phương trình đường thẳng đi qua hai điểm, lập phương trình đường thẳng biết hệ số góc…

    Xem thêm 100 Bài tập phương pháp tọa độ trong mặt phẳng

    1. Phương trình tham số của đường thẳng

    Một véc-tơ $\overrightarrow{u}\ne \vec{0}$ được gọi là véc-tơ chỉ phương của đường thẳng nếu nó có giá song song hoặc trùng với đường thẳng đó.

    • Phương trình tham số của đường thẳng $\Delta$ đi qua $M(x_{0},y_{0})$ và có một véc-tơ chỉ phương $\vec{u}(a,b)$ là:\[
      \begin{cases} x =x_{0}+at\\ y =y_{0}+bt \end{cases}, (t\in \mathbb{R})\]

    phương trình tham số của đường thẳng

    Ví dụ 1. Lập phương trình tham số của đường thẳng $d$ có véc-tơ chỉ phương là $ \vec{u}(3;4) $ và đi qua điểm $ M(7;2) $.

    Hướng dẫn.

    Phương trình tham số của đường thẳng $d$ có véc-tơ chỉ phương là $ \vec{u}(3;4) $ và đi qua điểm $ M(7;2) $ là $$ \begin{cases}
    x=3t+7\\
    y=4t+2
    \end{cases} (t\in \mathbb{R}) $$

    Nhận xét

    • Một đường thẳng có vô số vectơ chỉ phương và tất cả chúng đều cùng phương với nhau.
    • Nếu \(\overrightarrow{u}\) là một vectơ chỉ phương của đường thẳng \(d\) thì \(k.\overrightarrow{u}\) cũng là vectơ chỉ phương của \(d.\)

    2. Phương trình tổng quát của đường thẳng

    Một véc-tơ $\overrightarrow{n}\ne \vec{0}$ được gọi là véc-tơ pháp tuyến của đường thẳng nếu nó có giá vuông góc với đường thẳng đó.

    2.1. Phương trình tổng quát của đường thẳng

    phuong trinh tong quat của đường thẳng

    • Trong mặt phẳng tọa độ $Oxy$, phương trình tổng quát của đường thẳng có dạng $$ax+by+c=0$$ với $a,b$ không đồng thời bằng $0$ (có thể viết tắt là $a^2+b^2 \ne 0$).
    • Khi đó, một véc-tơ pháp tuyến của đường thẳng là $\vec{n}(a;b)$.
    • Lấy một điểm bất kì thuộc đường thẳng ta có thể cho $x$ nhận một giá trị tùy ý rồi tìm giá trị của $y$ tương ứng, hoặc cho $y$ một giá trị tùy ý rồi tìm $x$ tương ứng.

    Ví dụ 2. Cho đường thẳng $\Delta$ có phương trình $2x+3y-5=0$ thì chúng ta có:

    • Một véc-tơ pháp tuyến là $\vec{n}=(2;3)$.
    • Lấy một điểm thuộc $\Delta$. Cho $x=2$ thì có $2\cdot 2+3y-5=0$, do đó tìm được $y=\frac{1}{3}$. Vậy tọa độ một điểm thuộc đường thẳng $\Delta$ là $\left (2;\frac{1}{3}\right)$.

    2.2. Cách lập phương trình tổng quát của đường thẳng

    Ta cần tìm một véc-tơ pháp tuyến $\vec{n}$ và tìm tọa độ của một điểm $M$ thuộc đường thẳng. Sau đó sử dụng kết quả:

    Phương trình tổng quát của đường thẳng $\Delta$ có một véc-tơ pháp tuyến $\vec{n}(a,b)$ và đi qua điểm $M(x_{0},y_{0})$ là: \[ ax+by-(ax_{0}+by_{0})=0\]

    Ví dụ 3. Lập phương trình tổng quát của đường thẳng $\Delta$ biết nó có véc-tơ pháp tuyến $ \vec{n}(3;4) $ và đi qua điểm $ M(0;7) $.

    Hướng dẫn. Đường thẳng $\Delta$ có véc-tơ pháp tuyến $ \vec{n}(3;4) $ và đi qua điểm $ M(0;7) $ nên có phương trình tổng quát:
    $$ 3x+4y-(3\cdot 0+4\cdot 7)=0 $$ hay chính là $ 3x+4y-28=0 $.

    Ví dụ 4. Lập phương trình đường trung trực của đoạn thẳng $EF$ với $ E(1;9) $ và $ F(3;-3) $

    Hướng dẫn.

    • Gọi đường trung trực của $ EF $ là $ d $ thì đường thẳng $d$ vuông góc với $ EF $ và đi qua trung điểm của $ EF. $
    • Vì $d$ vuông góc với $ EF $ nên đường thẳng $d$ có véc-tơ pháp tuyến chính là $ \overrightarrow{EF}(2;-12) $.
    • Gọi trung điểm của $ EF $ là $ M $ thì tìm được $ M(2;3) $.
    • Đường thẳng $ d $ có véc-tơ pháp tuyến chính là $ \overrightarrow{EF}(2;-12) $ và đi qua điểm $ M(2;3) $ nên có phương trình tổng quát: $$ 2x-12y+32=0. $$

    2.3. Mối quan hệ giữa véc-tơ chỉ phương và véc-tơ pháp tuyến của đường thẳng

    • Véctơ chỉ phương và véc-tơ pháp tuyến của một đường thẳng thì vuông góc với nhau, do đó nếu véc-tơ pháp tuyến là $\vec{n}=(a,b)$ thì có thể chọn véc-tơ chỉ phương $\vec{u}=(-b,a)$ hoặc $\vec{u}=(b,-a);$ và ngược lại, nếu \(\overrightarrow{u}=(p,q)\) là một vectơ chỉ phương của một đường thẳng thì đường thẳng đó có một vectơ pháp tuyến là \(\overrightarrow{n}=(q,-p)\) hoặc \(\overrightarrow{n’}=(-q,p).\)
    • Hai đường thẳng song song thì có cùng các véc-tơ chỉ phương, cùng các véc-tơ pháp tuyến.
    • Hai đường thẳng vuông góc thì véc-tơ chỉ phương của đường thẳng này là véc-tơ pháp tuyến của đường thẳng kia và ngược lại.

    Nếu đường thẳng $\Delta$ có phương trình: $ax+by+c=0$ thì đường thẳng $\Delta’$

    • vuông góc với $\Delta$ là $\Delta’:-bx+ay+c’=0$ hoặc $\Delta’:bx-ay+c’=0$.
    • song song với $\Delta$ là $\Delta’:ax+by+c’=0$ với $ c\ne c’. $

    Ví dụ 5. Lập phương trình tổng quát của đường thẳng $ AB $ với $ A(1;2) $ và $ B(-3;5) $.

    Hướng dẫn.

    • Đường thẳng $ AB $ chứa $ \overrightarrow{AB}(-4;3) $ nên $ \overrightarrow{AB}(-4;3) $ chính là véc-tơ chỉ phương của đường thẳng $AB$.
    • Suy ra, đường thẳng $AB$ có véc-tơ pháp tuyến là $ \vec{n}(3;4) $.
    • Như vậy, đường thẳng $AB$ có véc-tơ pháp tuyến là $ \vec{n}(3;4) $ và đi qua điểm $ A(1;2) $ nên có phương trình tổng quát: $$ 3x+4y-11=0. $$

    3. Góc và khoảng cách lớp 10

    • Khoảng cách từ điểm $ M(x_0,y_0) $ đến đường thẳng $ \Delta:ax+by+c=0 $ là $$ d(M,\Delta)=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} $$
    • Góc giữa hai véc-tơ $ \vec{a},\vec{b} $ có $$\cos(\vec{a},\vec{b})=\frac{\vec{a}.\vec{b}}{|\vec{a}|.|\vec{b}|}=\frac{\text{tích vô hướng}}{\text{tích độ dài}} $$
    • Góc giữa hai đường thẳng $ \Delta $ và $ \Delta’ $ có $$\cos(\Delta,\Delta’)=\left|\cos(\vec{n},\vec{n’})\right|=\frac{|\vec{n}.\vec{n’}|}{|\vec{n}|.|\vec{n’}|}$$

    Góc giữa hai đường thẳng có cosin bằng trị tuyệt đối của tích vô hướng chia tích độ dài các véc-tơ pháp tuyến của hai đường thẳng.

    Ví dụ 6. Tính khoảng cách từ điểm $ A(1 , 3) $ đến đường thẳng $ \Delta: 3x – 4y + 4 = 0 $

    Hướng dẫn. Khoảng cách từ điểm $ A $ đến đường thẳng $\Delta$ là $$ d(A,\Delta) = \frac{\left|3\cdot 1-4\cdot 3 +4\right|}{\sqrt{3^2+(-4)^2}}=1 $$

    Ví dụ 7. Tính khoảng cách từ điểm $ P(3 , 12) $ đến đường thẳng $ \Delta:\begin{cases} x=2+t\\y=5-3t \end{cases} $

    Hướng dẫn. Trước tiên, chúng ta cần chuyển phương trình đường thẳng $\Delta$ từ dạng tham số về dạng tổng quát. Từ phương trình thứ nhất của hệ, chúng ta có $ t=x-2 $. Thế vào phương trình thứ hai của hệ ta được $ y=5-3(x-2) $ hay chính là $$ 3x+y-11=0 $$
    Đây chính là phương trình tổng quát của đường thẳng $\Delta$. Từ đó, khoảng cách cần tìm là $$ d(P,\Delta)=\frac{|3\cdot 3+ 12 -11|}{\sqrt{3^2+1^2}} = \sqrt{10} . $$

    Ví dụ 8. Tính khoảng cách giữa hai đường thẳng song song $ d : 5x + 3y – 5 = 0 $ và $ d’ : 5x + 3y + 8 = 0 $.

    Hướng dẫn. Vì hai đường thẳng đã cho song song với nhau, nên khoảng cách giữa chúng chính bằng khoảng cách từ một điểm bất kì thuộc đường thẳng này tới đường thẳng còn lại.

    Lấy một điểm bất kì thuộc đường thẳng $ d $, chẳng hạn $ M(1;0) $ thì khoảng cách cần tìm là \begin{align}
    d(d,d’) &= d(M,d’) \\
    &=\frac{|5\cdot 1+3\cdot 0+8|}{\sqrt{5^2+3^2}}\\
    & = \frac{13\sqrt{34}}{34}.
    \end{align}

    Ví dụ 9. Tính góc giữa hai đường thẳng $ \Delta: x-3y+5=0 $ và $ \Delta’:2x-3y+7=0 $.

    Hướng dẫn.

    • Đường thẳng $\Delta$ có véc-tơ pháp tuyến là $ \vec{n}(1;-3) $, đường thẳng $\Delta’$ có véc-tơ pháp tuyến là $ \vec{n}'(2;-3) $ nên góc giữa hai đường thẳng có \begin{align}
      \cos(\Delta,\Delta’)&=\frac{|\vec{n}\cdot \vec{n}’|}{\big|\vec{n}|\cdot|\vec{n}’\big|}\\
      &=\frac{\big|1\cdot 2+(-3)\cdot (-3)\big|}{\sqrt{1^2+(-3)^2}\cdot\sqrt{2^2+(-3)^2}}\\
      &= \frac{11}{\sqrt{130}}.
      \end{align}
    • Suy ra, góc giữa hai đường thẳng là $ (\Delta,\Delta’)\approx 15.26^\circ. $

    4. Các dạng phương trình đường thẳng lớp 10 khác

    4.1. Phương trình chính tắc của đường thẳng

    • Phương trình chính tắc của đường thẳng đi qua $ M(x_0,y_0) $ và có véc-tơ chỉ phương $ \vec{u}(a,b) $ mà $ ab\ne0 $ là $$\frac{x-x_{0}}{a}=\frac{y-y_{0}}{b}$$

    4.2. Phương trình đường thẳng biết hệ số góc

    • Đường thẳng đi qua điểm $M(x_{0},y_{0})$ và có hệ số góc $k$ có phương trình: $$y-y_{0}=k(x-x_{0})$$

    4.3. Phương trình đường thẳng đi qua 2 điểm

    • Nếu hai điểm $ A(x_A;y_A) $ và $ B(x_B;y_B) $ mà có $ x_B-x_A\ne 0 $ và $ y_B-y_A\ne 0 $ thì có phương trình
      $$ \frac{x-x_A}{x_B-x_A}=\frac{y-y_A}{y_B-yA} $$

    4.4. PT đường thẳng cắt hai trục tọa độ

    • Đường thẳng cắt hai trục tọa độ tại $A(a,0)$ và $B(0,b)$ có phương trình: $$\frac{x}{a}+\frac{y}{b}=1$$
    • Phương trình này được gọi là phương trình đoạn chắn.

    5. Bài tập phương trình đường thẳng lớp 10

    Quý thầy cô và các em học sinh tham khảo trong bài Bài tập phương pháp tọa độ trong mặt phẳng

  • ĐỀ CƯƠNG HỌC KÌ 2 TOÁN 10

    ĐỀ CƯƠNG HỌC KÌ 2 TOÁN 10

    ĐỀ CƯƠNG HỌC KÌ 2 TOÁN 10

    1. Nội dung ôn tập đề cương học kì 2 Toán 10

    2. Bài tập trắc nghiệm ôn tập HK2 môn Toán 10

    2.1. Tam thức bậc hai

    Câu 1: Tìm tập xác định của hàm số.

    A. $\left( -\infty ;\frac{1}{2} \right]$.

    B. $\left[ \frac{1}{2};2 \right]$.

    C. $\left( -\infty ;\frac{1}{2} \right]\cup \left[ 2;+\infty \right)$.

    D. $\left[ 2;+\infty \right)$.

    Câu 2: Tam thức nào dưới đây luôn dương với mọi giá trị của $x$?

    A. ${{x}^{2}}-10x+2$.
    B. ${{x}^{2}}-2x-10$.
    C. ${{x}^{2}}-2x+10$.
    D. $-{{x}^{2}}+2x+10$

    Câu 3: Giá trị nào của $m$ thì phương trình $\left( m-3 \right){{x}^{2}}+\left( m+3 \right)x-\left( m+1 \right)=0\,$ $\left( 1 \right)$ có hai nghiệm phân biệt?

    A. $m\in \mathbb{R}\backslash \left\{ 3 \right\}$
    B. $m\in \left( -\infty ;\,-\frac{3}{5} \right)\cup \left( 1;\,+\infty \right)\backslash \left\{ 3 \right\}$.
    C. $m\in \left( -\frac{3}{5};\,1 \right)$.
    D. $m\in \left( -\frac{3}{5};\,+\infty \right)$.

    Câu 4: Gọi $S$ là tập nghiệm của bất phương trình ${{x}^{2}}-8x+7\ge 0$. Trong các tập hợp sau, tập nào không là tập con của $S$?
    A. $\left[ 8;+\infty \right)$.
    B. $\left( -\infty ;-1 \right]$.
    C. $\left( -\infty ;0 \right]$.
    D. $\left[ 6;+\infty \right)$.

    Câu 5: Tìm nghiệm của tam thức bậc hai $f\left( x \right)={{x}^{2}}+4x-5$.

    A. $x=5$; $x=-1$.
    B. $x=-5$; $x=-1$.
    C. $x=5$; $x=1$.
    D. $x=-5$; $x=1$.

    Câu 6: Cho tam thức bậc hai $f\left( x \right)=-{{x}^{2}}-4x+5$. Tìm tất cả giá trị của $x$ để $f\left( x \right)\ge 0$.

    A. $x\in \left( -\infty ;\,-1 \right]\cup \left[ 5;\,+\infty \right)$.
    B. $x\in \left[ -1;\,5 \right]$.
    C. $x\in \left[ -5;\,1 \right]$.
    D. $x\in \left( -5;\,1 \right)$.

    Câu 7: Tìm tập nghiệm $S$ của bất phương trình ${{x}^{2}}-4>0$.

    A. $S=\left( -\infty ;-2 \right)\cup \left( 2;+\infty \right)$
    B. $S=\left( -2;2 \right)$
    C. $S=\left( -\infty ;-2 \right]\cup \left[ 2;+\infty \right)$.
    D. $S=\left( -\infty ;0 \right)\cup \left( 4;+\infty \right)$

    Câu 8: Tìm tập nghiệm $S$ của bất phương trình ${{x}^{2}}-4x+4>0$.

    A. $S=\mathbb{R}\backslash \left\{ 2 \right\}$.
    B. $S=\mathbb{R}$.
    C. $S=\left( 2;+\infty \right)$.
    D. $S=\mathbb{R}\backslash \left\{ -2 \right\}$.

    Câu 9: Tìm khẳng định đúng trong các khẳng định sau?

    A. $f\left( x \right)=3{{x}^{2}}+2x-5$ là tam thức bậc hai.
    B. $f\left( x \right)=2x-4$ là tam thức bậc hai.

    C. $f\left( x \right)=3{{x}^{3}}+2x-1$ là tam thức bậc hai.
    D. $f\left( x \right)={{x}^{4}}-{{x}^{2}}+1$ là tam thức bậc hai.

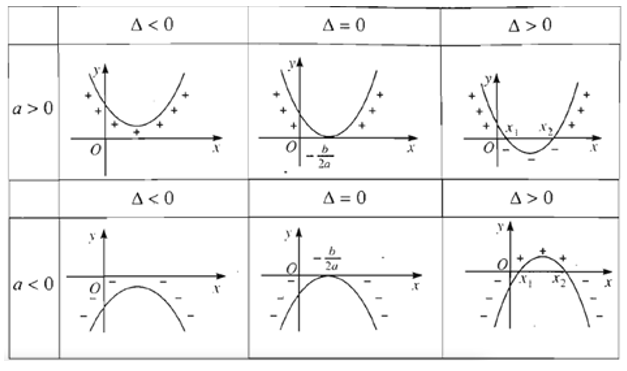
    Câu 10: Cho $f\left( x \right)=a{{x}^{2}}+bx+c$, $\left( a\ne 0 \right)$ và $\Delta ={{b}^{2}}-4ac$. Cho biết dấu của $\Delta $ khi $f\left( x \right)$ luôn cùng dấu với hệ số $a$ với mọi $x\in \mathbb{R}$.
    A. $\Delta <0$.
    B. $\Delta =0$.
    C. $\Delta >0$.
    D. $\Delta \ge 0$.

    Câu 11: Hệ bất phương trình $\left\{ \begin{align}
    & {{x}^{2}}-4<0 \\
    & \left( x-1 \right)\left( {{x}^{2}}+5x+4 \right)\ge 0 \\
    \end{align} \right.$ có số nghiệm nguyên là

    A. $2$.
    B. $1$.
    C. Vô số.
    D. $3$.

    Câu 12: Dấu của tam thức bậc hai $f\left( x \right)=-{{x}^{2}}+5x-6$ được xác định như sau

    A. $f\left( x \right)<0$ với $2<x<3$ và $f\left( x \right)>0$ với $x<2$ hoặc $x>3$.

    B. $f\left( x \right)<0$ với $-3<x<-2$ và $f\left( x \right)>0$ với $x<-3$ hoặc $x>-2$.

    C. $f\left( x \right)>0$ với $2<x<3$ và $f\left( x \right)<0$ với $x<2$hoặc $x>3$.

    D. $f\left( x \right)>0$ với $-3<x<-2$ và $f\left( x \right)<0$ với $x<-3$ hoặc $x>-2$.

    Câu 13: Số nghiệm nguyên của bất phương trình $2{{x}^{2}}-3x-15\le 0$ là

    A. $6$.
    B. $5$.
    C. $8$.
    D. $7$.

    Câu 14: Gọi $S$ là tập nghiệm của bất phương trình $\frac{{{x}^{2}}+x+3}{{{x}^{2}}-4}\ge 1$. Khi đó $S\cap \left( -2;\,2 \right)$ là tập nào sau đây?

    A. $\left( -2;\,-1 \right)$.
    B. $\left( -1;\,2 \right)$.
    C. $\varnothing $.
    D. $\left( -2;\,-1 \right]$.

    Câu 15: Để bất phương trình $5{{x}^{2}}-x+m\le 0$ vô nghiệm thì $m$ thỏa mãn điều kiện nào sau đây?

    A. $m\le \frac{1}{5}$.
    B. $m>\frac{1}{20}$.
    C. $m\le \frac{1}{20}$.
    D. $m>\frac{1}{5}$.

    Câu 16: Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=\sqrt{{{x}^{2}}-2mx-2m+3}$ có tập xác định là $\mathbb{R}$.

    A. $4$.
    B. $6$.
    C. $3$.
    D. $5$.

    Câu 17: Tập nghiệm của bất phương trình $\sqrt{8-x}\le x-2$ là

    A. $S=\left[ 4,\,+\infty \right)$.
    B. $S=\left( -\infty ;\,-1 \right)\cup \left( 4;\,8 \right)$.
    C. $S=\left[ 4;\,8 \right]$.
    D. $S=\left( -\infty ;\,-1 \right]\cup \left[ 4;\,+\infty \right)$.

    Câu 18: Cho hàm số $f\left( x \right)={{x}^{2}}+2x+m$. Với giá trị nào của tham số $m$ thì $f\left( x \right)\ge 0,\,\forall x\in \mathbb{R}$.

    A. $m\ge 1$.
    B. $m>1$.
    C. $m>0$.
    D. $m<2$.

    Câu 19: Với giá trị nào của $m$ thì phương trình $\left( m-1 \right){{x}^{2}}-2\left( m-2 \right)x+m-3=0$ có hai nghiệm ${{x}_{1}}$, ${{x}_{2}}$ thỏa mãn ${{x}_{1}}+{{x}_{2}}+{{x}_{1}}{{x}_{2}}<1$?
    A. $1<m<3$.
    B. $1<m<2$.
    C. $m>2$.
    D. $m>3$.

    Câu 20: Cho phương trình $\left( m-5 \right){{x}^{2}}+2\left( m-1 \right)x+m=0$ $\left( 1 \right)$. Với giá trị nào của $m$ thì $\left( 1 \right)$ có $2$ nghiệm ${{x}_{1}}$, ${{x}_{2}}$ thỏa ${{x}_{1}}<2<{{x}_{2}}$?
    A. $m\ge 5$.
    B. $m<\frac{8}{3}$.
    C. $\frac{8}{3}<m<5$.
    D. $\frac{8}{3}\le m\le 5$.
    Câu 21: Tìm tất cả các giá trị của tham số $m$ để bất phương trình $-{{x}^{2}}+x-m>0$ vô nghiệm.

    A. $m\ge \frac{1}{4}$.
    B. $m\in \mathbb{R}$.
    C. $m>\frac{1}{4}$.
    D. $m<\frac{1}{4}$.

    Câu 22: Tìm các giá trị thực của tham số $m$ để phương trình $\left( m-1 \right){{x}^{2}}-2mx+m=0$ có một nghiệm lớn hơn $1$ và một nghiệm nhỏ hơn $1$?
    A. $0<m<1$.
    B. $m>1$.
    C. $m\in \varnothing $.
    D. $\left\{ \begin{align}
    & m>0 \\
    & m\ne 1 \\
    \end{align} \right.$.

    Câu 23: Bất phương trình $\left( m-1 \right){{x}^{2}}-2\left( m-1 \right)x+m+3\ge 0$ với mọi $x\in \mathbb{R}$ khi

    A. $m\in \left[ 1;+\infty \right)$.
    B. $m\in \left( 2;+\infty \right)$.
    C. $m\in \left( 1;+\infty \right)$.
    D. $m\in \left( -2;7 \right)$.

    Câu 24: Tập nghiệm của bất phương trình $\left( {{x}^{2}}-3x \right)\sqrt{2{{x}^{2}}-3x-2}\ge 0$ là

    A. $\left[ \begin{matrix}
    x\ge 3\text{ } \\
    x=2\text{ } \\
    x\le -\frac{1}{2} \\
    \end{matrix} \right.$.
    B. $\left[ \begin{matrix}
    x\ge 3 \\
    x\le 0 \\
    \end{matrix} \right.$.
    C. $\left[ \begin{matrix}
    x\ge 2\text{ } \\
    x\le -\frac{1}{2} \\
    \end{matrix} \right.$.
    D. $x\in \left\{ -\frac{1}{2};0;2;3 \right\}$.

    Câu 25: Hệ bất phương trình $\left\{ \begin{align}
    & {{x}^{2}}-1\le 0 \\
    & x-m>0 \\
    \end{align} \right.$ có nghiệm khi
    A. $m>1$.
    B. $m<1$.
    C. $m\ne 1$.
    D. $m=1$.

    Câu 26: Xác định $m$ để phương trình $\left( x-1 \right)\left[ {{x}^{2}}+2\left( m+3 \right)x+4m+12 \right]=0$ có ba nghiệm phân biệt lớn hơn $-1$.

    A. $-\frac{7}{2}<m<-3$ và $m\ne -\frac{19}{6}$.
    B. $m<-\frac{7}{2}$.
    C. $-\frac{7}{2}<m<-1$ và $m\ne -\frac{16}{9}$.
    D. $-\frac{7}{2}<m<3$ và $m\ne -\frac{19}{6}$.

    Câu 27: Tìm tất cả các giá trị của tham số $m$ để phương trình ${{x}^{2}}-2mx+m+2=0$ có hai nghiệm ${{x}_{1}}$, ${{x}_{2}}$ thỏa mãn $x_{1}^{3}+x_{2}^{3}\le 16$.
    A. Không có giá trị của $m$.
    B. $m\ge 2$.
    C. $m\le -1$.
    D. $m\le -1$ hoặc $m=2$.

    Câu 28: Giải bất phương trình $\sqrt{-{{x}^{2}}+6x-5}>8-2x$ có nghiệm là

    A. $-5<x\le -3$.
    B. $3<x\le 5$.
    C. $2<x\le 3$.
    D. $-3\le x\le -2$.
    Câu 29: Giá trị lớn nhất của hàm số $f(x)=\sqrt{(x-1)(9-3x)}$ với $1 \leqslant  x \leqslant  3$ là:
    A. $\sqrt{2}$
    B. $0$
    C. $\sqrt{3}$
    D. $2$
    Câu 30: Cho hàm số $f\left( x \right)=-{{x}^{2}}-2\left( m-1 \right)x+2m-1$. Tìm tất cả các giá trị của tham số $m$ để $f\left( x \right)>0$, $\forall x\in \left( 0;\,1 \right)$.
    A. $m>1$.
    B. $m<\frac{1}{2}$.
    C. $m\ge 1$.
    D. $m\ge \frac{1}{2}$.

    2.2. CUNG, GÓC LƯỢNG GIÁ
    C. CÔNG THỨC LƯỢNG GIÁC

    Câu 1: Góc có số đo ${{108}^{\text{o}}}$đổi ra radian là
    A. $\frac{3\pi }{5}.$
    B. $\frac{\pi }{10}.$
    C. $\frac{3\pi }{2}.$
    D. $\frac{\pi }{4}.$

    Câu 2: Biết một số đo của góc $\left( Ou,Ov \right)=\frac{3\pi }{2}$. Giá trị tổng quát của góc $\left( Ou,Ov \right)$ là

    A. $\left( Ou,Ov \right)=\frac{3\pi }{2}+k\pi $
    B. $\left( Ou,Ov \right)=\pi +k2\pi $
    C. $\left( Ou,Ov \right)=\frac{\pi }{2}+k\pi $
    D. $\left( Ou,Ov \right)=\frac{-\pi }{2}+k2\pi $

    Câu 3: Góc có số đo $\frac{2\pi }{5}$đổi sang độ là
    A. ${{240}^{\text{o}}}$
    B. ${{135}^{\text{o}}}$
    C. ${{72}^{\text{o}}}$
    D. ${{270}^{\text{o}}}$

    Câu 4: Một đường tròn có bán kính $R=\frac{10}{\pi }\,\text{cm}$. Tìm độ dài của cung $\frac{\pi }{2}$ trên đường tròn.

    A. $10\,\text{cm}$
    B. $5\,\text{cm}$
    C. $\frac{20}{{{\pi }^{2}}}\,\text{cm}$
    D. $\frac{{{\pi }^{2}}}{20}\,\text{cm}$

    Câu 5: Tìm mệnh đề đúng trong các mệnh đề sau:

    A. Số đo của một cung lượng giác luôn là một số không âm.

    B. Số đo của một cung lượng giác luôn không vượt quá $2\pi $.

    C. Số đo của một cung lượng giác luôn là một số thực thuộc đoạn $\text{ }\!\![\!\!\text{ }0;2\pi \text{ }\!\!]\!\!\text{ }$.

    D. Số đo của một cung lượng giác là một số thực.

    Câu 6: Cho đường tròn có bán kính $6\ \text{cm}$. Tìm số đo (${rad}$) của cung có độ dài là $3\ \text{cm}$:

    A. 0,5
    B. 3
    C. 2
    D. 1

    Câu 7: Xét góc lượng giác $\left( OA;OM \right)=\alpha $, trong đó $M$ là điểm không nằm trên các trục tọa độ $Ox$ và $Oy$. Khi đó $M$ thuộc góc phần tư nào để $\sin \alpha $ và $\text{cos}\alpha $ cùng dấu

    A. (I) và (II)
    B. (I) và (III)
    C. (I) và (IV)
    D. (II) và (III)

    Câu 8: Cho $\alpha $ là góc tù. Điều khẳng định nào sau đây đúng?

    A. $\sin \alpha <0$
    B. $\cos \alpha >\text{0}$
    C. $\tan \alpha <0$
    D. $\cot \alpha >0$

    Câu 9: Chọn điểm $A\left( 1;0 \right)$làm điểm đầu của cung lượng giác trên đường tròn lượng giác. Tìm điểm cuối $M$ của cung lượng giác có số đo $\frac{25\pi }{4}$.

    A. $M$ là điểm chính giữa của cung phần tư thứ $\text{I}$.

    B.$M$là điểm chính giữa của cung phần tư thứ $\text{II}$.

    C. $M$ là điểm chính giữa của cung phần tư thứ $\text{III}$.

    D. $M$ là điểm chính giữa của cung phần tư thứ$\text{IV}$.

    Câu 10: Cho bốn cung (trên một đường tròn định hướng): $\alpha =-\frac{5\pi }{6}$, $\beta =\frac{\pi }{\text{3}}$, $\gamma =\frac{\text{25}\pi }{\text{3}}$, $\delta =\frac{\text{19}\pi }{\text{6}}$. Các cung nào có điểm cuối trùng nhau:

    A. $\alpha $ và $\beta $; $\gamma $và $\delta $.
    B. $\beta $ và $\gamma $; $\alpha $ và $\delta $.
    C. $\alpha $, $\beta $, $\gamma $.
    D. $\beta $, $\gamma $, $\delta $.

    Câu 11: Giá trị $k$ để cung $\alpha =\frac{\pi }{2}+k2\pi $ thỏa mãn $10\pi <\alpha <11\pi $ là

    A. $k=4.$
    B. $k=6.$
    C. $k=7.$
    D. $k=5.$

    Câu 12: Cung $\alpha $ có mút đầu là $A$ và mút cuối là $M$ thì số đo của $\alpha $ là

    A.$\frac{3\pi }{4}+k\pi. $

    B.$-\frac{3\pi }{4}+k\pi. $

    C. $\frac{3\pi }{4}+k2\pi. $

    D. $-\frac{3\pi }{4}+k2\pi. $

    Câu 13: Nếu góc lượng giác có $s\left( Ox,Oz \right)=-\frac{63\pi }{2}$thì hai tia $Ox$ và $Oz$

    A. Trùng nhau.
    B. Vuông góc.
    C. Tạo với nhau một góc bằng $\frac{3\pi }{4}$.
    D. Đối nhau.

    Câu 14: Một bánh xe có $72$ răng. Số đo góc mà bánh xe đã quay được khi di chuyển $10$ răng là

    A.${{30}^{\text{o}}}.$

    B.${{40}^{\text{o}}}.$

    C.${{50}^{\text{o}}}.$

    D.${{60}^{\text{o}}}.$

    Câu 15: Trong ${20}$ giây bánh xe của xe gắn máy quay được ${60}$ vòng.Tính độ dài quãng đường xe gắn máy đã đi được trong vòng $3$ phút, biết rằng bán kính bánh xe gắn máy bằng $6,5\text{ cm}$ (lấy $\pi =3,1416$).

    A. $22054\text{ cm}$.
    B. $22063\text{ cm}$.
    C. $22054\text{ mm}$.
    D. $22044\text{ cm}$

    Câu 16: Cho hai góc lượng giác có sđ$\left( Ox,Ou \right)={{45}^{\text{o}}}+m{{360}^{\text{o}}},m\in \mathbb{Z}$ và sđ$\left( Ox,Ov \right)=-{{135}^{\text{o}}}+n{{360}^{\text{o}}},n\in \mathbb{Z}$. Ta có hai tia $Ou$ và $Ov$

    A. Tạo với nhau góc ${{45}^{\text{o}}}$.
    B. Trùng nhau.
    C. Đối nhau.
    D. Vuông góc.

    Câu 17: Một đồng hồ treo tường, kim giờ dài $10,57\text{ cm}$ và kim phút dài $13,34\text{ cm}$.Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là:
    A. $2,77\text{ cm}$
    B. $2,9\text{ cm}$
    C. $2,76\text{ cm}$
    D. $2,8\text{ cm}$

    Câu 18: Cho $\frac{3\pi }{2}<a<2\pi $. Kết quả đúng là
    A. $\sin a>0$, $\cos a>0$.
    B. $\sin a<0$, $cosa<0$.
    C. $\sin a>0$, $cosa<0$.
    D. $\sin a<0$, $cosa>0$

    Câu 19: Trong các đẳng thức sau, đẳng thức nào đúng ?

    A. $\cos \left( {{180}^{0}}a \right)=\cos a$.
    B. $\sin \left( {{180}^{0}}a \right)=-\sin a$.
    C. $\sin \left( {{180}^{0}}a \right)=-\sin a$.
    D. $\sin \left( {{180}^{0}}a \right)=\cos a$.

    Câu 20: Chọn đẳng thức sai trong các đẳng thức sau

    A. $\sin \left( \frac{\pi }{2}-x \right)=\cos x$.
    B. $\sin \left( \frac{\pi }{2}+x \right)=-\cos x$.
    C. $\tan \left( \frac{\pi }{2}-x \right)=\cot x$.
    D. $\tan \left( \frac{\pi }{2}+x \right)=-\cot x$

    Câu 21: Trong các giá trị sau, $\sin \alpha $ có thể nhận giá trị nào?

    A. $-1,7$.
    B. $\frac{2}{3}$.
    C. $-\sqrt{3}$.
    D. $\frac{\sqrt{10}}{3}$.

    Câu 22: Trong các công thức sau, công thức nào sai?

    A. ${{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1$.

    B. $1+{{\tan }^{2}}\alpha =\frac{1}{{{\cos }^{2}}\alpha }\,\left( \alpha \ne \frac{\pi }{2}+k\pi ,\,k\in \mathbb{Z} \right)$.

    C. $1+{{\cot }^{2}}\alpha =\frac{1}{{{\sin }^{2}}\alpha }\ \left( \alpha \ne k\pi ,\,k\in \mathbb{Z} \right)$.

    D. $\tan \alpha +\cot \alpha =1\,\left( \alpha \ne \frac{k\pi }{2},\,k\in \mathbb{Z} \right)$.

    Câu 23: Cho biết $\tan \alpha =\frac{1}{5}$. Tính $\cot \alpha $

    A. $\cot \alpha =5$.
    B. $\cot \alpha =\frac{1}{25}$.
    C. $\cot \alpha =\frac{1}{5}$.
    D. $\cot \alpha =\sqrt{5}$

    Câu 24: Đơn giản biểu thức $A=\cos \left( \frac{\pi }{2}-\alpha \right)+\sin \left( \frac{\pi }{2}-\alpha \right)-\sin \left( \pi -\alpha \right)-\cos \left( \pi -\alpha \right)$, ta có:

    A. $A=2\sin a$.
    B. $A=2\cos a$.
    C. $A=\sin a\cos a$.
    D. $A=0$.

    Câu 25: Đơn giản biểu thức $A=\left( 1{{\cos }^{2}}x \right).{{\tan }^{2}}x+\left( 1{{\tan }^{2}}x \right),$ ta có

    A. $A={{\sin }^{2}}x$.
    B. $A={{\cos }^{2}}x$.
    C. $A={{\sin }^{2}}x$.
    D. $A=co{{s}^{2}}x$.

    Câu 26: Cho $\sin \alpha =\frac{4}{5}$ và $\frac{\pi }{2}<\alpha <\pi $. Giá trị của $\text{cos}\alpha $ là:
    A. $\frac{3}{5}$.
    B. $-\frac{3}{5}$.
    C. $\pm \frac{3}{5}$
    D. $\frac{9}{25}$.

    Câu 27: Cho $\tan \alpha =2$. Giá trị của $A=\frac{5\sin \alpha +\cos \alpha }{\sin \alpha -3\cos \alpha }$ là:
    A. $5$.
    B. $\frac{5}{3}$.
    C. $-11$.
    D. $\frac{-1}{3}$.

    Câu 28: Các cặp đẳng thức nào sau đây đồng thời xảy ra?

    A. $\sin \alpha =1$ và $\cos \alpha =1$.
    B. $\sin \alpha =\frac{1}{2}$ và $\cos \alpha =-\frac{\sqrt{3}}{2}$.

    C. $\sin \alpha =\frac{1}{2}$ và $\text{cos}\alpha =-\frac{1}{2}$.
    D. $\sin \alpha =\sqrt{3}$ và $\cos \alpha =0$.

    Câu 29: Cho $\cos \alpha =\frac{4}{5}$ với $0<\alpha <\frac{\pi }{2}$. Tính $\sin \alpha $.
    A. $\sin \alpha =\frac{1}{5}$.
    B. $\sin \alpha =-\frac{1}{5}$
    C. $\sin \alpha =\frac{3}{5}$
    D. $\sin \alpha =\pm \frac{3}{5}$.

    Câu 30: Đơn giản biểu thức $A\text{ }=\frac{2{{\cos }^{2}}x-1}{\sin x-\cos x}$ ta có

    A. $A=\cos x+\sin x$.
    B. $A=\cos x\sin x$.
    C. $A=\sin x\cos x$.
    D. $A=-\sin x\cos x$.

    Câu 31: Tính $\alpha $ biết $\cos \alpha =-1$

    A. $\alpha =k\pi \ \ \left( k\in \mathbb{Z} \right)$.
    B. $\alpha =k2\pi \ \ \left( k\in \mathbb{Z} \right)$.
    C. $\alpha =\frac{\pi }{2}+k2\pi \ \ \left( k\in \mathbb{Z} \right)$.
    D. $\alpha =-\pi +k2\pi \ \ \left( k\in \mathbb{Z} \right)$.

    Câu 32: Biết $\tan \alpha =2$ và ${{180}^{\circ }}<\alpha <{{270}^{\circ }}$. Giá trị $\cos \alpha +\sin \alpha $ bằng
    A. $-\frac{3\sqrt{5}}{5}$.
    B. $1\sqrt{5}$.
    C. $\frac{3\sqrt{5}}{2}$.
    D. $\frac{\sqrt{5}-1}{2}$.
    Câu 33: Giá trị của $A={{\cos }^{2}}\frac{\pi }{8}+{{\cos }^{2}}\frac{3\pi }{8}+{{\cos }^{2}}\frac{5\pi }{8}+{{\cos }^{2}}\frac{7\pi }{8}$ bằng
    A. $0$.
    B. $1$.
    C. $2$
    D. $-1$.

    Câu 34: Biểu thức $D={{\cos }^{2}}x.co{{t}^{2}}x+4{{\cos }^{2}}xco{{t}^{2}}x+3{{\sin }^{2}}x$ không phụ thuộc $x$ và bằng
    A. 2.
    B. $2$.
    C. 3.
    D. $3$.

    Câu 35: Biết $\sin \alpha +\cos \alpha =\frac{\sqrt{3}}{2}$. Trong các kết quả sau, kết quả nào sai ?
    A. $\sin \alpha. \cos \alpha =\frac{1}{8}$.
    B. $\sin \alpha -\cos \alpha =\pm \frac{\sqrt{5}}{2}$.
    C. ${{\sin }^{4}}\alpha +{{\cos }^{4}}\alpha =\frac{5}{4}$.
    D. ${{\tan }^{2}}\alpha +{{\cot }^{2}}\alpha =62$.

    Câu 36: Tính giá trị của biểu thức $A={{\sin }^{6}}x+{{\cos }^{6}}x+3{{\sin }^{2}}x{{\cos }^{2}}x$.
    A. $A=1$.
    B. $A=1$.
    C. $A=4$.
    D. $A=4$.

    Câu 37: Biểu thức $A=\frac{{{\left( 1-{{\tan }^{2}}x \right)}^{2}}}{4{{\tan }^{2}}x}-\frac{1}{4{{\sin }^{2}}x{{\cos }^{2}}x}$ không phụ thuộc vào $x$ và bằng
    A. $1$.
    B. $1$.
    C. $\frac{1}{4}$.
    D. $-\frac{1}{4}$.

    Câu 38: Biểu thức $C=2{{\left( {{\sin }^{4}}x+{{\cos }^{4}}x+{{\sin }^{2}}x{{\cos }^{2}}x \right)}^{2}}\left( {{\sin }^{8}}x+{{\cos }^{8}}x \right)$ có giá trị không đổi và bằng
    A. $2$.
    B. $2$.
    C. $1$.
    D. $1$.

    Câu 39: Trong các công thức sau, công thức nào sai?
    A. $\cot 2x=\frac{{{\cot }^{2}}x-1}{2\cot x}$.
    B. $\tan 2x=\frac{2\tan x}{1+{{\tan }^{2}}x}$.
    C. $\cos 3x=4{{\cos }^{3}}x-3\cos x$.
    D. $\sin 3x=3\sin x-4{{\sin }^{3}}x$

    Câu 40: Trong các công thức sau, công thức nào sai?
    A. $\cos 2a={{\cos }^{2}}a{{\sin }^{2}}a.$
    B. $\cos 2a={{\cos }^{2}}a+{{\sin }^{2}}a.$
    C. $\cos 2a=2{{\cos }^{2}}a1.$
    D. $\cos 2a=12{{\sin }^{2}}a.$

    Câu 41: Trong các công thức sau, công thức nào đúng?
    A. $\cos \left( ab \right)=\cos a.\cos b+\sin a.\sin b.$
    B. $\cos \left( a+b \right)=\cos a.\cos b+\sin a.\sin b.$
    C. $\sin \left( ab \right)=\sin a.\cos b+\cos a.\sin b.$
    D. $\sin \left( a+b \right)=\sin a.\cos b-\cos. \sin b.$

    Câu 42: Trong các công thức sau, công thức nào đúng?
    A. $\tan \left( a-b \right)=\frac{\tan a+\tan b}{1-\tan a\tan b}.$
    B. $\tan \left( ab \right)=\tan a-\tan b.$
    C. $\tan \left( a+b \right)=\frac{\tan a+\tan b}{1-\tan a\tan b}.$
    D. $\tan \left( a+b \right)=\tan a+\tan b.$

    Câu 43: Trong các công thức sau, công thức nào sai?
    A. $\cos a\cos b=\frac{1}{2}\left[ \cos \left( ab \right)+\cos \left( a+b \right) \right].$
    B. $\sin a\sin b=\frac{1}{2}\left[ \cos \left( ab \right)\cos \left( a+b \right) \right].$
    C. $\sin a\cos b=\frac{1}{2}\left[ \sin \left( ab \right)+\sin \left( a+b \right) \right].$
    D. $\sin a\cos b=\frac{1}{2}\left[ \sin \left( a-b \right)-\cos \left( a+b \right) \right].$

    Câu 44: Trong các công thức sau, công thức nào sai?

    A. $\cos a+\cos b=2\cos \frac{a+b}{2}.\cos \frac{a-b}{2}.$

    B. $\cos a\cos b=2\sin \frac{a+b}{2}.\sin \frac{a-b}{2}.$

    C. $\sin a+\sin b=2\sin \frac{a+b}{2}.\cos \frac{a-b}{2}.$

    D. $\sin a\sin b=2\cos \frac{a+b}{2}.\sin \frac{a-b}{2}.$

    Câu 45: Rút gọn biểu thức: $\sin \left( a17{}^\circ \right).\cos \left( a+13{}^\circ \right)\sin \left( a+13{}^\circ \right).\cos \left( a17{}^\circ \right)$, ta được:
    A. $\sin 2a.$
    B. $\cos 2a.$
    C. $-\frac{1}{2}.$
    D. $\frac{1}{2}.$

    Câu 46: Giá trị đúng của $\tan \frac{\pi }{24}+\tan \frac{7\pi }{24}$ bằng:
    A. $2\left( \sqrt{6}-\sqrt{3} \right).$
    B. $2\left( \sqrt{6}+\sqrt{3} \right).$
    C. $2\left( \sqrt{3}-\sqrt{2} \right).$
    D. $2\left( \sqrt{3}+\sqrt{2} \right).$

    Câu 47: Rút gọn biểu thức $\cos 54{}^\circ. \cos 4{}^\circ \cos 36{}^\circ. \cos 86{}^\circ $, ta được:
    A. $\cos 50{}^\circ. $
    B. $\cos 58{}^\circ. $
    C. $\sin 50{}^\circ. $
    D. $\sin 58{}^\circ. $

    Câu 48: Cho $x,\text{ }y$ là các góc nhọn, $\cot x=\frac{3}{4}$, $\cot y=\frac{1}{7}$. Tổng $x+y$ bằng:
    A. $\frac{\pi }{4}.$
    B. $\frac{3\pi }{4}.$
    C. $\frac{\pi }{3}.$
    D. $\pi. $

    Câu 49: Biểu thức $A={{\cos }^{2}}x+{{\cos }^{2}}\left( \frac{\pi }{3}+x \right)+{{\cos }^{2}}\left( \frac{\pi }{3}-x \right)$ không phụ thuộc $x$ và bằng:
    A. $\frac{3}{4}.$
    B. $\frac{4}{3}.$
    C. $\frac{3}{2}.$
    D. $\frac{2}{3}.$

    Câu 50: Cho $A$, $B$ , $C$ là ba góc của một tam giá
    C. Hãy chỉ ra hệ thức SAI.
    A. $\cos \frac{A+B}{2}=\sin \frac{C}{2}.$
    B. $\cos \left( A+B+2C \right)=\cos C.$
    C. $\sin \left( A+C \right)=\sin B.$
    D. $\cos \left( A+B \right)=\cos C.$

    Câu 51: Rút gọn biểu thức $A=\frac{\sin x+\sin 2x+\sin 3x}{\cos x+\cos 2x+\cos 3x}$
    A. $A=\tan 6x.$
    B. $A=\tan 3x.$
    C. $A=\tan 2x.$
    D. $A=\tan x+\tan 2x+\tan 3x.$

    Câu 52: Rút gọn biểu thức: $\cos \left( 120{}^\circ \text{ }x \right)+\cos \left( 120{}^\circ +\text{ }x \right)\cos x$ ta được kết quả là
    A. $0.$
    B. $\cos x.$
    C. $2\cos x.$
    D. $\sin x\cos x.$

    Câu 53: Cho $\cos a=\frac{3}{4}$; $\sin a>0$; $\sin b=\frac{3}{5}$; $\cos b<0$. Giá trị của $\cos \left( a+b \right).$ bằng:

    A. $\frac{3}{5}\left( 1+\frac{\sqrt{7}}{4} \right).$
    B. $-\frac{3}{5}\left( 1+\frac{\sqrt{7}}{4} \right).$
    C. $\frac{3}{5}\left( 1-\frac{\sqrt{7}}{4} \right).$
    D. $-\frac{3}{5}\left( 1-\frac{\sqrt{7}}{4} \right).$

    Câu 54: Biểu thức $\frac{\sin \left( a+b \right)}{\sin \left( a-b \right)}$ bằng biểu thức nào sau đây? (Giả sử biểu thức có nghĩa)

    A. $\frac{\sin \left( a+b \right)}{\sin \left( a-b \right)}=\frac{\sin a+\sin b}{\sin a-\sin b}.$
    B. $\frac{\sin \left( a+b \right)}{\sin \left( a-b \right)}=\frac{\sin a-\sin b}{\sin a+\sin b}.$

    C. $\frac{\sin \left( a+b \right)}{\sin \left( a-b \right)}=\frac{\tan a+\tan b}{\tan a-\tan b}.$
    D. $\frac{\sin \left( a+b \right)}{\sin \left( a-b \right)}=\frac{\cot a+\cot b}{\cot a-\cot b}.$

    Câu 55: Giá trị đúng của $\cos \frac{2k\pi }{7}+\cos \frac{4k\pi }{7}+\cos \frac{6k\pi }{7}$ ( k℃∈Z) bằng:
    A. $\frac{1}{2}.$
    B. $-\frac{1}{2}.$
    C. $\frac{1}{4}.$
    D. $-\frac{1}{4}.$

    Câu 56: Cho $A$, $B$, $C$ là các góc nhọn và $\tan A=\frac{1}{2}$, $\tan B=\frac{1}{5}$, $\tan C=\frac{1}{8}$. Tổng $A+B+C$ bằng:

    A. $\frac{\pi }{6}.$
    B. $\frac{\pi }{5}.$
    C. $\frac{\pi }{4}.$
    D. $\frac{\pi }{3}.$

    Câu 57: Cho $\cot a=15$, giá trị $\sin 2a$ có thể nhận giá trị nào dưới đây:
    A. $\frac{11}{113}.$
    B. $\frac{13}{113}.$
    C. $\frac{15}{113}.$
    D. $\frac{17}{113}.$

    Câu 58: Cho $A$, $B$, $C$ là ba góc của một tam giá
    C. Hãy chọn hệ thức đúng trong các hệ thức sau.

    A. ${{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1+\cos A.\cos B.\cos C.$
    B. ${{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1\cos A.\cos B.\cos C.$

    C. ${{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=1+2\cos A.\cos B.\cos C.$
    D. ${{\cos }^{2}}A+{{\cos }^{2}}B+{{\cos }^{2}}C=12\cos A.\cos B.\cos C.$

    Câu 59: Biểu thức $A=\frac{2{{\cos }^{2}}2\alpha +\sqrt{3}\sin 4\alpha -1}{2{{\sin }^{2}}2\alpha +\sqrt{3}\sin 4\alpha -1}$ có kết quả rút gọn là:

    A. $\frac{\cos \left( 4\alpha +30{}^\circ \right)}{\cos \left( 4\alpha -30{}^\circ \right)}.$
    B. $\frac{\cos \left( 4\alpha -30{}^\circ \right)}{\cos \left( 4\alpha +30{}^\circ \right)}.$
    C. $\frac{\sin \left( 4\alpha +30{}^\circ \right)}{\sin \left( 4\alpha -30{}^\circ \right)}.$
    D. $\frac{\sin \left( 4\alpha -30{}^\circ \right)}{\sin \left( 4\alpha +30{}^\circ \right)}.$

    Câu 60: Nếu $5\sin \alpha =3\sin \left( \alpha +2\beta \right)$ thì:

    A. $\tan \left( \alpha +\beta \right)=2\tan \beta. $
    B. $\tan \left( \alpha +\beta \right)=3\tan \beta. $
    C. $\tan \left( \alpha +\beta \right)=4\tan \beta. $
    D. $\tan \left( \alpha +\beta \right)=5\tan \beta. $

    2.3. PHƯƠNG TRÌNH ĐƯỜNG THẲNG (GÓC VÀ KHOẢNG CÁCH)

    Câu 1: Tìm côsin góc giữa $2$ đường thẳng ${{\Delta }_{1}}$: $10x+5y-1=0$và ${{\Delta }_{2}}$: $\left\{ \begin{align}
    & x=2+t \\ & y=1-t \\ \end{align} \right.$.
    A. $\frac{3}{10}$.
    B. $\frac{\sqrt{10}}{10}.$
    C. $\frac{3\sqrt{10}}{10}.$
    D. $\frac{3}{5}.$

    Câu 2: Khoảng cách từ điểm $M\left( 15;1 \right)$đến đường thẳng $\Delta: \left\{ \begin{align}
    & x=2+3t \\ & y=t \\ \end{align} \right.$ là
    A. $\sqrt{5}$.
    B. $\frac{1}{\sqrt{10}}$.
    C. $\sqrt{10}$.
    D. $\frac{16}{\sqrt{5}}$

    Câu 3: Có hai giá trị ${{m}_{1}},\,\,{{m}_{2}}$ để đường thẳng $mx+y-3=0$ hợp với đường thẳng $x+y=0$ một góc $60{}^\circ $.Tổng ${{m}_{1}}+{{m}_{2}}$ bằng
    A. $-3.$
    B. $3.$
    C. $4.$
    D. $-4.$

    Câu 4: Tìm tọa độ điểm $M$nằm trên trục $Ox$và cách đều $2$đường thẳng: ${{\Delta }_{1}}: 3x-2y-6=0$ và ${{\Delta }_{2}}: 3x-2y+3=0$

    A. $\left( 0;\sqrt{2} \right)$.
    B. $\left( \frac{1}{2};0 \right)$.
    C. $\left( 1;0 \right)$.
    D. $\left( \sqrt{2};0 \right)$.

    Câu 5: Tính chiều cao tương ứng với cạnh $BC$ của tam giác $ABC$ biết $A\left( 1;2 \right)$, $C\left( 4;0 \right)$, $B\left( 0;3 \right)$

    A. $3$.
    B. $\frac{1}{5}$.
    C. $\frac{1}{25}$.
    D. $\frac{3}{5}$.

    Câu 6: Khoảng cách giữa hai đường thẳng ${{\Delta }_{1}}: 5x-7y+4=0$ và ${{\Delta }_{2}}: 5x-7y+6=0$ là

    A. $\frac{4}{\sqrt{74}}$.
    B. $\frac{6}{\sqrt{74}}$.
    C. $\frac{2}{\sqrt{74}}$.
    D. $\frac{10}{\sqrt{74}}$.

    Câu 7: Cho đường thẳng đi qua hai điểm $A\left( 2;2 \right)$, $B\left( 5;1 \right)$. Tìm tọa độ điểm $C$ trên đường thẳng $\Delta: x-2y+8=0$ sao cho diện tích tam giác $ABC$ bằng $17$.

    A. $C\left( 12;10 \right)$ và$C\left( -\frac{76}{5};-\frac{18}{5} \right)$
    B. $C\left( -12;10 \right)$.
    C. $C\left( -4;2 \right)$.
    D. $C\left( \frac{1}{5};\frac{41}{10} \right)$.

    Câu 8: Trong mặt phẳng với hệ trục tọa độ $Oxy$$\Delta ABC$có đỉnh $A\left( 2;-3 \right),$$B\left( 3;-2 \right)$ và diện tích $\Delta ABC$bằng $\frac{3}{2}$. Biết trọng tâm $G$của $\Delta ABC$ thuộc đường thẳng $
    D. 3x-y-8=0$. Tìm tọa độ điểm $C$.

    A. $C\left( 1;-1 \right)$và $C\left( 4;8 \right)$.
    B. $C\left( 1;-1 \right)$và $C\left( -2;10 \right)$.
    C. $C\left( -1;1 \right)$và $C\left( -2;10 \right)$.
    D. $C\left( -1;1 \right)$và $C\left( 2;-10 \right)$.

    Câu 9: Cho hai điểm $A\left( 3;2 \right)$, $B\left( -2;2 \right)$. Tìm phương trình đường thẳng đi qua $A$ và cách $B$ một khoảng bằng $3$là:

    A. $3x+4y-17=0$ và $3x+7y-23=0$.
    B. $x+2y-7=0$và $3x-7y+5=0$

    C. $3x-4y-1=0$và $3x-7y+5=0$
    D. $3x+4y-17=0$.và $3x-4y-1=0$

    Câu 10: Trong mặt phẳng tọa độ vuông góc $Oxy$, cho hai đường thẳng ${{d}_{1}}: 2x-y-2=0$ và ${{d}_{2}}: 2x+4y-7=0$. Viết phương trình đường thẳng qua điểm $P\left( 3;1 \right)$ cùng với ${{d}_{1}}$, ${{d}_{2}}$ tạo thành tam giác cân có đỉnh là giao điểm của ${{d}_{1}}$ và ${{d}_{2}}$

    A. $\left[ \begin{align}
    &
    D. 3x+y-10=0 \\
    &
    D. x+3y=0 \\
    \end{align} \right.$.
    B. $\left[ \begin{align}
    &
    D. 3x-y-10=0 \\
    &
    D. x-3y=0 \\
    \end{align} \right.$.
    C. $\left[ \begin{align}
    &
    D. 2x+y-7=0 \\
    &
    D. x-2y-1=0 \\
    \end{align} \right.$.
    D. $\left[ \begin{align}
    &
    D. 3x+y-10=0 \\
    &
    D. x-3y=0 \\
    \end{align} \right.$.

    2.4. PHƯƠNG TRÌNH ĐƯỜNG TRÒN

    Câu 1: Trong mặt phẳng với hệ tọa độ $Oxy$ cho đường tròn $\left( C \right)$ có phương trình ${{x}^{2}}+{{y}^{2}}+2x+4y-4=0$. Tâm $I$ và bán kính $R$ của $\left( C \right)$ lần lượt là

    A. $I\left( 1;\,2 \right)$, $R=1$.
    B. $I\left( 1;\,-2 \right)$, $R=3$.
    C. $I\left( -1;\,-2 \right)$, $R=3$.
    D. $I\left( 2;\,-4 \right)$, $R=9$.

    Câu 2: Trong mặt phẳng $Oxy$, đường tròn nào sau đây đi qua điểm$A\left( 4;-2 \right)$?

    A. ${{x}^{2}}+{{y}^{2}}+2x-20=0$.
    B. ${{x}^{2}}+{{y}^{2}}-4x+7y-8=0$.
    C. ${{x}^{2}}+{{y}^{2}}-6x-2y+9=0$.
    D. ${{x}^{2}}+{{y}^{2}}-2x+6y=0$.

    Câu 3: Phương trình nào dưới đây là phương trình của đường tròn?

    A. ${{x}^{2}}+{{y}^{2}}+x+y+4=0$.
    B. ${{x}^{2}}-{{y}^{2}}+4x-6y-2=0$.
    C. ${{x}^{2}}+2{{y}^{2}}-2x+4y-1=0$.
    D. ${{x}^{2}}+{{y}^{2}}-4x-1=0$.

    Câu 4: Cho đường tròn $\left( C \right): {{x}^{2}}+{{y}^{2}}-2x+4y+1=0$. Chỉ ra mệnh đề sai trong các mệnh đề sau:

    A. $\left( C \right)$ có tâm $I\left( 1;\,-2 \right)$.
    B. $\left( C \right)$ đi qua $M\left( 1;\,0 \right)$.
    C. $\left( C \right)$ đi qua $A\left( 1;\,1 \right)$.
    D. $\left( C \right)$ có bán kính $R=2$.

    Câu 5: Cho đường tròn $\left( C \right)$ có tâm thuộc đường thẳng $
    D. \left\{ \begin{align}
    & x=1+2t \\
    & y=3-t \\
    \end{align} \right.$ và đi qua hai điểm $A\left( 1;1 \right)$ và $B\left( 0;-2 \right)$. Tính bán kính đường tròn $\left( C \right)$
    A. $R=\sqrt{565}$.
    B. $R=\sqrt{10}$.
    C. $R=2$.
    D. $R=25$.

    Câu 6: Trong mặt phẳng $Oxy$, cho đường tròn $\left( C \right): {{\left( x-3 \right)}^{2}}+{{\left( y-1 \right)}^{2}}=10$. Phương trình tiếp tuyến của $\left( C \right)$ tại điểm $A\left( 4;4 \right)$ là
    A. $x+3y-16=0$.
    B. $x+3y-4=0$.
    C. $x-3y+5=0$.
    D. $x-3y+16=0$.

    Câu 7: Cho đường tròn $\left( C \right): \,{{\left( x-1 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=10$ và đường thẳng $\Delta: x+y+1=0$ biết đường thẳng $\Delta $ cắt $\left( C \right)$ tại hai điểm phân biệt $A$, $B$. Độ dài đoạn thẳng $AB$ bằng
    A. $\frac{19}{2}$.
    B. $\sqrt{38}$.
    C. $\frac{\sqrt{19}}{2}$.
    D. $\frac{\sqrt{38}}{2}$.

    Câu 8: Cho đường tròn $\left( C \right): {{\left( x-1 \right)}^{2}}+{{\left( y+3 \right)}^{2}}=10$ và đường thẳng $\Delta: x+3y+m+1=0$. Đường thẳng $\Delta $ tiếp xúc với đường tròn $\left( C \right)$ khi và chỉ khi

    A. $m=1$ hoặc $m=-19$.
    B. $m=-3$ hoặc $m=17$.
    C. $m=-1$ hoặc $m=19$.
    D. $m=3$ hoặc $m=-17$.

    Câu 9: Cho đường tròn $\left( C \right): \,{{x}^{2}}+{{y}^{2}}-2x+2y-7=0$ và đường thẳng $
    D. \,x+y+1=0$. Tìm tất cả các đường thẳng song song với đường thẳng $
    D. và cắt đường tròn $\left( C \right)$ theo dây cung có độ dài bằng $2$.

    A. $x+y+4=0$ và $x+y-4=0$.
    B. $x+y+2=0$.
    C. $x+y+4=0$.
    D. $x+y+2=0$ và $x+y-2=0$.

    Câu 10: Cho đường tròn $\left( C \right): {{x}^{2}}+{{y}^{2}}+6x-2y+5=0$ và điểm $A\left( -4;2 \right)$. Đường thẳng $
    D. qua $A$ cắt $\left( C \right)$ tại $2$ điểm $M$, $N$ sao cho $A$ là trung điểm của $MN$ có phương trình là

    A. $x-y+6=0$.
    B. $7x-3y+34=0$.
    C. $7x-y+30=0$.
    D. $7x-y+35=0$

    2.5. ĐƯỜNG ELIP

    Câu 1: Trong các phương trình sau,phương trình nào là phương trình chính tắc của elip:

    A. $4x{}^\text{2}+8y{}^\text{2}=32$.
    B. $\frac{x{}^\text{2}}{\frac{1}{8}}+\frac{y{}^\text{2}}{\frac{1}{4}}=1$.
    C. $\frac{x{}^\text{2}}{64}+\frac{y{}^\text{2}}{16}=-1$.
    D. $\frac{x{}^\text{2}}{8}-\frac{y{}^\text{2}}{4}=1$.

    Câu 2: Elip $(E)$ có độ dài trục bé bằng $8$ và độ dài trục lớn bằng $12$ có phương trình chính tắc là:

    A. $\frac{x{}^\text{2}}{36}-\frac{y{}^\text{2}}{16}=1$.
    B. $\frac{x{}^\text{2}}{36}+\frac{y{}^\text{2}}{16}=1$.
    C. $\frac{x{}^\text{2}}{36}+\frac{y{}^\text{2}}{16}=-1$.
    D. $\frac{x{}^\text{2}}{144}+\frac{y{}^\text{2}}{64}=1$.

    Câu 3: Đường Elip $\left( E \right): \frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{6}=1$ có một tiêu điểm là:

    A. $\left( 0;3 \right)$.
    B. $(0\ ;\ \sqrt{3)}$.
    C. $(-\sqrt{3};0)$.
    D. $\left( 3;0 \right)$.

    Câu 4: Phương trình chính tắc của elip đi qua $A\left( 0;\,-4 \right)$ và có tiêu điểm $F\left( 3;\,0 \right)$ là:

    A. $\frac{x{}^\text{2}}{25}-\frac{y{}^\text{2}}{16}=1$.
    B. $\frac{x{}^\text{2}}{13}+\frac{y{}^\text{2}}{4}=1$.
    C. $\frac{x{}^\text{2}}{5}+\frac{y{}^\text{2}}{4}=1$.
    D. $\frac{x{}^\text{2}}{25}+\frac{y{}^\text{2}}{16}=1$.

    Câu 5: Tìm phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và có tiêu cự bằng $4\sqrt{3}$

    A. $\frac{{{x}^{2}}}{36}+\frac{{{y}^{2}}}{9}=1$.
    B. $\frac{{{x}^{2}}}{36}+\frac{{{y}^{2}}}{24}=1$.
    C. $\frac{{{x}^{2}}}{24}+\frac{{{y}^{2}}}{6}=1$.
    D. $\frac{{{x}^{2}}}{16}+\frac{{{y}^{2}}}{4}=1$.

    Câu 6: Cho elip có phương trình $16{{x}^{2}}+\text{ }25{{y}^{2}}=\text{ }100$. Tính tổng khoảng cách từ điểm $M$ thuộc elip có hoành độ bằng $2$ đến hai tiêu điểm.
    A. $\sqrt{3}.$
    B. $2\sqrt{2}.$
    C. $5$.
    D. $4\sqrt{3}.$

    Câu 7: Trong mặt phẳng ${Oxy}$,cho (E) có hai tiêu điểm F_1 (-4;0); F_2 (4;0) và đi qua điểm A(0;3). Điểm $M$ nào sau đây thuộc (E) thỏa$M{{F}_{1}}=3M{{F}_{2}}$.

    A. $M\left( -\frac{25}{8};\frac{\sqrt{551}}{8} \right)$.
    B. $M\left( \frac{25}{8};\frac{\sqrt{551}}{8} \right)$.
    C. $M\left( -\frac{25}{8};-\frac{\sqrt{551}}{8} \right)$.
    D. $M\left( \frac{25}{4};\frac{\sqrt{551}}{4} \right)$.

    Câu 8: Cho $\left( E \right): \frac{{{x}^{2}}}{20}+\frac{{{y}^{2}}}{16}=1$. Một đường thẳng đi qua điểm $A\left( 2;2 \right)$ và song song với trục hoành cắt $\left( E \right)$ tại hai điểm phân biệt $M$ và $N$. Tính độ dài $MN$.
    A. $3\sqrt{5}.$
    B. $15\sqrt{2}.$
    C. $2\sqrt{15}.$
    D. $5\sqrt{3}.$

    Câu 9: Lập phương trình chính tắc của elip $\left( E \right),$ biết đi qua điểm $M\left( \frac{3}{\sqrt{5}};\frac{4}{\sqrt{5}} \right)$ và $\Delta M{{F}_{1}}{{F}_{2}}$ vuông tại $M$.

    A. $\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{4}=1$.
    B. $\frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{36}=1$.
    C. $\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{9}=1$.
    D. $\frac{{{x}^{2}}}{36}+\frac{{{y}^{2}}}{9}=1$.

    Câu 10: Trong mặt phẳng với hệ toạ độ ${Oxy}$ cho elíp $\left( E \right): \frac{{{x}^{2}}}{9}+\frac{{{y}^{2}}}{4}=1$ và hai điểm $A\left( -3;2 \right)$,$B\left( -3;-2 \right)$ Tìm trên $\left( E \right)$ điểm $C$ sao cho tam giác ${ABC}$ có diện tích lớn nhất.

    A. $C\left( 0;3 \right)$.
    B. $C\left( 0;2 \right)$.
    C. $C\left( 3;0 \right)$.
    D. $C\left( 2;0 \right)$.

    3. BÀI TẬP TỰ LUẬN ÔN TẬP HỌC KÌ 2 TOÁN 10

    Bài 1: Giải các hệ phương trình:

    1. $\left\{ \begin{align} & \frac{5x+2}{3}\ge 4-x \\ & \frac{6-5x}{13}<3x+1 \\ \end{align} \right.$
    2. $\left\{ \begin{align} & x-1\le 2x-3 \\ & 3x<x+5 \\ & \frac{5-3x}{2}\le x-3 \\ \end{align} \right.$

    Bài 2: Giải các bất phương trình sau:

    1. $\left( 2-x \right)\left( 2{{x}^{2}}-5x+2 \right)\ge 0$
    2. $\frac{{{x}^{2}}+3x-1}{2-x}>-x$
    3. $\left| x+1 \right|\le \left| x \right|-x+2$
    4. $\frac{3-3x}{15-2x-{{x}^{2}}}\ge 1$

    Bài 3: Tìm giá trị của tham số để phương trình sau nghiệm đúng với mọi $x$:

    1. $mx^2 –10x –5 < 0$
    2. $(m + 1)x^2 –2(m – 1)x +3m – 3\ge 0$

    Bài 4: Tìm giá trị của tham số để phương trình sau vô nghiệm:

    • $5x^2 – x + m \le 0$
    • $mx^2 -10x -5 \ge 0$

    Bài 5: Cho phương trình: $(m-5){{x}^{2}}-4mx+m-2=0$ với giá nào của $m$ thì

    • Phương trình có nghiệm?
    • Phương trình có 2 nghiệm trái dấu?
    • Phương trình có hai nghiệm phân biệt?
    • Có hai nghiệm dương phân biệt?

    Bài 6: Với giá trị nào của $m$ thì hệ sau có nghiệm: $$\left\{ \begin{align} & {{x}^{2}}-9x+20\le 0 \\ & 3x-2m>0 \\
    \end{align} \right.$
    $\left\{ \begin{align}
    & {{x}^{2}}-5x+4>0 \\
    & m-2x\ge 0 \\
    \end{align} \right.$$

    Bài 7: Giải các phương trình và bất phương trình sau

    1. $\sqrt{{{x}^{2}}+3x+2}={{x}^{2}}+3x-4$
    2. $\sqrt{{{x}^{2}}-4x}<x-3$ $c)|x+1|+|x+3|=x+4$
    3. $\sqrt{{{x}^{2}}-2x-15}=x-3$
    4. $\frac{2}{2x_{{}}^{2}-5x+3}>\frac{1}{x_{{}}^{2}-9}$
    5. $\frac{x_{{}}^{2}-4x+3}{3-2x}<1-x$
    6. $\sqrt{3{{x}^{2}}+24x+22}\ge 2x+1$

    Bài 8:

    1. Cho $cosx =\frac{-3}{5}$ và $180^\circ < x < 270^\circ$. Tính giá trị của $\sin x, \tan x, \cot x$.
    2. Cho $tan \alpha=\frac{3}{4}$ và $\pi <\alpha <\frac{3\pi }{2}$. Tính $\cot\alpha \sin\alpha $ và $\cos\alpha $.

    Bài 9. Cho $0<\alpha <\frac{\pi }{2}$. Xét dấu các biểu thức sau:

    1. $\cos (\alpha +\pi )$
    2. $\tan(\alpha +\pi )$
    3. $\sin\left( \alpha +\frac{2\pi }{5} \right)$

    Bài 10. Rút gọn các biểu thức:

    • $A=\frac{1-2{{\cos }^{2}}x}{\sin x-\cos x}$
    • $B=\sqrt{{{\sin }^{2}}x(1+\cot x)+{{\cos }^{2}}(1+\tan x)}$

    Bài 11. Tính giá trị của biểu thức:

    • $A=\frac{\cot \alpha +\tan \alpha }{\cot \alpha -\tan \alpha }$ biết $\sin\alpha = \frac{3}{5}$ và $0 < \alpha <\frac{\pi }{2}$.
    • Cho $\tan \alpha =3$. Tính $\frac{2\sin \alpha +3\cos \alpha }{4\sin \alpha -5\cos \alpha }$; $\frac{3\sin \alpha -2\cos \alpha }{5{{\sin }^{3}}\alpha +4{{\cos }^{3}}\alpha }$.

    Bài 12. Chứng minh các đẳng thức sau:

    1. $\frac{\sin x}{1+\cos x}+\frac{1+\cos x}{\sin x}=\frac{2}{\sin x}$
    2. $\sin4x+\cos4x=1-2\sin2x\cos2x$
    3. $\frac{1}{\cos x}-\frac{\cos x}{1+\sin x}=\tan x$
    4. $\sin6x + \cos6x = 1 – 3\sin2x\cos2x$
    5. $\frac{{{\cos }^{2}}x-{{\sin }^{2}}x}{{{\cot }^{2}}x-{{\tan }^{2}}x}={{\sin }^{2}}x.{{\cos }^{2}}x$
    6. $\frac{1+{{\sin }^{2}}x}{1-{{\sin }^{2}}x}=1+2{{\tan }^{2}}x$

    Bài 13. Tính $\cos \left( \frac{\pi }{3}-\alpha \right)$ nếu $\sin \alpha =-\frac{12}{13}$ và $\frac{3\pi }{2}<\alpha <2\pi $.

    Bài 14. Chứng minh rằng:

    1. $\frac{1-\tan x}{1+\tan x}=\tan \left( \frac{\pi }{4}-x \right)$
    2. $\frac{1+\tan x}{1-\tan x}=\tan \left( \frac{\pi }{4}+x \right)$

    Bài 15. Tính giá trị của các biểu thức

    • $A=\sin \frac{\pi }{24}.\cos \frac{\pi }{24}.\cos \frac{\pi }{12}.\cos \frac{\pi }{6}$
    • $B=2{{\cos }^{2}}{{75}^{0}}-1$
    • $C=\left( \cos {{15}^{0}}-\sin {{15}^{0}} \right).\left( \cos {{15}^{0}}+\sin {{15}^{0}} \right)$

    Bài 16. Rút gon biểu thức:

    • $A=\frac{\sin 2\alpha +\sin \alpha }{1+\cos 2\alpha +\cos \alpha }$
    • $B=\frac{4{{\sin }^{2}}\alpha }{1-{{\cos }^{2}}\frac{\alpha }{2}}$
    • $\frac{1+\cos \alpha -\sin \alpha }{1-\cos \alpha -\sin \alpha }$

    Bài 17. Chứng minh biểu thức sau không phụ thuộc vào $\alpha ,\beta $:

    1. $\sin 6\alpha. \cot 3\alpha -\cos 6\alpha $
    2. $(\tan \alpha -\tan \beta )\cot (\alpha -\beta )-\tan \alpha. \tan \beta $
    3. $\left( \cot \frac{\alpha }{3}-\tan \frac{\alpha }{3} \right).\tan \frac{2\alpha }{3}$

    Bài 18. Cho biết trung điểm ba cạnh của một tam giác là $M1(2; 1); M2 (5; 3); M3 (3; -4)$. Lập phương trình tổng quát của đường thẳng chứa mỗi cạnh của tam giác đó.

    Bài 19. Trong mặt phẳng tọa độ cho tam giác với $M (-1; 1)$ là trung điểm của một cạnh, hai cạnh kia có phương trình là: $x + y -2 = 0$ và $2x + 6y +3 = 0$. Xác định tọa độ các đỉnh của tam giác.

    Bài 20. Lập phương trình tổng quát của đường thẳng $d$ trong các trường hợp sau:

    • $d$ đi qua điểm $M (1; -2)$ và vuông góc với đường thẳng $\Delta: 3x + y = 0$
    • $d$ đi qua gốc tọa độ và song song với đường thẳng $\left\{ \begin{align} & x=2-5t \\ & y=1+t \\ \end{align} \right.$

    Bài 21. Xét vị trí tương đối của mỗi cặp đường thẳng sau:

    • $d_1: 2x – 5y +6 = 0$ và $d_2: – x + y – 3 = 0$
    • $d_1: \left\{ \begin{align} & x=-1-5t \\ & y=2+4t \\ \end{align} \right.$ và $d_2: \left\{ \begin{align}
      & x=-6+5u \\ & y=2-4u \\ \end{align} \right.$
    • $d_1: 8x + 10y – 12 = 0$ và $d_2: \left\{ \begin{align} & x=-6+5t \\
      & y=6-4t \\ \end{align} \right.$

    Bài 22. Cho điểm $M(1; 2)$ và đường thẳng $d: 2x – 6y + 3 = 0$. Viết ptrình đường thẳng $d’$ đi qua $M$ và tạo với $d$ một góc $45^\circ$.

    Bài 23. Cho hai điểm $M(2; 5)$ và $N(5; 1)$. Viết phương trình đường thẳng $d$ đi qua $M$ và cách điểm $N$ một khoảng bằng $3$.

    Bài 24. Cho đường thẳng $\Delta: 2x – y – 1 = 0$ và điểm $M(1; 2)$.

    1. Viết phương trình đường thẳng $(\Delta’) $ đi qua $M$ và vuông góc với $\Delta $.
    2. Tìm tọa độ hình chiếu $H$ của $M$ trên $\Delta $.
    3. Tìm điểm $M’$ đối xứng với $M$ qua $\Delta $.

    Bài 25. Cho đường thẳng $\Delta $ có phương trình tham số: $\left\{ \begin{align} & x=2+2t \\ & y=3+t \\
    \end{align} \right.$

    • Tìm điểm $M$ nằm trên $\Delta $ và cách điểm $A(0 ;1)$ một khoảng bằng $5$.
    • Tìm tọa độ giao điểm của đường thẳng $\Delta $ với đường thẳng $x + y + 1 = 0$.
    • Tìm điểm $M$ trên $\Delta $ sao cho $AM$ là ngắn nhất.

    Bài 26. Cho phương trình $$x^2 + y2 – 2mx – 2(m- 1)y + 5 = 0 $$ với $m$ là tham số. Với giá trị nào của $m$ thì phương trình trên là phương trình đường tròn? Khi đó hãy tìm tọa độ tâm và bán kính của đường tròn theo $m$.

    Bài 27. Viết phương trình đường tròn đi qua 3 điểm $A(2; 0); B(0; – 1)$ và $C(- 3; 1)$.

    Bài 28. Tìm tọa độ giao điểm của đường thẳng $\Delta: \left\{ \begin{align} & x=1+2t \\ & y=-2+t \\ \end{align} \right.$ và đường tròn $(C): (x – 1)^2 + (y – 2)^2 = 16$.

    Bài 29. Viết phương trình đường tròn đi qua $A(1; 1), B(0; 4)$ và có tâm thuộc đường thẳng $d: x – y – 2 = 0$.

    Bài 30. Viết phương trình đường tròn đi qua $A(2; 1), B(-4;1)$ và có bán kính $R=10$.

    Bài 31. Viết phương trình tiếp tuyến với đường tròn $(C ): {{(x-2)}^{2}}+{{(y-1)}^{2}}=13$ tại điểm $M$ thuộc đường tròn có hoành độ bằng 2.

    Bài 32. Cho đường tròn $(C): {{x}^{2}}+{{y}^{2}}-2x+6y+5=0$ và đường thẳng $d: 2x + y – 1 = 0$. Viết phương trình tiếp tuyến $\Delta $ biết $\Delta $ song song với $d$. Tìm tọa độ tiếp điểm.

    Bài 33. Cho đường tròn $(C): {{x}^{2}}+{{y}^{2}}-6x+2y+6=0$ và điểm $A(1; 3)$.

    • Chứng minh rằng $A$ nằm ngoài đường tròn $(C).$
    • Viết phương trình tiếp tuyến của $(C)$ kẻ từ $A$.
    • Viết phương trình tiếp tuyến của $(C )$ biết tiếp tuyến vuông góc với đường thẳng $d: 3x – 4y + 1 = 0$.
  • XÁC ĐỊNH HỆ SỐ HÀM SỐ BẬC 2 BẰNG MÁY TÍNH CASIO

    XÁC ĐỊNH HỆ SỐ HÀM SỐ BẬC 2 BẰNG MÁY TÍNH CASIO

    XÁC ĐỊNH HỆ SỐ HÀM SỐ BẬC 2 BẰNG MÁY TÍNH CASIO

    Hướng dẫn cách tìm các hệ số $a,b,c$ của hàm số hậc hai $y=ax^2+bx+c$ bằng máy tính biết parabol đi qua 3 điểm có tọa độ cụ thể cho trước.

    MUA MÁY TÍNH CASIO 580VNX GIÁ TỐT

    Xem thêm: Đề thi học kì 1 Toán 10 Xuân Trường B năm 2020

    Phương pháp xác định hệ số hàm số bậc 2 bằng máy tính

    https://www.youtube.com/watch?v=q_sXAtPfm3M&feature=emb_logo

    Phương pháp nhanh lập phương trình parabol đi qua ba điểm bằng máy tính CASIO fx 580 VNX hoặc máy tính VINACAL

    • Toán 10 lập phương trình hàm số bậc hai biết parabol đi qua ba điem có tọa độ cho trước. (Tìm phương trình parabol đi qua 3 điểm bằng máy tính cầm tay CASIO, VINACAL)
    • Xác định tìm phương trình của parabol biết tọa độ đỉnh, trục đối xứng và tọa độ một điểm đi qua.
    • Hướng dẫn giải đề thi thử đại học THPTQG môn toán năm 2021 trường Lương Thế Vinh Hà Nội và Trần Phú Hà Tĩnh
    • Một vật chuyển động trong 4 giờ với vận tốc v (km/ h) phụ thuộc thời gian t (h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật đi được trong 4 giờ kể từ lúc xuất phát.
    • Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là AB = 8m. Người ta treo một tấm phông hình chữ nhật có hai đỉnh M,N nằm trên Parbol và hai đỉnh P,Q nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho 1 m2 cần số tiền mua hoa là 200.000 đồng cho 1 m2 . Biết MN = 4m,MQ = 6m. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng gần với số tiền nào sau đây?
      • A. 3.735.300 đồng.
      • B. 3.437.300 đồng.
      • C. 3.734.300 đồng.
      • D. 3.733.300 đồng.

    Ở bài viết xác định nhanh các hệ số hàm số bậc 2 trên casio fx 580vnx ta đã biết cách sử dụng máy tính cầm tay CASIO fx 580VNX để tìm các hệ số của một hàm số bậc 2, mời các bạn cùng thực hành thao tác trên máy tính với bài toán tương tự trích trong một đề thi học kỳ.

  • So sánh 1 số với 2 nghiệm của phương trình bậc hai

    So sánh 1 số với 2 nghiệm của phương trình bậc hai

    So sánh 1 số với 2 nghiệm của phương trình bậc hai

    Để so sánh một số với hai nghiệm của phương trình bậc hai, chúng ta sử dụng định lý đảo về dấu tam thức bậc hai.

    1. So sánh 1 số với 2 nghiệm của phương trình bậc hai

    Cho tam thức bậc hai $ f(x)=ax^2+bx+c $, với $ a\ne 0 $, có hai nghiệm phân biệt $ x_1<x_2 $ và một số $ \alpha$. Khi đó, ta có các kết quả sau

    1.1. Số α nằm trong khoảng hai nghiệm

    • Số $\alpha$ nằm giữa hai nghiệm, tức là $ x_1<\alpha<x_2 $ điều kiện cần và đủ là $$a\cdot f(\alpha)<0$$

    1.2. Số α nằm ngoài khoảng hai nghiệm

    • Số $\alpha$ nằm về bên trái hai nghiệm $x_1,x_2$ (nói cách khác, số $\alpha$ bé hơn hai nghiệm), tức là $ \alpha<x_1<x_2$ điều kiện cần và đủ là $$\begin{cases} \Delta >0\\ a\cdot f(\alpha)>0\\ \alpha<\frac{S}{2} \end{cases}$$
    • Số $\alpha$ nằm về bên phải hai nghiệm $x_1,x_2$, (nói cách khác, số $\alpha$ lớn hơn hai nghiệm)tức là $ x_1<x_2<\alpha$ điều kiện cần và đủ là  $$ \begin{cases}
      \Delta >0\\ a\cdot f(\alpha)>0\\ \frac{S}{2}<\alpha \end{cases}$$

    1.3. So sánh nghiệm của phương trình bậc hai với số 0

    Đặc biệt, khi $\alpha=0$ chúng ta có các bài toán:

    • Tìm điều kiện để phương trình có hai nghiệm trái dấu: Tức là $x_1<0<x_2$, khi đó $f(\alpha) = f(0) =c$ nên điều kiện cần và đủ là $$ac<0$$
    • Tìm điều kiện để phương trình có hai nghiệm dương phân biệt khi và chỉ khi  $$ \begin{cases} \Delta >0\\ ac>0\\ -\frac{b}{a}>0\end{cases}$$
    • Tìm điều kiện để phương trình có hai nghiệm âm phân biệt khi và chỉ khi  $$ \begin{cases} \Delta >0\\ ac>0\\ -\frac{b}{a}<0\end{cases}$$

    Đôi khi, người ta còn đặt tổng 2 nghiệm là $x_1+x_2=S=-\frac{b}{a}$, tích hai nghiệm là $x_1 x_2=P=\frac{c}{a}$ thì các điều kiện trên trở thành:

    • Phương trình bậc 2 có hai nghiệm trái dấu khi và chỉ khi $P<0$.
    • Phương trình bậc 2 có hai nghiệm cùng dấu khi và chỉ khi $$ \begin{cases} \Delta >0\\ P>0\end{cases}$$
    • Phương trình bậc 2 có hai nghiệm dương phân biệt khi và chỉ khi  $$ \begin{cases} \Delta >0\\ P>0\\ S>0\end{cases}$$
    • Phương trình bậc 2 có hai nghiệm âm phân biệt khi và chỉ khi  $$ \begin{cases} \Delta >0\\ P>0\\ S<0\end{cases}$$

    2. So sánh nghiệm với hai số cho trước α < β

    • Phương trình có hai nghiệm thỏa mãn ${{x}_{1}}<\alpha <\beta <{{x}_{2}}\Leftrightarrow \left\{ \begin{align}   & af(\alpha )<0 \\ & af(\beta )<0 \\ \end{align} \right.$
    • Phương trình có hai nghiệm thỏa mãn ${{x}_{1}}<\alpha <{{x}_{2}}<\beta \Leftrightarrow \left\{ \begin{align}   & af(\alpha )<0 \\ & af(\beta )>0 \\ \end{align} \right.$
    • Phương trình có hai nghiệm thỏa mãn $\alpha <{{x}_{1}}<\beta <{{x}_{2}}\Leftrightarrow \left\{ \begin{align}   & af(\alpha )>0 \\  & af(\beta )<0 \\ \end{align} \right.$
    • Phương trình có hai nghiệm phân biệt và chỉ có một nghiệm thuộc khoảng $(\alpha;\beta)$ khi và chỉ khi $$f(\alpha).f(\beta) < 0$$
    • Phương trình có hai nghiệm phân biệt và $\alpha <{{x}_{1}}<{{x}_{2}}<\beta \Leftrightarrow \left\{ \begin{align}   & \Delta >0 \\  & af(\alpha )>0 \\  & af(\beta )>0 \\  & \frac{S}{2}-\alpha >0 \\  & \frac{S}{2}-\beta <0 \\ \end{align} \right.$

    3. Ví dụ về so sánh nghiệm phương trình bậc hai với một số

    Ví dụ 1. Tìm $m$ để phương trình: ${{x}^{2}}-2mx+m+2=0$

    • Có hai nghiệm trái dấu;
    • Có hai nghiệm cùng lớn hơn $1$.

    Hướng dẫn.

    • Phương trình có hai nghiệm trái dấu khi và chỉ khi $$P=\frac{c}{a}=m+2<0\Leftrightarrow m<-2$$
      Vậy $m<-2$ là giá trị cần tìm.
    • Phương trình có hai nghiệm ${{x}_{1}},{{x}_{2}}$ cùng lớn hơn 1 khi và chỉ khi $$ \begin{cases} \Delta >0\\ a.f(1)>0\\
      {-b}{2a}>0 \end{cases} $$ Giải hệ này ta tìm được đáp số $2\leqslant m<3$.

    Cách khác, không sử dụng định lý đảo về dấu tam thức bậc hai, mà chúng ta sử dụng định lí Viète:

    • Phương trình có hai nghiệm $x_1,x_2$ khi và chỉ khi $$\Delta’={{m}^{2}}-m-2\geqslant 0\Leftrightarrow m\in (-\infty,-1]\cup[2,+\infty)$$
    • Khi đó, cả hai nghiệm của phương trình đều lớn hơn $ 1$, tức là $ x_1-1>0$ và $ x_2-1>0$. Do đó, chúng ta có \begin{align*}
      \begin{cases} x_1-1>0\\ x_2-1>0 \end{cases} \Leftrightarrow \begin{cases}  (x_1-1)(x_2-1)>0\\ (x_1-1)+(x_2-1)>0
      \end{cases}\end{align*}
    • Nhân ra và sử dụng Viète, thay $ x_1x_2=m+2$ và $ x_1+x_2=2m$ chúng ta được hệ \begin{align}
      \begin{cases} m+2-2m+1>0\\2m-2>0 \end{cases} \Leftrightarrow 1<m<3 \end{align}
      Kết hợp với điều kiện ta có $2\leqslant m<3$ là những giá trị cần tìm.

    Ví dụ 2.  Cho phương trình $ {x^2} + 2mx – 3{m^2} = 0$. Tìm $ m$ để phương trình có hai nghiệm $ x_1, x_2$ thoả mãn $ {x1} < 1 < {x_2}.$
    Hướng dẫn. Đặt $ f\left( x \right) = {x^2} + 2mx – 3{m^2}$. Yêu cầu bài toán tương đương với
    $$ af\left( 1 \right) < 0 \Leftrightarrow 1 \cdot f\left( 1 \right) < 0 \Leftrightarrow {1^2} + 2m – 3{m^2} < 0 \Leftrightarrow – 3{m^2} + 2m + 1 < 0 \Leftrightarrow \left[ \begin{array}{l} m > 1\\ m < – \frac{1}{3} \end{array} \right. $$.

    Ví dụ 3. Cho phương trình $ {x^2} + 2mx – 3{m^2} = 0$. Tìm m để phương trình có hai nghiệm $ x_1, x_2$ và số $ \alpha =1$ nằm ngoài khoảng hai nghiệm.

    Hướng dẫn. Đặt $ f\left( x \right) = {x^2} + 2mx – 3{m^2}$. Ta có $ \Delta ‘ = {m^2} – \left( { – 3{m^2}} \right) = 4{m^2}$.
    Yêu cầu bài toán tương đương
    $$ \left\{ \begin{array}{l} \Delta ‘ > 0\\ af\left( \alpha \right) > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} 4{m^2} > 0\\ – 3{m^2} + 2m + 1 > 0 \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} m \ne 0\\ – \frac{1}{3} < m < 1 \end{array} \right. $$.

    4. Bài tập so sánh nghiệm phương trình bậc hai

    Bài 1. Tìm giá trị của $ m $ để phương trình sau có nghiệm cùng dấu. Khi đó hai nghiệm mang dấu gì?

    • $ x^2-2mx+5m-4=0; $
    • $ mx^2+mx+3=0. $

    Bài 2. Tìm $ m $ để phương trình $ (m+1)x^2+2(m+4)x+m+1=0 $ có một nghiệm, hai nghiệm phân biệt cùng dấu, hai nghiệm âm phân biệt?

    Bài 3. Tìm $ m $ để phương trình $ (m-4)x^2-2(m-2)x+m-1=0 $ có hai nghiệm cùng dấu, hai nghiệm trái dấu và nghiệm âm có giá trị tuyệt đối lớn hơn, đúng một nghiệm dương, hai nghiệm đối nhau?

    Bài 4. Tìm $m$ để phương trình $ mx^2-2(m-3)x+m-4=0 $ có đúng một nghiệm không dương.

    Bài 5. Tìm $ m $ để phương trình $ (m+1)x^2-2x+m-1=0 $ có ít nhất một nghiệm không âm.

    Bài 6. So sánh số $1$ với nghiệm của phương trình $ 2x^2 – 18x + 17 = 0$ [TD10BD70]
    Bài 7. So sánh số $- 2$ với nghiệm của phương trình $f(x) = (m^2 + 1)x^2 – 5(m^2 + 1)x – m^2 + m – 1 = 0$ [TD11BD70]
    Bài 8. Tìm $ m$ để các phương trình sau có hai nghiệm

    • $ mx^2 + (m – 1)x + 3 – 4m = 0$ và thoả mãn $ x_1 < 2 < x_2$ [VD1TTM19]
    • $ (m + 1)x^2 – (m – 3)x + m + 1 = 0$ và thoả mãn $ -1 < x_1 \leqslant x_2$
    • $ (m + 1)x^2 + mx + 3 = 0$ và thoả mãn $ x_1 < – 2 < 1 < x_2$ [VD-TTM27]
    • $ x^2 – 2mx + m = 0$ và thoả mãn $ x_1, x_2\in (-1;3)$
    • $ x^2 – 2x – 3m = 0$ và thoả mãn $\frac{m}{2}\le {{x}_{1}}<1<{{x}_{2}}$

    Bài 9. Tìm $ m$ để phương trình sau có nghiệm

    • $ (x^2 + 2x)2 – 4m(x^2 + 2x) + 3m + 1 = 0$ [VD1TTM23]
    • $ x^4 + mx^3 + 2mx^2 + mx + 1 = 0$ [VD!TTM31]

    Bài 10. Tìm $ m$ để phương trình $ (m + 1)x^2 – 3mx + 4m = 0$ có duy nhất một nghiệm lớn hơn $ 1$.

    Bài 11. Cho phương trình $ x^2 – (2m – 3)x + m2 – 3m = 0$. Xác định $ m$ để phương trình có hai nghiệm $ x_1 ; x_2$ thoả mãn $ 1 < x_1 < x_2 < 6$.

    Bài 12. Cho phương trình $ 2x^2 + (2m – 1)x + m – 1 = 0$. Xác định $ m$ để phương trình có hai nghiệm phân biệt $ x_1 ; x_2$ thoả mãn: $ – 1 < x_1 < x_2 < 1.$

    Bài 13. Cho $ f(x) = x^2 – 2(m + 2)x + 6m + 1.$

    • Chứng minh rằng phương trình $ f(x) = 0$ có nghiệm với mọi $ m$.
    • Đặt $ x = t + 2$. Tính $ f(x)$ theo $ t$, từ đó tìm điều kiện đối với $ m$ để phương trình $ f(x) = 0$ có hai nghiệm lớn hơn $ 2$.

    Bài 14. Cho phương trình bậc hai: $ x^2 + 2(a + 3)x + 4(a + 3) = 0$.

    • Với giá trị nào của tham số $ a$, phương trình có nghiệm kép. Tính các nghiệm kép.
    • Xác định $ a$ để phương trình có hai nghiệm phân biệt lớn hơn $ – 1$.

    Bài 15. Cho phương trình: $ x^2 + 2(m – 1)x – (m + 1) = 0$.

    • Tìm giá trị của $ m$ để phương trình có một nghiệm nhỏ hơn $ 1$ và một nghiệm lớn hơn $ 1$.
    • Tìm giá trị của $ m$ để phương trình có hai nghiệm nhỏ hơn $ 2$.

    Bài 16. Tìm $m$ để phương trình: $ x^2 – mx + m = 0$ có nghiệm thoả mãn $ x_1 \leqslant – 2 \leqslant x_2$

    Bài 17. Cho biểu thức \[ A=\left(1-\frac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{\sqrt{x}+2}{3-\sqrt{x}}+\frac{\sqrt{x}+2}{x-5\sqrt{x}+6}\right). \] Tìm $ m $ để có $ x $ thoả mãn $ A(\sqrt{x}+1)=m(x+1)-2 $.

    Bài 18. Tìm $ m $ để có $ x<0 $ sao cho \[ m=\frac{x(1-x^2)^2}{1+x^2}:\left[\left(\frac{1-x^3}{1-x}+x\right)\left(\frac{1+x^3}{1+x}-x\right)\right]. \]

    Bài 19. Tìm $ m $ để có $ x<0 $ sao cho \[ m=\sqrt{x}-\frac{\sqrt{4x}-9}{x-5\sqrt{x}+6}+\frac{2\sqrt{x}+1}{3-\sqrt{x}}+\frac{\sqrt{x}+3}{\sqrt{x}-2}. \]

  • Lý thuyết và bài tập dấu tam thức bậc hai

    Lý thuyết và bài tập dấu tam thức bậc hai

    Lý thuyết và bài tập dấu tam thức bậc hai

    Sử dụng kiến thức về dấu tam thức bậc hai, chúng ta có thể giải quyết được 2 dạng toán quan trọng sau:

    1. Tam thức bậc hai là gì?

    Tam thức bậc hai đối với biến $x$ là biểu thức có dạng $$f(x) = ax^2+ bx + c,$$ trong đó $a, b, c$ là những hệ số, $a \ne  0$.

    2. Định lí về dấu của tam thức bậc hai

    2.1. Định lí dấu tam thức bậc hai

    Cho tam thức bậc hai $ f(x)=ax^2+bx+c $ với $ a\ne 0 $ có $ \Delta=b^2-4ac $. Khi đó, có ba trường hợp xảy ra:

    • $ \Delta <0 $: $ f(x) $ cùng dấu với hệ số $ a $ với mọi $ x\in \mathbb{R}, $
    • $ \Delta =0 $: $ f(x) $ cùng dấu với hệ số $ a $ với mọi $ x\ne -\frac{b}{2a}, $
    • $ \Delta >0 $: $ f(x) $ có hai nghiệm phân biệt $ x_1,x_2 $ (giả sử $ x_1<x_2 $), và dấu của $ f(x) $ xác định bởi quy tắc trong trái — ngoài cùng, nghĩa là ở giữa hai số $0$ thì thì $ f(x) $ và hệ số $ a $ trái dấu, còn bên ngoài hai số $0$ thì cùng dấu.

    bảng xét dấu tam thức bậc hai

    2.2. Minh họa hình học của định lý dấu tam thức bậc hai

    Định lí về dấu của tam thức bậc hai có minh họa hình học sau

    định lí về dấu tam thức bậc hai

    2.3. Ứng dụng định lí dấu của tam thức bậc hai

    Nhận xét rằng trong cả hai trường hợp $ a>0 $ và $ a<0 $ thì

    • $ f(x) $ luôn có đủ hai loại dấu cả âm và dương nếu $ \Delta >0, $
    • $ f(x) $ chỉ có một loại dấu hoặc âm hoặc dương nếu $ \Delta \leqslant 0. $

    Do đó, chúng ta có các bài toán sau đây, với $ f(x)=ax^2+bx+c $ trong đó $ a\ne 0 $:

    • $ f(x) >0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta <0\\ a>0 \end{cases}$
    • $ f(x) <0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta <0\\ a<0 \end{cases}$
    • $ f(x) \geqslant 0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \leqslant 0\\ a>0 \end{cases}$
    • $ f(x) \leqslant 0\, \forall x\in \mathbb{R} \Leftrightarrow \begin{cases} \Delta \leqslant 0\\ a<0 \end{cases}$

    Chi tiết về vấn đề này, xin mời các em học sinh xem trong bài giảng Tìm điều kiện để tam thức bậc hai luôn dương, luôn âm

    2.4. Định lí đảo dấu tam thức bậc hai

    Cho tam thức bậc hai $ f(x)=ax^2+bx+c $, với $ a\ne 0 $, có hai nghiệm phân biệt $ x_1<x_2 $ và một số $ \epsilon $. Khi đó, ta có các kết quả sau

    • $ x_1<\epsilon <x_2 \Leftrightarrow a\cdot f(\epsilon)<0$
    • $ \epsilon <x_1<x_2 \Leftrightarrow \begin{cases}
      \Delta >0\\
      a\cdot f(\epsilon)>0\\
      \epsilon <\frac{S}{2}
      \end{cases}$
    • $ x_1<x_2<\epsilon \Leftrightarrow \begin{cases}
      \Delta >0\\
      a\cdot f(\epsilon)>0\\
      \frac{S}{2}<\epsilon
      \end{cases}$

    Ứng dụng của định lí đảo là dùng để so sánh một số với hai nghiệm của phương trình bậc hai. Chi tiết vấn đề này, mời các em tham khảo bài So sánh 1 số với 2 nghiệm của phương trình bậc hai

    3. Bài tập về dấu tam thức bậc hai

    Bài 1.  Xét dấu các tam thức sau

    1. $ f(x)=x^2-5x+6$
    2. $ g(x)=-x^2+4x+5$
    3. $ h(x)=6x^2+x+4$

    Hướng dẫn.

    1. Tam thức bậc hai $f(x)$ có hệ số $ a=6$ và có hai nghiệm $ x_1=2,x_2=3 $ nên có bảng xét dấu như sau:bảng xét dấu của tam thức bậc hai f(x)
    2. Tam thức bậc hai $ g(x)=-x^2+4x+5$ có hệ số $ a=-1$ và có hai nghiệm $ x_1=-1,x_2=5 $ nên có bảng xét dấu như sau: bảng xét dấu của g(x)
    3. Tam thức bậc hai $ h(x)=6x^2+x+4$ có hệ số $ a=6$ và có $ \Delta <0$ nên có bảng xét dấu như sau: bảng xét dấu của hx

    Bài 2. Giải các bất phương trình sau

    1. $x^2-2x+3>0$
    2. $x^2+9>6x$
    3. $6x^2-x-2 \geqslant 0$
    4. $\frac{1}{3}x^2+3x+6<0$
    5. $\dfrac{x^2+1}{x^2+3x-10}<0$
    6. $\dfrac{10-x}{5+x^2}>\dfrac{1}{2}$
    7. $\dfrac{x+1}{x-1}+2>\dfrac{x-1}{x}$
    8. $\dfrac{1}{x+1}+\dfrac{2}{x+3}<\dfrac{3}{x+2}$

    Hướng dẫn. Để giải các bất phương trình hữu tỉ, chúng ta biến đổi (rút gọn, quy đồng giữ lại mẫu) để được một bất phương trình tích, thương các nhị thức bậc nhất và tam thức bậc hai. Sau đó lập bảng xét dấu và căn cứ vào đó để kết luận.

    1. $x^2-2x+3>0.$
      Bất phương trình này chỉ gồm một tam thức bậc hai nên chúng ta lập bảng xét dấu luôn, được kết quả như sau:bảng xét dấu bất phương trình bậc hai
      Từ bảng xét dấu, chúng ta có tập nghiệm của bất phương trình là $\mathbb{R}$.
    2. $x^2+9>6x$. Biến đổi bất phương trình đã cho thành $$x^2+9-6x>0$$ Bảng xét dấu của vế trái như sau: bat phuong trinh bac hai 2
      Suy ra, tập nghiệm của bất phương trình đã cho là $\mathbb{R}\setminus \{0\}$.
    3. $6x^2-x-2 \geqslant 0$. Lập bảng xét dấu cho vế trái, ta được: bat phuong trinh đa thuc
      Suy ra, tập nghiệm của bất phương trình đã cho là $ S=\left(-\infty;-\frac{1}{2}\right]\cup \left[\frac{2}{3};+\infty\right)$.
    4. $\frac{1}{3}x^2+3x+6<0$. Bảng xét dấu của vế trái: bất phương trình hữu tỉ
      Kết luận, tập nghiệm của bất phương trình là $S=(-6;-3)$.
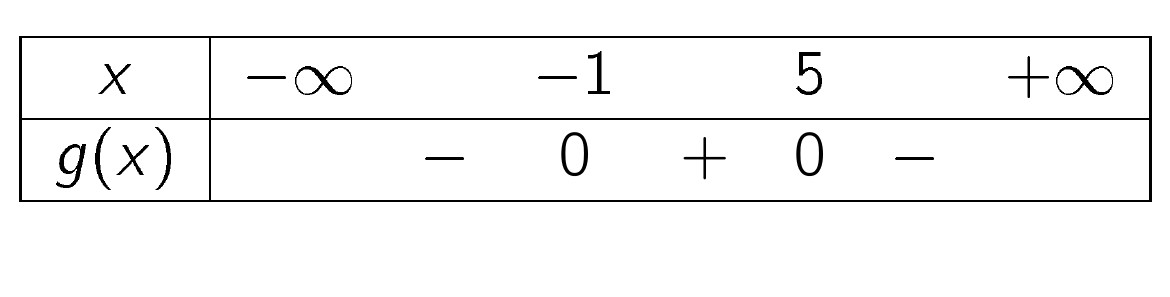
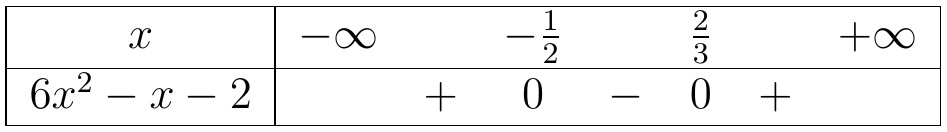
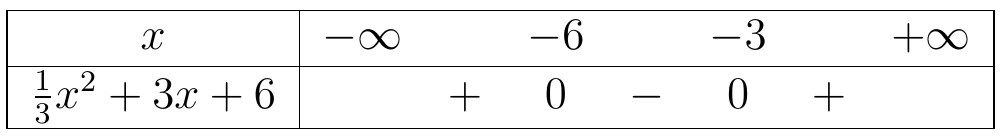
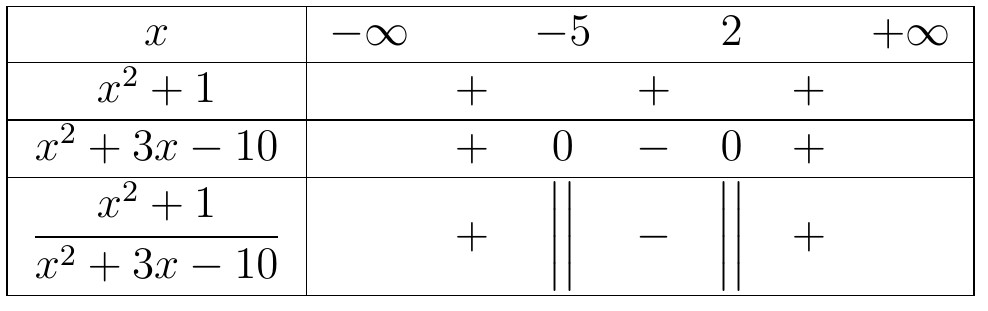    5. $\dfrac{x^2+1}{x^2+3x-10}<0$. Lập bảng xét dấu cho vế trái, chúng ta có bảng sau: bất phương trình phân thức hữu tỉKết luận, tập nghiệm của bất phương trình là $S=(-5;2)$.
    6. $\dfrac{10-x}{5+x^2}>\dfrac{1}{2}$. Chuyển vế, quy đồng giữ lại mẫu của bất phương trình đã cho, ta được bất phương trình tương đương $$\frac{-x^{2}-2x+15}{2\left( x^{2}+5\right) }>0$$ Lập bảng xét dấu cho vế trái bất phương trình này, ta được bảng sau:bất phương trình thươngKết luận, tập nghiệm của bất phương trình là $S=(-5;3)$.
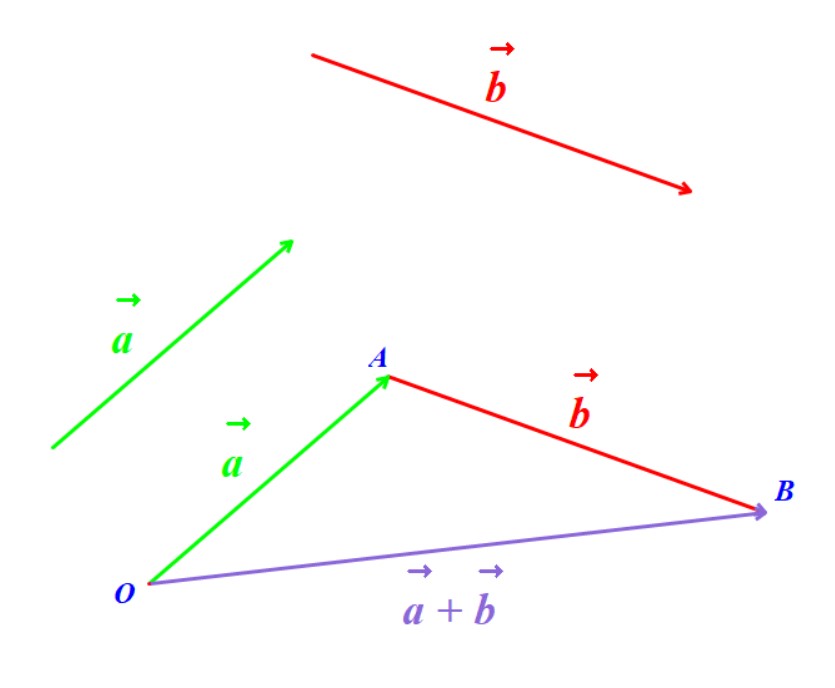
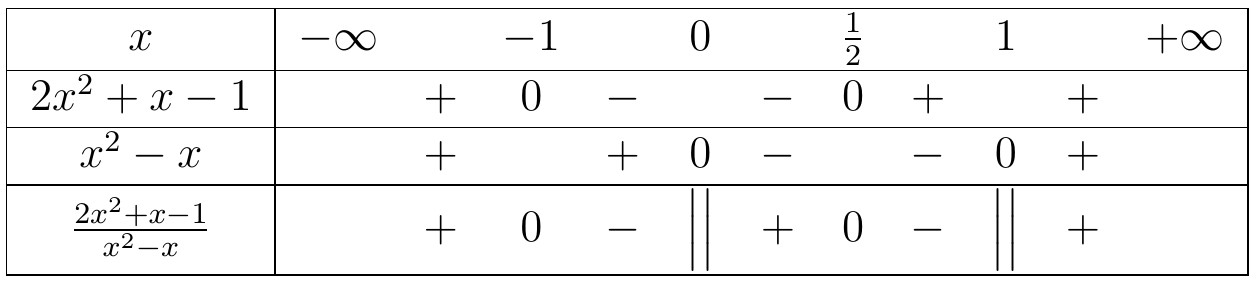    7. $\dfrac{x+1}{x-1}+2>\dfrac{x-1}{x}$. Chuyển vế, quy đồng giữ mẫu của bất phương trình này, ta được bất phương trình tương đương: $$\frac{2x^{2}+x-1}{x^{2}-x}>0$$Lập bảng xét dấu cho vế trái, ta được: bất phương trình hữu tỉKết luận, tập nghiệm của bất phương trình đã cho là $S= \left( -\infty ,-1\right) \cup \left( 0,\frac{1}{2}\right) \cup \left( 1,+\infty \right) $.
    8. $\dfrac{1}{x+1}+\dfrac{2}{x+3}<\dfrac{3}{x+2}$. Chuyển vế, quy đồng ta được bất phương trình tương đương: $$\frac{-x+1}{\left( x+3\right) \left( x+2\right) \left( x+1\right) }<0$$ Lập bảng xét dấu cho vế trái, ta được:bất phương trình chứa ẩn ở mẫu sử dụng tam thức bậc hai
      Căn cứ vào bảng xét dấu, chúng ta có tập nghiệm của bất phương trình đã cho là $S=\left( -\infty ,-3\right) \cup \left( -2,-1\right) \cup \left( 1,+\infty \right) $.

    Bài 3. Tìm các giá trị của tham số $m$ để các phương trình sau có 2 nghiệm dương phân biệt

    1. $(m^2+m+1)x^2+(2m-3)x+m-5=0$
    2. $x^2-6mx+2-2m+9m^2=0$

    Bài 4. Tìm $m$ để các bất phương trình sau vô nghiệm.

    1. $5x^2-x+m\leqslant 0$
    2. $mx^2-10x-5\geqslant 0$
    3. $(m-1)x^{2}-(2m+1)x>m-3$
    4. $x^{2}-2mx+m+12<0$
    5. $-2x^{2}-mx+m^{2}-1>0$
    6. $x^{2}+3mx-9<0$
    7. $2mx^{2}+x-3\geqslant 0$
    8. $x^{2}+3x-9m\leqslant 0$

    Bài 5. Tìm $m$ để các bất phương trình sau có nghiệm duy nhất.

    1. $x^{2}-2mx+m+12\leqslant 0$
    2. $-2x^{2}-mx+m^{2}-1\geqslant 0$
    3. $x^{2}+3mx-9\leqslant 0$
    4. $x^{2}+3x-9m\leqslant 0$
    5. $(m-1)x^{2}-(2m+1)x\geqslant -m-3$
    6. $2mx^{2}+x-3\geqslant 0$

    Bài 6. Tìm $m$ để các bất phương trình sau có tập nghiệm là $\mathbb{R}$.

    1. $5x^2-x+m>0$
    2. $mx^2-10x-5<0$
    3. $\dfrac{x^2-mx-2}{x^2-3x+4}>-1$
    4. $m(m+2)x^2+2mx+2>0$
    5. $x^{2}-2mx+m+12>0$
    6. $-2x^{2}-mx+m^{2}-1<0$
    7. $x^{2}+3mx-9\geqslant 0$
    8. $2mx^{2}+x-3\geqslant 0$
    9. $x^{2}+3x-9m>0$
    10. $(m-1)x^{2}>(2m+1)x-m-3$

    Bài 7. Tìm $m$ để hàm số sau xác định với mọi $x\in\mathbb{R}$.

    1. $y=\sqrt{x^{2}+3x-m^{2}+2}$
    2. $y=\sqrt{m(m+2)x^{2}+2mx+2}$
    3. $y=\dfrac{1}{\sqrt{mx^{2}+6mx-7}}$

    Bài 8. Giải các bất phương trình sau:

    1. $\dfrac{x^{2}-9x+14}{2-3x}\geqslant 0$
    2. $\dfrac{(2x-5)(x+2)}{-4x+3}>0$
    3. $\dfrac{x-3}{x+1}>\dfrac{x+5}{2-x}$
    4. $\dfrac{x-3}{x+5}<\dfrac{1-2x}{x-3}$
    5. $\dfrac{2x-1}{2x+1}\leqslant 1$
    6. $\dfrac{3x-4}{x-2}>1$
    7. $\dfrac{2x-5}{2-x}\geqslant -1$
    8. $\dfrac{2}{x-1}\leqslant \dfrac{5}{2x-1}$
    9. $\dfrac{1}{x}+\dfrac{1}{x+1}<\dfrac{2}{x^{2}+x}$
    10. $\dfrac{x^{2}}{x^{2}+1}+\dfrac{2}{x}<1$
    11. $\dfrac{11x^{2}-5x+6}{x^{2}+5x+6}<x$
    12. $\dfrac{1}{x+1}-\dfrac{2}{x^{2}-x+1}\leqslant \dfrac{1-2x}{x^{3}+1}$
    13. $\dfrac{2-x}{x^{3}+x}>\dfrac{1-2x}{x^{3}-3x}$
    14. $1<\dfrac{1+x}{1-x}\le2$
    15. $-1\leqslant \dfrac{x^{2}-5x+4}{x^{2}-4}\leqslant 1$

    Xem thêm: Phương trình chứa trị tuyệt đối

    Bài 9. Giải các phương trình sau.

    1. $|2x+1|-3=x$
    2. $|1-3x|+x-7=0$
    3. $|2x-13|+3x-1=0$
    4. $|x^{2}-x+2|=2-x$
    5. $|1-x-2x^{2}|+3x=5$
    6. $|2x^{2}-4x+1|+x-2=1$
    7. $|2x-1|+|1-x|+x=4$
    8. $|2x-1|+|2x+1|=4$
    9. $|x^{2}-3x+2|-2x=1$
    10. $|x^{2}+x-12|=x^{2}-x-2$
    11. $|x^{2}-2x|=2x^{2}-1$
    12. $|2x^{2}+3x-2|=|x^{2}-x-3|$

    Bài 10. Giải các phương trình, bất phương trình sau:

    1. $(x^{2}+4x+10)^{2}-7(x^{2}+4x+11)+7<0$
    2. $x^{4}+4x^{2}+2|x^{2}-2x|=4x^{3}+3$
    3. $2|x+1|-|x^{2}-2x-8|=-5-x+x^{2}$
    4. $|x+3|<x-6$
    5. $|2x-1|+5x-7\geqslant 0$
    6. $|x^{2}-3x+2|-3x-7\geqslant 0$
    7. $|2x-4|+|3x-6|\geqslant 2$
    8. $|x-1|\leqslant 2|-x-4|+x-2$
    9. $|x+2|+|1-2x|\leqslant x+1$
  • Đề thi học kì 1 Toán 10 Xuân Trường B năm 2020

    Đề thi học kì 1 Toán 10 Xuân Trường B năm 2020

    Đề thi học kì 1 Toán 10 Xuân Trường B năm 2020

    Xem thêm: Đề thi Hóa học 12 HK1 2020 SGD Nam Định

    1. Đề thi học kì 1 Toán 10 trắc nghiệm

    Câu 1: Cho tam giác $ABC$có $AB=5$, $AC=8$ và $A={{60}^{o}}.$ Giá trị của tích vô hướng $\overrightarrow{AB}.\overrightarrow{AC}$ bằng
    A. 40.
    B. $40\sqrt{3}.$
    C. $20.$
    D. $20\sqrt{3}.$
    Câu 2: Cho hàm số $y=\frac{x+2}{\sqrt{x-1}}+\sqrt{3-x}$. Tập xác định của hàm số là
    A. $\left( 1;3 \right)$.
    B. $\left[ 1;3 \right]$.
    C. $\left( 1;3 \right]$ .
    D. $\left[ 1;3 \right)$.
    Câu 3: Tất cả các giá trị của tham số $m$ để phương trình $m{{\text{x}}^{2}}+2m\text{x}+m+1=0$ có hai nghiệm phân biệt là
    A. $m<0.$
    B. $m\le 0.$
    C. $m>0.$
    D. $m\ge 0.$
    Câu 4: Số nghiệm của phương trình $\sqrt{x-2020}+x=\sqrt{2020-x}+2020$ là
    A. 2020.
    B. 1.
    C. 2.
    D. 0.
    Câu 5: Cho $\tan \alpha =2.$Giá trị của $A=\frac{3\sin \alpha -c\text{os}\alpha }{\sin \alpha +3c\text{os}\alpha }$ bằng
    A. $3.$
    B. $1.$
    C. $\frac{1}{2}.$
    D. $\pm \frac{2}{3}.$
    Câu 6: Cho hai vectơ $\overrightarrow{a}=(4;3),$và $\overrightarrow{b}=(1;7).$ Khi đó góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ bằng
    A. ${{45}^{o}}.$
    B. ${{90}^{o}}.$
    C. ${{60}^{o}}.$
    D. ${{30}^{o}}.$
    Câu 7: Trên mặt phẳng tọa độ $Oxy$ cho hình thang cân $ABC\text{D}$$(AB\parallel C\text{D}).$ Biết điểm $A(-1;1),$ $B(0;2),$ $C(3;1).$ Gọi điểm $D(x;y).$ Biểu thức ${{x}^{2}}-{{y}^{2}}$ bằng
    A. 9.
    B. $4.$
    C. $-4.$
    D. -9.
    Câu 8: Số các giá trị nguyên của $m$ để phương trình $\sqrt{x-1}=2\text{x}+m$ có hai nghiệm phân biệt là
    A. 1.
    B. 2.
    C. 0.
    D. 3.
    Câu 9: Tất cả các giá trị của tham số $m$ để phương trình ${{\text{x}}^{2}}-x-m=0$ có hai nghiệm phân biệt ${{x}_{1}},$${{x}_{2}}$thỏa mãn ${{x}_{1}}^{2}+{{x}_{2}}^{2}\le 3$ là
    A. $m\in \left[ -\frac{1}{4};1 \right)$
    B. $m\in \left( -\frac{1}{4};1 \right).$
    C. $m\in \left( -\frac{1}{4};1 \right].$
    D. $m\in \left[ -\frac{1}{4};1 \right].$
    Câu 10: Cho hàm số $y=\text{a}{{\text{x}}^{2}}+b\text{x}+c,$ với $a\ne 0$ . Khi đó tọa độ đỉnh của đồ thị hàm số là
    A. $\left( -\frac{b}{2a};\frac{-\Delta }{4\text{a}} \right)$.
    B. $\left( \frac{b}{2a};\frac{-\Delta }{4\text{a}} \right)$
    C. $\left( -\frac{b}{2a};\frac{\Delta }{4\text{a}} \right)$
    D. $\left( \frac{b}{2a};\frac{\Delta }{4\text{a}} \right)$
    Câu 11: Trên mặt phẳng tọa độ $(O;\overrightarrow{i},\overrightarrow{j})$ cho hai vectơ $\overrightarrow{a}=({{a}_{1}};b_{1}^{{}}),$và $\overrightarrow{b}=({{a}_{2}};{{b}_{2}}).$Trong các biểu thức sau, biểu thức nào dưới đây đúng?
    A. $\overrightarrow{a}.\overrightarrow{b}={{a}_{1}}{{b}_{2}}+{{a}_{2}}{{b}_{1}}.$
    B. $\overrightarrow{a}.\overrightarrow{b}={{a}_{1}}{{b}_{1}}-{{a}_{2}}{{b}_{2}}.$
    C. $\overrightarrow{a}.\overrightarrow{b}={{a}_{1}}{{b}_{1}}+{{a}_{2}}{{b}_{2}}.$
    D. $\overrightarrow{a}.\overrightarrow{b}={{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}.$
    Câu 12: Số các giá trị nguyên dương của $m$ để phương trình ${{x}^{2}}-x+{{m}^{2}}-4=0$có hai nghiệm trái dấu là
    A. 1.
    B. 2.
    C. 5.
    D. 3.
    Câu 13: Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn?
    A. $\left\{ \begin{align}
    & 3x-y-z=0 \\
    & 4x-5y=3 \\
    \end{align} \right.$
    B. $\left\{ \begin{align}
    & 3x-2y=1 \\
    & 4x-5y=-3 \\
    \end{align} \right.$
    C. $\left\{ \begin{align}
    & 3{{x}^{2}}-2y=11 \\
    & 4x-5{{y}^{2}}=3 \\
    \end{align} \right.$
    D. $\left\{ \begin{align}
    & 3x-2=0 \\
    & {{x}^{2}}-5x=3 \\
    \end{align} \right.$
    Câu 14: Số nghiệm nguyên của phương trình $\sqrt{{{x}^{2}}+x-6}=7-x$ là
    A. $\frac{11}{3}.$
    B. 2.
    C. 1.
    D. 0.
    Câu 15: Trên hệ trục tọa độ $Oxy$cho hình bình hành $ABCD$ có $A(-1;3),$$B(2;4),$$C(0;1)$. Tọa độ đỉnh D là
    A. $D(3;0).$
    B. $D(0;-3).$
    C. $D(0;3).$
    D. $D(-3;0).$
    Câu 16: Trong các hàm số sau, hàm số nào đồng biến trên $R$?
    A. $y={{x}^{2}}+1$.
    B. $y=3\text{x}-2$.
    C. $y=-{{x}^{2}}+1$.
    D. $y=2-3\text{x}$.
    Câu 17: Tập xác định của hàm số $y=\frac{1}{{{x}^{2}}-4\text{x}+4}$ là
    A. $\left[ 2;+\infty \right).$
    B. $\left( 2;+\infty \right).$
    C. $\mathbb{R}.$
    D. $\mathbb{R}\backslash \left\{ 2 \right\}.$
    Câu 18: Với điều kiện nào của $m$ thì phương trình $m(x-2)=3\text{x}+1$ có nghiệm duy nhất
    A. $m\ne 0.$
    B. $m=0.$
    C. $m=3.$
    D. $m\ne 3.$
    Câu 19: Phương trình ${{\left( x-4 \right)}^{2}}=x-2$ là phương trình hệ quả của phương trình nào sau đây
    A. ${{(x-2)}^{2}}=x-4.$
    B. $\sqrt{x-4}=x-2.$
    C. $\sqrt{x-2}=x-4.$
    D. $\sqrt{x-2}=\sqrt{x-4}.$
    Câu 20: Số nghiệm nguyên của phương trình $\frac{\left| 4-x \right|}{\sqrt{x-2}}=\frac{4-x}{\sqrt{x-2}}$ là
    A. 3.
    B. 1.
    C. 4.
    D. 2.
    Câu 21: Trong các đẳng thức sau, đẳng thức nào dưới đây đúng?
    A. $\sin ({{180}^{0}}-\alpha )=-\sin \alpha .$
    B. $\sin ({{180}^{0}}-\alpha )=\sin \alpha .$
    C. $\sin ({{180}^{0}}-\alpha )=c\text{os}\alpha .$
    D. $\sin ({{180}^{0}}-\alpha )=-\cos \alpha .$
    Câu 22: Cho $\text{cos}\alpha =-\frac{3}{5}.$Giá trị của$\sin \alpha $ bằng
    A. $-\frac{4}{5}.$
    B. $\frac{4}{5}.$
    C. $\frac{16}{25}.$
    D. $\pm \frac{4}{5}.$
    Câu 23: Trên mặt phẳng tọa độ $Oxy$ cho hai điểm $A(1;2),$$B(-3;1)$. Số điểm $C$ thuộc trục tung để tam giác $ABC$ cân tại $A$ là
    A. $2.$
    B. $1.$
    C. 0.
    D. 3.
    Câu 24: Số các giá trị nguyên dương của $m$ để phương trình $\frac{{{x}^{2}}-4\text{x}+m-1}{x-1}=0$ có hai nghiệm phân biệt là
    A. 4.
    B. 5.
    C. 6.
    D. 3.
    Câu 25: Cho ba điểm phân biệt $A,$$B,$$C.$ Nếu $\overrightarrow{AB}=-3\overrightarrow{AC}$ thì đẳng thức nào dưới đây đúng?
    A. $\overrightarrow{BC}=4\overrightarrow{AC}.$
    B. $\overrightarrow{BC}=-4\overrightarrow{AC}.$
    C. $\overrightarrow{BC}=-3\overrightarrow{AC}.$
    D. $\overrightarrow{BC}=3\overrightarrow{AC}.$

    2. Đề thi học kì 1 Toán 10 tự luận

    Câu 1. (2,0 điểm) Giải các phương trình sau:

    1. $\sqrt{{{x}^{2}}-x+7}=2x-1$
    2. $\sqrt{2-x}=\sqrt{x+1}+1$

    Câu 2. (1,0 điểm) Tìm tất cả các giá trị của tham số $m$ để phương trình sau có nghiệm:$$m{{x}^{2}}+(2x+1)m+5-5x=0$$

    Câu 3. (1,5 điểm) Trên mặt phẳng tọa độ $Oxy$ cho tam giác ABC có $A(1;1)$, $B(2;4)$, $C(10;-2)$ và đường cao $AH$.

    1. Chứng minh tam giác ABC vuông tại $A$;
    2. Tính cosin của góc $B$;
    3. Tìm tọa độ của điểm $H$.

    Câu 4. (0,5 điểm)

    Tìm tất cả các giá trị của tham số $m$ để phương trình sau có nghiệm duy nhất $$\sqrt{{{x}^{2}}-2m}+2\sqrt{{{x}^{2}}-1}=x$$

    ———-Hết———–