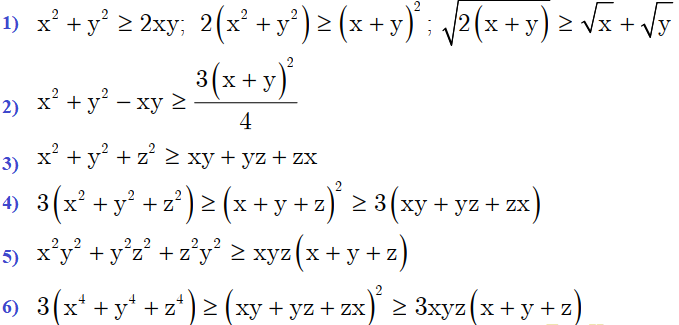Geogebra không chỉ là phần mềm vẽ hình Toán học cực kỳ tiện lợi mà còn là một phần mềm dùng để hỗ trợ học Toán, dạy Toán xuất sắc. Hãy cùng tìm hiểu nhanh cách sử dụng phần mềm Geogebra.
1. Hướng dẫn cài đặt phần mềm Geogebra
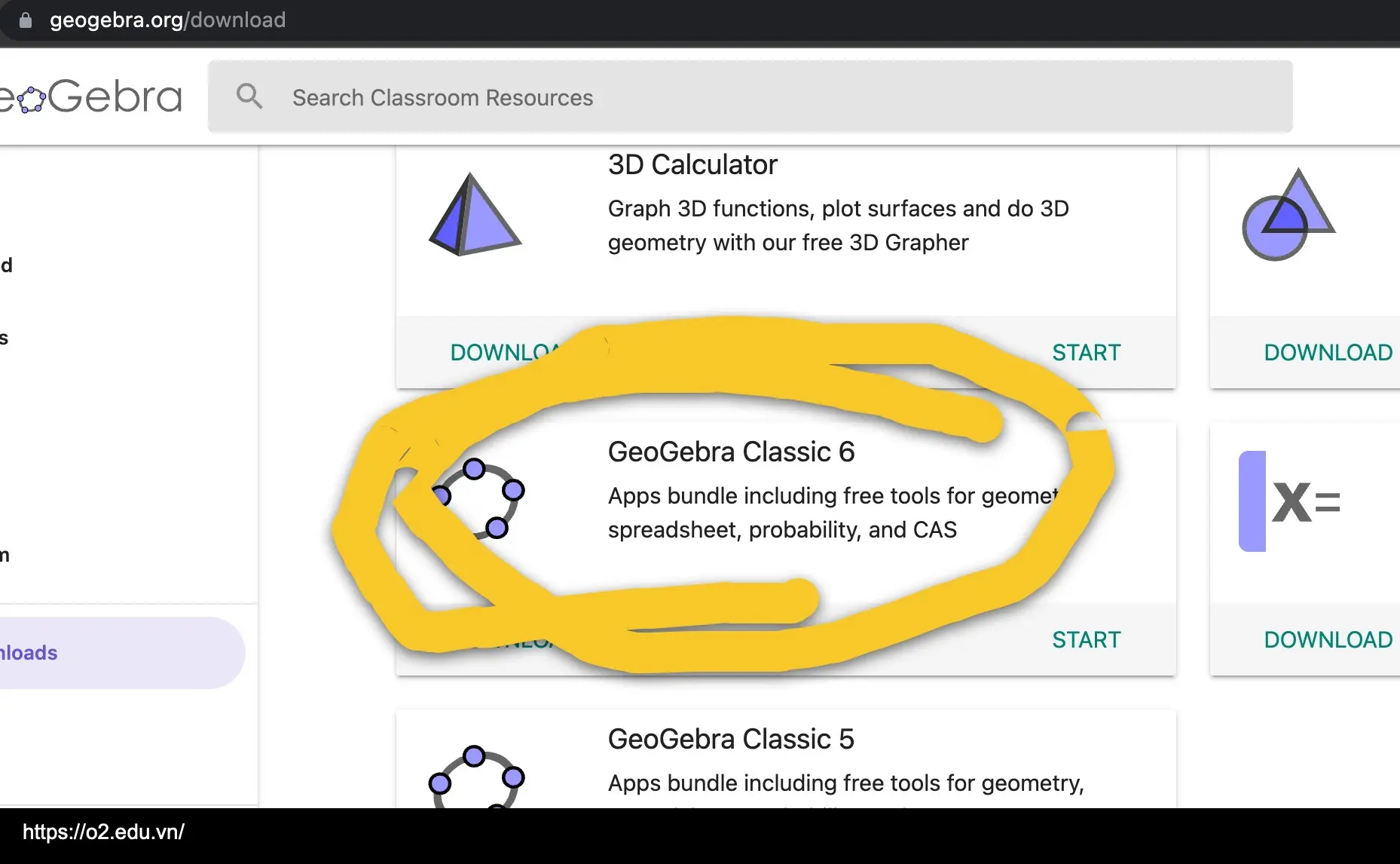
Đầu tiên, bạn truy cập link https://www.geogebra.org/download để tải phần mềm Geogebra. Chúng tôi gợi ý bạn nên chọn phiên bản GeoGebra Classic 6.
Nháy kép vào file vừa tải về, đợi một chút để chương trình cài đặt vào máy tính của bạn. Nếu bạn dùng Macbook thì có thể vào App store tìm và tải về.
2. Hướng dẫn sử dụng Geogebra
Đổi ngôn ngữ cho phần mềm
Phần mềm có hỗ trợ ngôn ngữ Tiếng Việt, bạn có thể cài đặt giao diện Tiếng Việt cho chương trình theo các bước sau: Bấm vào menu menu hamburger (dấu ba gạch ngang ở góc phải màn hình) → chọn Settings → chọn Language → chọn Vietnamese / Tiếng Việt.

Cách mở các môi trường làm việc
Khi bạn mở Geogebra Classic 6, phần mềm sẽ hiển thị môi trường mặc định là Graphing (vẽ đồ thị).
Để thay đổi môi trường làm việc, chẳng hạn bạn muốn làm việc với hình không gian 3D. Bạn bấm vào menu bảng chọn hồ sơ (dấu ba gạch ngang ở góc phải màn hình) → chọn Hiển thị → tích chọn Hiển thị dạng 3D và bỏ tích Vùng làm việc.

Với các môi trường làm việc khác, bạn có thể làm tương tự như vây.
Ngoài ra, các bạn có thể mở các file làm việc khác của bản thân hay của người dùng khác, bằng cách bấm vào menu → chọn Hồ sơ → chọn Mở.

Lúc này, bạn có 2 lựa chọn:
- Tìm kiếm tệp chương trình trên thư viện cộng đồng của Geogebra bằng cách gõ từ khóa vào ô tìm kiếm và bấm Enter (như trong hình là O2 Education đang tìm các file có từ khóa “đạo hàm”) → chọn chế độ View (chỉ xem) hoặc Chỉnh sửa;
- Mở một tệp trong máy tính của bạn.

Lưu, xuất bản chương trình làm việc
Sau khi bạn hoàn thành việc tạo các hình học hay đại số, bạn muốn lưu hoặc xuất chương trình làm việc này. Bạn vào menu, chọn Hồ sơ → Lưu lại (phải đăng nhập hoặc tạo tài khoản trên Geogebra)

Còn phần xuất bản, có rất nhiều định dạng file sau khi xuất ra dành cho bạn, chỉ cần chọn định dạng cần xuất bản, sau đó bấm lưu là được.
3. Các chức năng của phần mềm Geogebra 6
Giao diện của Geogebra

- Menu hamburger (bảng chọn, thực đơn): Cho phép người dùng tạo mới, mở, lưu, xuất bản, sao chép, tùy chọn tên, cỡ chữ, tùy biến thanh công cụ,… rất nhiều chức năng quan trọng của phần mềm đều nằm ở đây.
- Thanh công cụ: Đây là nơi để bạn lựa chọn các công cụ như tạo điểm, tạo đường thẳng, tạo các khối, hình không gian, dựng đường tròn,…
- Vùng làm việc: Đây là khu vực làm việc chính của chương trình, là nơi chứa sản phẩm cuối cùng của bạn. Các đối tượng bạn tạo ra sẽ xuất hiện ở đây
- Danh sách đối tượng: Vùng này sẽ hiển thị chi tiết thông tin của các đối tượng trong vùng làm việc của bạn (nếu máy bạn không có vùng này thì chọn Menu → Hiển thị → Tích chọn Hiển thị danh sách đối tượng).
- Khung nhập lệnh: Dùng để tạo các đối tượng bằng lệnh, ví dụ muốn tạo điểm A trên mặt phẳng có tọa độ (4,-5) thì chỉ cần nhập
A=(4,-5), muốn tìm nghiệm của phương trình thì có thể sử dụng lệnh Giai (Solve)…

Ở dấu cộng bên trái khung nhập lệnh, có một số chức năng như thêm văn bản hay thêm hình ảnh cho chương trình làm việc, bạn có thể viết minh họa hoặc tải hình ảnh lên để chương trình làm việc của bạn trở nên sinh động hơn.
Thanh công cụ của Geogebra

Các công cụ thuộc cùng một nhóm sẽ được gom lại, nếu không thấy công cụ mong muốn các bạn có thể di chuột lên từng công cụ để hiển thị thêm các công cụ khác. Chẳng hạn trong hình dưới, di chuột lên công cụ Đa giác sẽ xổ xuống menu cho phép bạn chọn Đa giác, Đa giác đều, Đa giác có hướng…

Khi bạn di chuột lên mỗi công cụ, chương trình đều hiển thị chức năng và các bước sử dụng của các công cụ này ở góc trái bên dưới chương trình. Nếu có vấn đề gì đó không hiểu hoặc gặp trục trặc, bạn hãy bấm vào phần trợ giúp.









Context Menu
Context Menu hay còn gọi là menu ngữ cảnh, trình đơn ngữ cảnh, là danh sách các lệnh khi bạn bấm chuột phải vào một đối tượng nào đó.
Muốn mở menu ngữ cảnh này, bạn hãy nhấp chuột phải vào đối tượng mà bạn muốn làm việc. Khi bạn nhấp chuột phải vào vùng làm việc, nó sẽ xuất hiện một menu mới, trong đó bao gồm nhiều chức năng dành cho vùng làm việc của bạn.
Còn nếu bạn nhấp chuột phải vào đối tượng làm việc, ví dụ như hình bên dưới, mình nhấp chuột phải vào điểm A. Sẽ xuất hiện một bảng menu khác với nhiều chức năng khác nhau.

4. Cách vẽ hình bằng Geogebra đơn giản
Vẽ hình học trên môi trường Graphing (không gian hai chiều)
Chúng ta hãy cùng bắt tay vào vẽ một hình tam giác đơn giản bằng GeoGebra Classic 6 nhé!
Trước hết, chúng ta hãy tắt tọa độ để vùng làm việc nhìn đơn giản hơn nhé. (Nếu ai cần khung tọa độ này thì đừng tắt).
Có hai cách để vẽ hình tam giác:
Cách 1: Sử dụng biểu tượng tam giác trên thanh công cụ để vẽ.
Trong nhóm biểu tượng hình tam giác, bạn hãy chọn công cụ đa giác. Sau đó chấm ba điểm lên vùng làm việc, như thế là đã hoàn thành vẽ hình tam giác.

Cách 2: Sử dụng điểm mới và đoạn thẳng để vẽ hình tam giác.
– Đầu tiên, bạn hãy chọn điểm mới trên thanh công cụ, sau đó chấm ba chấm lên vùng làm việc.

– Tiếp theo, chọn đoạn thẳng trên thanh công cụ rồi bấm vào các điểm vừa vẽ, sau đó di chuyển chuột để nối các điểm còn lại.

Tương tự với vẽ các hình học khác, bạn chỉ cần sử dụng các biểu tượng trên thanh công cụ là có thể tạo cho mình một vùng làm việc hoàn chỉnh.