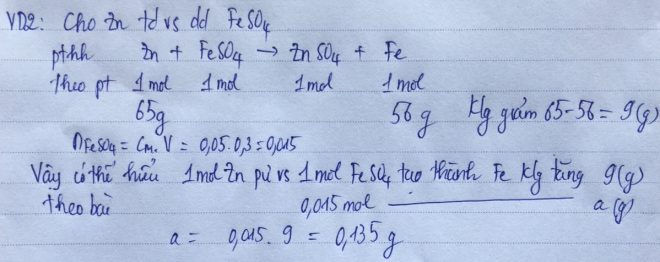O₂ Education

  • Tự học tiếng Do Thái – Giới thiệu và bảng chữ cái

    Tự học tiếng Do Thái – Giới thiệu và bảng chữ cái

    Tự học tiếng Do Thái – Giới thiệu và bảng chữ cái

    Do Thái là một trong những dân tộc thành công nhất thế giới. Một phần do gen, nhưng một phần do chính văn hoá của họ quyết định. Và, để thử tìm hiểu cách sinh hoạt, đời sống của dân tộc này, tôi tự mình mày mò học ngôn ngữ của họ. Vì đây là một ngôn ngữ không phổ biến nên có khá ít tài liệu, khoá học tiếng Do Thái. Phần lớn những kiến thức vụn vặt này là do tôi thu lượm trên mạng internet.

    Xem thêm:

    1. Giới thiệu chung về tiếng Do Thái

    Tiếng Hebrew (phiên âm tiếng Việt: Híp-ri, Hê-brơ, Hi-bru, hoặc Hy-bá-lai), cũng được gọi một cách đại khái là “tiếng Do Thái”, là một ngôn ngữ bản địa tại Israel, được sử dụng bởi hơn 9 triệu người trên toàn cầu, trong đó 5 triệu ở Israel. Về mặt lịch sử, đây là ngôn ngữ của người Israel cổ đại và tổ tiên họ, dù nó không được gọi là “Hebrew” trong Tanakh. Những mẫu viết chữ Cổ Hebrew cổ nhất có niên đại từ thế kỷ 10 Trước Công Nguyên. Tiếng Hebrew thuộc về nhánh Semit của ngữ hệ Phi-Á. Tiếng Hebrew được viết và đọc từ phải sang trái, giống tiếng Ả Rập và tiếng Ba Tư.

    2. Một số đặc điểm của tiếng Do Thái

    • Tiếng Do Thái viết từ phải sang trái, không có sự phân biệt chữ viết hoa và chữ viết thường.
    • Nguyên gốc, bảng chữ Hebrew cái gồm có 22 phụ âm, không có nguyên âm (xem hình sau), về sau các nhà ngôn ngữ học đưa thêm các nguyên âm (gọi là niqqud) để giúp việc đọc/phát âm trở nên dễ dàng hơn. Việc phát âm một từ Do Thái khá giống với ghép vần của tiếng Việt, tuy nhiên không có nguyên âm nên việc đọc có khó khăn hơn.
    • Đầu tiên và quan trọng nhất, chúng tôi khuyên bạn là nên học thuộc bảng chữ cái này cũng như cách phát âm từng chữ cái, đặc biệt là thuộc (nhận được mặt chữ và cách phát âm) kiểu viết dạng chữ in [đánh máy]. Sau khi thành thạo có thể học thêm kiểu chữ viết tay [script].

    3. Cách phát âm bảng chữ cái tiếng Do Thái

    Bang chu cai tieng Do Thai Hebrew

    4. Cách viết chữ Do Thái

    Cách viết, các bạn có thể tập theo hai hình vẽ sau:

    Cach viet Bang chu cai tieng Do Thai Hebrew
    Cach viet Bang chu cai tieng Do Thai Hebrew

    Tuy nhiên, phần lớn các văn bản bạn sẽ đọc là trên máy tính, điện thoại, do đó chúng tôi khuyên bạn nên học thuộc bảng chữ cái như trong hình sau:

    Tự học tiếng Do Thái - Giới thiệu và bảng chữ cái 1
  • Phụ âm và nguyên âm tiếng Do Thái

    Phụ âm và nguyên âm tiếng Do Thái

    Phụ âm và nguyên âm tiếng Do Thái

    Như bạn đã biết, trong bảng chữ cái tiếng Do Thái chỉ gồm có 22 phụ âm mà không có nguyên âm. Do đó khi phát âm gặp khá nhiều khó khăn và người ta đã bổ sung các nguyên âm niqqud. Tuy nhiên, trong bảng chữ cái tiếng Do Thái thì có một số phụ âm cũng được sử dụng gần như là các nguyên âm để giúp cho việc phát âm được dễ dàng. Bài viết này xin giới thiệu các nguyên âm tiếng Do Thái để bạn đọc dễ dàng phát âm hơn.

    hebrew alphabet

    Tiếng Do Thái trong Kinh thánh được viết như thế nào

    Người ta biết rằng chỉ có phụ âm được viết bằng chữ Hê-bơ-rơ. Tuyên bố này, tuy nhiên, chỉ đúng một phần. Mặc dù đúng là tất cả các ký tự của chữ Hê-bơ-rơ là phụ âm, nhưng không phải vì thế mà một văn bản trong tiếng Do Thái chứa ít thông tin về nguyên âm như một văn bản tiếng Anh mà từ đó tất cả các nguyên âm đã bị xóa. Về cơ bản, có hai tính năng trong hệ thống chữ viết cung cấp thêm thông tin:

    • Có một phụ âm không được viết bằng chữ Latinh mà bằng tiếng Do Thái. Vì không có chữ cái nào trong tiếng Latin, nên nó không có tên; Các nhà ngôn ngữ học gọi đó là điểm dừng glottal (glottal stop). Trong tiếng Anh, rất hiếm (ví dụ: khoảng nghỉ ngắn giữa hai nguyên âm “he eats” hay được phát âm nối liền mạch, hoặc trong “wa’er” được phát âm thành “water” bởi một người nói tiếng Cockney), trong các ngôn ngữ khác, nó khá phổ biến (ví dụ tiếng Đức : so sánh giữa “bereisen” (từ “Reise”) không có glottal stop và “vereisen” (từ “Eis”) với một glottal stop trước “ei”). Bây giờ, một từ tiếng Do Thái – giống như tiếng Đức – sẽ không bắt đầu bằng nguyên âm; nó có thể bắt đầu bằng một điểm dừng glottal – trái ngược với tiếng Đức – được viết bằng một chữ cái, Alef ( Alef). Do đó, bạn có thể nói [) DM] ( adam = người, người) từ [DM] ( dam= máu) bởi Alef ở đầu (tức là cạnh phải) của từ.
    • Phụ âm rất thường xuyên sử dụng để nguyên âm biểu thị: Yod ( Yod, một phụ âm “y”) có thể biểu thị cho nguyên âm “i” hay “e”, Waw ( Waw, phụ âm “v”) có thể biểu thị cho nguyên âm “u” hoặc “o”. Và, nếu từ này kết thúc bằng một nguyên âm chưa được biểu thị bằng Yod, Waw hoặc Alef cuối cùng, He ( Anh ta, phụ âm của chú họ) được thêm vào để biểu thị nguyên âm. Do đó, bạn có thể nói [DBWRH] ( dvora= bee, Deborah ) từ [DBR] ( davar= word, mối quan tâm ) bằng Waw bổ sung cho các oái oái và He bổ sung cho các trò chơi một tên lửa.

    Thí dụ:

    Bây giờ cả thế giới đã có một ngôn ngữ và một bài phát biểu chung. (Gen.11: 1, NIV)

    Trong ngôn ngữ Hebrew gốc, nhưng trong phiên mã Latin (với “ c” cho “tz” như trong “ tz ar” và “ x” cho “ch” như trong “Lo ch Ness”, cả hai để không làm cho một chữ cái Hebrew thêm hơn một chữ cái Latinh), ví dụ câu này có thể trông như thế này:

    wayehi kol haárec safa exat udvarim axadim

    Nếu chúng ta xóa bỏ các nguyên âm đi, nó sẽ trông như thế này:

    wyh kl hrc sf xt wdvrm xdm

    Trên thực tế, các chữ cái tiếng Hê-bơ-rơ được phiên âm (với dấu nháy đơn cho Alef) là:

    wyhy kl h'rc sfh 'xt wdvrym 'xdym

    đó là thông tin nhiều hơn đáng kể về nguyên âm ở đâu. Trong kịch bản tiếng Do Thái (được viết từ phải sang trái), nó trông như thế này:

    Gen.11: 1 (không tập trung)

    Khi người ta xem xét một kịch bản trong đó các nguyên âm bị bỏ đi, ít nhất đôi khi, người ta sẽ mong đợi hiệu ứng khó hiểu nhất khi các từ không liên quan được viết giống nhau, ví dụ bằng tiếng Anh: tan, ten, teen, tin, ton, giai điệu, điều chỉnh, điều chỉnh. Có bằng tiếng Anh, các từ nhận thức thường chia sẻ phụ âm của họ nhiều hơn nguyên âm của họ: trong ví dụ này, điều này có nghĩa là một phần mười ban phạm, có thể, và người hâm mộ, người hâm mộ, người hâm mộ, người hâm mộ, người hâm mộ, người hâm mộ. Trong tiếng Do Thái, điều tương tự cũng đúng với một mức độ lớn hơn: các nhận thức chỉ được nhận ra bởi gốc của chúng, nghĩa là, bởi mẫu phụ âm còn tồn tại khi tất cả các tiền tố và hậu tố bị loại bỏ. Nguyên âm đi vào để phân biệt các từ khác nhau chia sẻ cùng một gốc hoặc các hình thức ngữ pháp khác nhau của một từ; có một ví dụ gần cuối bài viết.

    Mọi người nên nhớ rằng một điều khá bình thường là không phải tất cả các tính năng của ngôn ngữ đều được phản ánh trong một hệ thống chữ viết: trong nhiều ngôn ngữ, ví dụ như tiếng Anh, trọng âm của từ và trọng âm câu không được đánh dấu và hầu hết các ngôn ngữ có nhiều âm vị hơn chữ cái trong bảng chữ cái của họ. Nó là đủ khi tập lệnh chứa đủ thông tin để cho phép đọc nó mà không cần đoán. Kinh nghiệm trong suốt lịch sử đã chỉ ra rằng thông tin có trong chữ viết tiếng Do Thái là đủ cho độc giả biết ngôn ngữ này.

    Hỗ trợ thêm để đọc

    Vâng, câu cuối cùng phải được thực hiện với một hạt muối. Nếu nó đã được như vậy, kịch bản sẽ không được phát triển để bao gồm thêm thông tin về nguyên âm. Vào thời hậu Kinh Thánh, người ta thường viết các Yod và Waws cho các nguyên âm ở nhiều nơi hơn là nơi chúng xuất hiện trong Kinh thánh, và Yod và Waw phụ âm thường được nhân đôi để phân biệt chúng với các nguyên âm. Mặc dù những thay đổi này là nhỏ, nhưng chúng đóng góp phần lớn vào khả năng đọc. Đây là cách tiếng Do Thái hiện đại thường được viết và tất cả các độc giả báo chí Israel chứng minh mỗi sáng rằng thông tin trong kịch bản nâng cao một chút này hoàn toàn đủ để đọc – một lần nữa cung cấp một người biết ngôn ngữ.

    Công việc của Masoretes

    Vào cuối thiên niên kỷ đầu tiên của kỷ nguyên chung, sau hàng ngàn năm di cư của người Do Thái, việc làm chủ hoàn hảo ngôn ngữ tiếng Do Thái và kiến ​​thức sâu sắc về Kinh thánh không còn có thể được mong đợi từ tất cả các thành viên của cộng đồng Do Thái, những người cần đọc Kinh thánh . Để hỗ trợ họ và giảm sự ra đời của nhiều bài đọc biến thể, một vài học giả Do Thái đã bắt đầu chuẩn hóa các văn bản và cách đọc của họ. Một phần của tác phẩm này là chú thích của văn bản phụ âm có dấu cho nguyên âm. Lược đồ được mô tả ngắn gọn trong phần trước, mặc dù được giới thiệu tốt vào thời điểm đó, không phù hợp cho mục đích này:

    • Nó không đủ chính xác – văn bản xuất hiện vẫn còn mơ hồ đối với độc giả có ít kiến ​​thức về ngôn ngữ và truyền thống học thuật của người Do Thái.
    • Nó sửa đổi Kinh thánh bằng cách giới thiệu thêm các chữ cái.

    Dự án được gọi là [MSWRH] ( masora= truyền thống ). Tên này nhấn mạnh rằng nó hiểu chính nó như là một bản ghi chép về cách Kinh Thánh luôn được đọc theo truyền thống trong cộng đồng Do Thái và không phải là một giới thiệu về những diễn giải mới cho một văn bản tối nghĩa trước đây. Cũng có thể là họ gặp phải truyền thống hoặc ý kiến ​​khác nhau về cách đọc một đoạn văn nhất định – đây là một quá trình bình thường trong các nhà phê bình văn bản. Nhưng mục tiêu là sửa chữa những gì là truyền thống sống và không bị gián đoạn.

    Về cơ bản, công việc của họ bao gồm các nhiệm vụ sau:

    • So sánh tất cả các bản thảo có sẵn và quyết định nên theo dõi cái nào nếu chúng phân kỳ (cực kỳ hiếm so với các tài liệu khác cùng tuổi, do sự thận trọng cao độ mà các nhà sao chép đã áp dụng).
    • Tạo các chú thích về các nguyên âm trong văn bản bằng cách giới thiệu các dấu phụ, [NQWDWT] ( nequdot= dấu phát âm ). Các dấu tương tự được sử dụng ngày nay khi cách phát âm là quan trọng, ví dụ như trong từ điển, cũng trong các bài thơ.
    • Tạo các chú thích về cấu trúc câu bằng các dấu phụ khác nhau, [+ (MYM] ( teamim= dấu cộng hưởng ), để cho phép đọc tụng và tụng kinh. Chúng được sử dụng độc quyền trong các văn bản Kinh Thánh.
    • Cung cấp thông tin bổ sung khi văn bản, để dễ hiểu, phải được đọc hơi khác so với những gì được viết. Điều này sẽ được chi tiết một chút trong phần tiếp theo.
    • Tạo một thống kê về số lượng từ và chữ cái trong mỗi cuốn Kinh thánh, dự định là một tổng kiểm tra cho các nhà sao chép.

    Văn bản của ví dụ trên trông như thế này với các dấu hiệu phát âm:

    Gen.11: 1 (phát âm)

    và với các dấu cộng hưởng bổ sung:

    Gen.11: 1 (phát âm và nhấn mạnh)

    Văn bản dưới dạng văn bản (Ketiv) và văn bản khi đọc (Qere)

    Trong một số trường hợp, vấn đề nảy sinh là văn bản Kinh thánh bằng văn bản sẽ có ý nghĩa hơn nếu được sửa đổi một chút. Truyền thống sau đó không phải là để sửa lỗi văn bản mà chỉ đọc nó như thể nó là bản sửa lỗi. Nói cách khác, người đọc dự kiến ​​sẽ đọc không chính xác những gì được viết. Đây là quá trình tương tự diễn ra khi ai đó đọc to từ một cuốn sách có lỗi chính tả. Trong các trường hợp như vậy, bạn có hai hình thức cho từ đang đề cập, thường chỉ khác nhau bởi một chữ cái: một là dạng viết, Ketiv ( [KTYB] ) chỉ có phụ âm và dạng còn lại là dạng được sử dụng khi đọc, Qere ( [QRY] ), với phụ âm và nguyên âm. Một giải pháp rõ ràng sẽ là đưa một trong những hình thức này vào văn bản đang chạy và một hình thức khác trong phần chú thích. Tuy nhiên, nó được thực hiện theo cách khác: văn bản đang chạy lấy Ketiv với nguyên âm của Qere và chú thích có các phụ âm của Qere. Thoạt nhìn điều này có vẻ kỳ lạ, nhưng nó rất hữu ích:

    • Các văn bản đang chạy không chứa sửa đổi của bản gốc.
    • Phần chú thích không chứa dấu phụ, chiếm không gian bổ sung và khó nhận biết khi sử dụng kích thước tập lệnh nhỏ.
    • Nếu chú thích bị bỏ qua, có tối đa thông tin trong văn bản đang chạy.

    Để làm ví dụ, chúng ta hãy xem Jer.8: 7. Chúng tôi đọc ở đó trong Kinh thánh của chúng tôi:

    Ngay cả những con cò trên bầu trời cũng biết các mùa được chỉ định của cô ấy, và chim bồ câu, chim én và tưa lưỡi quan sát thời gian di cư của chúng. (Giê-rê-mi 8: 7, NIV)

    mặc dù văn bản viết có [SW.S] ( sus= ngựa ) và không [SIYS] ( sis= swift ) trong số các động vật biết thời gian quay trở lại. Masoretes đã quyết định rằng đây có lẽ là một sai lầm của người sao chép vì vậy câu này sẽ được đọc với dòng chữ Swift nhanh trong đó. Phản ánh sự điều chỉnh này, bây giờ Kinh thánh tiếng Hê-bơ-rơ có [SIWS] nghĩa là các phụ âm Ketiv truyền thống có dấu phát âm không phù hợp, được trang bị một chú thích cho các phụ âm Qere [SYS] .

    Những trường hợp như vậy mà một từ hiện có được thay thế bằng một từ hiện có với một nghĩa khác thì không thường xuyên. Phần lớn các sửa chữa là cho các lỗi rõ ràng, chẳng hạn như các chữ cái bị mất hoàn toàn, hoặc cho các hình thức phi logic (ví dụ Ex.22: 4 (5?): Kiếm Nếu một người đàn ông chăn thả gia súc của cô ấy Thay (thay vì của anh ta ). thay thế một Waw hoặc ngược lại, vì hai ký tự thường gặp này chỉ khác nhau về độ dài của nét dọc. Trong một số trường hợp, hai phiên bản là các biến thể của cùng một từ và việc hiệu chỉnh được thực hiện ngay cả khi cả hai phiên bản đều có ý nghĩa, ví dụ như phiên bản đầu tiên từ Ps.77: 12 (11?) [) ZKYR] ( azkir = Tôi sẽ nhắc ) đã được sửa thành [) ZKWR] ( ezkor= Tôi sẽ nhớ) mà hình vuông tốt hơn với bối cảnh. (Đây đồng thời là một ví dụ về cách nhận thức chia sẻ gốc phụ âm của chúng, trong trường hợp này [ZKR] .)

    Tần suất sửa chữa như vậy thay đổi rất nhiều trong các sách của Kinh thánh; trung bình là khoảng một hoặc hai điều chỉnh mỗi chương. Con số này nói nhiều hơn về sự miễn cưỡng của Masoretes khi sửa đổi văn bản phụ âm truyền thống (đã được chuẩn hóa trong khoảng 850 năm) so với chất lượng của truyền thống văn bản: có nhiều biến thể hơn cho văn bản trên tất cả các bản thảo, nhưng trên mặt khác, nhiều lỗi rõ ràng có thể được sửa chữa một cách an toàn mà không để lại chú thích. Quá trình thực tế của truyền thống văn bản phức tạp hơn nhiều, và không phải là chủ đề của bài viết này chỉ liên quan đến hệ thống chữ viết.

    Một trường hợp hơi đặc biệt: theo truyền thống là không phát âm Tên thiêng liêng để giữ cho nó là thánh. Thay vào đó, một trong những từ [): QUẢNG CÁO] ( adonai= Chúa của tôi ) hoặc [): ELOHIYM] ( elohim= Chúa ) sẽ được đọc thay vào đó, sau này ở một vài nơi tương đối có hình thức [) FDOWN] ( adon= chúa, chủ) liền kề với Tên: Chúa tể, chúa tể của chúng tôi nghe có vẻ kỳ lạ trong tiếng Do Thái giống như tiếng Anh. Bây giờ, cách viết này trong văn bản Masoretic hoàn toàn giống với các dạng Ketiv / Qere khác: văn bản chứa Ketiv, trong trường hợp này là Tetragrammaton, với các nguyên âm của Qere. Vì việc này xảy ra thường xuyên đến mức bao gồm cả chú thích mỗi lần sẽ rất lãng phí, thực tế này đã dẫn đến sự nhầm lẫn với những độc giả không phải là người Do Thái, đã lấy nhầm nguyên âm của Qere là thuộc về Ketiv, do đó, Tetragrammaton phát âm sai yehovaMùi (hay tôn yehovi, tôn trọng.). Đầu tiên trong số này đã đi vào văn học Cơ đốc, chủ yếu là với một J J ban đầu (được phát âm giống như một tiếng Anh hiện đại dù sao đi nữa).

    Lưu ý về phiên âm tiếng Latin

    Việc phiên âm các từ tiếng Hê-bơ-rơ trong bài viết này dựa trên cách phát âm tiếng Do Thái hiện đại của người Do Thái không tốt hơn hoặc tệ hơn bất kỳ truyền thống nào khác. Ký hiệu theo sau ít nhiều cách phát âm tiếng Anh cho các phụ âm; các ngoại lệ được ghi chú rõ ràng. Cả hai đều được phát âm giống như tiếng Anh và kv. Các nguyên âm, tuy nhiên, không được phát âm như tiếng Anh, nhưng đại khái theo Bảng chữ cái ngữ âm quốc tế, hoặc tiếng Tây Ban Nha hoặc tiếng Đức. Điều này có nghĩa: Tùy thuộc vào chiều dài, “a” là khả năng phát âm như trong “b u t” hoặc “f một ther”, “e” như trong “b đ t” hoặc “b e d”, “i” như trong “f i sh” hay “b ee ”, “o” là “d o ll” hoặc tiếng Pháp “bistro ”và‘u’như trong‘b u tcher’hoặc‘c oo l’. Hầu hết các nguyên âm đều ngắn, trừ trừ i iv ở âm tiết cuối và tất cả các nguyên âm ở vị trí từ cuối cùng. Trọng âm nằm ở âm tiết cuối trừ khi có dấu hiệu cấp tính khác.

    Bài viết dịch từ https://hhr-m.userweb.mwn.de/he-vowels/

  • Ai là người nuôi cá? Câu đố của Einstein 98% dân số thế giới không giải được!

    Ai là người nuôi cá? Câu đố của Einstein 98% dân số thế giới không giải được!

    Ai là người nuôi cá? Câu đố của Einstein 98% dân số thế giới không giải được!

    Albert Einstein (14 tháng 3 năm 1879 – 18 tháng 4 năm 1955) là một nhà bác học thiên tài người Đức, ông là một trong những nhân vật quan trọng nhất với khoa học trong thế kỷ 20. Người ta ước tính ông có chỉ số IQ vào khoảng 160 đến 190 (IQ của Albert Einstein là bao nhiêu?).

    chỉ số iq của einstein

    Nhưng như người ta vẫn nói, thiên tài thì thường có phần… lập dị. Ngay từ khi còn nhỏ, Einstein đã tỏ ra thông tuệ khác người, có thể đưa ra những vấn đề không nhiều người đủ khả năng giải đáp. Như vào cuối thế kỷ XIX, Einstein – lúc này chỉ là một cậu bé – đã đưa ra câu đố cực kỳ hóc búa mà ông tự tin cho rằng chỉ 2% dân số thế giới có thể trả lời. Nó nổi tiếng đến mức được người đời sau này biết đến với tên gọi “câu đố của Einstein”.

    Câu đố này như thế nào mà chỉ có 2% trả lời được? Đó là một bài toán đề thì ngắn, mà có đến 15 gợi ý khác nhau. Hãy thử xem bạn có trả lời được không

    1. Câu đố của Einstein: Ai là người nuôi cá?

    • Có 5 ngôi nhà cạnh nhau, mỗi ngôi nhà được sơn một màu khác nhau.
    • Chủ sở hữu của mỗi ngôi nhà đến từ 5 quốc gia khác nhau.
    • Mỗi người chỉ thích một loại đồ uống, chỉ hút thuốc lá từ một hãng, và có nuôi một con vật. Tuy nhiên, tất cả không trùng nhau, nghĩa là không ai hút thuốc, uống nước hay có vật nuôi giống nhau.

    Tiếp theo là các gợi ý:

    1. Người Anh sống trong ngôi nhà màu đỏ.

    2. Người Thụy Điển nuôi chó.

    3. Người Đan Mạch thích uống trà.

    4. Ngôi nhà màu xanh lục nằm cạnh và bên trái ngôi nhà màu trắng.

    5. Chủ nhà xanh lục thích uống cà phê.

    6. Người hút thuốc hãng Pall Mall nuôi chim.

    7. Chủ nhà vàng hút thuốc Dunhill.

    8. Chủ nhà ở giữa dãy phố thích uống sữa.

    9. Người Na-Uy sống trong ngôi nhà đầu tiên.

    10. Người hút thuốc hãng Blends sống cạnh nhà người nuôi mèo.

    11. Người nuôi ngựa sống cạnh người hút thuốc lá Dunhill.

    12. Người hút thuốc Blue Master thích uống bia.

    13. Người Đức hút thuốc Prince.

    14. Người Na-Uy sống cạnh ngôi nhà màu xanh dương.

    15. Người hút thuốc Blends có người hàng xóm chỉ luôn uống nước lọc.

    Giờ thì các bạn hãy cùng lấy giấy, bút và thử trả lời bài toán hóc búa này của Einstein nhé!

    2. Lời giải câu đố của Einstein

    Để giải được câu đố này, bạn cần lập một bảng, sau đó suy luận để tìm ra các phương án hợp lý. Cách giải chi tiết xem trong video sau:

    CAU DO CUA EINSTEIN

    Đáp án: Người Đức nuôi cá.

    3. Các câu đố khác của nhà bác học Einstein

    3.1. Ai trộm bánh quy gừng?

    Câu đố của nhà Vật lý thiên tài Albert Einstein yêu cầu người giải suy luận để tìm ra câu trả lời đúng.

    • Holly, Cameron, Julieanne, Alex và Jackie là bạn bè. Mỗi người trong số họ trộm một chiếc bánh quy của thương hiệu họ yêu thích được đặt trong một cái lọ.
    • Mỗi người ăn nó tại một địa điểm cụ thể và uống kèm loại sữa khoái khẩu.
    • Jackie là ở cạnh người ăn bánh quy trên ghế dài.
    • Những chiếc bánh hiệu Arnotts được đựng trong chiếc lọ tròn.
    • Người ngồi cạnh Cameron ăn bánh trên bàn.
    • Người ăn bánh Oreos ở trong phòng chứa đồ.
    • Julieanne thích bánh quy hiệu Paradise.
    • Người uống sữa vị chuối ngồi ở giữa và sở hữu chiếc lọ cao cổ.
    • Người ngồi đầu tiên thích sữa vani.
    • Holly ngồi ngoài cùng bên phải.
    • Người ăn trong phòng ngủ uống sữa vị dâu tây.
    • Người sở hữu chiếc lọ cao cổ ngồi cạnh người sở hữu lọ hình vuông.
    • Cameron uống sữa caramel.
    • Người thích bánh quy hiệu Dick Smith ngồi cạnh người thích bánh quy hiệu Coles.
    • Người thích bánh quy thương hiệu No Frills ngồi cạnh người sở hữu chiếc lọ tròn.
    • Người lấy trộm bánh quy 100s & 1000s ngồi cạnh người sở hữu chiếc lọ bằng đồng.
    • Người thứ hai từ bên phải thích bánh hiệu No Frills và ngồi cạnh người sở hữu chiếc lọ tròn.
    • Người đầu tiên bên trái trộm bánh quy choc chip.
    • Người ăn bánh hiệu Dick Smith ngồi cạnh người ăn bánh hiệu Paradise.
    • Người thứ hai từ bên trái sở hữu chiếc lọ bằng đồng.
    • Julieanne ngồi bên phải người uống sữa vị dâu tây.
    • Người uống sữa vị sôcôla ngồi ở bàn.
    • Những chiếc bánh hiệu Paradise bị ăn trong phòng bếp.
    • Người ăn bánh Tiny Teddies không sở hữu chiếc lọ hình tròn.
    • Những chiếc bánh hiệu Coles được đặt trong lọ nhỏ.

    Bánh quy gừng bị đánh cắp. Vậy, ai đã trộm nó?

    3.2. Câu đố về 5 con tàu

    • Có 5 con tàu đang đỗ tại một bến cảng.
    • Chiếc tàu ở giữa có một ống khói màu đen. Tàu Anh rời cảnh lúc 9h.Tàu Hy Lạp rời cảng lúc 6h và chở cà phê.
    • Tàu Pháp có ống khói màu xanh dương, nằm bên trái chiếc tàu chở cà phê.
    • Bên phải chiếc tàu chở ca cao là tàu đi Marseille.
    • Tàu Brazil đi Manila.
    • Bên cạnh tàu chở gạo là tàu có ống khói màu lục.
    • Tàu đi Genoa rời cảng lúc 9h.
    • Tàu Tây Ban Nha rời cảng lúc 7h và nằm bên phải tàu đi Marseille.
    • Tàu có ống khói màu đỏ đi Hamburg.
    • Bên cạnh tàu rời cảng lúc 7h là tàu có ống khói mà trắng.
    • Tàu ở ngoài cùng chở ngô.
    • Tàu có ống khói màu đen rời cảng lúc 8h.
    • Tàu chở ngô thả neo cạnh tàu chở gạo.
    • Tàu đi Hamburg rời cảng lúc 6h.

    Như vậy, tàu nào đi Port Said? Tàu nào chở trà?

    Lưu ý, tàu đậu bên trái/phải không nhất thiết phải nằm bên cạnh (có thể tiến phía trước hoặc lùi phía sau hay cách một số tàu ở giữa).

  • 120 câu đố vui có lời giải

    120 câu đố vui có lời giải

    120 CÂU ĐỐ VUI CÓ ĐÁP ÁN

    Xem thêm 49 bài toán lớp 4 thử thách trí thông minh

    Câu đố 1: Bạn hãy tưởng tượng bạn đang đi trên 1 con thuyền trên 1 dòng sông có rất nhiều cá ăn thịt đến giữa dòng bỗng thuyền của bạn bị thủng 1 lỗ rất to, sau vài phút nữa thuyền sẽ chìm và chắc chắn bạn sẽ là bữa ăn những con cá này. Bạn làm cách nào đơn giản nhất để thoát ra khỏi cái hoàn cảnh chết tiệt này?

    Đáp án: Đừng tưởng tượng nữa.

    Câu đố 2: Một người đi vào rừng sâu để thám hiểm, thật không may cho ông ta khi bắt gặp 1 con đười ươi rất hung dữ muốn xé xác ông ta ra. Trong tay ông ta có 2 con dao, ông sợ quá vứt 2 con dao ra đó, con đười ươi nhặt lên và sau vài phút nó nằm vật xuống đất chết luôn. Bạn có biết tại sao không?

    Đáp án: Nó cầm dao và đâm vào ngực nó (đười ươi hay tự đấm vào ngực mình)                                                          

    Câu đố 3: Có một cây cầu có trọng tải là 10 tấn, có nghĩa là nếu vượt quá trọng tải trên 10 tấn thì cây cầu sẽ sập. Có một chiếc xe tải chở hàng, tổng trọng tải của xe 8 tấn + hàng 4 tấn = 12 tấn. Vậy đố các bạn làm sao bác tài qua được cây cầu này (Không được bớt hàng ra khỏi xe)?

    Đáp án: Bác tài cứ đi qua thôi, còn xe thì ở lại.

    Câu đố 4: Trên đồng cỏ có 6 con bò, đếm đi đếm lại chỉ có 12 cái chân. Tại sao?

    Đáp án: Con bò này cưỡi lên lưng con bò kia theo dây chuyền và vòng tròn nên mỗi con chỉ có 2 chân!

    Câu đố 5: Nếu chỉ có một que diêm, trong một ngày mùa đông giá rét, bạn bước vào căn phòng có một cây đèn, một bếp dầu, và một bếp củi, bạn thắp gì trước tiên?

    Đáp án: Que diêm.

    Câu đố 6: Một kẻ giết người bị kết án tử hình. Hắn ta phải chọn một trong ba căn phòng: phòng thứ nhất lửa cháy dữ dội, phòng thứ hai đầy những kẻ ám sát đang giương súng, và phòng thứ ba đầy sư tử nhịn đói trong ba năm. Phòng nào an toàn nhất cho hắn?

    Đáp án: Phòng 3 vì sư tử chết hết rồi

    Câu đố 7: 2 con vịt đi trước 2 con vịt, 2 con vịt đi sau 2 con vịt, 2 con vịt đi giữa 2 con vịt. Hỏi có mấy con vịt?

    Đáp án: 4.

    Câu đố 8: Con ma xanh đập 1 phát chết, con ma đỏ đập 2 phát thì chết. Làm sao chỉ với 2 lần đập mà chết cả 2 con?

    Đáp án: Đập con ma xanh trước là 1, con ma đỏ thấy thế sợ quá, mặt mày tái mét (chuyển sang xanh). Đập con ma xanh mới này nữa là đủ 2.

    Câu đố 9: Có 1 bà kia không biết bơi, xuống nước là bả chết. Một hôm bà đi tàu, bỗng nhiên tàu chìm, nhưng bà ko chết. Tại sao (ko ai cứu hết)?

    Đáp án: Bà ấy đi tàu ngầm.

    Câu đố 10: Cái gì đen khi bạn mua nó, đỏ khi dùng nó và xám xịt khi vứt nó đi?

    Đáp án: Than.

    Câu đố 11: Có 1 anh chàng làm việc trong 1 tòa nhà 50 tầng, nhưng anh ta lại chỉ đi thang máy lên đến tầng 35 rồi đoạn còn lại anh ta đi thang bộ.Tại sao anh ta lại làm như vậy?

    Đáp án: Vì cái thang máy đó không lên được tới tầng 50.

    Câu đố 12: Xã đông nhất là xã nào?

    Đáp án: Xã hội.

    Câu đố 13: Lịch nào dài nhất?

    Đáp án: Lịch sử.

    Câu đố 14: Con đường dài nhất là đường nào?

    Đáp án: Đường đời.

    Câu đố 15: Quần rộng nhất là quần gì?

    Đáp án: Quần đảo.

    Câu đố 16: Cái gì của chồng mà vợ thích cầm nhất (không nghĩ lung tung)?;

    Đáp án: Tiền!

    Câu đố 17: Cái gì mà đi thì nằm, đứng cũng nằm, nhưng nằm lại đứng?

    Đáp án: Bàn chân.

    Câu đố 18: Câu này nghĩa là gì: 1p’ => 4 = 1505

    Đáp án: 1 phút suy tư bằng 1 năm không ngủ.

    Câu đố 19: Núi nào mà bị chặt ra từng khúc?

    Đáp án: Thái Sơn.

    Câu đố 20: Bạn có thể kể ra ba ngày liên tiếp mà không có tên là thứ hai, thứ ba, thứ tư, thứ năm, thứ sáu, thứ bảy, chủ nhật?

    Đáp án: Hôm qua, hôm nay và ngày mai.

    Câu đố 21: Môn gì càng thắng càng thua?

    Đáp án: Môn đua xe đạp.

    Câu đố 22: Con gì đầu dê mình ốc?

    Đáp án: Con dốc.

    Câu đố 23: Con gì đập thì sống, không đập thì chết?

    Đáp án: Con tim.

    Câu đố 24: Có 1 đàn chuột điếc đi ngang qua, hỏi có mấy con?

    Đáp án: điếc là hư tai, hư tai là hai tư.

    Câu đố 25: Bỏ ngoài nướng trong, ăn ngoài bỏ trong là gì?

    Đáp án: Bắp ngô.

    Câu đố 26: Trong 1 cuộc thi chạy, nếu bạn vượt qua người thứ 2 bạn sẽ đứng thứ mấy?

    Đáp án: Thứ 2.

    Câu đố 27: Con gì không gáy ò ó o mà người ta vẫn gọi là gà?

    Đáp án: Gà con và gà mái.

    Câu đố 28: Có 1 con trâu. Đầu nó thì hướng về hướng mặt trời mọc, nó quay trái 2 vòng sau đó quay ngược lại sau đó lại quay phải hay vòng hỏi cái đuôi của nó chỉ hướng nào?

    Đáp án: Chỉ xuống đất.

    Câu đố 29: Con trai có gì quí nhất?

    Đáp án: Ngọc trai.

     Câu đố 30: Cơ quan quan trọng nhất của phụ nữ là gì?

    Đáp án: Hội Liên Hiệp Phụ Nữ.

    Câu đố 31: Sở thú bị cháy, con gì chạy ra đầu tiên?

    Đáp án: Con người.

    Câu đố 32: Khi Beckham thực hiện quả đá phạt đền, anh ta sẽ sút vào quả gì?

    Đáp án: Quả bóng.

    Câu đố 33: Có bao nhiêu chữ C trong câu sau đây: “Cơm, canh, cháo gì tớ cũng thích ăn!”

    Đáp án: 1 chữ C, ở chữ “Cơm”.

    Câu đố 34: Cái gì tay trái cầm được còn tay phải cầm không được?

    Đáp án: Tay phải.

    Câu đố 35: Có 2 người: 1 lớn, 1 bé đi lên đỉnh một quả núi. Người bé là con của người lớn, nhưng người lớn lại không phải cha của người bé, hỏi người lớn là ai?

    Đáp án: Mẹ.

    Câu đố 36: Từ gì mà 100% nguời dân Việt Nam đều phát âm sai?
    Đáp án: Từ “sai”.

    Câu đố 37: Tìm điểm sai trong câu: “Dưới ánh nắng sương long lanh triệu cành hồng khoe sắc thắm”

    Đáp án: Khoe sắc khoé!

    Câu đố 38: Ai cũng biết đỉnh núi Everest cao nhất thế giới, vậy sau khi đỉnh Everest được khám phá, đỉnh núi nào cao nhất thế giới?

    Đáp án: Everest.

    Câu đố 39 & Đáp án:

    Hôn con heo trong nhà gọi là -> Hôn thú

    Mong được hôn gọi là -> Cầu hôn

    Vừa mới hôn gọi là -> Tân hôn

    Hôn thêm cái nữa gọi là -> Tái hôn

    Đang hôn mà bị đẩy ra gọi là -> Từ hôn

    Không cho mà cứ hôn gọi là -> Ép hôn

    Hẹn sẽ hôn gọi là -> Hứa hôn

    Vua hôn gọi là -> Hoàng hôn

    Hôn chia tay gọi là -> Ly hôn

    Vừa hôn vừa ngửi gọi là -> Vị hôn

    Hôn vào không trung gọi là -> Hôn gió

    Hôn trong mơ gọi là -> Hôn ước

    Hôn mà mà quá sớm thì gọi là -> Tảo hôn

    Rất thích hôn gọi là -> Kết hôn

    Hôn mà bị hôn lại gọi là -> Đính hôn

    Câu đố 40: Trận chung kết của 1 cuộc thi vắt sữa bò (ai vắt được nhiều hơn thì thắng): người đàn bà vắt được 15 lít, người đàn ông vắt được 0 lít.

    Hỏi sao người đàn ông thắng?

    Đáp án: Người đàn bà vắt sữa con bò cái, còn người đàn ông vắt sữa con bò đực.

    Câu đố 41: Nắng ba năm ta chưa hề bỏ bạn. Là cái gì?

    Đáp án: Cái bóng.

    Câu đố 42: Một ly thuỷ tinh đựng đầy nước, làm thế nào để lấy nước dưới đáy ly mà không đổ nước ra ngoài?

    Đáp án: Dùng ống hút.

    Câu đố 43: Cái gì người mua biết , người dùng không bao giờ biết?

    Đáp án: Quan tài.

    Câu đố 44: Tại sao khi bắn súng người ta lại nhắm một mắt?

    Đáp án: Nhắm 2 mắt thì sẽ không thấy đường để bắn.

    Câu đố 45: Từ nào trong tiếng Việt có 9 từ?

    Đáp án: Chính hoặc chín.

    Câu đố 46: Hãy chứng minh 4 : 3 = 2

    Đáp án: 4 : 3 = tứ chia tam = tám chia tư = 8 : 4 = 2.

    Câu đố 47: Lại nước giải khát nào chứa sắt và canxi?

    Đáp án: Cafe (ca: canxi, Fe: sắt).

    Câu đố 48: Con cua đỏ dài 15 dm 1 phút chạy đua với con cua xanh dài 10 dm 1 phút. Con nào về đích trước?

    Đáp án: Con cua xanh, vì con cua đỏ đã bị luộc chín.

    Câu đố 49: Tại sao 30 người đàn ông và 2 người đàn bà đánh nhau tán loạn?

    Đáp án: Đang chơi cờ vua.

    Câu đố 50: Cái gì đánh bố, đánh mẹ , đánh anh, đánh chị, đánh em?

    Đáp án: Bàn chải đánh răng.

    Câu đố 51: Cái gì Adam có 2 mà Eva chỉ có 1?

    Đáp án: Chữ a.

    Câu đố 52: Cái gì của người con gái lúc nào cũng ẩm ướt?

    Đáp án: Cái lưỡi.

    Câu đố 53: Cái gì dài như trái chuối, cầm 1 lúc thì nó chảy nước ra?

    Đáp án: Que kem.

    Câu đố 54: Càng chơi càng ra nuớc?

    Đáp án: Chơi cờ.

    Câu đố 55: Làm sao để cái cân tự cân chính nó?

    Đáp án: Lật ngược cái cân lại.

    Câu đố 56: Những loài thú nào sau đây ăn cơm:

    1. sư tử                     b) cọp
    2. c) hà mã           d) voi

    Đáp án: Sư tử (con gái)

    Câu đố 57: Chứng minh: con gái = con dê.

    Đáp án: Con gái = thần tiên = tiền thân = trước khỉ = con dê.

    Câu đố 60: Câu chữ nào mà những người vui sướng khi nhìn thấy nó sẽ trở nên buồn bã và ngược lại, những người buồn bã u sầu khi thấy nó sẽ trở nên vui vẻ hơn.

    Đáp án: Điều đó rồi cũng qua đi.

    Câu đố 61: Hai người đào trong hai giờ thì được một cái hố. Vậy hỏi một người đào trong một giờ thì được mấy cái hố?

    Đáp án: 1 cái hố nhỏ hơn.

    Câu đố 62: Bên trái đường có một căn nhà xanh, bên phải đường có một căn nhà đỏ. Vậy, nhà trắng ở đâu?

    Đáp án: Ở Mỹ.

    Câu đố 63: Tại sao con chó không cắn được đuôi của mình:

    Đáp án: Vì đuôi nó không đủ dài.

    Câu đố 64: Trên nhấp dưới giật là đang làm gì?

    Đáp án: Đó là đang câu cá!

    Câu đố 65: Tay cầm cục thịt nắn nắn, tay vỗ mông là đang làm gì?

    Đáp án: Đó là bà mẹ đang cho con bú!

    Câu đố 66: Cái gì bằng cái vung, vùng xuống ao. Đào chẳng thấy, lấy chẳng được?

    Đáp án: Đó là mặt trăng!

    Câu đố 67: Con trai và đàn ong có điểm gì khác nhau?

    Đáp án: Con trai là con vật sống dưới nước, còn đàn ong sống trên cây!

    Câu đố 68: Cái gì trong trắng ngoài xanh trồng đậu trồng hành rồi thả heo vào?

    Đáp án: Bánh chưng

    Câu đố 69: Ở Việt Nam, rồng bay ở đâu và đáp ở đâu?

    Đáp án: Rồng bay ở Thăng Long và đáp ở Hạ Long!

    Câu đố 70: Nếu bạn nhìn thấy con chim đang đậu trên nhánh cây, làm sao để lấy nhánh cây mà không làm động con chim?

    Đáp án: Đợi con chim bay đi.

    Câu đố 71: 5 chia 3 bằng 2 khi nào?

    Đáp án: Khi ta làm sai.

    Câu đố 72: Hoa gì biết ăn, biết nói, biết hát …?

    Đáp án: Hoa hậu.

    Câu đố 73: Vua gọi hoàng hậu bằng gì?

    Đáp án: Bằng miệng.

    Câu đố 74: Một người đàn ông ngày nào cũng ăn xài cực kỳ hoang phí, tiêu tiền như tiêu nước, vậy mà bây giờ trở thành triệu phú. Hỏi tại sao?

    Đáp án: Tại vì trước đây ông ta là tỷ phú

    Câu đố 75: Người ta phát hiện ra xác chết của một chàng trai treo cổ chết ở nóc nhà. Dưới chân cậu ta cách khoảng 20 cm đến sàn nhà là một vũng nước lớn. Hỏi cậu ta làm sao để có thể leo lên nóc nhà mà tự tử được?

    Đáp án: Cậu ta tự tử bằng cách đứng lên tảng nước đá!

    Câu đố 76: Bệnh gì bác sỹ bó tay?

    Đáp án: Đó là bệnh gãy tay!

    Câu đố 77: Bà đó ,bả chết bả bay lên trời. Hỏi bà ấy chết năm bao nhiêu tuổi và tại sao bà ấy chết?

    Đáp án: bà đó là bò đá —> bò đá bà chết, bả bay là bảy ba–> bà ấy chết năm bà ấy 73 tuổi!

    Câu đố 78: Có 1 đàn chim đậu trên cành, người thợ săn bắn cái rằm. Hỏi chết mấy con?

    Đáp án: rằm là 15 —> chết 15 con

    Câu đố 79 : Con kiến bò lên tai con voi nói gì với con voi mà ngay tức khắc con voi nằm lăn ra chết!

    Đáp án: Nói là em đã có thai với anh rồi!

     

    Câu đố 80: Có 1 chiếc thuyền tối đa là chỉ chở được hai người, nếu thêm người thứ 3 sẽ bị chìm ngay lập tức. Người ta trông thấy ba người Mỹ đen và ba người Mỹ trắng ngồi trên chiếc thuyền đó mà không bị chìm. Hỏi tại sao?

    Đáp án: Bởi vì trên chiếc thuyền đó sự thật là có đúng 2 người đi. Đó là ba của người Mỹ đen và ba của người Mỹ trắng!

    Câu đố 81: Có một tàu điện đi về hướng nam. Gió hướng tây bắc. Vậy khói từ con tàu sẽ theo hướng nào?

    Đáp án: Tàu điện làm gì có khói

    Câu đố 82. Làm thế nào để không đụng phải ngón tay khi bạn đập búa vào một cái móng tay?

    Đáp án:  Cầm búa bằng cả 2 tay

    Câu đố 83. Cái đầu giống mèo, chân giống mèo, và tai giống con mèo, nhưng không phải con mèo. Vậy là con gì?

    Đáp án: Là mèo con.

    Câu đố 84: Miệng rộng nhưng không nói một từ, là gì? Con sông

    Câu đố 85: Không bố mẹ nào phản ứng khi giáo viên đánh những đứa trẻ trong lớp, tại sao?

    Đáp án:  Vì đây là lớp học trong trại mồ côi.

    Câu đố 86: Cái gì luôn ở phía trước bạn, mà bạn không bao giờ nhìn thấy?

    Đáp án:Tương lai

    Câu đố 87. Cái gì bạn không mượn mà trả?

    Đáp án: Lời cám ơn

    Câu đố 88: Cái gì luôn đi đến mà không bao giờ đến nơi?

    Đáp án: Ngày mai

    Câu đố 89: Vào lúc nào thì đồng hồ gõ 13 tiếng?

    Đáp án: Là lúc bạn nên đem đồng hồ đi sửa

    Câu đố 90: Lúc lý tưởng để ăn trưa?

    Đáp án: Sau bữa ăn sáng.

    Câu đố 91: Có ba quả táo trên bàn và bạn lấy đi hai quả. Hỏi bạn còn bao nhiêu quả táo?

    Đáp án: 2 quả (Vì bạn đã lấy đi 2 quả rồi còn gì).

    Câu đố 92: Bố mẹ có sáu người con trai, mỗi người con trai có một em gái. Hỏi gia đình đó có bao nhiêu người?

    Đáp án: 9 người (bao gồm 6 người con trai, 1 cô con gái và bố mẹ).

    Câu đố 93: 30 chia 1/2, và cộng thêm 10, bằng bao nhiêu?

    Đáp án: Bằng 70.

    Câu đố 94: Con số lớn nhất có duy nhất hai chữ số?

    Đáp án: 9^9 (= 9x9x9x9x9x9x9x9x9 lớn quá trời lớn)

    Câu đố 95: Có hai bình rộng miệng đựng đầy nước. Làm sao để cho tất cả nước vào trong một cái chậu mà vẫn biết nước nào của bình nào (không được cho cả bình hay bất kỳ dụng cụ đựng nước nào vào chậu)?

    Đáp án: Cho cả 2 vào tủ lạnh để đông thành đá rồi cho chung vào một chậu.

    Câu đố 96: Một anh chàng đẹp trai, nhưng trên đầu chỉ có 3 cọng tóc. Bỗng 1 ngày anh quyết định bứt 1 cọng giữa. Hỏi anh bứt để làm gì?

    Đáp án: Anh đẹp trai bứt 1 cọng để bổ giữa

    Câu đố 97: Ba thằng Què đi trước 1 thằng què. Hỏi có mấy thằng què?

    Đáp án: Có 1 thằng què

    Câu đố 98: Mèo trắng là bạn của mèo đen.Mèo trắng bỏ mèo đen theo mèo vàng.Một thời gian sau, mèo trắng gặp lại mèo đen.Mèo trắng sẽ nói gì?

    Đáp án: Mèo không biết nói thì phải

    Câu đố 99: Có 1 con rết 100 chân dang đi dạo mát bổng nhiên đụng phải một bãi phân trâu. Rết ngậm ngùi bước tiếp. Hỏi khi đi qua bãi phân châu rết còn mấy chân?

    Đáp án: Còn 98 chân, 2 chân nó bịt mũi rồi

    Câu đố 100: Không phải lúc nào cũng thấy nó, không phải lúc nào cũng chạm được nó?

    Đáp án: Cái bóng

    Câu đố 101: Hãy đối lại một câu trái nghĩa với câu này:”đất lành chim đậu”

    Đáp án: Đất gỗ chim đi.

    Câu đố 102: Con gì càng to càng nhỏ.

    Đáp án: Con cua

    Câu đố 103: Đố em cái gì khi xài thì quăng đi, không xài thì lấy lại?

    Đáp án: Cái neo thuyền

    Câu đố 104: Tôi chu du khắp thế giới mà tôi vẫn ở nguyên một chỗ, tôi là ai?

    Đáp án: Tem thư

    Câu đố 105: Con gì bỏ cái đuôi thành con ngựa?

    Đáp án: Con mèo, vì Mèo là Mão bỏ cái đuôi là bỏ chữ o thành Mã, Mã là con ngựa

    Câu đố 106: Cái gì chứa nhiều nước nhất mà không ướt?

    Đáp án: Bản đồ

    Câu đố 107: Trời đang âm u, có 3 thằng mù chung một cây dù , Hỏi thằng nào ướt?

    Đáp án: Không thằng nào cả

    Câu đố 108: Người da đen tắm biển đen , Vậy hỏi họ bị gì?

    Đáp án: Bị ướt

    Câu đố 109: 1 kg bông gòn và 1 kg sắt ,kg nào nặng hơn?

    Đáp án: Bằng nhau

    Câu đố 110: Nhà Lan có 3 anh em, người anh đầu tên là Nhất Hào, người thứ hai tên là Nhị Hào. Hỏi người thứ 3 tên gì?

    Đáp án: Lan là người thứ 3

    Câu đố 111: Có ông bố người da đen, mẹ người da trắng. Họ vừa mới sinh ra 1 em bé. Hỏi em bé đó có hàm răng màu gì?

    Đáp án: Em bé mới sinh nên chưa có răng. 

    Câu đố 112: Tại sao có những người đi taxi nhưng sao họ lại không trả tiền?

    Đáp án: Vì họ là tài xế taxi đó.

    Câu đố113: Có 3 người lùn xếp hàng dọc đi vào hang. Người đi sau cầm 1 cái xô, người đi giữa cầm 1 cái xẻng, hỏi người đi trước cầm gì?

    Đáp án: Người đó “cầm đầu” tức là đại ca cầm đầu, nó không phải cầm cái vật gì hết!

    Câu đố 114: Có một cây lê có 2 cành, mỗi cành có 2 nhánh lớn, mỗi nhánh lớn có 2 nhánh nhỏ, mỗi nhánh nhò có hai cái lá, cạnh mỗi cái lá có hai quả. Hỏi trên cây đó có mấy quả táo?

    Đáp án: Không có quả táo nào vì lê không thể ra quả táo nào trên cây được

    Câu đố 115: Có một rổ táo, trong rổ có ba quả, làm sao để chia cho 3 người, mỗi người một quả mà vẫn còn một quả trong rổ?

    Đáp án: Thì đưa cho 2 người đầu mỗi người 1 quả. Còn 1 quả trong rổ đưa nguyên cả cái rổ đựng quả táo cho người còn lại thì 3 người mỗi người đều có 1 quả, và cũng có 1 quả trong rổ.

    Câu đố 116: Ở một xứ nọ, có luật lệ rằng: Ai muốn diện kiến nhà vua thì phải nói một câu. Nếu câu nói thật thì sẽ bị chém đầu, còn nếu là dối thì bị treo cổ. Vậy để gặp được nhà vua của xứ đó, ta phải nói như thế nào?

    Đáp án: Để gặp được nhà vui, người đó phải nói “tôi sẽ bị treo cổ!”.Nếu như câu nói này là thật thì hắn ta sẽ bị chém đầu, nhưng nếu đem hắn ta đi chém đầu thì câu nói “tôi sẽ bị treo cổ” của hắn là dối, mà nếu vậy thì hắn sẽ bị treo cổ, mà nếu treo cổ hắn thì câu nói “tôi sẽ bị treo cổ” của hắn là thật .Nhờ vậy mà gã đó gặp được nhà vua trong khi vẫn bảo toàn được tính mạng.

    Câu đố 117: Giả sử ta có 1 khúc vải, cắt nó ra làm 100 khúc, thời gian để cắt 1 khúc vải là 5 giây. Hỏi nếu cắt liên tục không ngừng nghỉ thì trong bao lâu sẽ cắt xong?

    Đáp án: 495 giây bởi vì 99 khúc (khúc cuối cùng ko phải cắt) x 5 giây = 495 giây.

    Câu đố 118: Có 1 người đứng ở chân cầu. Ở giữa cầu có một con gấu rất hung dữ không cho ai qua cầu hết. Người đó sẽ mất hết 5 phút để đi từ chân cầu cho đến giữa cầu và con gấu cũng chỉ ngủ có 5 phút là tỉnh dậy. Hỏi người đó làm sao để qua được bên kia?

    Đáp án: Đi đến giữa cầu và quay mặt ngược lại. Con gấu thức dậy tưởng người đó từ bên kia qua nên rượt trở lại. Thế là người đó đã qua được cầu.

    Câu đố 119: Con gấu trúc ao ước gì mà không bao giờ được?
    Đáp án: Vì gấu trúc chỉ có 2 màu trắng đen nên nó ao ước được chụp hình màu.Vậy mà không thể được vì chụp cỡ nào cũng chỉ có trắng đen mà thôi!

    Câu đố 120: Con gì ăn lửa với nước than?

    Đáp án: Đó là con tàu.

  • Xác suất có điều kiện – Công thức Bayes

    Xác suất có điều kiện – Công thức Bayes

    xác suất có điều kiện, định lý công thức bayes

    Xác suất có điều kiện – Công thức Bayes

    Công thức tính Xác suất có điều kiện và định lý Bayes (Bayes’ Theorem) là các công cụ mạnh mẽ để tính xác suất xảy ra của một sự kiện (biến cố – event) ngẫu nhiên A khi biết sự kiện liên quan B đã xảy ra.

    Mời xem thêm bài tập xác suất thống kê của ĐH Bách Khoa HN:

    1. Xác suất có điều kiện

    1.1. Ví dụ về xác suất có điều kiện

    Xác suất có điều kiện (Conditional probability) là xác suất của một biến cố $ A$ nào đó khi biết rằng một biến cố $ B$ khác xảy ra. Ký hiệu $ \mathrm{P}(A|B)$, và đọc là “xác suất của $ A$, biết $ B$”.

    Chẳng hạn, rút một lá bài từ một bộ bài có $52$ lá, xác suất để lấy được một lá Át là $ 1/52$. Nhưng nếu người chơi đã rút được lá Át rồi, nếu tiếp tục rút thêm một lá bài nữa thì thì để nhận được một lá Át nữa, xác suất chỉ còn là $ 1/51.$

    Để hiểu rõ hơn, chúng ta xét tiếp các ví dụ nữa.

    Ví dụ 1. Một bình đựng 5 viên bi kích thước và chất liệu giống nhau, chỉ khác nhau về màu sắc. Trong đó có 3 viên bi xanh và 2 viên bi đỏ. Lấy ngẫu nhiên từ bình ra một viên bi ta được viên bi màu xanh, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được viên bi đỏ ở lần thứ hai.

    Hướng dẫn. Gọi $ A$ là biến cố: “Lấy được một viên bi đỏ ở lần thứ hai”. Vì một viên bi xanh đã được lấy ra ở lần thứ nhất nên còn lại trong bình 4 viên bi trong đó số viên bi đỏ là 2 và số viên bi xanh cũng là 2. Do đó, xác suất cần tìm là $$ \mathrm{P}(A)=\frac{2}{4}=0{,}5. $$

    Ví dụ 2. Gieo một con xúc xắc cân đối và đồng chất hai lần. Tính xác suất để lần đầu gieo được mặt 1 chấm biết rằng tổng số chấm trong hai lần gieo không vượt quá 3.

    Xác suất có điều kiện - Công thức Bayes 2

    Hướng dẫn. Không gian mẫu là $$ \Omega=\big\{\left(i, j\right): 1\leqslant i, j\leqslant 6\big\}, $$ trong đó cặp số $ \left(i, j\right)$ thể hiện việc lần gieo đầu xuất hiện mặt $ i$ chấm, lần sau xuất hiện mặt $ j$ chấm. Không gian mẫu có tất cả $6\times 6=36$ phần tử.

    Gọi $ A$ là biến cố: “Lần đầu gieo xuất hiện mặt 1 chấm”, $ B$ là biến cố: “Tổng số chấm trong hai lần gieo không vượt quá 3”. Chúng ta dễ dàng liệt kê được các phần tử thuận lợi cho từng biến cố là
    \begin{align}
    A=&\big\{\left(1, 1\right), \left(1, 2\right), \left(1, 3\right), \left(1, 4\right), \left(1, 5\right), \left(1, 6\right)\big\},\\
    B=&\big\{\left(1, 1\right), \left(1, 2\right), \left(2, 1\right)\big\},\\
    AB=&\big\{\left(1, 1\right), \left(1, 2\right)\big\}.
    \end{align}

    Dễ dàng đếm được số phần tử của $A,B,AB$ lần lượt là $6$, $3$, $2$. Do đó, theo định nghĩa cổ điển của xác suất thì ta có

    $$ \mathrm{P}(A)=\frac{6}{36}, \quad \mathrm{P}(B)=\frac{3}{36},\quad \mathrm{P}(AB)=\frac{2}{36} .$$

    Nếu biết rằng $ B$ đã xảy ra thì $ A$ xảy ra khi một trong hai kết quả $ \left(1, 1\right)$ và $ \left(1, 2\right)$ xảy ra. Do đó, xác suất của $ A$ với điều kiện $ B$ là $$ \mathrm{P}(A | B)=\frac{2}{3}. $$ Nhận xét rằng $$ \frac{2}{3}=\frac{{2}/{36}}{{3}/{36}}=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)} $$ hay chính là $$ \mathrm{P}(A | B)=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}. $$ Từ đó, chúng ta có công thức tính xác suất có điều kiện như sau đây.

    Nếu bài viết hữu ích, bạn có thể  tặng tôi 1 cốc cafe vào số tài khoản Agribank 3205 215 033 513.  Xin cảm ơn!

    1.2. Công thức tính xác suất có điều kiện

    Giả sử số các kết quả đồng khả năng có thể xảy ra khi thực hiện phép thử đó là $ N$, số kết quả thuận lợi cho biến cố $ B$ là $ m$ và số kết quả thuận lợi cho biến cố $ AB$ là $n $.

    Theo định nghĩa cổ điển của xác suất thì $$ \mathrm{P}(B)=\frac{m}{N}, \mathrm{P}(AB)=\frac{n}{N}. $$

    Khi biến cố $ B$ đã xảy ra thì số các kết quả đồng khả năng của phép thử có thể xảy ra đối với biến cố $ A$ là $ m$, trong đó có $ n$ kết quả thuận lợi cho $ A$ xảy ra. Do đó, xác suất của biến cố $ A$ khi biết $ B$ đã xảy ra là
    $$ \mathrm{P}(A | B)=\frac{n}{m}=\frac{n/N}{m/N}=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}. $$

    Từ đó, chúng ta có công thức tính xác suất có điều kiện như sau:

    Xác suất có điều kiện của biến cố $ A$ với điều kiện $ B$ là một số được ký hiệu là $ \mathrm{P}(A | B)$ xác định bởi công thức $$ \mathrm{P}(A | B)=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}, \mathrm{P}(B)>0. $$

    Từ định nghĩa trên ta dễ dàng nhận được các tính chất sau của xác suất có điều kiện:

    • $ \mathrm{P}(A | B)\geqslant 0.$
    • $ \mathrm{P}\left(\Omega | B\right)=\mathrm{P}\left(B | B\right)=1.$
    • Nếu $ A_1, A_2,\ldots, A_n$ là các biến cố xung khắc từng đôi một, nghĩa là $ A_iA_j=\varnothing$ với mọi $ i\neq j$, ta có $$ \mathrm{P} \left( \left(\bigcup\limits_{i=1}^{n}A_i \right) \Bigg| B \right)=\sum\limits_{i=1}^{n}\mathrm{P}\left(A_i | B\right). $$

    Ví dụ 3. Gieo đồng thời ba con xúc xắc cân đối đồng chất. Tính xác suất để tổng số chấm xuất hiện trên ba con bằng 8 biết rằng ít nhất có một con xuất hiện mặt 5 chấm.

    Hướng dẫn. Không gian mẫu gồm các phần tử $$ \Omega=\big\{\left(i, j, k\right): 1\leqslant i, j, k\leqslant 6\big\}, $$ trong đó bộ số $ \left(i, j, k\right)$ kí hiệu cho việc “con xúc xắc thứ nhất xuất hiện mặt $ i$ chấm, con xúc xắc thứ hai xuất hiện mặt $ j$ chấm và con xúc xắc thứ ba xuất hiện mặt $ k$ chấm”.

    Gọi $ A$ là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8”, $ B$ là biến cố: “Ít nhất một con xúc xắc ra 5 chấm”. Ta có $$ \mathrm{P}(A | B)=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}. $$

    Vì $ B$ là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm” nên $ \overline{B}$ là biến cố: “Không có con xúc xắc nào xuất hiện mặt 5 chấm”, do đó $$ \overline{B}=\big\{\left(i, j, k\right): 1\leqslant i, j, k\leqslant 6, i, j, k\neq 5\big\}. $$

    Suy ra $$ \mathrm{P}(\overline{B})=\frac{|\overline{B}|}{|\Omega|}=\frac{5^3}{6^3}. $$

    Do đó $$ \mathrm{P}(B)=1-\mathrm{P}(\overline{B})=1-\frac{5^3}{6^3}=\frac{91}{216}. $$

    Ta thấy $ AB$ là biến cố: “Tổng số chấm xuất hiện trên ba con xúc xắc bằng 8 và ít nhất một con xúc xắc ra 5 chấm”, do đó $$ AB=\big\{\left(1, 2, 5\right), \left(1, 5, 2\right), \left(2, 1, 5\right), \left(2, 5, 1\right), \left(5, 1, 2\right),\left(5, 2, 1\right)\big\}. $$

    Suy ra $$ \mathrm{P}(AB)=\frac{|AB|}{|\Omega|}=\frac{15}{6^3}=\frac{15}{216}. $$

    Vậy xác suất cần tìm là $$ \mathrm{P}(A | B)=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}=\frac{{15}/{216}}{{91}/{216}}=\frac{15}{91}. $$

    Ví dụ 4. Một gia đình có 2 đứa trẻ. Biết rằng có ít nhất 1 đứa trẻ là con gái. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu?

    Hướng dẫn. Chúng ta có các nhận xét sau:

    • Xác suất để một đứa trẻ là trai hoặc gái là bằng nhau và bằng $ 1/2$.
    • Giới tính cả 2 đứa trẻ là ngẫu nhiên và không liên quan đến nhau.

    Lời giải. Do gia đình có 2 đứa trẻ nên sẽ có thể xảy ra 4 khả năng:

    (trai, trai), (gái, gái), (gái, trai), (trai, gái).

    Gọi $ A$ là biến cố “Cả hai đứa trẻ đều là con gái” và $ B$ là biến cố “Có ít nhất một đứa trẻ là con gái” thì có $$ \mathrm{P}(A)=\frac{1}{4},\quad \mathrm{P}(B)=\frac{3}{4}. $$
    Do nếu xảy ra $ A$ thì đương nhiên sẽ xảy ra $ B$ nên ta có: $$ \mathrm{P}(AB) = \mathrm{P}(A) =\frac{1}{4}. $$
    Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là
    $$\mathrm{P}(A | B) = \dfrac{\mathrm{P}\left(A,B\right)}{\mathrm{P}(B)} = \dfrac{{1}/{4}}{{3}/{4}} = \frac{1}{3}.$$
    Bằng trực quan ta cũng có thể nhìn ra xác suất này. Khi biết một đứa trẻ là gái, giới tính của 2 đứa trẻ sẽ có 3 khả năng: (trai, gái), (gái, trai), (gái, gái).

    Ví dụ 5. Một hộp chứa 8 bi trắng, 2 bi đỏ. Lần lượt bốc từng bi. Giả sử lần đầu tiên bốc được bi trắng. Xác định xác suất
    lần thứ 2 bốc được bi đỏ.

    Hướng dẫn. Gọi $ B$ là biến cố lần 1 bốc được bi trắng, $ A$ là biến cố lần 2 bốc được bi đỏ. Xác suất lần 2 bốc được bi đỏ khi lần 1 đã bốc được bi trắng là $$ \mathrm{P}(A | B)=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}=\frac{8/10\times 2/9}{8/10}=\frac{2}{9}. $$

    2. Công thức nhân xác suất

    2.1. Công thức nhân xác suất

    Từ công thức tính xác suất có điều kiện $$ \mathrm{P}(A | B)=\frac{\mathrm{P}(AB)}{\mathrm{P}(B)}, \quad \mathrm{P}(B|A)=\frac{\mathrm{P}(AB)}{\mathrm{P}(A)},$$ ta suy ra công thức nhân xác suất $$ \mathrm{P}(AB)=\mathrm{P}(B)\mathrm{P}(A | B)=\mathrm{P}(A)\mathrm{P}\left(B | A\right), $$ với $ \mathrm{P}(A)>0{,} \mathrm{P}(B)>0$.

    Công thức nhân xác suất sử dụng trong một số trường hợp, khi mà chúng ta có thể biết ngay xác suất $ \mathrm{P}\left(B | A\right)$ hoặc $ \mathrm{P}(A | B)$ thì sẽ tính được xác suất $ \mathrm{P}(AB)$.

    Ví dụ 1. Trong hộp có 20 nắp chai bia Tiger, trong đó có 2 nắp ghi “Chúc mừng bạn đã trúng thưởng”. Bạn được chọn lên rút thăm lần lượt hai nắp chai bia, tính xác suất để cả hai nắp đều trúng thưởng.

    Hướng dẫn. Gọi $ A$ là biến cố “nắp chai bia thứ nhất trúng thưởng”, $ B$ là biến cố “nắp chai bia thứ hai trúng thưởng”, $ C$ là biến cố “cả 2 nắp đều trúng thưởng”.

    Khi bạn rút thăm lần đầu thì trong hộp có 20 nắp trong đó có 2 nắp trúng nên $$ \mathrm{P}(A)=\frac{2}{20}. $$

    Khi biến cố $ A$ đã xảy ra thì còn lại 19 nắp trong đó có 1 nắp trúng thưởng. Do đó $$ \mathrm{P}\left(B/A\right) = \frac{1}{19}. $$
    Suy ra, xác suất để cả hai nắp đều trúng thưởng là $$ \mathrm{P}\left(C\right) = \mathrm{P}(A). \mathrm{P}\left(B/A\right) = \frac{2/20}{1/19} = \frac{1}{190} \approx 0{,}0053. $$

    Ví dụ 2. Một bình đựng 5 viên bi kích thước, chất liệu như nhau, trong đó có 3 viên bi xanh và 2 viên bi trắng. Lấy ngẫu nhiên ra một viên bi, rồi lại lấy ngẫu nhiên ra một viên bi nữa. Tính xác suất để lấy được một viên bi xanh ở lần thứ nhất và một viên bi trắng ở lần thứ hai.

    Hướng dẫn. Gọi $ A$ là biến cố: “Lấy được một viên bi xanh ở lần thứ nhất”, $ B$ là biến cố: “Lấy được một viên bi trắng ở lần thứ hai”. Chúng ta cần tính xác suất $ \mathrm{P}(AB)$.

    Theo công thức nhân xác suất $$ \mathrm{P}(AB)=\mathrm{P}(A)\mathrm{P}\left(B | A\right). $$
    Vì có 3 viên bi xanh trong tổng số 5 viên bi nên $$ \mathrm{P}(A)=\frac{3}{5}=0{,}6. $$
    Nếu $ A$ đã xảy ra, tức là một viên bi xanh đã được lấy ra ở lần thứ nhất, thì còn lại trong bình 4 viên bi trong đó số viên bi trắng là 2, do đó $$ \mathrm{P}\left(B | A\right)=\frac{2}{4}=0{,}5. $$
    Vậy xác suất cần tìm là $$ \mathrm{P}(AB)=\mathrm{P}(A)\mathrm{P}\left(B | A\right)=0{,}6\times 0{,}5=0{,}3. $$

    2.2. Công thức nhân xác suất tổng quát

    Bằng phương pháp quy nạp, ta có công thức nhân xác suất tổng quát sau:

    Giả sử $ n\geqslant 2$ và $ A_1, A_2,\ldots, A_n$ là các biến cố sao cho $ \mathrm{P}\left(A_1A_2\ldots A_{n-1}\right)>0$. Khi đó ta có $$ \mathrm{P}\left(A_1A_2\ldots A_{n}\right)=\mathrm{P}\left(A_1\right)\mathrm{P}\left(A_2 | A_1\right)\mathrm{P}\left(A_3 | A_1A_2\right)\ldots\mathrm{P}\left(A_n | A_1A_2\ldots A_{n-1}\right). $$

    Ví dụ 3. Một thủ kho có một chùm chìa khóa gồm 9 chiếc bề ngoài giống hệt nhau trong đó chỉ có hai chiếc mở được cửa kho. Anh ta thử ngẫu nhiên từng chìa (chìa nào không đúng thì bỏ ra khỏi chùm chìa khóa). Tìm xác suất để lần thử thứ ba thì anh ta mới mở được cửa.

    Hướng dẫn. Gọi $ A_1$ là biến cố: “Không mở được cửa ở lần thử thứ 1”, $ A_2$ là biến cố: “Không mở được cửa ở lần thử thứ 2” và $ A_3$ là biến cố: “Mở được cửa ở lần thử thứ 3”. Ta phải tìm $ \mathrm{P}\left(A_1A_2A_3\right)$. Theo công thức nhân xác suất ta có $$ \mathrm{P}\left(A_1A_2A_3\right)=\mathrm{P}\left(A_1\right)\mathrm{P}\left(A_2|A_1\right)\mathrm{P}\left(A_3|A_1A_2\right). $$

    Ta có $$ \mathrm{P}\left(A_1\right)=\frac{7}{9}, \mathrm{P}\left(A_2|A_1\right)=\frac{6}{8}, \mathrm{P}\left(A_3|A_1A_2\right)=\frac{2}{7}. $$

    Do đó $$ \mathrm{P}\left(A_1A_2A_3\right)=\frac{7}{9}\times\frac{6}{8}\times\frac{2}{7}=\frac{1}{6}. $$

    Ví dụ 4. Một người săn thỏ trong rừng, khả năng anh ta bắn trúng thỏ trong mỗi lần bắn tỷ lệ nghịch với khoảng cách bắn. Anh ta bắn lần đầu ở khoảng cách 20 m với xác suất trúng thỏ là 0,5, nếu bị trượt anh ta bắn viên thứ 2 ở khoảng cách 30 m, nếu lại trượt anh ta bắn viên thứ 3 ở khoảng cách 50 m. Tính xác suất để người thợ săn bắn được thỏ.

    Hướng dẫn. Gọi $ A_k$ là biến cố “Người thợ săn bắn trúng thỏ ở lần thứ $ k$” với $ k=1,2,3.$ Theo đề bài, chúng ta có
    \begin{align}
    \mathrm{P}\left(A_1\right)&=0{,}5,\\
    \mathrm{P}\left(A_2|\overline{A_1}\right)&=\frac{20\times 0{,}5}{30}=\frac{1}{3},\\
    \mathrm{P}\left(A_3|\overline{A_1}.\overline{A_2}\right)&=\frac{20\times 0{,}5}{50}=\frac{1}{5}.
    \end{align}
    Gọi $ A$ là biến cố “Người thợ săn bắn trúng thỏ” thì $$ A=A_1\cup \overline{A_1}A_2\cup \overline{A_1}.\overline{A_2}.A_3. $$
    Vì các biến cố $ A_1, \overline{A_1}A_2, \overline{A_1}.\overline{A_2}.A_3$ xung khắc từng đôi một, nên ta có
    $$ \mathrm{P}(A)=\mathrm{P}\left(A_1\right)+\mathrm{P}\left(\overline{A_1}A_2\right)+\mathrm{P}\left(\overline{A_1}.\overline{A_2}.A_3\right) $$
    Theo công thức nhân xác suất thì
    $$ \mathrm{P}\left(\overline{A_1}A_2\right) = \mathrm{P}\left(\overline{A_1}\right)\mathrm{P}\left(A_2|\overline{A_1}\right)=\left(1-0{,}5\right)\times \mathrm{P}\left(A_2|\overline{A_1}\right)=\frac{1}{6}. $$
    $$ \mathrm{P}\left(\overline{A_1}.\overline{A_2}.A_3\right)= \mathrm{P}\left(\overline{A_1}\right) \mathrm{P}\left(\overline{A_2}|\overline{A_1}\right)\mathrm{P}\left(A_3|\overline{A_1}.\overline{A_2}\right)=\left(1-0{,5}\right)\left(1-\frac{1}{3}\right)\times \frac{1}{5} =\frac{1}{15}.$$
    Do đó, xác suất cần tìm là $$ \mathrm{P}(A)=0{,}5+\frac{1}{6}+\frac{1}{15}=\frac{11}{15}. $$

    3. Công thức xác suất đầy đủ

    3.1. Hệ đầy đủ các biến cố

    Hệ các biến cố $ \big\{B_1, B_2,\ldots, B_n\big\}$ được gọi là đầy đủ nếu thỏa mãn đồng thời hai điều kiện:

    • $ B_1, B_2,\ldots, B_n$ là các biến cố xung khắc từng đôi một, nghĩa là $ B_iB_j=\varnothing$ với mọi $ i\neq j$,
    • $ \Omega=B_1\cup B_2\cup\cdots\cup B_n$.

    Nhận xét rằng, hệ $ \big\{B, \overline{B}\big\}$ là một hệ đầy đủ, trong đó $ B$ là một biến cố bất kỳ.

    3.2. Công thức xác suất đầy đủ

    Giả sử $ \big\{B_1, B_2,\ldots, B_n\big\}$ là hệ đầy đủ các biến cố với $ \mathrm{P}\left(B_i\right)>0,\,\forall i=1,2,\ldots,n$. Khi đó với bất kỳ biến cố $ A$, ta có $$ \mathrm{P}(A)=\mathrm{P}\left(B_1\right)\mathrm{P}\left(A | B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A | B_2\right)+\cdots+\mathrm{P}\left(B_n\right)\mathrm{P}\left(A | B_n\right). $$

    Ví dụ 1. Có 3 hộp giống nhau. Hộp thứ nhất đựng 10 sản phẩm, trong đó có 6 chính phẩm, hộp thứ hai đựng 15 sản phẩm, trong đó có 10 chính phẩm, hộp thứ ba đựng 20 sản phẩm, trong đó có 15 chính phẩm. Lấy ngẫu nhiên một hộp và từ đó lấy ngẫu nhiên một sản phẩm. Tìm xác suất để lấy được chính phẩm.

    Hướng dẫn. Ký hiệu $ B_k$ là biến cố: “Sản phẩm lấy ra thuộc hộp thứ $ k$”, $ k=1, 2, 3$ và $ A$ là biến cố: “Lấy được chính phẩm”. Chúng ta có ngay $ \big\{B_1, B_2, B_3\big\} $là hệ đầy đủ các biến cố và

    • $ \mathrm{P}\left(B_1\right)=\frac{1}{3}, \mathrm{P}\left(B_2\right)=\frac{1}{3}, \mathrm{P}\left(B_3\right)=\frac{1}{3},$
    • $ \mathrm{P}\left(A | B_1\right)=\frac{6}{10}, \mathrm{P}\left(A | B_2\right)=\frac{10}{15}, \mathrm{P}\left(A | B_3\right)=\frac{15}{20}.$

    Theo công thức xác suất đầy đủ $$ \mathrm{P}(A)=\mathrm{P}\left(B_1\right)\mathrm{P}\left(A | B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A | B_2\right)+\mathrm{P}\left(B_3\right)\mathrm{P}\left(A | B_3\right) $$

    Thay các giá trị tính được ở trên vào công thức này ta thu được $$ \mathrm{P}(A)=\frac{1}{3}\times \frac{6}{10}+\frac{1}{3}\times \frac{10}{15}+\frac{1}{3}\times \frac{15}{20}=\frac{31}{45} $$
    Vậy xác suất để lấy được chính phẩm là $ {31}/{45}$.

    Ví dụ 2. Từ một hộp chứa $ m$ quả cầu trắng và $ n$ quả cầu đen, người ta rút ngẫu nhiên không hoàn lại từng quả một hai lần. Tính xác suất để quả lấy lần thứ hai là trắng.

    Hướng dẫn. Ký hiệu $ A$ là biến cố: “Lần thứ hai rút được quả cầu trắng”, $ B_1$ là biến cố: “Lần thứ nhất rút được quả cầu trắng”, $ B_2$ là biến cố: “Lần thứ nhất rút được quả cầu đen”.

    Ta có

    • $ \mathrm{P}\left(B_1\right)=\frac{m}{m+n}, \mathrm{P}\left(B_2\right)=\frac{n}{m+n},$
    • $ \mathrm{P}\left(A|B_1\right)=\frac{m-1}{m+n-1}, \mathrm{P}\left(A|B_2\right)=\frac{m}{m+n-1}.$

    Vì $ \big\{B_1, B_2\big\}$ là một hệ đầy đủ nên theo công thức xác suất đầy đủ, chúng ta có \begin{align}
    \mathrm{P}(A)&=\mathrm{P}\left(B_1\right)\mathrm{P}\left(A|B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A|B_2\right)\\
    =&\frac{m}{m+n}\times\frac{m-1}{m+n-1}+\frac{n}{m+n}\times\frac{m}{m+n-1}\\
    =&\frac{m\left(m-1\right)+mn}{\left(m+n\right)\left(m+n-1\right)}
    =&\frac{m\left(m+n-1\right)}{\left(m+n\right)\left(m+n-1\right)}
    =&\frac{m}{m+n}.
    \end{align}
    Vậy xác suất để quả lấy lần thứ hai là trắng là$ \frac{m}{m+n}$.

    Ví dụ 3. Có 10 chiếc túi đựng bi như sau:

    • 4 túi loại 1, trong mỗi túi loại 1 chứa 6 viên bi trắng và 4 viên bi đen,
    • 2 túi loại 2, trong mỗi túi loại 2 chứa 3 viên bi trắng và 7 viên bi đen,
    • 1 túi loại 3, trong mỗi túi loại 3 chứa 7 viên bi trắng và 3 viên bi đen,
    • 3 túi loại 4, trong mỗi túi loại 4 chứa 4 viên bi trắng và 6 viên bi đen.

    Chọn ngẫu nhiên 1 chiếc túi rồi lấy ngẫu nhiên 2 viên bi. Tính xác suất để lấy được hai viên bi cùng màu.

    Hướng dẫn. Ký hiệu $ B_k$ là biến cố “chọn được túi loại $ k$”, $ k=1, 2, 3, 4$ và $ A$ là biến cố “lấy được hai viên bi cùng màu”.

    Ta có $ \big\{B_1, B_2, B_3, B_4\big\} $ là hệ đầy đủ các biến cố và

    \begin{align}
    \mathrm{P}\left(B_1\right)=\frac{4}{10}, \mathrm{P}\left(B_2\right)=\frac{2}{10},\\
    \mathrm{P}\left(B_3\right)=\frac{1}{10}, \mathrm{P}\left(B_4\right)=\frac{3}{10},\\
    \mathrm{P}\left(A | B_1\right)=\frac{C_6^2+C_4^2}{C_{10}^2}=\frac{21}{45},\mathrm{P}\left(A | B_2\right)=\frac{C_3^2+C_7^2}{C_{10}^2}=\frac{24}{45},\\
    \mathrm{P}\left(A | B_3\right)=\frac{C_7^2+C_3^2}{C_{10}^2}=\frac{24}{45}, \mathrm{P}\left(A | B_4\right)=\frac{C_4^2+C_6^2}{C_{10}^2}=\frac{21}{45}.
    \end{align}

    Theo công thức xác suất đầy đủ
    $$ \mathrm{P}(A)=\mathrm{P}\left(B_1\right)\mathrm{P}\left(A | B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A | B_2\right)+\mathrm{P}\left(B_3\right)\mathrm{P}\left(A | B_3\right)+\mathrm{P}\left(B_4\right)\mathrm{P}\left(A | B_4\right) $$

    Suy ra $$ \mathrm{P}(A)=\frac{4}{10}\times \frac{21}{45}+\frac{2}{10}\times \frac{24}{45}+\frac{1}{10}\times \frac{24}{45}+\frac{3}{10}\times \frac{21}{45} =\frac{219}{450}. $$

    Vậy xác suất cần tìm là $ \frac{219}{450}$.

    Ví dụ 4. Có hai cái hộp. Hộp thứ nhất có 4 bi trắng và 5 bi đen. Hộp thứ hai có 5 bi trắng và 4 bi đen. Chọn ngẫu nhiên 3 viên bi ở hộp thứ nhất bỏ vào hộp thứ hai rồi sau đó chọn ngẫu nhiên một viên bi ở hộp thứ hai ra. Tính xác suất để lấy được bi trắng từ hộp thứ hai.

    Hướng dẫn. Gọi $ A$ là biến cố: “Lấy được bi trắng từ hộp thứ hai”, $ B_k$ là biến cố: “Trong 3 viên bi lấy ra từ hộp thứ nhất có $ k$ bi trắng”, $ k=0, 1, 2, 3$.

    Khi đó $ \big\{B_0{,} B_1, B_1, B_3\big\} $ là hệ đầy đủ các biến cố và ta có
    \begin{align}
    \mathrm{P}\left(B_0\right)&=\frac{C_5^3}{C_9^3}=\frac{10}{84},\\
    \mathrm{P}\left(B_1\right)&=\frac{C_4^1C_5^2}{C_9^3}=\frac{40}{84},\\
    \mathrm{P}\left(B_2\right)&=\frac{C_4^2C_5^1}{C_9^3}=\frac{30}{84},\\
    \mathrm{P}\left(B_3\right)&=\frac{C_4^3}{C_9^3}=\frac{4}{84}.
    \end{align}

    Theo công thức xác suất đầy đủ
    $$ \mathrm{P}(A)=\mathrm{P}\left(B_0\right)\mathrm{P}\left(A | B_0\right)+\mathrm{P}\left(B_1\right)\mathrm{P}\left(A | B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A | B_2\right)+\mathrm{P}\left(B_3\right)\mathrm{P}\left(A | B_3\right). $$

    Dễ thấy
    \begin{align}
    \mathrm{P}\left(A | B_0\right)=\frac{5}{12},\quad & \mathrm{P}\left(A | B_1\right)=\frac{6}{12},\\
    \mathrm{P}\left(A | B_2\right)=\frac{7}{12},\quad & \mathrm{P}\left(A | B_3\right)=\frac{8}{12}.
    \end{align}

    Thay các giá trị này vào công thức xác suất đầy đủ ta được $$ \mathrm{P}(A)=\frac{10}{84}\times\frac{5}{12}+\frac{40}{84}\times\frac{6}{12}+\frac{30}{84}\times\frac{7}{12}+\frac{4}{84}\times\frac{8}{12} =\frac{532}{1008} =\frac{19}{36}. $$

    Vậy xác suất cần tìm là $ {19}/{36}$.

    Ví dụ 5. Trong một cái hộp có $ n$ sản phẩm, ta bỏ vào cái hộp đó một sản phẩm tốt sau đó lấy ngẫu nhiên ra một sản phẩm. Tính xác suất để sản phẩm lấy ra là tốt nếu mọi giả thiết về trạng thái cấu thành ban đầu của hộp là đồng xác suất.

    Hướng dẫn. Gọi $ A$ là biến cố: “Lấy được sản phẩm tốt”, $ B_i$ là biến cố: “Lúc ban đầu hộp có $ i$ sản phẩm tốt”, $ i=0,1,\ldots,n$. Khi đó $ \big\{B_0{,} B_1,\ldots, B_n\big\} $ là hệ đầy đủ các biến cố.

    Theo giả thiết $$ \mathrm{P}\left(B_i\right)=\frac{1}{n+1}, i=0,1,\ldots,n.$$

    Ta có $ \mathrm{P}\left(A | B_i\right)=\frac{i+1}{n+1}$ với mọi $ i=0,1,\ldots,n$. Theo công thức xác suất đầy đủ

    $$ \mathrm{P}(A)=\sum\limits_{i=0}^{n}\mathrm{P}\left(B_i\right)\mathrm{P}\left(A | B_i\right). $$

    Thay vào ta được
    \begin{align}
    \mathrm{P}(A)&=\sum\limits_{i=0}^{n}\frac{i+1}{\left(n+1\right)^2}\\
    &=\frac{1+2+\cdots+\left(n+1\right)}{\left(n+1\right)^2}\\
    &=\frac{\left(n+1\right)\left(n+2\right)}{2\left(n+1\right)^2}\\
    &=\frac{n+2}{2\left(n+1\right)}.
    \end{align}

    4. Công thức Bayes – Định lý Bayes

    Giả sử $ \mathrm{P}(A)>0$ và $ \big\{B_1, B_2,\ldots, B_n\big\} $ là hệ đầy đủ các biến cố với $ \mathrm{P}\left(B_k\right)>0$ với mọi $ k=1,2,\ldots,n$. Khi đó với mọi $ k=1,2,\ldots,n$, ta có $$ \mathrm{P}\left(B_k | A\right)=\frac{\mathrm{P}\left(B_k\right)\mathrm{P}\left(A | B_k\right)}{\mathrm{P}\left(B_1\right)\mathrm{P}\left(A | B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A | B_2\right)+\cdots+\mathrm{P}\left(B_n\right)\mathrm{P}\left(A | B_n\right)}. $$

    Ví dụ 1. Dây chuyền lắp ráp nhận được các chi tiết do hai máy sản xuất. Trung bình máy thứ nhất cung cấp 60% chi tiết, máy thứ hai cung cấp 40% chi tiết. Khoảng 90% chi tiết do máy thứ nhất sản xuất là đạt tiêu chuẩn, còn 85% chi tiết do máy thứ hai sản xuất là đạt tiêu chuẩn. Lấy ngẫu nhiên từ dây chuyền một sản phẩm, thấy nó đạt tiêu chuẩn. Tìm xác suất để sản phẩm đó do máy thứ nhất sản xuất.

    Hướng dẫn. Gọi $ A$ là biến cố: “Chi tiết lấy từ dây chuyền đạt tiêu chuẩn”, $ B_1$ là biến cố: “Chi tiết do máy thứ nhất sản xuất” và $ B_2$ là biến cố: “Chi tiết do máy thứ hai sản xuất”. Ta cần tính xác suất $ \mathrm{P}\left(B_1|A\right)$.

    Theo công thức Bayes $$ \mathrm{P}\left(B_1|A\right)=\frac{\mathrm{P}\left(B_1\right)\mathrm{P}\left(A|B_1\right)}{\mathrm{P}\left(B_1\right)\mathrm{P}\left(A|B_1\right)+\mathrm{P}\left(B_2\right)\mathrm{P}\left(A|B_2\right)}. $$

    Theo điều kiện bài toán $$ \mathrm{P}(B_1)=0{,}6; \mathrm{P}(B_2)=0{,}4; $$
    $$ \mathrm{P}(A|B_1)=0{,}9; \mathrm{P}(A|B_2)=0{,}85. $$

    Thay vào ta có $$ \mathrm{P}\left(B_1|A\right)=\frac{0{,}6\times 0{,}9}{0{,}6\times 0{,}9+0{,}4\times 0{,}85}=0{,}614. $$

    Sau đây là một bài toán khá nổi tiếng trong xác suất thống kê, được giải theo nhiều cách khác nhau. Ta hãy thử giải bài toán này bằng định lý Bayes.
    Ví dụ 2.[Bài toán Tuesday Child] Một gia đình có hai đứa trẻ. Biết có ít nhất có một đứa trẻ là con gái và sinh vào thứ 3. Hỏi xác suất 2 đứa trẻ đều là con gái là bao nhiêu?

    Hướng dẫn. Chúng ta có nhận xét sau:

    • Xác suất để một đứa trẻ sinh vào một ngày nhất định trong tuần là $ 1/7$.
    • Giới tính của đứa trẻ và ngày sinh của nó là 2 sự kiện không liên quan đến nhau.

    Ta ký hiệu các biến cố như sau:

    • $ B$ là biến cố “Ít nhất 1 đứa trẻ là con gái sinh ra vào thứ 3”,
    • $ A$ là biến cố “Cả 2 đứa trẻ đều là con gái”, xác suất là $ \mathrm{P}(A)=1/4$,
    • $ A_1$ là biến cố “Chỉ một trong 2 đứa trẻ là con gái”, $ \mathrm{P}(A_1)=1/2$,
    • $ C $ là biến cố “Đứa trẻ sinh ra vào thứ 3”, $ \mathrm{P}(C)=1/7$,
    • $ \overline{C} $ là biến cố “Đứa trẻ sinh ra vào thứ 3”, $ \mathrm{P}(\overline{C})=6/7$.

    Để sử dụng định lý Bayes tính $ \mathrm{P}(A | B)$ ta cần tính được $ \mathrm{P}(B|A)$ và $ \mathrm{P}(B)$.

    $ \mathrm{P}(B|A)$ được hiểu là xác suất ít nhất 1 đứa trẻ là con gái sinh ra vào thứ 3 nếu biết trước 2 đứa trẻ là con gái.
    Ta sẽ tính xác suất phần bù $ \mathrm{P}(\overline{B}|A)$, đây là xác suất để không có đứa trẻ nào sinh ra vào thứ 3.
    $$ \mathrm{P}(\overline{B}|A) = \mathrm{P}(\overline{C}) \mathrm{P}(\overline{C}) = \dfrac{6}{7} \times \dfrac{6}{7} = \dfrac{36}{49} $$
    Như vậy ta có
    $$ \mathrm{P}(B|A) = 1 – \mathrm{P}(\overline{B}|A) = \dfrac{13}{49} $$
    $ \mathrm{P}(B)$ là xác suất sự ít nhất 1 đứa trẻ là con gái sinh ra vào thứ 3. Sự kiện này bao gồm 2 khả năng:

    • Cả 2 đứa trẻ đều là con gái $ A$,
    • Chỉ 1 đứa trẻ là con gái $ A_1$.

    Ta có \begin{align}
    \mathrm{P}(B) &= \mathrm{P}(BA) + \mathrm{P}(BA_1) \\
    &= \mathrm{P}(B|A)\mathrm{P}(A) + \mathrm{P}(B|A_1)\mathrm{P}(A_1)\\
    &= \dfrac{13}{49} \times \dfrac{1}{4} + \dfrac{1}{7} \times \dfrac{1}{2}\\
    &=\dfrac{27}{196}
    \end{align}

    Thay vào định lý Bayes, ta tính được
    $$ \mathrm{P}(A | B) = \dfrac{\mathrm{P}(B|A)\times \mathrm{P}(A)}{\mathrm{P}(B)} = \dfrac{\tfrac{13}{49} \times \tfrac{1}{4}}{\tfrac{27}{196}} = \dfrac{13}{27} \approx 0{,}481 $$
    Chúng ta có thể minh họa bằng hình vẽ sau đây, xác suất cần tìm chính bằng số ô màu xanh chia cho tổng số ô màu vàng và xanh.

    Ta dùng một đoạn code Python nho nhỏ để kiểm tra thử kết quả vừa tính được.

    import random

def random_kid():
   gender = random.choice(["boy", "girl"])
   birth_date = random.choice(["mon", "tue", "wed", "thu", "fri", "sat", "sun"])
   return (gender, birth_date)

both_girls = 0
tuesday_girl = 0

random.seed(0)
total = 100000
for _ in range(total):
   first_child = random_kid()
   second_child = random_kid()

if first_child == ("girl", "tue") or second_child == ("girl", "tue"):
   tuesday_girl += 1
if first_child[0] == "girl" and second_child[0] == "girl":
   both_girls += 1

print("both_girls = ", both_girls)
print("tuesday_girl = ", tuesday_girl)
print("P(both_girls|tuesday_girl) = ", both_girls / tuesday_girl)

    Đoạn code trên thực hiện random 100K dữ liệu. Thu được kết quả in ra như sau

    both_girls = 6506
tuesday_girl = 13637
P(both_girls|tuesday_girl) = 0.4770844027278727

    Xác suất tính ra tương đối sát với con số ta tính bằng định lý Bayes ở trên.

    Bài viết tổng hợp từ https://1upnote.me/post/2018/11/ds-ml-bayes-theorem/ và https://math4rum.wordpress.com/2013/04/01/bai-1-5-cong-thuc-xac-suat-day-du-cong-thuc-bayes/

  • 49 bài toán lớp 4 thử thách trí thông minh

    49 bài toán lớp 4 thử thách trí thông minh

    49 BÀI TOÁN LỚP 4

    O2 Education xin giới thiệu 54 bài toán lớp 4, các dạng toán đố, thử thách trí thông minh, toán suy luận dành cho HSG lớp 4. Các bài toán có lời giải được chúng tôi sưu tầm từ nhiều nguồn khác nhau.

    Bài 1: GIỎI CẢ HAI MÔN

    Lớp 4A có 42 học sinh. Trong đó có 25 HS giỏi toán, 23 HS giỏi Tiếng Việt và hai HS không giỏi môn nào. Hỏi có bao nhiêu HS giỏi cả hai môn?

    Hướng dẫn.

    Số HS giỏi ít nhất 1 môn là:

    42 – 2 = 40 (HS)

    Số HS giỏi cả hai môn là:

    (25 + 23) – 40 = 8 (HS)

    Đáp số: 8 HS.

    Bài 2: MÀU ÁO VÀ MÀU NƠ

    Ba bạn Hiền, Thi, Thoa mặc ba chiếu áo màu đỏ, vàng, xanh và cài ba cái nơ cũng màu đỏ, vàng, xanh.

    Biết rằng:

    1. Thoa cài nơ màu xanh.
    2. Chỉ có bạn Hiền là có màu áo và màu nơ giống nhau.
    3. Màu áo và màu nơ của Thi đều không phải màu đỏ.

    Hãy xác định xem ba bạn Hiền, Thi, Thoa mặc áo màu gì và cài nơ màu gì?

    Hướng dẫn.

    Từ a) và b) có màu áo của Thoa là đỏ hoặc vàng.

    Từ c) có màu nơ, màu áo của Thi là xanh hoặc vàng. Suy ra:

    • Màu áo của Thoa là màu vàng.
    • Màu áo và màu nơ của Hiền là màu đỏ. Còn lại Thi có áo màu xanh và nơ màu vàng.

    Đáp số:

    • Hiền mặc áo đỏ, cài nơ đỏ.
    • Thi mặc áo xanh, cài nơ vàng.
    • Thoa mặc áo vàng, cài nơ xanh.

    Bài 3: NGƯỜI LÁI THUYỀN THÔNG MINH

    Trên một dòng sông, có một người lái thuyền phải chở một con sói, một con dê và một chiếc bắp cải sang sông. Khó một nỗi là thuyền của bác nhỏ nên mỗi chuyến chỉ chở được một con sói, hoặc một con dê, hoặc một bắp cải. Nhưng nếu chó sói đứng cạnh dê thì chó sói sẽ ăn thịt dê, mà dê đứng cạnh bắp cải thì dê sẽ ăn bắp cải.

    Làm thế nào bay giờ? Bác lái thuyền suy nghĩ một lúc rồi bác reo lên: “Ta đã có cách.” Và rồi bác đã hoàn thành công việc thật xuất sắc.

    Đố bạn biết bác đã làm thế nào?

    bài toán 4 logic câu đố bài toán qua sông

    Hướng dẫn.

    Bác lái thuyền đã chở được cả sói, dê và bắp cải sang sông bằng cách:

    • Lần thứ nhất: Bác chở dê sang sông để sói và bắp cải ở lại vì sói không ăn bắp cải. Bác quay thuyền trở về.
    • Lần thứ hai: Bác chở sói sang sông nhưng khi đưa sói lên bờ đồng thời bác lại cho dê xuống thuyền về bên kia vì nếu để dê lại thì dê sẽ là miếng mồi ngon của sói.
    • Lần thứ ba: Bác chở bắp cải sang sông. Như vậy sói và bắp cải đã sang sông. Bác quay trở về bến cũ nơi có chú dê đang đợi.
    • Lần thứ tư: Bác chở nốt chú dê sang sông.

    Sau bốn lần, bác lái thuyền đã chở được sói, bắp cải và dê sang sông một cách an toàn. Đúng là một bác lái thuyền thông minh.

    Bài 4: AI LÀM HOA GÌ?

    Ba bạn Cúc, Đào, Hồng làm ba hoa giấy, hoa cúc, hoa đào, hoa hồng. Bạn làm hoa hồng nói với Cúc: thế là trong chúng ta không có ai làm hoa trùng với tên của mình.

    Các bạn thử đoán xem ai làm hoa gì?

    Hướng dẫn.

    • Bạn làm hoa hồng nói với Cúc nên Cúc không làm hoa hồng. Cúc không làm hoa trùng tên của mình nên Cúc không làm hoa cúc. Vậy Cúc làm hoa đào.
    • Bạn hồng không làm hoa đào vì hoa đào là bạn Cúc làm, Hồng không làm hoa trùng tên của mình nên Hồng không làm hoa hồng. Vậy Hồng làm hoa cúc.
    • Cuối cùng Đào làm hoa hồng.

    Bài 5: CÓ MẤY NGƯỜI CON?

    Ở một bản làng nọ có một gia đình có ba người con trai. Mỗi người con trai đều có một người chị gái và một người em gái.

    Cái bạn thử đoán xem gia đình đó có mấy người?

    Hướng dẫn.

    • Gia đình đó có một người con gái là con gái là con cả để ba người con trai đó có một chị gái.
    • Gia đình đó phải có một người con gái là con út để ba người con trai có một em gái.
    • Vậy gia đình đó có tổng số người con là: 1 + 3 + 1 = 5 (người con)

    Đáp số: 5 người con.

    Bài 6: LẤY ÍT NHẤT BAO NHIÊU?

    Trong hộp có 45 quả bóng gồm 20 màu đỏ, 15 quả màu xanh và 10 quả màu vàng. Hỏi phải lấy ra bao nhiêu quả bóng để chắc chắn có ba quả bóng:

    a) Màu đỏ.

    b) Cùng màu.

    c) Khác màu

    Hướng dẫn.

    a) Hộp đó có tất cả số bong xanh và vàng là: 15 + 10 = 25 (quả)

    Nếu lấy ra 25 quả bóng thì chưa chắc trong đó đã có bóng màu đỏ. Vậy mướn có chắc chắn 3 quả bóng màu đỏ được lấy ra thì ta phải lấy ít nhất số quả bóng là: 25 + 3 = 28 (quả)

    b) Số bóng trong hộp chỉ có ba màu đỏ, xanh và vàng nên nếu lấy ít nhất 7 quả thì chắc chắn sẽ có ba quả cùng màu.

    c) Hộp đó có tất cả số bóng đỏ và xanh là: 20 + 15 = 35 (quả)

    Nếu lấy ra 35 quả thì chưa chắc trong đó đã có bóng vàng. Vậy muốn chắc chắn có 3 quả bóng khác màu thì ta phải lấy ít nhất số quả bóng là: 35 + 1 = 36(quả)

    Đáp số: a) 28 quả. b) 7 quả. c) 36 quả.

    Bài 7: BỐN KHÁCH DU LỊCH

    Có bốn người cùng đi du lịch đến Pháp. Một người biết tiếng Pháp và tiếng Anh. Một người biết tiếng Đức và tiếng Nhật. Một người biết tiếng Nhật và tiếng Anh, còn người cuối cùng biết tiếng Trung Quốc và tiếng Đức. Cả bốn người họ cùng thuê phòng ở một khách sạn. Đến cửa khách sạn họ nhìn thấy một bảng thông báo.

    Làm thế nào để mọi người đều hiểu nội dung bảng thông báo được nhỉ? Chúng ta cùng nghĩ xem nhé.

    Hướng dẫn.

    • Nếu cả 4 người khách đều ở cùng một nước thì thật đơn giản. Người biết tiếng Pháp và tiếng Anh sẽ dịch bảng thông báo này ra thứ tiếng của nước mà họ ở. Khi đó cả 4 người đều hiểu nội dung bảng thông báo.
    • Nếu cả 4 người khách không phải là người cùng một nước thì ta giải quyết như sau:
      • Người biết tiếng Pháp và tiếng Anh sẽ dịch bảng thông báo này sang tiếng Anh để người biết tiếng Anh và tiếng Nhật hiểu.
      • Sau đó người biết tiếng Anh và tiếng Nhật sẽ dịch bảng bảng thông báo này sang tiếng Nhật để người biết tiếng Nhật và tiếng Đức hiểu.
      • Cuối cùng người biết tiếng Nhật và tiếng Đức sẽ dịch bảng bảng thông báo này sang tiếng Đức để người biết tiếng Đức và tiếng Trung Quốc hiểu.

    Như vậy là cả 4 người đều hiểu nội dung bảng thông báo.

    Bài 8: CÓ BAO NHIÊU CÁCH CHỌN?

    Có 8 người đăng kí tham gia trò chơi VUI ĐỂ HỌC trên đài truyền hình. Ban tổ chức muốn chọn ba người vào một vòng chơi.

    Đố các bạn có bao nhiêu cách chọn?

    Hướng dẫn.

    • Người thứ nhất có 8 cách chọn. Còn lại 7 người.
    • Người thứ hai có 7 cách chọn. Còn lại 6 người.
    • Người thứ ba có 6 cách chọn.
    • Cách chọn 3 người ABC cũng là ACB,BAC, BCA, CAB, CBA.
    • Sáu cách chọn trên chỉ là một cách. Do đó ta có số cách chọ là: (8 x 7 x 6) : 6 = 56 (cách chọn)

    Đáp số: 56 cách chọn.

    Bài 9: DŨNG ĐÚNG HAY TRÍ ĐÚNG?

    • Trường Tiểu học M tổ chức thi đấu bóng bàn, có 11 đấu thủ tham gia.
    • Dũng nói rằng: “Có thời điểm mỗi đấu thủ đều đấu đung 7 trận”
    • Trí nói rằng: “Dũng nói sai rồi”.
    • Dũng đúng hay Trí đúng? Các bạn hãy nghĩ xem!

    Hướng dẫn.

    Nếu mỗi đấu thủ đấu đúng 7 trận thì số trận đẫ đấu của giải là: (7 x 11 ) : 2 = 38,5 không phải là số tự nhiên.

    Vậy không có lúc nào mỗi đấu thủ đều đấu đúng 7 trận. Dũng nói sai. Trí nói đúng!

    Bài 10: BA ĐÔI VỚ

    Trong thùng có ba đôi vớ (bít tất) để lẫn lộn. Bạn Mai lấy ra 4 chiếc vớ.

    Hỏi có thể nói chắc chắn rằng trong 4 chiếc vớ bạn Mai vừa lấy ra có ít nhất 2 chiếc vớ cùng một đôi được không?

    Hướng dẫn.

    Số chiếc vớ có là: 2 x 3 = 6 (chiếc)

    Lấy ra 4 chiếc còn lại 2 chiếc. 2 chiếc vớ còn lại này của cùng một đôi hoặc hai đôi khác nhau. Do đó 4 chiếc vớ lấy ra phải có ít nhât 2 chiếc vớ của cùng một đôi.

    Bài 11: NƯỚNG CÁ

    Chị Trinh giúp mẹ nướng cá trên lò nướng. Cần phải nướng chín 3 con cá. Biết rằng : để nướng chín một con cá thì cần 4 phút và lò nướng chỉ có thể nướng được 2 con cá một lần.

    Chị Trinh cần ít nhất bao nhiêu phút để nướng chín 3 con cá này?

    Hướng dẫn.

    Chị Trinh cần ít nhất 6 phút để nướng hết số cá.

    Chị Trinh có thể nướng như sau:

    Con cá thứ nhất và thứ hai cùng nướng trong 2 phút, trở mặt dưới của con cá thứ nhất lên, đặt con cá thứ hai lên trên con cá thứ nhất và đặt con cá thứ ba vào lò nướng, nướng trong 2 phút con cá thứ nhất đã chín, lấy ra ngoài, trở mặt chưa nướng của con cá thứ hai và thứ ba xuống nướng trong 2 phút chín hai con cá này!

    Bài 12: BỐN SỐ KÌ DIỆU

    Anh Hai đố Bình viết lên bảng con, bốn số chẵn có ba chữ số mà sau khi xoay ngược bảng từ dưới lên trên thì vẫn được những số ấy. Bình loay hoay mãi không nổi một số. Các bạn hãy giúp Bình tìm ra bốn số kì diệu đó nhé!

    Hướng dẫn.

    • Trong mười chữ số chỉ có bốn chỉ có bốn chữ số 0 ; 6 ; 8 ; 9 là khi viết vào bảng con rồi xoay ngược bảng từ dưới lên trên vẫn đọc được.
    • Từ bốn số trên ta viết được bốn số chẵn có ba chữ số mà sau khi xoay ngược bảng từ dưới lên trên thì vẫn được chính số đó là:
    • 808 ; 888 ; 906 ; 986.
    • Bình hãy viết từng số lên bảng rồi làm đúng yêu càu của anh Hai xem nhé. Bình thấy chúng mình “siêu” chưa?

    Bài 13: SAO LẠI THẾ ?

    Cô giáo có ba tấm bìa nhỏ hình vuông, trên mỗi tấm bìa có ghi một chữ số. Cô đưa cả ba tấm bìa cho Tý và yêu cầu Tý tính tổng. Tý tìm ra kết quả là 22. Cô đưa lại ba tấm bìa đó cho Tèo và yêu cầu Tèo tính tổng. Tèo lại tìm ra kết quả là 25. Tuy nhiên cô giáo vẫn khen cả hai bạn tính đúng. Các bạn ơi ! Tại sao thế nhỉ?

    Hướng dẫn.

    Cô giáo khẳng định kết quả của cả Tý và Tèo đều đúng nên chắc chắn ba số ở ba tấm bìa sẽ có ít nhất một số một bạn đã so được với số của ban kia.

    Vì 25 – 22 = 3 nên sau khi xoay ngược só đó đã tăng lên hoặc giảm đi ba đơn vị. trong các chữ số khi xoay ngược vẫn đọc được chỉ có số 9 và số 6 hơn kém nhau 3 đơn vị. Ta có:

    8 + 8 + 6 = 22 và 8 + 8 + 9 = 25

    Do đó phép tính của Tý là 8 + 8 + 6 = 22 và Tèo đã xoay ngược số 6 thành số 9 nên phép tính của Tèo là 8 + 8 + 9 = 25

    Bài 14: TÍCH CÁC CHỮ SỐ

    Tuấn Anh cùng mẹ đến siêu thị sách. Tuấn Anh dừng chân tại khu sách tham khảo dành cho Tiểu học. Em cầm trên tay cuốn: “VUI HỌC TOÁN 4” và say sưa đọc các bài toán vui. Biết con mình thích cuốn sách này nên mẹ mua ngay cho Tuấn Anh. Nhìn vào tên cuốn sách mẹ chợt nảy ra một bài toán đố Tuấn Anh:

    “Nếu thay mỗi chữ cái bởi một chữ số, chữ cái giống nhau được thay bởi những số giống nhau, chữ cái khác nhau được thay bởi những số khác nhau và không có chữ số nào trùng với số 4. Tích các chữ số đó liệu có lớn hơn 2005 không?”.

    Tuấn Anh nhẩm tính một lúc rồi nói với mẹ:

    Tích là số lớn lắm, lớn hơn 2005 nhiều mẹ ạ.

    Theo bạn Tuấn Anh nói đúng hay sai?

    Hướng dẫn.

    Cuốn sách “VUI HỌC TOÁN 4” chỉ có 9 chữ cái khác nhau là V, U, I, H, O, C, T, A, N mà hông có chữ nào được thay bởi số 4 nên 9 chữ ấy phải thay bởi các chữ số 0,1,2,3,5,6,7,8,9.

    Tích của tất cả các chữ này bằng 0 vì có một thừa số bằng 0.

    Vậy Tuấn Anh đã nói sai.

    Bài 15: SỐ NÀO?

    Chị Hiền cho em Trí làm bài tính nhân một số tự nhiên với 9. Trí làm xong , chị Hiền ghi cho Trí số 4297 và nói đây là đáp số. Trí nhìn đáy số chị Hiền đưa ra và nói rằng “ Đáp số của chị còn thiếu một chữ số, nó nằm ở chính giữa số này !”

    Bạn hãy cho biết chị Hiền đã cho Trí số nào nhân với 9?

    Hướng dẫn.

    Gọi chữ số còn thiếu của đáp số đúng là A, ta có số 42A97 chia hết cho 9. Do đó 4 + 2 + A + 9 = 22 + A chia hết cho 9. Tính ra được A = 5.

    Số mà chị Hiền cho Trí nhân với 9 là:

    42597 : 9 = 4733

    Đáp số: 4733

    Bài 16: RỔ NÀO ĐỰNG CAM?

    Có hai rổ đựng cam, ba rổ đựng quýt với số quả cam và quả quýt có trong năm rổ là: 60; 45; 75; 65; 55.

    Không cho biết rổ nào đựng cam, rổ nào đựng quýt. Chỉ biết rằng số quả quýt gấp hai lần số quả cam.

    Hỏi rổ nào đựng cam?

    Hướng dẫn.

    Số quả quýt gấp hai lần số quả cam. Nên số quả quýt và cam gấp 3 lần số quả cam.

    bai toan lop 4 so do

    Số quả cam có là:

    (60 + 45 + 75 + 65 + 55) : 3 = 100 (quả)

    Dễ thấy 45 + 55 = 100 (quả)

    Vậy hai rổ đựng cam là rổ đựng 45 quả và rổ đựng 55 quả.

    Bài 17: CAM VÀ XOÀI.

    Một người bán sáu giỏ cam và xoài. Mỗi giỏ chỉ đựng hoặc là cam hoặc là xoài, với số lượng như sau: 36; 39; 40; 41; 42; 44. Biết rằng sau khi bán một giỏ xoài thì số cam còn lại gấp 4 lần số xoài còn lại.

    Hãy cho biết giỏ nào đựng xoài, giỏ nào đựng cam?

    Hướng dẫn.

    Vì số cam còn lại gấp 4 lần số xoài còn lại nên tổng số cam và số xoài còn lại là số chia hết cho 5.

    Số cam và xoài mang ra chợ là:

    36 + 39 + 40 + 41 + 42 + 44 = 242 (quả)

    Số 242 chia cho 5 còn dư 2.

    Vậy giỏ xoài bán đi có số quả là số chia cho 5 còn dư 2.

    Trong các số 36; 39; 40; 41; 42; 44 chỉ có số 42 chia cho 5 còn dư 2.

    Vậy số cam và xoài còn lại là;

    242 – 42 = 200 (quả)

    Số xoài còn lại là:

    200 : 5 = 40 (quả)

    Đáp số: Các giỏ xoài 40 quả và 42 quả

    Các giỏ cam: 36 quả; 39 quả; 41 quả; 44 quả.

    Bài 18: AI ĐÚNG? AI SAI?

    Toán đố Tuổi và Thơ: “ Không tính tông bạn hãy cho biết ngay tổng của 2005 số tự nhiên liên tiếp bắt đầu từ 1 là số chẵn hay số lẻ?”.

    Tuổi nói ngay: “Chắc chắn là số chẵn”.

    Thơ suy nghĩ một lúc rồi trả lời: “là một số lẻ”.

    Chắc chắn sẽ có một bạn nói đúng, một bạn nói sai phải không các bạn? Chúng ta cùng tìm xem ai đúng, ai sai nhé!

    Hướng dẫn.

    Các số tự nhiên liên tiếp từ 1 đến 2005 sẽ tạo thành dãy số sau:

    1; 2; 3; 4; 5; … ; 2003; 2004; 2005.

    Dãy số trên ta thấy cứ một số lẻ lại có một số chẵn, mà bắt đầu vào dãy là số lẻ và kết thúc cũng là số lẻ nên số các số lẻ nhiều hơn số các ố chẵn là một số.

    Từ 1 đến 2005 có 2005 số. Do đó, ta có:

    • Số các số chẵn là: (2005 -1) : 2 = 1002 (số)
    • Số các số lẻ là: 1002 + 1 = 1003 (số)
    • Tổng của 1002 số chẵn là một số chẵn
    • Tổng của 1003 số lẻ là một số lẻ.

    Do đó tổng của 2005 số tự nhiên liên tiếp từ 1 đến 2005 là một số lẻ.

    Vậy Thơ nói đúng và tuổi nói sai.

    Bài 19: CÁC SỐ VÀ CÁC Ô VUÔNG

    Hãy tìm cách viết vào mỗi ô vuông một trong các số tự nhiên từ 1 đến 10 để các phép tính sau đều đúng.

    cau do vui lop 4

    Hướng dẫn.

    Ô cuối cùng ở góc bên phải chỉ có thể là số 10. Do đó cột bên phải là 5 x 2 = 10.

    Bài 20: DỜI MỘT ĐỒNG TIỀN

    Bé Hoa đặt lên bà 6 đồng tiền thành hình chữ thập (hình bên)

    Bạn hãy dời một đồng tiền để tổng số tiền trên một đường thẳng là 4 đồng tiền.

    bai toan lop 4 di chuyen dong tien

    Hướng dẫn.

    Dời đồng tiền ở dưới cùng đạt chồng lên đồng tiền ở giữa.

    Bài 21: HAI MƯƠI CHỮ SỐ 1

    Bạn hãy dùng 20 chữ số 1 và đạt giữa chúng những dấu cộng (+) để được tổng bằng 200.

    Bạn hãy cho biết vì sao bạn làm được như vậy?

    Bài 22: SIÊU TOÁN

    Mão là một học sinh được bạn bè trong lớp suy tôn là siêu sao giải toán nhanh. Một hôm bạn Thân đố Mão tính tổng sau:

    99 + 199 + 299 + 399 + … + 899.

    Mão! … chỉ một thoáng đã đọc kết quả trước sự thán phục của Thân.

    Bí quyết nào giúp Mão thế? Bạn có biết không?

    Bài 23: AI ĐƯỢC THƯỞNG?

    Bác Tuấn nói rằng: “Ai giúp bác thay các chữ cái bằng các chữ số thích hợp ở phép tình sau, bác sẽ thưởng cho 10 triệu đồng”.

    bai toan lop 4 tim so abcde

    Ai được thưởng bạn có biết không?

    Bài 24: VUI HỌC.

    Các bạn có thay được các chữ cái bằng các chữ số thích hợp để được phép tính ở dưới không?

    bai toan lop 4 tim so VUIHOC

    Bài 25: AI LẤY SỐ CHẴN?

    Anh Quân có hai mảnh giấy giống hệt nhau, một mảnh anh ghi một số chắn, một mảnh anhh ghi một số lẻ. Anh đưa cho Lâm và Ly xem rồi gấp lại trộn đều và đưa cho Lâm và Ly bốc thăm.

    Bốc xong rồi Ly nhanh nhảu:

    • Để làm gì hở anh?

    Anh Quân cười:

    • Anh sẽ nói ngay được ai lấy số chẵn. Trước hết Lâm nhân số của mình với 5. Bí mật cộng hai tích đó lại và báo cho anh kết quả là số chẵn hay số lẻ.

    Lâm và Ly tính xong Lâm thông báo:

    • Kết quả là số lẻ anh ạ.

    Anh Quân nói luôn:

    • Vậy chính em lấy được số chẵn.

    Cả Lâm và Ly đều ngạc nhiên:

    • Sao anh giỏi thế!

    Các bạn ơi, Anh Quân đã tính thế nào nhỉ?

    Bài 26: BA CHÀNG CÂU CÁ

    Một ngày chủ nhật, được nghỉ học, ba bạn chơi thân với nhau là An, Phương, Minh rủ nhau đi câu cá. Khi về An thấy mình câu được nhiều cá bèn cho Phương và Minh một số cá bằng số cá bằng mỗi người hiện có. Khi ấy, Phương thấy mình nhiều cá quá liền cho lại An và Minh số cá bằng số cá của mỗi người hiện có. Sau lần đó , Minh thấy có nhiều cá hơn các ban nên cho lại An và Phương số cá bằng số cá hiện có củ mỗi người. Lúc này của số cá của ba người đều bằng nhau và họ cùng vui vẻ ra về.

    Bạn hãy tính xem mỗi người câu được bao nhiêu con cá, biết cả ba người câu được 24 con cá.

    Bài 27: SỐ CHẴN HAY SỐ LẺ?

    Anh Tuấn có 25 miếng bìa nhỏ, anh yêu cầu bé Lan viết các số tự nhiên liên tiếp từ 1 đến 55 lên mặt phải của 55 miếng bìa đó, sau đó, anh xáo trộn các miếng bìa và yêu cầu Lan viết lên mặt trái của miếng bìa lần lượt các số từ 1 đến 55 một lần nữa.

    Bây giờ các bạn hãy cộng hai số đã viết trên hai mặt của tấm bìa sau đó nhân 55 kết quả đó với nhau xem được số chẵn hay số lẻ?

    Bài 28: BAO NHIÊU NĂM NỮA?

    Cha nay bốn mốt tuổi rồi

    Con vừa mười bảy đang thời xuân xanh

    Bao nhiêu năm nữa đến phần

    Tuổi cha gấp đúng hai lần tuổi con?

    Bài 29: NHỮNG MIẾNG BÌA LANG THANG

    Cậu Mít cắt một tấm bìa thành hình tròn rất đẹp. Sau đó Mít chia tấm bìa thành 20 ô nhỏ, mỗi ô Mít viết một số hoặc một dấu trong các số 1,2,4,6,0,5 và trong các dấu +; – ; x ; : ; = để được phép tính đúng. Một lúc sau Mít lại hí hoáy cắt tấm bìa thành 7 miếng và thả chúng lang thang quanh bàn học của Mít. Bây giờ các bạn hãy xếp các miếng bìa lang thang này lại thành tấm bìa ban đầu của Mít nhé.

    Bài 30: PHÉP TÍNH CỘNG SAI!

    Cho phép cộng sau: Hãy giải thích phép tính cộng này là sai.

    1 8 * *

    + 3 7 * *

    4 6 * *

    1 * 5 * *

    Bài 31: BÂY GIỜ LÀ MẤY GIỜ?

    Vui hỏi Toán “Bây giờ là mấy giờ?

    Toán trả lời: “Từ 12 giờ trưa đến bây giờ, bằng thời gian từ bây giờ đến nửa đêm”

    Vui suy nghĩ và hớn hở nói rằng “ Tớ biết bây giờ là mấy giờ rồi!”

    Lúc đó là mấy giờ? Đố bạn biết đấy!

    Bài 32: CHIA THÙNG VÀ CHIA MẮM

    Ba bà Thược, Loan, Liên có tất cả 7 thùng đựng đầy mắm, 7 thùng đựng mắm đầy một nửa và 7 thùng không, bạn hãy giúp ba bà chia dều số mắm và số thùng để mỗi người đều được phần bằng nhau mà không phải rót mắm sang thùng khác đâu nhé?

    Bài 33: NGÀY 18 THÁNG 2 LÀ THỨ MẤY?

    Tồ đố Tèo: ‘Này nhé, tháng 2 năm 2004 có đến năm ngày chủ nhật, đố Tèo ngày 18 tháng 2 năm 2004 là thứ mấy”. Tèo liền đứng dậy, Tồ nắm giữ tay Tèo và hỏi “Cậu định đâu”.

    Tèo trả lời: “tớ đi tìm tờ lịch măm 2004 để trả lời cậu”.

    Tồ nói: “ Thế thì tớ đố làm gì? Không được xem lịch mà suy nghĩ để tìm câu trả lời”… Tèo đàng chịu thua.

    Các ban hãy giúp Tèo nhé.

    Bài 34: CHỈ MỘT LẦN CÂN

    Có mười cái túi đựng tiền vàng có hinhfdangj giống hệt nhau, trong đó có một túi đựng tiền giả. Những đồng tiền giả nhẹ hơn 1 gam so với đồng tiền thật nặng 10 gam.

    Bằng chiếc cân đồng hồ và chỉ một lần cân hãy tìm ra túi đồng tiền giả.

    Bài 35: BA CAN DẦU

    Cô Mai có 12 lít đựng đầy dầu và hai can 7 lít và 5 lít không đựng gì. Cô muốn chia số dầu có được của mình thành ba phần: 5 lít ; 4 lít ; 3 lít bằng ba cái can này.

    Bạn hãy giup cô Mai nhé!

    Bài 36: LẤY BẢY LÍT NƯỚC

    Bạn Tuyền có hai cái can: một can loại 5 lít và một can loại 3 lít.

    Tuyền muốn lấy đúng 7 lít nước từ 1 hồ (bể) nước.

    Tuyền cứ loay hoay maixmaf chưa lấy được đủ 7 lít nước.

    Các ban hãy giúp bạn Tuyền nhé!

    Bài 37: ĐỒNG HỒ HƯ

    Có một đồng hồ hư, cứ mỗi ngày (24 giờ =1440 phút) nó lại chạy chậm 10 phút. Đúng 7 giờ sáng hôm đó người ta vặn đồng hồtheo giờ đúng.

    Hỏi sau bao nhiêu ngày đồng trên chỉ đúng 7 giờ sáng?

    Bài 38: MỘT VIÊN BI LẠ

    Dũng có bốn viên bi, trong đó có ba viên nặng bằng nhau còn một viên không nặng như ba viên kia (có thể nặng hơn hoặc nhẹ hơn). Nhìn bề ngoài cả bốn viên bi giống hệt nhau nên không thể xác định được viên bi lạ này.

    Bạn nào có thể tìm được viên bi lạ ấy chỉ bằng nhiều nhất hai lần cân trên cân hai đĩa?

    Bài 39: CÁ NẶNG BAO NHIÊU?

    Thấy bố đang thịt một con cá rất ngon, Tí, Tồ đến bên và hỏi bố:

    Bố ơi, con cá này nặng bao nhiêu mà to thế?

    Bố Tí, Tồ mỉm cười nói:

    Đuôi của cá nặng 150 gam, đầu cá nặng bằng đuôi cá cộng nửa thân cá. Thân cá bằng đầu cá cộng với đuôi cá.

    Các con tính xem con cá nặng bao nhiêu gam?

    Tí, Tồ tính mãi mà không đúng. Các bạn hãy giúp Tí, Tồ nhé!

    Bài 40: TÌM ĐỒNG TIỀN GIẢ

    Có 27 đồng tiền kim loại giống hệt nhau trong đó có một đồng tiền giả nhẹ hơn đồng tiền thật. Các đồng tiền thật có cùng khối lượng.

    Bây giờ phải lấy ra được đồng tiền giả đó với ba lần cân và chỉ dùng chiếc cân hai đĩa. Vậy phải cân thế nào đậy?

    Bài 41: CÂN THẾ NÀO ĐÂY

    Một cửa hàng nhập vào 80 gói kẹo giống hệt nhau và được biết trong đó có một gói kẹo nhẹ hơn các gói kẹo khác. Bây giờ phải xác định được gói kẹo nhẹ đó, nhưng cửa hàng chỉ có một chiếc cân hai đĩa. Làm thế nào để chỉ 4 lần cân mà xác định được gói kẹo nhẹ đó?

    Các bạn hãy cùng trổ tài để giúp cô nhân viên bán hàng nhé!

    Bài 42: THỨ MẤY?

    Hùng nhớ mãi ngày lễ 20/11/2004 (ngày nhà giáo Việt Nam) vì hôm đó lớp Hùng tổ chức vui lắm. Các bạn chúc mừng cô giáo bằng lời ca tiến hát và những bông hoa điểm mười rực rỡ. Cô giáo vui mừng hỏi cả lớp

    “Hôm nay là thứ mấy?”

    Cả lớp đồng thanh trả lời: “ Hôm nay là thứ bảy ạ”.

    Cô hỏi tiếp: “ Đố các con 28 năm nữa thì ngày 20/11 là thứ mấy?”.

    Cả lớp im lặng suy nghĩ, và rồi chính Hùng trả lời được câu hỏi của cô sớm nhất.

    Hôm đó Hùng được cô thưởng quà và khen Hùng giỏi toán. Các bạn đoán xem câu trả lời của Hùng như thế nào nhé!

    Bài 43: HÃY GIÚP BẠN BỜM

    Bạn Bờm có chín số là: 1;3;5;9;11;13;15;17. Bờm muốn đặt mỗi số này vào một ô vuông ở bảng dưới đây để tổng các số trên ba cột lần lượt là: 25;30;26. Bờm loay hoay mãi mà vẫn chưa tìm được cách đặt các số vào các ô vuông. Các bạn hãy giúp bạn Bờm nhé!

    ma tran 3x3

    Bài 44: TÍNH DIỆN TÍCH HÌNH VUÔNG

    Tính diện tích hình vuông ABCD, biết rằng tổng các chu vi của sáu hình chữ nhật nhỏ ở hình bên là 50 cm.

    Bài 45: CHIA THẾ NÀO?

    Tam ngồi đăm chiêu trước một bàn cờ có 8 x 8 = 64 ô vuông. Tứ đến bên bạn hỏi: Bạn đang nghiên cứu gì ở bàn cờ mà say sưa thế?

    Tam quay sang Tứ nói: Anh Nam vừa đố tớ chia bàn cờ thành bảy hình chữ nhật khác nhau mà số ô đen và số ô trắng ở mỗi hình chữ nhật đều bằng nhau. Mình với bạn cùng nghĩ nhé.

    Hai bạn chụm đấu kẻ rồi lại xóa mãi mà không tìm ra kết quả. Các bạn có thể giúp hai bạn ấy không?


    chia bàn cờ vua 

    Bài 46: ĐIỀN SỐ VÀO Ô TRÒN

    Hãy viết các số tự nhiên liên tiếp từ 1 đến 6 vào các ô tròn trên các cạnh của tam giác sao cho tổng các số trên 3 cạnh đều bằng 9.

    bai toan lop 4 viet so vao cac hinh tron o dinh tam giac

    Bài 47: CHỈ VẼ MỘT NÉT

    1. Hãy vẽ một nét gồm 4 đoạn thẳng chứa 9 điểm (Hình a)
    2. Hãy vẽ một nét gồm 6 đoạn thẳng chứa 16 điểm (Hình b)
    3. Hãy vẽ một nét gồm 8 đoạn thẳng chứa 25 điểm (Hình c)

    ve hinh bang 1 net khong nhấc bút

     

    Bài 48: XẾP HÌNH CHỮ NHẬT

    Dịu có 16 que dài 1 cm, 16 que dài 2 cm, 15 que dài 3 cm. Dịu đưa số que này cho Dàng và đố Dàng xép thành một hình chữ nhật.

    Dàng khẳng định : “ Đơn giản tớ xếp được ngay”.

    Thế nhưng … Dàng hì hụi xếp mãi mà vẫn không được. Các bạn có xếp được không ?

    Bài 49: CHIA BÁNH CHƯNG XANH

    Có một chiếc bánh chưng xanh đã bóc lá. Bạn hãy chia chiếc bánh chưng đó thành 8 phàn bằng nhau bởi 3 chiếc lạt, sao cho mỗi phần đều có cả bánh lẫn nhân như nhau.

  • Phương pháp tăng giảm khối lượng

    Phương pháp tăng giảm khối lượng

    Phương pháp tăng giảm khối lượng

    I. Lý thuyết phương pháp tăng giảm khối lượng

    • Trong phản ứng hóa học khi chuyển từ chất này thành chất khác, khối lượng các chất có thể tăng hoặc giảm do khối lượng mol phân tử của các chất đó khác nhau. Dựa vào sự tăng giảm khối lượng của các chất ta có thể tìm được số mol các chất đó.
    • Sự tăng hoặc giảm khối lượng của các chất có mối quan hệ với số mol các chất đó.
    •  Có thể dùng phương pháp tăng giảm khối lượng thay cho phương pháp bảo toàn khối lượng để giải bài tập nhanh hơn (tuy nhiên khó hiểu hơn đối với một số HS).
    • Dấu hiệu: Đề bài cho khối lượng, mối quan hệ khối lượng giữa các chất trong phản ứng hóa học.
    • Các phản ứng thường áp dụng phương pháp tăng giảm khối lượng
      • Phản ứng kim loại tác dụng với dd axit HCl, H2SO4 loãng

    R + HX – muối + H2

    ∆m tăng = mgốc axit = mmuối – mKL (ngốc axit = naxit)

      • Phản ứng kim loại A tác dụng với muối của kim loại B

    A + muối B – muối A + B

        • MA > MB sau phản ứng khối lượng thanh KL A tăng (VD:…)
        • MA < MB sau phản ứng khối lượng thanh KL A giảm (VD:…)
      • Phản ứng muối cacbonat (hiđro cacbonat) tác dụng với dd axit HCl, H2SO4 loãng

    ∆m tăng = mmuối clorua – mmuối cacbonat = 11nCO2 (VD: …)

    ∆m tăng = mmuối sunfat – mmuối cacbonat = 36nCO2 (VD: …)

      • Phản ứng oxit kiam loại tác dụng với dd axit HCl, H2SO4 loãng
      • Phản ứng CO2 tác dụng với dung dịch Ca(OH)2
        • mkết tủa > mCO2 khối lượng dung dịch giảm so với ban đầu mdd giảm = mkết tủa – mCO2
        • mkết tủa < mCO2 khối lượng dung dịch giảm so với ban đầu mdd giảm = mCO2 – mkết tủa
      • Phản ứng CO/H2 tác dụng với oxit kim loại
        • m hỗn hợp khí tăng = mchất rắn giảm = moxi trong oxit phản ứng

    II. Vận dụng phương pháp tăng giảm khối lượng

    VD1: Ngâm một thanh magie vào 200ml dung dịch CuSO4 1M. Sau khi phản ứng xảy ra hoàn toànthì khối lượng thanh magie tăng hay giảm bao nhiêu gam? (ĐS: 0,2(64-24)=8g)

    Phương pháp bảo toàn khối lượng VD1

    Tính nhanh n = Δm/ΔM thay số 0,2 = Δm/(64-24) => Δm = 0,2.(64-24) = 8 gam

    VD2: Ngâm một lá kẽm vào 300ml dung dịch FeSO4 0,05M. Sau khi phản ứng xảy ra hoàn toànthì khối lượng lá kẽm tăng hay giảm bao nhiêu gam? (ĐS: 0,3.0,05(65-56)=0,135g)

    Phương pháp bảo toàn khối lượng VD2

    Tính nhanh n = Δm/ΔM thay số 0,2 = Δm/(65-56) => Δm = 0,2.(65-56) = 0,135 gam

    VD3: Ngâm một lá nhôm trong 150 ml CuSO4 1M. Sau khi phản ứng hoàn toàn khối lượng lá nhôm tăng hay giảm bao nhiêu gam. (ĐS: 6,9 gam)

    Phương pháp bảo toàn khối lượng VD3

    Tính nhanh n(CuSO4):3 = Δm/ΔM (vì hệ số của CuSO4 trong phương trình là 3)

    thay số 0,15:3 = Δm/(3.64-2.27)

    => Δm = 0,05.(3.64-2.27) = 6,9 gam

    VD4: Ngâm một lá sắt trong dung dịch CuSO4. Tính khối lượng đồng bám trên lá sắt biết khối lượng lá sắt tăng 1,2 gam. (ĐS: 9,6 gam)

    Phương pháp bảo toàn khối lượng VD4

    Tính nhanh n(Cu) = Δm/ΔM thay số n(Cu) = 1,2/(64-56) = 0,15 => m (Cu) = 0,15.64 = 9,6 gam

    VD5: Ngâm một thanh magie trong dung dịch AgNO3. Tính khối lượng bạc bám trên thanh magie biết khối lượng thanh magie tăng 15,36 gam. (ĐS: 17,28 gam)

    Phương pháp bảo toàn khối lượng VD5

    Tính nhanh n(Ag):2 = Δm/ΔM (Vì hệ số của Ag trong phương trình là 2)

    thay số n(Ag) = 2.(15,36/(2.108-24) = 0,16

    => m (Cu) = 0,16.108 = 17,28 gam

    VD6: Nhúng thanh Zn vào dung dịch chứa 5,64 gam Cu(NO3)2 và 3,4 gam AgNO3. Sau khi các phản ứng xảy ra hoàn toàn khối lượng thanh Zn tăng hay giảm bao nhiêu gam biết tất cả kim loại thoát ra đều bám vào thanh Zn. (ĐS: 1,48 gam)

    Phương pháp bảo toàn khối lượng VD6

    Nhúng thanh Zn vào dd AgNO3 thì khối lượng tăng Δm1 gam

    n(AgNO3) : 2 = Δm1/ΔM => Δm1 = (0,02:2).(2.108-65) = 1,51 gam

    Nhúng thanh Zn vào dd Cu(NO3)2 thì khối lượng giảm Δm2 gam

    n(Cu(NO3)2)  = Δm2/ΔM => Δm2 = 0,03.(65-64) = 0,03 gam

     Δm1 > Δm2 => Khối lượng thanh Zn tăng 1,51 – 0,03 = 1,48 gam

    III. Bài tập áp dụng phương pháp tăng giảm khối lượng

    ● Bài tập phương pháp tăng giảm khối lượng dành cho học sinh lớp 10

    Câu 1: Hòa tan hoàn toàn 2,43 gam hỗn hợp gồm Mg và Zn vào một lượng vừa đủ dung dịch H2SO4 loãng, sau phản ứng thu được 1,12 lít H2 (đktc) và dung dịch X. Khối lượng muối trong dung dịch X là

    A. 7,23 gam. B. 7,33 gam. C. 4,83 gam. D. 5,83 gam.

    (Đề thi tuyển sinh Đại học khối A năm 2012)

    Câu 2: Hòa tan hoàn toàn 20,6 gam hỗn hợp gồm Na2CO3 và CaCO3 bằng dung dịch HCl dư, thu được V lít khí CO2 (đktc) và dung dịch chứa 22,8 gam hỗn hợp muối. Giá trị của V là

    A. 1,79. B. 5,60. C. 2,24. D. 4,48.

    (Đề thi tuyển sinh Cao đẳng năm 2013)

    Câu 3: Hoà tan hoàn toàn 2,81 gam hỗn hợp gồm Fe2O3, MgO, ZnO trong 500 ml axit HCl 0,2M (vừa đủ). Sau phản ứng, hỗn hợp muối clorua khan thu được khi cô cạn dung dịch có khối lượng là :

    A. 6,81 gam. B. 4,76 gam. C. 3,81 gam. D. 5,56 gam.

    Câu 4: Cho dung dịch AgNO3 dư tác dụng với dung dịch hỗn hợp có hòa tan 6,25 gam hai muối KCl và KBr thu được 10,39 gam hỗn hợp AgCl và AgBr. Số mol các chất trong hỗn hợp đầu là :

    A. 0,08 mol. B. 0,06 mol. C. 0,03 mol. D. 0,055 mol.

    Câu 5*: Có hỗn hợp gồm NaI và NaBr. Hòa tan hỗn hợp vào nước. Cho brom dư vào dung dịch. Sau khi phản ứng thực hiện xong, làm bay hơi dung dịch, làm khô sản phẩm, thì thấy khối lượng của sản phẩm nhỏ hơn khối lượng hỗn hợp 2 muối ban đầu là m gam. Lại hòa tan sản phẩm vào nước và cho clo lội qua cho đến dư. Làm bay hơi dung dịch và làm khô chất còn lại người thấy khối lượng chất thu được lại nhỏ hơn khối lượng muối phản ứng là m gam. Thành phần phần trăm về khối lượng của NaBr trong hỗn hợp đầu là :

    A. 3,7%. B. 4,5%. C. 7,3%. D. 6,7%.

    Câu 6: Một bình cầu dung tích 448 ml được nạp đầy oxi rồi cân. Phóng điện để ozon hoá, sau đó nạp thêm cho đầy oxi rồi cân. Khối lượng trong hai trường hợp chênh lệch nhau 0,03 gam. Biết các thể tích nạp đều ở đktc. Thành phần % về thể tích của ozon trong hỗn hợp sau phản ứng là :

    A. 9,375%. B. 10,375%. C. 8,375%. D.11,375%.

    Câu 7: Cho một lượng bột Zn vào dung dịch X gồm FeCl2 và CuCl2. Khối lượng chất rắn sau khi các phản ứng xảy ra hoàn toàn nhỏ hơn khối lượng bột Zn ban đầu là 0,5 gam. Cô cạn phần dung dịch sau phản ứng thu được 13,6 gam muối khan. Tổng khối lượng các muối trong X là :

    A. 17,0 gam. B. 13,1 gam. C. 19,5 gam. D. 14,1 gam.

    (Đề thi tuyển sinh Đại học khối B năm 2008)

    Câu 8: Cho m gam hỗn hợp bột Zn và Fe vào lượng dư dung dịch CuSO4. Sau khi kết thúc các phản ứng, lọc bỏ phần dung dịch thu được m gam bột rắn. Thành phần phần trăm theo khối lượng của Zn trong hỗn hợp bột ban đầu là :

    A. 90,27%. B. 85,30%. C. 82,20%. D. 12,67%.

    (Đề thi tuyển sinh đại học khối B năm 2007)

    Câu 9: Lấy 2 thanh kim loại M hoá trị II. Thanh 1 nhúng vào 250 ml dung dịch FeSO4; thanh 2 nhúng vào 250 ml dung dịch CuSO4. Sau khi phản ứng kết thúc, thanh 1 tăng 16 gam, thanh 2 tăng 20 gam. Biết nồng độ mol/l của 2 dung dịch ban đầu bằng nhau. Vậy M là :

    A. Mg. B. Ni. C. Zn. D. Be.

    Câu 10*: Cho 3,78 gam bột Al phản ứng vừa đủ với dung dịch muối XCla tạo thành dung dịch Y. Khối lượng chất tan trong dung dịch Y giảm 4,06 gam so với dung dịch XCla. Công thức của muối XCla là :

    A. FeCl3. B. CuCl3. C. CrCl3. D. ZnCl2.

    ● Bài tập phương pháp tăng giảm khối lượng dành cho học sinh lớp 11

    Câu 11: Có 1 lít dung dịch hỗn hợp Na2CO3 0,1 mol/l và (NH4)2CO3 0,25 mol/l. Cho 43 gam hỗn hợp BaCl2 và CaCl2 vào dung dịch đó. Sau khi các phản ứng kết thúc ta thu được 39,7 gam kết tủa A và dung dịch B. Phần trăm khối lượng các chất trong A là :

    A. = 75%, = 25%. B. = 50,38%, = 49,62%.

    C. = 49,62%, = 50,38%. D. = 25%, = 75%.

    Câu 12: Hòa tan 5,94 gam hỗn hợp 2 muối clorua của 2 kim loại R và M vào nước được dung dịch X. Để làm kết tủa hết ion có trong dung dịch X, người ta cho dung dịch X tác dụng với dung dịch AgNO3 dư, thu được 17,22 gam kết tủa. Lọc bỏ kết tủa, thu được dung dịch Y. Cô cạn Y được m gam hỗn hợp muối khan. Giá trị m là :

    A. 6,36 gam. B. 6,15 gam. C. 9,12 gam. D. 12,3 gam.

    Câu 13*: Có một cốc đựng m gam dung dịch HNO3 và H2SO4. Hoà tan hết 3,64 gam kim loại M (có hoá trị không đổi) vào dung dịch trong cốc thì thu được 2,1504 lít (đktc) hỗn hợp 2 khí NO2 và X. Sau phản ứng, khối lượng các chất trong cốc giảm 1,064 gam. Kim loại M là :

    A. Fe. B. Cu. C. Al. D. Zn.

    Câu 14: Nung 6,58 gam Cu(NO3)2 trong bình kín không chứa không khí, sau một thời gian thu được 4,96 gam chất rắn và hỗn hợp khí X. Hấp thụ hoàn toàn X vào nước để được 300 ml dung dịch Y. Dung dịch Y có pH bằng

    A. 2. B. 3. C. 4. D. 1.

    (Đề thi tuyển sinh Đại học khối A năm 2009)

    Câu 15: Nhiệt phân hoàn toàn 29,6 gam một muối nitrat kim loại, sau phản ứng thu được 8 gam oxit kim loại. Công thức của muối nitrat là

    A. Cu(NO3)2. B. Fe(NO3)3. C. Pb(NO3)2. D. Mg(NO3)2­.

    (Đề thi thử đại học lần 4 – THPT Chuyên – Đại học Vinh, năm học 2010 – 2011)

    Câu 16*: Đốt cháy hoàn toàn 4,64 gam một hiđrocacbon X (chất khí ở điều kiện thường) rồi đem toàn bộ sản phẩm cháy hấp thụ hết vào bình đựng dung dịch Ba(OH)2. Sau các phản ứng thu được 39,4 gam kết tủa và khối lượng phần dung dịch giảm bớt 19,912 gam. Công thức phân tử của X là

    A. C3H4. B. CH4. C. C2H4. D. C4H10.

    (Đề thi tuyển sinh Đại học khối A năm 2012)

    Câu 17: Cho 13,8 gam chất hữu cơ X có công thức phân tử C7H8 tác dụng với một lượng dư dung dịch AgNO3 trong NH3, thu được 45,9 gam kết tủa. X có bao nhiêu đồng phân cấu tạo thỏa mãn tính chất trên ?

    A. 5. B. 4. C. 6. D. 2.

    (Đề thi tuyển sinh Đại học khối A năm 2011)

    Câu 18: Cho 5,76 gam axit hữu cơ X đơn chức, mạch hở tác dụng hết với CaCO3 thu được 7,28 gam muối của axit hữu cơ. Công thức cấu tạo thu gọn của X là :

    A. CH2=CHCOOH. B. CH3COOH.

    C. HCCCOOH. D. CH3CH2COOH.

    (Đề thi tuyển sinh Cao đẳng năm 2007)

    Câu 19: Cho 24,4 gam hỗn hợp gồm axit axetic, axit fomic, glixerol, ancol etylic tác dụng với Na dư. Sau khi phản ứng hoàn toàn thu được 6,72 lít khí H2 (đktc) và m gam muối. Giá trị của m là:

    A. 31 gam. B. 37,6 gam. C. 23,8 gam. D. 25 gam.

    (Đề thi thử Đại học lần 2 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2010 – 2011)

    Câu 20*: Cho m gam hỗn hợp axit axetic, axit benzoic, axit ađipic, axit oxalic tác dụng vừa đủ với dung dịch NaOH thu được a gam muối. Nếu cũng cho m gam hỗn hợp X nói trên tác dụng với Ca(OH)2 vừa đủ thì thu được b gam muối. Biểu thức liên hệ m, a, b là:

    A. 9m = 20a – 11b. B. 3m = 22b – 19a. C. 8m = 19a – 11b. D. m = 11b – 10a.

    (Đề thi thử đại học lần 3 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2011 – 2012)

    ● Bài tập phương pháp tăng giảm khối lượng dành cho học sinh lớp 12

    Câu 21: Để tác dụng hết với 100 gam lipit có chỉ số axit bằng 7 phải dùng 17,92 gam KOH. Khối lượng muối thu được là:

    A. 110,324 gam. B. 108,107 gam. C. 103,178 gam. D. 108,265 gam.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2010 – 2011)

    Câu 22: Cho 8,9 gam một hợp chất hữu cơ X có công thức phân tử C3H7O2N phản ứng với 100 ml dung dịch NaOH 1,5M. Sau khi phản ứng xảy ra hoàn toàn, cô cạn dung dịch thu được 11,7 gam chất rắn. Công thức cấu tạo thu gọn của X là :

    A. HCOOH3NCH=CH2. B. H2NCH2CH2COOH.

    C. CH2=CHCOONH4. D. H2NCH2COOCH3.

    (Đề thi tuyển sinh Đại học khối B năm 2008)

    Câu 23: Cho 1 mol amino axit X phản ứng với dung dịch HCl (dư), thu được m­1 gam muối Y. Cũng 1 mol amino axit X phản ứng với dung dịch NaOH (dư), thu được m2 gam muối Z. Biết m2 – m1 = 7,5. Công thức phân tử của X là:

    A. C4H10O2N2. B. C4H8O4N2. C. C5H9O4N. D. C5H11O2N.

    (Đề thi tuyển sinh Đại học khối A năm 2009)

    Câu 24*: Cho 0,16 mol axit A phản ứng vừa đủ với 160 ml dung dịch HCl 1M, thu được 22,32 gam muối. Mặt khác, cho 1,03 gam A phản ứng vừa với dung dịch KOH, thu được 1,41 gam muối khan. Số CTCT của A là:

    A. 7. B. 5. C. 4. D. 6.

    Câu 25: Nhúng một thanh sắt nặng 100 gam vào 100 ml dung dịch hỗn hợp gồm Cu(NO3)2 0,2M và AgNO3 0,2M. Sau một thời gian lấy thanh kim loại ra, rửa sạch làm khô cân được 101,72 gam (giả thiết các kim loại tạo thành đều bám hết vào thanh sắt). Khối lượng sắt đã phản ứng là

    A. 2,16 gam. B. 0,84 gam. C. 1,72 gam. D. 1,40 gam.

    (Đề thi tuyển sinh Đại học khối B năm 2009)

    Câu 26: Cho 8 gam hỗn hợp A gồm Mg và Fe tác dụng với dung dịch CuSO4 đến khi phản ứng kết thúc, thu được 12,4 gam chất rắn B và dung dịch D. Cho dung dịch D tác dụng với dung dịch NaOH dư, lọc và nung kết tủa ngoài không khí đến khối lượng không đổi thu được 8 gam oxit. Phần trăm khối lượng của Fe trong hỗn hợp A là :

    A. 35%. B. 30%. C. 70%. D. 65%.

    Câu 27: Cho 50 gam hỗn hợp MgCO3 và BaCO3 tác dụng với dung dịch H2SO4, thu được m gam chất rắn A, dung dịch B chứa 12 gam muối và 4,48 lít khí CO2 (đktc). Giá trị của m là :

    A. 45,2. B. 57,2. C. 64. D. 66,2.

    Câu 28: Cho 19,2 gam hỗn hợp Fe3O4, FexOy tác dụng với vừa hết 180 ml dung dịch H2SO4 2M (loãng), thu được dung dịch X. Khối lượng muối có trong X là :

    A. 30,4. B. 24. C. 48. D. 52.

    (Đề thi thử Đại học – THPT Chuyên Lê Hồng Phong – Nam Định, năm học 2012 – 2013)

    Câu 29*: Hòa tan hết 26,43 gam hỗn hợp bột A gồm Mg, Al, Al2O3 và MgO bằng 795 ml dung dịch hỗn hợp gồm HCl 0,5M và H2SO4 0,75M (vừa đủ). Sau phản ứng thu được dung dịch X và 4,368 lít khí H2 (ở đktc). Cô cạn dung dịch X thu được khối lượng muối khan là

    A. 95,92 gam. B. 86,58 gam. C. 100,52 gam. D. 88,18 gam.

    Câu 30*: Chia 9,6 gam hỗn hợp gồm CuO và Fe2O3 thành 2 phần bằng nhau : Phần 1 phản ứng với 100 ml dung dịch HCl x (mol/l), cô cạn hỗn hợp thu được 8,1 gam chất rắn. Phần 2 phản ứng với 200 ml dung dịch HCl x (mol/l), cô cạn hỗn hợp thu được 9,2 gam chất rắn. Giá trị của x và phần trăm về khối lượng CuO tương ứng là

    A. 1,2 và 33,33%. B. 0,5 và 33,33%. C. 0,5 và 66,66%. D. 1,2 và 66,66%.

    (Đề thi dự bị tuyển sinh Đại học khối B năm 2012)

    Câu 31: Hòa tan 14 gam hỗn hợp 2 muối M2CO3 và RCO3 bằng dung dịch HCl dư, thu được dung dịch A và 0,672 lít khí (đktc). Cô cạn dung dịch A thì thu được m gam muối khan. m có giá trị là :

    A. 16,33 gam. B. 14,33 gam. C. 9,265 gam. D. 12,65 gam.

    Câu 32: Hòa tan hết 23,2 gam hỗn hợp rắn X gồm FeO, Fe2O3, Fe3O4 trong dung dịch HCl loãng, dư. Cô cạn dung dịch sau phản ứng thu được 45,2 gam muối khan. Nếu khử hoàn toàn lượng X trên sẽ thu được bao nhiêu gam sắt?

    A. 11,6. B. 11,2. C. 16,8. D. 12,8.

    (Đề thi thử đại học lần 4 – THPT Chuyên – Đại học Vinh, năm học 2011 – 2012)

    Câu 33: Hỗn hợp X gồm NaBr và NaI. Cho hỗn hợp X tan trong nước thu được dung dịch A. Nếu cho brom dư vào dung dịch A, sau phản ứng hoàn toàn, cô cạn thấy khối lượng muối khan thu được giảm 7,05 gam. Nếu sục khí clo dư vào dung dịch A, phản ứng hoàn toàn, cô cạn dung dịch thấy khối lượng muối khan giảm 22,625 gam. Thành phần % khối lượng của một chất trong hỗn hợp X là

    A. 47,8%. B. 64,3%. C. 35,9%. D. 39,1%.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Bắc Ninh, năm học 2009 – 2010)

    Câu 34: Cho dung dịch chứa 6,03 gam hỗn hợp gồm hai muối NaX và NaY (X, Y là hai nguyên tố có trong tự nhiên, ở hai chu kì liên tiếp thuộc nhóm VIIA, số hiệu nguyên tử ZX < ZY) vào dung dịch AgNO3 (dư), thu được 8,61 gam kết tủa. Phần trăm khối lượng của NaX trong hỗn hợp ban đầu là

    A. 58,2%. B. 52,8%. C. 41,8%. D. 47,2%.

    (Đề thi tuyển sinh Đại học khối B năm 2009)

    Câu 35: Sau khi chuyển một thể tích khí oxi thành ozon thì thấy thể tích giảm đi 5 ml (biết các thể tích đo ở cùng điều kiện). Thể tích oxi đã tham gia phản ứng là bao nhiêu ?

    A. 14 ml. B. 16 ml. C. 17 ml. D. 15 ml.

    Câu 36*: Hỗn hợp X gồm SO2 và O2 có tỉ khối so với H2 bằng 28. Nung nóng hỗn hợp X một thời gian (có xúc tác V2O5) thu được hỗn hợp Y có tỉ khối so với X bằng 16/13. Hiệu suất của phản ứng tổng hợp SO3 là

    A. 62,5%. B. 75,0%. C. 50,0%. D. 60,0%.

    (Đề thi thử đại học lần 2 – THPT Chuyên – Đại học Vinh, năm học 2012 – 2013)

    Câu 37: Ngâm một lá Mg kim loại trong dung dịch Cu(NO3)2, sau một thời gian người ta nhận thấy khối lượng của lá kim loại đó tăng 1 gam so với ban đầu. Khối lượng của Cu kim loại đã bám lên bề mặt của lá kim loại đó là (giả thiết rằng toàn bộ Cu bị đẩy ra khỏi muối đã bám hết vào lá Mg kim loại)

    A. 1,60 gam. B. 1,28 gam. C. 1,20 gam. D. 2,40 gam.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Bắc Ninh, năm học 2008 – 2009)

    Câu 38: Cho m gam bột Zn vào 500 ml dung dịch Fe2(SO4)3 0,24M. Sau khi các phản ứng xảy ra hoàn toàn, khối lượng dung dịch tăng thêm 9,6 gam so với khối lượng dung dịch ban đầu. Giá trị của m là :

    A. 32,50. B. 20,80. C. 29,25. D. 48,75.

    (Đề thi tuyển sinh Đại học khối A năm 2011)

    Câu 39: Nhúng một thanh kẽm và một thanh sắt vào cùng một dung dịch CuSO4. Sau một thời gian lấy hai thanh kim loại ra thấy trong dung dịch còn lại có nồng độ mol ZnSO4 bằng 2,5 lần nồng độ mol FeSO4. Mặt khác, khối lượng dung dịch giảm 2,2 gam. Khối lượng đồng bám lên thanh kẽm và bám lên thanh sắt lần lượt là :

    A. 12,8 gam; 32 gam. B. 64 gam; 25,6 gam.

    C. 32 gam; 12,8 gam. D. 25,6 gam; 64 gam.

    Câu 40: Cho 2,7 gam hỗn hợp bột X gồm Fe và Zn tác dụng với dung dịch CuSO4. Sau một thời gian, thu được dung dịch Y và 2,84 gam chất rắn Z. Cho toàn bộ Z vào dung dịch H2SO4 (loãng, dư). sau khi các phản ứng kết thúc thì khối lượng chất rắn giảm 0,28 gam và dung dịch thu được chỉ chứa một muối duy nhất. Phần trăm khối lượng của Fe trong X là :

    A. 58,52%. B. 51,85%. C. 48,15%. D. 41,48%.

    (Đề thi tuyển sinh Đại học khối A năm 2011)

    Mời các thầy cô và các em download file word tại đây pp3 – tăng giảm khối lượng

     

    Website còn có bài tập trắc nghiệm cho tất cả các chương – chủ đề của cả 3 khối, các thầy cô và các em có thể xem cụ thể từng khối lớp tại các link sau

    Các phương pháp bảo toàn khác

    Hoặc các thầy cô có thể xem các tài liệu khác của website

  • Phương pháp bảo toàn khối lượng

    Phương pháp bảo toàn khối lượng

    Phương pháp bảo toàn khối lượng

    phuong phap bao toan khoi luong

    Xem thêm

    Phương pháp bảo toàn nguyên tố

    Phương pháp tăng giảm khối lượng

     

     

    CHUYÊN ĐỀ 2: PHƯƠNG PHÁP B ẢO TOÀN KHỐI LƯỢNG

    I. Lí thuyết

    – Nội dung định luật: Trong phản ứng hóa học, tổng khối lượng các chất tham gia phản ứng luôn bằng tổng khối lượng các sản phẩm tạo thành.

    – Hq1: Khi phản ứng xảy ra không hoàn toàn hoặc có chất hết chất dư, tổng khối lượng các chất trước phản ứng luôn bằng tổng khối lượng các chất sau phản ứng.

    – Hq2: Tổng khối lượng của một nguyên tố trước phản ứng bằng tổng khối lượng nguyên tố đó sau phản ứng.

    – Hq3: mdd sau pư = mdd trước pư + mct – mkhí, kết tủa (VD: Cho Ba vào dd BaSO4)

    – Hq4: Trong phản ứng của kim loại với dung dịch axit, khối lượng muối thu được bằng tổng khối lượng của kim loại và anion gốc axit tạo muối.

    – Hq5: Có thể dùng phương pháp tăng giảm khối lượng thay cho bảo toàn khối lượng.

    * Chú ý

    – Dấu hiệu: Đề bài cho nhiều dữ kiện về khối lượng không quy được thành số mol.

    – Một số công thức liên quan Axit HCl

    Axit H2SO4 loãng

    VD1: Trộn 5,4 gam Al với 6,0 gam Fe2O3 rồi nung nóng để thực hiện phản ứng nhiệt nhôm. Sau phản ứng ta thu được m gam hỗn hợp chất rắn. Giá trị của m là :

    A. 2,24 gam. B. 9,40 gam. C. 10,20 gam. D. 11,40 gam.

    VD1: Nhiệt phân 100g CaCO3 sau một thời gian thu được 93,4 gam chất rắn và thoát ra V lít khí ở đktc. Giá trị của V là:

    A. 2,24. B. 3,36. C. 4,48. D. 1,12.

    VD2: Nhiệt phân 20 gam CaCO3 sau một thời gian thấy còn lại a gam chất rắn và thấy thoát ra 0,615 lít khí khí ở 270C, 2atm. Tính a.

    A. 17,8. B. 18,7. C. 17,7. D. 18,8.

    VD3: Nhiệt phân a gam CaCO3 sau một thời gian thấy còn lại 79 gam chất rắn và thấy thoát ra 3,08 lít khí ở 27,30C, 2 atm. Giá trị của a là?

    A. 90. B. 80. C. 100. D. 95.

    VD4: Hòa tan hoàn toàn 5 gam hỗn hợp 2 kim loại bằng dung dịch HCl thu được dung dịch chứa 5,71 gam muối và V lít khí X ở đktc. Giá trị của V là : A. 2,24. B. 0,224. C. 4,48. D. 0,448.

    VD5: Hòa tan hoàn toàn 4,5 gam hỗn hợp 2 kim loại bằng dung dịch HCl thu được dung dịch chứa 5,21 gam muối và V lít khí X ở 00C 1,6atm . Giá trị của V là

    A. 1,14. B. 0,14. C. 1,4. D. 0,224.

    VD6: Cho 14,5 gam hỗn hợp Mg, Zn và Fe tác dụng hết với dung dịch HCl thu được 6,72 lít khí ở đktc. Cô cạn dung dịch sau phản ứng thu được m gam muối khan. Tính m

    A. 58,3 gam. B. 53,8 gam. C. 35,8 gam. D. 38,5 gam.

    VD7: Cho 12,1 gam hỗn hợp Zn, Fe, Mg tác dụng vừa đủ với m gam dung dịch HCl 10%. Cô cạn dung dịch sau phản ứng thu được 26,3 gam muối khan. Giá trị của m là?

    A. 116 gam. B. 126 gam. C. 146 gam. D. 156 gam.

    VD8: Hòa tan hoàn toàn 12,4 gam hỗn hợp 2 kim loại bằng V1 lít dung dịch HCl 1M vừa đủ thu được dung dịch chứa 13,82 gam muối và V2 lít khí H2 ở đktc. Giá trị V1, V2 lần lượt là?

    A. 0,2 & 2,24. B. 0,02 & 0,224. C. 0,4 & 4,48. D. 0,04 & 0,448.

    VD9: Cho 8 gam hỗn hợp bột gồm 2 kim loại Mg và Fe tác dụng hết với dung dịch HCl thấy thoát ra 5,6 lít khí H2 ở đktc. Khối lượng muối tạo thành trong dung dịch là

    A. 22,25 gam. B. 22,75 gam. C. 24,45 gam. D. 25,75 gam.

    VD10: Hòa tan m gam hỗn hợp Zn và Fe cần vừa đủ 1 lít dung dịch HCl 3,65M (d=1,19g/ml) thấy thoát ra một chất khí và thu được 1250 gam dung dịch A. Giá trị của m là

    A. 60,1 gam. B. 65,63 gam. C. 63,65 gam. D. Kết quả khác.

    VD11: Cho 24,4 gam h ỗn hợp Na2CO3, K2CO3 tác dụng vừa đủ với dung dịch BaCl2. Sau phản ứng thu được 39,4 gam kết tủa. Lọc tách kết tủa, cô cạn dung dịch thu được m gam muối clorua. Vậy m có giá trị là :

    A. 2,66 gam. B. 22,6 gam. C. 26,6 gam. D. 6,26 gam.

    VD12: Hoà tan hoàn toàn 23,8 gam hỗn hợp một muối cacbonat của các kim loại hoá trị (I) và muối cacbonat của kim loại hoá trị (II) trong dung dịch HCl. Sau phản ứng thu được 4,48 lít khí (đktc). Đem cô cạn dung dịch thu được bao nhiêu gam muối khan ?

    A. 13 gam. B. 15 gam. C. 26 gam. D. 30 gam.

    VD13: Cho 2,81 gam hỗn hợp A gồm 3 oxit Fe 2O3, MgO, ZnO tan vừa đủ trong 300 ml dung dịch H2SO4 0,1M. Cô cạn dung dịch sau phản ứng, khối lượng hỗn hợp các muối sunfat khan tạo ra l à :

    A. 3,81 gam. B. 4,81 gam. C. 5,21 gam. D. 4,8 gam.

    VD14: Hoà tan hết 38,60 gam hỗn hợp gồm Fe và kim loại M trong dung dịch HCl dư thấy thoát ra 14,56 lít H2 (đktc). Khối lượng hỗn hợp muối clorua khan thu được là :

    A. 48,75 gam. B. 84,75 gam. C. 74,85 gam. D. 78,45 gam.

    VD15: Cho 0,52 gam hỗn hợp 2 kim loại Mg v à Fe tan hoàn toàn trong dung d ịch H2SO4 loãng, dư thấy có 0,336 lít khí thoát ra (đktc). Khối lượng hỗn hợp muối sunfat khan thu được là :

    A. 2 gam. B. 2,4 gam. C. 3,92 gam. D. 1,96 gam.

    VD16: Hòa tan 10,14 gam hợp kim Cu, Mg, Al bằng một lượng vừa đủ dung dịch HCl thu được 7,84 lít khí A (đktc) và 1,54 gam chất rắn B và dung dịch C. Cô cạn dung dịch C thu được m gam muối, m có giá trị là :

    A. 33,45. B. 33,25. C. 32,99. D. 35,58.

    VD17: Cho 12 gam hỗn hợp kim loại Fe và Cu tác dụng hoàn toàn với dung dịch HNO3 63% sau phản ứng thu được dung dịch A và 11,2 lít khí NO2 (sản phẩm khử duy nhất – đktc). Biết axit HNO3 dùng dư 11% so với lượng cần thiết. Nồng độ % các chất có trong dung dịch A là:

    A. 24,20%, 18,80%, 6,93% B. 22,40%, 18,08%, 6,39%

    C. 24,40%, 18,80%, 9,36% D. 22,20%, 18,08%, 9,63%

    4. Bài tập áp dụng

    4.1. Bài tập dành cho học sinh lớp 10

    Câu 1: Khử hoàn toàn 6,64 gam h ỗn hợp gồm Fe, FeO, Fe 3O4, Fe2O3 cần dùng 2,24 lít CO (đktc).

    Khối lượng Fe thu được là :

    A. 5,04 gam. B. 5,40 gam. C. 5,05 gam. D. 5,06 gam.

    Câu 2: Cho 3,45 gam hỗn hợp muối natri cacbonat và kali cacbonat tác dụng hết với dung dịch HCl thu được V lít CO2 (đktc) và 3,78 gam muối clorua. Giá trị của V l à :

    A. 6,72 lít. B. 3,36 lít. C. 0,224 lít. D. 0,672 lít.

    Câu 3: Cho 9,125 gam muối hiđrocacbonat phản ứng hết với dung dịch H2SO4 (dư), thu được dung dịch chứa 7,5 gam muối sunfat trung hoà. Công thức của muối hiđrocacbonat là :

    A. NaHCO3. B. Mg(HCO3)2. C. Ba(HCO3)2. D. Ca(HCO3)2.

    Câu 4: Hòa tan hoàn toàn 3,22 gam hỗn hợp X gồm Fe, Mg v à Zn bằng một dịch H2SO4 loãng, thu được 1,344 lít hiđro (ở đktc) v à dung dịch chứa m gam muối. Giá trị của m l à :

    A. 9,52. B. 10,27. C. 8,98. D. 7,25.

    Câu 5: Hoà tan hoàn toàn 2,81 gam h ỗn hợp gồm Fe 2O3, MgO, ZnO trong 500 ml axit H 2SO4 0,1M (vừa đủ). Sau phản ứng, hỗn hợp muối sunfat khan thu được khi cô cạn dung dịch có khối lượng là :

    A. 6,81 gam. B. 4,81 gam. C. 3,81 gam. D. 5,81 gam.

    Câu 6: Cho 3,68 gam h ỗn hợp gồm Al và Zn tác dụng với một lượng vừa đủ dung dịch H 2SO4 10%,

    thu được 2,24 lít khí H 2 (đktc). Khối lượng dung dịch thu đ ược sau phản ứng l à :

    A. 97,80 gam. B. 101,48 gam. C. 88,20 gam. D. 101,68 gam.

    Câu 7: Hòa tan hoàn toàn m gam h ỗn hợp X gồm Al, Fe, Zn bằng dung dịch HCl dư. Dung dịch thu được sau phản ứng tăng l ên so với ban đầu (m – 2) gam. Khối lượng (gam) muối clorua tạo thàmh trong dung dịch là :

    A. m+71. B. m + 36,5. C. m + 35,5. D. m+ 73.

    Câu 8: Nung một hỗn hợp X gồm SO 2 và O2 có tỉ khối so với O 2 là 1,6 với xúc tác V2O5 thu được

    hỗn hợp Y. Biết tỉ khối của X so với Y l à 0,8. Tính hiệu suất của phản ứng tổng hợp SO 3 ?

    A. 66,7%. B. 50%. C. 75%. D. 80%.

    Câu 9: Hòa tan 5,94 gam h ỗn hợp 2 muối clorua của 2 kim loại A, B (đều có hoá trị II) v ào nước được dung dịch X. Để làm kết tủa hết ion Cl – có trong dung dịch X người ta cho dung dịch X tác dụng với dung dịch AgNO 3 thu được 17,22 gam kết tủa. Lọc bỏ kết tủa, thu được dung dịch Y. Cô cạn Y được m gam hỗn hợp muối khan. Giá trị m l à :

    A. 6,36 gam. B. 6,15 gam. C. 9,12 gam. D. 12,3 gam.

    III. Bài tập áp dụng

    1. Bài tập có lời giải

    ● Bài tập dành cho học sinh lớp 10

    Câu 1: Cho V lít Cl2 tác dụng với dung dịch NaOH vừa đủ ở điều kiện thường, cô cạn dung dịch thu được m1 gam muối khan. Cũng lấy V lít Cl2 cho tác dụng với dung dịch NaOH vừa đủ, đun nóng ở 80oC, cô cạn dung dịch thu được m2 gam muối. Thể tích khí Cl2 đo ở cùng điều kiện. Tỉ lệ m1 : m2 là

    A. 1 : 2. B. 1 : 1,5. C. 1 : 1. D. 2 : 1.

    (Đề thi thử Đại học lần 2 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2011 – 2012)

    Câu 2: Hoà tan hoàn toàn 23,8 gam hỗn hợp một muối cacbonat của các kim loại hoá trị I và muối cacbonat của kim loại hoá trị II trong dung dịch HCl. Sau phản ứng thu được 4,48 lít khí (đktc). Đem cô cạn dung dịch thu được bao nhiêu gam muối khan ?

    A. 13 gam. B. 15 gam. C. 26 gam. D. 30 gam.

    Câu 3: Hoà tan hoàn toàn 7,8 gam hỗn hợp Mg và Al bằng dung dịch HCl dư. Sau phản ứng thấy khối lượng dung dịch tăng thêm 7,0 gam so với ban đầu. Số mol axit đã tham gia phản ứng là :

    A. 0,8 mol. B. 0,08 mol. C. 0,04 mol. D. 0,4 mol.

    Câu 4: Hoà tan hoàn toàn 2,81 gam hỗn hợp gồm Fe2O3, MgO, ZnO trong 500 ml axit H2SO4 0,1M (vừa đủ). Sau phản ứng, hỗn hợp muối sunfat khan thu được khi cô cạn dung dịch có khối lượng là :

    A. 6,81 gam. B. 4,81 gam. C. 3,81 gam. D. 5,81 gam.

    (Đề thi tuyển sinh Đại học khối A năm 2007)

    Câu 5: Cho 3,68 gam hỗn hợp gồm Al và Zn tác dụng với một lượng vừa đủ dung dịch H2SO4 10%, thu được 2,24 lít khí H2 (ở đktc). Khối lượng dung dịch thu được sau phản ứng là:

    A. 101,48 gam. B. 101,68 gam. C. 97,80 gam. D. 88,20 gam.

    (Đề thi tuyển sinh Đại học khối A năm 2009)

    Câu 6: Cho m gam hỗn hợp kim loại gồm Al, Mg, Zn phản ứng hết với dung dịch H2SO4 loãng, dư thì thu được dung dịch X chứa 61,4 gam muối sunfat và 5m/67 gam khí H2. Giá trị của m là

    A. 10,72. B. 17,42. C. 20,10. D. 13,40.

    (Đề thi thử đại học lần 2 – THPT Chuyên – Đại học Vinh, năm học 2012 – 2013)

    Câu 7: Hỗn hợp A gồm CuSO4, FeSO4, Fe2(SO4)3, trong đó phần trăm khối lượng của S là 22%. Lấy 50 gam hỗn hợp A hoà tan trong nước, thêm dung dịch NaOH dư, kết tủa thu được đem nung ngoài không khí tới khối lượng không đổi. Lượng oxit sinh ra đem khử hoàn toàn bằng CO thu được m gam chất rắn. Giá trị của m là:

    A. 17 gam. B. 19 gam. C. 20 gam. D. 18 gam.

    (Đề thi thử Đại học lần 2 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2010 – 2011)

    Câu 8*: Đốt cháy hoàn toàn 8,96 lít H2S (đktc) trong oxi dư, rồi dẫn tất cả sản phẩm vào 50 ml dung dịch NaOH 25% (d = 1,28). Nồng độ phần trăm của muối trong dung dịch là :

    A. 47,92%. B. 42,98%. C. 42,69%. D. 46,43%.

    Câu 9*: Trộn lẫn 500 ml dung dịch H2SO4 0,3M với 200 ml dung dịch hỗn hợp NaOH aM, sau phản ứng thu được dung dịch X chỉ chứa 19,1 gam muối. Giá trị của a là :

    A. 0,5. B. 1. C. 1,5. D. 2.

    Câu 10*: Khi hoà tan b gam oxit kim loại hóa trị II bằng một lượng vừa đủ axit dung dịch H2SO4 15,8% người ta thu được dung dịch muối có nồng độ 18,21%. Vậy kim loại hoá trị II là :

    A. Ca. B. Ba. C. Be. D. Mg.

    ● Bài tập dành cho học sinh lớp 11

    Câu 11: Hoà tan 17 gam hỗn hợp NaOH, KOH, Ca(OH)2 vào nước được 500 gam dung dịch X. Để trung hoà 50 gam dung dịch X cần dùng 40 gam dung dịch HCl 3,65%. Cô cạn dung dịch sau khi trung hoà thu được khối lượng muối khan là :

    A. 3,16 gam. B. 2,44 gam. C. 1,58 gam. D. 1,22 gam.

    Câu 12: A là hỗn hợp khí gồm SO2 và CO2 có tỷ khối hơi so với H2 là 27. Dẫn a mol hỗn hợp khí A qua bình đựng 1 lít dung dịch KOH 1,5a M, sau phản ứng cô cạn dung dịch thu được m gam muối. Biểu thức liên hệ giữa m và a là:

    A. m=203a. B. m=193,5a. C. m=129a. D. m=184a.

    (Đề thi thử đại học lần 4 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2010 – 2011)

    Câu 13: Cho m gam hỗn hợp Al, Al2O3, Al(OH)3 tác dụng với dung dịch H2SO4 19,6% vừa đủ thu được dung dịch X có nồng độ là 21,302% và 3,36 lít H2 (đktc). Cô cạn dung dịch X thu được 80,37 gam muối khan. m có giá trị là :

    A. 24,18 gam. B. 28,98 gam. C. 18,78 gam. D. 25,09 gam.

    Câu 14: Cho 50 gam dung dịch BaCl2 20,8% vào 100 gam dung dịch Na2CO3, lọc bỏ kết tủa được dung dịch X. Tiếp tục thêm 50 gam dung dịch H2SO4 9,8% vào dung dịch X thấy thoát ra 0,448 lít khí (đktc). Biết các phản ứng xảy ra hoàn toàn. Khối lượng dung dịch sau cùng thu được là :

    A. 198,27. B. 189,27. C. 212,5. D. 286,72.

    Câu 15: Cho 7,68 gam Cu vào 200 ml dung dịch gồm HNO3 0,6M và H2SO4 0,5M. Sau khi các phản ứng xảy ra hoàn toàn (sản phẩm khử duy nhất là NO), cô cạn cẩn thận toàn bộ dung dịch sau phản ứng thì khối lượng muối khan thu được là :

    A. 20,16 gam. B. 19,76 gam. C. 19,20 gam. D. 22,56 gam.

    (Đề thi tuyển sinh Đại học khối A năm 2011)

    Câu 16: Đun nóng hỗn hợp khí X gồm 0,02 mol C2H2 và 0,03 mol H2 trong một bình kín (xúc tác Ni), thu được hỗn hợp khí Y. Cho Y lội từ từ vào bình nước brom (dư), sau khi kết thúc các phản ứng, khối lượng bình tăng m gam và có 280 ml hỗn hợp khí Z (đktc) thoát ra. Tỉ khối của Z so với H2 là 10,08. Giá trị của m là

    A. 0,328. B. 0,205. C. 0,585. D. 0,620.

    (Đề thi tuyển sinh Đại học khối A năm 2010)

    Câu 17: Hỗn hợp X gồm 0,15 mol vinylaxetilen và 0,6 mol H2. Nung nóng hỗn hợp X (xúc tác Ni) một thời gian, thu được hỗn hợp Y có tỉ khối so với H2 bằng 10. Dẫn hỗn hợp Y qua dung dịch brom dư, sau khi phản ứng xảy ra hoàn toàn, khối lượng brom tham gia phản ứng là

    A. 0 gam. B. 24 gam. C. 8 gam. D. 16 gam.

    (Đề thi tuyển sinh Đại học khối B năm 2012)

    Câu 18: Hỗn hợp X gồm hai ancol đơn chức, đồng đẳng kế tiếp. Đun nóng 16,6 gam X với H2SO4 đặc ở 140oC, thu được 13,9 gam hỗn hợp ete (không có sản phẩm hữu cơ nào khác). Biết với phản ứng xảy ra hoàn toàn. Công thức của hai ancol trong X là

    A. C3H7OH và C4H9OH. B. C2H5OH và C3H7OH.

    C. CH3OH và C2H5OH. D. C3H5OH và C4H7OH.

    (Đề thi tuyển sinh Cao đẳng khối A và khối B năm 2013)

    Câu 19: Cho m gam ancol đơn chức X qua ống đựng CuO dư, nung nóng. Sau khi phản ứng hoàn toàn, khối lượng chất rắn trong bình giảm 3,2 gam. Hỗn hợp hơi thu được có tỉ khối đối với hiđro là 19. Giá trị của m là

    A. 12. B. 6. C. 4,4. D. 8,8.

    Câu 20: Cho 2,16 gam axit cacboxylic đơn chức X tác dụng hoàn toàn với dung dịch chứa 0,02 mol KOH và 0,03 mol NaOH. Cô cạn dung dịch thu được sau khi phản ứng kết thúc còn lại 3,94 gam chất rắn khan. Công thức của X là

    A. CH3-CH2-COOH. B. CH2=CH-COOH. C. CHC-COOH. D. CH3-COOH.

    (Đề thi thử đại học lần 1 – THPT Chuyên – Đại học Vinh, năm học 2012 – 2013)

    ● Bài tập dành cho học sinh lớp 12

    Câu 21: Cho 4,48 gam hỗn hợp gồm CH3COOC2H5 và CH3COOC6H5 (có tỉ lệ mol 1:1) tác dụng với 800 ml dung dịch NaOH 0,1M thu được dung dịch X. Cô cạn dung dịch X thì khối lượng chất rắn thu được là :

    A. 4,88 gam. B. 5,6 gam. C. 6,40 gam. D. 3,28 gam.

    (Đề thi thử đại học lần 5 – THPT Chuyên – Đại học SPHN, năm học 2011 – 2012)

    Câu 22*: X là este đơn chức, mạch hở tác dụng vừa đủ với dung dịch KOH 11,666%. Sau phản ứng thu được dung dịch Y. Cô cạn Y thì phần hơi chỉ có H2O với khối lượng 86,6 gam, còn lại chất rắn Z có khối lượng là 23 gam. Có bao nhiêu đồng phân cấu tạo của X thoả mãn tính chất trên ?

    A. 1. B. 2. C. 3. D. 4.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2009 – 2010)

    Câu 23: Xà phòng hoá hoàn toàn 13,44 kg chất béo có chỉ số axit bằng 7 cần 120,064 kg dung dịch NaOH 15%. Khối lượng xà phòng thu được là :

    A. 17,66 kg. B. 31,41 kg. C. 17,69 kg. D. 31,45 kg.

    Câu 24: Khi thủy phân hoàn toàn 0,1 mol peptit X mạch hở (X tạo bởi từ các amino axit có một nhóm amino và một nhóm cacboxylic) bằng lượng dung dịch NaOH gấp đôi lượng cần phản ứng, cô cạn dung dịch thu được hỗn hợp chất rắn tăng so với khối lượng X là 78,2 gam. Số liên kết peptit trong X là :

    A. 9. B. 10. C. 18. D. 20.

    (Đề thi thử đại học lần 5 – THPT Chuyên – Đại học SPHN, năm học 2011 – 2012)

    Câu 25*: Dung dịch X chứa 0,01 mol ClH3NCH2COOH, 0,02 mol CH3CH(NH2)COOH; 0,05 mol HCOOC6H5. Cho dung dịch X tác dụng với 160 ml dung dịch KOH 1M đun nóng để phản ứng xảy ra hoàn toàn. Cô cạn dung dịch sau phản ứng thu được m gam chất rắn khan. Giá trị của m là:

    A. 16,335 gam. B. 8,615 gam. C. 12,535 gam. D. 14,515 gam.

    (Đề thi thử đại học lần 3 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2010 – 2011)

    Câu 26: Hỗn hợp X gồm Ca và 2 kim loại kiềm ở 2 chu kì liên tiếp. Lấy 9,1 gam hỗn hợp X tác dụng hết với H2O thu được dung dịch Y và 7,84 lít khí H2 (ở đktc). Đem dung dịch Y tác dụng với dung dịch HCl dư thu được dung dịch Z, cô cạn dung dịch Z thì thu được m gam chất rắn khan. Giá trị m là

    A. 21. B. 21,525. C. 27,17. D. 33,95.

    Câu 27: Hoà tan hoàn toàn 2,9 gam hỗn hợp gồm kim loại M và oxit của nó vào nước, thu được 500 ml dung dịch chứa một chất tan có nồng độ 0,04M và 0,224 lít khí H2 (ở đktc). Kim loại M là

    A. Ca. B. Ba. C. K. D. Na.

    (Đề thi tuyển sinh Đại học khối B năm 2009)

    Câu 28: Cho 5,35 gam hỗn hợp X gồm Mg, Fe, Al vào 250 ml dung dịch Y gồm H2SO4 0,5M và HCl 1M thu được 3,92 lít khí (đktc) và dung dịch A. Cô cạn dung dịch A trong điều kiện không có không khí, thu được m gam chất rắn khan. Giá trị của m là :

    A. 20,900. B. 26,225. C. 26,375. D. 28,600.

    Câu 29*: Hỗn hợp X gồm Na2O, Na2O2, Na2CO3, K2O, K2O2, K2CO3. Cho m gam hỗn hợp X tác dụng với dung dịch HCl dư thu được dung dịch Y chứa 50,85 gam chất tan gồm các chất tan có cùng nồng độ mol; 3,024 lít hỗn hợp khí Z (đktc) có tỉ khối so với hiđro là 20,889. Giá trị của m là :

    A. 30,492. B. 22,689. C. 21,780. D. 29,040.

    Câu 30*: Cho 250 gam dung dịch FeCl3 6,5% vào 150 gam dung dịch Na2CO3 10,6% thu được khí A, kết tủa B và dung dịch X, Thêm m gam dung dịch AgNO3 21,25% vào dung dịch X thu được dung dịch Y có nồng độ phần của NaCl là 1,138%. Giá trị của m là ?

    A. 200 gam. B. 120 gam. C. 140 gam. D. 160 gam.

    (Đề thi thử đại học lần 1 – THPT Chuyên Bến Tre, năm học 2012 – 2013)

    2. Bài tập chỉ có đáp án

    Câu 31: Cho 24,4 gam hỗn hợp Na2CO3, K2CO3 tác dụng vừa đủ với dung dịch BaCl2. Sau phản ứng thu được 39,4 gam kết tủa. Lọc tách kết tủa, cô cạn dung dịch thu được m gam muối clorua. Vậy m có giá trị là :

    A. 2,66 gam. B. 22,6 gam. C. 26,6 gam. D. 6,26 gam.

    Câu 32: Cho 3,45 gam hỗn hợp muối natri cacbonat và kali cacbonat tác dụng hết với dung dịch HCl thu được V lít CO2 (đktc) và 3,78 gam muối clorua. Giá trị của V là :

    A. 6,72 lít. B. 3,36 lít. C. 0,224 lít. D. 0,672 lít.

    Câu 33: Hoà tan hết 38,60 gam hỗn hợp gồm Fe và kim loại M trong dung dịch HCl dư thấy thoát ra 14,56 lít H2 (đktc). Khối lượng hỗn hợp muối clorua khan thu được là :

    A. 48,75 gam. B. 84,75 gam. C. 74,85 gam. D. 78,45 gam.

    Câu 34: Hòa tan 28,1 gam hỗn hợp X gồm Ag, Zn, Al bằng một lượng vừa đủ dung dịch HCl thu được 8,96 lít khí H2 (đktc); 16,2 gam chất rắn Y và dung dịch Z. Lọc bỏ chất rắn Y, cô cạn cẩn thận dung dịch Z thu được lượng muối khan là

    A. 39,5 gam. B. 40,3 gam. C. 33,9 gam. D. 56,3 gam.

    (Đề thi thử Đại học lần 2 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2012 – 2013)

    Câu 35: Hòa tan hoàn toàn m gam hỗn hợp X gồm Al, Fe, Zn bằng dung dịch HCl dư­. Dung dịch thu đ­ược sau phản ứng tăng lên so với ban đầu (m – 2) gam. Khối lư­ợng (gam) muối clorua tạo thàmh trong dung dịch là :

    A. m +71. B. m + 36,5. C. m + 35,5. D. m + 73.

    Câu 36: Hỗn hợp khí X gồm N2 và H2 có tỉ khối so với He bằng 1,8. Đun nóng X một thời gian trong bình kín (có bột Fe làm xúc tác), thu được hỗn hợp khí Y có tỉ khối so với He bằng 2. Hiệu suất của phản ứng tổng hợp NH3 là

    A. 50%. B. 36%. C. 40%. D. 25%.

    (Đề thi tuyển sinh Đại học khối A năm 2010)

    Câu 37: Hòa tan 5,94 gam hỗn hợp 2 muối clorua của 2 kim loại A, B (đều có hoá trị II) vào nước được dung dịch X. Để làm kết tủa hết ion có trong dung dịch X, người ta cho dung dịch X tác dụng với dung dịch AgNO3 dư, thu được 17,22 gam kết tủa. Lọc bỏ kết tủa, thu được dung dịch Y. Cô cạn Y được m gam hỗn hợp muối khan. Giá trị m là :

    A. 6,36 gam. B. 6,15 gam. C. 9,12 gam. D. 12,3 gam.

    Câu 38: Hoà tan a gam M2(CO3)n­ bằng một lượng vừa đủ dung dịch H2SO4 10% thu được dung dịch muối có nồng độ 15,09%. Công thức của muối cacbonat là :

    A. CuCO3. B. FeCO3. C. SrCO3. D. K2CO3.

    Câu 39: Cho 115,3 gam hỗn hợp hai muối MgCO3 và RCO3 vào 500 ml dung dịch H2SO4 loãng thấy có 4,48 lít CO2 (đktc) thoát ra, dung dịch A và chất rắn B. Cô cạn dung dịch A thu được 12 gam muối khan. Nung chất rắn B đến khối lượng không đổi thì thu được rắn B1 và 11,2 lít CO2 (đktc). Khối lượng chất rắn B và B1 là :

    A. 110,5 gam và 88,5 gam. B. 110,5 gam và 88 gam.

    C. 110,5 gam và 87 gam. D. 110,5 gam và 86,5 gam.

    Phân tích và hướng dẫn giải

    1C

    2C

    3A

    4A

    5A

    6D

    7A

    8B

    9B

    10D

    11B

    12C

    13D

    14B

    15B

    16A

    17B

    18B

    19A

    20B

    21C

    22D

    23A

    24A

    25A

    26D

    27B

    28A

    29D

    30D

    31C

    32B

    33B

    34B

    35A

    36D

    37C

    38A

    39A

    40B

    41D

    42A

    43B

    44D

    45B

    46D

    47D

    48C

    49C

    50B

    51A

    52A

    53C

    54A

    55A

    56C

    57C

    58D

    59D

    60A

    61C

    62C

    63A

    64C

    65C

    66D

    67B

    68A

    69A

    70C

     

    Mời các thầy cô và các em download file word tại đây

    pp2-bao toan khoi luong

     

    Xem thêm

    Tổng hợp các chuyên đề hóa học lớp 10

    Tổng hợp các chuyên đề hóa học lớp 11

    Tổng hợp các chuyên đề hóa học lớp 12

    Tổng hợp đề thi học kì 2 lớp 12 môn hóa học

    Tổng hợp đề thi học kì 2 lớp 10 môn hoá học

    Tổng hợp đề thi giữa học kì 2 cả ba khối 10 11 12

    Tổng hợp đề thi THPT QG 2021 file word có lời giải chi tiết

    Tổng hợp các phương pháp giải bài tập môn hoá học

    Tổng hợp đề thi HSG lớp 12 môn hoá học

    Phương pháp bảo toàn khối lượng đầy đủ

    Phương pháp bảo toàn nguyên tố

    Phương pháp bảo toàn khối lượng

    Phương pháp quy đổi este

    Phương pháp giải bài tập điện phân

    Phương pháp đồng đẳng hoá

  • Phương pháp bảo toàn nguyên tố

    Phương pháp bảo toàn nguyên tố

    Phương pháp bảo toàn nguyên tố

    phuong phap bao toan nguyen toXem thêm

    Phương pháp bảo toàn khối lượng

    Phương pháp tăng giảm khối lượng

    CHUYÊN ĐỀ 1: PHƯƠNG PHÁP B ẢO TOÀN NGUYÊN TỐ

    I. Lí thuyết

    – Nội dung định luật: Trong phản ứng hóa học, tổng số mol của một nguyên tố trước phản ứng bằng tổng số mol nguyên tố đó sau phản ứng.

    VD: Viết biểu thức định luật BTNT cho pt Mg + HCl; Cu + HNO3 loãng.

    – Trong phản ứng hóa học, tổng số khối lượng của một nguyên tố trước phản ứng bằng tổng số khối lượng nguyên tố đó sau phản ứng.

    – Đối với bài toán hỗn hợp bao gồm nhiều chất xảy ra theo nhiều quá trình khác nhau mà đề bài chỉ cho các dữ kiện liên quan đến chất đầu tiên và chất cuối cùng ta lập sơ đồ sau đó tính toán theo sơ đồ (bỏ qua các phản ứng trung gian).

    – Khi áp dụng định luật bảo toàn nguyên tố ta chỉ cần viết sơ đồ phản ứng, không cần cân bằng phương trình hóa học.

    * Chú ý

    – Dấu hiệu: Cho – hỏi nhiều dữ kiện về số mol của các chất liên quan đến một nguyên tố.

    – Khi nhiệt phân các hiđroxit không tạn (kết tủa) sản phẩm thu được là oxit tương ứng và nước (trừ trường hợp đặc biệt Fe(OH)2 khi nhiệt phân trong không khí – pthh minh họa)

    – Oxit kim loại + axit muối + H2O nH trong axit = 2nO trong oxit

    II. Vận dụng

    VD1: Cho a gam CuO tác dụng với dd H2SO4 loãng dư thu được 200 gam dd CuSO4 16%. Tính a (16g)

    VD2: Đốt cháy hoàn toàn m gam FeS trong oxi dư thu được a gam khí SO2. Oxi hóa hoàn toàn a gam SO2 thu được b gam SO3. Hấp thụ hết b gam SO3 vào nước thu được 50 gam dd H2SO4 12,25%. Tính m (5,5gam)

    VD3: Đốt cháy hoàn toàn 6 gam FeS2 trong oxi dư thu được a gam khí SO2. Oxi hóa hoàn toàn a gam SO2 thu được b gam SO3. Cho b gam SO3 tác dụng hết với dd NaOH dư thu được c gam Na2SO4. Cho c gam Na2SO4 tác dụng hết với dd Ba(OH)2 thu được d gam kết tủa. Tính d (23,3g)

    VD4: Cho hỗn hợp A gồm các chất rắn Fe, FeO, Fe3O4, Fe2O3 tan hoàn toàn vào dung dịch HCl dư thu được dung dịch B. Cho dung dịch B tác dụng với dung dịch NaOH dư, lọc kết tủa nung trong không khí đến khối lượng không đổi thu được m gam chất rắn. Tính m nếu số mol mỗi chất là 0,05 mol (28g)

    VD5: Cho hỗn hợp 5,6 gam Fe, 6,5 gam Zn, 4,8 gam Mg tác dụng hết với dung dịch HCl thu được dung dịch A. Nhỏ dung dịch NaOH vào dung dịch A đến khi thu được kết tủa lớn nhất B, nung kết tủa B trong không khí đến khối lượng không đổi thu được m gam chất rắn. Tính m.

    VD6: Cho 11,2 gam Fe và 2,4 gam Mg tác dụng với dung dịch H2SO4 loãng dư thu được dung dịch A. Cho dung dịch NaOH dư vào dung dịch A thu được kết tủa B. Nung B trong không khí đến khối lượng không đổi thu được m gam chất rắn C. (20g)

    VD7: Hoàn tan hoàn toàn 0,2 mol Fe, 0,1 mol Fe2O3 và 0,2 mol Al2O3 vào dung dịch HCl dư thu được dung dịch A. Cho dung dịch A tác dụng với dung dịch NaOH đến khi thu được lượng kết tủa lớn nhất B. Nung B trong không khí đến khối lượng không đổi thu được m gam chất rắn C. Tính m. (52,4g)

    VD8: Đem đốt cháy hết x gam Fe ở dạng bột thu được hỗn hợp gồm 3 oxit của sắt. Đem hoàn tan hết lượng oxit này bằng dd HCl dư, sau đó cô cạn dd thu được 162,5 gam FeCl3 và 38,1 gam FeCl2. Tính x (72,8 g)

    VD9: Hấp thụ hết V lít CO2(đktc) vào 300 ml dung dịch NaOH x mol/l được 10,6 gam Na2CO3 và 8,4 gam NaHCO3. Tính giá trị của V, x là? (4,48lít và 1M)

    VD10: Cho hỗn hợp Fe và FeS tác dụng với dung dịch HCl (dư), thu được 2,464 lít hỗn hợp khí ở điều kiện tiêu chuẩn. Dẫn hỗn hợp khí này qua dung dịch Pb(NO3)2 dư, sinh ra 23,9 gam kết tủa đen. Phần trăm khối lượng của Fe và FeS trong hỗn hợp lần lượt là :

    A. 5,98% và 94,02%. B. 94,02% và 5,98%. C. 25% và 75%. D. 75% và 25%.

    VD11: Cho hỗn hợp gồm 0,3 mol Fe, 0,15 mol Fe2O3 và 0,1 mol Fe3O4 tác dụng hết với dung dịch H2SO4 loãng thu được dung dịch A. Cho dung dịch A tác dụng với dung dịch NaOH dư, lọc kết tủa đem nung trong không khí đến khối lượng không đổi thu đ ược m gam chất rắn C. Tính m

    A. 70. B. 72. C. 65. D. 75.

    VD12: Hòa tan hoàn toàn a gam 1 oxit sắt FexOy bằng dd H2SO4 đặc, nóng, vừa đủ có chứa 0,075 mol H2SO4 thu được b gam muối và 168 ml khí không màu mùi hắc (khí SO2) (đktc). CTPT của oxit là?

    Bài tập dành cho học sinh lớp 10

    Câu 1: Cho hỗn hợp gồm 0,15 mol Fe, 0,075 mol Fe 2O3 và 0,05 mol Fe3O4 tác dụng hết với dung dịch H2SO4 loãng thu được dung dịch A. Cho dung dịch A tác dụng hết với dung dịch NaOH dư, lọc kết tủa đem nung trong không khí đến khối lượng không đổi th u được m gam chất rắn C. Giá trị của m là :

    A. 36. B. 72. C. 65. D. 75.

    Câu 2: Khử 16 gam Fe2O3 bằng H2 thu được hỗn hợp A gồm Fe, Fe2O3, FeO, Fe3O4. Cho A tác dụng hết với dung dịch H2SO4 đặc, nóng. Khối lượng muối sunfat tạo r a trong dung dịch là :

    A. 48 gam. B. 50 gam. C. 32 gam. D. 40 gam.

    Câu 3: Hòa tan hoàn toàn hỗn hợp gồm 0,1 mol Fe 2O3 và 0,2 mol FeO vào dung dịch HCl dư thu được dung dịch A. Cho NaOH dư vào dung dịch A thu được kết tủa B. Lọc lấy kết tủa B rồi đem nung trong không khí đ ến khối lượng không đổi được m gam chất rắn, m có giá trị l à:

    A. 16 gam. B. 32 gam. C. 48 gam. D. 52 gam.

    Câu 4: Cho hỗn hợp X gồm SO 2 và O2 theo tỷ lệ số mol 1:1 đi qua V 2O5 xúc tác, đun nóng thu đư ợc hỗn hợp Y có khối lượng 19,2 gam. Hoà tan Y vào nư ớc sau đó thêm Ba(NO3)2 dư thu được 37,28 gam kết tủa. Hiệu suất phản ứng SO 2 + O2 là :

    A. 40%. B. 75%. C. 80%. D. 60%.

     

    III. Bài tập áp dụng

    1. Bài tập có lời giải

    ● Bài tập dành cho học sinh lớp 10

    Câu 1: Cho hỗn hợp X gồm 0,15 mol Fe, 0,075 mol Fe2O3 và 0,05 mol Fe3O4 tác dụng hết với dung dịch HCl loãng, thu được dung dịch Y. Cho dung dịch Y tác dụng hết với dung dịch KOH dư, lọc kết tủa đem nung trong không khí đến khối lượng không đổi thu được m gam chất rắn Z. Giá trị của m là :

    A. 36. B. 72. C. 65. D. 75.

    Câu 2: Cho 1,56 gam hỗn hợp gồm Al và Al2O3 phản ứng hết với dung dịch HCl (dư), thu được V lít khí H2 (đktc) và dung dịch X. Nhỏ từ từ dung dịch NH3 đến dư vào dung dịch X thu được kết tủa, lọc hết lượng kết tủa, nung đến khối lượng không đổi thu được 2,04 gam chất rắn. Giá trị của V là :

    A. 0,672. B. 0,224. C. 0,448. D. 1,344.

    (Đề thi tuyển sinh Cao đẳng năm 2010)

    Câu 3: Cho V lít hỗn hợp khí gồm H2S và SO2 tác dụng với dung dịch brom dư. Thêm dung dịch BaCl2 dư vào hỗn hợp trên thì thu được 2,33 gam kết tủa. Giá trị của V là :

    A. 0,112 lít. B. 2,24 lít. C. 1,12 lít. D. 0,224 lít.

    Câu 4: Cho hỗn hợp Fe và FeS tác dụng với dung dịch HCl (dư), thu được 2,464 lít hỗn hợp khí (đktc). Dẫn hỗn hợp khí này qua dung dịch Pb(NO3)2 dư, sinh ra 23,9 gam kết tủa đen. Phần trăm khối lượng của Fe và FeS trong hỗn hợp lần lượt là :

    A. 94,02% và 5,98%. B. 5,98% và 94,02%.

    C. 25% và 75%. D. 75% và 25%.

    Câu 5: Cho hỗn hợp X gồm SO2 và O2 theo tỷ lệ số mol 1:1 đi qua V2O5 xúc tác, đun nóng thu được hỗn hợp Y có khối lượng 19,2 gam. Hoà tan Y vào nước sau đó thêm Ba(NO3)2 dư thu được 37,28 gam kết tủa. Hiệu suất phản ứng giữa SO2 và O2 là :

    A. 40%. B. 75%. C. 80%. D. 60%.

    Câu 6: Hòa tan hỗn hợp X gồm 11,2 gam Fe và 2,4 gam Mg bằng dung dịch H2SO4 loãng (dư), thu được dung dịch Y. Cho dung dịch NaOH dư vào Y thu được kết tủa Z. Nung Z trong không khí đến khối lượng không đổi, thu được m gam chất rắn. Biết các phản ứng đều xảy ra hoàn toàn. Giá trị của m là

    A. 24. B. 20. C. 36. D. 18.

    (Đề thi tuyển sinh Đại học khối B năm 2013)

    Câu 7: Đem 11,2 gam Fe để ngoài không khí, sau một thời gian thu được một hỗn hợp gồm Fe và các oxit. Hòa tan hoàn toàn hỗn hợp đó trong dung dịch H2SO4 đặc, nóng dư thu được 3,36 lít khí SO2 (đktc). Số mol H2SO4 đã tham gia phản ứng là :

    A. 0,4 mol. B. 0,3 mol. C. 0,5 mol. D. 0,45 mol.

    Câu 8: Cho 6 lít hỗn hợp CO2 và N2 (đktc) đi qua dung dịch KOH tạo ra 2,07 gam K2CO3 và 6 gam KHCO3. Thành phần phần trăm về thể tích của CO2 trong hỗn hợp là :

    A. 42%. B. 56%. C. 28%. D. 50%.

    Câu 9: Dùng khí CO để khử hoàn toàn 2,88 gam hỗn hợp X gồm Fe, FeO, Fe2O3 thu được 2,24 gam chất rắn. Mặt khác, để hòa tan hết 2,88 gam X cần vừa đủ 100 ml dung dịch HCl, kết thúc thí nghiệm thu được 224 ml khí (đktc). Nồng độ mol/lít của dung dịch HCl là :

    A. 1. B. 0,5. C. 1,6. D. 0,8.

    (Đề thi thử đại học lần 2 – THPT Chuyên – Đại học SPHN, năm học 2011 – 2012)

    Câu 10: Hỗn hợp X gồm Fe3O4, FeO, Fe2O3, CuO. Lấy 46,7 gam X khử hóa hoàn toàn bằng H2 thì thu được 9 gam H2O. Cũng lấy 46,7 gam X tác dụng với dung dịch HCl dư, rồi cô cạn dung dịch sau phản ứng thì thu được khối lượng muối khan thu được là

    A. 64,95 gam. B. 82,2 gam. C. 74,2 gam. D. 96,8 gam.

    (Đề thi thử đại học lần 1 – THPT Chuyên – Đại học Vinh, năm học 2011 – 2012)

    ● Bài tập dành cho học sinh lớp 11

    Câu 11: Cho m gam hỗn hợp Mg, Al vào 250 ml dung dịch X chứa hỗn hợp axit HCl 1M và axit H2SO4 0,5M, thu được 5,32 lít H2 (ở đktc) và dung dịch Y (coi thể tích dung dịch không đổi). Dung dịch Y có pH là :

    A. 1. B. 6. C. 7. D. 2.

    (Đề thi tuyển sinh Đại học khối A năm 2007)

    Câu 12: Cho 150 ml dung dịch KOH 1,2M tác dụng với 100 ml dung dịch AlCl3 nồng độ x mol/l, thu được dung dịch Y và 4,68 gam kết tủa. Loại bỏ kết tủa, thêm tiếp 175 ml dung dịch KOH 1,2M vào Y, thu được 2,34 gam kết tủa. Giá trị của x là

    A. 1,2. B. 0,8. C. 0,9. D. 1,0.

    (Đề thi tuyển sinh Đại học khối B năm 2010)

    Câu 13: Hoà tan hoàn toàn hỗn hợp m gam hỗn hợp gồm FeS2 và Cu2S vào axit HNO3 (vừa đủ), thu được dung dịch X (chỉ chứa hai muối sunfat) với tổng khối lượng là 72 gam. Giá trị của m là :

    A. 80. B. 20. C. 60. D. 40.

    (Đề thi thử đại học lần 4 – THPT Chuyên – Đại học Vinh, năm học 2010 – 2011)

    Câu 14: Đun nóng m gam hỗn hợp Cu và Fe có tỉ lệ khối lượng tương ứng 7 : 3 với một lượng dung dịch HNO3. Khi các phản ứng kết thúc, thu được 0,75m gam chất rắn, dung dịch X và 5,6 lít hỗn hợp khí (đktc) gồm NO và NO2 (không có sản phẩm khử khác của N+5). Biết lượng HNO3 đã phản ứng là 44,1 gam. Giá trị của m là :

    A. 44,8. B. 40,5. C. 33,6. D. 50,4.

    (Đề thi tuyển sinh Đại học khối A năm 2011)

    Câu 15*: Hấp thụ hết V lít khí CO2 vào dung dịch chứa 0,42 mol Ca(OH)2 thu được a gam kết tủa. Tách lấy kết tủa, sau đó thêm tiếp 0,6V lít khí CO2 nữa, thu thêm 0,2a gam kết tủa. Thể tích các khí đo ở đktc. Giá trị của V là:

    A. 7,84 lít. B. 5,60 lít. C. 6,72 lít. D. 8,40 lít.

    (Đề thi thử đại học lần 4 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2011 – 2012)

    Câu 16: Đốt cháy hoàn toàn m gam hỗn hợp X gồm C2H2, C3H6, C6H6 cần vừa đúng V lít không khí (đktc). Hấp thụ toàn bộ sản phẩm cháy vào bình đựng nước vôi trong dư thu được a gam kết tủa. Biết không khí gồm có 20% oxi và 80% nitơ theo thể tích. Biểu thức liên hệ giữa m với V và a là

    A. B. C. D.

    Đề thi thử đại học lần 1 – THPT Đô Lương 1 – Nghệ An, năm học 2012 – 2013)

    Câu 17: Cho 0,5 lít hỗn hợp gồm hiđrocacbon và khí cacbonic vào 2,5 lít oxi (lấy dư) rồi đốt. Thể tích của hỗn hợp thu được sau khi đốt là 3,4 lít. Cho hỗn hợp qua thiết bị làm lạnh, thể tích hỗn hợp khí còn lại 1,8 lít và cho lội qua dung dịch KOH chỉ còn 0,5 lít khí. Thể tích các khí được đo trong cùng điều kiện. Tên gọi của hiđrocacbon là :

    A. propan. B. xiclobutan. C. propen. D. xiclopropan.

    Câu 18: Cho 224,00 lít metan (đktc) qua hồ quang được V lít hỗn hợp A (đktc) chứa 12% C2H2; 10% CH4; 78% H2 (về thể tích). Giả sử chỉ xảy ra 2 phản ứng :

    2CH4 ® C2H2 + 3H2 (1)

    CH4 ® C + 2H2 (2)

    Giá trị của V là :

    A. 407,27. B. 448,00. C. 520,18. D. 472,64.

    Câu 19: Đốt cháy hoàn toàn m gam hỗn hợp X gồm hai ancol, thu được 13,44 lít khí CO2 (đktc) và 15,3 gam H2O. Mặt khác, cho m gam X tác dụng với Na (dư), thu được 4,48 lít khí H2 (đktc). Giá trị của m là

    A. 12,9 . B. 15,3. C. 12,3. D. 16,9.

    (Đề thi tuyển sinh Đại học khối B năm 2012)

    Câu 20*: Hỗn hợp X gồm 0,01 mol HCOONa và a mol muối natri của hai axit no, đơn chức, mạch hở là đồng đẳng liên tiếp. Đốt cháy hoàn toàn hỗn hợp X, cho sản phẩm khí và hơi lần lượt qua bình 1 đựng H2SO4 đặc, bình 2 đựng KOH thấy khối lượng bình 2 tăng nhiều hơn bình một là 3,51 gam. Phần chất rắn còn lại sau khi đốt cháy X có khối lượng là 2,65 gam. Công thức phân tử của hai muối natri là :

    A. C2H5COONa và C3H7COONa. B. C3H7COONa và C4H9COONa.

    C. CH3COONa và C2H5COONa. D. CH3COONa và C3H7COONa.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2009 – 2010)

    ● Bài tập dành cho học sinh lớp 12

    Câu 21: Cho 0,1 mol CH3COOH vào cốc chứa 30 ml dung dịch ROH 20% (d =1,2 g/ml, R là một kim loại kiềm). Cô cạn dung dịch sau phản ứng, rồi đốt cháy hoàn toàn chất rắn khan còn lại. Sau khi đốt cháy thì còn lại 9,54 gam chất rắn và có m gam hỗn hợp gồm CO2, hơi nước bay ra. Giá trị của m là :

    A. 10,02. B. 9,3. C. 7,54. D. 8,26.

    (Đề thi thử Đại học lần 1 – THPT Chuyên KHTN, năm học 2011 – 2012)

    Câu 22*: Cho 2,76 gam chất hữu cơ X gồm C, H, O tác dụng với dung dịch NaOH vừa đủ sau đó chưng khô thì phần bay hơi chỉ có nước và còn lại 2 muối của Na có khối lượng 4,44 gam. Nung nóng 2 muối này trong oxi dư, phản ứng hoàn toàn thu được 2,464 lít CO2 (đktc); 3,18 gam Na2CO3 và 0,9 gam H2O. Biết công thức phân tử của X trùng với công thức đơn giản nhất. Cho 2,76 gam X tác dụng với 80 ml dung dịch KOH 1M, cô cạn dung dịch thu được m gam chất rắn. m có giá trị là :

    A. 6,88. B. 6,52. C. 7,24. D. 6,16.

    (Đề thi thử Đại học lần 2 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2009 – 2010)

    Câu 23: Đun nóng m gam hỗn hợp X gồm các chất có cùng một loại nhóm chức với 600 ml dung dịch NaOH 1,15M, thu được dung dịch Y chứa muối của một axit cacboxylic đơn chức và 15,4 gam hơi Z gồm các ancol. Cho toàn bộ Z tác dụng với Na dư, thu được 5,04 lít khí H2 (đktc). Cô cạn dung dịch Y, nung nóng chất rắn thu được với CaO cho đến khi phản ứng xảy ra hoàn toàn, thu được 7,2 gam một chất khí. Giá trị của m là

    A. 40,60. B. 22,60. C. 34,30. D. 34,51.

    (Đề thi tuyển sinh Đại học khối B năm 2012)

    Câu 24: Cho X là hexapeptit Ala-Gly-Ala-Val-Gly-Val và Y là tetrapeptit Gly-Ala-Gly-Glu. Thủy phân hoàn toàn m gam hỗn hợp gồm X và Y thu được 4 amino axit, trong đó có 30 gam glyxin và 28,48 gam alanin. Giá trị của m là

    A. 77,6. B. 83,2. C. 87,4. D. 73,4.

    (Đề thi tuyển sinh Đại học khối A năm 2013)

    Câu 25*: Cho V lít CO2 (đktc) hấp thụ hết trong dung dịch chứa 0,2 mol Ba(OH)2 và 0,1 mol NaOH. Sau phản ứng hoàn toàn thu kết tủa và dung dịch chứa 21,35 gam muối. Giá trị của V là :

    A. 7,84. B. 8,96. C. 6,72. D. 7,84 hoặc 6,72.

    Câu 26: Hòa tan hết m gam ZnSO4 vào nước được dung dịch X. Cho 110 ml dung dịch KOH 2M vào X, thu được a gam kết tủa. Mặt khác, nếu cho 140 ml dung dịch KOH 2M vào X thì cũng thu được a gam kết tủa. Giá trị của m là

    A. 20,125. B. 12,375. C. 22,540. D. 17,710.

    (Đề thi tuyển sinh Đại học khối A năm 2009)

    Câu 27*: Cho 500 ml dung dịch Ba(OH)2 0,1M vào V ml dung dịch Al2(SO4)3 0,1M; sau khi các phản ứng kết thúc thu được 12,045 gam kết tủa. Giá trị của V là

    A. 75. B. 150. C. 300. D. 200.

    (Đề thi tuyển sinh Đại học khối A năm 2012)

    Câu 28: Hòa tan 14 gam hỗn hợp Cu, Fe3O4 vào dung dịch HCl, sau phản ứng còn dư 2,16 gam hỗn hợp chất rắn và dung dịch X. Cho X tác dụng với AgNO3 dư thu được bao nhiêu gam kết tủa ?

    A. 45,92. B. 12,96. C. 58,88. D. 47,4.

    (Đề thi thử đại học lần 2 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2011 – 2012)

    Câu 29: Cho 8,96 lít hỗn hợp 2 khí H2 và CO (đktc) đi qua ống sứ đựng 0,2 mol Al2O3 và 0,3 mol CuO nung nóng đến phản ứng hoàn toàn thu được chất rắn X. X phản ứng vừa đủ trong 0,5 lít dung dịch HNO3 có nồng độ aM (sản phẩm khử là khí NO duy nhất). Giá trị của a là

    A. 2,00. B. 2,80. C. 3,67. D. 4,00.

    (Đề thi thử đại học lần 4 – THPT Chuyên – Đại học Vinh, năm học 2010 – 2011)

    Câu 30: Hòa tan hết 10,24 gam Cu bằng 200 ml dung dịch HNO3 3M được dung dịch A. Thêm 400 ml dung dịch NaOH 1M vào dung dịch A. Lọc bỏ kết tủa, cô cạn dung dịch rồi nung chất rắn đến khối lượng không đổi thu được 26,44 gam chất rắn. Số mol HNO3 đã phản ứng với Cu là :

    A. 0,48 mol. B. 0,58 mol. C. 0,56 mol. D. 0,4 mol.

    (Đề thi thử đại học lần 2 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2010 – 2011)

    2. Bài tập chỉ có đáp án

    Câu 31: Điện phân nóng chảy Al2O3 khi đó tại anot thoát ra một hỗn hợp khí gồm O2 10%; CO 20% và CO2 70%. Tổng thể tích khí là 6,72 m3 (tại nhiệt độ 819oC và áp suất 2,0 atm). Tính khối lượng Al thu được tại catot?

    A. 2,16 kg. B. 5,40 kg. C. 4,86 kg. D. 4,32 kg.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2010 – 2011)

    Câu 32: Cho m gam hỗn hợp Al, Fe vào 300 ml dung dịch HCl 1M và H2SO4 0,5M, thu được dung dịch X và 5,6 lít H2 (đktc). Tính thể tích dung dịch NaOH 1M cần cho vào dung dịch X để thu được kết tủa có khối lượng lớn nhất ?

    A. 300 ml. B. 500 ml. C. 400 ml. D. 600 ml.

    Câu 33: Cho 2,13 gam hỗn hợp X gồm ba kim loại Mg, Cu và Al ở dạng bột tác dụng hoàn toàn với oxi thu được hỗn hợp Y gồm các oxit có khối lượng 3,33 gam. Thể tích dung dịch HCl 2M vừa đủ để phản ứng hết với Y là :

    A. 90 ml. B. 57 ml. C. 75 ml. D. 50 ml.

    (Đề thi tuyển sinh Đại học khối A năm 2008)

    Câu 34: Cho 20 gam hỗn hợp X gồm Fe, FeO, Fe3O4, Fe2O3 tan vừa hết trong 700 ml dung dịch HCl 1M thu được 3,36 lít H2 (đktc) và dung dịch D. Cho dung dịch D tác dụng với NaOH dư, lọc kết tủa và nung trong không khí đến khối lượng không đổi thu được chất rắn Y. Khối lượng Y là :

    A. 16 gam. B. 32 gam. C. 8 gam. D. 24 gam.

    Câu 35: Cho V lít dung dịch NaOH 2M vào dung dịch chứa 0,1 mol Al2(SO4)3 và 0,1 mol H2SO4 đến khi phản ứng hoàn toàn, thu được 7,8 gam kết tủa. Giá trị lớn nhất của V để thu được lượng kết tủa trên là :

    A. 0,35. B. 0,25. C. 0,45. D. 0,05.

    (Đề thi tuyển sinh Đại học khối A năm 2008)

    Câu 36: Hỗn hợp Z gồm có Al và Al4C3. Nếu cho hỗn hợp Z tác dụng với H2O thu được 31,2 gam Al(OH)3. Nếu cho hỗn hợp Z tác dụng với dung dịch HCl, người ta thu được một muối duy nhất và 20,16 lít hỗn hợp khí (đktc). Khối lượng của Al và Al4C3 trong Z là :

    A. 14,4 gam và 10,8 gam. B. 10,8 gam và 14,0 gam.

    C. 10,8 gam và 14,4 gam. D. 5,4 gam và 7,2 gam.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2012 – 2013)

    Câu 37: Hòa tan hết một lượng Na vào dung dịch HCl 10% thu được 46,88 gam dung dịch gồm NaCl và NaOH và 1,568 lít H2 (đktc). Nồng độ % NaCl trong dung dịch thu được là :

    A. 14,97. B. 12,48. C. 12,68. D. 15,38.

    Câu 38: Hòa tan m gam hỗn hợp gồm K và Ca vào nước thu được dung dịch A và 5,6 lít H2 (đktc). Hấp thụ 8,96 lít khí CO2 (đktc) vào dung dịch A thu được 10 gam kết tủa và dung dịch B. Cô cạn dung dịch B thu được 22,5 gam chất rắn khan gồm hai chất có cùng khối lượng mol. Giá trị của m là :

    A. 12,85 gam. B. 16,75 gam. C. 10,85 gam. D. 14,80 gam.

    Câu 39: Hấp thụ hoàn toàn 2,24 lít CO2 (đktc) vào 100 ml dung dịch gồm K2CO3 0,2M và KOH x mol/lít , sau khi các phản ứng xảy ra hoàn toàn thu được dung dịch Y. Cho toàn bộ Y tác dụng với dung dịch BaCl2 (dư), thu được 11,82 gam kết tủa. Giá trị của x là :

    A. 1,0. B. 1,2. C. 1,4. D. 1,6.

    (Đề thi tuyển sinh Đại học khối B năm 2011)

    Câu 40: Cho 3,36 lít khí CO2 vào 200,0 ml dung dịch chứa NaOH xM và Na2CO3 0,4M thu được dung dịch X chứa 19,98 gam chất tan. Xác định nồng độ mol/l của NaOH trong dung dịch ?

    A. 0,70M. B. 0,75M. C. 0,60M. D. 0,50M.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2010 – 2011)

    Câu 41: Hấp thụ hết V lít khí CO2 (đktc) vào 300 ml dung dịch hỗn hợp chứa đồng thời Ba(OH)2 1M và KOH 1M, thu được 19,7 gam kết tủa và dung dịch X. Cho KOH dư vào dung dịch X lại thấy xuất hiện thêm m gam kết tủa nữa. Giá trị của V và m lần lượt là :

    A. 17,92 và 39,4. B. 17,92 và 19,7. C. 17,92 và 137,9. D. 15,58 và 39,4.

    (Đề thi thử đại học lần 1 – THPT Chuyên – Đại học Vinh, năm học 2011 – 2012)

    Câu 42*: Cho m gam hỗn hợp X gồm Ba, BaO, Ba(OH)2 có cùng số mol vào nước thu được 500 ml dung dịch Y và V lít H2 (đktc). Hấp thụ 3,6V lít CO2 (đktc) vào 500 ml dung dịch Y thu được 37,824 gam kết tủa. Giá trị của m là :

    A. 41,49 gam. B. 36,88 gam. C. 32,27 gam. D. 46,10 gam.

    Câu 43*: Trong một cốc nước có hoà tan a mol Ca(HCO3)2 và b mol Mg(HCO3)2. Để làm mềm nước trong cốc cần dùng V lít nước vôi trong, nồng độ pM. Biểu thức liên hệ giữa V với a, b, p là :

    A. V = (a +2b)/p. B. V = (a + b)/2p. C. V = (a + b)/p. D. V = (a + b)p.

    Câu 44: Cho m gam Al4C3 phản ứng vừa hết với lượng dung dịch có 0,03 mol HCl, được dung dịch X. Mặt khác cho m’ gam Al4C3 kể trên phản ứng vừa hết với dung dịch có 0,04 mol KOH được dung dịch Y. Trộn lẫn toàn bộ X và Y kể trên với nhau được hỗn hợp Z chứa bao nhiêu mol muối nhôm ?

    A. 0,025 mol. B. 0,01 mol. C. 0,04 mol. D. 0,08 mol.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2011 – 2012)

    Câu 45*: Hoà tan hết m gam Al2(SO4)3 vào nước được dung dịch X. Cho 360 ml dung dịch NaOH 1M vào X, thu được 2a gam kết tủa. Mặc khác, nếu cho 400 ml dung dịch NaOH 1M vào X, cũng thu được a gam kết tủa. Các phản ứng xảy ra hoàn toàn, giá trị của m là:

    A. 18,81. B. 15,39. C. 20,52. D. 19,665.

    (Đề thi thử đại học lần 2 – THPT Chuyên Nguyễn Huệ – Hà Nội, năm học 2011 – 2012)

    Câu 46*: Cho 240 ml dung dịch Ba(OH)2 1M vào 200 ml dung dịch hỗn hợp AlCl3 a mol/l và Al2(SO4)3 2a mol/l thu được 51,3 gam kết tủa. Giá trị của a là :

    A. 0,12 . B. 0,16 . C. 0,15 . D. 0,2.

    Câu 47*: Hòa tan 30 gam hỗn hợp gồm Al, Zn, Mg trong dung dịch HNO3 dư. Sau phản ứng thu được hỗn hợp khí gồm 0,1 mol NO, 0,1 mol N2O và dung dịch X. Cô cạn dung dịch X thu được 127 gam chất rắn. Số mol HNO3 đã tham gia phản ứng là bao nhiêu ?

    A. 1,7. B. 1,4. C. 1,9. D. 1,8.

    Câu 48: Đốt nóng một hỗn hợp gồm Al và 16 gam Fe2O3 (trong điều kiện không có không khí) đến khi phản ứng xảy ra hoàn toàn, thu được hỗn hợp rắn X. Cho X tác dụng vừa đủ với V ml dung dịch NaOH 1M sinh ra 3,36 lít H2 (đktc). Giá trị của V là :

    A. 150. B. 100. C. 200. D. 300.

    Câu 49: Hỗn hợp X gồm Fe, FeO, Fe2O3 và Fe3O4. Hoà tan hoàn toàn X trong 400 ml dung dịch HCl 2M thấy thoát ra 2,24 lít H2 và còn lại 2,8 gam sắt (duy nhất) chưa tan. Hãy cho biết nếu cho toàn bộ hỗn hợp X vào dung dịch HNO3 đặc, nóng dư thu được bao nhiêu lít khí NO2 ?

    A. 4,48 lít. B. 10,08 lít. C. 16,8 lít. D. 20,16 lít.

    Câu 50*: Hoà tan hoàn toàn một lượng hỗn hợp X gồm Fe3O4 và FeS2 trong 63 gam HNO3, thu được 1,568 lít NO2 (đktc). Dung dịch thu được cho tác dụng vừa đủ với 200 ml dung dịch NaOH 2M, lọc kết tủa đem nung đến khối lượng không đổi thu được 9,76 gam chất rắn. Nồng độ % của dung dịch HNO3 có giá trị là :

    A. 47,2%. B. 46,2%. C. 46,6%. D. 44,2%.

    (Đề thi HSG Tỉnh Thái Bình, năm học 2011 – 2012)

    Câu 51: Khử hoàn toàn m gam FexOy bằng CO thu được 8,4 gam kim loại Fe và khí CO2. Hấp thụ hoàn toàn khí CO2 và 500 ml dung dịch Ba(OH)2 0,35M thì thu được kết tủa. Lọc kết tủa, cho dung dịch Na2SO4 dư vào dung dịch sau phản ứng thu được 5,825 gam kết tủa trắng. Công thức của oxit là :

    A. FeO hoặc Fe2O3. B. Fe2O3 hoặc Fe3O4.

    C. Fe3O4. D. FeO hoặc Fe3O4.

    Câu 52: Cho 2,56 gam Cu vào bình chứa 25,2 gam dung dịch HNO3 60% đến khi phản ứng xảy ra hoàn toàn. Thêm tiếp 210 ml dung dịch KOH 1M vào bình. Phản ứng xong, cô cạn bình phản ứng, nung chất rắn thu được tới khối lượng không đổi được 20,76 gam chất rắn. Tính số mol HNO3 tham gia phản ứng hòa tan đồng.

    A. 0,12 mol. B. 0,1 mol. C. 0,15 mol. D. 0,08 mol.

    (Đề thi thử Đại học lần 1 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2011 – 2012)

    Câu 53: Đốt cháy hoàn toàn một hợp chất hữu cơ X (C, H, N) bằng lượng không khí vừa đủ (gồm 1/5 thể tích O2, còn lại là N2) được khí CO2 , H2O và N2. Cho toàn bộ sản phẩm cháy qua bình đựng dung dịch Ba(OH)2 dư thấy có 39,4 gam kết tủa, khối lượng dung dịch giảm đi 24,3 gam. Khí thoát ra khỏi bình có thể tích 34,72 lít (đktc). Biết < 2. CTPT của X là :

    A. C2H7N. B. C2H8N. C. C2H7N2. D. C2H4N2.

    Câu 54: Đốt cháy hoàn toàn một hiđrocacbon A. Sản phẩm thu được hấp thụ hoàn toàn vào 200 ml dung dịch Ca(OH)2 0,2M thấy thu được 3 gam kết tủa. Lọc bỏ kết tủa, cân lại phần dung dịch thấy khối lượng tăng lên so với ban đầu là 0,28 gam. Hiđrocacbon trên có CTPT là :

    A. C5H12. B. C2H6. C. C3H8 . D. C4H10.

    Câu 55: Cho 400 ml một hỗn hợp gồm nitơ và một hiđrocacbon vào 900 ml oxi (dư) rồi đốt. Thể tích hỗn hợp thu được sau khi đốt là 1,4 lít. Sau khi cho nước ngưng tụ còn 800 ml hỗn hợp, người ta cho lội qua dung dịch KOH thấy còn 400 ml khí. Các thể tích khí đều đo ở cùng điều kiện nhiệt độ, áp suất. Công thức phân tử của chất hữu cơ là :

    A. C3H8. B. C2H4. C. C2H2. D. C2H6.

    Câu 56: Đốt cháy hoàn toàn một thể tích khí thiên nhiên gồm metan, etan, propan bằng oxi không khí (trong không khí, oxi chiếm 20% thể tích), thu được 7,84 lít khí CO2 (ở đktc) và 9,9 gam nước. Thể tích không khí (ở đktc) nhỏ nhất cần dùng để đốt cháy hoàn toàn lượng khí thiên nhiên trên là :

    A. 70,0 lít. B. 78,4 lít. C. 84,0 lít. D. 56,0 lít.

    Câu 57: Đốt cháy 2 gam hiđrocacbon A (khí trong điều kiện thường) được CO2 và 2 gam H2O. Mặt khác 2,7 gam A tác dụng với dung dịch AgNO3/NH3 dư được m gam kết tủa. Giá trị m là :

    A. 8,05 gam. B. 7,35 gam. C. 16,1 gam. D. 24 gam.

    Câu 58: Đun nóng m gam hỗn hợp X gồm C2H2, C2H4 và H2 với xúc tác Ni đến phản ứng xảy ra hoàn toàn, thu được 8,96 lít (đktc) hỗn hợp Y (có tỉ khối so với hiđro bằng 8). Đốt cháy hoàn toàn cùng lượng hỗn hợp X trên, rồi cho sản phẩm cháy hấp thụ hoàn toàn trong dung dịch nước vôi trong dư thì khối lượng kết tủa thu được là

    A. 20 gam. B. 40 gam. C. 30 gam. D. 50 gam.

    (Đề thi HSG Tỉnh Thái Bình, năm học 2009 – 2010)

    Câu 59: Đốt cháy hoàn toàn 3 lít hỗn hợp X gồm 2 anken kế tiếp nhau trong dãy đồng đẳng cần vừa đủ 10,5 lít O2 (các thể tích khí đo trong cùng điều kiện nhiệt độ, áp suất). Hiđrat hóa hoàn toàn X trong điều kiện thích hợp thu được hỗn hợp ancol Y, trong đó khối lượng ancol bậc hai bằng 6/13 lần tổng khối lượng các ancol bậc một. Phần trăm khối lượng của ancol bậc một (có số nguyên tử cacbon lớn hơn) trong Y là

    A. 46,43%. B. 31,58%. C. 10,88%. D. 7,89%.

    (Đề thi tuyển sinh Đại học khối A năm 2012)

    Câu 60: Đốt cháy hoàn toàn 0,1 mol anken X thu được CO2 và hơi nước. Hấp thụ hoàn toàn sản phẩm bằng 100 gam dung dịch NaOH 21,62% thu được dung dịch mới trong đó nồng độ của NaOH chỉ còn 5%. Công thức phân tử đúng của X là :

    A. C2H4. B. C3H6. C. C4H8. D. C5H10.

    Câu 61: Cho hỗn hợp A gồm 1 anken và 2 ankan là đồng đẳng liên tiếp vào một bình có dung tích 5,6 lít chứa O2 ở 0oC và 2 atm. Bật tia lửa điện để đốt cháy hết hiđrocacbon, sau đó đưa bình về 273oC thì áp suất trong bình là p. Nếu cho khí trong bình sau phản ứng lần lượt đi qua bình 1 đựng dung dịch H2SO4 đặc và bình 2 đựng dung dịch NaOH thấy khối lượng bình 1 tăng 3,6 gam, bình 2 tăng 7,92 gam. Tính p biết dung tích bình thay đổi không đáng kể.

    A. 3,04. B. 4,8. C. 5,0. D. 5,2.

    Câu 62: Đốt cháy hoàn toàn hỗn hợp gồm 0,1 mol etilenglicol và 0,2 mol ancol X cần dùng 0,95 mol khí oxi. Sau phản ứng thu được 0,8 mol khí CO2 và 1,1 mol H2O. Công thức phân tử của X là:

    A. C3H6(OH)2. B. C3H5(OH)3. C. C3H5OH. D. C3H7OH.

    (Đề thi thử Đại học lần 2 – THPT Chuyên Hùng Vương – Phú Thọ, năm học 2010 – 2011)

    Câu 63: Cho hỗn hợp khí X gồm HCHO và H2 đi qua ống sứ đựng bột Ni nung nóng. Sau khi phản ứng xảy ra hoàn toàn, thu được hỗn hợp Y gồm hai chất hữu cơ. Đốt cháy hết Y thì thu được 11,7 gam H2O và 7,84 lít khí CO2 (ở đktc). Phần trăm theo thể tích của H2 trong X là:

    A. 65,00%. B. 46,15%. C. 35,00%. D. 53,85%.

    (Đề thi tuyển sinh Đại học khối A năm 2009)

    Câu 64: Cho a mol hỗn hợp X gồm HCHO, OHC – CHO và H2 đi qua ống đựng bột Ni nung nóng, sau một thời gian thu được hỗn hợp Y gồm khí và hơi. Đốt cháy hoàn toàn hỗn hợp Y, sinh ra 8,1 gam nước. Giá trị của a là :

    A. 0,3. B. 0,25. C. 0,45. D. 0,5.

    (Đề thi thử đại học lần 3 – THPT Chuyên – Đại học Vinh, năm học 2011 – 2012)

    Câu 65: Đốt cháy hoàn toàn 1 mol hỗn hợp X gồm 1 ancol đơn chức và một anđehit đơn chức cần 76,16 lít O2 (đktc) tạo ra 54 gam H2O. Tỉ khối hơi của X đối với H2 là :

    A. 32,4. B. 36,5. C. 28,9. D. 25,4.

    Câu 66: Hỗn hợp X gồm axit fomic, axit acrylic, axit oxalic và axit axetic. Cho m gam X phản ứng hết với dung dịch NaHCO3 thu được 1,344 lít CO2 (đktc). Đốt cháy hoàn toàn m gam X cần 2,016 lít O2 (đktc), thu được 4,84 gam CO2 và a gam H2O. Giá trị của a là

    A. 1,62. B. 1,80. C. 3,60. D. 1,44.

    (Đề thi tuyển sinh Đại học khối A năm 2012)

    Câu 67: Đốt cháy hoàn toàn 3,42 gam hỗn hợp gồm axit acrylic, vinyl axetat, metyl acrylat và axit oleic, rồi hấp thụ toàn bộ sản phẩm cháy vào dung dịch Ca(OH)2 (dư). Sau phản ứng thu được 18 gam kết tủa và dung dịch X. Khối lượng X so với khối lượng dung dịch Ca(OH)2 ban đầu đã thay đổi như thế nào ?

    A. Tăng 2,70 gam. B. Giảm 7,74 gam. C. Tăng 7,92 gam. D. Giảm 7,38 gam.

    (Đề thi tuyển sinh Đại học khối A năm 2011)

    Câu 68: Hỗn hợp X gồm 1 mol aminoaxit no, mạch hở và 1 mol amin no, mạch hở. X có khả năng phản ứng tối đa với 2 mol HCl hoặc 2 mol NaOH. Đốt cháy hoàn toàn X thu được 6 mol CO2, x mol H2O và y mol N2. Các giá trị x, y tương ứng là

    A. 8 và 1,0. B. 8 và 1,5. C. 7 và 1,0. D. 7 và 1,5.

    (Đề thi tuyển sinh Đại học khối A năm 2010)

    Câu 69*: Hỗn hợp X gồm 2 amino axit no (chỉ có nhóm chức –COOH và –NH2 trong phân tử), trong đó tỉ lệ Để tác dụng vừa đủ với 3,83 gam hỗn hợp X cần 30 ml dung dịch HCl 1M. Mặt khác, đốt cháy hoàn toàn 3,83 gam hỗn hợp X cần 3,192 lít O2 (đktc). Dẫn toàn bộ sản phẩm cháy (CO2, H2O và N2) vào nước vôi trong dư thì khối lượng kết tủa thu được là

    A. 20 gam. B. 13 gam. C. 10 gam. D. 15 gam.

    (Đề thi tuyển sinh Đại học khối A năm 2012)

    Câu 70*: Tripeptit M và tetrapeptit Q đều được tạo ra từ một amino axit X mạch hở, phân tử có một nhóm -NH2. Phần trăm khối lượng của N trong X là 18,667%. Thuỷ phân không hoàn toàn m gam hỗn hợp M, Q (tỉ lệ mol 1 : 1) trong môi trường axit thu được 0,945 gam M; 4,62 gam đipeptit và 3,75 gam X. Giá trị của m là

    A. 8,389. B. 58,725. C. 5,580. D. 9,315.

    (Đề thi thử đại học lần 4 – THPT Chuyên – Đại học Vinh, năm học 2010 – 2011)

    Phân tích và hướng dẫn giải

    1A

    2A

    3D

    4B

    5C

    6A

    7D

    8C

    9A

    10C

    11A

    12A

    13D

    14D

    15C

    16D

    17A

    18A

    19B

    20A

    21D

    22B

    23A

    24A

    25A

    26A

    27B

    28C

    29D

    30C

    31C

    32D

    33C

    34D

    35C

    36C

    37A

    38A

    39C

    40D

    41A

    42B

    43A

    44B

    45A

    46C

    47C

    48D

    49C

    50B

    51D

    52A

    53A

    54A

    55D

    56A

    57A

    58B

    59D

    60A

    61B

    62B

    63B

    64C

    65D

    66D

    67D

    68C

    69B

    70A

     

    Mời các thầy cô và các em download file word tại đây

    pp1-bao toan nguyen to

     

    Xem thêm

    Tổng hợp các chuyên đề hóa học lớp 10

    Tổng hợp các chuyên đề hóa học lớp 11

    Tổng hợp các chuyên đề hóa học lớp 12

    Tổng hợp đề thi học kì 2 lớp 12 môn hóa học

    Tổng hợp đề thi học kì 2 lớp 10 môn hoá học

    Tổng hợp đề thi giữa học kì 2 cả ba khối 10 11 12

    Tổng hợp đề thi THPT QG 2021 file word có lời giải chi tiết

    Tổng hợp các phương pháp giải bài tập môn hoá học

    Tổng hợp đề thi HSG lớp 12 môn hoá học

    Phương pháp bảo toàn khối lượng đầy đủ

    Phương pháp bảo toàn nguyên tố

    Phương pháp bảo toàn khối lượng

    Phương pháp quy đổi este

    Phương pháp giải bài tập điện phân

    Phương pháp đồng đẳng hoá