Quan sát các hiện tượng tự nhiên ta thấy có những hiện tượng thường xảy ra, có những hiện tượng ít xảy ra. Xác suất là một đại lượng thể hiện mức độ xảy ra (thường xuyên hay ít khi) của một biến cố. Trong lịch sử Toán học đã có nhiều định nghĩa cho khái niệm xác suất. Trong phần này, ta sẽ xem xét một số định nghĩa tiêu biểu.
Nhắc lại các khái niệm cơ bản
Chúng ta nhắc lại một số kiến thức sau:
- Tập các kết quả có thể xảy ra của một thí nghiệm (phép thử) được gọi là không gian mẫu (ký hiệu: Ω).
- Mỗi phần tử ω trong Ω được gọi là một kết quả (một điểm hay phần tử trong không gian mẫu).
- Mỗi tập con của Ω được gọi là một biến cố.
Bạn có thể xem chi tiết trong bài Phép thử là gì? Biến cố là gì?
Ví dụ, tung đồng xu kết quả có thể là sấp hoặc ngửa. Gọi S là biến cố “sấp” và N là biến cố “ngửa”. thì phép thử “tung đồng xu hai lần” có không gian mẫu là Ω={SS,SN,NS,NN}. Biến cố lần tung đầu tiên xuất hiện mặt sấp là A={SS,SN}.

Đặt ω là vận tốc của một chiếc xe máy, khi đó chúng ta có thể đặt không gian mẫu là
Ω=R=(−∞,+∞)
Xác suất là gì?
Có rất nhiều cách định nghĩa xác suất, dưới đây chúng tôi giới thiệu một vài cách tiếp cận.
Định nghĩa cổ điển của xác suất
Đây là cách định nghĩa xác suất mà học sinh phổ thông sử dụng. Cho \(A_1, A_2,…, A_n\) là nhóm các biến cố đầy đủ và có cùng khả năng xảy ra. Khi đó xác suất để xảy ra biến cố \(A_i\) là: \[P(A_i) = \frac{1}{n}\]
Nếu biến cố A nào đó là tổng của m biến cố thuộc nhóm các biến cố đầy đủ trên thì xác suất của biến cố A là: \[P(A) = \frac{m}{n}\]
Như vậy, xác suất xuất hiện biến cố A là tỷ số giữa số các trường hợp thuận lợi để biến cố A xảy ra và số trường hợp cùng khả năng có thể xảy ra khi thực hiện phép thử.
Ví dụ, từ một hộp có 13 bi đỏ và 7 bi trắng có kích thước như nhau, lấy ngẫu nhiên 1 bi. Khi đó, xác suất để lấy được bi đỏ là \[P(A)=\frac{13}{20}.\]
Bạn có thể tham khảo thêm các bài tập trong bài viết 1000 bài toán Tổ hợp Xác Suất có lời giải.
Định nghĩa xác suất theo tiên đề
Xác suất là một hàm số thực định lượng khả năng xảy ra của mỗi biến cố A xảy ra trong không gian mẫu Ω, mỗi biến cố A sẽ được gán một con số thực Pr(A), đôi khi còn kí hiệu là P(A), để định lượng khả năng (hay còn gọi là độ đo xác suất). Mỗi xác suất của mỗi biến cố phải thỏa mãn 3 tiên đề Kolmogorov sau:
- Tiên đề 1: Pr(A)≥0, với mọi biến cố A
- Tiên đề 2: Pr(Ω)=1
- Tiên đề 3: Nếu hai biến cố A và B rời nhau (disjoint – không giao nhau) \(A \cap B = \emptyset\) thì \[\Pr(A \cap B) = \Pr(A) + \Pr(B) \] Tổng quát, nếu như \(A_{1}, A_{2},…\) rời nhau thì:\[\Pr \left( \bigcup\limits_{i = 1}^\infty {{A_i}} \right) = \sum\limits_{i = 1}^\infty \Pr\left( {{A_i}} \right)\]
Định nghĩa thống kê về xác suất
Tần số của một biến cố $ A $, kí hiệu $ n_A $, là tần số (số lần) xuất hiện của nó sau $ n $ lần thực hiện phép thử. $$ f_n(A) = \frac{n_A}{n} $$
Định nghĩa xác suất theo định luật số lớn là giới hạn của tần số biến cố khi số lần thử lên tới vô hạn. $$ P(A) = \lim\limits_{n \to \infty}f_n(A) $$
Trên thực tế ta không đủ thời gian và điều kiện để thực hiện vô hạn số lần gieo phép thử và $ n $ đủ lớn thì tần số $ f_n(A) $ sẽ tiến tới một giá trị gần như không thay đổi nhiều nên người ta chọn giá trị xấp xỉ đó là xác suất: $$ |P(A) – f_n(A)| < \epsilon $$ với $ \epsilon $ là một số dương rất bé.
Định nghĩa hình học của xác suất
Khi n(Ω) là vô hạn, ta không thể áp dụng định nghĩa cổ điển để tính xác suất. Trong nhiều trường hợp, ta có thể sử dụng định nghĩa xác suất theo quan điểm hình học như sau:
Định nghĩa: Giả sử một điểm được rơi ngẫu nhiên vào một miền D, A là một miền con của D. Khi đó xác suất để điểm rơi ngẫu nhiên vào miền A được xác định bởi công thức:
\[P(A) = \frac{sd(A)}{sd(D)}\]
Trong đó sd(A), sd(D) là số đo của miền A, D (có thể là độ dài, diện tích hay thể tích tùy thuộc vào miền xét trên đường thẳng, mặt phẳng hay trong không gian 3 chiều theo từng bài toán cụ thể).
Ví dụ “Bài toán gặp gỡ”
Hai người bạn hẹn gặp nhau tại một địa điểm đã định trước trong khoảng thời gian từ 19 đến 20 giờ. Hai người đến chỗ hẹn độc lập với nhau và qui ước rằng người đến trước sẽ chỉ đợi người đến sau 10 phút, nếu không gặp thì sẽ rời đi. Tính xác suất để hai người có thể gặp nhau?
Gọi A là biến cố hai người gặp nhau.
Gọi x là số phút tại thời điểm người thứ nhất đến điểm hẹn: 0 ≤ x ≤ 60.
Gọi y là số phút lúc người thứ hai đến điểm hẹn: 0 ≤ y ≤ 60.
Nếu ta biểu diễn số phút x theo trục hoành và số phút y theo trục tung.
Như vậy số phút lúc đến của cả hai người được biểu diễn bằng một điểm có tọa độ (x, y) nằm trong hình vuông có cạnh là 60 (ta lấy phút làm đơn vị). Đó chính là miền D.
D = {(x,y): 0 ≤x ≤ 60; 0 ≤ y ≤ 60}
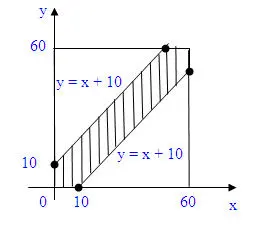
Để hai người gặp nhau thì số phút lúc đến x, y của mỗi người phải thỏa mãn điều kiện: |x-y| ≤ 10 hay x-10 ≤ y ≤ x+10.
Như vậy các điểm (x, y) thích hợp cho việc gặp nhau là các điểm nằm trong phần A có gạch chéo nằm giữa hai đường thẳng y = x – 10 và y = x + 10 (như hình vẽ).
Theo công thức xác suất hình học, ta đi tính diện tích của miền gạch chéo và diện tích hình vuông cạnh 60. Từ đó tìm được xác suất \[P(A) = \frac{60^2-50^2}{60^2}=\frac{11}{36}.\]
Tính chất của xác suất
Từ đây ra có thể rút ra được 1 vài điều sau:
- Xác suất của biến cố $ A $ bất kì luôn nằm trong đoạn [0, 1];
- Xác suất của biến cố không thể bằng 0: $$ P(\emptyset) = 0; $$
- Xác suất của biến cố chắc chắn hay không gian biến cố bằng 1 $$ P(\Omega) = 1 $$
- Xác suất hợp của 2 biến cố độc lập $ A, B $ là tổng của chúng $$ P(A+B) = P(A) + P(B) $$
- Xác suất kéo theo $ A \subseteq B $ thì $$ P(A) \le P(B). $$

