Cách tính Khoảng cách giữa hai đường thẳng chéo nhau trong không gian
Muốn tính được khoảng cách giữa hai đường thẳng chéo nhau thì các em học sinh cần nắm vững cách tính khoảng cách từ điểm tới một mặt phẳng và cách dựng hình chiếu vuông góc của một điểm lên mặt phẳng. Chi tiết về vấn đề này, mời các em xem trong bài viết Cách tính khoảng cách từ một điểm đến một mặt phẳng.
1. Các phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau
Để tìm khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\) trong không gian, chúng ta có 3 hướng xử lý như sau:
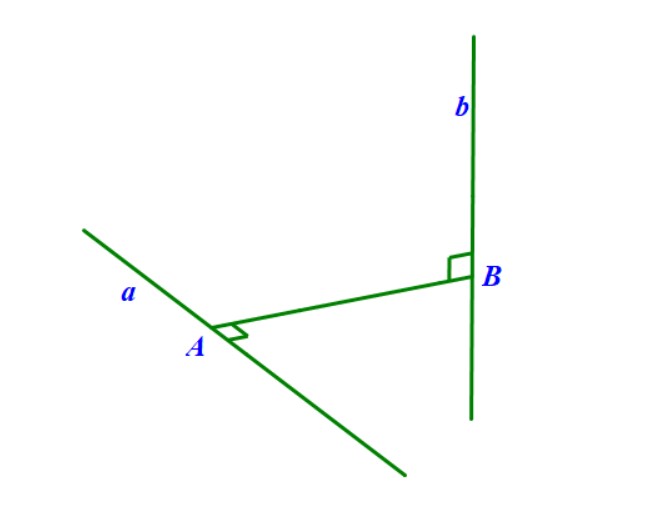
- Cách 1. Dựng đoạn vuông góc chung của hai đường thẳng và tính độ dài đoạn vuông góc chung đó. Nói thêm, đường vuông góc chung của hai đường thẳng là một đường thẳng mà cắt cả hai và vuông góc với cả hai đường thẳng đã cho. $$ \begin{cases}
AB \perp a\\ AB \perp b\\
AB \cap a = A\\ AB \cap b = B
\end{cases} \Rightarrow d(a,b)=AB$$
- Cách 2. Chuyển về tính khoảng cách từ đường thẳng thứ nhất tới mặt phẳng song song với nó và chứa đường thẳng thứ hai. $$ \begin{cases}
a \parallel (P)\\ b \subset (P)
\end{cases} \Rightarrow d(a,b) = d(a,(P))$$ Trong thực tế, việc tạo ra mặt phẳng \((P)\) song song với đường thẳng $a$ thường được thực hiện bằng cách, dựng hoặc tìm một đường thẳng $a’$ nào đó song song với $a$ và cắt đường thẳng $b$. Lúc này, mặt phẳng \((P)\) chính là mặt phẳng xác định bởi hai đường thẳng cắt nhau \(a’\) và \(b\). Và, việc tính khoảng cách tiếp tục quy về khoảng cách từ một điểm tới một mặt phẳng bằng cách lấy một điểm $M$ bất kỳ thuộc đường thẳng $a$ và tính khoảng cách từ $M$ tới $(P)$.
Trong thực tế, việc tạo ra mặt phẳng \((P)\) song song với đường thẳng $a$ thường được thực hiện bằng cách, dựng hoặc tìm một đường thẳng $a’$ nào đó song song với $a$ và cắt đường thẳng $b$. Lúc này, mặt phẳng \((P)\) chính là mặt phẳng xác định bởi hai đường thẳng cắt nhau \(a’\) và \(b\). Và, việc tính khoảng cách tiếp tục quy về khoảng cách từ một điểm tới một mặt phẳng bằng cách lấy một điểm $M$ bất kỳ thuộc đường thẳng $a$ và tính khoảng cách từ $M$ tới $(P)$. - Cách 3. Chuyển về tính khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đã cho. $$ \begin{cases}
a\subset (P)\\
b\subset (Q)\\
(P)\parallel (Q)
\end{cases} \Rightarrow d(a,b)=d((P),(Q))$$

Cách 1 thì chỉ nên sử dụng khi hai đường thẳng \(a\) và \(b\) vuông góc với nhau. Lúc đó việc dựng đoạn vuông góc chung là khá dễ dàng, còn khi \(a\) và \(b\) không vuông góc với nhau thì dựng đường vuông góc chung rất phức tạp. Xin xem phần 2.3 để biết thêm về cách dựng đoạn vuông góc chung.
Cách 2 thường được sử dụng nhiều hơn cả, cách 3 chỉ sử dụng khi việc kẻ đường thẳng song song với một trong hai đường thẳng ban đầu gặp khó khăn.
Sau đây chúng ta cùng nhau tìm hiểu các ví dụ minh họa về tính khoảng cách giữa hai đường chéo nhau trong không gian.
2. Các ví dụ minh họa xác định khoảng cách 2 đường thẳng chéo nhau
2.1. Tính khoảng cách giữa hai đường thẳng chéo nhau bằng cách đưa về khoảng cách giữa đường thẳng và mặt phẳng song song
Ví dụ 1. [Câu 40, Đề minh họa Tốt nghiệp 2020] Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với đáy \( (ABC) \), \( SA=a \), tam giác \(ABC\) vuông tại \( A\) và \( AB=2a,\) \(AC=4a \). Gọi \( M \) là trung điểm của \( AB \). Tính khoảng cách giữa hai đường thẳng \( SM \) và \( BC \).
Phân tích. Để dựng một mặt phẳng chứa một trong hai đường thẳng \( SM \) và \( BC \) đồng thời vuông góc với đường còn lại thì chúng ta cần xem xét, việc dựng mặt phẳng song song với đường thẳng nào dễ dàng hơn.
Rõ ràng việc kẻ một đường thẳng cắt \(SM\) và song song với \(BC\) rất đơn giản, chỉ việc qua \( M \) kẻ đường thẳng song song với \( BC \), đường thẳng này chính là đường trung bình của tam giác \( ABC \). Do đó, chúng ta sẽ ưu tiên chọn cách làm này.
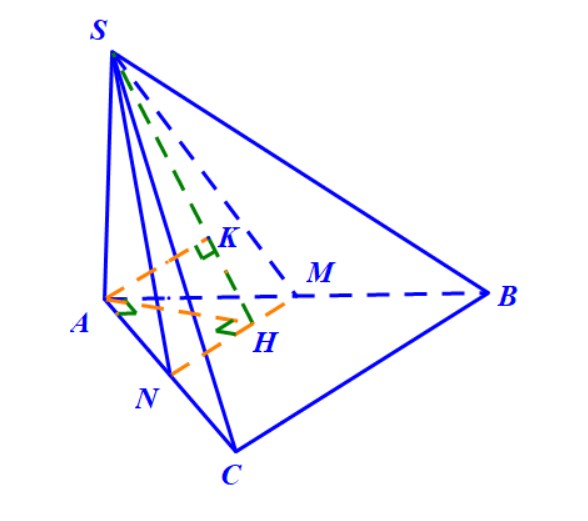
Hướng dẫn. Gọi \( N \) là trung điểm \( AC \) thì ta có
$$ \begin{cases}
BC\parallel MN\\
MN\subset (SMN)
BC \not \subset (SMN)
\end{cases} $$ Do đó, khoảng cách cần tìm $$ d(BC,SM)=d(BC,(SMN) =d(B,(SMN))$$ Tuy nhiên, đường thẳng \( AB \) lại cắt mặt phẳng \( (SMN) \) tại trung điểm \( M \) của \( AB \) nên
$$ \frac{d(B,(SMN))}{d(A,(SMN))} =\frac{BM}{AM}=1 $$ hay \( d(B,(SMN))=d(A,(SMN))\) và chúng ta chỉ cần đi tính khoảng cách từ điểm \( A \) tới mặt phẳng \( (SMN) \) là xong. Đây lại là một bài toán khá cơ bản, chỉ việc kẻ vuông góc hai lần \( AH\perp MN \) và \( AK\perp SH \), hoặc áp dụng trực tiếp kết quả đối với trường hợp hình chóp có ba tia \( AS,\) \(AC,\) \(AB \) đồng quy và đôi một vuông góc với nhau. Tóm lại, khoảng cách cần tìm chính là độ dài đoạn \( AK \) như trong hình vẽ và có $$ \frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AN^2} $$ Thay số vào và tìm được \( d(BC,SM)=AK= \frac{2a}{3}.\)
Ví dụ 2. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $ a, $ cạnh $ SA=a$ và vuông góc với đáy. Tính khoảng cách giữa $ AB $ và $ SC. $
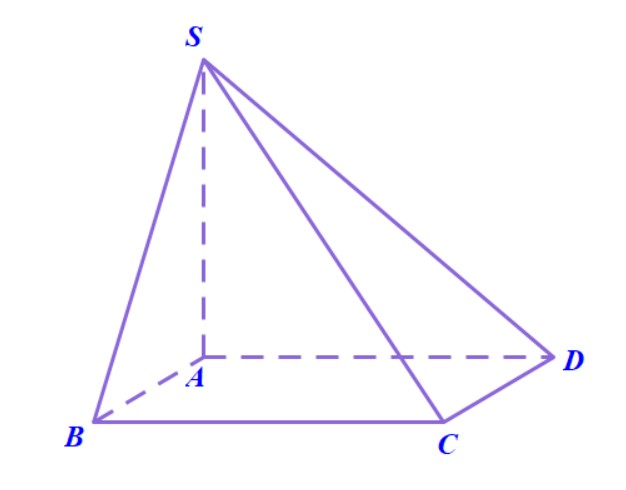
Hướng dẫn. Có $ AB\parallel CD $ nên $ AB\parallel (SCD) $. Do đó $$ d(AB,SC)=d(AB,(SCD))=d(A,(SCD))$$
Đây chính là bài toán tính khoảng cách cơ bản, kẻ đường cao $AK$ của tam giác $SAD$ thì khoảng cách cần tìm $$d(A,(SCD))=AK=\frac{a}{\sqrt{2}} $$
Nếu bài viết hữu ích, bạn có thể tặng tôi 1 cốc cafe vào số tài khoản Agribank 3205215033513. Xin cảm ơn!
Ví dụ 3. [Đề Đại học Khối D năm 2008] Cho lăng trụ đứng tam giác $ ABC.A’B’C’ $ có đáy $ ABC $ là tam giác vuông với $ BA=BC=a $, cạnh bên $ AA’=a\sqrt{2}. $ Gọi $ M $ là trung điểm của $ BC $. Tính khoảng cách giữa hai đường thẳng $ AM $ và $ B’C $.
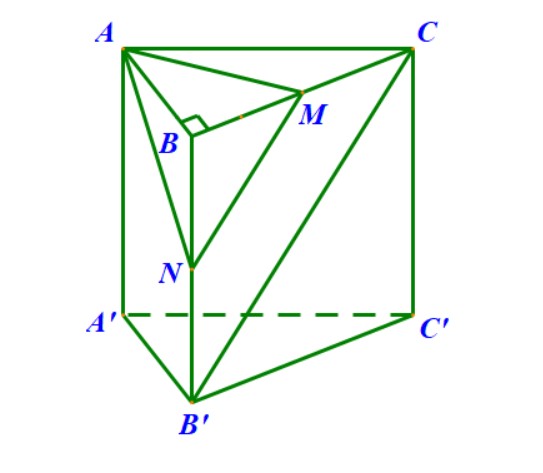
Hướng dẫn. Lấy $ N $ là trung điểm của $ BB’ $, ta có $ MN $ là đường trung bình của tam giác $ B’BC $ nên $ B’C $ song song với $ MN $. Như vậy đường thẳng $ B’C $ song song với mặt phẳng $ (AMN) $, và do đó
\[ {d}(B’C,AM)={d}(B’C,(AMN))={d}(B'(AMN)) \] Lại có $ BB’ $ cắt mặt phẳng $ (AMN) $ tại trung điểm $ N $ của $ BB’ $ nên
\[ {d}(B’,(AMN))={d}( B,(AMN))\] Hình chóp $ B.AMN $ có ba tia $ BA,BM,BN $ đồng quy và đôi một vuông góc nên đặt $d=d(B,(AMN))$ thì có \[ \frac{1}{d^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BN^2}=\frac{7}{a^2} \] Từ đó tìm được khoảng cách từ giữa $B’C $ và $ AM $ là $ \frac{a}{\sqrt{7}}. $
Ví dụ 4. Cho hình chóp đều $S.ABCD$ có đáy là hình vuông cạnh $ a, $ cạnh $ SA=a\sqrt{2}$. Tính khoảng cách giữa $ AB $ và $ SC. $

Hướng dẫn. Có $ AB\parallel CD $ nên $ AB\parallel (SCD) $. Do đó, gọi $ O $ là tâm hình vuông thì có $$ {d}(AB,SC)={d}(AB,(SCD))={d}(A,(SCD)) $$ Nhưng đường thẳng \( AO \) cắt mặt phẳng \( (SCD) \) tại điểm \( C \) nên có
$$ \frac{d(A,(SCD))}{d(O,(SCD))}=\frac{AC}{OC}=2$$ Suy ra \( d(A,(SCD))=2d(O,(SCD)) \). Đây chính là bài toán 1, kẻ vuông góc hai lần và tìm được đáp số $ \mathrm{d}(AB,SC)=\frac{2a\sqrt{21}}{7}. $
Ví dụ 5. [Đề ĐH khối A năm 2006] Cho hình lập phương $ ABCD.A’B’C’D’ $ có các cạnh bằng 1. Gọi $ M , N $ lần lượt là trung điểm của $ AB $ và $ CD $. Tính khoảng cách giữa hai đường thẳng chéo nhau $ A C’ $ và $ MN $.

Hướng dẫn. Chúng ta có \( MN\) song song với mặt phẳng \( (ADC’B’) \), mà mặt phẳng \( (ADC’B’) \) chứa đường thẳng \( AC’ \) nên suy ra $$ d(MN,AC’)=d(MN,(ADC’B’))=d(N,(ADC’B’) ).$$ Để dựng hình chiếu vuông góc của \( N \) lên mặt phẳng \( (ADC’B’) \) ta chú ý rằng \( N \) nằm trong mặt phẳng \( (CDD’C’) \) mà hai mặt phẳng \( (ADC’B’) \) và \( (CDD’C’) \) vuông góc với nhau và cắt nhau theo giao tuyến \( C’D \). Do đó, chúng ta chỉ cần tìm hình chiếu vuông góc của \( N \) lên giao tuyến \( C’D \) là được. Giả sử hình chiếu vuông góc đó là điểm \( H \) thì có $$ d(N,(ADC’B’))=NH=\frac{1}{2} CD’ $$ Từ đó tìm được đáp số $ d(MN,AC’)=\frac{a\sqrt{2}}{4}. $
Ví dụ 6. [Đề ĐH khối A năm 2004] Cho hình chóp tứ giác $ S.ABCD $ có đáy là hình thoi đường chéo $ AC=4,SO=2\sqrt{2}$ và $ SO $ vuông góc với đáy $ ABCD $, ở đây $ O $ là giao điểm của $ AC $ và $ BD$. Gọi $ M $ là trung điểm của $ SC $. Tìm khoảng cách giữa hai đường thẳng chéo nhau $ SA $ và $ BM. $

Hướng dẫn. Ta có $ MO $ là đường trung bình của tam giác $ SAC $ nên $ SA $ song song với $ MO. $ Do đó $ SA $ song song với mặt phẳng $ (MBD). $ Dẫn tới \[ {d}( SA,MB)={d}(SA,(MBD))={d}( S,(MBD)) \] Mặt khác $ SC $ cắt mặt phẳng $ (MBD) $ tại trung điểm $ M $ nên
\[ {d}( S,(MBD))={d}( C,(MBD)) \] Gọi $ K $ là chân đường vuông góc hạ từ $ C $ xuống $ MO $ thì chứng minh được $ K $ là hình chiếu vuông góc của $ C $ lên mặt phẳng $ (MBD). $
Bây giờ, để tính được độ dài đoạn \( CK \) thì ta sẽ tính diện tích tam giác \( MOC \) theo hai cách. Có
$$ S_{\Delta MOC} =\frac{1}{4} S_{\Delta SAC}=\frac{1}{8}SO\cdot AC$$ Nhưng mặt khác $$ S_{\Delta MOC} =\frac{1}{2} CK \cdot OM=\frac{1}{4}CK\cdot SA$$ Từ đó suy ra
$$ CK=\frac{SO\cdot AC}{2 SA}= \frac{2\sqrt{6}}{3}.$$ Vậy khoảng cách giữa hai đường thẳng $ SA $ và $ BM $ là $\frac{2\sqrt{6}}{3}$.
Ví dụ 7. Cho hình chóp $ S.ABC $ có đáy $ ABC $ là tam giác vuông tại $ B,$ $ AB = 2a,$ $\widehat{BAC}=60^\circ, $ cạnh bên $ SA $ vuông góc với đáy và $ SA=a\sqrt{3}. $ Gọi $ M $ là trung điểm của cạnh $ AB $. Tính theo $ a $ khoảng cách giữa hai đường thẳng $ SB $ và $ CM $.

Hướng dẫn.
Gọi $ N $ là trung điểm $ SA $ thì $ MN\parallel SB $ nên $$ d(SB,CM)=d(SB,(CMN))=d(B,(CMN)). $$ Lại có đường thẳng \( AB \) cắt mặt phẳng \( (CMN) \) tại trung điểm \( M \) của \( AB \) nên suy ra $$ d(B,(CMN))=d(A,(CMN)) $$ Tính khoảng cách từ điểm \( A \) tới mặt phẳng \( (CMN) \) chúng ta sử dụng bài toán 1.
Hạ $ AE\perp MC $ thì chú ý rằng, tam giác $ AMC $ có góc $\widehat{M} $ tù nên $ E $ nằm ngoài đoạn $ MC. $ Sử dụng tam giác đồng dạng hoặc tính diện tích tam giác $ AMC $ theo hai cách, tính được $ AE=\frac{2a\sqrt{3}}{\sqrt{29}}. $ Tiếp tục hạ $ AH\perp AE $ thì tính được $$ d(A,(CMN))=AH=\frac{2a\sqrt{3}}{\sqrt{29}}.$$
Ví dụ 8. Cho hình chóp đều $ S.ABC $ có $ SA=2a,AB=a $. Gọi $ M $ là trung điểm của cạnh $ BC $. Tính theo $ a $ khoảng cách giữa hai đường thẳng $ AM,SB $.
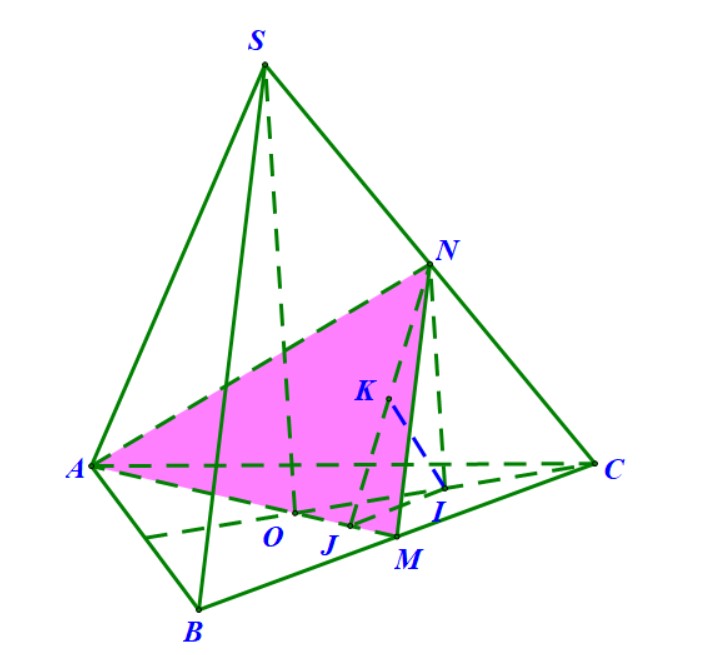
Hướng dẫn. Gọi $ O $ là tâm tam giác đều $ ABC $. Gọi $ N $ là trung điểm $ SC $ thì $ MN\parallel SB $ nên $$ d(AM,SB)=d(SB,(AMN))=d(B,(AMN))$$ Mặt khác, vì $ M $ là trung điểm $ BC $ nên $d(B,(AMN))=d(C,(AMN))$.
Gọi $ I $ là trung điểm $ OC $ thì $ NI\perp (ABC) $, hơn nữa $ d(C,(AMN))=2d(I,(AMN)). $ Từ $ I $ hạ $ IJ $ vuông góc xuống $ OM $ thì $ J $ là trung điểm $ OM. $ Tiếp tục hạ $ IK$ vuông góc xuống $NJ $ thì ta có $$ d(I,(AMN))=IK=a\sqrt{\frac{11}{188}} $$ Từ đó tìm được đáp số $d(AM,SB)= \frac{a\sqrt{517}}{47}. $
2.2. Tính khoảng cách giữa hai đường thẳng chéo nhau bằng cách đưa về khoảng cách giữa 2 mặt phẳng song song
Ví dụ 9. [Đề ĐH Khối B năm 2002] Cho hình lập phương $ ABCD.A’B’C’D’ $ cạnh $ a $. Tính theo $ a $ khoảng cách giữa hai đường thẳng $ A’B $ và $ B’D. $
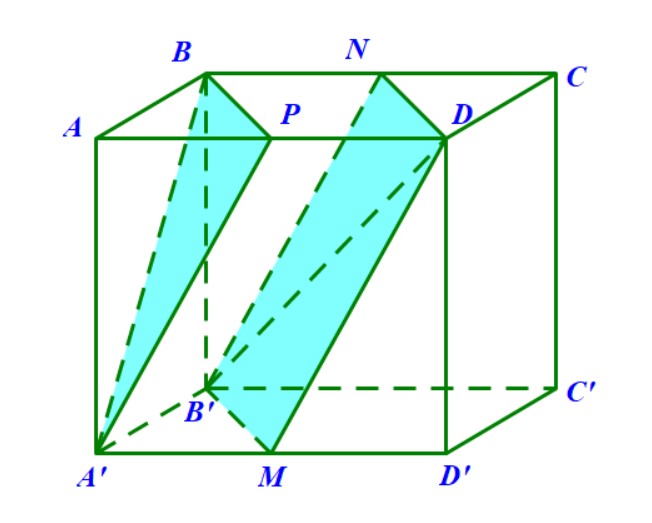
Hướng dẫn. Gọi $ M , N , P $ lần lượt là trung điểm các đoạn thẳng $ A’ D ‘ ,BC , AD $ thì dễ dàng chứng minh được hai mặt phẳng \( (A’BP) \) và \( B’NDM \) song với nhau và lần lượt chứa hai đường thẳng \( A’B \) và \( B’D \). Do đó, khoảng cách cần tìm
\[ d(A’B,B’D)=d( (A’PB),(MDNB’))\] Khoảng cách này lại bằng khoảng cách từ một điểm bất kì trên mặt phẳng này tới mặt phẳng còn lại, ở đây chúng ta chọn điểm \(D \), thì có $$ d( (A’PB),(MDNB’))= =d( D,(A’PB))$$ Nhưng, đoạn thẳng \( AD \) cắt mặt phẳng \( (A’PB) \) tại trung điểm \( P \) nên có $$ d( D,(A’PB))=d(A,(A’PB))=d$$ Rõ ràng \( AB,AP,AA’ \) là ba tia đồng quy và đôi một vuông góc nên có ngay $$ \frac{1}{d^2}=\frac{1}{AB^2}+\frac{1}{AP^2}+\frac{1}{A’A^2}$$ Thay số vào tìm được đáp số $d(A’B,B’D)=\frac{a}{3}. $
Ví dụ 10. Cho hình hộp đứng \( ABCD.A’B’C’D’ \) có đáy là hình bình hành với \( AB=a \), \( AD=2a \), góc \(BAD\) bằng \( 60^\circ \) và \( AA’=a\sqrt{3}. \) Gọi \( M,N,P \) lần lượt là trung điểm của \( A’B’ \), \( BD \) và \( DD’ \). Gọi \(H \) là hình chiếu vuông góc của \( B \) lên \( AD \). Tính khoảng cách giữa hai đường thẳng chéo nhau \( MN \) và \( HP \).

Hướng dẫn. Gọi \( Q \) là trung điểm của \( AB \) thì có ngay hai mặt phẳng \( (MNQ) \) và \( (ADD’A’) \) song song với nhau. Hơn nữa, hai mặt phẳng này còn lần lượt chứa hai đường thẳng \( MN \) và \( HP \) nên $$ d(MN,HP)=d((MNQ),(ADD’A’)) $$ Khoảng cách giữa hai mặt phẳng song song này chính bằng khoảng cách từ \( Q \) tới mặt phẳng \( (ADD’A’) \) và bằng một nửa khoảng cách từ \( B \) tới mặt phẳng \( (ADD’A’) \). Từ đó tìm được đáp số \( d(MN,HP)=\frac{a\sqrt{3}}{4}.\)
2.3. Tính khoảng cách giữa hai đường thẳng chéo nhau bằng cách dựng đoạn vuông góc chung
Trong trường hợp đặc biệt khi hai đường thẳng \(a\) và \(b\) chéo nhau đồng thời lại vuông góc với nhau, thì thường tồn tại một mặt phẳng $(\alpha)$ chứa \(a\) và vuông góc với \(b\). Ta dựng đoạn vuông góc chung qua hai bước sau:
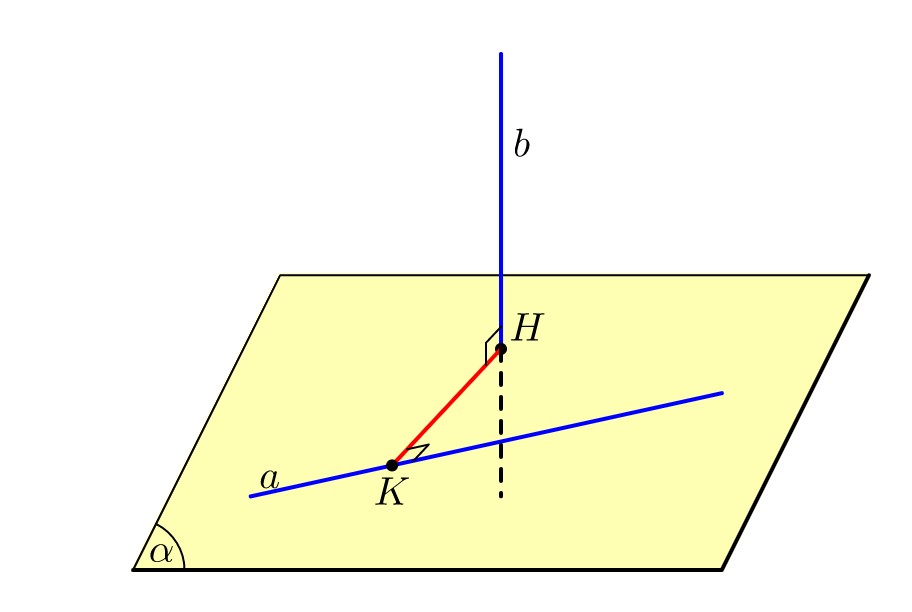
- Tìm giao điểm \(H\) của đường thẳng \(b\) và mặt phẳng \((\alpha)\).
- Trong mặt phẳng \((\alpha)\), dựng \(HK\) vuông góc với \(a\) tại \( K\) thì \( HK\) chính là đoạn vuông góc chung.
Tổng quát, việc dựng đoạn vuông góc chung của hai đường thẳng chéo nhau được thực hiện như sau:

- Dựng mặt phẳng \( (\alpha) \) chứa đường thẳng \( b \) và song song với đường thẳng \( a \).
- Tìm hình chiếu vuông góc \( a’ \) của \( a \) trên mặt phẳng \((\alpha)\).
- Tìm giao điểm \( N \) của \( a’ \) và \( b \), dựng đường thẳng qua \( N \) và vuông góc với \( (\alpha) \), đường thẳng này cắt \( a \) tại \( M \).
Kết luận: Đoạn \( MN \) chính là đoạn vuông góc chung của hai đường thẳng chéo nhau \( a \) và \( b \).
Ví dụ 11. Cho tứ diện đều $ ABCD $ có độ dài các cạnh bằng $ 6\sqrt{2} $cm. Hãy xác định đường vuông góc chung và tính khoảng cách giữa hai đường thẳng chéo nhau $ AB $ và $ CD $.
Hướng dẫn. Gọi $ M , N $ lần lượt là trung điểm các cạnh $ AB , CD $. Chứng minh được $ MN $ là đường vuông góc chung của hai đường thẳng $ AB,CD $ và khoảng cách giữa chúng là $ MN=6 $cm.
Ví dụ 12. Cho hình chóp $ S.ABC $ có đáy là tam giác vuông tại $ B , AB=a , BC=2a $, cạnh $ SA $ vuông góc với đáy và $ SA=2a. $ Hãy xác định đường vuông góc chung và tính khoảng cách giữa hai đường thẳng chéo nhau $ AB $ và $ SC $.
Hướng dẫn. Lấy điểm $ D $ sao cho $ ABCD $ là hình chữ nhật thì $ AB $ song song với $ (SCD). $ Gọi $ E $ là chân đường vuông góc hạ từ $ A $ xuống $ SD $ thì chứng minh được $ E $ là hình chiếu vuông góc của $ A $ lên $ (SCD). $
Qua $ E $ kẻ đường thẳng song song với $ CD $ cắt $ SC $ tại $ N $, qua $ N $ kẻ đường thẳng song song với $ AE $ cắt $ AB $ tại $ M $ thì $ MN $ là đường vuông góc chung cần tìm. Đáp số $ a\sqrt{2}. $
Leave a Reply