Hình 9: Góc ở tâm, số đo cung trong đường tròn

Góc ở tâm, số đo cung trong đường tròn là một kiến thức hình học quan trọng của lớp 9, thường xuất hiện trong các kì thi tuyển sinh vào lớp 10.

Mời các em tham khảo thêm một số dạng toán thường xuất hiện trong kì thi vào 10:

• Giải bài toán bằng cách lập hệ phương trình
• Giải bài toán bằng cách lập phương trình
• Các dạng toán về căn bậc hai

1. Lý thuyết góc ở tâm, số đo cung

Góc ở tâm là gì?

Trong đường tròn, góc có đỉnh trùng với tâm đường tròn gọi là góc ở tâm.

Số đo cung trong đường tròn

Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó $\left( \widehat{AOB}=sđ\overset\frown{AB} \right)$.

1. Số đo của cung lớn bằng hiệu giữa $360^\circ $ và số đo của cung nhỏ.
2. Số đo của nửa đường tròn bằng $180^\circ $.

Chú ý: Cung nhỏ có số đo nhỏ hơn $180^\circ $, cung lớn có số đo lớn hơn $180^\circ $.

Trong một đường tròn hay hai đường tròn bằng nhau:

1. Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
2. Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

Nếu $C$ là một điểm nằm trên cung $AB$ thì $$sđ\stackrel{⌢}{AB}=sđ\stackrel{⌢}{AC}+sđ\stackrel{⌢}{CB}$$

Ví dụ. Cho đường tròn $\left( O\,;R \right)$, trên$\left( O \right)$ lấy các điểm $A,\,B,\,C$sao cho $AB=R$, $BC=R\sqrt{2}$, tia $BO$ nằm giữa hai tia $BA$ và $BC$.

1. Tính số đo $\widehat{BOC}$.
2. Tính số đo các cung $\overset\frown{AB}\,,\,\overset\frown{AC},\,\overset\frown{BC}$.
3. Cho điểm $D$ là điểm nằm trên cung lớn $AC$sao cho $sđ\overset\frown{CD}=120^\circ $. Tính số đo cung $AD$.

Lời giải

a) Xét $\mathrm{\Delta }OBC$ cân tại $O$ ($OB=OC=R$),  ta có #$CB^{2}={{\left( R\sqrt{2} \right)}^{2}}=2{{R}^{2}};\,\,O{{B}^{2}}+O{{C}^{2}}={{R}^{2}}+{{R}^{2}}=2{{R}^{2}}$$ Suy ra $O{{B}^{2}}+O{{C}^{2}}=B{{C}^{2}}$ $\Rightarrow \Delta OBC$ vuông cân tại $O$.

Như vậy $\widehat{COB}=90^\circ $.

b) Ta có $\widehat{COB}=90^\circ $ $\Rightarrow $sđ $\overset\frown{CB}=90^\circ $
Tam giác $ABC$ đều nên $\widehat{AOB}=60^\circ $ $\Rightarrow $sđ $\overset\frown{AB}=60^\circ $
$\widehat{AOC}=\widehat{AOB}+\widehat{BOC}=150^\circ $ $\Rightarrow $sđ $\overset\frown{AC}=150^\circ $.

c) $\widehat{DOA}=360^\circ -\left( \widehat{AOC}+\widehat{COD} \right)=360^\circ -\left( 150^\circ +120^\circ \right)=90^\circ $ $\Rightarrow $sđ $\overset\frown{DA}=90^\circ $.

2. Bài tập Góc ở tâm, số đo cung trong đường tròn

Bài 1. Cho $\mathrm{\Delta }ABC$ cân tại $A$ có $\hat{A}={70}^{\circ }$. Vẽ đường tròn $(A;AB)$, $D$ là điểm trên $\left(A\right)$ sao cho sđ$\stackrel{⌢}{CD}={30}^{\circ }$. Tính số đo $\widehat{BAD}$.

Lời giải

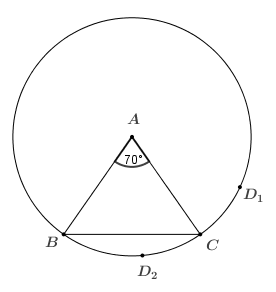
TH1: Điểm $D$ nằm trong cung lớn $CB$ khi đó $D\equiv {{D}_{1}}$
$\widehat{BA{D}_1}=\widehat{BAC}+\widehat{CA{D}_1}={70}^{\circ }+{30}^{\circ }={100}^{\circ }$
TH2: Điểm $D$ nằm trong cung nhỏ $CB$ khi đó $D\equiv {{D}_{2}}$
$\widehat{BA{D}_2}=\widehat{BAC}-\widehat{D_{2}AC}={70}^{\circ }-{30}^{\circ }={40}^{\circ }$

Bài 2. Cho điểm $A$ nằm ngoài đường tròn $(O;R)$, $OA=2R$. Vẽ $AB,AC$ là các tiếp tuyến của đường tròn $\left(O\right)$. Tính sđ$\stackrel{⌢}{BC}$, độ dài cạnh $BC$ theo $R$.

Lời giải

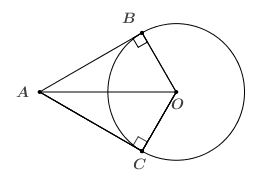
Xét tam giác $AOB$ vuông tại $B$ có $AO=2BO$ nên $\widehat{OAB}=30^\circ,\,\,\widehat{AOB}=60^\circ $
$\Rightarrow \widehat{OAC}=\widehat{BOA}=60^\circ \Rightarrow \widehat{BOC}=120^\circ $ $\Rightarrow $sđ $\overset\frown{BC}=120^\circ $.

Bài 3. Cho đường tròn $(O;R)$, $AB$ là dây cung $(AB\ne 2R)$. Trên cung nhỏ $AB$ lấy các điểm $E,F$sao cho $\stackrel{⌢}{AE}=\stackrel{⌢}{EF}=\stackrel{⌢}{FB}$. Bán kính $OE,OF$ cắt $AB$ lần lượt tại $C$ và $D$. Chứng minh rằng $AC=BD>CD$.

Lời giải

Ta có: $OA=OB\Rightarrow \Delta OAB$ cân tại $O$ $\Rightarrow \widehat{OAC}=\widehat{OBD}$.
Khi đó: $\widehat{OAC}=\widehat{OBD};OA=OB;\widehat{AOC}=\widehat{BOD}$
$\Rightarrow \mathrm{\Delta }OCA=\mathrm{\Delta }ODB$(g-c-g).
$\Rightarrow AC=BD$.
Xét $\Delta OBC$ có phân giác $OD$ $\Rightarrow \frac{OC}{OB}=\frac{DC}{DB}$.
Mà $OC<OB\Rightarrow CD<BD$.

Bài 4. Cho đường tròn $(O;R)$, $AB$ là dây cung $(AB\ne 2R)$. Trên dây $AB$ lấy hai điểm $C$ và $D$ sao cho $AC=CD=DB$. Vẽ bán kính $OE$ qua $C$, bán kính $OF$ qua $D$. Chứng minh rằng:
a) $\stackrel{⌢}{AE}=\stackrel{⌢}{BF}$.
b) $\stackrel{⌢}{AE}<\stackrel{⌢}{EF}$.

Lời giải

a) Ta có: $OA=OB\Rightarrow \Delta OAB$ cân tại $O$ $\Rightarrow \widehat{A}=\widehat{B}$.
Khi đó: $AC=BD;\widehat{A}=\widehat{B};OA=OB\Rightarrow \Delta OAC=\Delta OBD\Rightarrow \widehat{AOC}=\widehat{BOD}$.

b) Từ câu a ta có $\Delta OAC=\Delta OBD\Rightarrow OC=OD$$\Rightarrow \Delta OCD$ cân tại $O$.
khi đó $\widehat{CDO}<90^\circ \Rightarrow \widehat{CDF}>90^\circ $ ($\widehat{CDF}+\widehat{CDO}=180^\circ $)
$\Rightarrow CF>CD$ hay $CF>AC$ ($AC=CD$).
Xét $\Delta OAC$ và $\Delta OCF$ có $OA=OF$; $OC$ chung và $CF>AC$ $\Rightarrow \widehat{COF}>\widehat{COA}$.

Bài 5. Cho $\mathrm{\Delta }ABC$ đều. Về phía ngoài $\mathrm{\Delta }ABC$ vẽ nửa đường tròn$\left(O\right)$ đường kính $BC$. Trên nửa đường tròn $\left(O\right)$lấy các điểm $M,N$ sao cho $\stackrel{⌢}{BM}=\stackrel{⌢}{MN}=\stackrel{⌢}{NC}$, $AM$ và $AN$ cắt $BC$ lần lượt tại $E$ và $F$. Chứng minh: $BE=BF=FC$.
Lời giải
$OB=OM;\widehat{BOM}=60^\circ $ $\Rightarrow \Delta OBM$ đều.
$AB=AC;\widehat{ABM}=\widehat{ACN}=120^\circ ;BM=CN$$\Rightarrow \Delta ABM=\Delta ACN$(c-g-c)
$\Rightarrow \widehat{BAM}=\widehat{CAN}$.
$\widehat{BAE}=\widehat{CAF};AB=AC;\widehat{ABE}=\widehat{ACF}=60^\circ \Rightarrow \Delta ABE=\Delta ACF$ (g-c-g)
$\Rightarrow BE=CF$ (1).

$\Delta OBM$ đều nên $AC=2BO=2BM\Rightarrow \frac{BM}{AC}=\frac{1}{2}$.
Xét $\Delta EBM;\Delta ECA$ có $\widehat{BEM}=\widehat{CEA};\widehat{MBE}=\widehat{ACE}=60^\circ $
$\Rightarrow \Delta EBM\backsim \Delta ECA$$\Rightarrow \frac{EB}{EC}=\frac{BM}{AC}=\frac{1}{2}$; $BE=CF$
$\Rightarrow BE=EF$ (2).
Từ (1) và (2) suy ra: $BE=EF=FC$.