Bài toán mũ và logarit trong các đề thi năm 2020
Xem thêm Nguyên Hàm – Tích Phân trong đề thi 2020
Ví dụ 1. [Chuyên KHTN năm 2020] Cho $ m$ là tham số thực. Phương trình $ 4^x-(m+4)\cdot 2^x+2=0$ có hai nghiệm thực $ x_1,x_2 $ thỏa mãn $ (x_1+2)(x_2+2)=4$. Tính giá trị của $ m$.
Hướng dẫn. Đặt $ t=2^x$, điều kiện $ t>0$ ta được phương trình bậc hai $$ t^2-(m+4)t+2=0 $$ Theo định lí Viét ta có $$ \begin{cases}
t_1+t_2=m+4,\\t_1\cdot t_2=2.
\end{cases}$$ Suy ra $$ 2=2^{x_1}\cdot 2^{x_2} =2^{x_1+x_2}$$ nên có $ x_1+x_2=1$. Kết hợp với giả thiết $ (x_1+2)(x_2+2)=4 $ ta tìm được $$ \begin{cases}
x_1=-1\\x_2=2
\end{cases} $$ Do đó, $ m+4=t_1+t_2=2^{x_1}+2^{x_2}=\frac{9}{2}$. Từ đó tìm được $ m=\frac{1}{2}$. Thử lại thấy nếu $ m=\frac{1}{2}$ thì phương trình đã cho có hai nghiệm thỏa mãn yêu cầu (cần phải thử lại vì ở đây chúng ta chưa tìm điều kiện cho phương trình $ t^2-(m+4)t+2=0 $ có hai nghiệm $ t>0$ ).
Ví dụ 2. Xét các số thực $ a,b>1$ và các số thực $x,y>0$ thỏa mãn $$ a^x=b^y=b^2\sqrt{a}. $$ Tính giá trị nhỏ nhất của biểu thức $ p=2020x+y$.
Hướng dẫn. Từ đẳng thức $ a^x=b^y=b^2\sqrt{a}$, lần lượt lấy logarit cơ số $ a,b$ hai vế ta được $$ \begin{cases}
x=\log_a\left(b^2\sqrt{a}\right)=2\log_a b+\frac{1}{2}\\
y=\log_b \left(b^2\sqrt{a}\right)=2+\frac{1}{2}\log_b a
\end{cases} $$ Suy ra, biểu thức cần tìm giá trị nhỏ nhất là $$ p= 2020\cdot \left(2\log_a b+\frac{1}{2}\right)+2+\frac{1}{2}\log_b a$$ Đặt $ t=\log_a b $ thì $ a,b>1$ nên $ t>0$ và biểu thức trên trở thành $$ p=2020\left(2t+\frac{1}{2}\right) +2+\frac{1}{2t}$$
Khảo sát hàm số này trên khoảng $ (0,+\infty)$, hoặc sử dụng bất đẳng thức AM–GM, ta tìm được giá trị nhỏ nhất của $ p$ là $ 1012+2\sqrt{2020}$.
Ví dụ 3. Có bao nhiêu số nguyên $ x$ để tồn tại số thực $ y$ thỏa mãn $$ \log_2 \frac{x}{x^2+y^2} =x^2+y^2 -4x-2$$
Hướng dẫn. Điều kiện $$\frac{x}{x^2+y^2}>0 \Leftrightarrow x>0 $$ Với điều kiện đó thì đẳng thức đã cho trở thành \begin{align}
\frac{x}{x^2+y^2} &= 2^{x^2+y^2-4x-2}\\
\Leftrightarrow \frac{x}{x^2+y^2} &=\frac{2^{x^2+y^2}}{2^{4x+2}}\\
\Leftrightarrow 4x\cdot 2^{4x}&=\left(x^2+y^2\right)\cdot 2^{x^2+y^2}
\end{align} Hàm số $ f(t)=t\cdot 2^t$ trên $ (0,+\infty)$ là một hàm đồng biến. Do đó $ f(4x)=f\left(x^2+y^2\right)$ xảy ra khi và chỉ khi $$ 4x=x^2+y^2. $$ Suy ra $ 4x-x^2=y^2 \geqslant 0$. Giải bất phương trình này, tìm được $ 0 \leqslant x \leqslant 4$. Mà $ x$ nguyên dương nên chọn được các giá trị là $ 1,2,3,4$.
Ví dụ 4. [Chuyên ĐHSP HN năm 2020] Cho các số thực $ x,y$ thỏa mãn $ x>y>0$ và $$ \ln (x-y)+\frac{1}{2}\ln (xy)=\ln(x+y). $$ Giá trị nhỏ nhất của biểu thức $ M=x+y$ bằng bao nhiêu?
Hướng dẫn. Biến đổi đẳng thức đã cho thành \begin{align}
\ln (x-y)^2+\ln(xy)&=\ln(x+y)^2\\
\Leftrightarrow (x-y)^2\cdot xy&=(x+y)^2\\
\Leftrightarrow \left((x+y)^2-4xy\right)\cdot xy& = (x+y)^2\\
\Leftrightarrow (x+y)^2(1-xy)&=4(xy)^2
\end{align} Nhận xét nếu $ xy=1 $ thì đẳng thức trên dẫn tới điều vô lý, do đó $ xy\ne 1$. Chia hai vế cho $ (1-xy)$ ta được $$ (x+y)^2=\frac{4(xy)^2}{1-xy} $$Đặt $ t=xy$ ta xét hàm số $ f(t)= \frac{4t^2}{t-1}$ trên khoảng $ (0;+\infty)$. Bảng biến thiên của hàm số này như sau

Suy ra $ (x+y)^2 \geqslant 16 \Leftrightarrow x+y \geqslant 4$ hay giá trị nhỏ nhất của $ M$ là $ 4$.
Cách khác, chúng ta có thể sử dụng điều kiện có nghiệm của phương trình bậc hai.
Đặt $ t=xy $, điều kiện $ t>0$, ta được phương trình bậc hai ẩn $ t$ là \begin{align}
(M^2-4t)t&=M^2\\
\Leftrightarrow -4t^2+M^2t-M^2&=0
\end{align} Phương trình này có nghiệm $ t>0$ khi và chỉ khi hoặc là có hai nghiệm dương, hoặc là có hai nghiệm trái dấu. Nhưng khả năng hai nghiệm trái dấu không xảy ra do $P=4M^2>0 $, nên chỉ xảy ra khả năng hai nghiệm dương. Điều kiện cần và đủ là $$ \begin{cases}
\Delta \geqslant 0\\
S>0\\ P>0
\end{cases} \Leftrightarrow \begin{cases}
M^4-16M^2 \geqslant 0\\ \frac{M^2}{4}>0\\ 4M^2>0
\end{cases}$$ Giải hệ này, ta cũng tìm được giá trị nhỏ nhất của $ M$ là $ 4.$
Ví dụ 5. [Lương Thế Vinh – HN Lần 2 năm 2020] Cho các số thực $ x,y$ thỏa mãn $ \ln y \geqslant \ln (x^3+2)-\ln 3$. Tìm giá trị nhỏ nhất của biểu thức $$ H=e^{4y-x^3-x-2}-\frac{x^2+y^2}{2}+x(y+1)-y. $$
Hướng dẫn. Trước tiên, ta có điều kiện xác định của các biểu thức là $$ \begin{cases}
x > \sqrt[3]{-2}\\ y >0
\end{cases} $$ Với điều kiện đó, bất đẳng thức đã cho trở thành $$ 3y \geqslant x^3+2 $$ Biến đổi biểu thức $ H$ ta được \begin{align}
H&=e^{y-x}\cdot e^{3y-x^3-2} -\frac{(y-x)^2}{2}-(y-x)\\
&\geqslant e^{y-x} -\frac{(y-x)^2}{2}-(y-x)
\end{align} Đặt $ t=y-x$ thì ta có \begin{align}
t=y-x \geqslant \frac{x^3+2}{3}-x
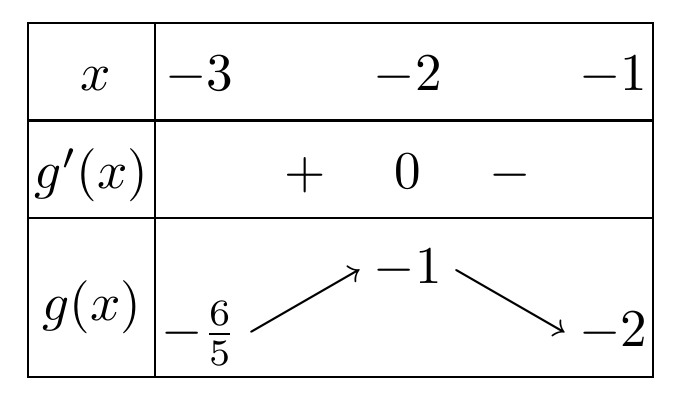
\end{align} Xét hàm số $ f(x)=\frac{x^3+2}{3}-x$ trên khoảng $ \sqrt[3]{-2}$ ta có bảng biến thiên sau

Suy ra điều kiện của biến $ t$ là $ t \geqslant 0$. Tiếp tục lập bảng biến thiên của hàm số $ H=e^t-\frac{t^2}{2}-t$ trên nửa khoảng $ [0;+\infty)$ ta tìm được giá trị nhỏ nhất của $ H $ là $ 1.$
Ví dụ 6. [SGD Vĩnh Phúc năm 2020] Cho hai số thực dương $ x,y$ thỏa mãn $ 2+2\log_2 x=\frac{1}{2}\log_{\sqrt{2}}y$. Tìm giá trị nhỏ nhất của biểu thức $ P=10x^2-2(x+y)-3$.
Hướng dẫn. Biến đổi đẳng thức $ 2+2\log_2 x=\frac{1}{2}\log_{\sqrt{2}}y$, chúng ta có \begin{align}
\log_2 \left(4x^2\right)&=\log_2 y\\
\Leftrightarrow 4x^2&=y
\end{align} Thay vào biểu thức $ P$ ta được \begin{align}
P&=10x^2-2(x+4y^2)-3 \\
&=2\left(x-\frac{1}{2}\right)^2-\frac{7}{2}
\end{align} Suy ra, giá trị nhỏ nhất của $ P$ là $ -\frac{7}{2}.$
Ví dụ 7. [Chuyên Thái Bình Lần 4 năm 2020] Cho hai số thực dương $ x,y$ thỏa mãn $ \log_2 x +x(x+y)=\log_2 (6-y)+6x$. Tìm giá trị nhỏ nhất của biểu thức $ T=x^3+3y$.
Hướng dẫn. Biến đổi đẳng thức đã cho ta được \begin{align}
\log_2 x+x^2 &=\log_2 (6-y) +x(6-y)\\
\Leftrightarrow 2 \log_2 x +x^2 &= \log_2 x+ \log_2 (6-y) +x(6-y)\\
\Leftrightarrow \log_2 x^2 + x^2 &= \log_2 \big(x(6-y)\big) +x(6-y)
\end{align} Hàm số $ f(t)=\log_2 t+t$ với $ t>0$ là một hàm số đồng biến nên ta có $$ f(x^2)=f\big(x(6-y)\big) $$ xảy ra khi và chỉ khi $ x^2=x(6-y)$. Mà $ x>0$ nên điều này đồng nghĩa với $ x=6-y$ hay $ y=6-x$. Lúc này, biểu thức $ T$ trở thành $$ T=x^3+3(6-x) $$ Bảng biến thiên của $T$ trên $ (0,+\infty)$ như sau

Suy ra, giá trị nhỏ nhất của biểu thức $ T$ là $ 16.$
Ví dụ 8.
Hướng dẫn.
Ví dụ 9.
Hướng dẫn.
Ví dụ 10.
Hướng dẫn.