Cách tính góc giữa hai vectơ trong mặt phẳng

1. Cách xác định góc giữa hai vectơ trong mặt phẳng

Cho hai véc-tơ $ \vec{a}$ và $\vec{b}$ đều khác $ \vec{0}$. Từ một điểm $ O$ bất kỳ, dựng $ \overrightarrow{OA}=\vec{a}$ và $ \overrightarrow{OB}=\vec{b}$ thì góc $ \widehat{AOB}$ được gọi là góc giữa hai véc-tơ $ \vec{a}$ và $\vec{b}$, kí hiệu là $ \left(\vec{a},\vec{b}\right)$.

Nhận xét.

• Trong định nghĩa thì điểm $ O$ được lấy tuỳ ý. Tuy nhiên, trong lúc giải toán ta có thể chọn O trùng với điểm gốc của vectơ $ \overrightarrow{a}$ hoặc $ \overrightarrow{b}$ cho đơn giản.
• Hiểu một cách đơn giản, để xác định góc giữa hai véc-tơ ta thay thế hai vectơ đã cho bởi hai vecto mới có chung điểm gốc.

2. Tính chất góc giữa hai véc-tơ trong mặt phẳng

• Góc giữa hai vecto bất kì luôn nằm trong đoạn từ $ 0^\circ $ đến $180^\circ$.
• Góc giữa hai véc tơ bằng $0^\circ$ khi và chỉ khi hai véc tơ đó cùng chiều.
• Góc giữa hai véc tơ bằng $180^\circ$ khi và chỉ khi hai véc tơ đó ngược chiều.
• Góc giữa hai véc tơ bằng $90^\circ$ khi và chỉ khi hai véc tơ đó vuông góc.

3. Bài tập xác định góc giữa hai vectơ trong mặt phẳng

Ví dụ 1. Cho tam giác đều $$ABC$  có$ $$H$$là trung điểm $$BC$$ Tính góc giữa các cặp vectơ sau:

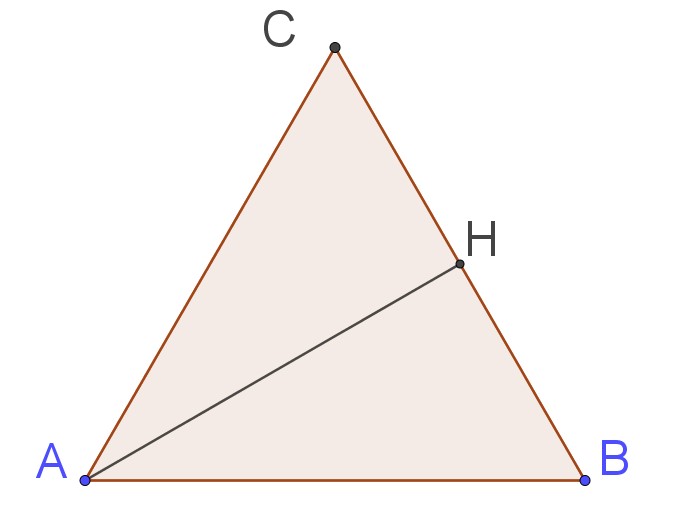
1. $ \overrightarrow{AH}$ và $ \overrightarrow{BC}$;
2. $ \overrightarrow{AB}$ và $ \overrightarrow{AC}$;
3. $ \overrightarrow{AB}$ và $ \overrightarrow{CA}$;
4. $ \overrightarrow{AB} $ và $  \overrightarrow{AH}$;
5. $ \overrightarrow{AB} $ và $ \overrightarrow{HA}$;
6. $ \overrightarrow{AB}$ và $ \overrightarrow{BC}$.

Ví dụ 2. Cho tam giác $ABC$ vuông tại $A$, cạnh $AB=3,AC=4$. Tính góc giữa các cặp vectơ:

1. $ \overrightarrow{AB}, \overrightarrow{AC}$;
2. $ \overrightarrow{AB}, \overrightarrow{BC}$.

Ví dụ 3. Cho hình vuông $ABCD$, tính góc giữa các véc-tơ:

1. $ \overrightarrow{AB},\overrightarrow{AD}$;
2. $ \overrightarrow{AC},\overrightarrow{BD}$;
3. $ \overrightarrow{AB},\overrightarrow{CB}$;
4. $ \overrightarrow{AD},\overrightarrow{DC}$.