Đề thi THPT QG 2021 file word có lời giải chi tiết
|
ĐỀ MINH HỌA SỐ 03 |
KỲ THI TRUNG HỌC PHỔ THÔNG QUỐC GIA NĂM 2021 Bài thi: Khoa học tự nhiên; Môn: Hóa Học Thời gian làm bài: 50 phút, không kể thời gian phát đề |
Cho biết nguyên tử khối của các nguyên tố: H=1; O=16; S=32; F=19; Cl=35,5; Br=80; I=127; N=14; P=31; C=12; Si=28; Li=7; Na=23; K=39; Mg=24; Ca=40; Ba=137; Sr=88; Al=27;Fe=56, Cu=64; Pb=207; Ag=108.
Câu 1: Cho sơ đồ phản ứng sau:
Biết rằng X là chất khí dùng nạp cho các bình cứu hỏa, Y là khoáng sản dùng để sản xuất vôi sống. Vậy Y, X, Z, T lần lượt là:
A. CO2, CaC2, Na2CO3, NaHCO3. B. CaCO3, CO2, Na2CO3, NaHCO3.
C. CaCO3, CO2, NaHCO3, Na2CO3. D. CO2, CaO, NaHCO3, Na2CO3.
Câu 2: Thực hiện một số thí nghiệm với 4 oxit, thu được kết quả như sau:
-
Oxit
Thuốc thử
X
Y
Z
T
H2O
có xảy ra phản ứng
không xảy ra phản ứng
có xảy ra phản ứng
không xảy ra phản ứng
Dung dịch HCl
không tạo thành muối
có tạo thành muối
có tạo thành muối
có tạo thành muối
Dung dịch NaOH
có tạo thành muối
có tạo thành muối
không tạo thành muối
không xảy ra phản ứng
X, Y, Z, T lần lượt là:
A. CrO3, Na2O, Fe3O4, Al2O3. B. CrO3, Al2O3, Na2O, Fe3O4.
C. CrO3, Al2O3, Fe3O4, Na2O. D. CrO3, Fe3O4, Na2O, Al2O3.
Câu 3: Cho phản ứng :
Các hệ số a, b, c, d, e là những số nguyên, đơn giản nhất thì tổng (a+b) bằng
A. 6. B. 4. C. 3. D. 5.
Câu 4: Oxit lưỡng tính là
A. CaO. B. MgO. C. Cr2O3. D. CrO.
Câu 5: Dung dịch metylamin trong nước làm
A. phenolphtalein không đổi màu. B. quì tím không đổi màu.
C. phenolphtalein hoá xanh. D. quì tím hoá xanh.
Câu 6: Nguyên liệu chính dùng để sản xuất nhôm là
A. quặng boxit. B. quặng pirit. C. quặng đolomit. D. quặng manhetit.
Câu 7: Cho dãy các chất: CH3NH2, NH3, C6H5NH2 (anilin), NaOH. Chất có lực bazơ nhỏ nhất trong dãy là
A. NaOH. B. NH3. C. C6H5NH2. D. CH3NH2.
Câu 8: Amilozơ được tạo thành từ các gốc
A. β-glucozơ. B. β-fructozơ. C. α-glucozơ. D. α-fructozơ.
Câu 9: Tính chất hoá học đặc trưng của kim loại là
A. tính oxi hoá và tính khử. B. tính khử.
C. tính oxi hoá. D. tính bazơ.
Câu 10: Cặp chất không xảy ra phản ứng là
A. K2O và H2O. B. dung dịch NaNO3 và dung dịch MgCl2.
C. dung dịch NaOH và Al2O3. D. Na và dung dịch KCl.
Câu 11: Dãy gồm các chất đều tác dụng với dung dịch NaOH là
A. metyl axetat, glucozơ, etanol. B. glixerol, glyxin, anilin.
C. etanol, fructozơ, metylamin. D. metyl axetat, alanin, axit axetic.
Câu 12: Cho chất X có công thức phân tử C4H8O2 tác dụng với dung dịch NaOH sinh ra chất Y có công thức phân tử C2H3O2Na. Công thức của X là
A. C2H5COOCH3. B. CH3COOC2H5. C. HCOOC3H5. D. HCOOC3H7.
Câu 13: Cho 3 thí nghiệm sau:
(1) Cho từ từ dung dịch AgNO3 đến dư vào dung dịch Fe(NO3)2.
(2) Cho bột sắt từ từ đến dư vào dung dịch FeCl3.
(3) Cho từ từ dung dịch AgNO3 đến dư vào dung dịch FeCl3.
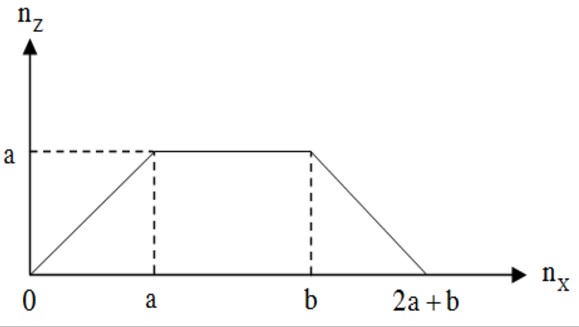
Trong mỗi thí nghiệm, số mol ion Fe3+ biến đổi tương ứng với đồ thị nào sau đây?

A. 1-b, 2-a, 3-c. B. 1-a, 2-c, 3-b. C. 1-c, 2-b, 3-a. D. 1-a, 2-b, 3-c.
Câu 14: Để hoà tan hoàn toàn hỗn hợp gồm hai kim loại Cu và Zn, ta có thể dùng một lượng dư dung dịch
A. AgNO3. B. AlCl3. C. CuSO4. D. HCl.
Câu 15: Phát biểu nào sau đây là sai?
A. Ozon trong không khí là nguyên nhân chính gây ra sự biến đổi khí hậu.
B. Clo được dùng để diệt trùng nước trong hệ thống cung cấp nước sạch.
C. Amoniac được dùng để điều chế nhiên liệu cho tên lửa.
D. Lưu huỳnh đioxit được dùng làm chất chống thấm nước.
Câu 16: Dãy gồm các kim loại đều phản ứng với nước ở nhiệt độ thường tạo ra dung dịch có môi trường kiềm là
A. Na, Fe, K. B. Na, Cr, K. C. Na, Ba, K. D. Be, Na, Ca.
Câu 17: Cho dãy các kim loại: Al, Cr, Hg, W. Hai kim loại có nhiệt độ nóng chảy thấp nhất và cao nhất tương ứng là:
A. Al, Cr. B. Hg, W. C. W, Cr. D. Hg, Al.
Câu 18: Phát biểu nào sau đây đúng?
A. Chất béo là trieste của glixerol với axit béo.
B. Glucozơ là đồng phân của saccarozơ.
C. Cacbohiđrat là những hợp chất hữu cơ đơn chức.
D. Xà phòng là hỗn hợp muối natri hoặc kali của axit axetic.
Câu 19: Tơ được sản xuất từ xenlulozơ là
A. tơ visco. B. tơ tằm. C. tơ capron. D. tơ nilon-6,6.
Câu 20: Hai kim loại có thể điều chế bằng phương pháp nhiệt luyện là
A. Ca và Fe. B. Mg và Zn. C. Na và Cu. D. Fe và Cu.
Câu 21: Để phân biệt hai dung dịch KNO3 và Zn(NO3)2 đựng trong hai lọ riêng biệt, ta có thể dùng dung dịch
A. HCl. B. NaOH. C. NaCl. D. MgCl2.
Câu 22: Dãy gồm các chất đều không tham gia phản ứng tráng bạc là:
A. saccarozơ, tinh bột, xenlulozơ. B. fructozơ, tinh bột, anđehit fomic.
C. anđehit axetic, fructozơ, xenlulozơ. D. axit fomic, anđehit fomic, glucozơ.
Câu 23: Đun nóng 250 gam dung dịch glucozơ với dung dịch AgNO3 /NH3 thu được 15 gam Ag, nồng độ của dung dịch glucozơ là
A. 10%. B. 15%. C. 30%. D. 5%.
Câu 24: Để tác dụng hết với dung dịch chứa 0,01 mol KCl và 0,02 mol NaCl thì thể tích dung dịch AgNO3 1M cần dùng là
A. 10 ml. B. 40 ml. C. 30 ml. D. 20 ml.
Câu 25: Trung hòa hoàn toàn 14,16 gam một amin X (bậc 1) bằng axit HCl, tạo ra 22,92 gam muối. Amin X là
A. H2NCH2CH2CH2NH2. B. H2NCH2CH2NH2.
C. CH3CH2NHCH3. D. CH3CH2CH2NH2.
Câu 26: Cho một lượng hỗn hợp X gồm Ba và Na vào 200 ml dung dịch Y gồm HCl 0,1M và CuCl2 0,1M. Kết thúc các phản ứng, thu được 0,448 lít khí (đktc) và m gam kết tủa. Giá trị của m là
A. 0,64. B. 1,28. C. 0,98. D. 1,96.
Câu 27: Hòa tan m gam hỗn hợp FeO, Fe(OH)2, FeCO3 và Fe3O4 (trong đó Fe3O4 chiếm 1/3 tổng số mol hỗn hợp) vào dung dịch HNO3 loãng (dư), thu được 8,96 lít (đktc) hỗn hợp khí gồm CO2 và NO (sản phẩm khử duy nhất của N+5) có tỉ khối so với H2 là 18,5. Số mol HNO3 phản ứng là
A. 3,8. B. 2,0. C. 3,2. D. 1,8.
Câu 28: Ba chất hữu cơ X, Y, Z mạch hở có cùng công thức phân tử C2H4O2 và có tính chất sau:
– X tác dụng được với Na2CO3 giải phóng CO2.
– Y tác dụng được với Na và có phản ứng tráng gương.
– Z tác dụng được với dung dịch NaOH, không tác dụng được với Na.
Các chất X, Y, Z là:
A. X: HCOOCH3; Y: CH3COOH; Z: CH2(OH)CHO.
B. X: CH3COOH; Y: CH2(OH)CHO; Z: HCOOCH3.
C. X: CH2(OH)CHO; Y: CH3COOH; Z: HCOOCH3.
D. X: CH3COOH; Y: HCOOCH3; Z: CH2(OH)CHO.
Câu 29: Cho 10 gam hỗn hợp X gồm etanol và etyl axetat tác dụng vừa đủ với 50 gam dung dịch natri hiđroxit 4%. Phần trăm khối lượng của etyl axetat trong hỗn hợp là
A. 44%. B. 50%. C. 51%. D. 22%.
Câu 30: Cho các phát biểu sau:
(a) Đốt cháy hoàn toàn este no, đơn chức, mạch hở luôn thu được số mol CO2 bằng số mol H2O.
(b) Trong hợp chất hữu cơ nhất thiết phải có cacbon và hiđro.
(c) Những hợp chất hữu cơ có thành phần nguyên tố giống nhau, thành phần phân tử hơn kém nhau một hay nhiều nhóm CH2 là đồng đẳng của nhau.
(d) Dung dịch glucozơ bị khử bởi AgNO3 trong NH3 tạo ra Ag.
(e) Saccarazơ chỉ có cấu tạo mạch vòng.
Số phát biểu đúng là
A. 5. B. 3. C. 4. D. 2.
Câu 31: Đốt cháy hoàn toàn m gam FeS2 bằng một lượng O2 vừa đủ, thu được khí X. Hấp thụ hết X vào dung dịch Ba(OH)2 dư sau phản ứng hoàn toàn thu được 43,4 gam kết tủa. Giá trị của m là
A. 13,2. B. 48,0. C. 12,0. D. 24,0.
Câu 32: Hỗn hợp X gồm Mg (0,10 mol), Al (0,04 mol) và Zn (0,15 mol). Cho X tác dụng với dung dịch HNO3 loãng (dư), sau phản ứng khối lượng dung dịch tăng 13,23 gam. Số mol HNO3 tham gia phản ứng là
A. 0,6975 mol. B. 0,6200 mol. C. 0,7750 mol. D. 1,2400 mol.
Câu 33: Điện phân 400 ml (không đổi) dung dịch gồm NaCl, HCl và CuCl2 0,02M (điện cực trơ, màng ngăn xốp) với cường độ dòng điện bằng 1,93A. Mối liên hệ giữa thời gian điện phân và pH của dung dịch điện phân được biểu diễn dưới đây:

Giá trị của t trên đồ thị là
A. 1200. B. 3600. C. 1800. D. 3000.
Câu 34: Khi thủy phân hoàn toàn 0,2 mol peptit A mạch hở (A tạo bởi các amino axit có một nhóm amino và một nhóm cacboxylic) bằng lượng dung dịch KOH gấp đôi lượng cần phản ứng, cô cạn dung dịch thu được hỗn hơp chất rắn tăng so với khối lượng A là 108,4 gam. Số liên kết peptit trong A là
A. 4. B. 10. C. 9. D. 5.
Câu 35: Khi trùng ngưng 65,5 gam axit ε – aminocaproic thu được m gam polime và 7,2 gam nước. Hiệu suất của phản ứng trùng ngưng là
A. 80%. B. 70%. C. 75%. D. 90%.
Câu 36: Đốt cháy hoàn toàn 1 mol chất béo, thu được lượng CO2 và H2O hơn kém nhau 6 mol. Mặt khác, a mol chất béo trên tác dụng tối đa với 600 ml dung dịch Br2 1M. Giá trị của a là
A. 0,20. B. 0,30. C. 0,18. D. 0,15.
Câu 37: X, Y, Z, T là các peptit đều được tạo bởi các α-amino axit no, chứa một nhóm –NH2 và 1 nhóm –COOH và có tổng số nguyên tử oxi là 12. Đốt cháy 13,98 gam hỗn hợp E chứa X, Y, Z, T cần dùng 14,112 lít O2 (đktc) thu được CO2, H2O, N2. Mặt khác, đun nóng 0,135 mol hỗn hợp E bằng dung dịch NaOH (lấy dư 20% so với phản ứng), cô cạn dung dịch sau phản ứng thu được lượng chất rắn khan là
A. 31,5 gam. B. 24,51 gam. C. 25,84 gam. D. 36,05 gam.
Câu 38: Điện phân dung dịch hỗn hợp NaCl và 0,05 mol CuSO4 bằng dòng điện một chiều có cường độ 2A (điện cực trơ, có màng ngăn). Sau thời gian t giây thì ngừng điện phân, thu được khí ở hai điện cực có tổng thể tích là 2,352 lít (đktc) và dung dịch X. Dung dịch X hoà tan được tối đa 2,04 gam Al2O3. Giả sử hiệu xuất điện phân là 100%, các khí sinh ra không tan trong dung dịch. Giá trị của t là
A. 9408. B. 8685. C. 7720. D. 9650.
Câu 39: Cho m gam Na vào 250 ml dung dịch hỗn hợp gồm HCl 0,5M và AlCl3 0,4M. Sau phản ứng thu được kết tủa có khối lượng là (m – 3,995) gam. m có giá trị là
A. 10,304. B. 10,235. C. 12,788. D. 7,728.
Câu 40: Hợp chất hữu cơ X đa chức có công thức phân tử C9H14O6. Thực hiện phản ứng xà phòng hóa hoàn toàn X sản phẩm thu được là hỗn hợp 2 muối của 2 axit hữu cơ đơn chức (trong đó có 1 axit có mạch cacbon phân nhánh) và hợp chất hữu cơ đa chức Y. Đem 13,08 gam X tham gia phản ứng tráng bạc thì khối lượng Ag lớn nhất thu được là
A. 27 gam. B. 25,92 gam. C. 12,96 gam. D. 6,48 gam.
———————————————–
———– HẾT ———-
O2 education gửi các thầy cô link download file word đề và lời giải chi tiết
Xem thêm
Tổng hợp đề thi THPT QG 2021 file word có lời giải chi tiết
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 1
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 2
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 3
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 4
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 5
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 6
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 7
Đề thi THPT QG 2021 file word có lời giải chi tiết đề số 8







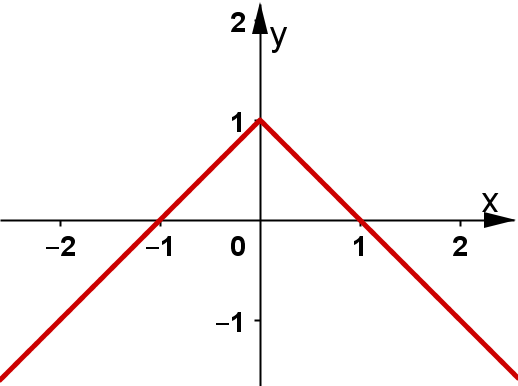
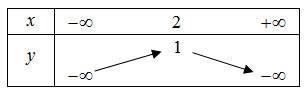 A. $ y=-{{x}^{2}}+4x-3.$
A. $ y=-{{x}^{2}}+4x-3.$