Điểm và đường thẳng trong không gian
1. Tóm tắt lý thuyết về điểm và đường thẳng trong không gian
Ba cách xác định một mặt phẳng
- Qua ba điểm không thẳng hàng $ A,B,C $; kí hiệu là $ (ABC) $ hoặc $ mp(ABC). $

- Qua đường thẳng $ d$ và điểm $M\notin d$; kí hiệu là $ mp(d,M) $

- Qua hai đường thẳng $ d_1,d_2 $ cắt nhau; kí hiệu là $ mp(d_1,d_2) $

Quy tắc vẽ hình biểu diễn của hình không gian
- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau.
- Hình biểu diễn phải giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.
- Đường nhìn thấy vẽ nét liền, đường bị che khuất vẽ nét đứt.
- Trên cùng một đường thẳng} hoặc trên hai đường thẳng song song} thì tỉ lệ về độ dài được giữ nguyên. Đặc biệt, hình biểu diễn của trung điểm là trung điểm.
Các tính chất thừa nhận
- Có một và chỉ một đường thẳng qua hai điểm phân biệt
- Nếu một đường thẳng có hai điểm nằm trong mặt phẳng thì tất cả các điểm còn lại của đường thẳng đó đều thuộc mặt phẳng đã cho.
- Nếu hai mặt phẳng phân biệt có một điểm chung , thì chúng còn có điểm chung khác nữa. Do đó, chúng có chung một đường thẳng, gọi là giao tuyến của hai mặt phẳng.
- Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.
- Có ít nhất bốn điểm không đồng phẳng.
Hình chóp
- Cho đa giác $ A_1A_2…A_n $ nằm trên mặt phẳng $(P)$ và điểm $ S $ nằm ngoài mặt phẳng $(P)$ thì hình chóp $ S.A_1A_2…A_n $ là hình gồm đa giác $ A_1A_2…A_n $ và $ n $ tam giác có $ S $ là đỉnh chung: $ SA_1A_2,SA_2A_3,… SA_nA_1. $

- Ta gọi tên hình chóp tùy theo số cạnh của đa giác đáy, ví dụ hình chóp tam giác, hình chóp tứ giác, hình chóp ngũ giác…
- Tứ diện là hình gồm có bốn điểm không đồng phẳng.

Một số hình không gian thường gặp
Để học tốt hình học không gian, việc đầu tiên là các em cần vẽ hình đúng các quy tắc. Khi vẽ hình đúng rồi, chúng ta cần lựa chọn cách vẽ làm sao cho dễ nhìn nhất có thể. Dưới đây là cách vẽ hình chuẩn của một số hình không gian thường gặp.
- Hình chóp tam giác, tứ diện
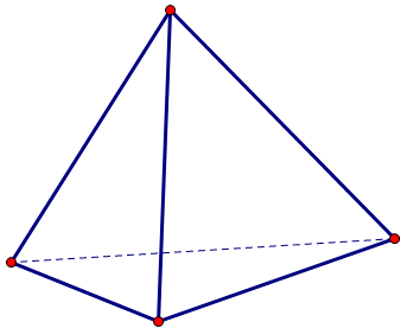
- Hình chóp tứ giác có đáy không là hình thang (đáy là một tứ giác bất kì)

- Hình chóp tứ giác có đáy là hình thang

- Hình chóp tứ giác có đáy là hình bình hành, hình chữ nhật, hình vuông

- Hình chóp ngũ giác

- Hình chóp lục giác

2. Bài tập điểm và đường thẳng trong không gian
Dạng 1. Tìm giao tuyến của hai mặt phẳng
Mời thầy cô và các em xem chi tiết trong bài Cách tìm giao tuyến của hai mặt phẳng
Dạng 2. Tìm giao điểm của đường thẳng và mặt phẳng
Mời thầy cô và các em xem chi tiết trong bài Tìm giao điểm của đường thẳng và mặt phẳng
Dạng 3. Chứng minh thẳng hàng, đồng quy
Mời thầy cô và các em xem chi tiết trong bài Cách chứng minh thẳng hàng trong hình học không gian
Dạng 4. Xác định giao tuyến của hình chóp khi cắt bởi một mặt phẳng
Mời thầy cô và các em học sinh xem chi tiết trong các bài viết sau:


